Примеры на сложение дробей с одинаковыми знаменателями – Сложение и вычитание дробей

Сложение и вычитание дробей с одинаковыми знаменателями

Технологическая карта урока № 1

Учитель: Логинова Галина Петровна

Предмет: Математика

Класс: 5 класс

Учебник: Математика. 5 класс: учеб. для общеобразовательных учреждений / С.М.Никольский

Тип урока: получение новых знаний

Тема. «Сложение и вычитание дробей с одинаковыми знаменателями»

Цели:

Образовательные

Создать условия для овладения навыками сложения дробей на основе алгоритма сложения обыкновенных дробей с одинаковыми

знаменателями;

Развивающие

Развивать умения анализировать, сравнивать, обобщать, делать выводы, развивать внимание.

Воспитательные

Продолжить воспитание в учащихся доброжелательности друг к другу, уважения к мнению других, умения слушать. Развивать познавательный интерес через игровые моменты взаимоконтроля, взаимопроверки

Формировать УУД:

Личностные: определять и высказывать самые простые, общие для всех людей правила поведения при совместной работе и сотрудничестве способность к самооценке на основе критерия успешности учебной деятельности.

Регулятивные: умение определять и формулировать цель на уроке с помощью учителя; проговаривать последовательность действий на уроке; работать по плану; оценивать правильность выполнения действия на уровне адекватной оценкой.

Коммуникативные: слушать и понимать речь других; совместно договариваться о правилах поведения и общения в школе и следовать им.

Познавательные: добывать новые знания: находить ответы на вопросы, используя учебник; извлекать информацию, представленную в разных формах; перерабатывать полученную информацию: наблюдать и делать самостоятельные выводы.

Формы урока: фронтальная и индивидуальная работа, работа в парах.

Методы обучения: наглядные, коммуникационные, частично-поисковые, проблемные.

Оборудование: учебник, мультимедийный проектор, интерактивная доска, карточки, презентация.

Приветствие, проверка подготовленности к учебному занятию, организация внимания детей.

Включаются в деловой ритм урока

Актуализация знаний и умений

Актуализация опорных знаний и способов действий

Устный счет. Выполните сложение и вычитание чисел

1. Сумма двух чисел 85. Найди первое слагаемое, если второе равно 35.

Чему равно уменьшаемое, если вычитаемое 17, а разность 24?

Чему равна сумма двух чисел, если первое число 52, а другое на 25 больше?

Какое число надо вычесть из 57, чтобы получилось 8?

Сумма двух чисел равна 47. Одно слагаемое больше другого на 10. Найди эти слагаемые.

2. Выполните удобным способом

• а) 21+22+23

• б) 69+43+37

• в) 72-39+18

• г) 25+37-5

• д) 37-(7+16)

3. Придумать 3 примера по два действия для устных вычислений для соседа по парте. Проверить.

В тетрадях пишут ответы (взаимопроверка).

Считают устно

Выполняют задания в парах

Целеполагание и мотивация

Обеспечение мотивации учения детьми, принятия ими целей урока

Проблемная ситуация

Как вычислить сложение чисел

Что заметили интересного?

Какая цель нашего урока?

Состоит из одинаковых знаменателей

Узнать, как складывать дроби с одинаковыми знаменателями.

Усвоение новых знаний и способов усвоения

Обеспечение восприятия, осмысления и первичного запоминания детьми изучаемой темы: определения смешанного числа

Сложение и вычитание дробей с одинаковыми знаменателями

Как выполняется данное действие?

Тогда как называется тема нашего урока?

Записываем в рабочий лист тему урока

1. Организует работу по самостоятельному изучению и анализу решения задачи 1 учебника.

2. Задача на нахождение разности дробей с одинаковыми знаменателями.

Проблема: как вычесть из одной дроби другую?

-Что заметили?

-Как вы думаете, это правило без исключений?

2) Приведите свой по примеру на сложение и вычитание дробей с одинаковыми знаменателями, прочитайте соседу и пусть он его запишет.

Физкультминутка

Мы писали, мы писали,
Наши пальчики устали,
А сейчас мы отдохнём,
Сделаем зарядку.
«1» подняться, подтянуться.
«2» согнуться, разогнуться.
«3» в ладоши 3 хлопка, головою 3 кивка.
«4» руки шире.
«5» руками помахать.
«6» тихонько за парту сесть.

Тема урока “ Сложение и вычитание дробей с одинаковыми знаменателями”.

Самостоятельно, в парах изучают решение задачи, анализируют, высказывают свое мнение, делают вывод о том, каким образом можно выполнить сложение двух дробей. Самостоятельно формулируют правило.

Читают правило из учебника, производят сравнительный анализ с ранее сформулированными самостоятельно. Рассказывают друг другу.

По аналогии с суммой вычисляют разность дробей с одинаковыми знаменателями.

Делают вывод:

Знаменатель оставляем тот же.

Правило без исключений, только числитель уменьшаемого должен быть больше числителя вычитаемого.

(a>c)

Приводят примеры, работая в парах.

Записывают в тетрадях.

Выполняют упражнения.

Организация первичного контроля

Выявление качества и уровня усвоения знаний и способов действий, а также выявление недостатков в знаниях и способах действий, установление причин выявленных недостатков

Самостоятельная работа

А сейчас возьмите листочки на краю стола и в них же выполните небольшую самостоятельную работу.

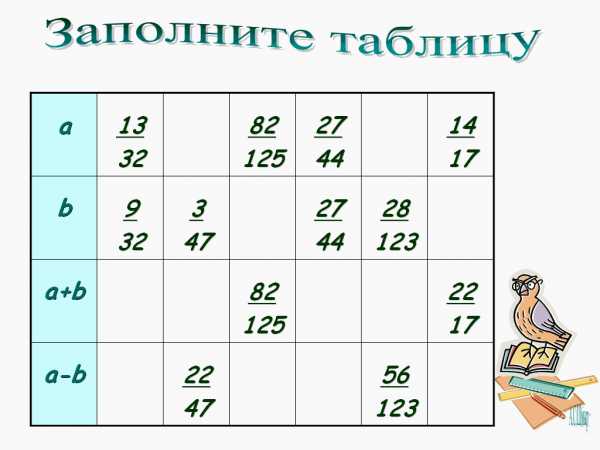
Ребята, давайте сверимся с доской (решение записано на слайде).

Выполняют задания на листах.

Сверяются с доской, выставляют себе отметки (критерий оценивания на доске).

Подведение итогов урока

Дать качественную оценку работы класса и отдельных обучаемых

Что изучали сегодня на уроке?

Отвечают на вопросы.

Информация о домашнем задании

Обеспечение понимания детьми цели, содержания и способов выполнения домашнего задания

Поясняет выполнение номеров.

Открывают дневники, записывают домашнее задание, задают вопросы.

Рефлексия

Инициировать рефлексию детей по их собственной деятельности и взаимодействия с учителем и другими детьми в классе

Задает вопросы:

— Кто хорошо понял тему и может поделиться своими знаниями?

— Кому нужно еще потренироваться?

— Какое у вас настроение сейчас?

— Изменилось ли оно?

Выставляют оценки.

Отвечают на вопросы учителя

infourok.ru

Сложение и вычитание дробей с одинаковыми знаменателями

Карлсон съел всех яблок, а Малыш — всех яблок. Какая часть всех яблок достанется Фрекен Бок?

В полном мешке было 48 кг картофеля. В первый день израсходовали мешка картофеля, во второй день — на мешка меньше, чем в первый день. Сколько килограммов картофеля израсходовано за эти два дня? И сколько килограммов картофеля осталось в мешке?

Туристы за три дня прошли 64 км. В первый день они прошли всего пути, а во второй — всего пути. Сколько километров туристы прошли в третий день?

Расстояние от города до села, равное 32 км, велосипедист проехал за 3 часа. За первый час он проехал  этого расстояния, за второй час  этого расстояния. Сколько километров велосипедист проехал за третий час.

За три дня было продано 800 кг репы. В первый день было продано , а во второй день этой репы. Сколько килограммов репы было продано в третий день?

В первый день похода туристы прошли намеченного пути. Во второй день – на части пути больше. А в третий — на части меньше, чем во второй. Какую часть пути прошли туристы за три дня? Какую часть пути им ещё осталось пройти?

Найдите периметр участка земли прямоугольной формы, если его длина км , а ширина на км меньше.

Из чисел составить числовое выражение так, чтобы его значение было равно .

Задумано число. К нему прибавили . Из этой суммы вычли и в результате получилось . Какое число задумано?

multiurok.ru

Сложение и вычитание дробей | Cubens

Сложение дробей

Сложение дробей с одинаковыми знаменателями

Чтобы добавить две дроби с одинаковыми знаменателями, нужно добавить их числители, а знаменатели оставить без изменений:

Примеры сложения дробей с одинаковыми знаменателями

Пример 1: Добавить две дроби с равными знаменателями: и

Ответ:

Пример 2: Добавить две дроби с равными знаменателями: и

Ответ:

Сложение дробей с разными знаменателями

Чтобы добавить две дроби с разными знаменателями, нужно:

Примеры сложения дробей с разными знаменателями

Пример 3: Добавить две дроби с разными знаменателями:

и

 

Ответ:

Пример 4: Добавить две дроби с разными знаменателями: и

Ответ:

Сложение смешанных чисел

Чтобы добавить два смешанных числа, нужно:

Примеры сложения смешанных чисел

Пример 5: Добавить два смешанных числа: и

Ответ:

Вычитание дробей

Вычитание дробей с одинаковыми знаменателями

Чтобы вычесть две дроби с одинаковыми знаменателями, нужно вычесть из числителя первой дроби числитель второй, а знаменатель оставить без изменений:

 

Примеры вычитания дробей с одинаковыми знаменателями

Пример 1: Вычесть две дроби с равными знаменателями: и

 

Ответ:

Вычитание дробей с разными знаменателями

Чтобы вычесть две дроби с разными знаменателями, нужно:

Примеры вычитания дробей с разными знаменателями

Пример 2: Вычесть две дроби с разными знаменателями: и

Ответ:

Вычитание смешанных чисел

Чтобы вычесть два смешанных числа, нужно:

• привести дробные части этих чисел к наименьшему общему знаменателю;
• если дробная часть уменьшаемого меньше дробной части вычитателя, превратить ее в неправильную дробь, уменьшил на единицу, целую часть;
• отдельно выполнить вычитание целых частей и отдельно дробных частей;
• сократить полученную дробь.

Примеры вычитания смешанных чисел

Пример 5: Добавить два смешанных числа: и

Ответ:

Сложение и вычитание десятичных дробей

Сложение и вычитание десятичных дробей выполняется поразрядно. Удобно это выполнять в столбик.

Подробная информация и примеры решения на сложение и вычитание десятичных дробей читайте здесь

cubens.com

Урок математики по теме «Сложение и вычитание дробей с одинаковыми знаменателями» (5 класс)

Тема урока: Сложение и вычитание дробей с одинаковыми знаменателями

Тип урока: объяснение новой темы.

Цель: обучающие — ознакомить учащихся с действиями сложения и вычитания дробей с одинаковыми знаменателями;

развивающие — развитие логического и математического мышления, а также познавательного интереса учащихся;

воспитательные – формирование дисциплинированности, организованности, а также развитие интереса к предмету, вычислительные навыки.

Оборудование: доска, компьютер, проектор, экран, учебная и научная литература.

Материалы: презентация урока – Приложение 1, карточки с заданиями – Приложение 2.

Ход урока

I. Организационный момент.

II. Устная работа с классом:

1) Сравните величины: 2ч 30мин и 150 мин

А) 2ч 30мин < 150 мин;

Б) 2ч 30мин = 150 мин;

В) 2ч 30мин > 150 мин;

Г) Сравнить нельзя.

Слайд 3

2) Определить, какая часть фигуры заштрихована?

Слайды 4-5

3) Даны числа:

Слайд 6

Вопросы к слайду 6

1) Как называются числа, записанные на доске? (Обыкновенные дроби.)
2) Из чего состоит дробь? (Числитель и знаменатель.)
3) Что показывает числитель и знаменатель дроби? (Знаменатель дроби показывает на сколько равных долей делят, а числитель – сколько таких долей взято.)
4) На какие две группы вы можете разбить данные дроби? (Правильные и неправильные.)

5) Какие дроби называются правильными, а какие неправильными? (Дроби, в которых числитель меньше знаменателя, называют правильными. Дроби, в которых числитель больше знаменателя или равен ему, называют неправильными.)

6) Какие операции вы можете выполнять с дробями? (Сравнивать.)

4) Сравнение дробей

Слайд 7

III. Объяснение новой темы: «Сложение и вычитание дробей с одинаковыми знаменателями»

На экране показана шоколадка из 12 долек. Сначала съели 3 дольки, а затем ещё 2. У учащихся спрашивается какую часть съели, когда взяли 3 дольки, а затем 2. Учащиеся отвечают .Вопрос: сколько всего съели шоколада?

Слайд 8

Итак, при сложении дробей с одинаковыми знаменателями числители складывают, а знаменатель оставляют тот же.

На доске записывается правило сложения дробей с одинаковыми знаменателями с помощью букв: .

На экране появляется круг разделенный на 8 равных частей, 4 части взяли. Какая часть круга осталась?

А потом от оставшейся части взяли ещё 3 части. Какая часть круга теперь осталась?

Слайд 9

При вычитании дробей с одинаковыми знаменателями из числителя уменьшаемого вычитают числитель вычитаемого, а знаменатель остается тот же.

На доске записывается правило вычитания дробей с одинаковыми знаменателями с помощью букв: .

Слайд 10 Запомни: При сложении (вычитании) обыкновенных дробей с одинаковыми знаменателями числители складываем (вычитаем), а знаменатель оставляем тот же.

Физминутка:

Мы сегодня рано встали (шаги на месте)
И зарядку делать стали.
Руки — вверх! Руки — вниз!
Влево-вправо повернись!

IV. Закрепление изученной темы:

1. Вычисли:

Затем на экране появляются ответы.

Слайд 11

2. Найти дорожку

Учащиеся считают и находят дорожки.

Слайд 12

3. Работа по учебнику (Виленкин Н.Я., Математика 5 кл., Мнемозина, 2008): № 1012 (а)

Слайд 13

4. Сравните дроби.

Слайды 14-19

5. Найти все значения x, при которых дробь , будет правильной.

Слайд 20

6. Выполните действия:

: А) , Б) , В)

Слайды 21-23

7. Выполните действия:

: А) , Б) , В)

Слайды 24-26

V. Работа в группах (задания на карточках ответы БЕРКУТ и БАРСУК). (Приложение 2)

VI. Домашнее задание:

Учебник «Математика» 5 класс, Виленкин Н.Я.; П. 26, стр. 161, № 1039, 1041(а, б, в), 1045.

Слайд 27

VII. Подведение итогов урока:

• Как выполняется сложение и вычитание дробей с одинаковыми знаменателями?

• Какие ошибки можно допустить при выполнении сложения и вычитания дробей с одинаковыми знаменателями?

Слайд 28

ПРИЛОЖЕНИЕ 2

Задание к карточке 1

№1 Среди дробей 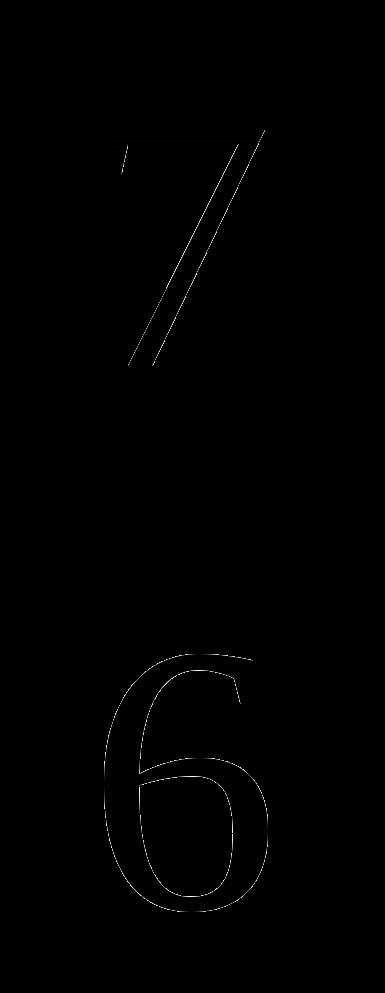; ; ; . Выберите правильную дробь.

№2 Сравните числа и , выберите наибольшее.

№3 Маша прочитала всей книги. Сколько страниц во всей книги, если она прочитала 240 страниц?

№4 Выполните действие: +

№5 Длина прямоугольника равна см. Ширина его на см меньше длины. Вычислите ширину прямоугольника?

№6 Выполните действие: — +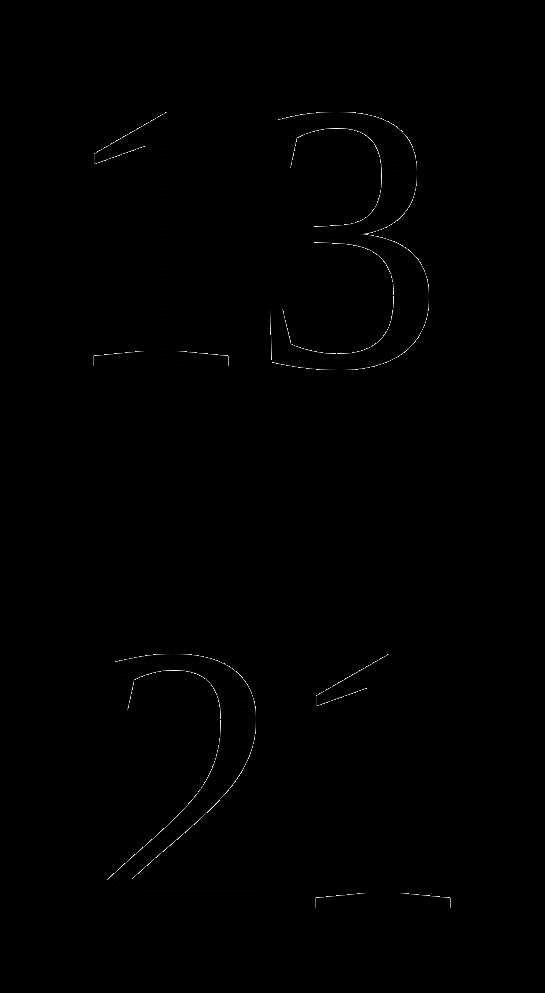

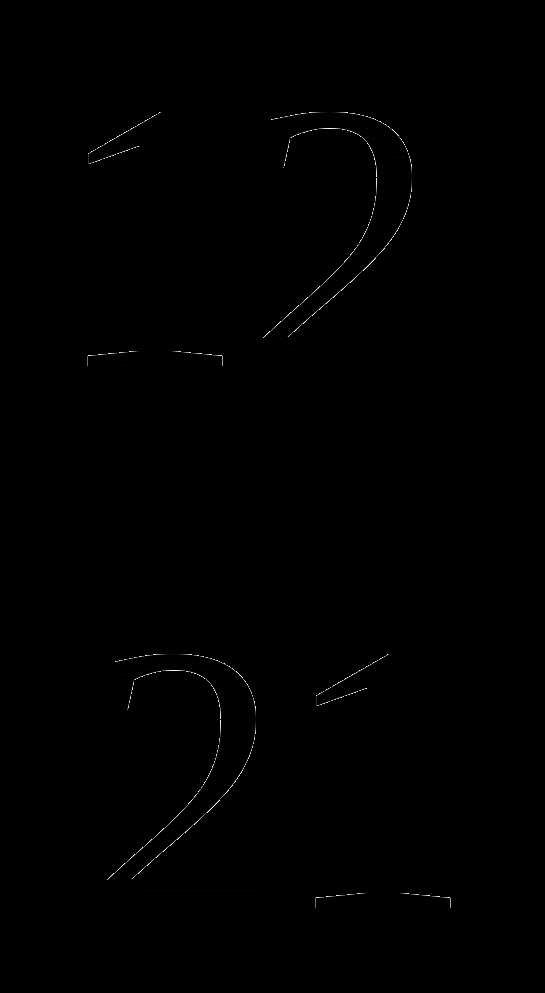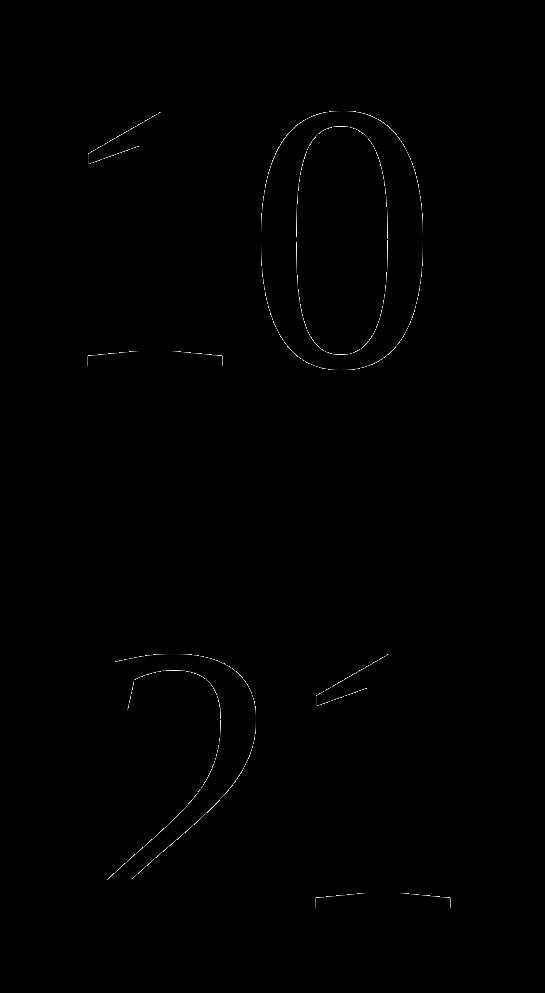
Номер задания

А

К

У

Б

Р

С

1

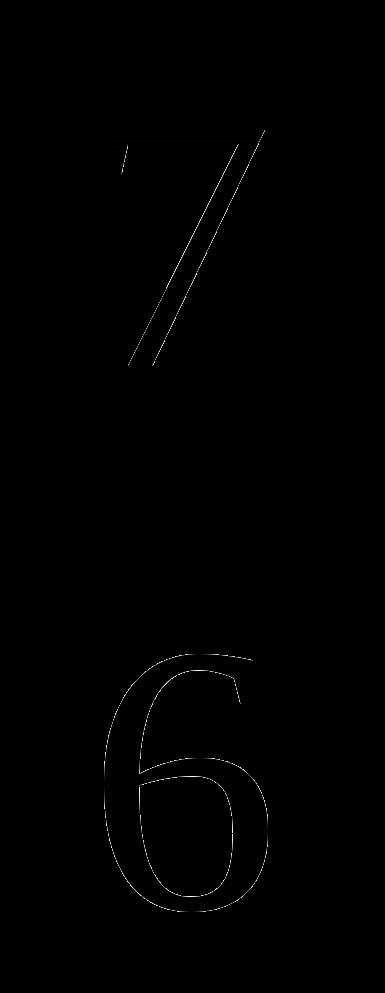
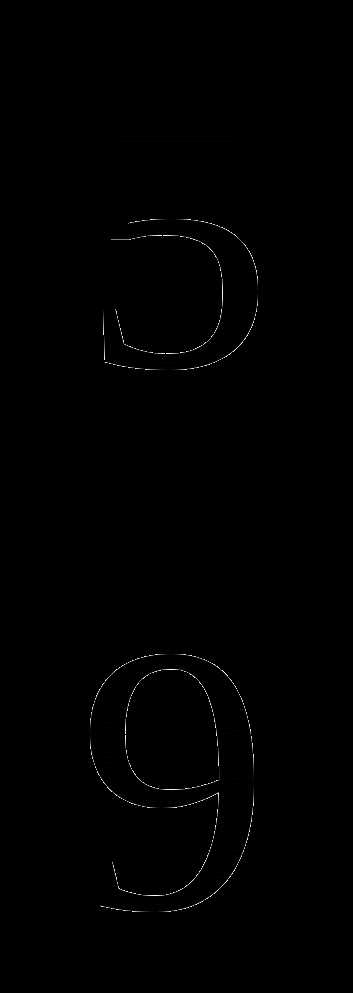
2

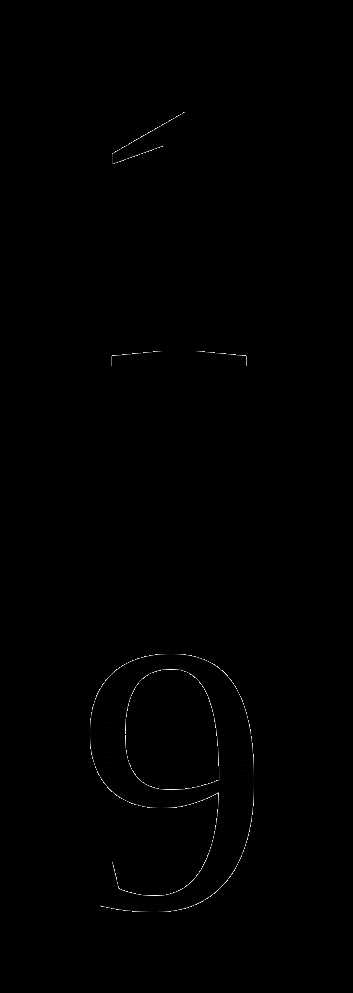
3

240

180

300

100

320

80

4

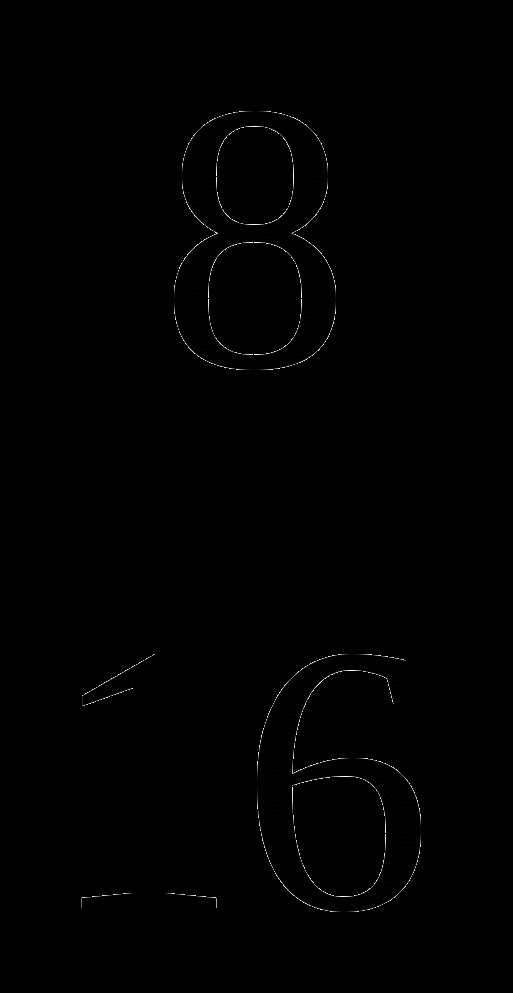
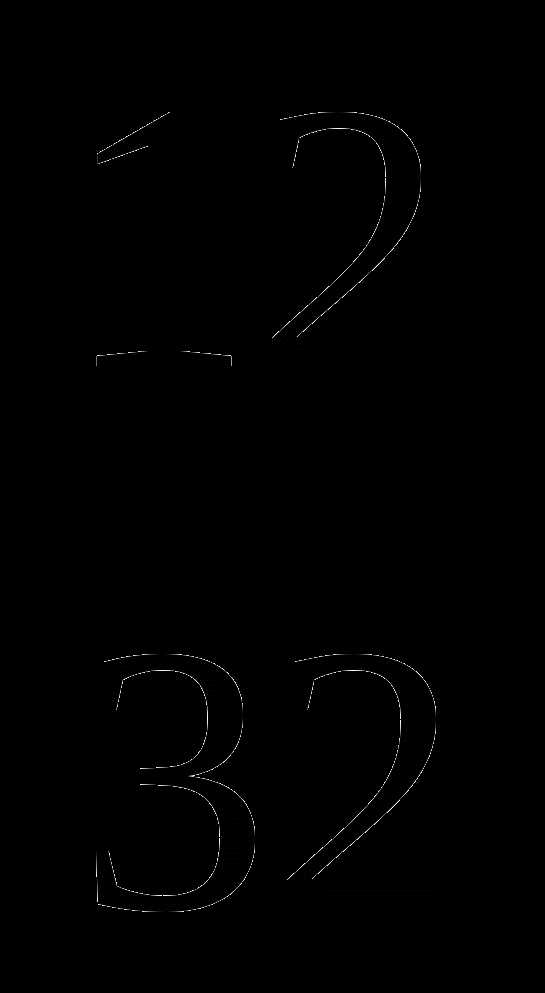
5

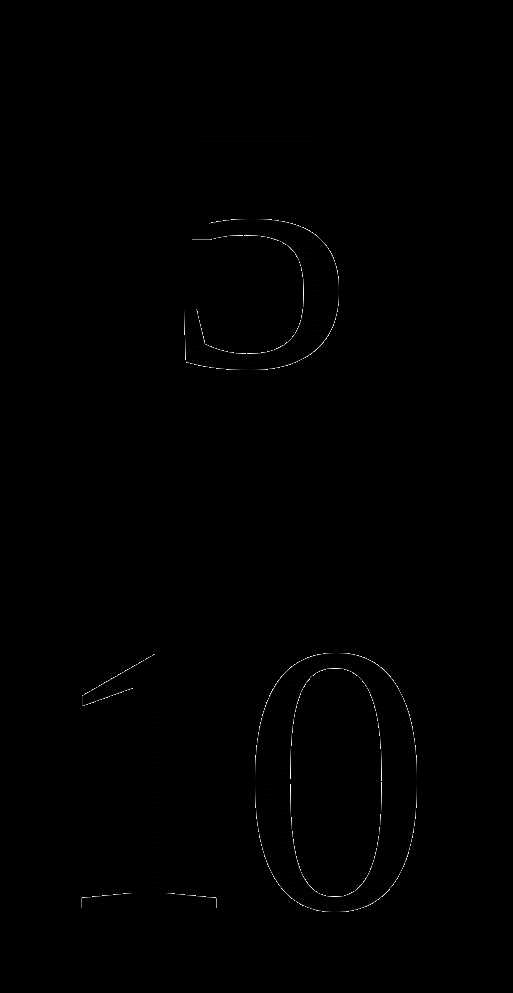
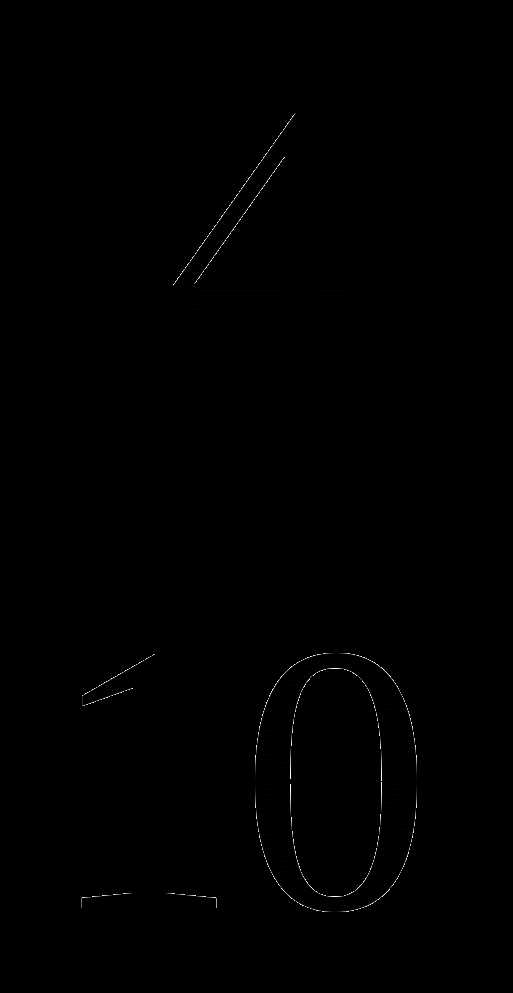
6

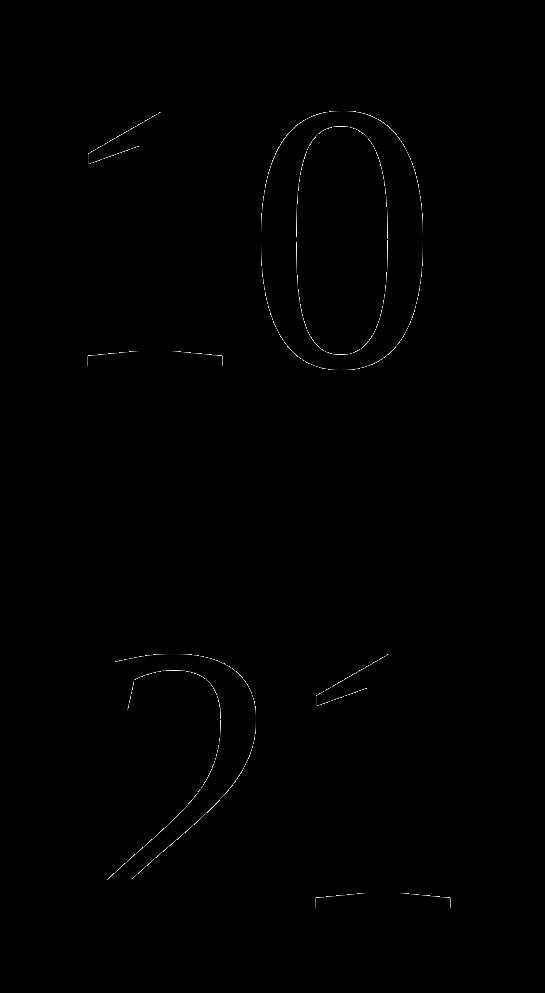
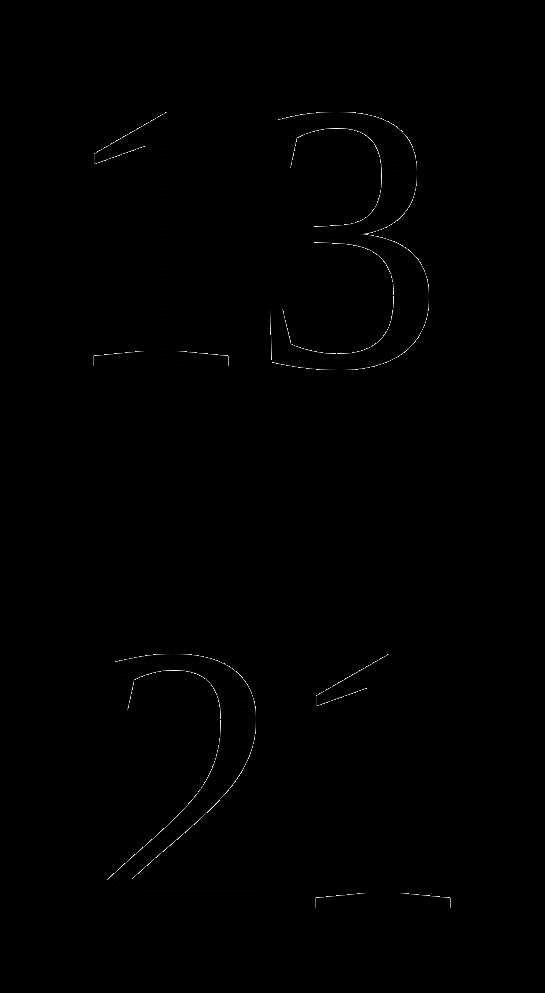
Задание к карточке 2

№1 Среди дробей ; ; ; 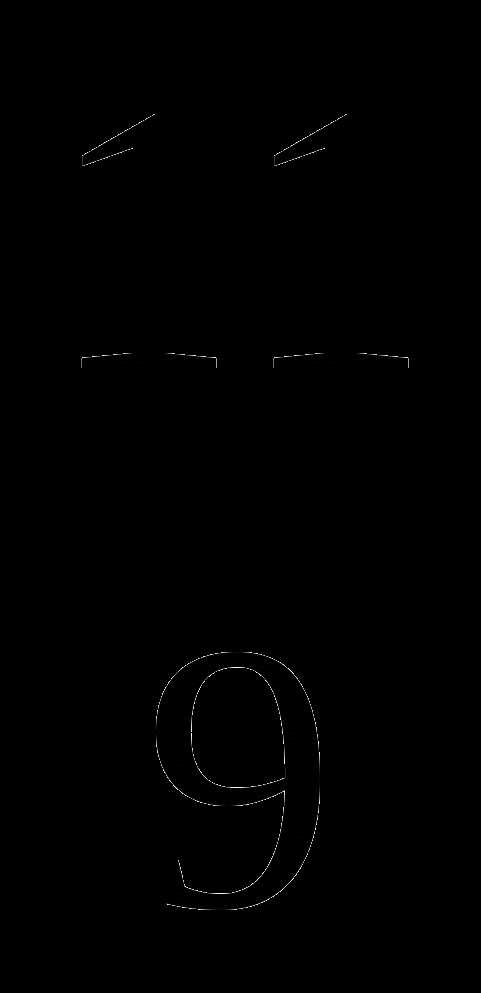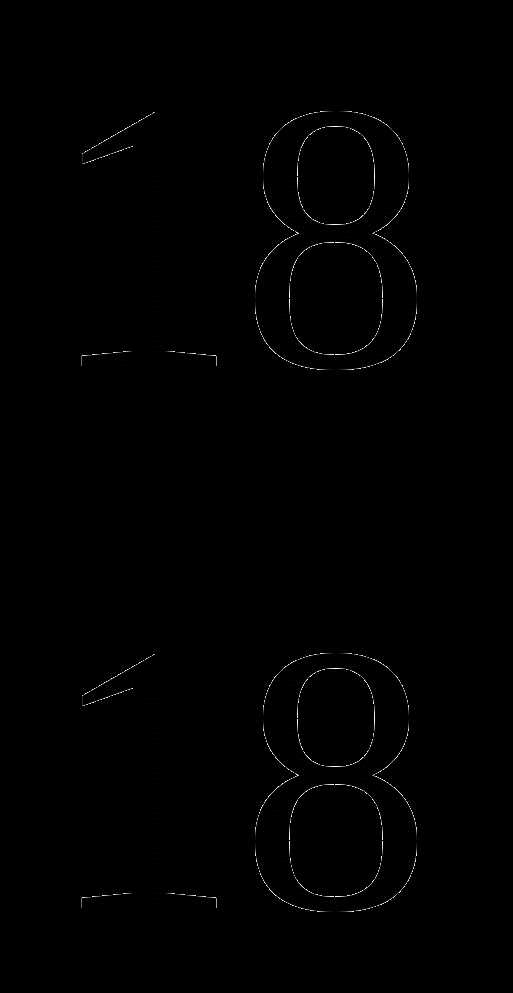. Выберите правильную дробь.

№2 Сравните числа 1 и , выберите большее.

№3 В книге 240 страниц. Вася прочитал книги. Сколько страниц ему осталось прочитать?

№4 Выполните действие: +

№5 Выполните действие: — .

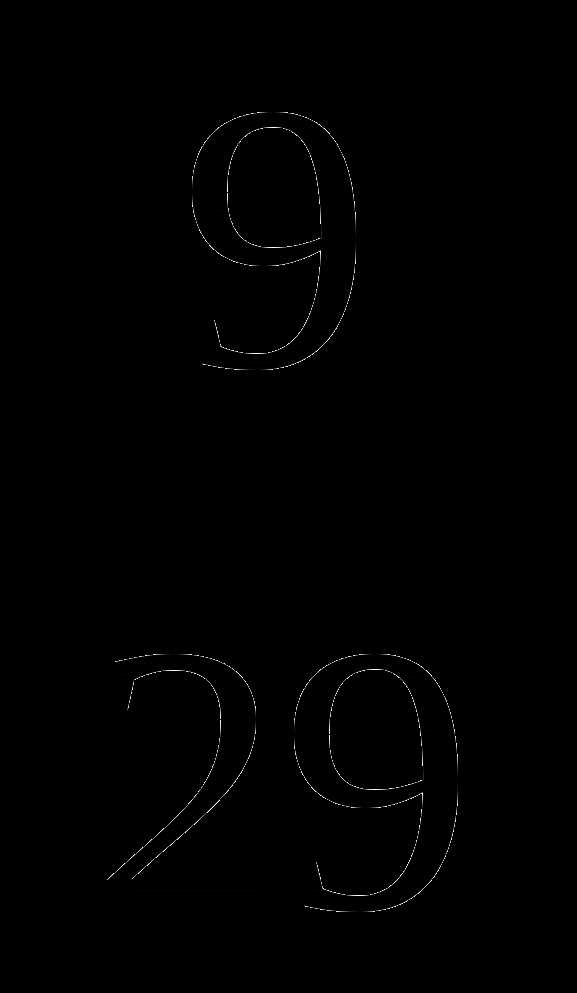№6 Выполните действие: + —.

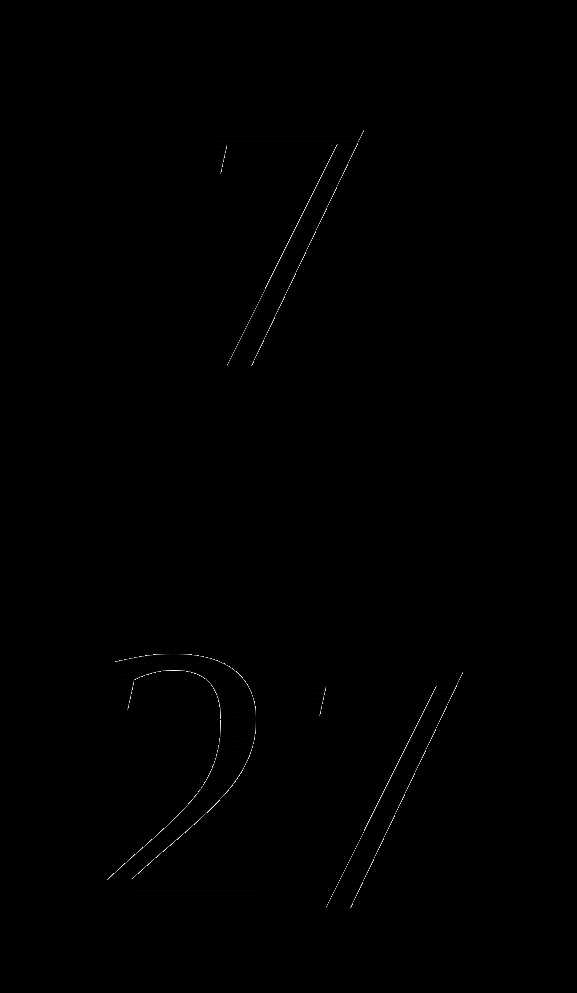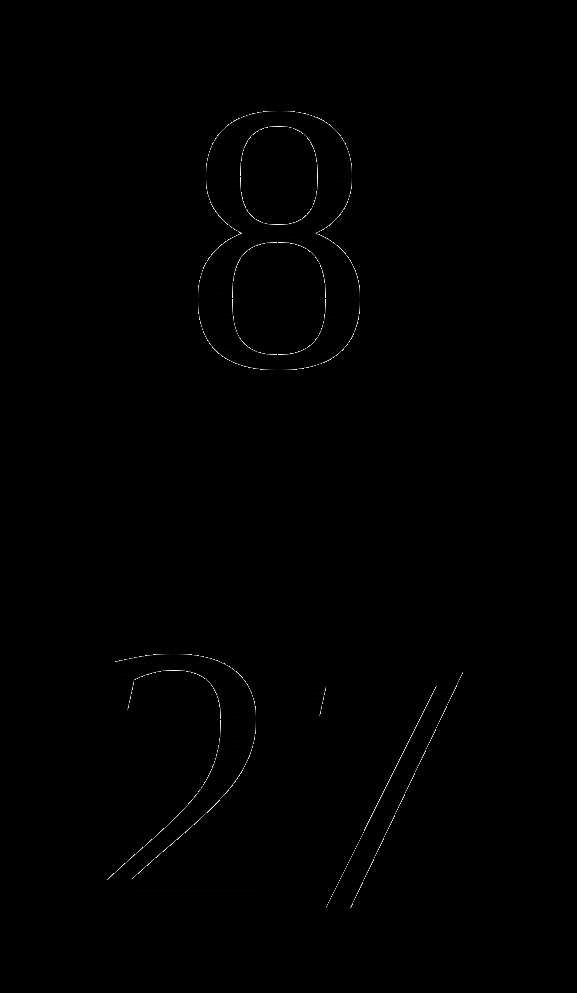Номер задания

Р

Б

Т

К

Е

У

1

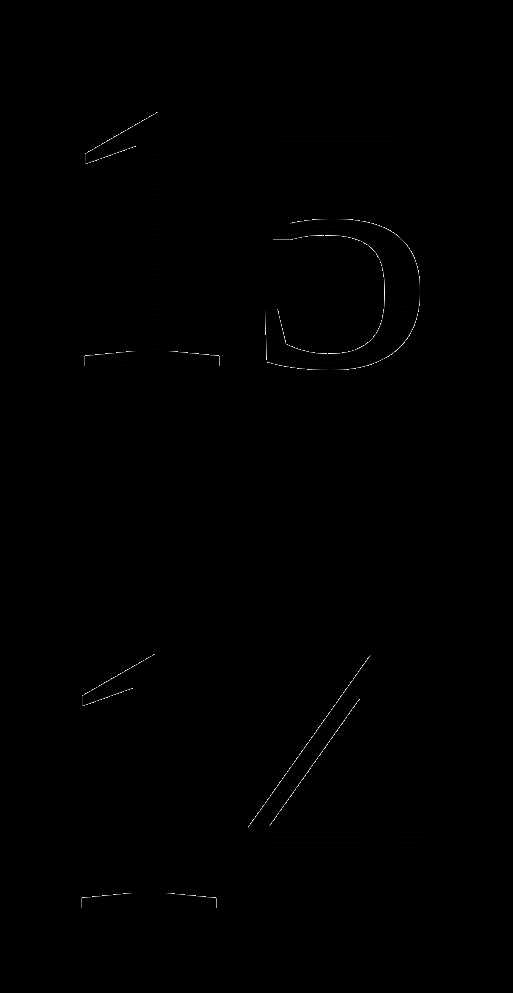
2

1

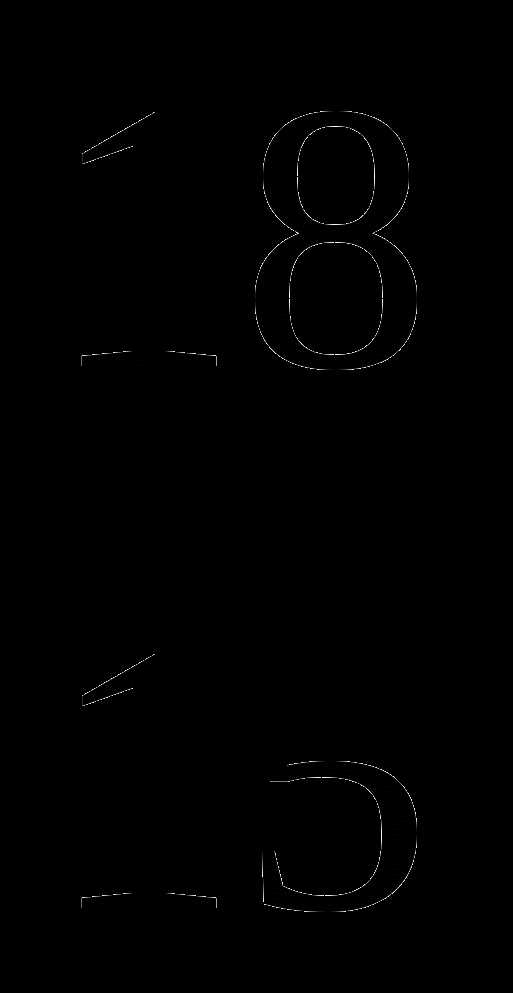
3

80

200

40

160

100

300

4

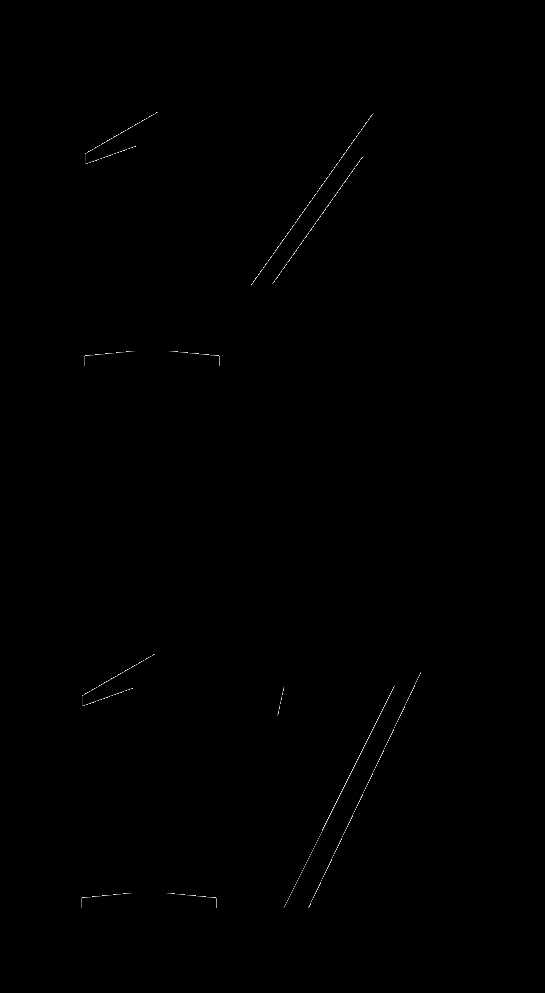
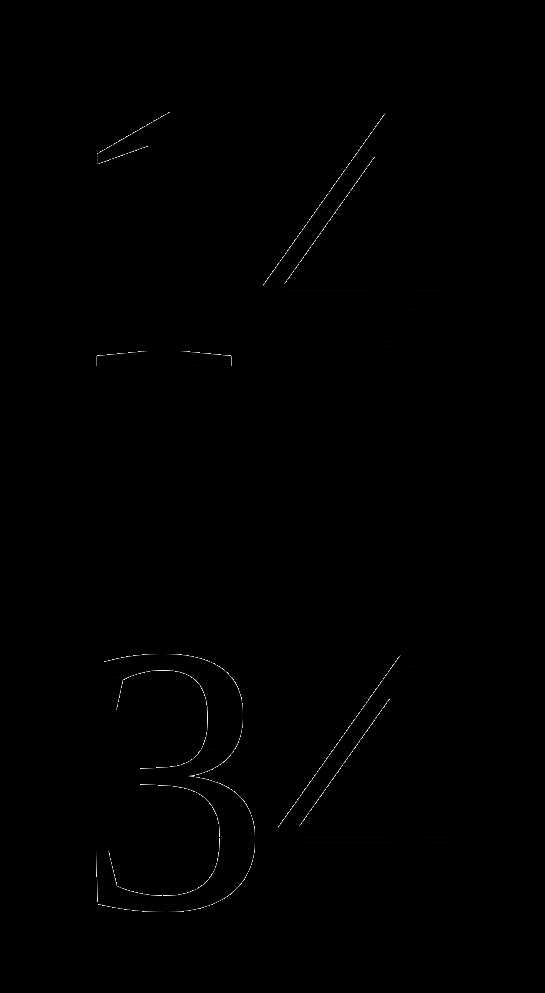
5

17

6

infourok.ru

Сложение смешанных дробей | Математика

Рассмотрим, как выполнить сложение смешанных дробей с одинаковыми знаменателями.

Правило.

Чтобы сложить смешанные дроби, надо:

1) отдельно сложить их целые части;

2) отдельно сложить дробные части.

Если при сложении дробных частей получается неправильная дробь, надо выделить из нее целую частьи прибавить ее к уже имеющейся целой части.

С помощью букв правило сложения смешанных дробей с одинаковыми знаменателями можно записать так:

   

Примеры.

Выполнить сложение смешанных дробей:

   

   

   

   

   

   

Решение:

   

Обычно сложение целых частей и сложение дробных частей выполняют устно и пишут короче:

   

   

Здесь дробная часть второго слагаемого равна нулю.

   

В этом примере равна нулю целая часть второго слагаемого.

   

Так как при сложении дробных частей получили неправильную дробь, выделяем целую часть и добавляем ее к уже полученной целой части:

   

   

   

   

   

www.for6cl.uznateshe.ru

Сложение и вычитание обыкновенных дробей

Сложение и вычитание дробей с одинаковыми знаменателями
Сложение и вычитание дробей с разными знаменателями
Понятие о НОК
Приведение дробей к одному знаменателю
Как сложить целое число и дробь

1 Сложение и вычитание дробей с одинаковыми знаменателями

Чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить тот же, например:

Чтобы вычесть дроби с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить тот же, например:

Чтобы сложить смешанные дроби, надо отдельно сложить их целые части, а затем сложить их дробные части, и записать результат смешанной дробью,

 

Если при сложении дробных частей получилась неправильная дробь, выделяем из нее целую часть и прибавляем ее к целой части, например:

2 Сложение и вычитание дробей с разными знаменателями

Для того, чтобы сложить или вычесть дроби с разными знаменателями, нужно сначала привести их к одному знаменателю, а дальше действовать, как указано в начале этой статьи. Общий знаменатель нескольких дробей — это НОК (наименьшее общее кратное). Для числителя каждой из дробей находятся дополнительные множители с помощью деления НОК на знаменатель этой дроби. Мы рассмотрим пример позже, после того, как разберемся, что же такое НОК.

3 Наименьшее общее кратное (НОК)

Наименьшее общее кратное двух чисел (НОК) — это наименьшее натуральное число, которое делится на оба эти числа без остатка. Иногда НОК можно подобрать устно, но чаще, особенно при работе с большими числами, приходится находить НОК письменно, с помощью следующего алгоритма:

Для того, чтобы найти НОК нескольких чисел, нужно:

1. Разложить эти числа на простые множители
2. Взять самое большое разложение, и записать эти числа в виде произведения
3. Выделить в других разложениях числа, которые не встречаются в самом большом разложении (или встречаются в нем меньшее число раз), и добавить их к произведению.
4. Перемножить все числа в произведении, это и будет НОК.

Например, найдем НОК чисел 28 и 21:

4Приведение дробей к одному знаменателю

Вернемся к сложению дробей с разными знаменателями.

Когда мы приводим дроби к одинаковому знаменателю, равному НОК обоих знаменателей, мы должны умножить числители этих дробей на дополнительные множители. Найти их можно, разделив НОК на знаменатель соответствующей дроби, например:

Таким образом, чтобы привести дроби к одному показателю, нужно сначала найти НОК (то есть наименьшее число, которое делится на оба знаменателя) знаменателей этих дробей, затем поставить дополнительные множители к числителям дробей. Найти их можно, разделив общий знаменатель (НОК) на знаменатель соответствующей дроби. Затем нужно умножить числитель каждой дроби на дополнительный множитель, а знаменателем поставить НОК.

5Как сложить целое число и дробь

Для того, чтобы сложить целое число и дробь, нужно просто добавить это число перед дробью, при этом получится смешанная дробь, например:

Если мы складываем целое число и смешанную дробь, мы прибавляем это число к целой части дроби, например:

mentalar.ru

Дробь с одинаковыми числителем и знаменателем

Дробь с одинаковыми числителем и знаменателем

Тема дроби объяснение.

Чему равна дробь, числитель которой равен знаменателю? Как сравнивать, складывать, вычитать и умножать дроби с одинаковыми числителем и знаменателем?

Рассмотрим на примерах дроби с одинаковыми числителем и знаменателем.

Проработайте примеры дробей внимательно.

Чему равна дробь, числитель которой равен знаменателю?

Дробь числитель которой равен знаменателю равна единице.

Пример.

Почему дробь, числитель которой равен знаменателю, равна единице?

Дробь – это другой способ записи деления. Смотрите в Дроби объяснение.

Значит дробь мы можем представить в виде деления:

Сравнение дробей с одинаковыми числителями и знаменателями

Дроби с одинаковыми числителями и знаменателями всегда равны.

Сложение дробей с одинаковыми знаменателями и числителями

Сложение дробей с одинаковыми знаменателями и числителями делается так: числители складываются, а знаменатель остается неизменным.

Пример.

5	+	5	=	5 + 5	=	10	= 2
5		5		5		5

Вычитание дробей с одинаковыми числителями и знаменателями

Вычитание дробей с одинаковыми числителями и знаменателями всегда дает ноль.

Пример.

5	—	5	= 1 — 1 = 0
5		5

Умножение дробей с одинаковыми знаменателями и числителями

Умножение дробей с одинаковыми знаменателями и числителями всегда дает единицу.

Пример.

5	*	5	= 1 * 1 = 1
5		5

www.sbp-program.ru