Расчет допусков и посадок подшипникового соединения. Пример решения задачи.
Примеры решения задач по метрологии
Расчет подшипникового соединения
Требуется определить:
1. Систему данного соединения.2. Верхние и нижние отклонения посадочного внутреннего диаметра подшипника и диаметра вала.
3. Предельные размеры посадочных диаметров подшипника и вала.
4. Допуски на изготовление внутреннего диаметра подшипника и вала (сначала подсчитать через их предельные размеры, а затем проверить через отклонения).
5. Предельные натяги или зазоры данного соединения.
6. Допуск посадки (сначала подсчитать через натяги или зазоры, а затем проверить через допуски на изготовление подшипника и шейки вала).
7. Выполнить графическое изображение полей допуска данного соединения в масштабе 1:1000, на котором показать их отклонения, предельные размеры и величины натяга или зазора.
Решение:
1. Данное соединение выполнено в системе отверстия, при этом отверстием является внутреннее кольцо подшипника, а валом – шейка чашки дифференциала заднего моста.
2. В соответствии с ГОСТ 3325-85 для подшипников класса точности 0 в основных типах соединений в системе отверстия применяется посадка L0/m6. При этом предельные отклонения отверстия и вала номинальным диаметром свыше 50 мм до 80 мм составляют:
Отверстие, |
Вал, |
||
Верхнее отклонение, |
Нижнее отклонение, |
Верхнее отклонение, |
Нижнее отклонение, |
0 |
-15 |
+45 |
+11 |
3. Исходя из величины предельных отклонений для отверстия и вала, определяем предельные размеры посадочных диаметров:
- Dmax = Dn = 75 мм;
- Dmin = Dn + EI = 75 + (- 0,015) = 74,985 мм;
- dmax = dn + es = 75 + 0,045 = 75,045 мм;
- dmin = dn – ei = 75 + 0,011 = 75,011 мм.
4. Определяем допуски через предельные размеры:
— на изготовление внутреннего диаметра подшипника:
TD = Dmax – Dmin = 75,0 – 74,985 = 0,015 мм = 15 мкм;
— на изготовление вала:
Td = dmax – dmin = 75,045 – 75,011 = 0,034 мм = 34 мкм.
Проверяем допуски на изготовление внутреннего диаметра подшипника и вала через предельные отклонения:
- TD =ES – EI = 0 – (-0,015) = 0,015 мм = 15 мкм;
- Td =es – ei = 0,045 – 0,011 = 0,034 мм = 34 мкм.
Результат проверочного расчета совпадает с предыдущим результатом, значит, расчет выполнен правильно.
5. Определяем предельные натяги или зазоры соединения.
Smax = Dmax – dmin = 75 – 75,011 = — 0,011 мм = -11 мкм.
Поскольку значение максимального зазора получилось отрицательным, следовательно, в посадке присутствует гарантированный натяг:
- Nmin = dmin – Dmax = 75,011- 75,0 = 0,011 мм = 11мкм;
- Nmax = dmax – Dmin = 75,045 – 74,985 = 0,060 мм = 60 мкм.
6. Определяем допуск посадки, который для данного соединения равен допуску натяга или разности максимального или минимального натягов:
ТП = Nmax – Nmin = 60 – 11 = 49 мкм = 0,049 мм.
Проверяем расчет через допуски на изготовление подшипника и шейки вала:
ТП = ТD + Тd = 15 + 34 = 49 мкм = 0,049 мм.
Результат проверочного расчета совпадает с предыдущим результатом, значит, расчет выполнен правильно.
7. По результатам расчетов выполняем графическое изображение полей допуска данного соединения в масштабе 1:1000, на котором показываем их отклонения, предельные размеры и величины натяга или зазора (см. рисунок 1).
Расположение полей допусков отверстия и вала указывает, что посадка выполнена с гарантированным натягом.
***
Пример решения задачи на расчет допусков и посадок резьбового соединения
k-a-t.ru
Решение задач по метрологии
Решение задач по метрологии
(смотрите также решение задач по статистике)
Для того, чтоб работать с любыми явлениями, объектами, схемами и проектами в материальном мире, необходимы измерения. Без измерений невозможно перевести представление об объекте в форму, понятную для какой-то абстрактной работы. С самого детства мы знакомы с измерительными приборами: линейкой измеряем расстояние, часами – время, весами – массу, спидометром – скорость и так далее. Однако метрология – это не чисто эмпирические измерения, а целая система знаний об измерениях. Сюда же входит и умение анализировать полученные измерениями данные. Поэтому метрология – не просто сводка единиц измерения, а ещё и целая собственная методология.
Если кратко, метрология – это наука, изучающая меры и измерительные инструменты. Выделить для них целую науку – это правильно: ведь только на мерах и измерительных инструментах можно построить научное знание и применить абстрактные формулы и исчисления к реальному миру.
Пример оформления курсовой работы по метрологии нашими специалистами:
Поэтому в метрологию входит не только знание формул, соотношений и названий различных единиц измерения. Знать надо также историю различных стран и их культуру (чтобы понять корни различных систем измерения), физику и химию (чтобы грамотно применять метрологические знания к реальному миру) и не только. Здесь нужно не только чисто научное, но и инженерное мышление, чтобы понять, как проводить некоторые виды измерений и как получить нужные данные.
Решение задач по метрологии, стандартизации и сертификации касается не только метрологии теоретической (которую обычно и преподают в различных ВУЗах на технических факультетах), но и метрологии прикладной, призванной решать различные практические проблемы. Правильное решение метрологии – это решение множества проблем, это и получение точных данных путём измерений, и более рациональные системы мер, и новации в рациональном использовании различных ресурсов. Большая часть метрологии основана на теории, а её задачи решаются простым приложением теоретических знаний к практике. Но часто этого недостаточно.
Любая техническая специальность немыслима без прикладной метрологии. Любой ВУЗ или факультет, готовящий студентов по техническим специальностям, уделяет много внимания метрологии, стандартизации и сертификации. Это касается и строителей, и физиков, и инженеров-электронщиков, и многих других. Кроме теоретических задач, в курс обучения входит и метрологическая практика, которая требует серьёзного освоения теории, а также применения знаний из смежных областей. Если решение задач по метрологии вызывает у вас проблемы, то вы можете обратиться к специалистам и решить задачи по метрологии на заказ. Опытный специалист сможет за сумму, которую вы оговорите, решить ваши конкретные задачи, пояснить последовательность выполняемых действий, а также оформить решение задачи так, как требуется в вашем ВУЗе.
Нет, вы, конечно, и сами понимаете важность изучения метрологии как науки и как инструмента других наук. И вы сознавали, что вам придётся уделить метрологии много вниманияю Но так получается, увы, не всегда: сессия содержит много экзаменов и зачётов, и к каждому надо готовиться, а в сутках – сколько в сутках часов? На таком уровне с метрологией знакомы все.
Вот и получается, что в условиях ограниченного времени решение задач по метрологии лучше доверить специалистам. Если же вы позже захотите уделить предмету больше времени и улучшить свои знания, вам на помощь могут прийти и частные репетиторы, и преподаватели, которые смогут на договорной основе привить вам понимание сути метрологии и фактические знания по теме.
Такое решение метрологии на заказ часто становится настоящим спасением для студентов в сложной ситуации. Примеры задач по метрологии с решениями могут стать не только образцом для механического переноса условий, но и ключом к пониманию науки в целом.
Заказать нам работу!
dx-dy.ru
Информатики и радиоэлектроники
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Кафедра метрологии и стандартизации
Метрология и измерения Учебно — методическое пособие
для индивидуальной работы студентов
всех специальностей
Под общей редакцией С.В. Лялькова
Минск 1999
УДК 621.317(075)
ББК 30:10
М 54
Авторы: А.П. Белошицкий, М.Ю. Дерябина, А.М. Кострикин, С.В. Ляльков, В.Т. Ревин
Метрология и измерения: Учебно-методическое пособие для индивидуальной работы студентов/ А.П. Белошицкий и др.; под общ. ред. С.В. Лялькова. — Мн.: БГУИР, 1999. -72 с.: ил. 1. ISBN 985-444-103-2
Учебно-методическое пособие «Метрология и измерения» предназначено для индивидуальной работы студентов, изучающих курсы измерений. Оно содержит краткие методические указания, список рекомендуемой литературы и НТД, контрольные вопросы, решения типовых задач и задачи для самостоятельного решения.
Пособие может быть использовано при проведении практических и лабораторных занятий, связанных с оценкой погрешностей получаемых результатов. Оно также будет полезно самому широкому кругу студентов, аспирантов и научно-педагогических работников при решении ими конкретных практических задач метрологии и стандартизации.
УДК 621.317(075)
ББК 30:10
ISBN 985-444-103-2 © Коллектив авторов, 1999
Содержание
1 | Погрешности средств измерений …………………………… | 4 |
2 | Обработка результатов измерений с однократными наблюдениями …………………………………………………… | 10 |
3 | Обработка результатов многократных наблюдений при прямых измерениях ………………………………………………… | 17 |
4 | Обработка результатов многократных наблюдений при косвенных измерениях ………………………………… | 30 |
5 | Обработка результатов наблюдений при совокупных и совместных измерениях………………………………….…. | 35 |
6 | Измерение напряжениЙ………………………………………………….…. | 40 |
7 | Измерение частоты, периода, интервалов времени и фазовых сдвигов………………………………………………….………. | 44 |
8 | Измерение параметров пассивных линейных двухполюсников …..……………………………………………. | 49 |
Литература …………………………………………………………………………..…… | 57 | |
1 ПОгрешности средств измерений
Рекомендуемая литература: [1, c.230-248], [3, с.15-19] [4, c.49-55], [5, c.51-61], [6, c.11-20, 32-36], [7, c.13-15], [11], [12]
Методические указания
При изучении темы необходимо особо обратить внимание на следующее:
— формы представления погрешностей средств измерений;
— правила выбора нормирующего значения ХN;
— способы нормирования и формы выражения пределов допускаемых погрешностей;
— обозначение классов точности средств измерений.
Контрольные вопросы
1 Что такое погрешность средства измерений?
2 Что такое основная и дополнительная погрешности средств измерений?
3 Какие существуют формы представления погрешностей средств измерений?
4 Какие существуют правила выбора нормирующего значения ХN?
5 Как регламентируются способы нормирования и формы выражения пределов допускаемых погрешностей?
6 Что такое класс точности средства измерения и чем он определяется?
7 Как обозначаются классы точности?
Решение типовых задач
Задача № 1
Определить пределы инструментальных абсолютной и относительной погрешностей измерения тока I = 67 мA, если измерения проводились магни-тоэлектрическим миллиамперметром с нулем в начале шкалы, классом точности 1.0 и пределом измерения А = 100 мA.
Решение
Для магнитоэлектрического миллиамперметра класс точности определяется
значением максимальной приведенной погрешности, т.е. = ±1,0 %.
Так как
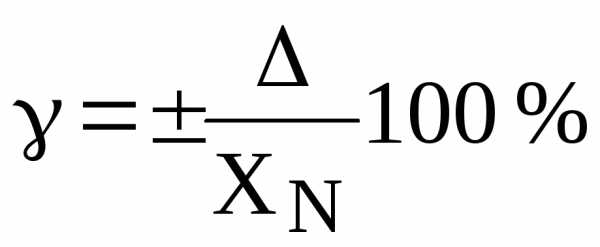 ,
,
то предел инструментальной абсолютной погрешности
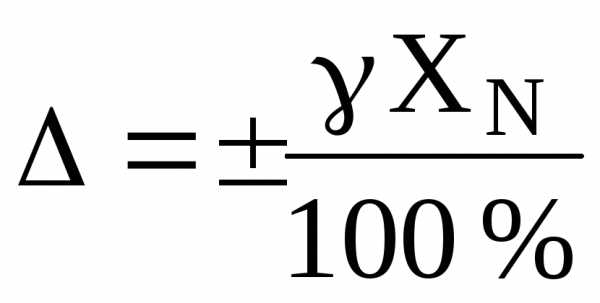 (мА).
(мА).
Миллиамперметр имеет равномерную шкалу с нулем в начале шкалы, и поэтому XN = A = 100 мA:
.
Предел инструментальной относительной погрешности
.
Задача № 2
Определить пределы инструментальных абсолютной и относительной погрешностей измерения напряжения U=8,6 B, если измерения проводились магнитоэлектрическим вольтметром с нулем в середине шкалы, классом точности 2,5 и пределами измерения А = ± 25 В.
Решение
Как и в предыдущей задаче, предел абсолютной погрешности находится из формулы:
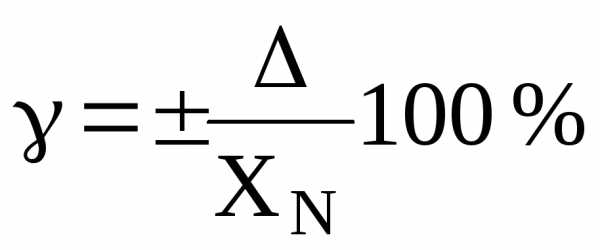 .
.
Вольтметр имеет равномерную шкалу с нулем в середине шкалы. Поэтому
XN = |25| + |25| = 50 (B),
= ±(2,550)/100 %=±1,25 (В).
Найдем предел относительной погрешности измерения:
= ±(/U)100 %= ±(1,25100)/8,6 ±15 (%).
Задача № 3
Oценить инструментальные погрешности измерения тока двумя магни-тоэлектрическими миллиамперметрами с классами точности 0,5 и 1.0 и указать, какой из результатов получен с большей точностью, а также, могут ли показания I1 = 19,0 мA и I2 = 18,6 мA исправных приборов отличаться так, как задано в условии? Миллиамперметры имеют нули в начале шкалы и пределы A1 =
= 50 мA и A2 = 20 мA.
Решение
Инструментальные абсолютные погрешности можно найти из формул:
1 = ±(1 ХN1)/100 %= ±(1 A1)/100 %= ±(0,550)/100 = ±0,25 (мA),
2 = ±(2 ХN2)/100 %= ±(2 A2)/100 %= ±(1,020)/100 = ±0,20 (мA).
Для определения, какое из измерений проведено с большей точностью, необходимо определить инструментальные относительные погрешности:
1 = ±(1/I1) 100 % = ±(0,25/19,0)100 % ±1,3 %,
2 = ±(2/I2) 100 % = ±(0,20/18,6)100 % ±1,1 %.
Видно, что второе измерение проведено с большей точностью, так как точность обратно пропорциональна модулю относительной погрешности.
В наихудшем случае (когда погрешности приборов будут иметь противоположные знаки) модуль разницы между результатами измерений || = |I1 — I2| не должен превышать сумму модулей абсолютных погрешностей, т.е.
|| < |1| + |2| .
Получаем
|| = 0,4 (мA) < |1| + |2| = 0,45 (мA).
Таким образом, при исправных миллиамперметрах можно получить указанные значения I1 и I2.
studfiles.net
Решение задач по метрологии [DOC]
Кумертауский филиал УГАТУ, 3 курс, 6 семестр, преподаватель Вдовыкина О. В, специальность 210200 «Автоматизация технологических процессов и производств. Дисциплина — метрология стандартизация сертификация. Также вложены две лабораторные работы, вопросы по дисциплине и методичка.
- 1,52 МБ
- дата добавления неизвестна
- изменен
БГТУ, ПГС. Определения основных элементов сопряжения, условное обозначение посадок и квалитетов на чертежах и расчет калибров. Расчет и выбор посадок подвижных и неподвижных соединений. Расчет допусков и посадок шпоночных соединений. Расчет и выбор посадок деталей под подшипники качения. Допуски и посадки шлицевых соединений.
- 602,63 КБ
- дата добавления неизвестна
- изменен
Метрология, стандартизация и сертификация. Расчет абсолютной и относительной погрешности, математическое ожидание. 27 примеров.
- 32,87 КБ
- дата добавления неизвестна
- изменен
В каждой части по 10 задач по различным темам курса «Метрология, стандартизация и сертификация». Первая часть состоит из трех разделов: метрология, стандартизация и сертификация. В первой части для решения различных задач используют различные формулы, коэффициенты, графики для определения результатов измерения, оценки его точности и, например, для задачи №1- границ доверительного…
- 907,44 КБ
- дата добавления неизвестна
- изменен
ОНПУ заочное. стр. -13 Построение схемы полей допусков гладкого цилиндрического соединения. Расчёт и выбор посадок подшипника качения на валу и в отверстии корпуса. Расчёт размерных цепей. Расчёт предельного контура резьбового профиля для резьбового соединения, построение резьбового профиля и схемы полей допусков.
- 585,18 КБ
- дата добавления неизвестна
- изменен
Иркутский государственный университет путей сообщения. Электротехнический факультет. 3 курс. Преподаватель Жигулина Е. Н. Вариант 91. Включает в себя задачи: Погрешности средств измерений, Определение погрешности результата косвенных измерений, Применение масштабных измерительных преобразователей для измерения тока и напряжения, Выбор измерительной аппаратуры, Измерение…
- 136,77 КБ
- дата добавления неизвестна
- изменен
www.twirpx.com
Сборник примеров и задач по метрологии 5 страница
Сборник примеров и задач по метрологии 5 страницаОтвет: IВ = 5 мА.
6.2.12. Какой верхний предел измерения должен быть у вольтметра класса точности К = 0,5, чтобы напряжение в диапазоне U = 10…25, В измерялось с погрешностью ?
Ответ: UВ = 40 В.
6.2.13. Высокоомным компенсатором постоянного тока класса точности c/d = 0,02/0,01, имеющего верхний предел измерения UВ = 1,6 В, измерено напряжение U = 0,80126 В. Определите предельную погрешность измерения (в нормальных условиях) и запишите результат измерения (формулы 6.4, 6.5).
Ответ: ( ) мВ.
6.2.14. На отсчетном устройстве цифрового вольтметра класса точности c/d = 0,5/0,2 с автоматическим выбором диапазона измерения отсчитано показание U = 54,68 В. Определите предельные абсолютную и относительную погрешности результата измерения.
Ответ: , В; .
6.2.15. Каким прибором будет точнее измерено напряжение U = 7,5 В, если имееется:
а) электромеханический вольтметр класса точности К1 = 0,1 с верхним пределом измерения UВ1 = 15 В;
б) цифровой вольтметр класса точности c2/d2 = 0,2/0,1 с верхним пределом измерения UВ2 = 10 В?
Ответ: первым.
6.2.16. Каким прибором будет точнее измерено напряжение U = 9 В, если имеется:
а) электромеханический вольтметр класса точности К1 = 0,1 с верхним пределом измерения UВ1 = 30 В;
б) цифровой вольтметр класса точности c2/d2 = 0,2/0,1 с верхним пределом измерения UВ2 = 10 В?
Ответ: вторым.
6.2.17. Для измерения напряжения U = 20 В можно использовать один из четырех вольтметров:
а) электромеханический вольтметр класса точности К1 = 1,5 с верхним пределом измерения UВ1 = 30 В;
б) электромеханический вольтметр класса точности К2 = 0,5 с диапазоном измерения Uд2 = (-20 ÷ +20) В;
в) электромеханический вольтметр класса точности К3 = 0,5 с диапазоном измерения Uд3 = (10 ÷ 30) В;
г) цифровой вольтметр класса точности c4/d4 = 0,5/0,1 с верхним пределом измерения UВ4 = 100 В?
Какой из приборов нужно выбрать, чтобы было выполнено точнее?
Решение. Из перечисленных приборов следует выбрать тот, у которого при измерении напряжения U = 20 В будет меньшая относительная погрешность.
а) Относительную погрешность определим по формуле:
,
где — приведенная погрешность первого прибора;
— его нормируещее значение, равное в этом случае верхнему пределу измерения:
б) Во втором случае используем ту же формулу, только нормируещее значение будет равно В
Следовательно, .
в) В третьем случае также используется та же формула, но нормирующее значение будет равно В.
Следовательно, .
г) в четвертом случае воспользуемся формулой
.
Сравнение показывает, что относительная погрешность получается меньше в четвертом случае. Следовательно, нужно выбрать цифровой вольтметр.
6.2.18. В паспорте цифрового вольтметра записана формула для определения приведенной . К какому классу точности он относится? (формулы 6.1, 6.2).
Ответ: c/d = 0,1/0,05.
6.2.19. Напишите обозначение класса точности c/d цифрового вольтметра, если известно, что предельное значение основной погрешности при конечном значении измеряемой величины составляет , а при значении, равном половине конечного, — .
Ответ: c/d = 0,01/0,005
6.2.20. Цифровой вольтметр с пределом измерения UВ = 100В при измерении напряжений U1 = 50 В и U2 = 25 В имеет относительные погрешности и . К какому классу точности c/d он относится?
Ответ: c/d = 0,2/0,1
6.2.21. У цифрового вольтметра В7-18 относительная погрешность нормирована формулой , где UВ – верхний предел измерения. К какому классу точности он относится? (формулы 6.1, 6.3).
Ответ: c/d = 0,1/0,02 (0,07/0,02).
6.2.22. Имеются два цифровых вольтметра: V1 – класс точности c1/d1 = 0,1/0,05 и V2 – класс точности c2/d2 = 0,15/0,025; оба с верхним пределом измерения UВ = 1В. При каких значениях измеряемого напряжения выгоднее применять V1 (меньше допускаемая погрешность)?
Ответ: В
6.2.23. Определите значения аддитивной и мультипликативной составляющих погрешностей цифрового вольтметра класса точности c/d = 0,1/0,05 при показании U = 5 В и верхнем пределе измерения UВ = 10 В (формулы 6.8 – 6.11).
Ответ: .
6.2.24. Определите значения аддитивной и мультипликативной составляющих погрешностей цифрового моста класса точности c/d = 0,05/0,02 при верхнем пределе измерения RВ = 1000 Ом и показании R = 500 Ом.
Ответ: .
6.2.25. Относительная погрешность измерительного преобразователя перемещения выражается трехчленной формулой (6.7) . Определите абсолютные значения аддитивной , мультипликативной и квадратической составляющих погрешности измерения перемещения Х = 1 м (формула 6.6).
Ответ: м; м; м.
6.2.26. Относительная погрешность моста для измерения сопротивлений выражается трехчленной формулой . Определите абсолютные значения аддитивной , мультипликативной и квадратической составляющих погрешности измерения сопротивления R = 2,4 кОм.
Ответ: Ом; Ом; Ом.
Библиографический список
1. Артемьев Б.Г., Голубев С.М. Справочное пособие для работников метрологических служб. Кн. 1. М.: Издательство стандартов, 1986.
2. Новицкий П.В., Зограф И.А. Оценка погрешностей результатов измерений. Л.: Энергоатомиздат, 1991.
3. Основы метрологии и электрические измерения / Под ред. Е.М. Душина. Л.: Энергоатомиздат, 1987.
4. Сборник задач и упражнений по электрическим и электронным измерениям / Под ред. Э.Г, Атамалян. М.: Высшая школа, 1980.
5. Белянина Е.К., Федорова Е.В. Основы метрологии, стандартизации и измерительной техники. Сборник задач: Учебное пособие. М.: МИРЭА, 1993.
6. Демидова-Панферова Р.М., Малиновский В.Н., Солодов Ю.С. Задачи и примеры расчетов по электроизмерительной технике. М.: Энергоатомиздат, 1990.
7. Тартаковский Д.Ф., Ястребов А.С., Метрология, стандартизация и технические средства измерений. М.: Высшая школа, 2001.
8. Косторниченко В.Г., Лапшин В.Б. Введение в метрологию, стандартизацию и сертификацию. Учебное пособие. Таганрог, изд-во ТРТУ, 2003.
9. Лапшин В.Б., Пахомкин Б.И., Рогозов Ю.И. Сборник примеров и задач по метрологии: Учебное пособие. Таганрог: Изд-во ТРТУ, 1999.
10. Кузнецов В.А., Ялунина Г.В. Метрология (теоретические прикладные и законодательные основы): Учебн. пособие. – М.: ИПК Издательство стандартов, 1998.
Приложение
Интеграл вероятности
Таблица I
| t | P(t) | t | P(t) | t | P(t) | t | P(t) |
| 0.00 | 0.00000 | 1.00 | 0.68269 | 2.00 | 0.95450 | 3.0 | 0.99730 |
| 0.05 | 0.03988 | 1.05 | 0.70628 | 2.05 | 0.95964 | 3.10 | 0.99806 |
| 0.10 | 0.07966 | 1.10 | 0.72867 | 2.10 | 0.96427 | 3.20 | 0.99863 |
| 0.15 | 0.11924 | 1.15 | 0.74986 | 2.15 | 0.96844 | 3.30 | 0.99903 |
| 0.20 | 0.15852 | 1.20 | 0.76986 | 2.20 | 0.97219 | 3.40 | 0.99933 |
| 0.25 | 0.19741 | 1.25 | 0.78870 | 2.25 | 0.97555 | 3.50 | 0.99953 |
| 0.30 | 0.23582 | 1.30 | 0.80640 | 2.30 | 0.97855 | 3.60 | 0.99968 |
| 0.35 | 0.27366 | 1.35 | 0.82298 | 2.35 | 0.98123 | 3.70 | 0.99978 |
| 0.40 | 0.31084 | 1.40 | 0.83849 | 2.40 | 0.98360 | 3.80 | 0.99986 |
| 0.45 | 0.34729 | 1.45 | 0.85294 | 2.45 | 0.98571 | 3.90 | 0.99990 |
| 0.50 | 0.38292 | 1.50 | 0.86635 | 2.50 | 0.98758 | 4.00 | 0.99994 |
| 0.55 | 0.41768 | 1.55 | 0.87886 | 2.55 | 0.98922 | 4.10 | 0.99996 |
| 0.60 | 0.45149 | 1.60 | 0.89040 | 2.60 | 0.99069 | 4.20 | 0.99997 |
| 0.65 | 0.48431 | 1.65 | 0.90106 | 2.65 | 0.99195 | 4.30 | 0.99999 |
| 0.70 | 0.51607 | 1.70 | 0.91087 | 2.70 | 0.99307 | 4.40 | 0.99999 |
| 0.75 | 0.54675 | 1.75 | 0.91988 | 2.75 | 0.99404 | 4.50 | 0.99999 |
| 0.80 | 0.57629 | 1.80 | 0.92814 | 2.80 | 0.99489 | ||
| 0.85 | 0.60468 | 1.85 | 0.93569 | 2.85 | 0.99563 | ||
| 0.90 | 0.63188 | 1.90 | 0.94257 | 2.90 | 0.99627 | ||
| 0.95 | 0.65789 | 1.95 | 0.94882 | 2.95 | 0.99682 |
Таблица II
Интегральная функция нормального распределения.
Значения t для различных F(t)
| F(t) | t | F(t) | t | F(t) | t |
| 0,0005 | -3,2905 | 0,35 | -0,3853 | 0,75 | +0,6745 |
| 0,005 | -2,5750 | 0,40 | -0,2533 | 0,80 | +0,8416 |
| 0,01 | -2,3267 | 0,45 | -0,1257 | 0,85 | +1,0364 |
| 0,05 | -1,6449 | 0,50 | -0,0000 | 0,90 | +1,2816 |
| 0,10 | -1,2816 | 0,50 | +0,0000 | 0,95 | +1,6449 |
| 0,15 | -1,0364 | 0,55 | +0,1257 | 0,99 | +2,3267 |
| 0,20 | -0,8416 | 0,60 | +0,2533 | 0,995 | +2,5750 |
| 0,25 | -0,6745 | 0,65 | +0,3853 | 0,9995 | +3,2905 |
| 0,30 | -0,5244 | 0,70 | +0,5244 |
Таблица III
Интеграл вероятности по закону Стьюдента
| Число изме-рений n | Значения tS при PS | |||||||
| 0,50 | 0,60 | 0,70 | 0,80 | 0,90 | 0,95 | 0,98 | 0,99 | |
| 1,000 | 1,376 | 1,963 | 3,078 | 6,134 | 12,706 | 31,821 | 63,657 | |
| 0,816 | 1,061 | 1,336 | 1,886 | 2,920 | 4,303 | 6,965 | 9,925 | |
| 0,765 | 0,978 | 1,250 | 1,638 | 2,353 | 3,182 | 4,541 | 5,841 | |
| 0,741 | 0,941 | 1,190 | 1,533 | 2,132 | 2,776 | 3,747 | 4,604 | |
| 0,727 | 0,920 | 1,156 | 1,476 | 2,015 | 2,570 | 3,365 | 4,032 | |
| 0,718 | 0,906 | 1,134 | 1,440 | 1,943 | 2,447 | 3,143 | 3,707 | |
| 0,711 | 0,896 | 1,119 | 1,415 | 1,895 | 2,365 | 2,998 | 3,499 | |
| 0,706 | 0,889 | 1,108 | 1,397 | 1,860 | 2,306 | 2,896 | 3,355 | |
| 0,703 | 0,883 | 1,100 | 1,383 | 1,833 | 2,262 | 2,821 | 3,250 | |
| 0,697 | 0,876 | 1,088 | 1,363 | 1,796 | 2,201 | 2,718 | 3,106 | |
| 0,694 | 0,870 | 1,079 | 1,350 | 1,771 | 2,160 | 2,650 | 3,012 | |
| 0,691 | 0,866 | 1,074 | 1,340 | 1,753 | 2,131 | 2,602 | 2,947 | |
| 0,688 | 0,861 | 1,066 | 1,328 | 1,729 | 2,093 | 2,539 | 2,861 | |
| 0,686 | 0,858 | 1,061 | 1,321 | 1,717 | 2,074 | 2,508 | 2,819 | |
| 0,685 | 0,857 | 1,059 | 1,318 | 1,711 | 2,064 | 2,429 | 2,797 | |
| 0,683 | 0,854 | 1,055 | 1,311 | 1,699 | 2,045 | 2,462 | 2,756 |
Таблица IV
Предельные значения tТ для оценки анормальности результатов измерения
| Объем выборки n | Предельные значения tS при уровне значимости q | |||
| 0,100 | 0,075 | 0,050 | 0,025 | |
| 1,15 | 1,15 | 1,15 | 1,15 | |
| 1,42 | 1,44 | 1,46 | 1,48 | |
| 1,60 | 1,64 | 1,67 | 1,72 | |
| 1,73 | 1,77 | 1,82 | 1,89 | |
| 1,83 | 1,88 | 1,94 | 2,02 | |
| 1,91 | 1,96 | 2,03 | 2,13 | |
| 1,98 | 2,04 | 2,11 | 2,21 | |
| 2,03 | 2,10 | 2,18 | 2,29 | |
| 2,09 | 2,14 | 2,23 | 2,36 | |
| 2,13 | 2,20 | 2,29 | 2,41 | |
| 2,17 | 2,24 | 2,33 | 2,47 | |
| 2,21 | 2,28 | 2,37 | 2,50 | |
| 2,25 | 2,32 | 2,41 | 2,55 | |
| 2,28 | 2,35 | 2,44 | 2,58 | |
| 2,31 | 2,38 | 2,48 | 2,62 | |
| 2,34 | 2,41 | 2,50 | 2,66 | |
| 2,36 | 2,44 | 2,53 | 2,68 | |
| 2,38 | 2,46 | 2,56 | 2,71 |
Таблица V
Квантили распределения d. Критерий 1.
| Объем выборки n | ||||
| 0,01 | 0,05 | 0,95 | 0,99 | |
| 0,9137 | 0,8884 | 0,7236 | 0,6829 | |
| 0,9001 | 0,8768 | 0,7304 | 0,6950 | |
| 0,8901 | 0,8686 | 0,7360 | 0,7040 | |
| 0,8826 | 0,8625 | 0,7404 | 0,7110 | |
| 0,8769 | 0,8578 | 0,7440 | 0,7167 | |
| 0,8722 | 0,8540 | 0,7470 | 0,7216 | |
| 0,8682 | 0,8508 | 0,7496 | 0,7256 | |
| 0,8648 | 0,8481 | 0,7518 | 0,7291 |
Таблица VI
Значения mт и , соответствующие различным n и q. Критерий 2.
| Объем выборки n | mт | при уровне значимости q2 равном | ||
| 0,01 | 0,02 | 0,05 | ||
| 0,98 | 0,98 | 0,96 | ||
| 11-14 | 0,99 | 0,98 | 0,97 | |
| 15-20 | 0,99 | 0,99 | 0,98 | |
| 21-22 | 0,98 | 0,97 | 0,96 | |
| 0,98 | 0,98 | 0,96 | ||
| 24-27 | 0,98 | 0,98 | 0,97 | |
| 28-32 | 0,99 | 0,98 | 0,97 | |
| 33-35 | 0,99 | 0,98 | 0,98 | |
| 36-49 | 0,99 | 0,99 | 0,98 |
Оглавление
Введение. 2
1. Международная система единиц (СИ) 3
1.1. Основные сведения. 3
1.2. Задачи и примеры.. 3
2. Виды измерений. 5
2.1. Основные сведения. 5
2.2. Задачи и примеры.. 6
3. Погрешность измерений. 9
3.1. Основные сведения. 9
3.2. Задачи и примеры.. 10
4. Случайные погрешности и обработка результатов измерений. 14
4.1. Основные сведения. 14
4.2. Задачи и примеры.. 21
5. Оценка погрешности результата косвенных измерений. 32
5.1. Основные сведения. 32
5.2. Задачи и примеры.. 34
6. Методы нормирования погрешностей средств измерений. 43
6.1. Основные сведения. 43
6.2. Задачи и примеры.. 48
Библиографический список. 54
Приложение. 55
Дата добавления: 2015-10-02; просмотров: 419 | Нарушение авторских прав
Сборник примеров и задач по метрологии 1 страница | Сборник примеров и задач по метрологии 2 страница | Сборник примеров и задач по метрологии 3 страница |
mybiblioteka.su — 2015-2019 год. (0.02 сек.)
mybiblioteka.su
Примеры решения типовых задач
1. Определить значение сопротивления R4 (рис. 8.1) при балансе моста, если R2 = 1 кОм, R3 = 5 кОм. Измерения осуществляются на постоянном токе.
Рис. 8.1. Мостовая схема измерения сопротивлений
Решение.
При балансе моста ток через амперметр равен нулю, это означает, что Uc = Uд. Напряжение на сопротивлении R3 равно в момент баланса напряжению на сопротивлении R4, т. е. I1R3 = I2R4. Значения токов
Окончательно уравнение баланса моста R2R3 = R1R4, откуда
2. Определить добротность последовательного колебательного контура, если ток в момент резонанса I0 = 10 мА, напряжение на конденсаторе
UCO = 5 В, а частота контура f0 = 1 МГц, сопротивление потерь rk = 5 Ом
Решение.
Ом
3. Определить погрешность измерения сопротивления Rx = 100 Ом методом вольтметра-амперметра, если Rv = 1 МОм.
Решение.
Задачи
1. Определить погрешность измерения сопротивления Rx = 1 кОм
омметром с классом точности 1,0, если Rом = 100 Ом.
2. Определить индуктивность катушки, если модель ее полного сопротивления на частоте f = 1 МГц равен 100 Ом, а сопротивление катушки RL = 5 Ом.
3. Общая индуктивность при согласном включении двух катушек L0 = 10 мкГн, а при встречном включении общая индуктивность Lв = 18 мкГн. Определить взаимную индуктивность.
4. Определить активное сопротивление контура, если образцовое сопротивление Rобр = 10 Ом, а показания вольтметра при резонансе U1 = 2 В, а при включении в контуре образцового резистора U2 = 1 В.
5. Определить чувствительность мостовой схемы (рис. 8.1), если при измерении сопротивления одного из плеч моста на ΔR = 100 Ом напряжение в измерительной диагонали изменилось на величину ΔU = 0,3 В.
6. Оценить абсолютное отклонение величины сопротивления R4 (рис. 8.1) при резонансе моста, если величина тока резонанса I = 0,1 А, напряжение питания моста U = 5 В, сопротивление измерительного прибора Rн = 100 Ом,
R1 = 1 кОм, R2 = 2 кОм, R3 = 2 кОм, R4 = 4 кОм.
7. Определить активное сопротивление катушки индуктивности, измеренное мостовой схемой, если Lx = 1 мкГн, C1 = 1 нФ, Rв = 10 Ом, R1 = 200 Ом.
8. Определить сопротивление потерь катушки индуктивности, если частота последовательного колебательного контура f = 1 МГц, значение образцового конденсатора C0 = 1 нФ, а добротность контура Q = 100.
9. Определить тангенс диэлектрических потерь конденсатора и погрешность его определения, если Cобр1 = 1,5 нФ, Cобр2 = 1 нФ, Q1 = 50, Q2 = 30. Погрешность измерения добротности составляет σQ1 = 0,5 %, σQ2 = 0,7 %.
10. Определить погрешность измерения частоты косвенным методом, если погрешности измерения индуктивности и емкости равны σL = 0,5 %,
σC = 0,2 %.
11. При двукратных измерениях исследуемой катушки на частотах f1 = 1 МГц и f2 = 1,5 МГц, значения образцовых конденсаторов Cобр1=1нФ, Cобр2 = 0,1 нФ. Определить собственную емкость и индуктивность катушки.
12. Определить сопротивление резистора, измеряемого методом преобразования его во временный интервал, если число импульсов, подсчитанных счетчиком, N = 20, период следования импульсов Tк= 0,1 мкс, образцовый конденсатор С = 0,1 нФ.
13. Определить добротность контура, измеряемую косвенным методом, если относительный уровень A = 0,707, резонансная частота f0 = 1 МГц, полоса пропускания Df = 10 МГц.
14. Определить добротность контура, измеряемую цифровым куметром, если логарифмический декремент затухания q = 1000 рад/с, а время измерения tx= 1 мкс.
15. В момент t = 0 в колебательном контуре возникают затухающие колебания по закону u(t) = 10e-50tcos(2p · 106t). Определить момент времени tx, когда значение огибающей данного колебания будет равно амплитуде постоянного напряжения u2 = 10e—p, подаваемого на вход устройства сравнения.
ИЗМЕРЕНИЕ ПАРАМЕТРОВ ЦЕПЕЙ СВЧ.
ПОГРЕШНОСТЬ ИЗМЕРЕНИЯ
Примеры решения типовых задач
1. Определить длину основной волны в прямоугольном волноводе, если длина волны в свободном пространстве l0 = 3 см, а
Решение.
2. Определить входное сопротивление короткозамкнутой линии передачи с волновым сопротивлением 50 Ом длиной 10 см на частоте 3 ГГц.
Решение.
3. Волновое сопротивление тракта Zв = 50 Ом. Длина волны в волноводе
lв = 40 мм. Смещение ближайшего минимума Dl = 18 мм. Коэффициент бегущей волны КБВ = 0,5. Определить сопротивление нагрузки.
Решение.
По круговой диаграмме сопротивлений, соединив точку прямой с центром диаграммы, получаем точку А в месте пересечения с КБВ = 0,5.
По диаграмме определяем в точке значение R/Zв = 0,55 и X/Zв= 0,24
Определяем сопротивление нагрузки
Задачи
1. Определить волновое сопротивление коаксиальной линии, у которой D/d = 3,6, а диэлектрическая проницаемость диэлектрика e = 2,2.
2. Значения lв, Dl, КБВ измерены с помощью измерительной линии. Определить Zн/Zв, если lв = 4 см, Dl = 0,04 см, КБВ = 0,5.
3. Определить сопротивление нагрузки, если Zв = 50 Ом, КСВ = 1,2, длина волны в линии передачи l = 4 см, смещение ближайшего минимума Dl = 0,4 см.
4. Оценить погрешность измерения сопротивления нагрузки примера 3, если погрешность измерения КСВ составляет sКСВ = 0,5 %, погрешность измерения длины волны sl = 0,7 % и погрешность измерения смещения составляет sсм = 0,3 %.
5. Определить входное сопротивление разомкнутой линии передачи длиной 5 см с волновым сопротивлением 50 Ом на частотах f = 3 ГГц; 5 ГГц; 10 ГГц.
6. КБВ в линии передачи равен 0,6. Определить коэффициент отражения.
7. Определить волновое сопротивление линии передачи с параметрами:
R = 5 Ом, L = 5 мкГн, G = 0,5 См, C = 5 нФ на частоте f = 10 ГГц. Оценить погрешность измерения, если пренебречь величинами R и G.
8. Показания индикатора в минимуме и максимуме напряженности поля равны соответственно Amin = 1,5; Amax = 5. Определить КБВ в линии передачи при квадратичной характеристике детектора.
9. Волновое сопротивление линии передачи Zв = 50 Ом. Определить коэффициент отражения от нагрузки Zн = 30 Ом; 100 Ом; 150 Ом.
10. Значения напряженности поля падающей и отраженной волн равны
Eпад= 0,5 В; Eотр = 0,3 В. Определить КБВ в линии передачи.
11. Определить входное сопротивление линии передачи, если Zв = 50 Ом,
l = 3 см, l = 7,5 см, а Zн = 100 Ом; (50 + j20) Ом; (100 – j10) Ом.
12. Определить волновое сопротивление l/4-трансформатора, если
Zв1 = 50 Ом, а Zв2 = 100 Ом.
13. Определить коэффициент распространения в прямоугольном медном волноводе на основной волне H10 на l0 = 3 см.
14. Определить коэффициент распространения в круглом медном волноводе на основной волне H11 на l0 = 3 см.
15. Определить сопротивление Zн, если волновое сопротивление линии передачи Zв = 50 Ом; КСВ = 1,5; x = 5 см, Dl = 0,08 см.
ЭКЗАМЕНАЦИОННЫЕ ВОПРОСЫ
1. Понятие об измерении. Основные элементы процесса измерения.
2. Классификация измерений. Особенности электрорадиоизмерений.
3. Классификация погрешностей.
4. Оценивание и способы уменьшения случайных погрешностей.
5. Способы оценивания и исключение систематических ошибок.
6. Формы представления результатов измерения и показатели точности.
7. Классификация средств измерения.
8. Классификация методов измерения.
9. Обобщенные структурные схемы измерительных приборов.
10. Общие сведения и классификация аналоговых приборов.
11. Обобщенная структурная схема цифрового измерительного прибора.
12. Общие методы повышения точности средств измерений.
13. Нормирование метрологических характеристик средств измерений.
14. Аналоговые электромеханические измерительные преобразователи и приборы.
15. Магнитоэлектрические измерительные механизмы.
16. Электродинамические приборы.
17. Электромагнитные приборы.
18. Электростатические приборы.
19. Логометры.
20. Термоэлектрические приборы.
21. Выпрямительные приборы. Измерение тока.
22. Пиковые детекторы. Параметры переменного напряжения.
23. Детектор среднеквадратического значения.
24. Детектор средневыпрямленного значения.
25. Аналого-цифровые преобразователи.
26. Цифро-аналоговые преобразователи.
27. Цифровые отсчетные устройства.
28. Общие замечания об измерении тока и напряжения. Классификация вольтметров.
29. Структурные схемы и принцип действия электронных вольтметров.
30. Цифровые вольтметры.
31. Измерение постоянных напряжений.
32. Измерение переменных напряжений.
33. Вольтметры среднеквадратических значений.
34. Вольтметры средневыпрямленных значений.
35. Специальные типы вольтметров.
36. Измерение мощности в цепях постоянного тока.
37. Измерение мощности в цепях переменного тока.
38. Измерение мощности на высоких и сверхвысоких частотах.
39. Измерение мощности с помощью терморезисторов.
40. Калориметрический метод измерения мощности.
41. Пондемоторный метод измерения мощности.
42. Измерение проходящей мощности.
43. Метод измерения мощности, основанный на эффекте Холла.
44. Метод измерения мощности, использующий неоднородный разогрев носителей зарядов в полупроводниках.
45. Измерение импульсной мощности.
46. Измерение частоты. Метод дискретного счета.
47. Гетеродинный метод измерения частоты.
48. Резонансный метод. Метод заряда и разряда конденсатора.
49. Измерение фазового сдвига.
50. Цифровые фазометры.
51. Осциллографы. Структурная схема.
52. Виды осциллографических разверток.
53. Основные узлы электронно-лучевого осциллографа.
54. Скоростные и запоминающие осциллографы.
55. Анализ частотного спектра.
56. Измерение нелинейных искажений.
57. Измерение коэффициента амплитудной модуляции.
58. Измерение параметров сигнала с угловой модуляцией.
59. Измерение вероятностных характеристик случайных процессов.
60. Измерение корреляционных функций.
61. Резонансные методы измерения параметров линейных компонентов.
62. Измерение параметров линейных компонентов методами дискретного счета.
63. Измерение параметров транзисторов.
64. Измерение амплитудно-частотных характеристик.
65. Измерительные генераторы.
66. Измерение параметров цепей с распределенными постоянными.
67. Автоматизация радиоэлектронных измерений.
68. Автоматизация процессов управления в осциллографе.
69. Цифровые осциллографы.
70. Автоматизированный анализатор спектра.
71. Интерфейс RS-232C.
72. Отечественная стандартизация.
73. Методы стандартизации.
СЛОВАРЬ НОВЫХ ТЕРМИНОВ
Аналогово-цифровой преобразователь – измерительный преобразователь, в котором непрерывная измеряемая величина автоматически преобразуется в дискретную и подвергается цифровому кодированию.
Аналоговый измерительный прибор – прибор, показания которого являются непрерывной функцией измеряемой величины.
Болометр – металлический терморезистор, обладающий свойством сильно изменять свое сопротивление при изменении температуры.
Времяимпульсный метод – метод, заключающийся в предварительном линейном преобразовании значения измеряемой величины во временной интервал с последующим непосредственным кодированием временного интервала.
Девиация частоты – амплитуда отклонения частоты несущей.
Динамическая погрешность – погрешность, возникающая при переменной во времени измеряемой величине.
Жидкокристаллический индикатор – индикатор, который модулирует внешний световой поток под действием электрического поля или тока.
Измерение – нахождение значения физической величины опытным путем с помощью специальных технических средств – средств измерений.
Измерительная линия – вспомогательная линия передачи для измерения параметров СВЧ-цепей.
Измерительная система – совокупность средств измерений (мер, измерительных преобразователей, измерительных приборов) и вспомогательных устройств, соединенных между собой каналами связи, предназначенная для выработки сигналов измерительной информации в форме, удобной для автоматической обработки, передачи или использования в автоматических системах управления.
Измерительная установка – совокупность средств измерений (мер, измерительных преобразователей, измерительных приборов) и вспомогательных устройств, предназначенная для выработки сигналов измерительной информации в форме, удобной для непосредственного восприятия наблюдателем и расположенная в одном месте.
Измерительный преобразователь – средство измерений, предназначенное для выработки сигнала измерительной информации в форме, удобной для передачи, дальнейшего преобразования, обработки или хранения, но не поддающейся непосредственному восприятию наблюдателем.
Измерительный прибор – средство измерения, предназначенное для выработки сигнала измерительной информации в форме, доступной для непосредственного восприятия наблюдателем.
Инструментальная погрешность – погрешность из-за несовершенства средств измерения, их схемы, конструкции, состояния в процессе эксплуатации.
Калибратор – мера, с помощью которой градуируют или проверяют градуировочные характеристики осей (шкал) экрана осциллографа.
Калориметрический метод – метод измерения мощности СВЧ-сигнала, заключающийся в определении количества тепла, которое выделяется при рассеивании электромагнитной энергии.
Коррелометр– прибор для измерения корреляционных функций сигналов.
Косвенные измерения – измерения, при которых искомое значение величины находят на основании известной математической зависимости между этой величиной и величиной-аргументом, полученными при прямых измерениях.
Коэффициент амплитудной модуляции – отношение максимального отклонения напряжения к среднему значению напряжения.
Логометр – прибор, предназначенный для измерения отношения двух величин.
Мера – средство измерений, которое служит для воспроизведения физической величины заданного размера.
Метод измерений – совокупность приемов использования принципов и средств измерений обеспечивающая сравнение измеряемой величины с единицей.
Метод поразрядного уравновешивания – метод, состоящий в поочередном сравнении измеряемой величины с суммой образцовых дискретных величин, изменяющихся по определенному закону.
Метрология – наука об измерениях.
Объект измерения – физическая величина, которая подлежит измерению.
Пиковый детектор – измерительный преобразователь, на выходе которого постоянная составляющая непосредственно соответствует пиковому значению напряжения на входе.
Пиксел – минимальный дискретный элемент цифрового изображения на экране дисплея.
Погрешность – отклонение результата измерения от истинного значения измеряемой величины.
Пондемоторный метод – метод измерения мощности СВЧ-сигналов, основанный на использовании механического действия электромагнитного поля.
Принцип измерений – совокупность физических явлений, на которых основаны измерения.
Прямые измерения – измерения, при которых искомое значение величины у находят непосредственно из опытных данных.
Систематическая погрешность – составляющая погрешности измерения, которая остается постоянной или закономерно изменяется при повторных измерениях одной и той же величины в одних и тех же условиях.
Случайная погрешность – составляющая погрешности измерения, которая при повторных измерениях в одних и тех же условиях изменяется случайным образом.
Совместные измерения – производимые одновременно измерения двух или нескольких неодноименных величин для нахождения зависимости между ними.
Совокупные измерения – производимые одновременно измерения нескольких одноименных величин, при которых искомые значения величин находят решением систем уравнений, получаемых при прямых измерениях различных сочетаний этих величин.
Спейсеры – зазорозадающие распорные элементы в жидкокристаллических индикаторах.
Средства измерений – технические средства, используемые для целей измерений и имеющие нормированную точность.
Статическая погрешность – погрешность, возникающая при неизменной во времени измеряемой величине.
Термопара – слой, состоящий из двух разнородных проводников.
Устройство сравнения – средство измерения, предназначенное для осуществления сравнения измеряемой величины с мерой.
Цифро-аналоговый преобразователь – преобразователь двоичного кода в аналоговый сигнал.
Частотно-импульсный метод – метод, основанный на преобразовании значения измеряемой величины в пропорциональное значение частоты с последующим преобразованием в код.
Эталоны единиц – средства измерений, обеспечивающие воспроизведение и хранение единицы с целью передачи ее размера нижестоящим по поверочной схеме средствам измерений, выполняемые по особой спецификации и официально утвержденные в установленном порядке в качестве эталона.
ЛИТЕРАТУРА
1. Архипенко А.Г., Белошицкий А.П., Ляльков С.В. Метрология, стандартизация и сертификация: Учеб. пособие. В 3 ч. – Мн.: БГУИР, 1997.
2. Архипенко А.Г. Основы метрологии и измерительная техника: Тексты лекций. В 2 ч. – Мн.: МРТИ, 1989.
3. Белошицкий А.П. и др. Метрология и измерения: Учеб.-метод. пособие для индивидуальной работы студ. / Под общ. ред. С.В. Лялькова. – Мн.: БГУИР, 1999.
4. Винокуров В.И., Капкин С.И., Петилин И.Г. Электрорадиоизмерения: Учеб. пособие для радиотехнических спец. вузов / Под ред. В.И. Винокурова. 2-е изд. – М.: Высш. шк., 1986.
5. Верник С.М., Кушнир Ф.В., Рудницкий В.Б. Повышение точности измерения в технике связи. – М.: Радио и связь, 1981.
6. Горлач А.А., Минц М.Я., Чинков В.Н. Цифровая обработка сигналов в измерительной технике. – Киев: Техника, 1985.
7. Грановский В.А., Сирая Т.М. Методы обработки экспериментальных данных при экспериментах. – Л.: Энергоатомиздат, 1990.
8. Гутников В.С. Интегральная электроника в измерительных устройствах. – Л.: Энергоатомиздат, 1988.
9. Кукуш В.Д. Электрорадиоизмерения. – М.: Радио и связь, 1985.
10. Моисеев Ю.Г., Хромой Б.П. Электрорадиоизмерения. – М.: Радио и связь, 1985.
11. Малиновский В.П. Электрические измерения. – М.: Энергоатомиздат, 1985.
12. Новицкий П.В., Зограф И.А. Оценка погрешности результатов измерений. – Л.: Энергоатомиздат, 1985.
13. Основы метрологии и электрические измерения: Учеб. для вузов / Под ред. Е.М. Душина. – Л.: Энергоатомиздат, 1987.
14. Самарин А.В. Жидкокристаллические дисплеи. – М.: Солон-Р, 2002.
15. Сапаров В.Е. Системы стандартов и электросвязи в радиоэлектронике: Учеб. пособие для институтов. – М.: Радио и связь, 1985.
16. Татур Т.А. Основы теории электромагнитного поля. – М.: Высш. шк., 1989.
17. Телор Дж. Введение в теорию ошибок: Пер. с англ. – М.: Мир, 1985.
18. Цифровая осциллография / Под ред. А.М. Беркутова и Е.М. Прошина. – М.: Энергоатомиздат, 1987.
19. Закон Республики Беларусь «Об обеспечении единства измерений».
20. Закон Республики Беларусь «О стандартизации».
Учебное издание
МЕТРОЛОГИЯ И РАДИОИЗМЕРЕНИЯ
УЧЕБНО-МЕТОДИЧЕСКИЙ КОМПЛЕКС
для студентов специальности 1-39 01 01
«Радиотехника»
Составитель
ЯНУШКЕВИЧ Виктор Францевич
Редактор Г.А. Тарасова
Дизайн обложки И.С. Васильевой
| Подписано в печать 9.09.05. Формат 60х84 1/16. Гарнитура Таймс. Бумага офисная. Отпечатано на ризографе. Усл. печ. л. 17,64. Уч.-изд. л. 18,76. Тираж 60. Заказ 849. |
Издатель и полиграфическое исполнение:
Учреждение образования «Полоцкий государственный университет»
ЛИ № 02330/0133020 от 30.04.04 ЛП № 02330/0133128 от 27.05.04
211440 г. Новополоцк, ул. Блохина, 29
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
zdamsam.ru
Задачи по метрологии Задача 11
Выбор измерительных средств для контроля размеров
Условие. Выбрать универсальные измерительные средства для размеров отверстия и вала, указанных в задаче 1 (табл. 1.1) или полученных в задачах 2 или 3 (в зависимости от задания по гладким цилиндрическим соединениям).
Указания к решению
Для выбора средств и методов измерений линейных размеров от 1 до 500 мм при приемке изделий ГОСТ 8.051-81 устанавливает допускаемые погрешности измерений () в зависимости от допуска на изготовление изделия IT по квалитету и номинальному измеряемому размеру (табл. 11.1). Погрешности измерения являются наибольшими погрешностями измерений, включающими в себя все составляющие, зависящие от измерительных средств, установочных мер, температурных деформаций, базирования и т.д.
При допусках на изготовление, не соответствующих значениям, указанным в табл. 11.1, допускаемая погрешность выбирается по ближайшему меньшему значению допуска для соответствующего размера.
Существует связь между относительной погрешностью измерения
Амет() = мет/ IT (где мет – среднее квадратичное отклонение погрешности измерения), количеством m принятия бракованных деталей в качестве годных, количеством n неправильно забракованных деталей и вероятным предельным значением С выхода размера за каждую границу поля допуска у неправильно принятых деталей.
Предельные значения m, n и С приведены в табл. 11.2.
При определении параметров m, n и С рекомендуется принимать для квалитетов 2-7 Амет () = 0,16; для квалитетов 8-9 Амет () = 0,12; для квалитетов 10 и грубее Амет () = 0,1.
В случае отсутствия измерительного средства с требуемой погрешностью измерения СИ назначают приемочные границы путем смещения их внутрь допуска на деталь на величину С.
Предельное значение С можно рассчитать по формуле С = Сдоп — Спр,
где Сдоп – допустимое значение С, определяемое по табл. 11.2 в зависимости от допуска на изготовление IT;
Спр – принятое значение С, определяемое по тому допуску IT, который по табл. 11.1 соответствует погрешности измерения СИ выбранного измерительного средства.
Результаты выбора измерительного средства заносятся в табл. 11.3.
Справочные данные для выбора измерительных средств приведены в табл. 11.4.
Таблица 11.1
Допускаемые погрешности измерений для линейных размеров (гост 8.051-81, ст сэв 303-76)
Номинальные размеры, мм | К в а л и т е т ы | |||||||||||||
2 | 3 | 4 | 5 | 6 | 7 | 8 | ||||||||
м к м | ||||||||||||||
1Т | | 1Т | | 1Т | | 1Т | | 1Т | | 1Т | | 1Т | | |
До 3 | 1,2 | 0,4 | 2,0 | 0,8 | 3 | 1,0 | 4 | 1,4 | 6 | 1,8 | 10 | 3,0 | 11 | 3,0 |
Св. 3 до 6 | 1,5 | 0,6 | 2,5 | 1,0 | 4 | 1,4 | 5 | 1,6 | 8 | 2,0 | 12 | 3,0 | 18 | 4,0 |
Св.6 до 10 | 1,5 | 0,6 | 2,5 | 1,0 | 4 | 1,4 | 6 | 2,0 | 9 | 2,0 | 15 | 4,0 | 22 | 5,0 |
Св.10 до 18 | 2,0 | 0,8 | 3,0 | 1,2 | 5 | 1,6 | 8 | 2,8 | 11 | 3,0 | 18 | 5,0 | 27 | 7,0 |
Св.18 до 30 | 2,5 | 1,0 | 4,0 | 1,4 | 6 | 2,0 | 9 | 3,0 | 13 | 4,0 | 21 | 6,0 | 38 | 8,0 |
Св.30 до 50 | 2,5 | 1,0 | 4,0 | 1,4 | 7 | 2,4 | 11 | 4,0 | 16 | 5,0 | 25 | 7,0 | 39 | 10,0 |
Св.50 до 80 | 3,0 | 1,2 | 5,0 | 1,8 | 8 | 2,8 | 13 | 4,0 | 19 | 5,0 | 30 | 9,0 | 46 | 12,0 |
Св.80 до 120 | 4,0 | 1,6 | 6,0 | 2,0 | 10 | 3,0 | 15 | 5,0 | 22 | 6,0 | 35 | 10,0 | 54 | 12,0 |
Св.120 до 180 | 5,0 | 2,0 | 8,0 | 2,8 | 12 | 4,0 | 18 | 6,0 | 25 | 7,0 | 40 | 12,0 | 63 | 16,0 |
Св.180 до 250 | 7,0 | 2,8 | 10,0 | 4,0 | 14 | 5,0 | 20 | 7,0 | 29 | 8,0 | 46 | 12,0 | 72 | 18,0 |
Св.250 до 315 | 8,0 | 3,0 | 12,0 | 4,0 | 16 | 5,0 | 23 | 8,0 | 32 | 10,0 | 52 | 14,0 | 81 | 20,0 |
Св.315 до 400 | 9,0 | 3,0 | 13,0 | 5,0 | 18 | 6,0 | 25 | 9,0 | 36 | 10,0 | 57 | 16,0 | 89 | 24,0 |
Св.400 до 500 | 10,0 | 4,0 | 15,0 | 5,0 | 20 | 6,0 | 27 | 9,0 | 40 | 12,0 | 63 | 18,0 | 97 | 26,0 |
Окончание табл. 11.1
Номинальные размеры, мм | К в а л и т е т ы | |||||||||||||||||
9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | ||||||||||
м к м | ||||||||||||||||||
1Т | | 1Т | | 1Т | | 1Т | | 1Т | | 1Т | | 1Т | | 1Т | | 1Т | | |
До 3 | 25 | 6 | 40 | 8 | 60 | 12 | 100 | 20 | 140 | 30 | 250 | 50 | 400 | 80 | 600 | 120 | 1000 | 200 |
Св. 3 до 6 | 30 | 8 | 48 | 10 | 75 | 16 | 120 | 30 | 180 | 40 | 300 | 60 | 480 | 100 | 750 | 160 | 1200 | 240 |
Св.6 до 10 | 36 | 9 | 58 | 12 | 90 | 18 | 150 | 30 | 220 | 50 | 360 | 80 | 580 | 120 | 900 | 200 | 1500 | 300 |
Св.10 до 18 | 43 | 10 | 70 | 14 | 110 | 30 | 180 | 40 | 270 | 60 | 430 | 90 | 700 | 140 | 1100 | 240 | 1800 | 380 |
Св.18 до 30 | 52 | 12 | 84 | 18 | 130 | 30 | 210 | 50 | 330 | 70 | 520 | 120 | 840 | 180 | 1300 | 280 | 2100 | 440 |
Св.30 до 50 | 62 | 16 | 100 | 20 | 160 | 40 | 250 | 50 | 390 | 80 | 620 | 140 | 1000 | 200 | 1600 | 320 | 2500 | 500 |
Св.50 до 80 | 74 | 18 | 120 | 30 | 190 | 40 | 300 | 60 | 460 | 100 | 740 | 160 | 1200 | 240 | 1900 | 400 | 3000 | 600 |
Св.80 до 120 | 87 | 20 | 140 | 30 | 220 | 50 | 350 | 70 | 540 | 120 | 870 | 180 | 1400 | 280 | 2200 | 440 | 3500 | 700 |
Св.120 до 180 | 100 | 30 | 160 | 40 | 250 | 50 | 400 | 80 | 630 | 140 | 1000 | 200 | 1600 | 320 | 2500 | 500 | 4000 | 800 |
Св.180 до 250 | 115 | 30 | 185 | 40 | 290 | 60 | 400 | 100 | 720 | 160 | 1150 | 240 | 1850 | 380 | 2900 | 600 | 4600 | 1000 |
Св.250 до 315 | 130 | 30 | 210 | 50 | 320 | 70 | 520 | 120 | 810 | 180 | 1300 | 260 | 2100 | 440 | 3200 | 700 | 5200 | 1100 |
Св.315 до 400 | 140 | 40 | 230 | 50 | 360 | 80 | 570 | 120 | 890 | 180 | 1400 | 280 | 2300 | 460 | 3600 | 800 | 5700 | 1200 |
Св.400 до 500 | 155 | 40 | 250 | 50 | 400 | 80 | 630 | 140 | 970 | 200 | 1550 | 320 | 2500 | 500 | 4000 | 800 | 6300 | 1400 |
Примечание. Разрешается увеличение допускаемой погрешности измерения при уменьшении размера, учитывающего это увеличение, а также в случае разделения на размерные группы для селективной сборки.
Таблица 11.2
Амет () | m | n | C/IT | Амет () | m | n | C/IT |
% | % | ||||||
1,6 3,0 5,0 8,0 | 0,37 — 0,39 0,87 — 0,90 1,60 — 1,70 2,60 — 2,80 | 0,70 — 0,75 1,20 — 1,30 2,00 — 2,25 3,40 — 3,70 | 0,01 0,03 0,06 0,10 | 10,0 12,0 16,0 | 3,10 — 3,50 3,75 — 4,11 5,00 — 5,40 | 4,50 — 4,75 5,40 — 5,80 7,80 — 8,25 | 0,14 0,17 0,25 |
Примечание. Первые значенияmиnсоответствуют закону нормального распределения погрешности измерения, вторые – закону равной вероятности. При неизвестном законе распределения погрешности измерения значенияmиnможно определять как среднее из приведенных значений.
Пример. Выбрать универсальные измерительные средства для измерения диаметра отверстия 100Н8, диаметра вала 100f7 и длины вала l = 80 мм по среднему классу точности.
studfiles.net
