обозначение знака и способы набора на клавиатуре
Корнем называют не только часть растения, но и математический элемент. По умолчанию он предназначен для расчётов и вычисления именно квадратного корня, то есть числа в степени одна вторая. У этого математического элемента есть и другое название – радикал, произошедшее, вероятно, от латинского слова radix. Поэтому в некоторых случаях радикал обозначается буквой r.
Что такое корень и его назначение
В общих чертах его знак похож на латинскую букву V, с тем лишь отличием, что правая часть длиннее левой. Связано это с тем, что справа пишется число большее, чем левое. И как было сказано выше – левое часто не пишут (если речь идет о квадратном корне).
- Пример 1. √16 = 4. Полная запись выглядела бы так: 2√16 = 4. Как видно из примера, двойка по умолчанию не пишется. Она обозначает то, сколько раз число 4 было умножено на само себя. Иными словами – 4, умноженное на 4 равняется числу 16.
- Пример 2. 3√8 = 2. Тут уже вычисляется кубический корень (третьей степени). Число 8 получается из умножения числа 2 на само себя три раза – 2*2*2 = 8.
Немного истории
Современное обозначение извлечения квадратного корня из восьми, где восьмёрка находится под правым «крылышком» корня (знака), раньше имело бы выражение вида r8 с чёрточкой над восьмёркой. Но это было не всегда удобно по ряду причин.
Изменить выражение на современный лад впервые предложил в 1525 году авторитетный немецкий математик Кристоф Рудольф. Этот человек внёс большой вклад в развитие алгебры в целом, излагая сложные математические формулы доступным и ясным языком. Его труд примечателен еще и тем, что изобилует доступными и наглядными примерами. Поэтому даже спустя два века на его работу ссылаются многие учебники.
 На данный момент в типографике знак корня почти не отличается в разных странах, так как вариант Рудольфа пришёлся по вкусу большинству.
На данный момент в типографике знак корня почти не отличается в разных странах, так как вариант Рудольфа пришёлся по вкусу большинству.
Применение
Разумный вопрос, который рано или поздно возникает у человека, только начавшего изучать математику – зачем вообще нужен квадратный корень? Конечно, он, может, никогда и не пригодится уборщице тёте Люсе или дворнику дяде Васе, но для более образованного человека квадратный корень всё же нужен.
Начнём с того, что квадратный корень нужен для вычисления диагонали прямоугольника. Ну и что с того? – спросят многие. А с того, что это нужно для качественного ремонта, чтобы правильно и аккуратно разложить линолеум, сделать навесной потолок и для проведения многих других работ в сфере строительства.
Ведь дома и квартиры строят люди, вещи и материалы для ремонта изготавливают люди, либо машины, которыми управляют опять-таки люди. А человеку свойственно ошибаться. Поэтому вычисление квадратного корня может существенно сэкономить нервы и деньги при ремонте какого-либо помещения.
Квадратный корень также необходим физикам, математикам, программистам и другим профессионалам, чья профессия связана с вычислениями и наукой. Без подобных знаний наука стояла бы на месте. Однако даже простому человеку никогда не помешают базовые знания о корне. Ведь эти знания развивают мозг, заставляют его работать, образуя новые нейронные связи. Чем больше знаний в голове – тем больше человек запомнит.
Как набирать
Знак корня на клавиатуре
В электронном виде этот символ может понадобиться как студентам, учителям, научным деятелям. Связано это может быть с докладом, проектом, рефератом и так далее. В стандартной раскладке клавиатуры нет символа квадратного корня, так как он не является популярным или часто используемым. Но его можно набрать и другими способами.
Самые распространённые программы для работы с документами – это пакет MS Office, в частности, Microsoft Word. Набрать квадратный корень в этой программе можно несколькими способами, которые по аналогии могут подойти и к другим программам, с небольшими различиями в интерфейсе.
Способы набора символа в Ворде
Можно использовать следующие варианты:
- При помощи набора специального кода. В самом низу клавиатуры находится клавиша с названием Alt. Этих клавиш две, подойдёт любая из них. В правой части клавиатуры есть цифры, над которыми находится клавиша Num Lock. Эту клавишу нужно предварительно нажать, чтобы активировать цифры, находящиеся под ней. Затем зажимаем клавишу Alt и не отпуская клавишу, набираем: 251. После этого на экране появится нужный значок.
- Ещё один способ связан с меню «вставка-символ». После того как будет найден нужный знак, его можно будет повторять, как ранее использованный. Его код в меню поиска — 221A, (латинская буква). Предварительно лучше включить Юникод.
- Самый «красивый» символ набирается с помощью компонента Microsoft Equation 3.0. Для этого надо зайти в «вставка-объект-Microsoft Equation 3.0», после чего найти там нужный знак и использовать его. При этом методе знак смотрится лучше всего, так как тут он отображается правильно с типографической и математической точки зрения.
liveposts.ru
О знаке квадратного корня. Историческая справка репетитора по математике
Ззнак квадратного корня знаком всем. Его используют школьники и студенты, преподаватели и репетиторы по математике, доктора наук и академики. Однако не все знают, что современная форма и появилась не сразу. Эволюция знака радикала длилась почти пять веков, начиная с в далекого XIII в., когда итальянские и некоторые европейские математики впервые называли квадратный корень латинским словом Radix (корень) или сокращенно R.
В XV в. Н.Шюке писал вместо . Современный знак корня произошел от обозначения, применяемого немецкими математиками XV-XVI вв., называвшие алгебру — наукой «Косс», а математиков -алгебраистов «коссистами». (Математики XII-XV вв. писали все свои труды исключительно на латинском языке. Они называли неизвестное — res (вещь). Итальянские математики перевели слово res как cosa. Последний термин заимствовали немцы, от которых и появилось коссисты и косс.)
В XV в. некоторые немецкие коссисты для обозначения квадратного корня пользовались точкой перед выражением или числом. В скорописи эти точки заменялись черточками, а позже они перешли в символ
Один такой знак означал обычный квадратный корень. Если нужно было обозначить корень четвертой степени, то применялся сдвоенный знак знак Для обозначения кубического корня использовали утроенный знак
Комментарий репетитора по математике: остается только гадать, как именно обозначался корень восьмой степени. Если брать аналогию с четвертой степенью, то этот знак должен был отождествлять трехкратное извлечение квадратного корня, то есть для этого нужно было поставить три квадратика. Однако, это обозначение занято кубическим корнем.
Скорее всего, в последствии от таких обозначений как раз и образовался знак V, близкий по записи к знакомому школьникам современному знаку, но без верхней черты. Впервые этот знак был замечен в немецкой алгебре «Красивый и быстрый счет при помощи искусных правил алгебры»:
 Автором этого труда был преподаватель математики из Вены, уроженец Чехии Криштоф Рудольф. Книга пользовалась большим успехом и постоянно переиздавалась на протяжении всего XVI в. и после аж до 1615г. Знаком корня, предложенного Криштофом пользовались А.Жирар, С.Стевин (он писал показатель корня справа от знака радикала в кружке: V (2) или V (3).
Автором этого труда был преподаватель математики из Вены, уроженец Чехии Криштоф Рудольф. Книга пользовалась большим успехом и постоянно переиздавалась на протяжении всего XVI в. и после аж до 1615г. Знаком корня, предложенного Криштофом пользовались А.Жирар, С.Стевин (он писал показатель корня справа от знака радикала в кружке: V (2) или V (3).
В 1626г. нидерландский математик А.Жирар видоизменил знак корня Рудольфа и ввел совсем близкое к современному обозначение Такая форма записи начала вытеснять прежний знак R. Однако некоторое время знак корня писали разрывая верхнюю черту, а именно так: .
И только в 1637 году Рене Декарт соединил горизонтальную черту с галочкой, применив новое обозначение в своей книге «геометрия».
Но и здесь не было точной копии современной формы. Запись Декарта несколько отличалась от той, к который мы с вами привыкли одной деталью. У него было записано: , где буква С, поставленная сразу после радикала, указывала на запись кубического корня. В современном виде это выражение выглядело бы так: .
Самое близкое к современному написанию радикала применял Ньютон в своей «Универсальной арифметике» (1685 г.) Впервые запись корня, полностью совпадающая с сегодняшней, встречается в книге французского математика Ролля «Руководство алгебры», вышедшей в 1690 г. Только через некоторое время после ее написания математики планеты принята, наконец, единую и окончательная форма записи квадратного корня:
Колпаков А.Н. Профессиональный репетитор по математике.
Метки: Алгебра
ankolpakov.ru
Преобразование выражений с корнями (внесение множителя под знак корня)
Тема: Функция . Свойства квадратного корня
Урок: Преобразование выражений с корнями (внесение множителя под знак корня)
Начнем урок с повторения теории.
Определение. Квадратным корнем из неотрицательного числа называется такое неотрицательное число , квадрат которого равен .
.
Из определения следует тождество при .
Пример 1. Вычислите , т. к. .
Пример 2. Решите уравнение
Решение. Уравнение может показаться очевидным и выполненным всегда при всех значениях переменной . Действительно, мы уже знакомы с тождеством, которое представляет собой это уравнение, однако, важно помнить, что оно выполнено при , что и будет являться решением уравнения. Это тот случай, в котором решением уравнения может являться не одно или несколько чисел, как мы привыкли, а целая числовая полуось.
Ответ..
Основные свойства квадратного корня:
а)
б)
в)
Рассмотрим две важнейшие типовые задачи урока, на методе решения которых будет базироваться подход к другим подобным задачам.
Пример 3. Внесите множитель под знак корня: а) , б) .
Решение. Задачи отличаются только знаком выражения, которое является множителем перед корнем, но это принципиальный аспект дальнейшего решения.
а) Внесение положительного множителя под знак корня. Если , то , тогда .
б) Внесение отрицательного множителя под знак корня. Если , то (т. к. ), тогда .
Ответ.
Как видно из приведенного примера, знак вносимого под корень выражения важен, и если он отрицательный, то перед корнем после внесения множителя должен остаться минус, в случае внесения положительного множителя, значение выражения остается положительным.
Когда нам известны два принципиальных подхода к решению задач, можем перейти к различным примерам.
Пример 4. Внесите множитель под знак корня: а) , б) , в) .
Решение. а) Т. к. множитель перед корнем положительный, то .
б) Т. к. множитель перед корнем отрицательный, то .
в) В этой задаче может показаться, что решение имеет различные варианты, т. к. знак выражения перед корнем не известен, но следует заметить, что такое же выражение находится и под знаком корня, т. е. оно неотрицательно по определению квадратного корня (). Имеем вариант для внесения неотрицательного числа .
Ответ.; ; .
Пример 5. Внесите множитель под знак корня и упростите: а) , б) .
Решение. Задачи похожи, однако, отличаются знаками вносимых под корень множителей, подход к решению нам уже известен, применим его.
а) , тогда .
б) , тогда .
Ответ..
Пример 6. Внесите множитель под знак корня и упростите: а) , б) .
Решение. а) По определению квадратного корня , т. к. если произведение трех одинаковых чисел неотрицательно, то и эти числа неотрицательны, тогда вносим под корень неотрицательное число: .
б) По определению квадратного корня , тогда вносим под корень отрицательное число: .
Ответ.; .
На следующем уроке рассмотрим более сложные задачи на преобразования выражений с корнями, в которых нам понадобятся знания обо всех основных свойствах квадратного корня.
Список литературы
1. Башмаков М.И. Алгебра 8 класс. – М.: Просвещение, 2004.
2. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.
3. Никольский С.М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра 8 класс. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2006.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. Старая школа (Источник).
2. Фестиваль педагогических идей «Открытый урок» (Источник).
3. Обучающие курсы (Источник).
Домашнее задание
1. №318, 319, 332, 339, 340, 343. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.
2. Внесите множитель под знак корня: а) , б) , в) .
3. Внесите множитель под знак корня, если известно, что : а) , б) .
4. Расположите в порядке возрастания числа: а) , б) .
interneturok.ru
Правила квадратного корня — Квадратный Корень
Применение операции корня к числам
Квадратный корень из числа — это такое число, квадрат которого (результат умножения на себя) равен , то есть решение уравнения относительно переменной .[1][2] Часто под этим понятием подразумевают более узкое — т. н. арифметический квадратный корень — неотрицательное число.
Рациональные числа
Корень из рационального числа является рациональным числом, только если и (после сокращения общих множителей) являются квадратами натуральных чисел.
Непрерывная дробь корня из рационального числа всегда является периодической (возможно с предпериодом) что позволяет с одной стороны легко вычислять хорошие рациональные приближения к ним с помощью линейных рекуррент, а с другой стороны ограничивает точность приближения: , где зависит от [3][4]. Верно и обратное: любая периодическая цепная дробь является квадратичной иррациональностью.
Действ
www.sites.google.com
Преобразование выражений с корнями (вынесение множителя из-под знака корня)
Тема: Функция . Свойства квадратного корня
Урок: Преобразование выражений с корнями (вынесение множителя из-под знака корня)
Напомним определение квадратного корня:
квадратным корнем из неотрицательного числа называется такое число неотрицательное число , квадрат которого равен : .
Из определения квадратного корня сразу следует следующее тождество:
.
Рассмотрим несколько примеров на вычисление корней: , т. к. ; , т. к. ; , т. к. ; .
Напомним также основные свойства квадратного корня:
1. (). Если и – неотрицательные числа, то корень из их произведения равен произведению корней.
2. (). Если – неотрицательное число, а – положительное число, то корень из их отношения равен отношению корней.
3. ().
Примеры:
1. .
2. .
Докажем теперь ещё одно не менее важное свойство квадратного корня:
, т. е.: .
Доказательство:
Напомним вначале определение модуля: . Примеры: , , .
Рассмотрим два случая:
1. , т. к. – можно пользоваться определением корня квадратного из неотрицательного числа.
2. . В этом случае: . Тогда для числа можем воспользоваться результатами первого случая: .
Утверждение доказано
Естественным обобщением данного свойства является формула:
.
Рассмотрим типовые задачи на применение указанного свойства.
Примеры:
1.
.
2.
.
3.
.
4.
.
Необходимо понимать, что во всех рассмотренных примерах значение корней всегда получается неотрицательным (несмотря на наличие перед некоторыми ответами знака . К примеру, в примере 4 ответ положительный, так как знак выражения , а перед самим выражением стоит ещё один . Как известно, минус на минус даёт плюс.
Решим ещё несколько примеров, в которых фигурируют уже несколько переменных:
5.
( – по условию, – всегда, так как квадрат всегда неотрицательный).
6.
( – по условию, – всегда, так как квадрат всегда неотрицательный).
7.
( – по условию, – так как ).
8.
( – по условию, – так как ).
Итак, мы рассмотрели вынесение множителя из-под знака корня. Мы научились выносить множитель из-под корня с учётом его знака, а также решили несколько примеров.
На следующем уроке мы научимся вносить множитель под знак квадратного корня.
Список литературы
1. Башмаков М.И. Алгебра 8 класс. – М.: Просвещение, 2004.
2. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.
3. Никольский С.М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра 8 класс. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2006.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. Фестиваль педагогических идей «Открытый урок» (Источник).
2. ЕГЭ! Сдам! (Источник).
3. Единая коллекция цифровых образовательных ресурсов (Источник).
Домашнее задание
1. №336-338 Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.
2. Упростить выражение: а) ; б) ; в) ; г) .
3. Упростить выражение: а) , б) , в) .
interneturok.ru
[Билет 33] Корень n-й степени из числа. Алгебраический и арифметический корни. Функция √
Корень n-й степени из числа.Определение корня. Безусловно, все так или иначе знакомы с интуитивным понятием квадратного корня — это такое число, квадрат которого равен a. Аналогично определяется корень n-й степени из числа a, где n — положительное число.
Определение. Корнем n-й степени из числа a называется такое число, n-я степень которого равна a.
Согласно данному определению корень n-й степени из числа а — это решение уравнения xn=a. Число корней этого уравнения зависит от n и от а.
Рассмотрим функцию f(x)=x^n. Как известно, на промежутке [0; ∞) эта функция при любом n возрастает и принимает все значения промежутка [0; inf). По теореме о корне уравнение xn=a для любого а, принадлежащего промежутку [0; ∞), имеет неотрицательный корень и только один. Его называют арифметическим корнем n-й степени из числа n и обозначают n√a Число n называют показателем корня, а само число a — подкоренным выражением. Знак корня √ так же называют радикалом.
Алгебраический и арифметический корни.
Арифметическим корнем n–й степени из неотрицательного числа a называется неотрицательное число, n–я степень которого равна a .
Алгебраическим корнем n–й степени из данного числа называется множество всех корней из этого числа. Алгебраический корень чётной степени имеет два значения: положительное и отрицательное, например:
Функция √
Квадратный корень из числа a — это такое число, квадрат которого (результат умножения на себя) равен a, то есть решение уравнения x2 = aотносительно переменной x
Квадратный корень как элементарная функция
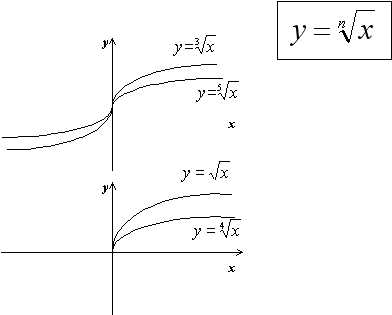
Свойства функции y=3x
Функция y=nx .
Степенная функция с положительным дробным показателем.
Степенная функция с положительным дробным показателем это функция, заданная формулой y = xr, где r — положительная несократимая дробь.
Свойства функции y = xr:
- Область определения — луч [о;+) .
- Функция общего вида, т.е. ни четная, ни нечетная.
- Функция y = xr возрастает на [о;+) .
[о;+) .
Подобный вид имеет любой график функции вида y = xr, где r > 1, а график любой степенной функции y = xr, где 0r y = x2/3.
Степенная функция с отрицательным дробным показателем.
Степенная функция с отрицательным дробным показателем это функция, заданная формулой y = x — r,
где r — положительная несократимая дробь.
- Облать определения — промежуток (о;+) .
- Функция общего вида, т.е. ни четная, ни нечетная.
- Функция y = x — r убывает на (о;+) .
- График функции y = x — r подобен ветке гиперболы, построенной на положительных значениях аргумента функции.
fizmatinf.blogspot.com
Арифметический квадратный корень. Вынесение, внесение множителя под знак корня
Математика->Модуль числа. Корень числа->квадратный корень->Тестирование онлайн
Квадратный корень. Вычисления
Квадратный корень. Вычисления (часть 2)
Квадратный корень. Алгебраические выражения и преобразования
Квадратный корень. Алгебраические выражения и преобразования (часть 2)
Квадратный корень. Алгебраические выражения и преобразования (часть 3)
Тождество
Вынесение множителя из-под знака квадратного корня
Внесение множителя под знак квадратного корня
Значение переменной в выражении с квадратным корнем
Вынесение и внесение множителя (средний уровень)
Алгебраические преобразования с квадратным корнем (выше среднего)
Алгебраические преобразования, вычисление. Повторение (выше среднего)
Арифметический квадратный корень
Обозначение знака квадратного арифметического корня , подразумеваем , но «2» не пишется.
Неотрицательный квадратный корень из числа a называется арифметическим квадратным корнем из числа a. Например,
Выражения не имеют смысла!
Тождество
При любом значении a имеет место равенство
Согласно определению модуля получим
Вынесение и внесения множителя под знак корня
При любом значении a и при любом положительном значении b верно равенство
Обратное равенство имеет вид
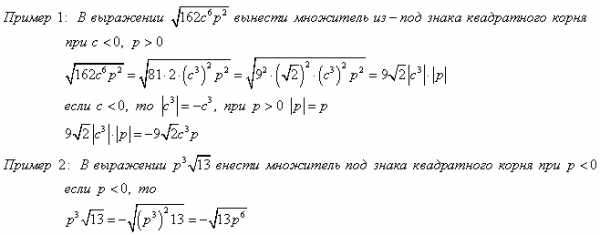
Среднее арифметическое и среднее геометрическое чисел
Средним арифметическим двух чисел a и b называется выражение
Средним геометрическим двух неотрицательных чисел a и b называется выражение
Среднее арифметическое неотрицательных чисел a и b не меньше их среднего геометрического.
Если среднее арифметическое двух неотрицательных чисел равно их среднему геометрическому, то эти числа равны.
fizmat.by