Приведение определителя к треугольному виду
Для того что бы вычислить определитель матрицы четвертого порядка или выше можно разложить определитель по строке или столбцу или применить метод Гаусса и привести определитель к треугольному виду. Рассмотрим приведение определителя матрицы к треугольному виду.
Для того чтобы привести матрицу к треугольному используйте свойства определителя для элементарных преобразований над строками и столбцами. Для нахождения определителя нужно умножить все элементы на главной диагонали.
Пример
Найдем определитель матрицы четвертого порядка.
Сделаем элемент a2,1 равный нулю.
Из строки №2 вычтем строку №1, умноженную на 1 элемент строки №2, т.е. на 3
Сделаем элемент a3,1 равный нулю.
Из строки №3 вычтем строку №1, умноженную на 1 элемент строки №3, т.е. на 8
Сделаем элемент a4,1 равный нулю.
Из строки №4 вычтем строку №1, умноженную на 1 элемент строки №4, т.е. на 6
Сделаем элемент a3,2 равный нулю.
Из строки №3 вычитаем строку №2, умноженную на 5
Сделаем элемент a4,2 равный нулю.
Из строки №4 вычитаем строку №2, умноженную на 2
Сделаем элемент a4,3 равный нулю.
Из строки №4
вычтем строку №3, умноженную на 9/21.Умножим элементы матрицы находящиеся на диагонали.
www.mozgan.ru
теоремы и примеры нахождения определителей
Задание. Вычислить определитель $\Delta=\left| \begin{array}{rrrr}{-2} & {1} & {3} & {2} \\ {3} & {0} & {-1} & {2} \\ {-5} & {2} & {3} & {0} \\ {4} & {-1} & {2} & {-3}\end{array}\right|$ приведением его к треугольному виду.
Решение. Сначала делаем нули в первом столбце под главной диагональю. Все преобразования будет выполнять проще, если элемент $a_{11}$ будет равен 1. Для этого мы поменяем местами первый и второй столбцы определителя, что, согласно свойствам определителя, приведет к тому, что он сменит знак на противоположный:
$$\Delta=\left| \begin{array}{rrrr}{-2} & {1} & {3} & {2} \\ {3} & {0} & {-1} & {2} \\ {-5} & {2} & {3} & {0} \\ {4} & {-1} & {2} & {-3}\end{array}\right|=-\left| \begin{array}{rrrr}{1} & {-2} & {3} & {2} \\ {0} & {3} & {-1} & {2} \\ {2} & {-5} & {3} & {0} \\ {-1} & {4} & {2} & {-3}\end{array}\right|$$
Далее получим нули в первом столбце, кроме элемента $a_{11}$ , для этого из третьей строки вычтем две первых, а к четвертой строке прибавим первую, будем иметь:
$$\Delta=-\left| \begin{array}{rrrr}{1} & {-2} & {3} & {2} \\ {0} & {3} & {-1} & {2} \\ {0} & {-1} & {-3} & {-4} \\ {0} & {2} & {5} & {-1}\end{array}\right|$$
Далее получаем нули во втором столбце на месте элементов, стоящих под главной диагональю. И снова, если диагональный элемент будет равен $\pm 1$ , то вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на противоположный знак определителя):
$$\Delta=\left| \begin{array}{rrrr}{1} & {-2} & {3} & {2} \\ {0} & {-1} & {-3} & {-4} \\ {0} & {3} & {-1} & {2} \\ {0} & {2} & {5} & {-1}\end{array}\right|$$
Далее делаем нули во втором столбце под главной диагональю, для этого поступаем следующим образом: к третьей строке прибавляем три вторых, а к четвертой — две вторых строки, получаем:
$$\Delta=\left| \begin{array}{rrrr}{1} & {-2} & {3} & {2} \\ {0} & {-1} & {-3} & {-4} \\ {0} & {0} & {-10} & {-10} \\ {0} & {0} & {-1} & {-9}\end{array}\right|$$
Далее из третьей строки выносим (-10) за определитель и делаем нули в третьем столбце под главной диагональю, а для этого к последней строке прибавляем третью:
$$\Delta=-10 \left| \begin{array}{rrrr}{1} & {-2} & {3} & {2} \\ {0} & {-1} & {-3} & {-4} \\ {0} & {0} & {1} & {1} \\ {0} & {0} & {-1} & {-9}\end{array}\right|=$$
$$=-10 \cdot \left| \begin{array}{cccc}{1} & {-2} & {3} & {2} \\ {0} & {-1} & {-3} & {-4} \\ {0} & {0} & {1} & {1} \\ {0} & {0} & {0} & {-8}\end{array}\right|=(-10) \cdot 1 \cdot(-1) \cdot 1 \cdot(-8)=-80$$
Ответ. $\Delta=-80$
www.webmath.ru
6. Вычисление определителей
6.1 Приведение матрицы к треугольному виду
Смотрим рис. 16 позиция 1. На нём квадратная матрица четвёртого порядка. Нам надо эту матрицу привести к треугольному виду (рис. 16, позиция 2), потому что определитель
треугольной матрицы равен простому произведению диагональных элементов, и его легко вычислить. Товарищ Белоусов описывал такие матрицы в примерах 4.2
и 4.3 и там же доказал это (утверждение). Я надеюсь, что всем понятно, что такое матрица в треугольном виде. У неё все элементы, расположенные ниже диагональных, равны нулю. Сначала вспомним два правила. Первое: если переставить местами две строки (или столбца)
определителя, то он сохранит абсолютное значение, но поменяет знак на противоположный. Второе: если к элементам строки определителя прибавить
соответствующие элементы другой его строки, умноженные на произвольное число, то определитель не изменится. Итак, начнём. Смотрим на первый столбец первоначальной матрицы. Если бы все его элементы были равны нулю, то всю последущую работу нам не нужно было бы проводить, потому что определитель матрицы с таким столбиком (с одними нулями) равен нулю. Мы это с вами уже проходили. В нашей же матрице нам надо добиться, чтобы первый (верхний) элемент столбика не был равен нулю, а все остальные были равны нулю. Сначала делаем перестановку строк (результат на рис. 16, позиция 3). Я сделал перестановку строк два раза, а не один, чтобы знак определителя не изменился. Далее нам надо добиться, чтобы вместо пятерки на нижней зелёной строке появился нуль. Используем второе правило. (Напоминаю, смотрим позицию 3, первый столбец). Вопрос: на сколько нужно умножить 2, чтобы получившееся произведение прибавить к 5, и в итоге получился нуль? Ответ: -5/2 . Умножаем, прибавляем, и первый столбик приобретает нужный нам вид. Но нам придётся все остальные элементы первой строки тоже умножить на -5/2 и прибавить к соответствующим элементам последней строки. Делаем это и получаем матрицу на рис 16, поз. 4 . Элементы первой строки в дальнейших преобразованиях уже не участвуют. Первый же столбик от дальнейших преобразований не изменится. Вы в этом убедитесь. Далее преобразуем второй столбик. Если бы все его элементы, расположенные ниже первой строки, были равны нулю, то тогда и определитель был бы равен нулю. (Объяснение для крутых математиков: в этом случае два первых столбика оказались бы пропорциональными, и, согласно свойствам определителей,
studfiles.net
Приведение матрицы к треугольному виду
Ниже два калькулятора для приведения матриц к треугольному, или ступенчатому, виду. Первый использует для этого метод Гаусса, второй — метод Барейса. Описание методов и немного теории — под калькуляторами.
Знаков после запятой: 4
Треугольная матрица (метод Гаусса)
Треугольная матрица (метод Гаусса с выбором максимума в столбце)
Треугольная матрица (метод Гаусса с выбором максимума по всей матрице)
Сохранить share extension
3 2 3 4 4 4 3 2 1 4 4 3 2 3 1 1МатрицаТочность вычисленияЗнаков после запятой: 4
Треугольная матрица (метод Барейса)
Треугольная матрица (метод Барейса с выбором максимума в столбце)
Треугольная матрица (метод Барейса с выбором максимума по всей матрице)
Сохранить share extension
Итак, для начала определимся с понятием треугольной, или ступенчатой матрицы:
Матрица имеет ступенчатый вид, если:
- Все нулевые строки матрицы стоят последними
- Первый ненулевой элемент строки всегда находится строго правее первого ненулевого элемента предыдущей строки
- Все элементы столбца под первым ненулевым элементом строки равны нулю (это впрочем следует из первых двух пунктов)
Пример ступенчатой матрицы:
1 0 2 5
0 3 0 0
0 0 0 4
Понятие треугольной матрицы более узкое, оно используется только для квадратных матриц (хотя я думаю, что это не строго), и формулируется проще: треугольная матрица — квадратная матрица, в которой все элементы ниже главной диагонали равны нулю. Строго говоря, это даже определение верхнетреугольной матрицы, но мы будем использовать его. Понятно, что такая верхнетреугольная матрица является также и ступенчатой.
Пример треугольной (верхнетреугольной) матрицы:
1 0 2 5
0 3 1 3
0 0 4 2
0 0 0 3
Кстати, определитель треугольной матрицы вычисляется простым перемножением ее диагональных элементов.
Чем же так интересны ступенчатые (и треугольные) матрицы, что к ним надо приводить все остальные? — спросите вы.
У них есть замечательной свойство, а именно, любую прямоугольную матрицу можно с помощью элементарных преобразований привести к ступенчатой форме.
Что же такое элементарные преобразования? — спросите вы.
Элементарными преобразованиями матрицы называют следующие операции:
- перестановка любых двух строк (столбцов) матрицы
- умножение любой строки (столбца) на призвольное, отличное от нуля, число
- сложение любой строки (столбца) с другой строкой (столбцом), умноженной (умноженным) на произвольное, отличное от нуля, число.
И что? — спросите вы.
А то, что элементарные преобразования матрицы сохраняют эквивалентность матриц. А если вспомнить, что системы линейных алгебраический уравнений (СЛАУ) записывают как раз в матричной форме, то это означает, что элементарные преобразования матрицы не изменяют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица.
Приведя матрицу системы линейных уравнений AX=B к треугольной форме A’X = B’, то есть, с соответствующими преобразованиями столбца B, можно найти решение этой системы так называемым «обратным ходом».
Чтобы было понятно, используем треугольную матрицу выше и перепишем систему уравнений в более привычной форме (столбец B я придумал сам):
Понятно, что сначала мы найдем , потом, подставив его в предыдущее уравнение, найдем и так далее — двигаясь от последнего уравнения к первому. Это и есть обратный ход.
Алгоритм приведения матрицы к ступенчатой форме с помощью элементарных преобразований называют методом Гаусса. Метод Гаусса — классический метод решения систем линейных алгебраических уравнений. Также его еще называют Гауссовым исключением, так как это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к эквивалентной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.
Теперь про сам метод.
Собственно, как можно занулить переменную во втором уравнении? Вычтя из него первое, домноженное на коэффициент
Поясним на примере:
Зануляем во втором уравнении:
Во втором уравнении больше не содержится
Обобщенно алгоритм метода Гаусса можно представить следующим образом:
где N — число строк,
— i-тая строка,
— элемент, находящийся в i-той строке, j-том столбце
И все бы ничего, да и метод отличный, но. Дело все в делении на , присутствующем в формуле. Во-первых, если диагональный элемент будет равен нулю, то метод работать не будет. Во-вторых, в процессе вычисления будет накапливаться погрешность, и чем дальше, тем больше. Результат будет отличаться от точного.
Для уменьшения погрешности используют модификации метода Гаусса, которые основаны на том, что погрешность тем меньше, чем больше знаменатель дроби. Эти модификации — метод Гаусса с выбором максимума в столбце и метод Гаусса с выбором максимума по всей матрице. Как следует из названия, перед каждым шагом исключения переменной по столбцу (всей матрице) ищется элемент с максимальным значением и проводится перестановка строк (строк и столбцов), таким образом, чтобы он оказался на месте .
Но есть еще более радикальная модификация метода Гаусса, которая называется методом Барейса (Bareiss).
Как можно избавиться от деления? Например, умножив перед вычитанием строку на . Тогда вычитать надо будет строку , домноженную только на , без всякого деления.
.
Уже хорошо, но возникает проблема с ростом значений элементов матрицы в ходе вычисления.
Барейс предложил делить выражение выше на и показал, что если исходные элементы матрицы — целые числа, то результатом вычисления такого выражения тоже будет целое число. При этом принимается, что для нулевой строки .
Кстати, то, что в случае целочисленных элементов исходной матрицы алгоритм Барейса приводит к треугольной матрице с целочисленными элементами, то есть без накопления погрешности вычислений — довольно важное свойство с точки зрения машинной арифметики.
Алгоритм Барейса можно представить следующим образом:
Алгоритм, аналогично методу Гаусса, также можно улучшить поиском максимума по столбцу(всей матрице) и перестановкой соответствующих строк (строк и столбцов).
С отличной лекцией на эту тему можно ознакомиться здесь
planetcalc.ru
1. Методы вычисления определителей n – го порядка.
Основываясь на понятиях определителей второго и третьего порядков, можно аналогично ввести понятие определителя порядка n. Определители порядка выше третьего вычисляются, как правило, с использованием свойств определителей, сформулированных в п. 1.3., которые справедливы для определителей любого порядка.
Используя свойство определителей номер 90 введем определение определителя 4-го порядка:
.
Пример 2. Вычислить, используя подходящее разложение.
.
Аналогично вводится понятие определителя 5-го, 6-го и т.д. порядка. Значит определитель порядка n :
.
Все свойства определителей 2-го и 3-го порядков, рассмотренные раннее, справедливы и для определителей n-го порядка.
Рассмотрим основные методы вычисления определителей n-го порядка.
Метод понижения порядка определителя основан на следующем соотношении (i фиксированное число):
 ,
где Аik алгебраические дополнения к
,
где Аik алгебраические дополнения к  (разложение определителя поi-ой
строке). Либо
(разложение определителя поi-ой
строке). Либо  (разложение поj-тому
столбцу).
(разложение поj-тому
столбцу).
Замечание: прежде чем применять этот метод, полезно, используя основные свойства определителей, обратить в нуль все, кроме одного, элементы его некоторой строки или столбца. (Метод эффективного понижения порядка)
Метод приведения к треугольному виду заключается в таком преобразовании определителя, когда все его элементы, лежащие по одну сторону от главной диагонали, становятся равными нулю. В этом случае определитель равен произведению элементов его главной диагонали.
Пример 3. Вычислить, приведением к треугольному виду.
Пример 4. Вычислить, используя метод эффективного понижения порядка
.
Решение: по свойству 40 определителей из первой строки вынесем множитель 10, а затем будем последовательно умножать вторую строку на 2, на 2, на 1 и складывать соответственно с первой, с третьей и четвертой строками (свойство 80).
.
Полученный определитель можно разложить по элементам первого столбца. Он будет сведен к определителю третьего порядка, который вычисляется по правилу Саррюса (треугольника).
Пример 5. Вычислить определитель, приведением к треугольному виду.
.
Пример 3. Вычислить, используя рекуррентные соотношения.
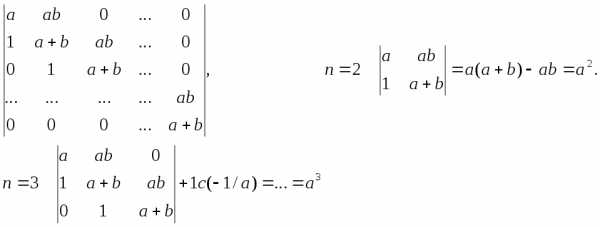 .
.
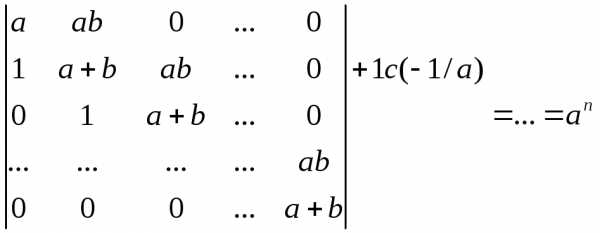 .
.
Лекция 4. Обратная матрица. Ранг матрицы.
1. Понятие обратной матрицы
Определение 1. Квадратная матрица А порядка n называется невырожденной, если ее определитель |A| ≠ 0. В случае, когда |A| = 0, матрица А называется вырожденной.
Только для квадратных невырожденных матриц А вводится понятие обратной матрицы А-1.
Определение 2. Матрица А-1 называется обратной для квадратной невырожденной матрицы А, если А-1А = АА-1 = Е, где Е – единичная матрица порядка n.
Определение 3. Матрица  называетсяприсоединенной, ее элементами являются алгебраические
дополнения
называетсяприсоединенной, ее элементами являются алгебраические
дополнения  транспонированной матрицы
транспонированной матрицы .
.
Алгоритм вычисления обратной матрицы методом присоединенной матрицы.
Находим определитель исходной матрицы. Если определитель равен нулю, то обратной матрицы не существует. Если определитель отличен от нуля, то матрица А невырожденная и обратная матрица существует.
Находим присоединенную матрицу А*, элементы которой являются алгебраическими дополнениями элементов транспонированной матрицы А.

Вычислим обратную матрицу по формуле
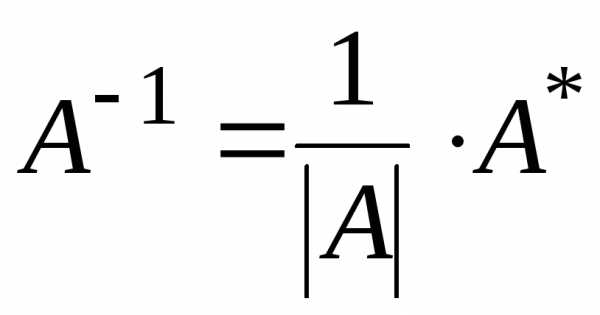 ,
где
,
где  .
.
Проверяем правильность вычисления А-1А = АА-1 = Е. (Е – единичная матрица)
Матрицы А и А-1взаимообратные. Если |A| = 0, то обратная матрица не существует.
Пример
1. Дана
матрица А. Убедиться, что она невырожденная,
и найти обратную матрицу 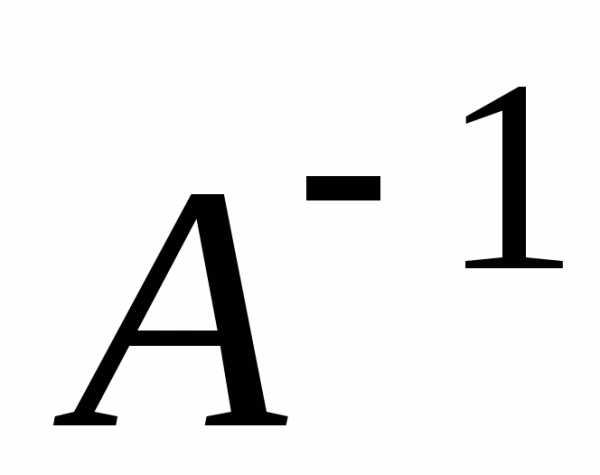 .
.
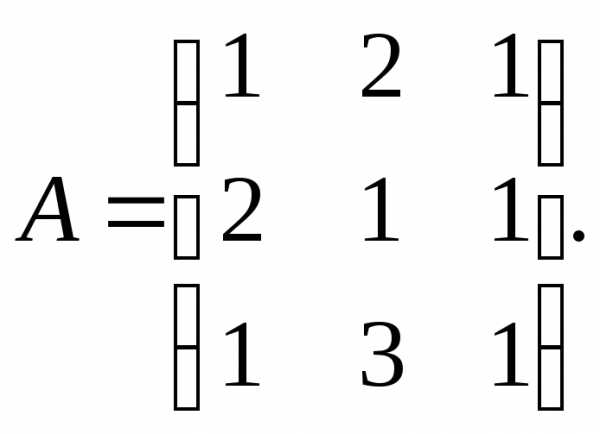
Решение: . Следовательно матрица невырожденная.
Найдем обратную матрицу. Составим алгебраические дополнения элементов матрицы А.
Получаем 
 .
.
studfiles.net
Свойства определителей
1. Определитель не меняется при транспонировании.
2. Если одна из строк определителя состоит из нулей, то определитель равен нулю.
3. Если в определителе переставить две строки, определитель поменяет знак.
4. Определитель, содержащий две одинаковые строки, равен нулю.
5. Если все элементы некоторой строки определителя умножить на некоторое число k, то сам определитель умножится на k.
6. Определитель, содержащий две пропорциональные строки, равен нулю.
7. Если все элементы i-й строки определителя представлены в виде суммы двух слагаемых ai j = bj + cj (j=), то определитель равен сумме определителей, у которых все строки, кроме i-ой, — такие же, как в заданном определителе, а i-я строка в одном из слагаемых состоит из элементов bj, в другом — из элементов cj.
8. Определитель не меняется, если к элементам одной из его строк прибавляются соответствующие элементы другой строки, умноженные на одно и то же число.
Замечание. Все свойства остаются справедливыми, если вместо строк взять столбцы.
Минором Mi j элемента ai j определителя d n-го порядка называется определитель порядка n-1, который получается из d вычеркиванием строки и столбца, содержащих данный элемент.
Алгебраическим дополнением элемента ai j определителя d называется его минор Mi j, взятый со знаком (-1) i + j. Алгебраическое дополнение элемента ai j будем обозначать Ai j. Таким образом, Ai j = (-1) i + j Mi j.
Способы практического вычисления определителей, основанные на том, что определитель порядка n может быть выражен через определители более низких порядков, дает следующая теорема.
Теорема (разложение определителя по строке или столбцу).
Определитель равен сумме произведений всех элементов произвольной его строки (или столбца) на их алгебраические дополнения. Иначе говоря, имеет место разложение d по элементам i-й строки
d = ai 1 Ai 1 + ai 2 Ai 2 +… + ai n Ai n (i= )
или j- го столбца
d = a1 j A1 j + a2 j A2 j +… + anj Anj (j = ).
В частности, если все элементы строки (или столбца), кроме одного, равны нулю, то определитель равен этому элементу, умноженному на его алгебраическое дополнение.
Формула вычисления определителя третьего порядка.
Для облегчения запоминания этой формулы:
Мінори та алгебраїчні доповнення.Минором Mi j элемента ai j определителя d n-гопорядка называется определитель порядка n-1, который получается из d вычеркиванием строки и столбца, содержащих данный элемент.
Алгебраическим дополнением элемента ai j определителя d называется его минор Mi j, взятый со знаком (-1) i + j. Алгебраическое дополнение элемента ai j будем обозначать Ai j. Таким образом, Ai j = (-1) i + j Mi j.
Визначник діагонального, трикутного та ступінчатого виду. Обчислення визначників спеціального виду.
Треугольные матрицы
Определение
Матрица называется верхней треугольной матрицей, если все элементы ниже главной диагонали равны нулю.
Матрица называется нижней треугольной матрицей, если все элементы выше главной диагонали равны нулю.
Замечание. Диагональная матрица — это пример матрицы, которая является одновременно верхне- и нижнетреугольной.
Приведение определителя к треугольному виду.
Некоторые определители удобно вычислять, используя метод приведения к треугольному виду. А, как известно, определитель треугольного вида равен произведению элементов главной диагонали.
.
Решение.Легко увидеть, что в этом определителе сумма элементов каждой строки (столбца) одна и та же. Следовательно, прибавляя все строки определителя к первой, получим
.
Вынесем общий множитель элементов первой строки за знак определителя. Имеем:
.
Из каждой строки, начиная со второй, вычтем первую. Мы получили определитель треугольного вида:
studfiles.net
Видеоурок 5. Вычисление определителя методом приведения матрицы определителя к треугольному виду
Видеокурс высшей математики. Урок 1. Определители 2 и 3 порядков
Урок: 1Видеоурок 2. Вычисление определителя методом разложения по элементам его строки или столбца
Урок: 2Высшая математика 3. Вычисление определителя третьего порядка. Правило треугольников
Урок: 3Видеоурок 4. Вычисление определителя третьего порядка методом присоединения строк (столбцов)
Урок: 4Видеоурок 5. Вычисление определителя методом приведения матрицы определителя к треугольному виду
Урок: 5Видеоурок 6. Решение систем двух линейных уравнений с двумя неизвестными методом Крамера
Урок: 6Видеоурок 7. Решение систем трех линейных уравнений с тремя неизвестными методом Крамера
Урок: 7Видеокурс высшей математики. Урок 8. Примеры решения систем трех линейных уравнений методом Крамера
Урок: 8Видеокурс высшей математики. Урок 9. Алгебраическая форма записи комплексного числа
Урок: 9Видеокурс высшей математики. Урок 10. 1 часть. Тригонометрическая форма записи комплексного числа
Урок: 10Видеокурс высшей математики. Урок 10. 2 часть. Тригонометрическая форма записи комплексного числа
Урок: 11Видеокурс высшей математики. Урок 11. Показательная форма записи комплексного числа
Урок: 12Видеокурс высшей математики. 12. Разложение многочлена на множители
Урок: 13Видеокурс высшей математики. 13. Разложение рациональной дроби на сумму простейших дробей
Урок: 14Высшая математика. 14. Часть 1. Примеры разложения рациональной дроби на сумму простейших дробей
Урок: 15Высшая математика. 14. Часть 2. Примеры разложения рациональной дроби на сумму простейших дробей
Урок: 16Видеокурс высшей математики. Урок 15. Матрицы. Виды матриц
Урок: 17Видеокурс высшей математики. Урок 16. Сложение и вычитание матриц. Умножение матрицы на число
Урок: 18Видеокурс высшей математики. Урок 17. Умножение матриц. Возведение матрицы в степень
Урок: 19Видеокурс высшей математики. Урок 18. Приведение матрицы к ступенчатому виду
Урок: 20Видеокурс высшей математики. Урок 19. Ранг матрицы. Ранг системы векторов
Урок: 21Видеокурс высшей математики. Урок 20. Вычисление определителей высоких порядков
Урок: 22Видеокурс высшей математики. Урок 21. Часть 1. Обратная матрица
Урок: 23Видеокурс высшей математики. Урок 21. Часть 2. Обратная матрица
Урок: 24Видеокурс высшей математики. Урок 22. Матричные уравнения
Урок: 25Видеокурс высшей математики. Урок 23. Системы линейных неоднородных уравнений. Общая теория
Урок: 26Видеокурс высшей математики. Урок 24. Метод обратной матрицы решения системы линейных уравнений
Урок: 27Видеокурс высшей математики. Урок 25. Метод Крамера решения системы линейных уравнений
Урок: 28Видеокурс высшей математики. Урок 26. Часть 1. Решений систем линейных уравнений методом Гаусса
Урок: 29Видеокурс высшей математики. Урок 26. Часть 2. Решений систем линейных уравнений методом Гаусса
Урок: 30Видеокурс высшей математики. Урок 27. Фундаментальная система решений
Урок: 31Видеокурс высшей математики. Урок 28. Примеры построения фундаментальной системы решений
Урок: 32Видеокурс. Урок 29. Задача: найти общее и одно частное решения системы лин неоднородных уравнений
Урок: 33Видеокурс высшей математики. Урок 30. Собственные значения и собственные векторы (теория)
Урок: 34Высшая математика. 31. Собственные значения и собственные векторы. Простое собственное значение
Урок: 35Высшая математика. 32. Собственные значения и собственные векторы. Комплексно-сопряженные значения
Урок: 36Видеокурс. 33. Собственные значения и собственные векторы. Случай кратного собственного значения
Урок: 37Высшая математика. 34. Собственные значения и собственные векторы. Присоединенные векторы
Урок: 38Видеокурс высшей математики. Урок 35. Часть 1. Линейные векторные пространства
Урок: 39Видеокурс высшей математики. Урок 35. Часть 2. Линейные векторные пространства
Урок: 40Видеокурс высшей математики. Урок 36. Преобразование координат. Матрица перехода
Урок: 41Видеокурс высшей математики. Урок 37. Евклидовы пространства
Урок: 42Видеокурс высшей математики. Урок 38. Квадратичные формы
Урок: 43Видеокурс высшей математики. Урок 39. Квадратичные формы. Преобразование переменных
Урок: 44Видеокурс высшей математики. Урок 40. Приведение квадратичной формы к каноническому виду
Урок: 45www.videxp.com

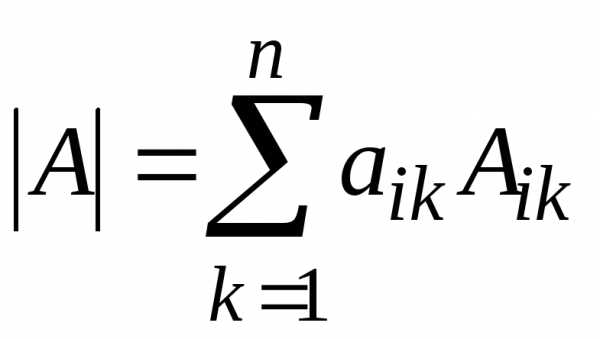 ,
где Аik алгебраические дополнения к
,
где Аik алгебраические дополнения к 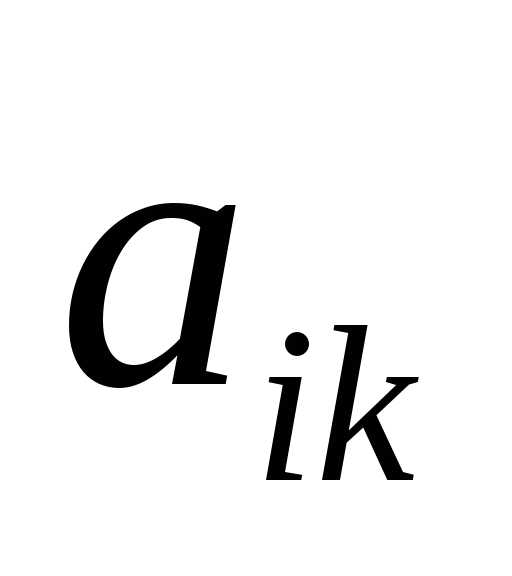 (разложение определителя поi-ой
строке). Либо
(разложение определителя поi-ой
строке). Либо 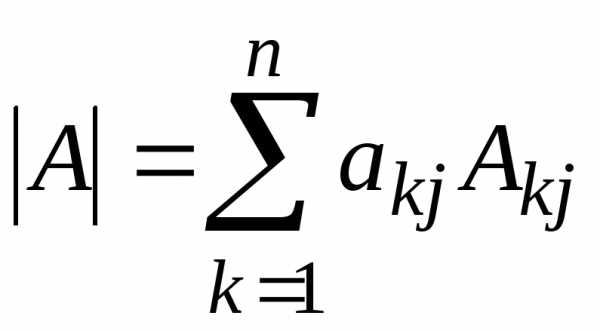 (разложение поj-тому
столбцу).
(разложение поj-тому
столбцу).