Процентное отношение двух чисел: онлайн калькулятор
Отношение двух любых чисел x и y – это их частное, то есть дробь вида x/y. Процентным соотношением таких чисел является частное, умноженное на 100.
История понятия
Процент происходит от латинского выражения «pro cento», которое в переводе означает «на сотню». В математике процент — это сотая часть числа. Выражение частей от целого было актуально еще в античные времена, когда люди впервые начали использовать дроби. В Древнем Египте широкой популярностью пользовались так называемые египетские дроби, которые представляли собой сумму нескольких различных дробей, обязательно содержащих в числителе единицу. Например, выражение 13/84 египетские математики выразили бы в виде суммы 1/12 + 1/14. Однако 1/100 — наиболее удобный способ выражать части числа.
Проценты зародились в Древнем Риме, задолго до возникновения арабской системы чисел. Многие бытовые вопросы, как то мера товаров или размер налога, определялись как сотая часть от целого. В России такие вычисления были введены гораздо позже Петром Первым, ведь русская система мер использовала числа, не кратные сотне. Проценты до сих пор активно используются в реальной жизни и занимают важное место во многих сферах деятельности.
Что такое процент
Итак, процент — это одна сотая часть чего либо. Если у нас есть 100 яблок, то 5 фруктов из них — это пять частей от сотни или 5 %. Если у нас есть 200 персиков, то 23 % от них означает 23 части по 2 фрукта каждая или 46 персиков. Очевидно, что эти показатели можно выразить в виде обыкновенных дробей. В случае с яблоками мы получим дробь 5 / 100 = 5 %, а в ситуации с персиками — 46 / 200 = 23 %. Используя данное уравнение, мы можем найти процентное соотношение двух чисел. И не только.
Процентное соотношение двух чисел
Процент — это соотношение двух чисел, переведенное в десятичную дробь и умноженное на 100. В математической записи это выглядит следующим образом:
m / n × 100 = p,
где m – размер части, n – размер целого, p – процент.
Зная два из трех параметров, мы можем легко определить третий. Наш калькулятор использует данное выражение для поиска процента, целого или части числа. Соответственно, в программе часть обозначена как числитель, целое — как знаменатель, а процент остается процентом. На практике это выглядит следующим образом.
Примеры расчета процентов
Допустим, у нас есть 200 кг сахара. Мы хотим узнать:
- сколько сахара необходимо отгрузить, если требуется поставить 37 % от исходной массы;
- 3 кг сахара просыпалось, и требуется указать процент потерянного товара.
Итак, в первой задаче нам уже известен процент p = 37, а также размер целой части n = 200. У нас есть знаменатель и процент, а требуется найти числитель. Для этого выбираем в меню калькулятора опцию «вычислить числитель» и вводим параметры процента и знаменателя. В ответе получаем 74 кг.
Во второй задаче у нас опять же есть значение целого (знаменатель, равный 200), а так же размер части (числитель, равный 3). Для решения задачи требуется определить процент. Для этого в меню программы выбираем «вычислить процент», вводим соответствующие значения и видим мгновенный результат в виде 2 %.
Есть и третья задача. Допустим, мы не знаем, сколько сахара было изначально, но хотим это выяснить. Нам известно, что 56 кг — это 18 % от первоначального объема. Теперь нам требуется найти целое или знаменатель. Выберем соответствующий пункт калькулятора и введем известные параметры, то есть процент и числитель. Таким образом, изначально на складе было 311 кг сахара.
Процентная разница между числами
Наш калькулятор также позволяет определить процентную разницу между числами. Для вычисления данного параметра используется простая формула:
(a − b) / (0,5 × (a + b)) × 100 %.
Если вам для решения практических задач требуется вычислить процентную разницу между двумя значениями, то достаточно выбрать необходимый пункт в меню калькулятора и рассчитать требуемый показатель.
Пример
Допустим, за первый месяц работы вы получили чистую прибыль в размере 500 $, а во втором — 650 $. Давайте узнаем, на сколько процентов изменился ваш доход за месяц. Для этого выберите в меню программы тип калькулятора «разница в процентах» и введите заданные показатели прибыли. При этом неважно, в какую из ячеек вы вобьете числа, так как разница в любом случае будет одинакова. В результате мы получим ответ — прибыль изменилась на 26 %. В нашем случае она увеличилась.
Заключение
Проценты занимают важное место в нашей жизни — расчет этих параметров необходим в практически любой деятельности человека: от продвижения сайтов до расчета технологических процессов. Используйте наши калькуляторы в своей деятельности — программы пригодятся вам как в учебе, так и на работе.
bbf.ru
Что процентное отношение. Как посчитать процентное соотношение чисел
Процентное соотношение (или отношение) двух чисел — это отношение одного числа к другому умноженное на 100%.
Процентное отношение двух чисел можно записать следующей формулой:
Пример процентного отношения
Например есть два числа: 750 и 1100.
Процентное отношение 750 к 1100 равно
Число 750 составляет 68.18% от 1100.
Процентное отношение 1100 к 750 равно
Число 1100 составляет 146.67% от 750.
Пример-задача 1
Норма завода по производству автомобилей составляет 250 машин в месяц. Завод собрал за месяц 315 машин. Вопрос: на сколько процентов завод перевыполнил план?
Процентное отношение 315 к 250 = 315:250*100 = 126% .
План выполнен на 126% . План перевыполнен на 126% — 100% = 26% .
Пример-задача 2
Прибыль компании за 2011 год составила 126 млн $, в 2012 году прибыль составила 89 млн $. Вопрос: на сколько процентов упала прибыль в 2012 году?
Процентное отношение 89 млн к 126 млн = 89:126*100 = 70.63%
Прибыль упала на 100% — 70.63% = 29.37%
Правило. Чтобы найти процентное отношение двух чисел, нужно одно число разделить на другое, а результат умножить на 100.
Например, вычислить, сколько процентов составляет число 52 от числа 400.
По правилу: 52: 400 * 100 — 13 (%).
Обычно такие отношения встречаются в задачах, когда величины заданы, а нужно определить, на сколько процентов вторая величина больше или меньше первой (в вопросе задачи: на сколько процентов перевыполнили задание; на сколько процентов выполнили работу; на сколько процентов снизилась или повысилась цена и т. д.).
Решения задач на процентное отношение двух чисел редко предполагают только одно действие. Чаше решение таких задач состоит из 2-3 действий.
Примеры.
1. Завод должен был за месяц изготовить 1 200 изделий, а изготовил 2 300 изделий. На сколько процентов завод перевыполнил план?
1-й вариант
Решение:
1 200 изделий — это план завода, или 100% плана.
1) Сколько изделий изготовил завод сверх…
0 0
Быстрая навигация по статье
Простые задачи
Для того чтобы правильно провести…
0 0
Сравнительную характеристику двух величин, показывающую насколько одна из них отличается от другой, называют их соотношением. Если одну из сравниваемых величин (или их сумму) принять равной ста процентам, то различия между величинами тоже можно выразить в процентах. Такое сравнение будет называться процентным соотношением.
Как правильно посчитать процентное соотношение
Сформулируйте задачу в соответствии с логикой, если вам не задано точной формулировки. Например, если есть результат тестирования (80 правильных ответов и 20 неправильных), то за 100 процентов следует принимать сумму известных величин (80+20=100). Исходя из этого, можно определить процентное соотношение двух величин как 80% к 20%. А если по условиям задачи известно количество правильных ответов (80) и число вопросов (100), то за 100 процентов следует принимать одну из известных величин, а не их сумму. Определив, какую величину следует считать стопроцентным…
0 0
Благодаря такому онлайн калькулятору у вас получается возможность быстро рассчитать процентное соотношение нескольких чисел. Для начала математической операции вам понадобится знать всего лишь два числа. Собственно говоря, между ними и будет производиться расчёт процентного соотношения. После того, как вы нажмёте на специальную кнопку, то расчёт будет завершён. В итоге вы получите ответ в графе под названием “Рост составляет”.
Такое приложение может быть использовано в процессе решения достаточно широкого круга задач, ведь рассчитать насколько процентов одно число больше другого необходимо достаточно часто. Это могут быть и бухгалтерские подсчёты, и школьные математические задачи, а также много и многое другое.
0 0
Считаем процентное соотношение — пример и формулы.
Любой современный человек должен уметь хорошо считать. Конечно, сегодня существуют специальные приспособления, которые помогают людям производить расчёты, однако не стоит забывать, что счёт в уме во все времена считался самой эффективной зарядкой для ума.
Простейшие алгоритмы математических расчётов могут пригодиться любому культурному человеку. В качестве примера, попробуем посчитать процентное соотношение.
Простые задачи
Посчитать процентное соотношение бывает необходимо для того, чтобы показать сравнительную характеристику этих величин. С помощью такого соотношения можно наглядно увидеть, насколько одна величина превышает другую и то действительно очень удобно и просто.
Говорят, что если одну из сравниваемых величин принять за сто процентов, то соотношение между этой величиной и сравниваемой (выраженное в процентах) и будут называть процентным соотношением.
Для того чтобы правильно…
0 0
Сегодня в современном мире без процентов невозможно обойтись. Даже в школе, начиная с 5 класса, дети узнают данное понятие и решают задачи с этой величиной. Проценты встречаются в любой сфере современных структур. Взять, к примеру, банки: размер переплаты кредита зависит от указанной в договоре величины; на размерность прибыли также влияет процентная ставка. Поэтому жизненно необходимо знать, что такое процент.
Понятие процента
Согласно одной легенде, процент появился из-за глупой опечатки. Наборщик должен был выставить число 100, но перепутал и поставил так: 010. Это послужило причиной того, что первый ноль немного приподнялся, а второй опустился. Единица превратилась в обратный слеш. Такие манипуляции послужили тому, что появился знак процента. Конечно, есть и другие легенды о происхождении этой величины.
О процентах индусы знали еще в V веке. В Европу же десятичные дроби, с которыми тесно взаимосвязано наше понятие, появились спустя тысячелетие….
0 0
Отношение двух любых чисел x и y – это их частное, то есть дробь вида x/y. Процентным соотношением таких чисел является частное, умноженное на 100.
История понятия
Процент происходит от латинского выражения «pro cento», которое в переводе означает «на сотню». В математике процент — это сотая часть числа. Выражение частей от целого было актуально еще в античные времена, когда люди впервые начали использовать дроби. В Древнем Египте широкой популярностью пользовались так называемые египетские дроби, которые представляли собой сумму нескольких различных дробей, обязательно содержащих в числителе единицу. Например, выражение 13/84 египетские математики выразили бы в виде суммы 1/12 + 1/14. Однако 1/100 — наиболее удобный способ выражать части числа.
Проценты зародились в Древнем Риме, задолго до возникновения арабской системы чисел. Многие бытовые вопросы, как то мера товаров или размер налога, определялись как сотая часть от целого. В России такие вычисления…
0 0
Вычи
www.torgural66.ru
Предложения со словосочетанием ПРОЦЕНТНОЕ СООТНОШЕНИЕ
Он был не из тех политиков, кто, как и многие генералы, живёт в мире статистики, процентных соотношений, графиков, стрелок и топографических карт. Всё это процентное соотношение было подробно расписано на зелёных флакончиках. Большое значение для диагностики имеет так называемая лейкоцитарная формула — процентное соотношение отдельных форм лейкоцитов. Для полноты картины сюда же можно добавить амортизационные, хозяйственные и другие расходы в процентном соотношении на каждую услугу. Способность удерживать воду в большой степени зависит от вида и количества вяжущих, процентного соотношения высокодисперсных (золы, глины и т.Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: потанцевать — это что-то нейтральное, положительное или отрицательное?
Положительное
Отрицательное
 Ограничьте себя сотней пунктов, так вам будет проще выявить процентное соотношение ценностных ориентиров.
Очень хорошим примером может служить дача в лесу, там вообще растений в процентном соотношении во много раз больше, чем в квартире.
Уместно ли дать расклад сил в процентном соотношении?
Но сказать о процентном соотношении можно.
Буквально за несколько десятков лет процентное соотношение суши и океана увеличилось в пять раз в пользу суши.
Например, в одном человеке могут быть и экстраверт, и интроверт — всё дело в процентном соотношении.
Мы убеждены, что передача меньших районов на основе более высокого процентного соотношения явится нецелесообразной.
Их процентное соотношение оговорено в уставе общества и не изменяется от того, являешься ли ты сотрудником детского центра или уже нет. Процентное соотношение различных видов лейкоцитов в крови получило название лейкоцитарной формулы.
И хотя потери среди мирного населения удалось минимизировать в процентном соотношении, в абсолютных величинах они были огромны.
Очень важно и процентное соотношение злаков, овощей, бобовых, морепродуктов.
Поэтому для анализа нашей деятельности правильнее оценивать не количество, а процентное соотношение записавшихся от позвонивших.
Таким образом, понятие «тариф» используется в случае необходимости установить процентное соотношение расчётной базы страхового взноса.
Саму оплату можно производить частями в процентном соотношении от общей стоимости работы.
Всё дело в пропорциях, в процентном соотношении реализованного и нереализованного. Процентное соотношение этих начал у всех людей абсолютно своё собственное.
Для соблюдения процентного соотношения, если я правильно понял, пол многоножкам назначался.
Разбирать процентное соотношение, отнимая тем самым хлеб у определённого рода публики, я не стану — нас в данном случае интересует иное.
Шаг третий: определитесь, в каком процентном соотношении вы будете наполнять ваш портфель акциями или иными активами.
Жирно-кислотный состав в процентном соотношении приведены в таблице 1. 3 -LSB- 1. 12 — 1. 16 -RSB-.
Таблица 1. 3. Жирно-кислотный состав в процентном соотношении.
Скорость их разложения и температура зависят от процентного соотношения составляющих.
Лейкоцитарная формула (лейкограмма) — это процентное соотношение различных видов лейкоцитов (как мы помним, их пять видов). Процентное соотношение женщин и мужчин 70: 30 в области связей с общественностью предъявляет к образовательным учреждениям крайне высокие требования.
Вопрос лишь в том, каково процентное соотношение между ними и чему мы выбираем отдать предпочтение.
В процентном соотношении принято выделять такую структуру.
В таблице показано процентное соотношение, а в скобках даются абсолютные цифры.
Если вам удобно, можно даже вывести процентное соотношение разных типов деятельности.
Если есть проблемы со здоровьем, процентное соотношение определит врач-диетолог и назначит, при необходимости, подходящую диету. Процентное соотношение массы воды к массе сухой древесины называется относительной влажностью.
Если в организме меняется процентное соотношение соли, будут происходить изменения и в сознании.
По сути, конверсия — это процентное соотношение выигранных торгов к тем, в которых фирма участвовала.
Под структурой ассортимента понимается процентное соотношение выделенных по определённому признаку совокупностей товаров в их суммарном количестве.
При обработке результатов этой методики подсчитывается процентное соотношение высказываний первого и второго типов.
Круговая диаграмма предназначена для демонстрации процентных соотношений, сравнения количественных показателей и т.
Поэтому, чтобы знать, как консистенция мёда изменится в будущем, нужно иметь сведения о процентном соотношении этих веществ.
Тем не менее статистика позволяет наблюдать достаточно устойчивую картину процентного соотношения нарушений среди различных возрастных групп.
Они выражаются в процентном соотношении семян, которые проросли или наклюнулись в отведённое для этого время, к их общему количеству посевного материала (табл.
Переменными являлись средние значения или процентные соотношения ответов на различные вопросы о ценностях.
Качество бронзы зависело от процентного соотношения олова.
Ограничьте себя сотней пунктов, так вам будет проще выявить процентное соотношение ценностных ориентиров.
Очень хорошим примером может служить дача в лесу, там вообще растений в процентном соотношении во много раз больше, чем в квартире.
Уместно ли дать расклад сил в процентном соотношении?
Но сказать о процентном соотношении можно.
Буквально за несколько десятков лет процентное соотношение суши и океана увеличилось в пять раз в пользу суши.
Например, в одном человеке могут быть и экстраверт, и интроверт — всё дело в процентном соотношении.
Мы убеждены, что передача меньших районов на основе более высокого процентного соотношения явится нецелесообразной.
Их процентное соотношение оговорено в уставе общества и не изменяется от того, являешься ли ты сотрудником детского центра или уже нет. Процентное соотношение различных видов лейкоцитов в крови получило название лейкоцитарной формулы.
И хотя потери среди мирного населения удалось минимизировать в процентном соотношении, в абсолютных величинах они были огромны.
Очень важно и процентное соотношение злаков, овощей, бобовых, морепродуктов.
Поэтому для анализа нашей деятельности правильнее оценивать не количество, а процентное соотношение записавшихся от позвонивших.
Таким образом, понятие «тариф» используется в случае необходимости установить процентное соотношение расчётной базы страхового взноса.
Саму оплату можно производить частями в процентном соотношении от общей стоимости работы.
Всё дело в пропорциях, в процентном соотношении реализованного и нереализованного. Процентное соотношение этих начал у всех людей абсолютно своё собственное.
Для соблюдения процентного соотношения, если я правильно понял, пол многоножкам назначался.
Разбирать процентное соотношение, отнимая тем самым хлеб у определённого рода публики, я не стану — нас в данном случае интересует иное.
Шаг третий: определитесь, в каком процентном соотношении вы будете наполнять ваш портфель акциями или иными активами.
Жирно-кислотный состав в процентном соотношении приведены в таблице 1. 3 -LSB- 1. 12 — 1. 16 -RSB-.
Таблица 1. 3. Жирно-кислотный состав в процентном соотношении.
Скорость их разложения и температура зависят от процентного соотношения составляющих.
Лейкоцитарная формула (лейкограмма) — это процентное соотношение различных видов лейкоцитов (как мы помним, их пять видов). Процентное соотношение женщин и мужчин 70: 30 в области связей с общественностью предъявляет к образовательным учреждениям крайне высокие требования.
Вопрос лишь в том, каково процентное соотношение между ними и чему мы выбираем отдать предпочтение.
В процентном соотношении принято выделять такую структуру.
В таблице показано процентное соотношение, а в скобках даются абсолютные цифры.
Если вам удобно, можно даже вывести процентное соотношение разных типов деятельности.
Если есть проблемы со здоровьем, процентное соотношение определит врач-диетолог и назначит, при необходимости, подходящую диету. Процентное соотношение массы воды к массе сухой древесины называется относительной влажностью.
Если в организме меняется процентное соотношение соли, будут происходить изменения и в сознании.
По сути, конверсия — это процентное соотношение выигранных торгов к тем, в которых фирма участвовала.
Под структурой ассортимента понимается процентное соотношение выделенных по определённому признаку совокупностей товаров в их суммарном количестве.
При обработке результатов этой методики подсчитывается процентное соотношение высказываний первого и второго типов.
Круговая диаграмма предназначена для демонстрации процентных соотношений, сравнения количественных показателей и т.
Поэтому, чтобы знать, как консистенция мёда изменится в будущем, нужно иметь сведения о процентном соотношении этих веществ.
Тем не менее статистика позволяет наблюдать достаточно устойчивую картину процентного соотношения нарушений среди различных возрастных групп.
Они выражаются в процентном соотношении семян, которые проросли или наклюнулись в отведённое для этого время, к их общему количеству посевного материала (табл.
Переменными являлись средние значения или процентные соотношения ответов на различные вопросы о ценностях.
Качество бронзы зависело от процентного соотношения олова.kartaslov.ru
Процентное соотношение Википедия
У этого термина существуют и другие значения, см. Отношение.Соотношение в математике (отношение, пропорция) — это взаимосвязь между двумя числами одного рода[1] (предметами, действиями, явлениями, свойствами (признаками), понятиями, объектами, например, людьми (студентами), чайными ложками, единицами чего-либо одинаковой размерности), обычно выражаемое как «a к b» или a:b{\displaystyle a:b}, а иногда выражаемое арифметически как безразмерное отношение (результат деления) двух чисел[2], непосредственно отображающее, сколько раз первое число содержит второе (не обязательно целое).[3]
Проще говоря, соотношение показывает для каждого количества чего-то одного сколько есть чего-то другого. Например, предположим, что у кого-то есть 8 апельсинов и 6 лимонов в вазе для фруктов, соотношение апельсинов и лимонов составит 4:3 (что эквивалентно 8:6), а соотношение лимонов и апельсинов составит 3:4. Кроме того, количество апельсинов относительно общего количества фруктов составит 4:7 (что эквивалентно 8:14). Соотношение 4:7 можно преобразовать в дробь 4/7, показывающую, какую долю от общего числа фруктов составляют апельсины.
Обозначения и термины
Соотношение чисел A и B можно представить как:[2]
Числа A и B в данном контексте иногда называют членами (terms), где A — антецедент, а B — консеквент.
Пропорция, выражающая равенство соотношений A:B и C:D, записывается как A:B=C:D или A:B::C:D. Читается:
- A относится к B как C относится к D.
И в данном случае, A, B, C, D называются членами пропорции. A и D — крайние члены пропорции, а B и C — средние члены. Равенство трёх и более соотношений называется непрерывной пропорцией (continued proportion, ряд отношений).[2]
Иногда в соотношениях три и более членов. Например, размеры предмета с сечением два к четырём и длиной десять сантиметров составят 2:4:10.
История и этимология
Невозможно проследить истоки концепции соотношения, поскольку идеи, из которых она развилась, должны были быть известны дописьменным культурам. Например, идея того, что одна деревня вдвое больше другой, настолько базовая, что была бы понятна даже в доисторическом обществе.[4]
Для обозначения отношения греки использовали термин др.-греч. λόγος, которое латиняне передавали как ratio («разумное основание»; как в слове «рациональный») или как proportio. (Рациональное число можно представить как результат отношения двух целых чисел.) Более современная интерпретация евклидова значения ближе к «вычисление» или «расчёт».[3]Боэций («Основы арифметики», «Основы музыки», начало VI в.) использовал слово proportio (наряду с ratio, comparatio и habitudo) для обозначения отношения и proportionalitas (перевод др.-греч. ἀναλογία) для обозначения пропорции (отношения отношений)[5]. Такое терминоупотребление (в связи с широчайшей распространённостью «Арифметики» и «Музыки» Боэция) практиковалось и в Средние века.
Евклид объединил в «Началах» результаты из более ранних источников. Пифагорейцы развили теорию соотношения и пропорции в приложении к числам[6]. Пифагорейская концепция числа включая лишь то, что сейчас называют рациональными числами, что навело сомнения на применимость теории в геометрии, где, как также обнаружили пифагорейцы, существуют несоизмеримые размеры, соответствующие иррациональным числам. Открытие теории отношений, не предполагавшей соизмеримость, вероятно, принадлежит Евдоксу Книдскому. В Книге VII «Начал» приведена и более ранняя теория отношений соизмеримых величин[7].
Существование нескольких теорий выглядит ненужным усложнением для современного взгляда, поскольку соотношения, во многом, определяются результатом деления. Однако, это довольно недавнее открытие, что можно увидеть на примере того, что современные учебники по геометрии до сих пор используют различную терминологию для соотношений (ratio) и результатов деления (quotient, частное). Причин для этого две. Во-первых, существовало вышеупомянутое нежелание признавать иррациональные числа как истинные числа. Во-вторых, нехватка широко используемых символов (обозначений) для замены уже устоявшейся терминологии соотношений задержало полное принятие дробей как альтернативы вплоть до XVI века.[8]
Определения Евклида
В книге V «Начал» Евклида 18 определений, касающихся соотношений[9]. Кроме того, Евклид использует идеи, которые были в настолько широком употреблении, что он не даёт им определений. Первые два определения гласят, что часть количества есть другое количество, которое «измеряет» его, и наоборот, кратное для количества есть другое количество, измеряемое им. В современных терминах, это означает, что кратное для количества есть это количество, умноженное на целое число, большее единицы, а часть количества (то есть делитель) при умножении на число, большее единицы, даёт то количество.
Эвклид не даёт определения слова «измерять». Тем не менее, можно предположить, что, если количество принимается за единицу измерения, а другое количество представлено как общее количество таких единиц измерения, то первое количество измеряет второе. Заметим, эти определения повторяются почти слово в слово как определения 3 и 5 в книге VII.
Определение 3 разъясняет, что такое соотношение в общем смысле. Оно не является математически строгим и некоторые исследователи приписывают его редакторам, а не самому Евклиду.[10] Евклид определяет соотношение между двумя количествами одного вида, например двух отрезков или двух площадей, но не соотношение длины к площади. Определение 4 указывает это ещё более строго. Оно утверждает, что соотношение между двумя количествами существует, если есть кратное для каждого, превышающее другое. В современных терминах: соотношение между количествами p и q существует, если существуют целые числа m и n такие, что mp>q и nq>p. Это условие известно как аксиома Архимеда.
Определение 5 наиболее сложное и трудное для понимания. Оно объясняет, что означает равенство для двух соотношений. Сегодня можно просто заявить, что соотношения равны, если равны результаты деления членов, но Евклид не признавал существование результатов деления для несоизмеримых величин, поэтому для него такое определение было бы бессмысленным. Поэтому требовалось более тонкое определение для случая количеств, не измеряющих друг друга напрямую. Хотя может быть невозможно присвоить соотношению рациональное значение, но вполне возможно сравнить соотношение с рациональным числом. А именно, для двух количеств p и q, а также рационального числа m/n, мы можем сказать, что соотношение p к q меньше, равно или больше m/n, когда np меньше, равно или больше mq, соответственно. Евклидово определение равенства можно сформулировать так: два соотношения равны, когда они одинаково себя ведут, будучи одновременно меньше, равны или больше любого рационального числа. В современной нотации это выглядит так: для данных количеств p, q, r и s выполняется p:q::r:s, если для любых положительных целых чисел m и n выполняется отношение np<mq, np=mq, np>mq в соответствии с nr<ms, nr=ms, nr>ms. Есть примечательное сходство между этим определением и теорией Дедекиндова сечения, используемого в современной теории иррациональных чисел[11].
Определение 6 гласит, что количества с одинаковым соотношением пропорциональны или состоят в пропорции. Евклид использует греческое слово ἀναλόγον (analogon), с тем же корнем, что и λόγος, от которого произошло слово «аналог».
Определение 7 объясняет, что значит для соотношения быть меньше или больше другого, и основывается на идеях из определения 5. В современной нотации: для данных количеств p, q, r и s выполняется p:q>r:s, если существуют положительные целые числа m и n такие, что np>mq и nr≤ms.
Как и в случае с определением 3, определение 8 некоторыми исследователями рассматривается как позднее включение редакторов. Оно гласит, что три члена p, q и r находятся в пропорции, если p:q::q:r. Это расширяется на 4 члена p, q, r и s как p:q::q:r::r:s и т. д. Последовательности, обладающие таким свойством, что соотношения последовательных членов равны, называются геометрическими прогрессиями. Определения 9 и 10 применяют это, говоря, что, если p, q и r состоят в пропорции, то p:r есть двойное отношение (duplicate ratio, отношение квадратов) для p:q, а если p, q, r и s находятся в пропорции, то p:s есть тройное отношение (triplicate ratio, отношение кубов) для p:q. Если p, q и r находятся в пропорции, то q называется средним пропорциональным (или геометрическим средним) для p и r. Подобным образом, если p, q, r и s находятся в пропорции, то q и r называют средними пропорциональными для p и s.
Процентное соотношение
Если умножить все количества в соотношении на одно и то же число, то соотношение не изменится. Например, соотношение 3:2 есть то же самое, что 12:8. Обычно члены пропорции уменьшают до наименьшего общего знаменателя либо выражают их в долях ста (процент). Иногда для удобства сравнения соотношения представляют в виде n:1 или 1:n.
Если смесь содержит вещества A, B, C и D в соотношении 5:9:4:2, то в ней 5 частей A приходится на каждые 9 частей B, 4 части C и 2 части D. Поскольку 5+9+4+2=20, то всего смесь содержит 5/20 A (5 частей из 20), 9/20 B, 4/20 C и 2/20 D. Если эти числа, деленные на общую сумму, умножить на 100, то получаем проценты: 25 % A, 45 % B, 20 % C и 10 % D (эквивалентно написанию соотношения в виде 25:45:20:10).
Пропорции
Если два или более количества, состоящих в пропорциональном соотношении, являются всеми количествами, задействованными в конкретной ситуации, например, два яблока и три апельсина в корзине, в которой нет других фруктов, то можно сказать, что «целое» содержит пять частей, состоящих из двух частей яблок и трёх частей апельсинов. В данном случае, 25{\displaystyle {\tfrac {2}{5}}}, или 40 % целого, — это яблоки, а 35{\displaystyle {\tfrac {3}{5}}}, или 60 % целого, — это апельсины. Такое сравнение определённого количества с «целым» иногда называют пропорцией. Пропорции иногда выражают в процентах, как указано выше.
Другие применения
- Соотношения часто используются для простых растворов в химии и биологии (степень разбавления).
- Шансы выигрыша в играх выражают в виде соотношения.
- Возможны соотношения количеств, измеряемых в разных единицах измерения.
См. также
Примечания
- ↑ Wentworth, p. 55
- ↑ 1 2 3 New International Encyclopedia
- ↑ 1 2 Penny Cyclopedia, p. 307
- ↑ Smith, p. 477
- ↑ А. М. С. Боэций. Основы музыки / Подготовка текста, перевод с латинского и комментарий С. Н. Лебедева. М.: Научно-издательский центр «Московская консерватория», 2012, pp. xxxiv-xxxv, 276.
- ↑ Heath, 1908, p. 112.
- ↑ Heath, 1908, p. 113.
- ↑ Smith, p. 480
- ↑ Heath, 1908, reference for section.
- ↑ «Geometry, Euclidean» Encyclopædia Britannica Eleventh Edition p682.
- ↑ Heath, 1908, p. 125.
Литература
- Отношение // Большая Советская энциклопедия (в 30 т.) / А. М. Прохоров (гл. ред.). — 3-е изд. — М: Сов. энциклопедия, 1974. — Т. XVIII. — С. 629. — 632 с.
- Отношение, в математике // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- «Ratio» The Penny Cyclopædia vol. 19, The Society for the Diffusion of Useful Knowledge (1841) Charles Knight and Co., London pp. 307ff
- «Proportion» New International Encyclopedia, Vol. 19 2nd ed. (1916) Dodd Mead & Co. pp270-271
- «Ratio and Proportion» Fundamentals of practical mathematics, George Wentworth, David Eugene Smith, Herbert Druery Harper (1922) Ginn and Co. pp. 55ff
- The thirteen books of Euclid’s Elements, vol 2 / trans. Sir Thomas Little Heath. — Cambridge Univ. Press, 1908. — P. 112ff.
- D.E. Smith, History of Mathematics, vol 2 Dover (1958) pp. 477ff
wikiredia.ru
процентное соотношение — Перевод на английский — примеры русский
На основании Вашего запроса эти примеры могут содержать грубую лексику.
На основании Вашего запроса эти примеры могут содержать разговорную лексику.
В государственном секторе структура расходов и процентное соотношение налоговых поступлений и национального дохода отражают степень и тип проводимой правительством деятельности.
In the public sector, the composition of expenditures and percentage of tax revenue over national income reflect the degree and type of government intervention.А. Население, процентное соотношение женщин и мужчин
Высокое процентное соотношение женщин отмечается только в частных учебных заведениях (53%).
It is in private educational establishments that a high proportion of women students is seen (53 per cent).Одним из отличительных аспектов современных войн и конфликтов является большое процентное соотношение некомбатантов к общему числу жертв.
One of the extraordinary aspects of contemporary wars and conflicts is the large proportion of non-combatants among the victims.(Число и процентное соотношение правительств, решающих при содействии ЮНЕП приоритетные вопросы отходов)
(Number and percentage of Governments assisted by UNEP to address priority waste issues)(Число и процентное соотношение стран, сообщающих о применении при содействии ЮНЕП схем промышленной отчетности, способствующих рациональному регулированию химических веществ и отходов)
(Number and percentage of countries assisted by UNEP reporting the use of industry reporting schemes to promote sound chemicals and waste management)Таблица 15 показывает, что процентное соотношение между женщинами и мужчинами, директорами государственных дневных школ, составило 69,6% в 2003/04 учебном году, что было самым высоким показателем и оставалось на уровне примерно 67,5% в 2007/08 учебном году.
The figures in Table 15 show that the proportion of directors of public day schools who were women was at an all-time high in 2003/04 — 69.6 per cent — and stood at 67.5 per cent in 2007/08.Просьба представить информацию о распространенности небезопасных абортов, с разбивкой по регионам и показателям экономического статуса женщин, а также число и процентное соотношение находящихся в местах заключения женщин, осужденных за незаконные аборты.
Please provide data on the prevalence of unsafe abortion, disaggregated by region and the economic status of the women, and the number and proportion of women in detention after a conviction for illegal abortion.Кроме того, она хотела бы узнать процентное соотношение женщин, работающих на предприятиях, выпускающих экспортную продукцию, и какими правами пользуются трудящиеся-мигранты, занятые на таких предприятиях.
In addition, she wanted to know what percentage of women worked in enterprises engaged in export production and what were the rights of migrant workers employed in such factories.Также можно считать, что не имеют гарантий занятости еще 15 процентов работающего населения, занятого в оптовой или розничной торговле (86 процентов рабочих мест в этом секторе), причем процентное соотношение женщин и мужчин примерно одинаково).
In the same vain, 15% of the total working population engaged in wholesale or retail trade can be considered as in vulnerable employment (86% of all employment in that sector — roughly same proportion for men and women).Очевидно, что достигнут существенный прогресс в том, что касается документов Секретариата, в том плане, что в пределах установленных сроков было выпущено гораздо большее число и процентное соотношение документов, чем в предшествующие годы.
It is obvious that significant progress had been made as far as the Secretariat documents are concerned, in that a much larger number and percentage of documents were issued within the mandated time frame than in previous years.Такое же процентное соотношение применяется ОЭСР/КСР.
Такой доклад не был представлен Исполнительному совету, а процентное соотношение по-прежнему остается неизменным.
No such report was ever submitted to the Executive Board, while the percentage has remained stable.За последние 25 лет процентное соотношение членства в профсоюзах оставалось неизменным.
The proportion of trade union members has remained at about the same level for the past 25 years.Например, наблюдается следующее процентное соотношение сотрудников из числа женщин:
Если взглянуть на процентное соотношение женщин, занятых в спортивной индустрии, то ситуация выглядит неоднородной.
If we look at the proportion of women who work in the sports industry, we see a varied picture.В таблице 4 показано процентное соотношение женщин и мужчин среди кандидатов.
Table 4 shows the female percentage to their male counterparts.Касаясь пункта 101 доклада, он просит сообщить процентное соотношение между студентами тибетского и ханьского происхождения, обучающимися в Тибетском университете.
Referring to paragraph 101 of the report, he enquired about the respective percentages of students of Tibetan and Han origin at Tibet University.Это процентное соотношение оставалось достаточно стабильным в последние годы.
This percentage has remained fairly stable over the past years.В то же время предлагаем установить процентное соотношение между ценовыми и неценовыми критериями.
context.reverso.net
Как посчитать процентное соотношение | Сделай все сам
Сравнительную отзыв 2-х величин, показывающую насколько одна из них отличается от иной, называют их соотношением. Если одну из сопоставляемых величин (либо их сумму) принять равной ста процентам, то отличия между величинами тоже дозволено выразить в процентах. Такое сопоставление будет именоваться процентным соотношением.
Инструкция
1. Сформулируйте задачу в соответствии с логикой, если вам не задано точной формулировки. Скажем, если есть итог тестирования (80 верных результатов и 20 неправильных), то за 100 процентов следует принимать сумму вестимых величин (80+20=100). Исходя из этого, дозволено определить процентное соотношение 2-х величин как 80% к 20%. А если по условиям задачи знаменито число положительных результатов (80) и число вопросов (100), то за 100 процентов следует принимать одну из знаменитых величин, а не их сумму. Определив, какую величину следует считать стопроцентным стандартом, дозволено переходить к фактическому вычислению итога.
2. Обнаружьте соотношение 2-х величин, поделив одну на иную, а после этого умножьте полученный итог на 100, дабы выразить это соотношение в процентах. Если изготавливать такие расчеты в уме не представляется допустимым, то используйте, скажем, калькулятор, встроенный в поисковую систему Google. Для этого перейдите на основную страницу этого веб-источника и наберите соответствующий запрос. Скажем, если нужно рассчитать процентное соотношение положительных результатов (37) к всеобщему их числу (52), то введите «37 / 52 * 100» и увидите верный результат (71.1538462).
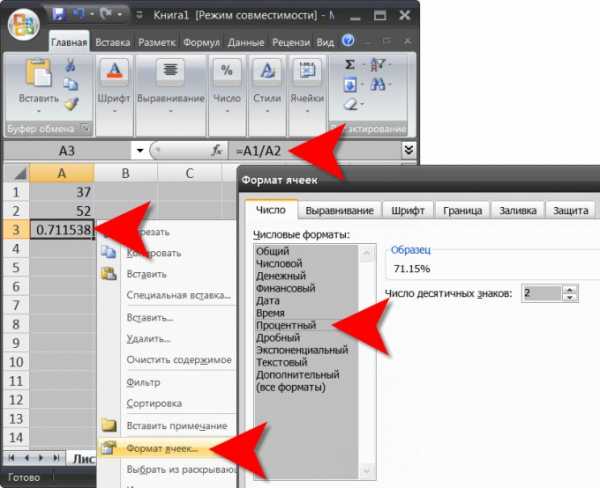
3. Используйте, скажем, табличный редактор Microsoft Excel, если хотите обойтись без интернета. Запустив его, введите необходимые для расчета данные. Скажем, в первой ячейке укажите число положительных результатов (37), а во 2-й – всеобщее число результатов (52). В третьей ячейке нажмите клавишу со знаком равенства, после этого щелкните первую ячейку, нажмите клавишу с косой чертой (слэш), щелкните вторую ячейку и нажмите Enter. Редактор рассчитает примитивное соотношение 2-х величин. Дабы перевести его в проценты задайте этой ячейке процентный формат. Для этого щелкните ее правой кнопкой мыши и выберите в контекстном меню строку «Формат». В списке «Числовые форматы» кликните строку «Процентный» и в поле «Число десятичных знаков» укажите, до которого знака нужно округлять итог. После этого нажмите кнопку «OK».
Видео по теме
jprosto.ru
Как посчитать процентное соотношение | Праздник
Считаем процентное соотношение — пример и формулы.
Любой современный человек должен уметь хорошо считать. Конечно, сегодня существуют специальные приспособления, которые помогают людям производить расчёты, однако не стоит забывать, что счёт в уме во все времена считался самой эффективной зарядкой для ума.
Простейшие алгоритмы математических расчётов могут пригодиться любому культурному человеку. В качестве примера, попробуем посчитать процентное соотношение.
Простые задачи
Посчитать процентное соотношение бывает необходимо для того, чтобы показать сравнительную характеристику этих величин. С помощью такого соотношения можно наглядно увидеть, насколько одна величина превышает другую и то действительно очень удобно и просто.
Говорят, что если одну из сравниваемых величин принять за сто процентов, то соотношение между этой величиной и сравниваемой (выраженное в процентах) и будут называть процентным соотношением.
Для того чтобы правильно провести необходимые расчёты, следует грамотно сформулировать условие задачи (конечно, это необходимо делать только в том случае, если подобной постановки задачи у вас не имеется).
Задача может звучать таким образом: было проведено тестирование, в результате которого имеется 70 правильных ответов и 30 неправильных. Исходя из логики, за сто процентов следует принять сумму правильных и неправильных ответов, так как эта величина получается известная.
А дальше посчитать процентное соотношение не составляет большого труда. Понятно, что правильных ответов получено 70 %, а неправильных – 30%. Но не всегда можно привести задачу к такому логически понятному окончанию.
Расчёты
Если сложно обозначить подобную постановку задачи, то процентное соотношение определяется следующим образом: необходимо одну величину разделить на другую и результат умножить на 100 – таким образом и будет получен искомый результат.
Причем, в таком случае следует применять правила округления, но при этом помнить, что в полученном процентном соотношении сумма процентов всегда должна быть 100 (это проверка правильности проведения расчётов).
В том случае, если в уме произвести деление сложно, всегда можно воспользоваться либо калькулятором, либо применить электронную таблицу Excel.
getonholiday.com
