Линейные дифференциальные уравнения первого порядка
Определение. Линейным уравнением первого порядка
называется уравнение, линейное
относительно искомой функции и ее
производной. Общий вид линейного д.у.1:
непрерывные функции или постоянные.
Если ,
то уравнениерешается как дифференциальное уравнение
с разделяющимися переменными.
,
то уравнениерешается как дифференциальное уравнение
с разделяющимися переменными.
Рассмотрим уравнения:
1) Это уравнение является линейным по определению
,но лучше рассматривать его как уравнение с разделяющимися переменными:
2) Это уравнение не является линейным, т. к. функцияy в уравнении имеет не первую степень, а выше
Уравнение является
линейным по определению. Но проще
рассматривать его как однородное д.у.1: 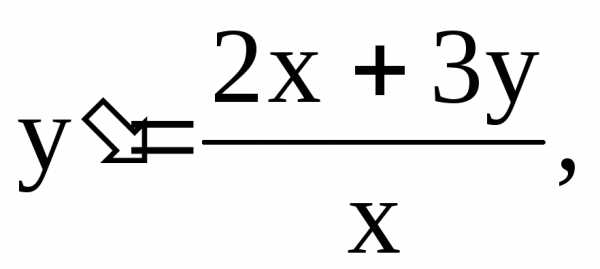 где
где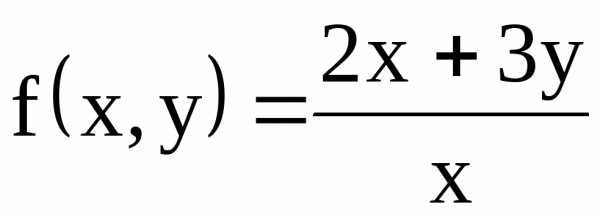 – однородная функция нулевого измерения.
– однородная функция нулевого измерения.
4)  Запишем уравнение в виде.
Это линейное д.у.1.
Запишем уравнение в виде.
Это линейное д.у.1.
Решение линейного дифференциального уравнения первого порядка
Общее решение ищется в виде гденекоторые функции.
Покажем на
примере, что любую функцию  можно представить в виде произведения
двух функций, одна из которых выбирается
произвольно, а вторая зависит от этого
выбора.
можно представить в виде произведения
двух функций, одна из которых выбирается
произвольно, а вторая зависит от этого
выбора.
Пусть 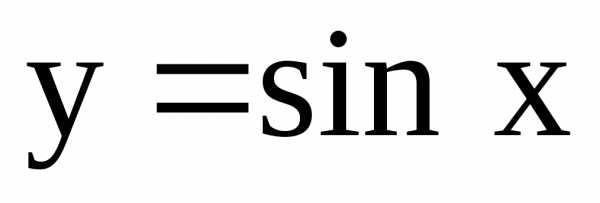
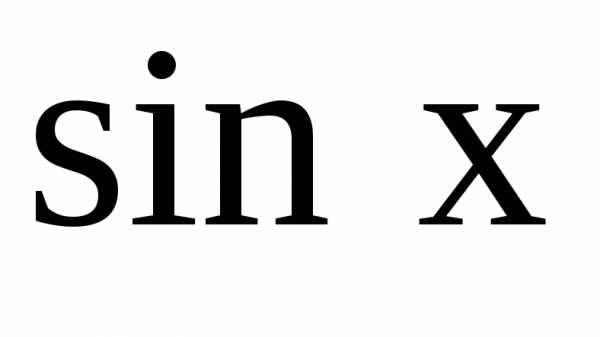 представить в виде различных пар
множителей:
представить в виде различных пар
множителей:где первый множитель выбирается произвольно.
Указанная подстановка приводит линейное д.у.1 к решению двух д.у. с разделяющимися переменными. Покажем это в общем виде. В линейное уравнениеподставимПолучим
или
. (4)
Выберем функцию u такой, чтобы
(5)
Уравнение (5) – дифференциальное уравнение с разделяющимися переменными:
Интегрируя, найдем
функцию 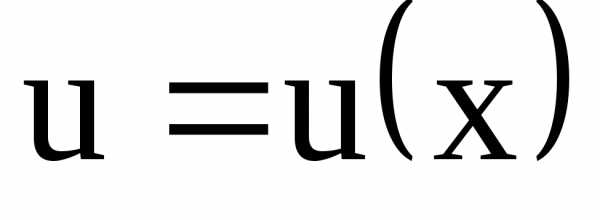
учета произвольной
постоянной. Подставим найденную функцию 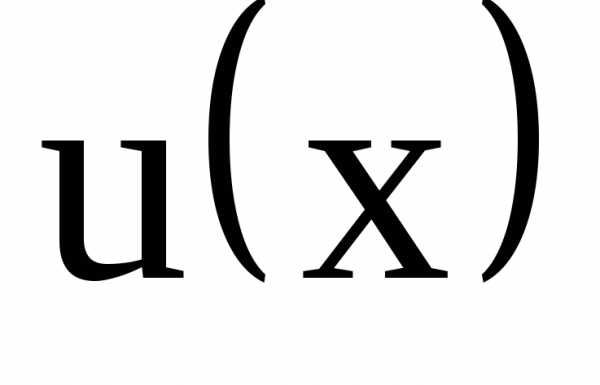 в уравнение (4) и получимдифференциальное уравнение с разделяющимися
переменными (3). Его общее решение
позволит получить второй множитель
в уравнение (4) и получимдифференциальное уравнение с разделяющимися
переменными (3). Его общее решение
позволит получить второй множитель
Тогда общее решение линейного д. у. 1.
Пример 1. Найти общее решение уравнения 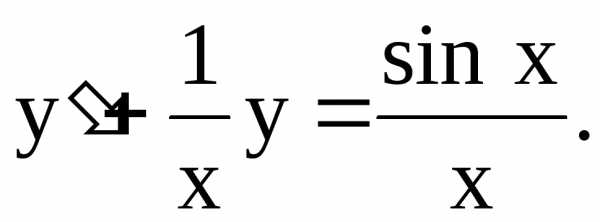
Решаем подстановкой
(6)
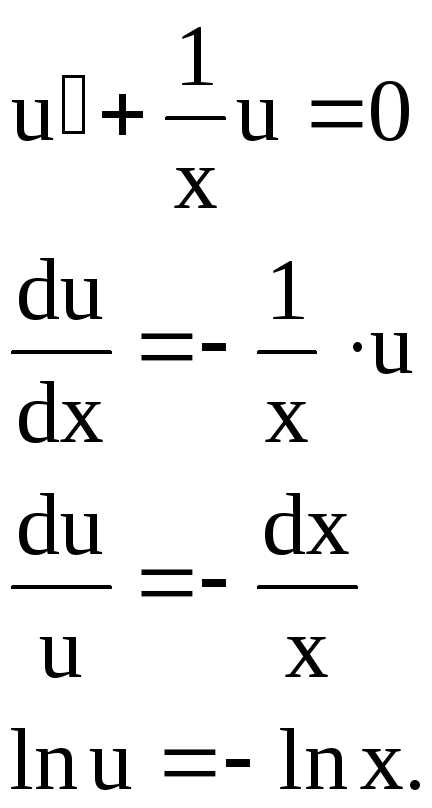
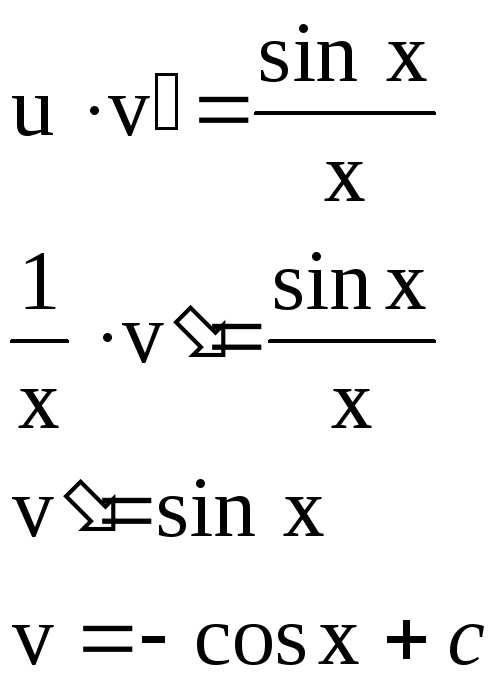
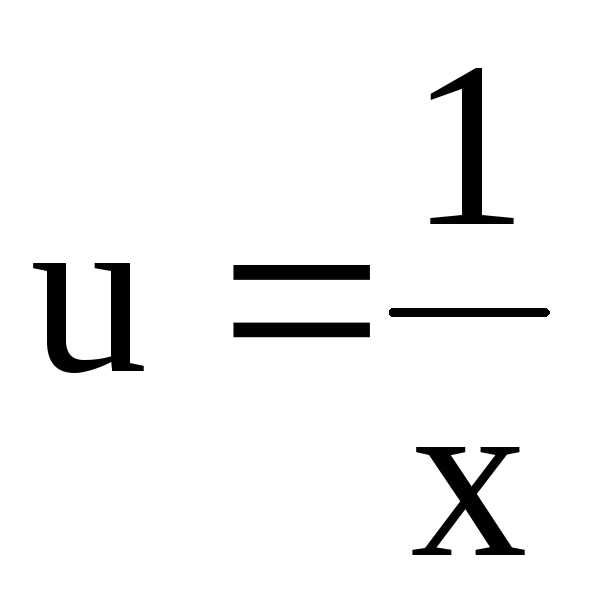 подставим в (6).
подставим в (6).
Общее решение:
Пример 2. Найти частное решение дифференциального уравнения
Подстановка: .
(7)
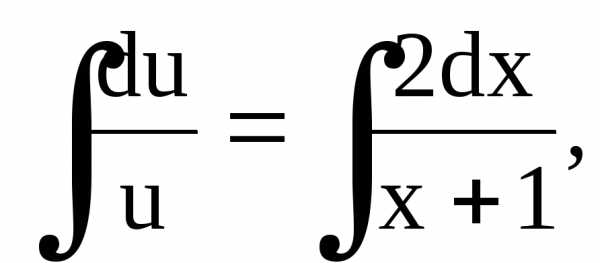
Подставим найденную функцию u в уравнение (7):
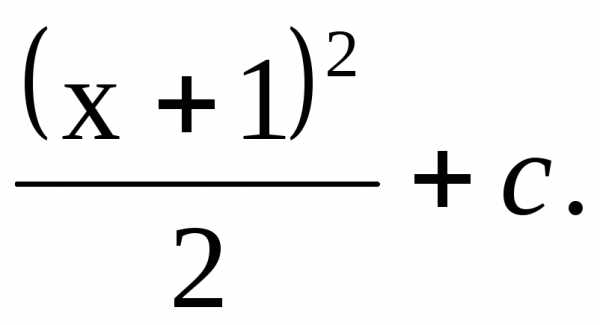
или
Найдем частное решение дифференциального решения, удовлетворяющее начальному условию
Следовательно, искомое частное решение такое:
Уравнения, приводящиеся к линейным (уравнения Бернулли)
Уравнение вида
называется уравнением Бернулли. Здесь n
– действительное число, причем при n
= 0 получим линейное уравнение; при 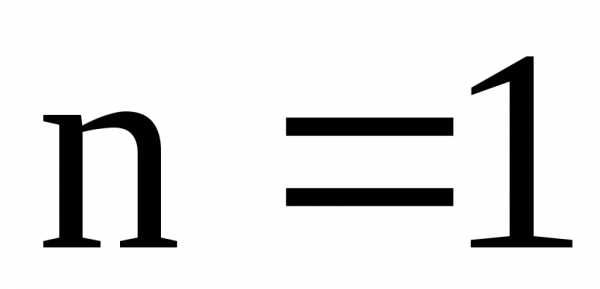 получим уравнение с разделяющимися
переменными. Приуравнение Бернулли приводится к
линейному, поэтому решается подстановкой
получим уравнение с разделяющимися
переменными. Приуравнение Бернулли приводится к
линейному, поэтому решается подстановкой
Пример. Найти общее решение уравнения
Разделив левую и правую части уравнения на х
, представим его в виде 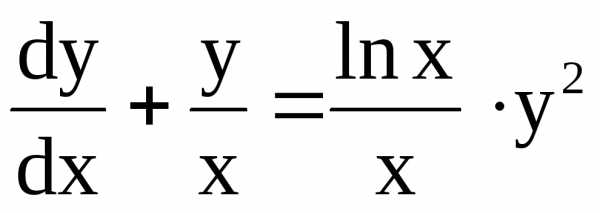 .
Можно утверждать, что это уравнение
имеет общий вид
.
Можно утверждать, что это уравнение
имеет общий вид
т. е. является уравнением Бернулли. Решаем его подстановкой
где – вспомогательные функции.
Подставим в исходное уравнение:
(8)
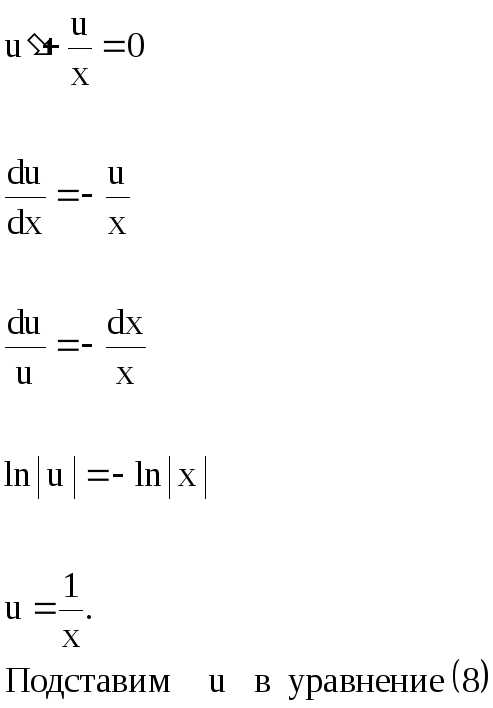
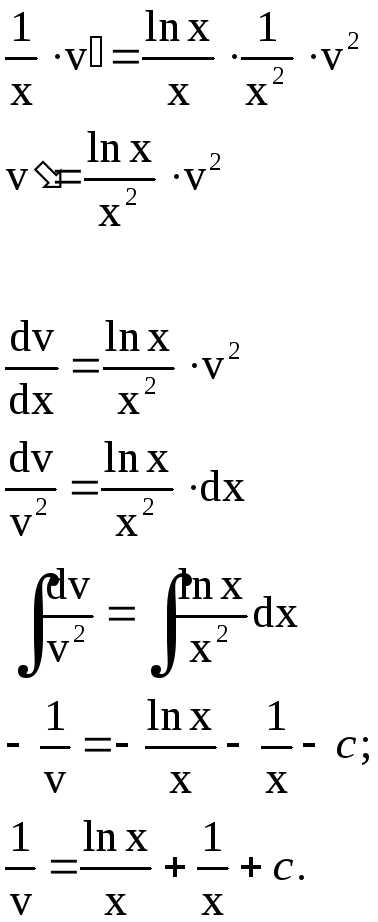
Для получения общего интеграла найдем
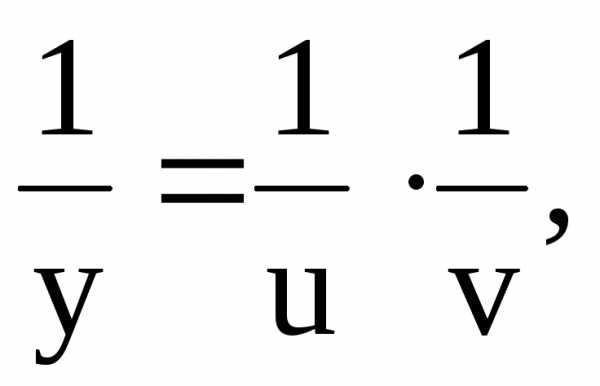
или
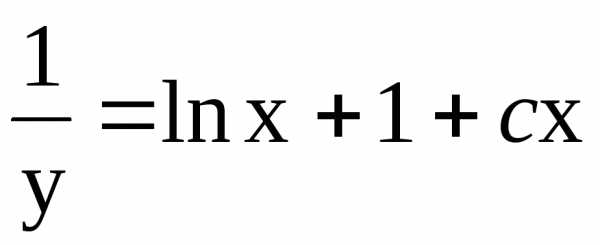 .
.
Замечание. Неопределенный интеграл 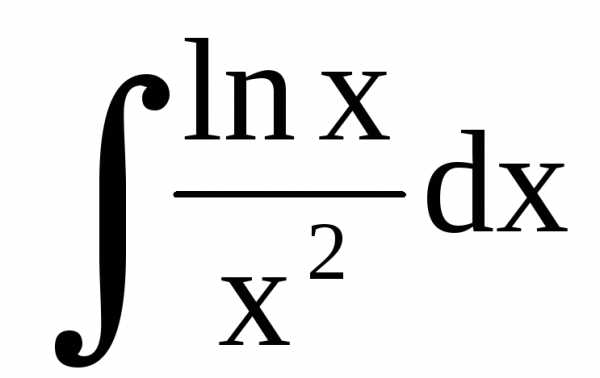 найден с применением
найден с применением
формулы интегрирования по частям:
Производим подстановку
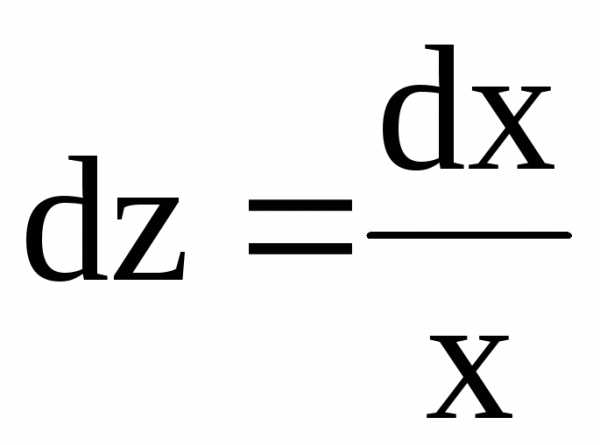 ;
;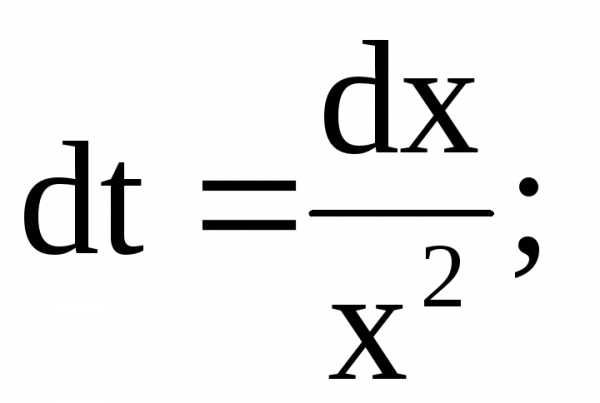
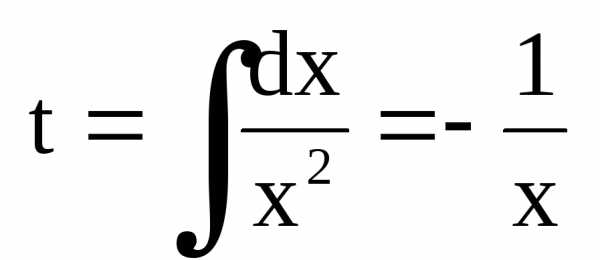 .
.
Тогда 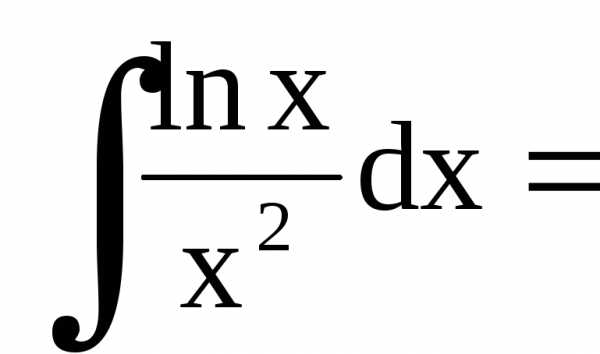
studfiles.net
Приводящиеся к линейным дифференциальные уравнения первого порядка

Рассмотрены дифференциальные уравнения, приводящиеся к линейным дифференциальным уравнениям первого порядка. Дан пример подробного решения дифференциального уравнения, приводящегося к линейному уравнению.
К линейным уравнениям первого порядка приводится уравнения вида:
(1) ,
где z – функция от y; p и q – функции от x.
Действительно, по правилу дифференцирования сложной функции:
.
Подставляя в (1), получаем уравнение, линейное относительно z:
.
Дифференциальные уравнения, линейные относительно переменной x
Ранее мы рассматривали уравнения, линейные относительно переменной y. То есть мы считали, что x является независимой переменной, а y является зависимой переменной. Однако, всегда стоит иметь в виду, что возможен противоположный подход. То есть можно считать переменную y независимой переменной, а x – зависимой переменной. На практике часто встречаются задачи, в которых уравнение линейно относительно переменной x, а не y. В общем виде такое уравнение можно записать так:
где P, Q, R –функции от y.
Покажем, что это уравнение линейно относительно переменной x. Для этого выполняем преобразования. Представим производную в виде отношения дифференциалов:
.
Тогда уравнение (2) примет вид:
.
Умножаем на и выполняем алгебраические преобразования:
;
.
Разделив на R(y), приводим уравнение к виду:
,
где .
Это – линейное относительно x дифференциальное уравнение.
Пример решения дифференциального уравнения, приводящегося к линейному уравнению первого порядка
Решить уравнение:
(П.1) .
Решение
Подставим в (П.1):
.
Считаем, что y – это независимая переменная, а x – зависимая. То есть x – это функция от y. Умножим на :
(П.2) .
Делаем подстановку:
.
Здесь z – сложная функция от y, .
Дифференцируем по y. По правилу дифференцирования сложной функции:
.
Подставляем в (П.2):
;
.
Это линейное, относительно z, дифференциальное уравнение. Решаем его с помощью интегрирующего множителя. Умножаем уравнение на интегрирующий множитель e y:
;
;
.
Интегрируем по частям:
;
;
;
.
Переходим к переменной x:
;
.
Ответ
.
Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.
Автор: Олег Одинцов. Опубликовано: Изменено:
Линейные дифференциальные уравнения первого порядка
Линейные однородные и неоднородные ДУ первого порядка
Функции и , входящие в уравнение, являются непрерывными на некотором интервале , на котором ищется решение рассматриваемого уравнения.
Решение неоднородных дифференциальных уравнений первого порядка
1. Метод Бернулли. Общее решение неоднородного дифференциального уравнения (1) ищется в виде
Отсюда
После подстановки в уравнение (1), будем иметь:
Функции и подбираются таким образом, чтобы выражение , стоящее в скобках второго слагаемого, равнялось нулю. То есть уравнение (3) распадается на два уравнения:
Первое из уравнений системы является дифференциальным уравнением с разделяющимися переменными:
Второе уравнение системы принимает вид:
Отсюда
А тогда
2. Метод вариации произвольной постоянной (метод Лагранжа). Данный метод заключается в следующем:
1) Вначале ищется общее решение однородного дифференциального уравнения (2):
2) Далее C считается не константой, а некоторой функцией от переменной x:
Находим производную и в заданное неоднородное дифференциальное уравнение подставляем полученное выражение для и . Из полученного уравнения находим функцию .
3) В общее решение (4) однородного уравнения вместо C подставляем найденное выражение .
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Линейные уравнения первого порядка
Такое дифференциальное уравнение можно решить методом разделения переменных. Представим его в стандартном виде метода: $y’=-P\left(x\right)\cdot y$, где $f_{1} \left(x\right)=-P\left(x\right)$ и $f_{2} \left(y\right)=y$.
Вычислим интеграл $I_{1} =\int f_{1} \left(x\right)\cdot dx =-\int P\left(x\right)\cdot dx $.
Вычислим интеграл $I_{2} =\int \frac{dy}{f_{2} \left(y\right)} =\int \frac{dy}{y} =\ln \left|y\right|$.
Запишем общее решение в виде $\ln \left|y\right|+\int P\left(x\right)\cdot dx =\ln \left|C_{1} \right|$, где $\ln \left|C_{1} \right|$ — произвольная постоянная, взятая в удобном для дальнейших преобразований виде.
Выполним преобразования:
\[\ln \left|y\right|-\ln \left|C_{1} \right|=-\int P\left(x\right)\cdot dx ; \ln \frac{\left|y\right|}{\left|C_{1} \right|} =-\int P\left(x\right)\cdot dx .\]Используя определение логарифма, получим: $\left|y\right|=\left|C_{1} \right|\cdot e^{-\int P\left(x\right)\cdot dx } $. Это равенство, в свою очередь, эквивалентно равенству $y=\pm C_{1} \cdot e^{-\int P\left(x\right)\cdot dx } $.
Заменив произвольную постоянную $C=\pm C_{1} $, получим общее решение линейного однородного дифференциального уравнения: $y=C\cdot e^{-\int P\left(x\right)\cdot dx } $.
Решив уравнение $f_{2} \left(y\right)=y=0$, найдем особые решения. Обычной проверкой убеждаемся, что функция $y=0$ является особым решением данного дифференциального уравнения.
Однако это же решение можно получить из общего решения $y=C\cdot e^{-\int P\left(x\right)\cdot dx } $, положив в нём $C=0$.
Таким образом, окончательный результат: $y=C\cdot e^{-\int P\left(x\right)\cdot dx } $.
Общий метод решения линейного однородного дифференциального уравнения первого порядка можно представить в виде следующего алгоритма:
- Для решения данного уравнения его сначала следует представить в стандартном виде метода $y’+P\left(x\right)\cdot y=0$. Если добиться этого не удалось, то данное дифференциальное уравнение должно решаться иным методом.
- Вычисляем интеграл $I=\int P\left(x\right)\cdot dx $.
- Записываем общее решение в виде $y=C\cdot e^{-I} $ и при необходимости выполняем упрощающие преобразования.
Решение одного сложного линейного неоднородного дифференциального уравнения может быть сведено к решению двух более простых дифференциальных уравнений. Для этого искомую функцию $y$ следует заменить произведением двух вспомогательных функций $u$ и $v$, то есть положить $y=u\cdot v$.
Выполняем дифференцирование принятой замены: $\frac{dy}{dx} =\frac{du}{dx} \cdot v+u\cdot \frac{dv}{dx} $. Подставляем полученное выражение в данное дифференциальное уравнение: $\frac{du}{dx} \cdot v+u\cdot \frac{dv}{dx} +P\left(x\right)\cdot u\cdot v=Q\left(x\right)$ или $\frac{du}{dx} \cdot v+u\cdot \left[\frac{dv}{dx} +P\left(x\right)\cdot v\right]=Q\left(x\right)$.
Отметим, что если принято $y=u\cdot v$, то в составе произведения $u\cdot v$ одну из вспомогательных функций можно выбирать произвольно. Выберем вспомогательную функцию $v$ так, чтобы выражение в квадратных скобках обратилось в нуль. Для этого достаточно решить дифференциальное уравнение $\frac{dv}{dx} +P\left(x\right)\cdot v=0$ относительно функции $v$ и выбрать для неё простейшее частное решение $v=v\left(x\right)$, отличное от нуля. Это дифференциальное уравнение является линейным однородным и решается оно вышерассмотренным методом.
Полученное решение $v=v\left(x\right)$ подставляем в данное дифференциальное уравнение с учетом того, что теперь выражение в квадратных скобках равно нулю, и получаем еще одно дифференциальное уравнение, но теперь относительно вспомогательной функции $u$: $\frac{du}{dx} \cdot v\left(x\right)=Q\left(x\right)$. Это дифференциальное уравнение можно представить в виде $\frac{du}{dx} =\frac{Q\left(x\right)}{v\left(x\right)} $, после чего становится очевидно, что оно допускает непосредственное интегрирование. Для этого дифференциального уравнения необходимо найти общее решение в виде $u=u\left(x,\; C\right)$.
Теперь можно найти общее решение данного линейного неоднородного дифференциального уравнения первого порядка в виде $y=u\left(x,C\right)\cdot v\left(x\right)$.
Общий метод решения линейного неоднородного дифференциального уравнения первого порядка можно представить в виде следующего алгоритма:
- Для решения данного уравнения его сначала следует представить в стандартном виде метода $y’+P\left(x\right)\cdot y=Q\left(x\right)$. Если добиться этого не удалось, то данное дифференциальное уравнение должно решаться иным методом.
- Вычисляем интеграл $I_{1} =\int P\left(x\right)\cdot dx $, записываем частное решение в виде $v\left(x\right)=e^{-I_{1} } $, выполняем упрощающие преобразования и выбираем для $v\left(x\right)$ простейший ненулевой вариант.
- Вычисляем интеграл $I_{2} =\int \frac{Q\left(x\right)}{v\left(x\right)} \cdot dx $, посля чего записываем выражение в виде $u\left(x,C\right)=I_{2} +C$.
- Записываем общее решение данного линейного неоднородного дифференциального уравнения в виде $y=u\left(x,C\right)\cdot v\left(x\right)$ и при необходимости выполняем упрощающие преобразования.
Задача 2
Найти общее решение дифференциального уравнения $y’-\frac{y}{x} =3\cdot x$.
Имеем линейное неоднородное уравнение первого порядка в стандартном виде, для которого $P\left(x\right)=-\frac{1}{x} $ и $Q\left(x\right)=3\cdot x$.
Вычисляем интеграл $I_{1} =\int P\left(x\right)\cdot dx =-\int \frac{1}{x} \cdot dx=-\ln \left|x\right| $.
Записываем частное решение в виде $v\left(x\right)=e^{-I_{1} } $ и выполняем упрощающие преобразования: $v\left(x\right)=e^{\ln \left|x\right|} $; $\ln v\left(x\right)=\ln \left|x\right|$; $v\left(x\right)=\left|x\right|$. Вибираем для $v\left(x\right)$ простейший ненулевой вариант: $v\left(x\right)=x$.
Вычисляем интеграл $I_{2} =\int \frac{Q\left(x\right)}{v\left(x\right)} \cdot dx =\int \frac{3\cdot x}{x} \cdot dx=3\cdot x $.
Записываем выражение $u\left(x,C\right)=I_{2} +C=3\cdot x+C$.
Окончательно записываем общее решение данного линейного неоднородного дифференциального уравнения в виде $y=u\left(x,C\right)\cdot v\left(x\right)$, то есть $y=\left(3\cdot x+C\right)\cdot x$.
spravochnick.ru
Линейные дифференциальные уравнения первого порядка [wiki.eduVdom.com]
subjects:diffury:линейные_уравнения_первого_порядка
Линейным дифференциальным уравнением 1-ого порядка называется уравнение, линейное относительно неизвестной функции и её производной $$ \frac{dy}{dx} +p(x)y =Q(x) \qquad (1)$$
Решение линейного уравнения ищем в виде $y=u(x)v(x)$
Подставляя в (1), после преобразования получаем $$ u \left ( \frac{dv}{dx} + p(x)v \right ) +V\frac{du}{dx} =Q(x) $$
Выберем v такой чтобы $\frac{dv}{dx} + p(x)v =0$ найдём u(x) , и следовательно получим решение $y=uv$
Пример 1
Решить дифференциальное уравнение: ${xy}’-2y=4x^{4}-x$
Решение дифференциального уравнения:
Пример 2. Решить задачу Коши $$ {y}’-y=-e^{-x} \,,\, y|_{x=0}=2 $$
Решение. Это линейное уравнение. Ищем общее решение в виде $y=u(x)v(x)$ , имеем ${y}’={u}’v+u{v}’$ . Подставляя выражения для y и ${y}’$ в данное уравнение, будем иметь
$$
u({v}’-v)+{u}’v=-e^{-x}
\\
u \left (
\frac{dv}{dx} -v
\right )
+\frac{du}{dx}v
=e^{-x}
\\
\frac{dv}{dx}-v=0
\;;\;
\frac{dv}{v}=dx
\;;\;
\ln{|v|}=x
\;;\;
v=e^{x}
$$
Для определения u имеем уравнение
$$
{u}’v=-e^{-x}
\\
\frac{du}{dx}e^{x}=-e^{-x}
\;;\;
\frac{du}{dx}=-e^{-2x}
\;;\;
u=\frac{ e^{-2x} }{2} +c
\\
y=uv=e^{x} \left(
\frac{ e^{-2x} }{2} +c
\right )
=\frac{ e^{-x} }{2} +Ce^{x}
$$
Найдём C: $2=\frac{1}{2}+c \,,\, c=\frac{3}{2}$;
Итак, решением поставленной задачи Коши будет $$ y=\frac{1}{2} \left ( \frac{1}{e^{x}} +3e^{x} \right ) $$
subjects/diffury/линейные_уравнения_первого_порядка.txt · Последние изменения: 2014/12/15 20:27 — ¶
www.wiki.eduvdom.com
Конспект лекции_6 Дифференциальные уравнения первого порядка
Учреждение образования «Белорусская государственная
сельскохозяйственная академия»
Кафедра высшей математики
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
Конспект лекции для студентов бухгалтерского факультета
заочной формы получения образования (НИСПО)
Горки, 2013
Дифференциальные уравнения первого порядка
Понятие дифференциального уравнения. Общее и частное решения
При изучении различных явлений часто не удаётся найти закон, который непосредственно связывает независимую переменную и искомую функцию, но можно установить связь между искомой функцией и её производными.
Соотношение, связывающее независимую переменную, искомую функцию и её производные, называется дифференциальным уравнением:
. (1)
Здесь x – независимая переменная, y – искомая функция, — производные искомой функции. При этом в соотношении (1) обязательно наличие хотя бы одной производной.
Порядком дифференциального уравнения называется порядок старшей производной, входящей в уравнение.
Рассмотрим дифференциальное уравнение
. (2)
Так в это уравнение входит производная только первого порядка, то оно называется дифференциальным уравнением первого порядка.
Если уравнение (2) можно разрешить относительно производной и записать в виде
, (3)
то такое уравнение называется дифференциальным уравнением первого порядка в нормальной форме.
Во многих случаях целесообразно рассматривать уравнение вида
, (4)
которое называется дифференциальным уравнением первого порядка, записанным в дифференциальной форме.
Так
как 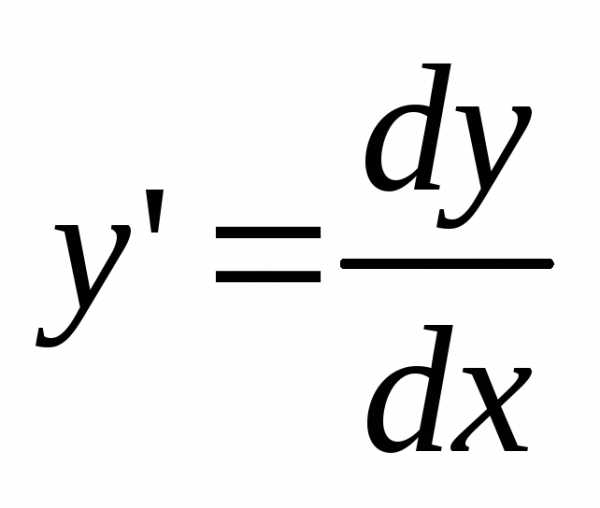 ,
то уравнение (3) можно записать в виде
,
то уравнение (3) можно записать в виде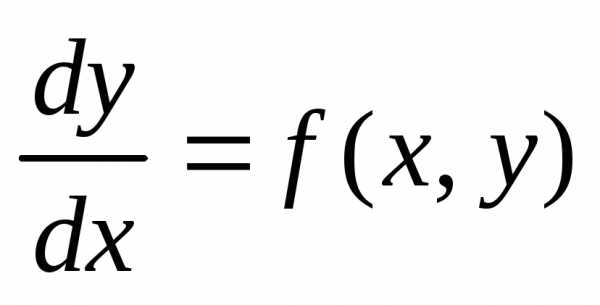 или,
где можно считатьи.
Это означает, что уравнение (3) преобразовано
в уравнение (4).
или,
где можно считатьи.
Это означает, что уравнение (3) преобразовано
в уравнение (4).
Запишем
уравнение (4) в виде
.
Тогда,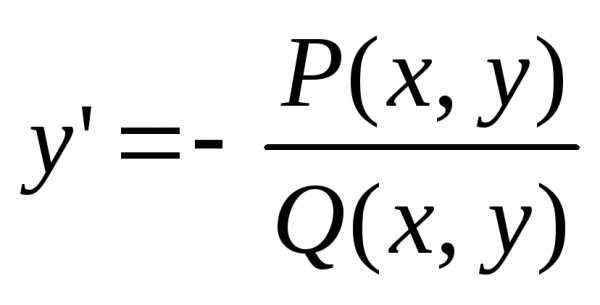 ,,
где можно считать
,,
где можно считать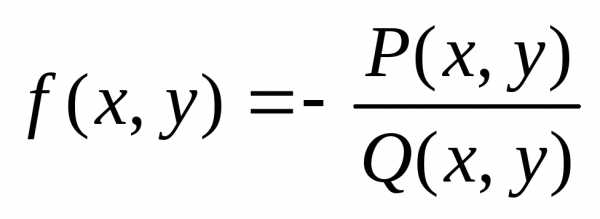 , т.е. получено уравнение вида (3). Таким
образом, уравнения (3) и (4) равносильны.
, т.е. получено уравнение вида (3). Таким
образом, уравнения (3) и (4) равносильны.
Решением
дифференциального уравнения (2) или (3) называется любая функция 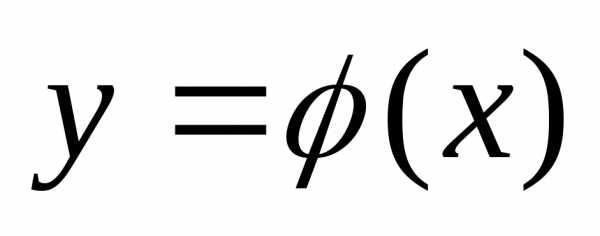 ,
которая при подстановке её в уравнение
(2) или (3) обращает его в тождество:
,
которая при подстановке её в уравнение
(2) или (3) обращает его в тождество:
или .
Процесс
нахождения всех решений дифференциального
уравнения называется его интегрированием,
а график решения 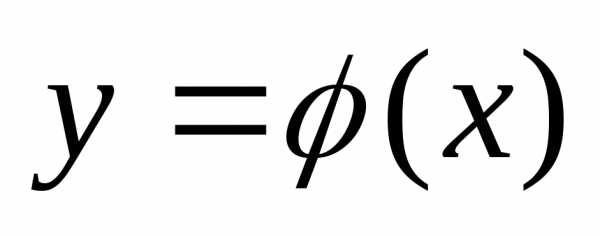 дифференциального уравнения называетсяинтегральной
кривой этого уравнения.
дифференциального уравнения называетсяинтегральной
кривой этого уравнения.
Если решение дифференциального уравнения получено в неявном виде , то оно называетсяинтегралом данного дифференциального уравнения.
Общим решением дифференциального уравнения первого порядка называется семейство функций вида , зависящее от произвольной постояннойС, каждая из которых является решением данного дифференциального уравнения при любом допустимом значении произвольной постоянной С. Таким образом, дифференциальное уравнение имеет бесчисленное множество решений.
Частным
решением дифференциального уравнения называется
решение, получаемое из формулы общего
решения при конкретном значении
произвольной постоянной С,
включая 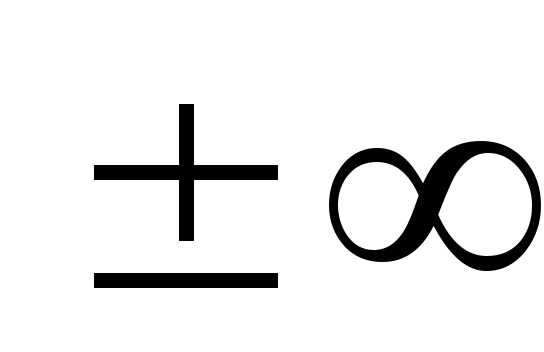 .
.
Задача Коши и её геометрическая интерпретация
Уравнение (2) имеет бесчисленное множество решений. Чтобы из этого множества выделить одно решение, которое называется частным, нужно задать некоторые дополнительные условия.
Задача отыскания частного решения уравнения (2) при заданных условиях называется задачей Коши. Эта задача является одной из важнейших в теории дифференциальных уравнений.
Формулируется
задача Коши следующим образом: среди
всех решений уравнения (2) найти такое
решение  ,
в котором функция
,
в котором функция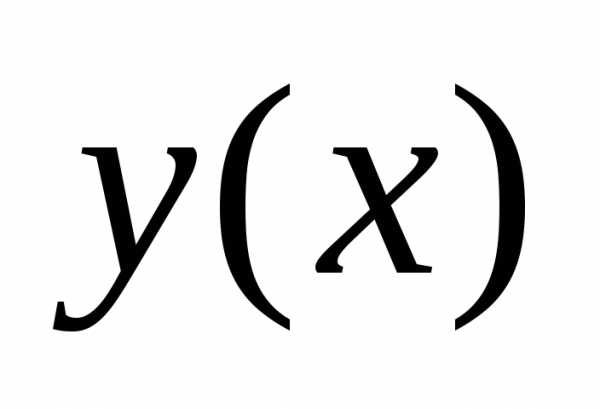 принимает заданное числовое значение
принимает заданное числовое значение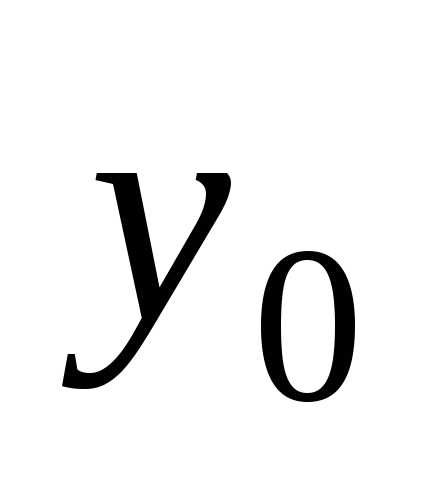 ,
если независимая переменнаяx принимает заданное числовое значение
,
если независимая переменнаяx принимает заданное числовое значение 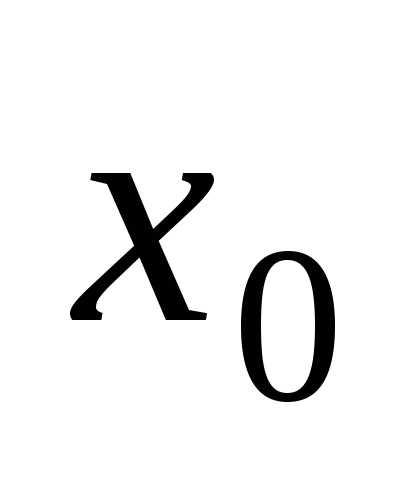 ,
т.е.
,
т.е.
, , (5)
где D – область определения функции  .
.
Значение 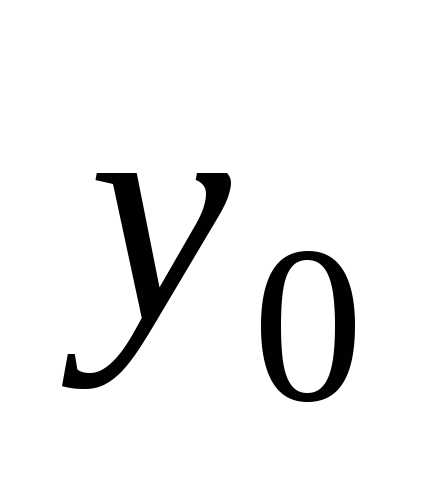 называетсяначальным
значением функции,
а
называетсяначальным
значением функции,
а 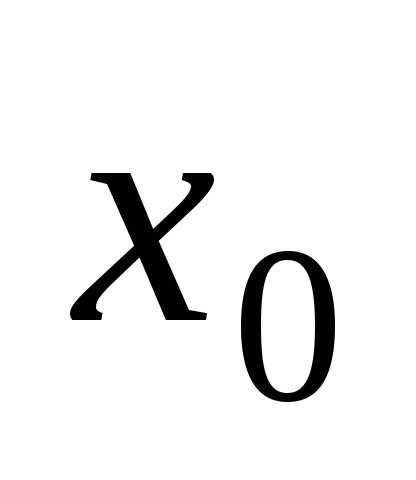 – начальным
значением независимой переменной.
Условие (5) называется начальным
условием или условием
Коши.
– начальным
значением независимой переменной.
Условие (5) называется начальным
условием или условием
Коши.
С геометрической точки зрения задачу Коши для дифференциального уравнения (2) можно сформулировать следующим образом: из множества интегральных кривых уравнения (2) выделить ту, которая проходит через заданную точку .
Дифференциальные уравнения с разделяющимися переменными
Одним из простейших видов дифференциальных уравнений является дифференциальное уравнение первого порядка, не содержащее искомой функции:
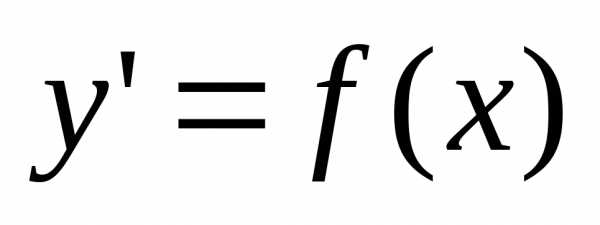 .
(6)
.
(6)
Учитывая,
что 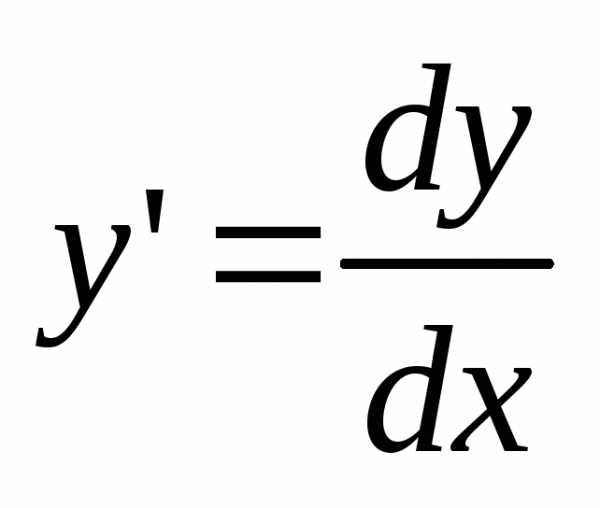 ,
запишем уравнение в виде
,
запишем уравнение в виде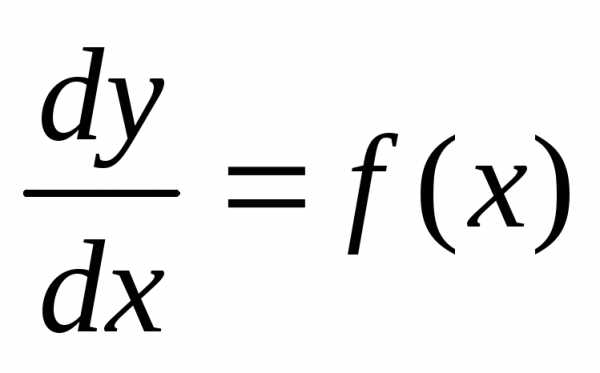 или.
Интегрируя обе части последнего
уравнения, получим:или
или.
Интегрируя обе части последнего
уравнения, получим:или
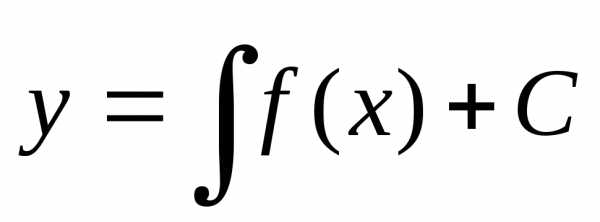 .
(7)
.
(7)
Таким образом, (7) является общим решением уравнения (6).
Пример 1. Найти общее решение дифференциального уравнения .
Решение.
Запишем уравнение в виде 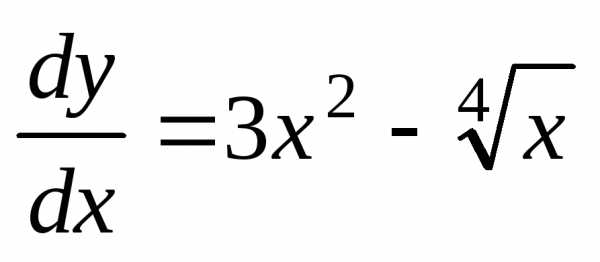 или
или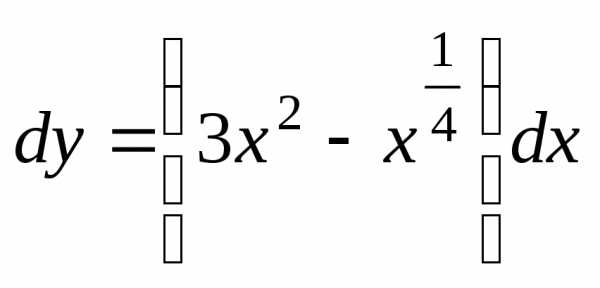 .
Проинтегрируем обе части полученного
уравнения:
.
Проинтегрируем обе части полученного
уравнения: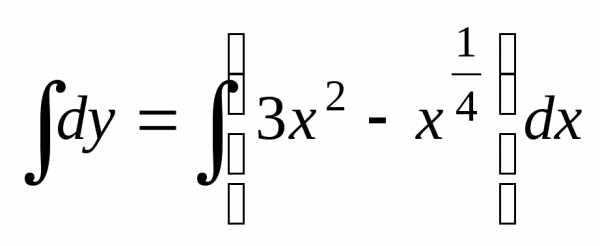 ,
,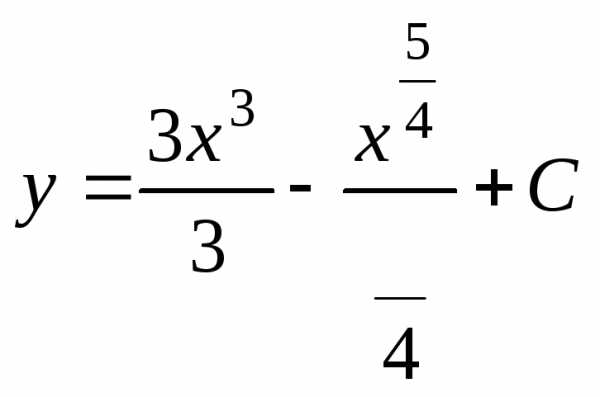 .
Окончательно запишем
.
Окончательно запишем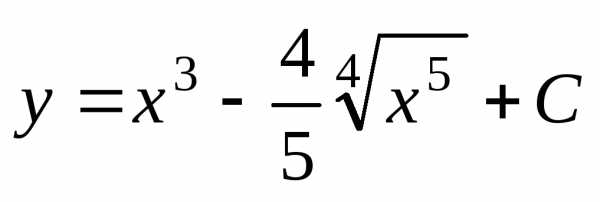 .
.
Пример
2.
Найти решение уравнения 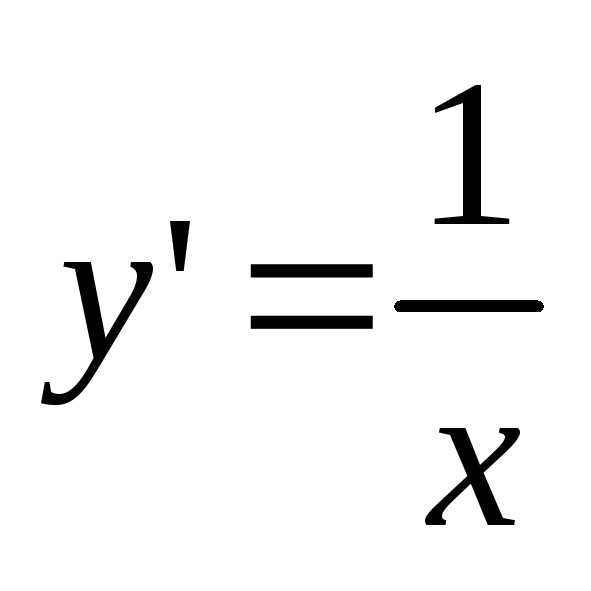 при условии
при условии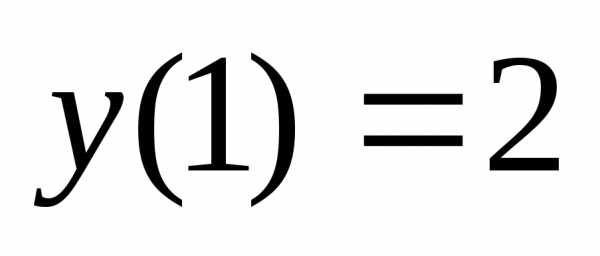 .
.
Решение.
Найдём общее решение уравнения: 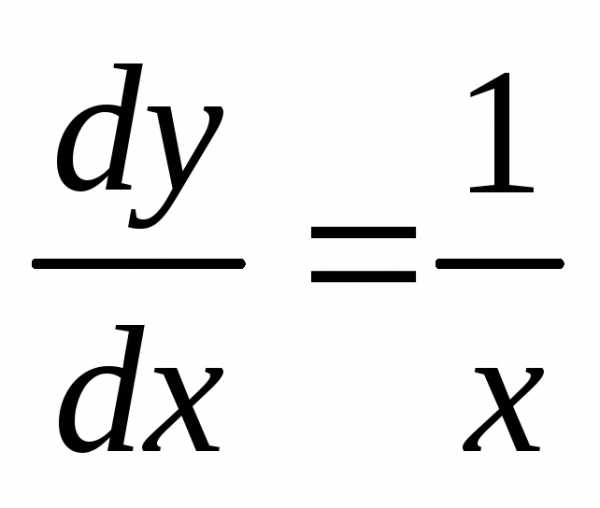 ,
,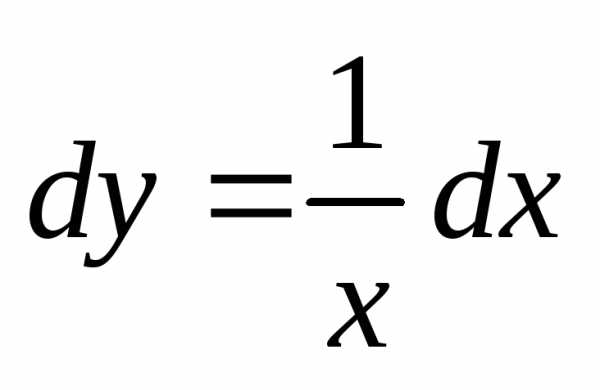 ,
, ,.
По условию
,.
По условию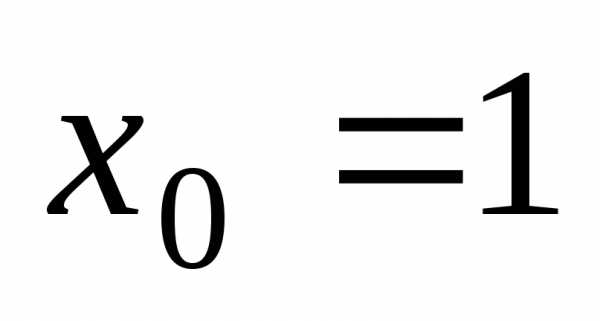 ,
,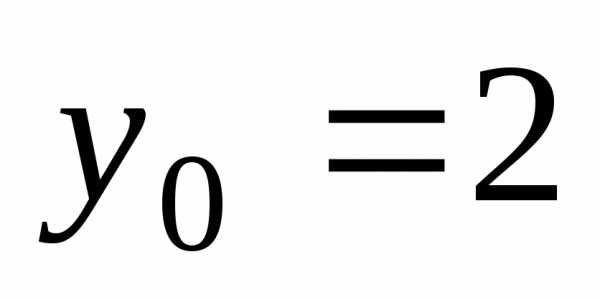 .
Подставим в общее решение:или
.
Подставим в общее решение:или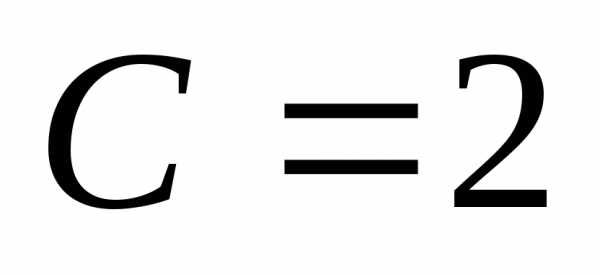 .
Найденное значение произвольной
постоянной подставим в формулу общего
решения:
.
Найденное значение произвольной
постоянной подставим в формулу общего
решения: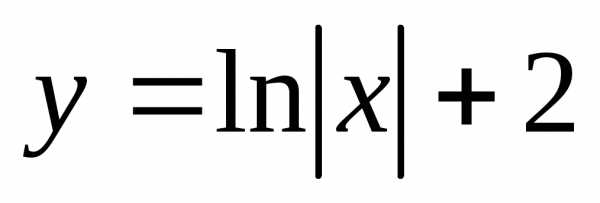 .
Это и есть частное решение дифференциального
уравнения, удовлетворяющее заданному
условию.
.
Это и есть частное решение дифференциального
уравнения, удовлетворяющее заданному
условию.
Уравнение
 (8)
(8)
Называется дифференциальным
уравнением первого порядка, не содержащим
независимой переменной.
Запишем его в виде 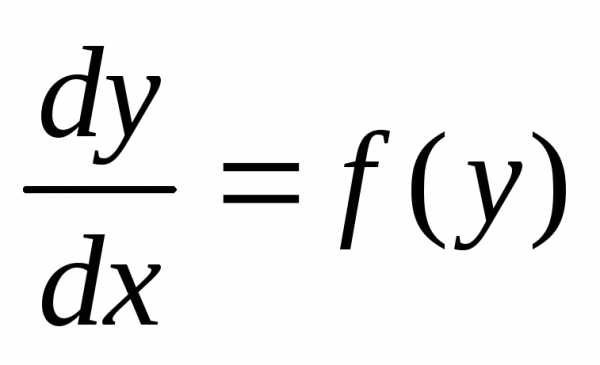 или
или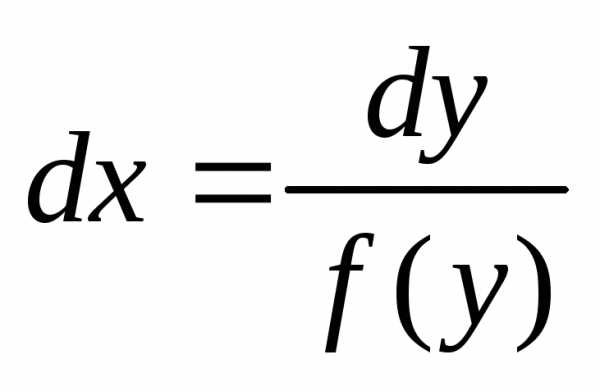 .
Проинтегрируем обе части последнего
уравнения:
.
Проинтегрируем обе части последнего
уравнения: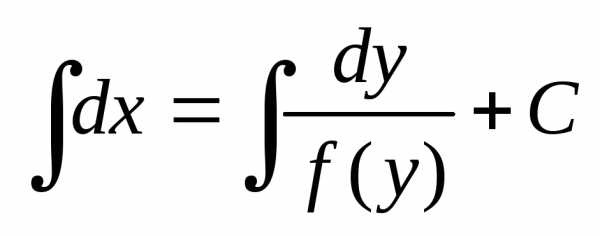 или
или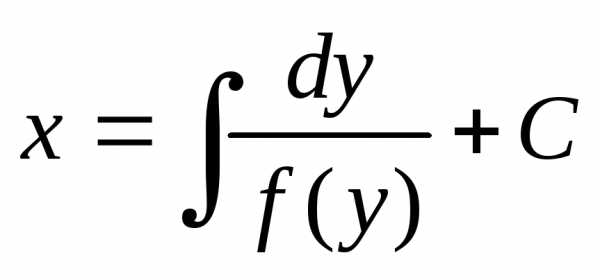 — общее решение уравнения (8).
— общее решение уравнения (8).
Пример.
Найти общее решение уравнения 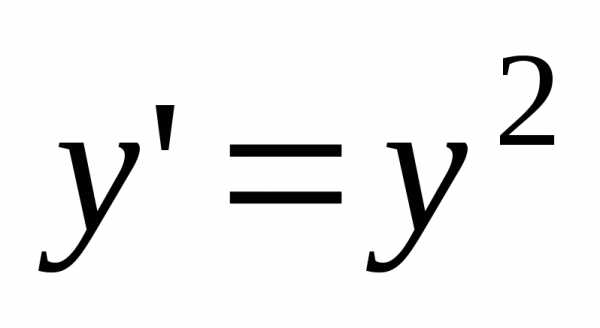 .
.
Решение.
Запишем это уравнение в виде:  или
или .
Тогда
.
Тогда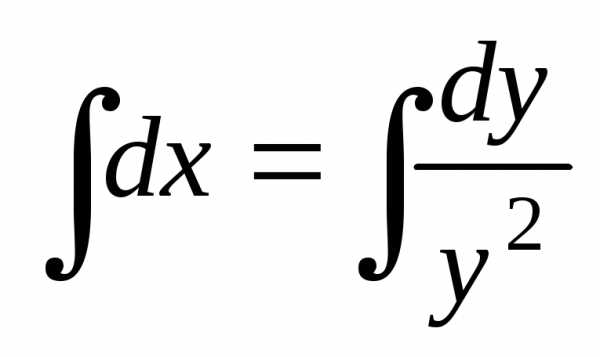 ,
,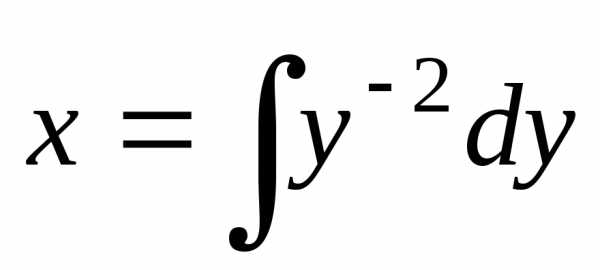 ,
, ,
,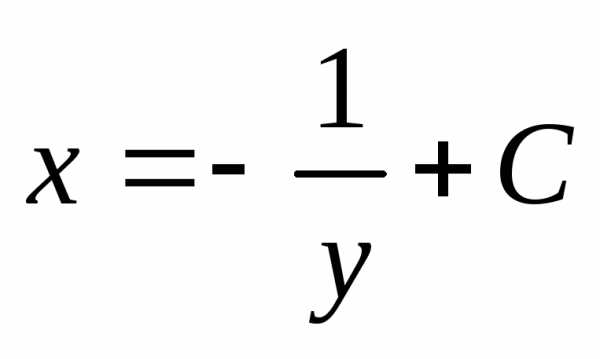 .
Таким образом,
.
Таким образом,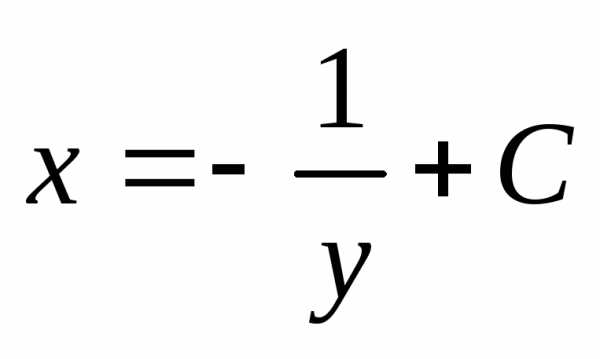 – общее решение данного уравнения.
– общее решение данного уравнения.
Уравнение вида
(9)
интегрируется
с помощью разделения переменных. Для
этого уравнение запишем в виде 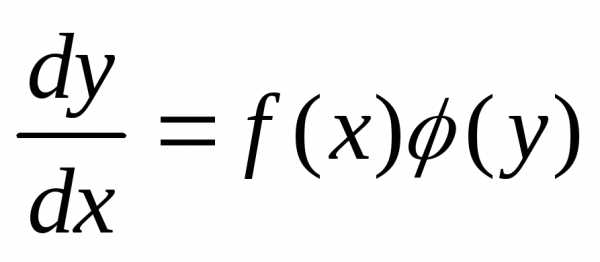 ,
а затем с помощью операций умножения и
деления приводим его к такой форме,
чтобы в одну часть входила только функция
отх и дифференциал dx,
а во вторую часть – функция от у и дифференциал dy.
Для этого обе части уравнения нужно
умножить на dx и разделить на
,
а затем с помощью операций умножения и
деления приводим его к такой форме,
чтобы в одну часть входила только функция
отх и дифференциал dx,
а во вторую часть – функция от у и дифференциал dy.
Для этого обе части уравнения нужно
умножить на dx и разделить на 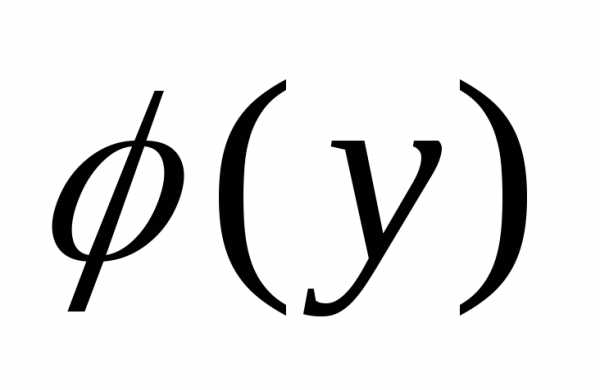 .
В результате получим уравнение
.
В результате получим уравнение
 ,
(10)
,
(10)
в котором переменные х и у разделены. Проинтегрируем обе части уравнения (10): . Полученное соотношение является общим интегралом уравнения (9).
Пример 3. Проинтегрировать уравнение .
Решение.
Преобразуем уравнение и разделим
переменные: 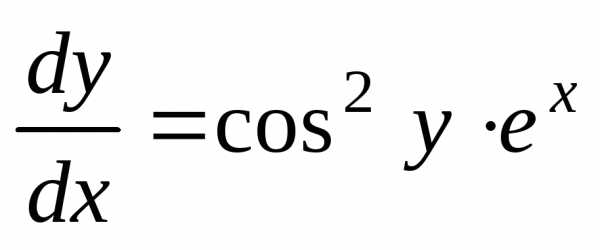 ,
,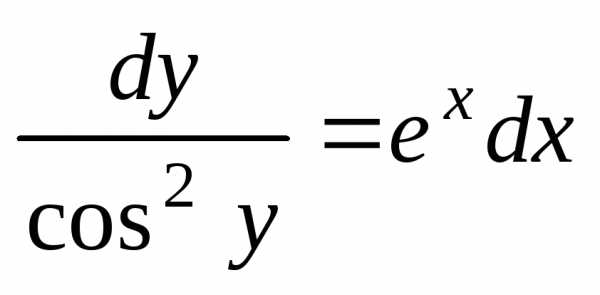 .
Проинтегрируем:
.
Проинтегрируем: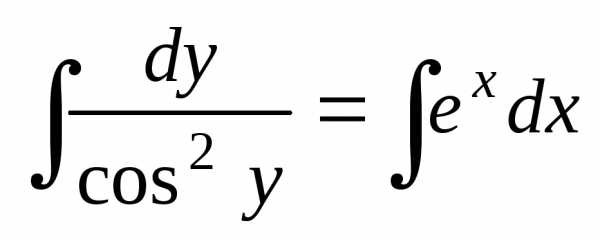 ,или – общий интеграл данного уравнения..
,или – общий интеграл данного уравнения..
Пусть уравнение задано в виде
. (11)
Такое уравнение называется дифференциальным уравнением первого порядка с разделяющимися переменными в симметрической форме.
Для разделения переменных нужно обе части уравнения разделить на :
. (12)
Полученное уравнение называется дифференциальным уравнением с разделёнными переменными. Проинтегрируем уравнение (12):
. (13)
(13)
Соотношение (13) является общим интегралом дифференциального уравнения (11).
Пример 4. Проинтегрировать дифференциальное уравнение .
Решение. Запишем уравнение в виде
и
разделим обе его части на  ,.
Полученное уравнение:
,.
Полученное уравнение: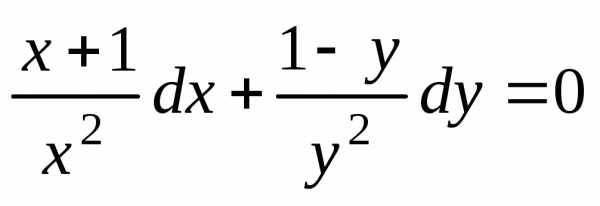 является уравнением с разделёнными
переменными. Проинтегрируем его:
является уравнением с разделёнными
переменными. Проинтегрируем его:
, ,
, . Последнее равенство является общим интегралом данного дифференциального уравнения.
Пример
5.
Найти частное решение дифференциального
уравнения
,
удовлетворяющее условию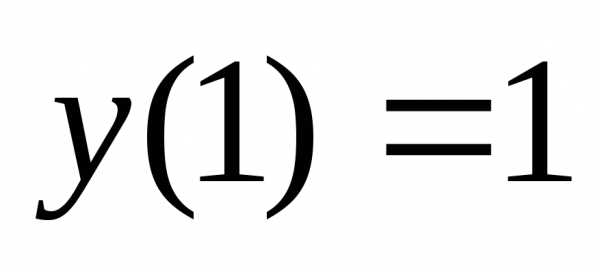 .
.
Решение.
Учитывая, что  ,
запишем уравнение в виде
,
запишем уравнение в виде или.
Разделим переменные:
или.
Разделим переменные: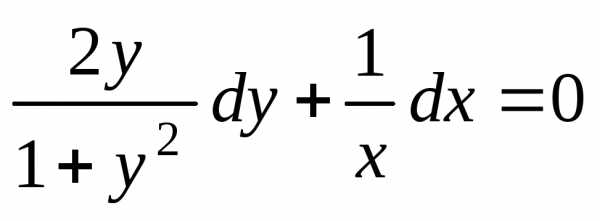 .
Проинтегрируем это уравнение:,,.
Полученное соотношение является общим
интегралом данного уравнения. По условию.
Подставим в общий интеграл и найдёмС:
,С=1.
Тогда выражение
является частным решением данного
дифференциального уравнения, записанным
в виде частного интеграла.
.
Проинтегрируем это уравнение:,,.
Полученное соотношение является общим
интегралом данного уравнения. По условию.
Подставим в общий интеграл и найдёмС:
,С=1.
Тогда выражение
является частным решением данного
дифференциального уравнения, записанным
в виде частного интеграла.
Линейные дифференциальные уравнения первого порядка
Уравнение
(14)
называется линейным
дифференциальным уравнением первого
порядка.
Неизвестная функция 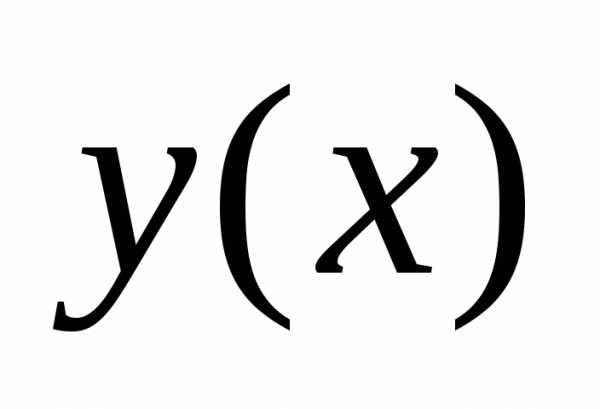 и её производная входят в это уравнение
линейно, а функции
и её производная входят в это уравнение
линейно, а функции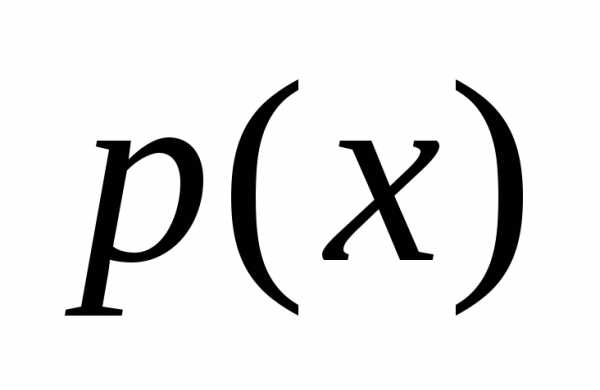 и
и непрерывны.
непрерывны.
Если  ,
то уравнение
,
то уравнение
(15)
называется линейным
однородным.
Если  ,
то уравнение (14) называетсялинейным
неоднородным.
,
то уравнение (14) называетсялинейным
неоднородным.
Для нахождения решения уравнения (14) обычно используют метод подстановки (Бернулли), суть которого в следующем.
Решение уравнения (14) будем искать в виде произведения двух функций
, (16)
где 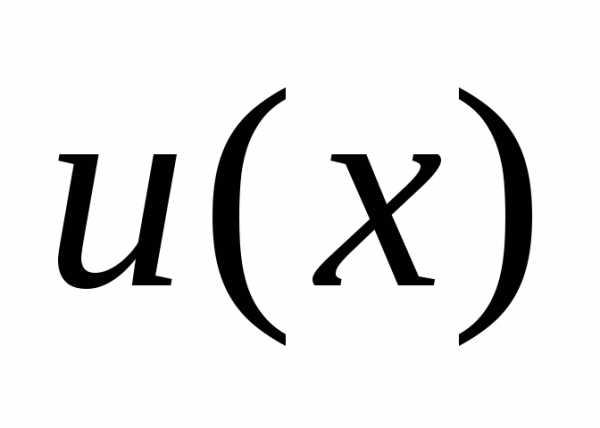 и
и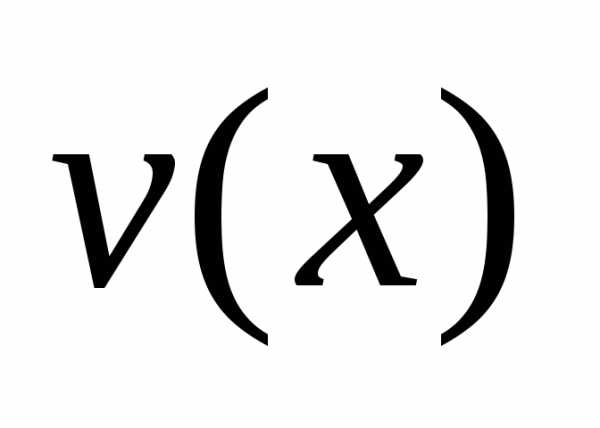 —
некоторые непрерывные функции. Подставим
—
некоторые непрерывные функции. Подставим и производнуюв уравнение (14):
и производнуюв уравнение (14):
или
Функцию v будем подбирать таким образом, чтобы выполнялось условие . Тогда. Таким образом, для нахождения решения уравнения (14) нужно решить систему дифференциальных уравнений

Первое
уравнение системы является линейным
однородным уравнением и решить его
можно методом разделения переменных: 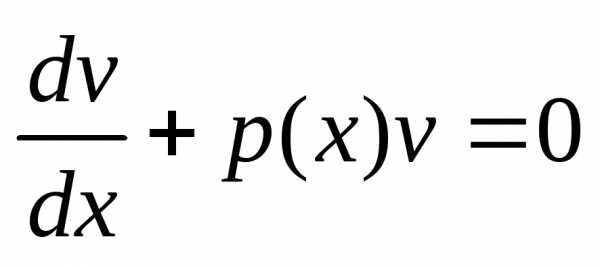 ,
,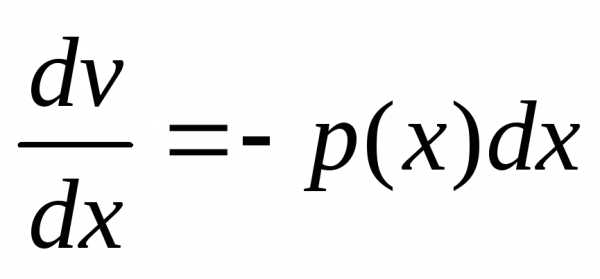 ,
,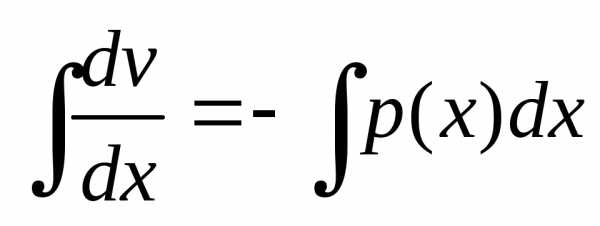 ,,.
В качестве функции
,,.
В качестве функции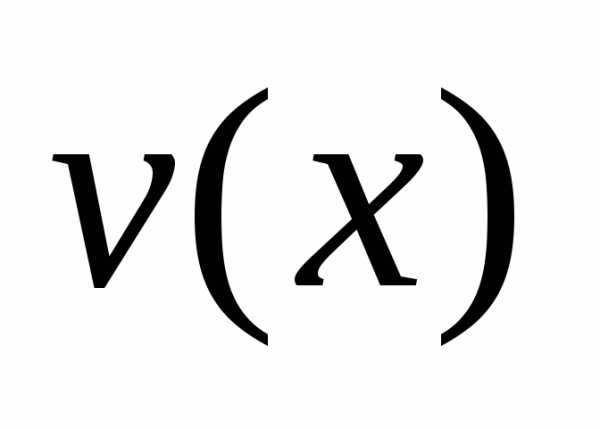 можно
взять одно из частных решений однородного
уравнения, т.е. приС=1:
можно
взять одно из частных решений однородного
уравнения, т.е. приС=1: 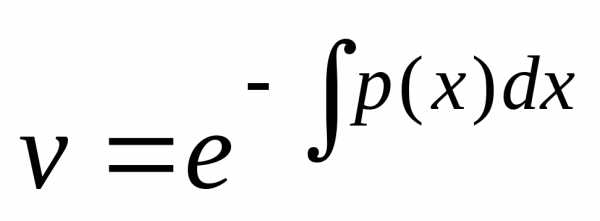 .
Подставим во второе уравнение системы:или.Тогда.
Таким образом, общее решение линейного
дифференциального уравнения первого
порядка имеет вид.
.
Подставим во второе уравнение системы:или.Тогда.
Таким образом, общее решение линейного
дифференциального уравнения первого
порядка имеет вид.
Пример
6.
Решить уравнение 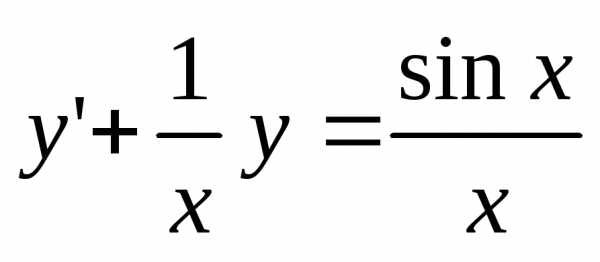 .
.
Решение.
Решение уравнения будем искать в виде 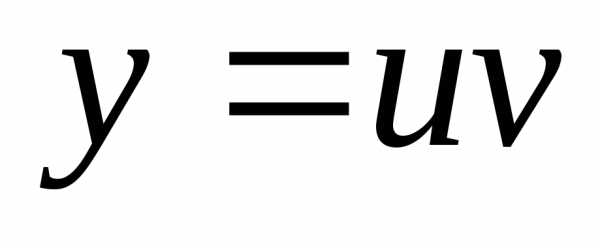 .
Тогда.
Подставим в уравнение:
.
Тогда.
Подставим в уравнение:
или
.
Функциюv выберем таким образом, чтобы выполнялось
равенство  .
Тогда
.
Тогда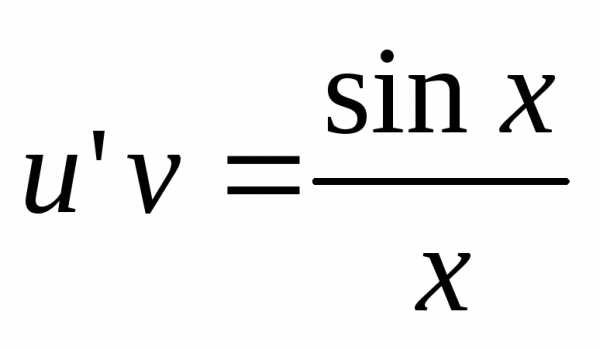 .
Решим первое из этих уравнений методом
разделения переменных:
.
Решим первое из этих уравнений методом
разделения переменных: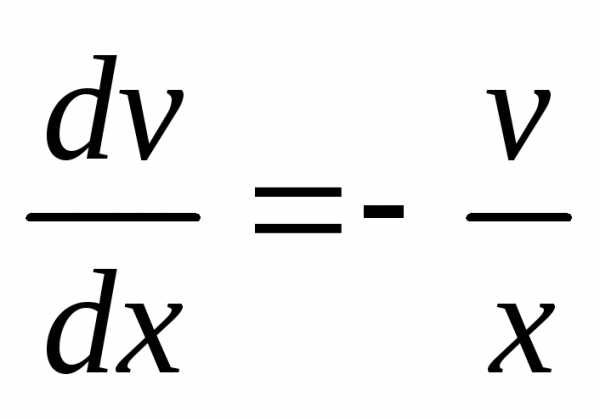 ,
,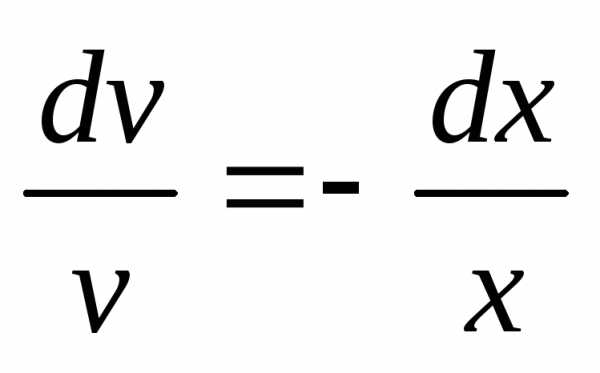 ,
,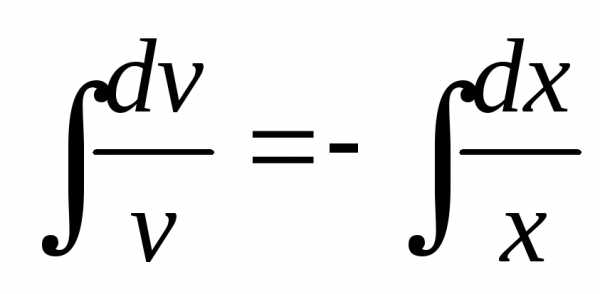 ,,
,,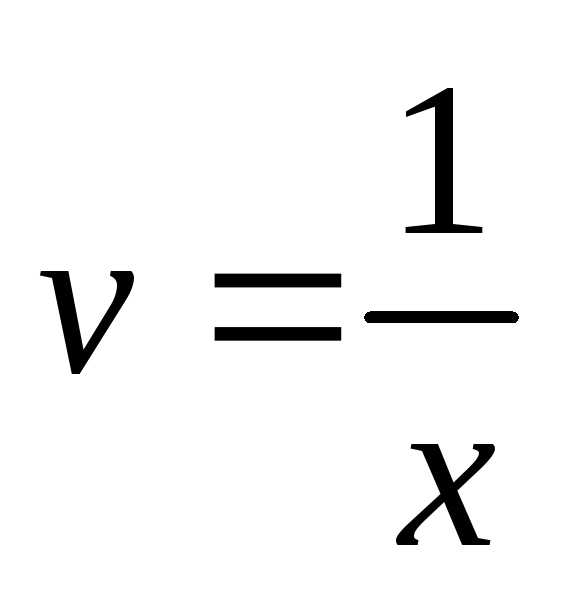 .
Функциюv подставим во второе уравнение:
.
Функциюv подставим во второе уравнение: 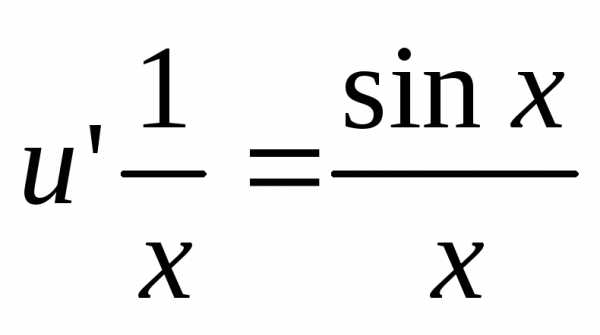 ,,
,,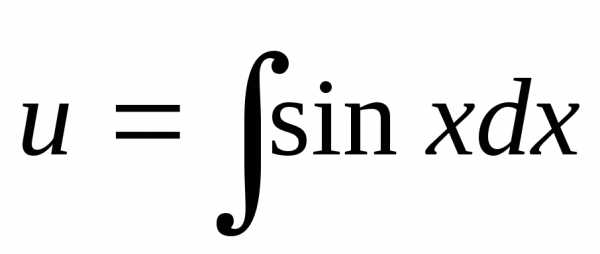 ,.
Общим решением данного уравнения
является
,.
Общим решением данного уравнения
является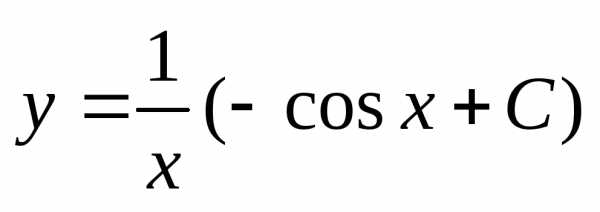 .
.
Вопросы для самоконтроля знаний
Что называется дифференциальным уравнением?
Что называется порядком дифференциального уравнения?
Какое дифференциальное уравнение называется дифференциальным уравнением первого порядка?
Как записывается дифференциальное уравнение первого порядка в дифференциальной форме?
Что называется решением дифференциального уравнения?
Что называется интегральной кривой?
Что называется общим решением дифференциального уравнения первого порядка?
Что называется частным решением дифференциального уравнения?
Как формулируется задача Коши для дифференциального уравнения первого порядка?
Какова геометрическая интерпретация задачи Коши?
Как записывается дифференциальное уравнение с разделяющимися переменными в симметрической форме?
Какое уравнение называется линейным дифференциальным уравнением первого порядка?
Каким методом можно решить линейное дифференциальное уравнение первого порядка и в чём суть этого метода?
Задания для самостоятельной работы
Решить дифференциальные уравнения с разделяющимися переменными:
а) ; б);
в) ; г).
2. Решить линейные дифференциальные уравнения первого порядка:
а) 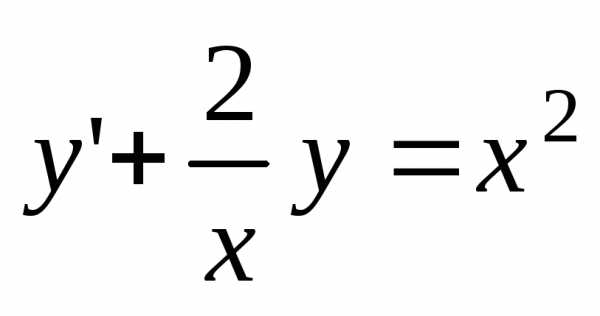 ;
б);
в)
;
б);
в)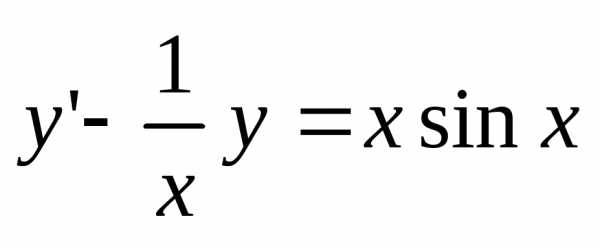 ;
;
г)
;
д) .
.
12
studfiles.net
Линейные и однородные дифференциальные уравнения первого порядка. Примеры решения
Думаю, нам стоит начать с истории такого славного математического инструмента как дифференциальные уравнения. Как и все дифференциальные и интегральные исчисления, эти уравнения были изобретены Ньютоном в конце 17-го века. Он считал именно это своё открытие настолько важным, что даже зашифровал послание, которое сегодня можно перевести примерно так: «Все законы природы описываются дифференциальными уравнениями». Это может показаться преувеличением, но всё так и есть. Любой закон физики, химии, биологии можно описать этими уравнениями.

Огромный вклад в развитие и создание теории дифференциальных уравнений внесли математики Эйлер и Лагранж. Уже в 18-м веке они открыли и развили то, что сейчас изучают на старших курсах университетов.
Новая веха в изучении дифференциальных уравнений началась благодаря Анри Пуанкаре. Он создал «качественную теорию дифференциальных уравнений», которая в сочетании с теорией функций комплексного переменного внесла значительный вклад в основание топологии — науки о пространстве и его свойствах.

Что такое дифференциальные уравнения?
Многие боятся одного словосочетания «дифференциальное уравнение». Однако в этой статье мы подробно изложим всю суть этого очень полезного математического аппарата, который на самом деле не так сложен, как кажется из названия. Для того чтобы начать рассказывать про дифференциальные уравнения первого порядка, следует сначала познакомиться с основными понятиями, которые неотъемлемо связаны с этим определением. И начнём мы с дифференциала.
Дифференциал
Многие знают это понятие ещё со школы. Однако всё же остановимся на нём поподробнее. Представьте себе график функции. Мы можем увеличить его до такой степени, что любой его отрезок примет вид прямой линии. На ней возьмём две точки, находящиеся бесконечно близко друг к другу. Разность их координат (x или y) будет бесконечно малой величиной. Ее и называют дифференциалом и обозначают знаками dy (дифференциал от y) и dx (дифференциал от x). Очень важно понимать, что дифференциал не является конечной величиной, и в этом заключается его смысл и основная функция.
А теперь необходимо рассмотреть следующий элемент, который нам пригодится при объяснении понятия дифференциального уравнения. Это — производная.
Производная
Все мы наверняка слышали в школе и это понятие. Говорят, что производная — это скорость роста или убывания функции. Однако из этого определения многое становится непонятным. Попробуем объяснить производную через дифференциалы. Давайте вернёмся к бесконечно малому отрезку функции с двумя точками, которые находятся на минимальном расстоянии друг от друга. Но даже за это расстояние функция успевает измениться на какую-то величину. И чтобы описать это изменение и придумали производную, которую иначе можно записать как отношение дифференциалов: f(x)’=df/dx.
Теперь стоит рассмотреть основные свойства производной. Их всего три:
- Производную суммы или разности можно представить как сумму или разность производных: (a+b)’=a’+b’ и (a-b)’=a’-b’.
- Второе свойство связано с умножением. Производная произведения — это сумма произведений одной функции на производную другой: (a*b)’=a’*b+a*b’.
- Производную разности записать можно в виде следующего равенства: (a/b)’=(a’*b-a*b’)/b2.
Все эти свойства нам пригодятся для нахождения решений дифференциальных уравнений первого порядка.
Также бывают частные производные. Допустим, у нас есть функция z, которая зависит от переменных x и y. Чтобы вычислить частную производную этой функции, скажем, по x, нам необходимо принять переменную y за постоянную и просто продифференцировать.
Интеграл
Другое важное понятие — интеграл. По сути это прямая противоположность производной. Интегралы бывают нескольких видов, но для решения простейших дифференциальных уравнений нам понадобятся самые тривиальные неопределённые интегралы.
Итак, что такое интеграл? Допустим, у нас есть некоторая зависимость f от x. Мы возьмём от неё интеграл и получим функцию F(x) (часто её называют первообразной), производная от которой равна первоначальной функции. Таким образом F(x)’=f(x). Отсюда следует также, что интеграл от производной равен первоначальной функции.
При решении дифференциальных уравнений очень важно понимать смысл и функцию интеграла, так как придётся очень часто их брать для нахождения решения.
Уравнения бывают разными в зависимости от своей природы. В следующем разделе мы рассмотрим виды дифференциальных уравнений первого порядка, а потом и научимся их решать.
Классы дифференциальных уравнений
«Диффуры» делятся по порядку производных, участвующих в них. Таким образом бывает первый, второй, третий и более порядок. Их также можно поделить на несколько классов: обыкновенные и в частных производных.
В этой статье мы рассмотрим обыкновенные дифференциальные уравнения первого порядка. Примеры и способы их решения мы также обсудим в следующих разделах. Будем рассматривать только ОДУ, потому что это самые распространённые виды уравнений. Обыкновенные делятся на подвиды: с разделяющимися переменными, однородные и неоднородные. Далее вы узнаете, чем они отличаются друг от друга, и научитесь их решать.
Кроме того, эти уравнения можно объединять, чтобы после у нас получилась система дифференциальных уравнений первого порядка. Такие системы мы тоже рассмотрим и научимся решать.
Почему мы рассматриваем только первый порядок? Потому что нужно начинать с простого, а описать всё, связанное с дифференциальными уравнениями, в одной статье просто невозможно.
Уравнения с разделяющимися переменными
Это, пожалуй, самые простые дифференциальные уравнения первого порядка. К ним относятся примеры, которые можно записать так: y’=f(x)*f(y). Для решения этого уравнения нам понадобится формула представления производной как отношения дифференциалов: y’=dy/dx. С помощью неё получаем такое уравнение: dy/dx=f(x)*f(y). Теперь мы можем обратиться к методу решения стандартных примеров: разделим переменные по частям, т. е. перенесём всё с переменной y в часть, где находится dy, и так же сделаем с переменной x. Получим уравнение вида: dy/f(y)=f(x)dx, которое решается взятием интегралов от обеих частей. Не стоит забывать и о константе, которую нужно ставить после взятия интеграла.
Решение любого «диффура» — это функция зависимости x от y (в нашем случае) или, если присутствует численное условие, то ответ в виде числа. Разберём на конкретном примере весь ход решения:
y’=2y*sin(x)
Переносим переменные в разные стороны:
dy/y=2*sin(x)dx
Теперь берём интегралы. Все их можно найти в специальной таблице интегралов. И получаем:
ln(y) = -2*cos(x) + C
Если требуется, мы можем выразить «игрек» как функцию от «икс». Теперь можно сказать, что наше дифференциальное уравнение решено, если не задано условие. Может быть задано условие, например, y(п/2)=e. Тогда мы просто подставляем значение этих переменных в решение и находим значение постоянной. В нашем примере оно равно 1.
Однородные дифференциальные уравнения первого порядка
Теперь переходим к более сложной части. Однородные дифференциальные уравнения первого порядка можно записать в общем виде так: y’=z(x,y). Следует заметить, что правая функция от двух переменных однородна, и её нельзя разделить на две зависимости: z от x и z от y. Проверить, является ли уравнение однородным или нет, достаточно просто: мы делаем замену x=k*x и y=k*y. Теперь сокращаем все k. Если все эти буквы сократились, значит уравнение однородное и можно смело приступать к его решению. Забегая вперёд, скажем: принцип решения этих примеров тоже очень прост.
Нам нужно сделать замену: y=t(x)*x, где t — некая функция, которая тоже зависит от x. Тогда мы можем выразить производную: y’=t'(x)*x+t. Подставляя всё это в наше исходное уравнение и упрощая его, мы получаем пример с разделяющимися переменными t и x. Решаем его и получаем зависимость t(x). Когда мы ее получили, то просто подставляем в нашу предыдущую замену y=t(x)*x. Тогда получаем зависимость y от x.
Чтобы было понятнее, разберём пример: x*y’=y-x*ey/x.
При проверке с заменой всё сокращается. Значит, уравнение действительно однородное. Теперь делаем другую замену, о которой мы говорили: y=t(x)*x и y’=t'(x)*x+t(x). После упрощения получаем следующее уравнение: t'(x)*x=-et. Решаем получившийся пример с разделёнными переменными и получаем: e-t=ln(C*x). Нам осталось только заменить t на y/x (ведь если y=t*x, то t=y/x), и мы получаем ответ: e-y/x=ln(x*С).

Линейные дифференциальные уравнения первого порядка
Пришло время рассмотреть ещё одну обширную тему. Мы разберём неоднородные дифференциальные уравнения первого порядка. Чем они отличаются от предыдущих двух? Давайте разберёмся. Линейные дифференциальные уравнения первого порядка в общем виде можно записать таким равенством: y’ + g(x)*y=z(x). Стоит уточнить, что z(x) и g(x) могут являться постоянными величинами.
А теперь пример: y’ — y*x=x2.
Существует два способа решения, и мы по порядку разберём оба. Первый — метод вариации произвольных констант.
Для того чтобы решить уравнение этим способом, необходимо сначала приравнять правую часть к нулю и решить получившееся уравнение, которое после переноса частей примет вид:
y’ = y*x;
dy/dx=y*x;
dy/y=xdx;
ln|y|=x2/2 + C;
y=ex2/2*уС=C1*ex2/2.
Теперь надо заменить константу C1 на функцию v(x), которую нам предстоит найти.
y=v*ex2/2.
Проведём замену производной:
y’=v’*ex2/2-x*v*ex2/2.
И подставим эти выражения в исходное уравнение:
v’*ex2/2 — x*v*ex2/2 + x*v*ex2/2 = x2.
Можно видеть, что в левой части сокращаются два слагаемых. Если в каком-то примере этого не произошло, значит вы что-то сделали не так. Продолжим:
v’*ex2/2 = x2.
Теперь решаем обычное уравнение, в котором нужно разделить переменные:
dv/dx=x2/ex2/2;
dv = x2*e—x2/2dx.
Чтобы извлечь интеграл, нам придётся применить здесь интегрирование по частям. Однако это не тема нашей статьи. Если вам интересно, вы можете самостоятельно научиться выполнять такие действия. Это не сложно, и при достаточном навыке и внимательности не отнимает много времени.
Обратимся ко второму способу решения неоднородных уравнений: методу Бернулли. Какой подход быстрее и проще — решать только вам.
Итак, при решении уравнения этим методом нам необходимо сделать замену: y=k*n. Здесь k и n — некоторые зависящие от x функции. Тогда производная будет выглядеть так: y’=k’*n+k*n’. Подставляем обе замены в уравнение:
k’*n+k*n’+x*k*n=x2.
Группируем:
k’*n+k*(n’+x*n)=x2.
Теперь надо приравнять к нулю то, что находится в скобках. Теперь, если объединить два получившихся уравнения, получается система дифференциальных уравнений первого порядка, которую нужно решить:
n’+x*n=0;
k’*n=x2.
Первое равенство решаем, как обычное уравнение. Для этого нужно разделить переменные:
dn/dx=x*v;
dn/n=xdx.
Берём интеграл и получаем: ln(n)=x2/2. Тогда, если выразить n:
n=ex2/2.
Теперь подставляем получившееся равенство во второе уравнение системы:
k’*ex2/2=x2.
И преобразовывая, получаем то же самое равенство, что и в первом методе:
dk=x2/ex2/2.
Мы также не будем разбирать дальнейшие действия. Стоит сказать, что поначалу решение дифференциальных уравнений первого порядка вызывает существенные трудности. Однако при более глубоком погружении в тему это начинает получаться всё лучше и лучше.
Где используются дифференциальные уравнения?
Очень активно дифференциальные уравнения применяются в физике, так как почти все основные законы записываются в дифференциальной форме, а те формулы, которые мы видим — решение этих уравнений. В химии они используются по той же причине: основные законы выводятся с их помощью. В биологии дифференциальные уравнения используются для моделирования поведения систем, например хищник — жертва. Они также могут использоваться для создания моделей размножения, скажем, колонии микроорганизмов.
Как дифференциальные уравнения помогут в жизни?
Ответ на этот вопрос прост: никак. Если вы не учёный или инженер, то вряд ли они вам пригодятся. Однако для общего развития не помешает знать, что такое дифференциальное уравнение и как оно решается. И тогда вопрос сына или дочки «что такое дифференциальное уравнение?» не поставит вас в тупик. Ну а если вы учёный или инженер, то и сами понимаете важность этой темы в любой науке. Но самое главное, что теперь на вопрос «как решить дифференциальное уравнение первого порядка?» вы всегда сможете дать ответ. Согласитесь, всегда приятно, когда понимаешь то, в чём люди даже боятся разобраться.
Основные проблемы при изучении
Основной проблемой в понимании этой темы является плохой навык интегрирования и дифференцирования функций. Если вы плохо берёте производные и интегралы, то, наверное, стоит ещё поучиться, освоить разные методы интегрирования и дифференцирования, и только потом приступать к изучению того материала, что был описан в статье.
Некоторые люди удивляются, когда узнают, что dx можно переносить, ведь ранее (в школе) утверждалось, что дробь dy/dx неделима. Тут нужно почитать литературу по производной и понять, что она является отношением бесконечно малых величин, которыми можно манипулировать при решении уравнений.
Многие не сразу осознают, что решение дифференциальных уравнений первого порядка — это зачастую функция или неберущийся интеграл, и это заблуждение доставляет им немало хлопот.
Что ещё можно изучить для лучшего понимания?
Лучше всего начать дальнейшее погружение в мир дифференциального исчисления со специализированных учебников, например, по математическому анализу для студентов нематематических специальностей. Затем можно переходить и к более специализированной литературе.
Стоит сказать, что, кроме дифференциальных, есть ещё интегральные уравнения, так что вам всегда будет к чему стремиться и что изучать.

Заключение
Надеемся, что после прочтения этой статьи у вас появилось представление о том, что такое дифференциальные уравнения и как их правильно решать.
В любом случае математика каким-либо образом пригодится нам в жизни. Она развивает логику и внимание, без которых каждый человек как без рук.
fb.ru
