Как находить производные: Как найти производную функции, примеры решения

Что такое производная. правила вычисления производных.

 

Что такое производная?

Таблица производных.

 

Производная — одно из главных понятий высшей математики. В этом уроке мы познакомимся с этим понятием. Именно познакомимся, без строгих математических формулировок и доказательств.

Это знакомство позволит:

— понимать суть несложных заданий с производной;

— успешно решать эти самые несложные задания;

— подготовиться к более серьёзным урокам по производной.

 

Сначала — приятный сюрприз.)

Строгое определение производной основано на теории пределов и штука достаточно сложная. Это огорчает. Но практическое применение производной, как правило, не требует таких обширных и глубоких знаний!

Для успешного выполнения большинства заданий в школе и ВУЗе достаточно знать всего несколько терминов — чтобы понять задание, и всего несколько правил — чтобы его решить. И всё. Это радует.

Приступим к знакомству?)

 

Термины и обозначения.

В элементарной математике много всяких математических операций. Сложение, вычитание умножение, возведение в степень, логарифмирование и т.д. Если к этим операциям добавить ещё одну, элементарная математика становится высшей. Эта новая операция называется дифференцирование. Определение и смысл этой операции будут рассмотрены в отдельных уроках.

Здесь же важно понять, что дифференцирование — это просто математическая операция над функцией. Берём любую функцию и, по определённым правилам, преобразовываем её. В результате получится новая функция. Вот эта новая функция и называется: производная.

Дифференцирование — действие над функцией.

Производная — результат этого действия.

Так же, как, например, сумма — результат сложения. Или частное — результат деления.

Зная термины, можно, как минимум, понимать задания.) Формулировки бывают такие: найти производную функции; взять производную; продифференцировать функцию; вычислить производную

 и т. п. Это всё одно и то же.Разумеется, бывают и более сложные задания, где нахождение производной (дифференцирование) будет всего лишь одним из шагов решения задания.

Обозначается производная с помощью штришка вверху справа над функцией. Вот так: y’ или f'(x) или S'(t) и так далее.

Читается игрек штрих, эф штрих от икс, эс штрих от тэ, ну вы поняли…)

Штрих также может обозначать производную конкретной функции, например: (2х+3)’, (x³)’, (sinx)’ и т.д. Часто производная обозначается с помощью дифференциалов, но такое обозначение в этом уроке мы рассматривать не будем.

 

Предположим, что понимать задания мы научились. Осталось всего ничего — научиться их решать.) Напомню ещё раз: нахождение производной — это 

преобразование функции по определённым правилам. Этих правил, на удивление, совсем немного.

Чтобы найти производную функции, надо знать всего три вещи. Три кита, на которых стоит всё дифференцирование. Вот они эти три кита:

1. Таблица производных (формулы дифференцирования).

2. Правила дифференцирования.

3. Производная сложной функции.

Начнём по порядку. В этом уроке рассмотрим таблицу производных.

 

Таблица производных.

В мире — бесконечное множество функций. Среди этого множества есть функции, которые наиболее важны для практического применения. Эти функции сидят во всех законах природы. Из этих функций, как из кирпичиков, можно сконструировать все остальные. Этот класс функций называется элементарные функции. Именно эти функции и изучаются в школе — линейная, квадратичная, гипербола и т.п.

Дифференцирование функций «с нуля», т.е. исходя из определения производной и теории пределов — штука достаточно трудоёмкая. А математики — тоже люди, да-да!) Вот и упростили себе (и нам) жизнь. Они вычислили производные элементарных функций до нас. Получилась таблица производных, где всё уже готово.)

Вот она, эта табличка для самых популярных функций. Слева — элементарная функция, справа — её производная.

 

	Функция  y	Производная функции y y’
1	C   (постоянная величина)	C’ = 0
2	x	x’ = 1
3	xn   (n — любое число)	(xn)’ = nxn-1
	x2   (n = 2)	(x2)’ = 2x
4	sin x	(sin x)’ = cosx
	cos x	(cos x)’ = — sin x
	tg x
	ctg x
5	arcsin x
	arccos x
	arctg x
	arcctg x
4	ax
	ex
5	loga x
	ln x     (a = e)

 

Рекомендую обратить внимание на третью группу функций в этой таблице производных. Производная степенной функции — одна из самых употребительных формул, если только не самая употребительная! Намёк понятен?) Да, таблицу производных желательно знать наизусть. Кстати, это не так трудно, как может показаться. Попробуйте решать побольше примеров, таблица сама и запомнится!)

Найти табличное значение производной, как вы понимаете, задание не самое трудное. Поэтому очень часто в подобных заданиях встречаются дополнительные фишки. Либо в формулировке задания, либо в исходной функции, которой в таблице — вроде и нету…

Рассмотрим несколько примеров:

1. Найти производную функции y = x³

Такой функции в таблице нет. Но есть производная степенной функции в общем виде (третья группа). В нашем случае n=3. Вот и подставляем тройку вместо n и аккуратно записываем результат:

(x³)‘ = 3·x^3-1 = 3x²

Вот и все дела.

Ответ: y’ = 3x²

 

2.

Найти значение производной функции y = sinx в точке х = 0.

Это задание означает, что надо сначала найти производную от синуса, а затем подставить значение х = 0 в эту самую производную. Именно в таком порядке! А то, бывает, сразу подставляют ноль в исходную функцию… Нас же просят найти не значение исходной функции, а значение её производной. Производная, напомню — это уже новая функция.

По табличке находим синус и соответствующую производную:

y’ = (sin x)’ = cosx

Подставляем ноль в производную:

y'(0) = cos 0 = 1

Это и будет ответ.

 

3. Продифференцировать функцию:

Что, внушает? ) Такой функции в таблице производных и близко нет.

Напомню, что продифференцировать функцию — это просто найти производную этой функции. Если забыть элементарную тригонометрию, искать производную нашей функции достаточно хлопотно. Таблица не помогает…

Но если увидеть, что наша функция — это косинус двойного угла, то всё сразу налаживается!

Да-да! Запомните, что преобразование исходной функции до дифференцирования вполне допускается! И, случается, здорово облегчает жизнь. По формуле косинуса двойного угла:

Т.е. наша хитрая функция есть не что иное, как y = cosx. А это — табличная функция. Сразу получаем:

Ответ: y’ = — sin x.

 

Пример для продвинутых выпускников и студентов:

4. Найти производную функции:

Такой функции в таблице производных нет, разумеется. Но если вспомнить элементарную математику, действия со степенями… То вполне можно упростить эту функцию. Вот так:

А икс в степени одна десятая — это уже табличная функция! Третья группа, n=1/10. Прямо по формуле и записываем:

Вот и всё. Это будет ответ.

 

 

 

 

Как найти производную?

Правила дифференцирования.

 

Чтобы найти производную от любой функции, надо освоить всего три понятия:

1. Таблица производных.

2. Правила дифференцирования.

3. Производная сложной функции.

Дифференцирование — это операция нахождения производной. Более за этим термином ничего не кроется. Т.е. выражения «найти производную функции» и «продифференцировать функцию» — это одно и то же.

Выражение «правила дифференцирования» относится к нахождению производной от арифметических операций. Такое понимание очень помогает избежать каши в голове.

Сосредоточимся и вспомним все-все-все арифметические операции. Их четыре). Сложение (сумма), вычитание (разность), умножение (произведение) и деление (частное). Вот они, правила дифференцирования:

	Действие	Производная
1	Производная суммы	(U+V)’ = U’+V’
2	Производная разности	(U-V)’ = U’- V’
3	Производная произведения	(U·V)’ = U’·V +U·V’
4	Производная от произведения на постоянное число	(C·V)’ = CV’
5	Производная частного

В табличке приведено пять правил на четыре арифметических действия.  Просто правило 4 — это элементарное следствие из правила 3. Но оно настолько популярно, что имеет смысл записать (и запомнить!) его как самостоятельную формулу.

Под обозначениями U и V подразумеваются какие-то (совершенно любые!) функции U(x) и V(x).

 

Рассмотрим несколько примеров. Сначала — самые простые.

Найти производную функции y=sinx — x²

Здесь мы имеем разность двух элементарных функций. Применяем правило 2. Будем считать, что sinx — это функция U, а x² — функция V. Имеем полное право написать:

y’ = (sinx — x²)’ = (sinx)’- (x²)’

Уже лучше, правда?) Осталось найти производные от синуса и квадрата икса. Для этого существует таблица производных. Просто ищем в таблице нужные нам функции (sinx и x²), смотрим, какие у них производные и записываем ответ:

y’ = (sinx)’ — (x²)’ = cosx — 2x

Вот и все дела. Правило 1 дифференцирования суммы работает точно так же.

А если у нас несколько слагаемых? Ничего страшного.) Разбиваем функцию на слагаемые и ищем производную от каждого слагаемого независимо от остальных. Например:

Найти производную функции y=sinx — x²+cosx — x +3

Смело пишем:

y’ = (sinx)’ — (x²)’ + (cosx)’ — (x)’ + (3)’

Опять лезем в таблицу, находим там производные синуса, квадрата икса, косинуса, чистого икса и тройки. Что, тройки нет в таблице!? Ну да.) Тройка — постоянная величина, в таблице обозначена буквой «С». Производная любой постоянной величины равна нулю. Можно сразу записать ответ:

y’ = cosx — 2x — sinx — 1

Как видим, первые два правила дифференцирования просты и безотказны.)

 

Переходим к примерам на правило 3. Производная произведения чуть посложнее, да…) Главное здесь — увидеть в исходной функции, что взять за U, а что — за V. Например:

Найти производную функции y=sinx · cosx.

Здесь всё очевидно. sinx — это U, cosx — это V. Пишем прямо по правилу:

y’ = (sinx)’ ·cosx + sinx · (cosx)’ = cosx·cosx — sinx·sinx = cos²x — sin²x

Вот здесь, частенько, возникает вопрос: оставить результат, как есть, или преобразовывать и упрощать дальше? Ответ зависит исключительно от задания и пожеланий преподавателя.) Производную мы уже нашли. Обычно, если упрощение простое и очевидное, его нужно сделать. В нашем случае получилась формула косинуса двойного угла. Можно написать ответ:

y’ = cos²x — sin²x = cos2x

Рассмотрим следствие из правила 3, т.е. правило 4. Эта формула получается прямо из производной для умножения функций. Если y=CU, где С — какое-то постоянное число, а U — любая функция, то:

y’ =(C·U)’ = C’·U + C·U’ = 0·U + C·U’ = C·U’

Словами говорят, что постоянную можно вынести из под знака производной.

Это маленькая, но очень полезная формулка. Позволяет делать кучу действий в уме. Например, по этому правилу все производные от выражений, типа 5х, 3,4х, -2х и так далее, сразу же превращаются в постоянные числа:

(5х)’ = 5·(x)’ = 5·1 = 5

(-2х)’ = -2·(x)’ = -2·1 = -2

Ну, вы поняли.) Пример посложнее:

Найти производную функции y=5sinx — 3x².

Если расписывать подробно, получится вот так:

y’ = (5sinx — 3x²)’ = (5sinx)’- (3x²)’

В скобках — произведения функций (постоянное число — тоже функция!). К первой и второй скобкам надо бы использовать правило 3, но сокращённый вариант (правило 4) — куда приятнее! Просто выносим числа за знак производной:

y’ = (5sinx)’- (3x²)’ = 5(sinx)’- 3(x²)’

Далее находим в таблице значения производных и результат просто умножаем на эти числа:

y’ = 5(sinx)’- 3(x²)’ = 5cosx — 3·2x = 5cosx — 6x

 

Переходим к производной частного. Правило 5 — самое злое, да…) Расписывать да считать подольше приходится. Но… тут уж ничего не поделаешь. Против законов математики протестовать глупо.) Хотя, в качестве бонуса, помогу.) Расскажу, чуть ниже, о случаях, когда эту формулу применять не надо. Так как есть более простые варианты. А сейчас — пример:

Найти производную функции

Расписываю по правилу 5. Подробно, со всеми скобочками и штрихами:

Берём производные (они табличные) в правой части:

Приводим к приличному виду:

Если требуется дальнейшее упрощение, можно в числителе вынести икс за скобки и сократить с иксом в знаменателе. Получим ответ:

Вот мы и рассмотрели, как находить производные функций с помощью правил дифференцирования.

 

Разумеется, сумма, разность, частное и произведение могут комбинироваться в самых разных сочетаниях. Например:

Продифференцировать функцию:

y=(x²+2) · (x³-4)

Здесь под функцией U скрывается выражение (x²+2), а под функцией V — выражение (x³-4). Расписываем прямо по правилу:

y’ = (x²+2)’ · (x³-4) + (x²+2) · (x³-4)‘

Теперь нужно довести дело до конца, т.е. вычислить производные от скобок. Штрих поставить — не означает «взять производную»…) В первых скобках будет сумма функций:

(x²+2)’ = (x²)’ + 2′ = 2x

Во вторых — разность функций:

(x³-4)‘ = (x³)’ — 4′ = 2x

Можно записать ответ:

y’ = 2х · (x³-4) + (x²+2) · 3x²

Упрощаем, т.е. перемножаем и приводим подобные:

y’ = 2x⁴-8х + 3x⁴+6x² = 5x⁴+6x²—8х

Вот и всё. Достаточно производную от злой функции расписать подробно, со всеми скобочками и штрихами, по подходящему правилу. Затем последовательно брать производные от скобочек. Всё и получится.

 

Всё просто, но. .. могут случиться и сюрпризы. Попадётся, например, вот такое задание:

Найти производную функции y=x³· sinx · cosx.

Здесь у нас умножаются три функции. Нет подходящего правила. Ничего страшного. Нас спасут… скобочки!) Мы вправе превратить умножение трёх функций в произведение двух, чтобы правило 3 в дело запустить. Просто возьмём за U и V то, что нам нужно. Например, пусть

U=x³· sinx

Тогда

V = cosx

Выделим эти U и V скобочками в исходной функции:

y=(x³· sinx) · (cosx).

Скобки никак не меняют исходную функцию, можно брать производную по правилу 3:

y’=((x³· sinx) · (cosx))’= (x³· sinx)‘· (cosx)+(x³· sinx) · (cosx)’

Теперь видно, что в скобках (x³· sinx)‘ у нас опять произведение функций. Но уже двух, что попроще. ) Можно расписать производную этих скобок отдельно. Теперь за U у нас пойдёт x³, а за V — sinx:

(x³· sinx)’ = (x³)’ · sinx +x³· (sinx)’= 3x²· sinx + x³· cosx

Вот практически и всё. Возвращаемся к исходной функции и вставляем наш результат промежуточного дифференцирования на своё место. Сразу же и производную от косинуса во втором слагаемом возьмём:

y’= (3x²· sinx + x³· cosx) · cosx + (x³· sinx) · (-sinx)

Производную нашли. Если требуется, перемножаем скобки и записываем ответ:

y’= 3x²· sinx · cosx + x³· cos²x — x³· sin²x

Замечу, что в этом примере U и V можно было выбрать по другому. За U взять x³, а за V — sinx · cosx. Это без разницы. Результат будет тот же самый.

Теперь — заслуженный бонус к правилу 5. В примерах постоянно приходится дифференцировать дроби. Что огорчает.) Но, если в знаменателе дроби — постоянное число, правила 5 можно избежать! Действия с дробями гласят, что деление можно заменить на умножение. Вот так:

Это даёт возможность вместо правила 5 использовать куда более простое и удобное правило 4. Например:

Найти производную функции:

В процессе дифференцирования слегка преобразуем исходную функцию. Превратим деление в умножение:

Вот так. Арифметика из младших классов ещё никому не мешала!)

Кстати, преобразование исходной функции перед дифференцированием вполне возможно и, иногда, очень помогает. Скажем, производная от функции:

берётся достаточно хлопотно. Таблицы производных и правил дифференцирования здесь недостаточно. Это сложная функция. Но если её преобразовать до дифференцирования, пример решается в уме.

В конце урока дам советы по облегчению жизни при дифференцировании. )

 

Практические советы:

1. Перед дифференцированием смотрим, нельзя ли упростить исходную функцию.

2. В замороченных примерах расписываем решение подробно, со всеми скобочками и штрихами.

3. При дифференцировании дробей с постоянным числом в знаменателе, превращаем деление в умножение и пользуемся правилом 4.

 

 

 

 

Как найти производную векторной функции — Криста Кинг Математика

Сосредоточьтесь на коэффициентах, чтобы найти производную вектор-функции

Чтобы найти производную вектор-функции, нам просто нужно найти производные коэффициентов, когда вектор-функция имеет вид

???r(t )=r(t)_1\жирный i+r(t)_2\жирный j+r(t)_3\жирный k???

Привет! Я Криста.

Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.

С векторной функцией в этой форме производная равна

???r'(t)=r'(t)_1\bold i+r'(t)_2\bold j+r'(t)_3\ смелый к???

Если вектор-функция имеет вид

???r(t)=\left\langle{r(t)_1,r(t)_2,r(t)_3}\right\rangle???

мы можем просто прикрепить каждый из номеров направления к ???\жирный i???, ???\жирный j??? и ???\жирный k??? преобразовать его в форму

???r(t)=r(t)_1\жирный i+r(t)_2\жирный j+r(t)_3\жирный k???

и потом взять производные от коэффициентов. В качестве альтернативы, мы можем просто взять производные каждого числа направления, оставив функцию в ее первоначальном виде. Обязательно дайте ответ, соответствующий форме исходной векторной функции. Другими словами,

Учитывая???r(t)=r(t)_1\bold i+r(t)_2\bold j+r(t)_3\bold k???, ответ должен быть ? ??r'(t)=r'(t)_1\жирный i+r'(t)_2\жирный j+r'(t)_3\жирный k???

Учитывая ???r(t)=\left\langle{r(t)_1,r(t)_2,r(t)_3}\right\rangle???, ответ должен быть ???r (t)=\left\langle{r'(t)_1,r'(t)_2,r'(t)_3}\right\rangle???

Как найти производную векторной функции

Пройти курс

Хотите узнать больше об исчислении 3? У меня есть пошаговый курс для этого. 🙂

Еще один пошаговый пример, как взять производную вектор-функции

Пример

Найти производную вектор-функции. 93\cos{(4t)}}\rangle???

Получить доступ к полному курсу Calculus 3

Learn mathКриста Кинг 18 июня 2021 г. математика, выучить онлайн, онлайн-курс, онлайн-математика, исчисление 3, исчисление iii, вычисление 3, вычисление iii, векторное исчисление, векторные функции, производная векторной функции, производная векторной функции, производные векторов, векторных производных

0 лайков

Common Derivatives — Статистика How To

1. Список общих производных:
   • Постоянные функции (например, y = 1, y = 44)
   • Производное X
   • Производная от 2x
   • Производная от 3x
     • ТИ-89 Пример
   • Производные e и e ^x
   • лн (натуральное бревно)
   • Грех 3x
2. Общие производные правила

Производная sin

³ x

Производная sin ³ x is 3sin ² x cos x.
Существует два основных способа получения производной: либо с помощью определения предела (длинный путь), либо с помощью упрощенного метода, называемого общим степенным правилом. Существуют короткие пути, так что вы можете пропустить длинный путь поиска производной: определение предела. Общая форма степенного правила помогает различать функции вида [u(x)] ⁿ ], например sin3x, который можно переписать как [sin x] ³ , который имеет внутреннюю функцию «sin x” и внешняя функция x ³ . Общая форма степенного правила:
Если y-u ⁿ , то y = nu ^{n – 1} *u’, где «u» — внутренняя функция.

Пример задачи : Найдите производную Sin3x

Шаг 1: Перепишите уравнение так, чтобы оно представляло собой степенную функцию:
sin ³ x = [sin x]

4

3 Найдите производную для «внутренней» части функции , sin x. По общим правилам дифференцирования производная от sin x равна cos x:
f’ sin x = cos x

Шаг 3: Перепишите функцию в соответствии с общим степенным правилом. Другими словами, запишите общее правило мощности, заменив его в вашей функции, где это уместно. Последняя половина общего правила мощности — это производная внутренней функции, которую вы разработали на шаге 2:
f- = 3[sin x] ^3-1 [cos x] = 3[sin x] ² [ cos x]

Шаг 4: Перепишите с помощью алгебры :
3[sin x] ² [cos x] = 3sin ² x cos x

Вот и все!

Совет: Исчисление использует много алгебры и тригонометрии. Если ваши навыки алгебры слабы, этот курс, вероятно, станет трудным. Вместо того, чтобы сосредотачиваться на запоминании правил дифференцирования, сосредоточьтесь на улучшении своих навыков алгебры. Возможность взглянуть на функцию и увидеть, какое правило может применяться, если вы манипулируете уравнением (например, зная, что квадратный корень можно переписать как «в степени 1/2»), является ключом к вычислению производных.

Наверх.

Это список наиболее распространенных производных (те, которые вы обычно найдете в приложении к учебнику).
Степень х

с = 0

х = 1

x n = n x (n-1)

 

Таблица экспоненциальных/логарифмических производных b ^x = b ^x ln(b) ln(x) = 1/x

 

Тригонометрический

sin x = cos x	csc x = -csc x детская кроватка x
cos x = – sin x	сек х = сек х тангенс х
тангенс x = сек 2 x	детская кроватка x = – csc 2 x

 

Обратный тригонометрический

arcsin x =	1 / (√ (1- х 2 ))
arccsc х =	-1 / (|х| √ (х 2 – 1))
arccos х =	-1 / (√ (1- х 2 ))
угловых секунды х =	1 / (|х| √ (х 2 ) – 1)
арктангенс х =	1 / (1 + х 2 )
дуга х =	(-1 / 1 +x 2 )

 

Гиперболические функции

ш х = ш х	csch x = – cth x csch x
ш х = ш х	сек х = – танх х сек х
танх x = 1 – тангенс 2 x	ткань x = 1 – ткань 2 x

Выше приведен список наиболее распространенных деривативов, которые вы найдете в таблице деривативов. Если вы не нашли здесь производную, которая вам нужна, возможно, искомая производная не является универсальной производной (т. е. вам действительно нужно вычислить производную с нуля). Если это так, и вам нужно найти производную, выполните поиск на этом сайте или попробуйте онлайн-калькулятор, подобный этому, от Wolfram Alpha.

Наверх.

Посмотрите видео или прочитайте ниже:

Производная от x

Посмотрите это видео на YouTube.

Видео не видно? Кликните сюда.

Производная от x = 1. Точно так же производная от -x = 1.

Почему производная от x равна всего 1 ?

Определение производной – это наклон касательной в любой точке графика. Функция y = x является постоянной функцией. Она имеет положительный наклон ровно 1 во всех точках графика, поэтому производная для всей функции определяется как 1.

График -x показывает, что это убывающая функция с отрицательным наклоном ровно -1 во всех точках:

График y=-x (красная линия) и производной, -1 (зеленая линия) .

Если вы вложите в голову идею о том, что производная — это просто наклон касательной, это сделает поиск многих общих производных чрезвычайно простым. Если бы все производные в исчислении были такими простыми!

Как насчет других функций с константами?

Производная любой другой функции с некоторым значением x, умноженная на константу, является просто константой. Например:

• Производная от 12x равна 12,
.
• Производная от 10 000x равна 10 000.

Вы можете применить это правило к любому x значению, умноженному на константу, включая π (см. производную пи), e (число Эйлера), десятичные числа, дроби и другие константы.

Наверх.

Посмотрите видео или прочитайте ниже:

Производное от 2x

Посмотрите это видео на YouTube.

Видео не видно? Кликните сюда.

Формула

Производная любого значения x, умноженная на константу, является самой константой.
В виде формулы это: [cx]′ = c
Другими словами, если у вас есть значение x, умноженное на любую константу , производная (обозначается символом ′, которая называется «простая запись “) — это просто константа.

Например, производная от 2x равна 2, или производная от 100 x равна 100. Вы можете применить это правило к любому x значению, умноженному на константу, включая:

• пи,
• е,
• десятичных знаков,
• дробей.

Правило можно легко расширить, чтобы найти производную от 3x (что равно 3), производную от 4x (что равно 4) …∞. Просто отбросьте «х», и у вас есть производная.

Почему производная от 2х просто «2»?

Производная — это касательная в точке. Другими словами, найдите наклон в точке, и вы получите производную. Наклон линии 2x равен 2, независимо от того, какую точку вы выберете, чтобы найти наклон. Следовательно, производная всей функции равна 2.

График y = 2x (красная линия) и производной 2x (зеленая линия).

Совет : На всякий случай, если вам нужно освежить в памяти формулу наклона: изменение y / изменение x. Вы можете использовать эту формулу, чтобы получить среднее значение наклона в двух точках; поскольку наклон для линейного графика (например, 2x) постоянен, нахождение наклона между двумя точками также даст вам производную от 2x.

Наверх.

Посмотрите видео или прочитайте ниже:

Производная от 3x

Посмотрите это видео на YouTube.

Видео не видно? Кликните сюда.

Производная от 3x равна 3.

Производная от любое x, умноженное на константу, есть просто константа. Например:

• Производная от 99x равна 99,
.
• Производная от 101х равна 101.

Почему производная от 3x равна 3?

Производная — это касательная в точке. Другими словами, для таких прямолинейных функций все, что вам нужно сделать, это найти наклон в определенной точке, и это значение является производной.

Вы можете найти наклон линии между двумя точками, используя формулу наклона:

Наклон = изменение y / изменение x.

Как вы, вероятно, можете сделать вывод из формулы, невозможно найти наклон в точке … потому что нет никаких изменений! В исчислении, если вы хотите найти наклон в точке, вы просто выбираете пару точек, равных 9.0131 очень близко к точке, для которой вы хотите найти уклон. Насколько близко достаточно близко? Обычно это вопрос личного мнения, но пока вы находитесь «в этом районе» (другими словами, пока вы достаточно близко), вы должны быть «достаточно близко».

Например, если вы хотите найти производную от 3x (это просто наклон), вы можете выбрать точку x = 3, в которой будет найдена производная. Чтобы использовать формулу наклона, вам нужно две точки, поэтому вы можете выбрать x = 2 и x = 4 (что составляет 1 единицу по обе стороны от 3). Линейная функция имеет постоянный наклон, поэтому на самом деле не имеет значения, какие точки вы выбираете: функция имеет одну и ту же постоянную производную.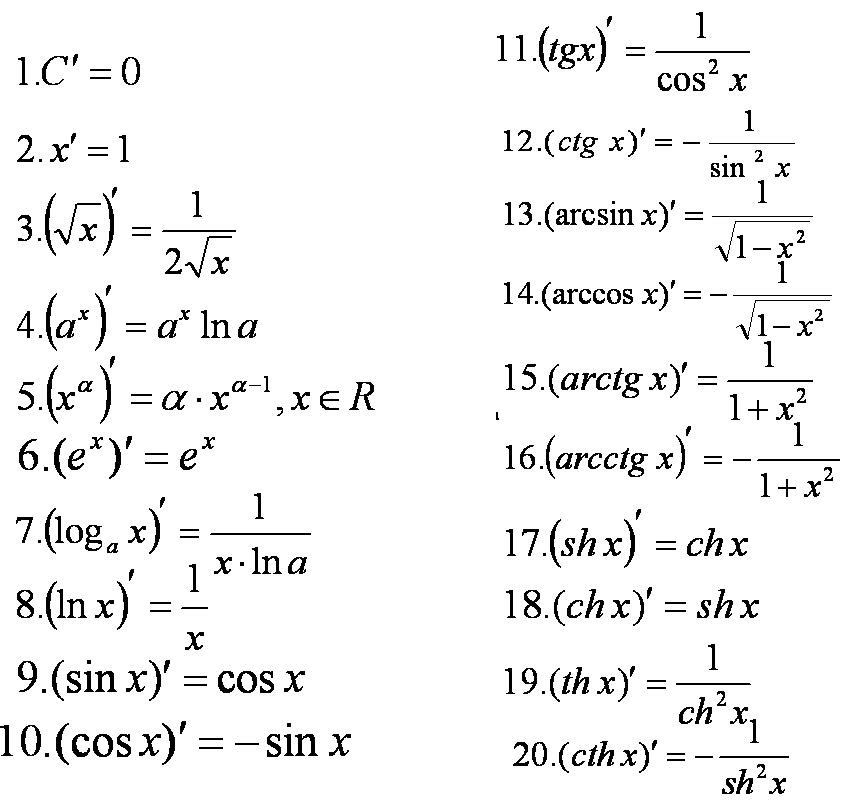

Наклон линии 3x равен 3, независимо от того, какие точки вы выберете, чтобы найти наклон. Следовательно, производная от 3x в точках от x = 2 до x = 4 является производной всей функции.

Функция 3x имеет постоянный наклон 3.

Пример задачи: Найдите производную f(x) = 3x на TI 89.

Шаг 1: Нажмите кнопку F3.

Шаг 2: Выберите «1: d(дифференцировать». Вы можете либо использовать клавишу со стрелкой вниз или введите номер, чтобы выбрать его.

Шаг 3: Нажмите ENTER. Калькулятор заполнит командную строку на главном экране d(

Шаг 4: Введите имя функции, а затем запятую. Например, если ваша функция 3x, введите «3x». Синтаксис теперь будет выглядеть так:

Шаг 5: Введите X. Это сообщает калькулятору, что вы проводите дифференцирование по отношению к X.

Шаг 6: Введите символ закрывающей скобки. 0076

Шаг 7: Нажмите ENTER. Решение показано в правой части экрана.

Производная от 3x равна 3.

Предупреждение : буква d для производной не совпадает с буквой D на вашей клавиатуре. Другими словами, вы не можете просто ввести «d(» на главном экране. Вам нужно нажать клавишу F3 (вы также можете найти ее в каталоге, но зачем делать это так долго?).

Наверх

Содержимое:

1. Производное e
2. Производное e ^x

Производная от e

Производная от e равна 0.

Почему?

Потому что производная любой постоянной функции равна 0.

Число Эйлера (e), иногда называемое константой Непера, не является переменной, как x или y. Это константа, как π. Его значение составляет примерно 2,718.

На этом графике показана постоянная функция y = e (красный) и y = e ^x (зеленый):

Если вы посмотрите на график e, вы увидите, что наклон равен нулю для всех точек на линии; Горизонтальная линия всегда имеет нулевой наклон. Следовательно, производная всегда равна нулю для постоянных функций (таких как e), которые на графике образуют горизонтальную линию.

Наверх.

Производная от e ^x равна e ^x .

Почему?
Это необычная функция, потому что является собственной производной. Другими словами, наклон такой же, как выход функции (значение y) для всех точек на графике. Чтобы было понятнее, попробуйте построить график функции и найти наклон в определенных точках.

На изображении выше показано, что производная (т. е. наклон касательной) в точке (0, 1) равна 1. Давайте представим, что вы начали строить график своей производной. Для этой единственной точки вашей функции (0, 1) первая точка вашей производной функции будет лежать на линии функции y = 1. Эта точка показана на красной линии ниже:
Наклон равен 1 в точке (0, 1).

Пока у нас есть только одна точка на нашей производной. Нам нужно еще несколько, чтобы начать рисовать производную функцию. Далее, давайте посмотрим на наклон для x = 1:

Производная функций e с использованием цепного правила

Производная e ^x на самом деле является частным случаем немного более сложного правила, называемого цепным правилом. Вы используете правило, когда степень е является функцией х, а не только переменной х сама по себе.

Когда e в сочетании с другой функцией. Например, вас могут попросить найти производную функции e, которая выглядит следующим образом: e ^5x или x ^{2x 2} . Для этих функций необходимо использовать цепное правило.

Далее: Цепное правило.

Наверх.

Общие производные: ссылки

Рон Ларсон, Брюс Х. Эдвардс. Исчисление. Cengage Learning, 16 января 2009 г. Получено 12 июня 2019 г. с: https://books.google.com/books?id=Xn9.rXyPSrzAC
Правила исчисления – функции одной переменной.