Онлайн расчет цепей – Расчет электрической цепи постоянного тока

Содержание

Мотопутешествия / Онлайн программа Расчёт размера длины цепи

	Нашли ошибку? Пожалуйста сообщите
Укажите значения по документации (умолчанию / СТОК) или же значения которые установлены сейчас на мотоцикле
Выберите шаг цепи (тип цепи)	тип: 530 шаг: 15.875тип: 215 шаг: 7тип: 219 шаг: 7.774тип: 350 шаг: 9.525тип: 415 шаг: 12.7тип: 420 шаг: 12.7тип: 428 шаг: 12.7тип: 520 шаг: 15.875тип: 525 шаг: 15.875тип: 530 шаг: 15.875тип: 630 шаг: 19.05тип: 632 шаг: 19.05
Размер передней звезды (кол-во зубов)	15891011121314151617181920212223242526272829
Размер задней звезды (кол-во зубов)	49222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119
Количество звеньев цепи	104161820222426283032343638404244464850525456586062646668707274767880828486889092949698100102104106108110112114116118120122124126128130132134136138140142144146148150152154156158160162164166168170172174176178180182184186188190192194196198200202204206208210212214216218220222224226228230232234236238240242244246248250252254256258260262264266268270272274276278280282284286288290292294296298
Укажите желаемые / подбираемые / новые значения
Выберите шаг цепи (тип цепи)	тип: 530 шаг: 15.875тип: 215 шаг: 7тип: 219 шаг: 7.774тип: 350 шаг: 9.525тип: 415 шаг: 12.7тип: 420 шаг: 12.7тип: 428 шаг: 12.7тип: 520 шаг: 15.875тип: 525 шаг: 15.875тип: 530 шаг: 15.875тип: 630 шаг: 19.05тип: 632 шаг: 19.05
Размер передней звезды (кол-во зубов)	17891011121314151617181920212223242526272829
Размер задней звезды (кол-во зубов)	52222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119

www.life4t.ru

Расчёты электрических цепей

Расчёт электрических цепей онлайн. Популярные и часто применяемые формулы для расчётов.

Для удобства есть более быстрый сервер — зеркало — Расчёт электрических цепей онлайн.

Достаточно вписать значения и кликнуть мышкой в таблице.

Расчёт реактивного сопротивления катушки индуктивности L и емкости конденсатора С.

Реактивное сопротивление ёмкости

Xc = 1/(2Pi*F*C)

Реактивное сопротивление индуктивности

XL = 2Pi*F*L

Расчёт параллельного соединения двух резисторов и последовательного соединения двух конденсаторов. Общее сопротивление.

Параллельное соединение двух сопротивлений

R =R1*R2/(R1+R2)

Последовательное соединение двух ёмкостей

C = C1*C2/(C1+C2)

Расчёт резистивного и ёмкостного делителей напряжения. Резистивный делитель. Емкостный делитель.

Расчёт резистивного делителя напряжения

U1 = U*R1/(R1+R2)

Расчёт емкостного делителя напряжения

U1 = U*C2/(C1+C2)

Резонансная частота. Расчёт частоты резонанса контура и фильтра RC. Частота среза ФНЧ и ФВЧ фильтра.

Частота резонанса колебательного контура LC

F = 1/(2*Pi*√(LC))

Постоянная времени τ цепочки RC и частота среза RC-фильтра

τ = R*C ; Fср = 1/(2Pi* τ)

Расчёт реактивных потерь и компенсации. Компенсация реактивной мощности и потерь в цепях переменного тока.

Реактивная мощность Q = √((UI)²-P²)
Реактивное сопротивление X = U²/Q
Компенсирующая ёмкость C = 1/(2Pi*F*X)

После сброса ввести два любых известных параметра

I=U/R; U=IR; R=U/I; P=UI;
P=U²/R; P=I²R; R=U²/P; R=P/I² U=√(PR) I= √(P/R)

Полезные статьи: Сайт создан в системе uCoz

horef.narod.ru

Расчет размерных цепей онлайн. Прямая задача.

Укажите звенья размерной цепи

Имя размерной цепи

Размер, мм

select

↑ Увеличивающее звено
↓ Уменьшающее звено

Требуемый допуск по умолчанию

по умолчанию
+ положительный
— отрицательный
± симметричный

Добавить Отклонения известны

expert-i.ru

Закон Ома. Онлайн расчёт для постоянного и переменного тока.

Онлайн расчёт электрических величин напряжения, тока и мощности для:
участка цепи, полной цепи с резистивными, ёмкостными и индуктивными
элементами.

— А любите ли Вы закон Ома так, как люблю его я? — спросил учитель физики стоящего рядом с щитком и разглядывающего свой обугленный палец электрика, — Всеми силами души Вашей, со всем энтузиазмом и исступлением, к которому только способна пылкая молодость, — никак не угомонялся он, сверкая из-под очков пытливым взглядом.

— Мужик, ты что, дурак? – вежливо поинтересовался обиженный противоестественным вопросом электрик и пошёл, насвистывая «Калинку-Малинку» в направлении ближайшего супермаркета — не ради пьянства окаянного, а дабы залечить свой увечный палец.

А тем временем, закон Ома является в электротехнике основным законом, который устанавливает связь силы электрического тока с сопротивлением и напряжением.

Формулировка закона Ома для участка цепи может быть представлена так: сила тока в проводнике прямо пропорциональна напряжению (разности потенциалов) на его концах и обратно пропорциональна сопротивлению этого проводника и записана в следующем виде:
I=U/R,

где
I – сила тока в проводнике, измеряемая в амперах [А];
U – электрическое напряжение (разность потенциалов), измеряемая в вольтах [В];

R – электрическое сопротивление проводника, измеряемое в омах [Ом].

Производные от этой формулы приобретают такой же незамысловатый вид: R=U/I и U=R×I.

Зная любые два из трёх приведённых параметров можно легко произвести расчёт и величины мощности, рассеиваемой на резисторе.
Мощность является функцией протекающего тока I(А) и приложенного напряжения U(В) и вычисляется по следующим формулам, также являющимся производными от основной формулы закона Ома:
P_(Вт) = U_(В)×I_(А) = I²_(А)×R_(Ом) = U²_(В)/R_(Ом)

Можно, конечно, описывая закон Ома обойтись и вообще без формул, а вместо них пользоваться словами или картинками:

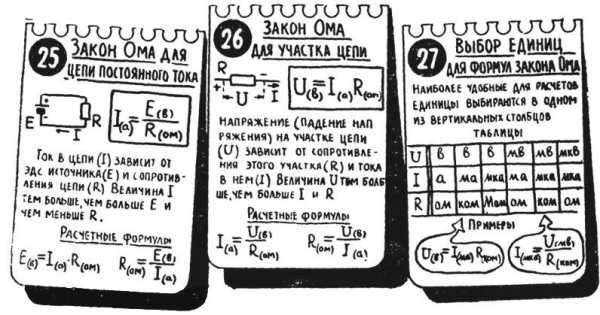
С другой стороны, формулы настолько просты, что не стоят выеденного яйца и, возможно, вообще не заслуживают отдельной крупной статьи на страницах уважающего себя сайта.

Не заслуживают, так не заслуживают. Калькулятор Вам в помощь, дамы и рыцари!
Считайте, учитывайте размерность, не стирайте из памяти, что:
1В=1000мВ=1000000мкВ;
1А=1000мА=1000000мкА;
1Ом=0.001кОм=0.000001МОм;
1Вт=1000мВт=100000мкВт.

Ну и так, на всякий случай, чисто для проверки полученных результатов, приведём незамысловатую таблицу, позволяющую в онлайн режиме проверить расчёты, связанные со знанием формул закона Ома.

ТАБЛИЦА ДЛЯ ПРОВЕРКИ РЕЗУЛЬТАТОВ РАСЧЁТОВ ЗАКОНА ОМА.

Вводить в таблицу нужно только два имеющихся у Вас параметра, остальные посчитает таблица.

Все наши расчёты проводились при условии, что значение внешнего сопротивления R значительно превышает внутреннее сопротивление источника напряжения r_внутр.
Если это условие не соблюдается, то под величиной R следует принять сумму внешнего и внутреннего сопротивлений: R = R_внешн + r_внутр , после чего закон приобретает солидное название — закон Ома для полной цепи:
I=U/(R+r) .

Для многозвенных цепей возникает необходимость преобразования её к эквивалентному виду:

Значения последовательно соединённых резисторов просто суммируются, в то время как значения параллельно соединённых резисторов определяются исходя из формулы: 1/R_ll = 1/R₄+1/R₅.
А онлайн калькулятор для расчёта величин сопротивлений при параллельном соединении нескольких проводников можно найти на странице ссылка на страницу.

Теперь, что касается закона Ома для переменного тока.
Если внешнее сопротивление у нас чисто активное (не содержит ёмкостей и индуктивностей), то формула, приведённая выше, остаётся в силе.
Единственное, что надо иметь в виду для правильной интерпретации закона Ома для переменного тока — под значением U следует понимать действующее (эффективное) значение амплитуды переменного сигнала.

А что такое действующее значение и как оно связано с амплитудой сигнала переменного тока?
Приведём диаграммы для нескольких различных форм сигнала.

Слева направо нарисованы диаграммы синусоидального сигнала, меандра (прямоугольный сигнал со скважностью, равной 2), сигнала треугольной формы, сигнала пилообразной формы.
Глядя на рисунок можно осмыслить, что амплитудное значение приведённых сигналов — это максимальное значение, которого достигает амплитуда в пределах положительной, или отрицательной (в наших случаях они равны) полуволны.

Рассчитываем действующее значение напряжение интересующей нас формы:

Для синуса U = Uд = Uа/√2;
для треугольника и пилы U = Uд = Uа/√3;
для меандра U = Uд = Uа.

С этим разобрались!

Теперь посмотрим, как будет выглядеть формула закона Ома при наличии индуктивности или ёмкости в цепи переменного тока.
В общем случае смотреться это будет так:

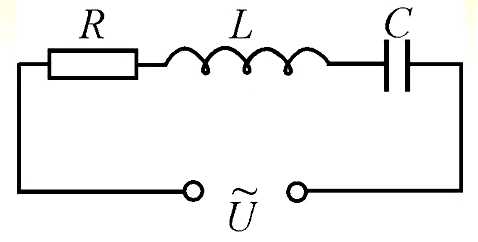
А формула остаётся прежней, просто в качестве сопротивления R выступает полное сопротивление цепи Z, состоящее из активного, ёмкостного и индуктивного сопротивлений.
Поскольку фазы протекающего через эти элементы тока не одинаковы, то простым арифметическим сложением сопротивлений этих трёх элементов обойтись не удаётся, и формула приобретает вид:
Реактивные сопротивления конденсаторов и индуктивностей мы с Вами уже рассчитывали на странице ссылка на страницу и знаем, что величины эти зависят от частоты, протекающего через них тока и описываются формулами: X_C = 1/(2πƒС) , X_L = 2πƒL .

Нарисуем таблицу для расчёта полного сопротивления цепи для переменного тока.
Количество вводимых элементов должно быть не менее одного, при наличии индуктивного или емкостного элемента — необходимо указать значение частоты f !

КАЛЬКУЛЯТОР ДЛЯ ОНЛАЙН РАСЧЁТА ПОЛНОГО СОПРОТИВЛЕНИЯ ЦЕПИ.

Теперь давайте рассмотрим практический пример применения закона Ома в цепях переменного тока и рассчитаем простенький бестрансформаторный источник питания.

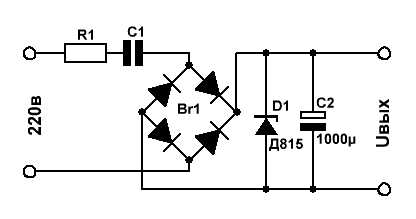
Токозадающими цепями в данной схеме являются элементы R1 и С1.

Допустим, нас интересует выходное напряжение Uвых = 12 вольт при токе нагрузки 100 мА.
Выбираем стабилитрон Д815Д с напряжением стабилизации 12В и максимально допустимым током стабилизации 1,4А.
Зададимся током через стабилитрон с некоторым запасом — 200мА.
С учётом падения напряжения на стабилитроне, напряжение на токозадающей цепи равно 220в — 12в = 208в.
Теперь рассчитаем сопротивление этой цепи Z для получения тока, равного 200мА: Z = 208в/200мА = 1,04кОм.
Резистор R1 является токоограничивающим и выбирается в пределах 10-100 Ом в зависимости от максимального тока нагрузки.
Зададимся номиналами R1 — 30 Ом, С1 — 1 Мкф, частотой сети f — 50 Гц и подставим всё это хозяйство в таблицу.
Получили полное сопротивление цепи, равное 3,183кОм. Многовато будет — надо увеличивать ёмкость С1.
Поигрались туда-сюда, нашли нужное значение ёмкости — 3,18 Мкф, при котором Z = 1,04кОм.

Всё — закон Ома выполнил свою функцию, расчёт закончен, всем спать полчаса!

vpayaem.ru