7.3. Выражение векторного произведения через координаты
Мы будем использовать таблицу векторного произведения векторов i,j иk:
если направление кратчайшего пути от первого вектора к второму совпадает с направлением стрелки, то произведение равно третьему вектору, если не совпадает — третий вектор берется со знаком «минус».
Пусть заданы два вектора а=ахi +ayj +azk и b =bxi +byj +bzk . Найдем векторное произведение этих векторов, перемножая их как многочлены (согласно свойств векторного произведения):Полученную формулу можно записать еще короче:так как правая часть равенства (7.1) соответствует разложению определителя третьего порядка по элементам первой строки.Равенство (7.2) легко запоминается.
7.4. Некоторые приложения векторного произведения
Установление коллинеарности векторов. Нахождение площади параллелограмма и треугольника
Согласно определению векторного произведения векторов а и b |а хb | = |а| * |b |sing , т. е. S пар = |а х b |. И, значит, DS =1/2|а х b |.
Определение момента силы относительно точки
Пусть в точке А приложена сила F =АВ и пусть О — некоторая точка пространства Из физики известно, что моментом си лы F относительно точки О называется вектор М, который проходит через точку О и:
1) перпендикулярен плоскости, проходящей через точки О, А, В;
2) численно равен произведению силы на плечо 3) образует правую тройку с векторами ОА и A В.
Стало быть, М=ОА х F . Нахождение линейной скорости вращения
Скорость v точки М твердого тела, вращающегося с угловой скоростью w вокруг неподвижной оси, определяется формулой Эйлера v =w хr , где r =ОМ, где О—некоторая неподвижная точка оси (см. рис. 21).
Угол между векторами
Из определения скалярного произведения двух векторов следует, что Если векторы и заданы координатами и , то формула (1.6.3.1) запишется в виде:
Площадь параллелограмма,построенных на векторах
Задачи на измерение длин отрезков, расстояний между точками, площадей поверхностей и объемов тел относятся к важному классу проблем, которые принято называть метрическими. В предыдущем разделе мы познакомились с тем, как использовать векторную алгебру для вычисления длин отрезков и расстояний между точками. Теперь мы собираемся найти способы вычисления площадей и объемов. Векторная алгебра позволяет ставить и решать подобные задачи только для достаточно простых случаев. Для вычисления площадей произвольных поверхностей и объемов произвольных тел требуются методы анализа. Но методы анализа в свою очередь существенным образом опираются на те результаты, которые дает векторная алгебра.
Для решения поставленной задачи, мы избрали достаточно долгий и непростой путь, подсказанный Гильбертом Стренгом [19], связанный с многочисленными геометрическими преобразованиями и кропотливыми алгебраическими вычислениями. Мы избрали этот путь несмотря на то, что существуют другие подходы, которые быстрее приводят к цели потому, что он показался нам прямым и естественным. Прямой путь в науке не всегда оказывается самым простым. Люди искушенные знают об этом и предпочитают пути окольные, но если не попытаться пройти прямиком, то можно так и остаться в неведении относительно некоторых тонкостей теории.
На избранном нами пути естественным образом появляются такие понятия как ориентация пространства, определитель, векторное и смешанное произведения. Особенно наглядно, как под микроскопом, проявляется геометрический смысл определителя и его свойств. Традиционно понятие определителя вводится в теории систем линейных уравнений, но именно для решения таких систем определитель почти бесполезен. Геометрический же смысл определителя существенен для векторной и тензорной алгебры.
А теперь запасемся терпением и начнем с самых простых и понятных случаев.
1. Векторы ориентированы вдоль координатных осей декартовой системы координат.
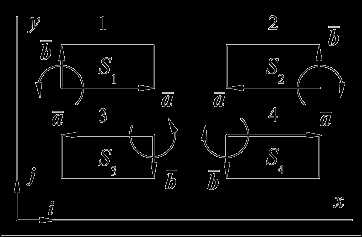
Векторы a и b в координатной форме:Где a и b означают модуль соответствующего вектора, а – знак координаты вектора.
Поскольку векторы ортогональны, то параллелограммы, построенные на них, являются прямоугольниками. Их площади равны просто произведению их сторон. Выразим эти произведения через координаты векторов для всех четырех случаев.
Все четыре формулы для вычисления площади одинаковы за исключением знака. Можно было бы просто закрыть на это глаза и записать, что во всех случаях. Однако более продуктивной оказывается другая возможность: придать знаку какой-то смысл. Посмотрим внимательно на рис. 21. В тех случаях, когда, поворот вектора к вектору осуществляется по часовой стрелке. В тех же случаях, когда мы вынуждены использовать в формуле знак минус, поворот вектора к вектору осуществляется против часовой стрелки. Это наблюдение позволяет связать знак в выражениях для площади с ориентацией плоскости.
Площадь прямоугольника, построенного на векторах aиb, со знаком плюс или минус будем считать ориентированной площадью, при этом знак будем связывать с ориентацией, задаваемой векторами. Для ориентированной площади мы можем записать единую формулу для всех рассмотренных четырех случаев:. Знак «векторной» черты над буквой S вводится для того, чтобы отличить обычную площадь, которая всегда положительна, от ориентированной.
При этом, очевидно, что те же самые векторы, взятые в другом порядке, определяют противоположную ориентацию, поэтому, . Просто площадь будем по-прежнему обозначать буквой S и, следовательно, .
Теперь, когда
казалось бы ценой расширения понятия
площади, мы получили общее выражение,
внимательный читатель скажет, что мы
рассмотрели не все возможности.
Действительно, кроме четырех вариантов
расположения векторов, представленных
на рис. 21, имеются еще четыре (рис. 22) 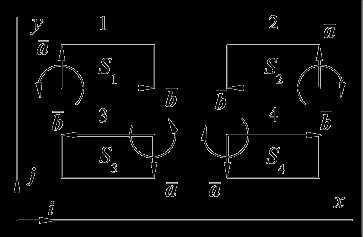
То есть, ориентированная площадь прямоугольника, построенного на векторах, как на сторонах, равна определителю, составленному из координат векторов, как из столбцов.
Мы полагаем, что с теорией определителей читатель знаком, поэтому, мы не останавливаемся подробно на этом понятии. Тем не менее, мы даем соответствующие определения, для того чтобы изменить акценты и показать, что к этому понятию можно прийти из чисто геометрических соображений.Итак, , , , – различные формы обозначения для одного и того же понятия – определителя, составленного из координат векторов, как из столбцов. Равенство может быть принято за его определение для двухмерного случая.
Теперь мы можем считать, что для всех частных случаев расположения векторов относительно декартовой системы координат у нас есть общее выражение для ориентированной площади.
2. Вектор b не параллелен оси x; вектор a/ является произвольным вектором.
Для того чтобы свести этот случай к уже известным, рассмотрим некоторые геометрические преобразования параллелограмма, построенного на векторах и (рис. .смешанные произведения векторов и его свойства
studfiles.net
Выражение скалярного произведения через координаты векторов.
Теорема 3. Если два вектора определены своими декартовыми прямоугольными координатами а={x1,y1,z1}, b={x2,y2,z2}, то их скалярное произведение равно сумме попарных произведений их соответствующих координат, т.е.a·b=x1x2+y1y2+z1z2 (5)
Доказательство. Т.к. базисные векторы являются попарно ортогональными и имеют единичную длину, то: .
=12сos 0˚=1,
Учитывая, что а=x1i+y1j+z1k, b= x2i+y2j+z2k, получим
a·b=(x1i+y1j+z1k)(x2
При a=b получаем a·а=|а|2=.
Следствие 1. Векторы а={x1,y1,z1} и b={x2,y2,z2} являются ортогональными тогда и только тогда, когда x1x2+y1y2+z1z2=0.
Пример. Проверить, являются ли ортогональными векторы а=(0;6;-3) и b=(2;4;8). A·b=0·2+6·4+(-3)·8=0
Следствие 2.
Угол между двумя векторами: cos φ=. (6)
Пример. Найти угол между векторами а=(1;2;-3) и b
=(2;4;0)cos φ=, φ=arccos 1/28
Векторное произведение векторов. Правые и левые тройки векторов и системы координат.
Определение 1. Упорядоченную тройку некомпланарных векторов abc называется правой, если направление вектора а совмещается с направлением вектора b при помощи кратчайшего поворота вектора а в плоскости этих векторов, который со стороны вектора с совершается против хода часовой стрелки. В противном случае (поворот по ходу часовой стрелки) эту тройку называют левой.
Всего из векторов а,b и c можно составить 3 правые: abc, bca, cab; и 3 левые
bac, acb, cba – тройки векторов.
Определение 2. Аффинная или декартова система координат называется правой (левой), если три базисных вектора образуют правую (левую) тройку векторов.
Определение 3.
|с|=|а||b|sin φ, где φ – угол между векторами а и b; (7)
вектор с ортогонален векторам а и b;
векторы а, b и с образуют правую тройку векторов.
с=[a,b]=a×b
Механический смысл. Если вектор изображает приложенную в некоторой точке М силу, а векторидет из некоторой точки О в точку М, то векторс=[a,b] представляет собой момент силы относительно точки О.
Геометрические свойства векторного произведения.
Теорема 4. Два вектора являются коллинеарными тогда и только тогда, когда их векторное произведение равно нулю.
Доказательство. Необходимость. Следует из определения векторного произведения, т.к. если векторы а и b коллинеарные, то угол между ними равен 0, а sin 0=0.
Достаточность. Пусть a×b=0. покажем, что векторы а и b коллинеарные. Исключим тривиальный случай, когда хотя бы один из векторов илиравен 0. Если оба вектора ненулевые, то>0,>0из равенства a×b=0 и (7) следует, что sin =0, т.е. векторы иколлинеарны. Ч.т.д.
Теорема 5. Длина (модуль) векторного произведения a×b равна площади параллелограмма, построенного на приведенных к общему началу векторах a и b.
Доказательство. Следует из (7), т.к. площадь параллелограмма равна S=|а||b|sin(a^b)=|a×b|. Ч.т.д.
Площадь соответствующего треугольника: SΔ=1/2|a×b|.
Определение. Ортом произвольного ненулевого вектора с называется единичный вектор, коллинеарный с и имеющий одинаковое с ним направление.
Следствие. Если е – орт векторного произведения a×b, а S – площадь параллелограмма, построенного на приведенных к общему началу векторах a и b, то для векторного произведения a×b справедлива формула: a×b=Sе (8).
Замечание. Из определений орта и векторного произведения вытекает, что тройка abe является правой (т.к. тройка aba×b является правой).
Теорема 6. Если с – некоторый вектор, — любая содержащая его плоскость, е – единичный вектор, лежащий в плоскости и ортогональный к с, g – единичный вектор, ортогональный к плоскости и направленный так, что тройка есg является правой, то для любого лежащего в плоскости вектора а справедлива формула
a×с=преас g (9)
Доказательство. Достаточно доказать, что векторы, стоящие в левой и правой частях (9): 1) имеют одинаковую длину, 2) коллинеарны, 3) имеют одинаковое направление.
S=|a×с| — площадь построенного на приведенных к общему началу векторах а и с параллелограмма. Длина вектора, стоящего в правой части (9), равна преас, т.е. тоже равна S, т.к. если за основание указанного параллелограмма принять вектор с, то высота его h будет равна преа.
Коллинеарность векторов, стоящих в левой и правой частях (9), вытекает из того, что оба эти вектора ортогональны плоскости (вектор a×с в силу определения векторного произведения, а вектор преас g в силу того, что вектор g по условию ортогонален к плоскости ).
Проверим, что векторы, стоящие в левой и правой частях (9) имеют одинаковое направление. Векторы a×с и g одинаково направлены (противоположно направлены), когда тройка aсg является правой (левой), т.е. когда векторы а и е лежат по одну сторону (по разные стороны) от с и проекция преа является положительной (отрицательной), но это и означает, что векторы a×с и преас g всегда одинаково направлены. Ч.т.д.
studfiles.net
5.6.6 Координаты вектора; скалярное произведение векторов; угол между векторами
Видеоурок: Скалярное произведение векторов
Лекция: Координаты вектора; скалярное произведение векторов; угол между векторами
Координаты вектора
Итак, как уже говорилось ранее, вектора – это направленный отрезок, у которого есть собственное начало и конец. Если начало и конец представлены некоторыми точками, значит на плоскости или в пространстве у них есть свои координаты.
Если же у каждой точки есть свои координаты, то мы можем получить и координаты целого вектора.
Допустим, мы имеем некоторый вектор, у которого начало и конец вектора имеют следующие обозначения и координаты: A(Ax; Ay) и B(Bx; By)
Чтобы получить координаты данного вектора, необходимо из координат конца вектора вычесть соответствующие координаты начала:
Для определения координаты вектора в пространстве следует воспользоваться следующей формулой:
Скалярное произведение векторов
Существует два способа определения понятия скалярного произведения:
- Геометрический способ. Согласно ему, скалярное произведение равно произведению величин данных модулей на косинус угла между ними.
- Алгебраический смысл. С точки зрения алгебры, скалярное произведение двух вектором – это некая величина, которая получается в результате суммы произведений соответствующих векторов.
Если векторы заданы в пространстве, то следует воспользоваться аналогичной формулой:
Свойства:
- Если умножить два одинаковых вектора скалярно, то их скалярное произведение будет не отрицательным:
- Если же скалярное произведение двух одинаковых векторов получилось равным нулю, то эти векторы считаются нулевыми:
- Если некоторый вектор умножить на себя же, то скалярное произведение получится равным квадрату его модуля:
- Скалярное произведение имеет коммуникативное свойство, то есть от перестановки векторов скалярное произведение не изменится:
- Скалярное произведение ненулевых векторов может быть равно нулю только в том случае, если вектора перпендикулярны друг другу:
- Для скалярного произведения векторов справедлив переместительный закон в случае с умножением одного из векторов на число:
- При скалярном произведении так же можно использовать дистрибутивное свойство умножения:
Угол между векторами
Если два вектора выходят из одной точки, то угол между ними – это угол, который описывает вектор при переходе по кратчайшему пути из своего первоначального положения в положение, при котором он будет сонаправленным.
Обобщив алгебраическую и геометрическую формулировку скалярного произведения можно получить, чему равен косинус угла между двумя векторами:
cknow.ru
Свойства векторного произведения Геометрические свойства
Векторное произведение
 равно нулю тогда и только тогда, когда
эти векторы коллинеарны:
равно нулю тогда и только тогда, когда
эти векторы коллинеарны:
||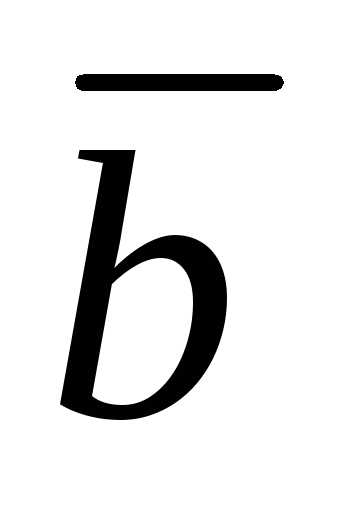 .
.
Доказательство. Пусть угол между векторами  и
и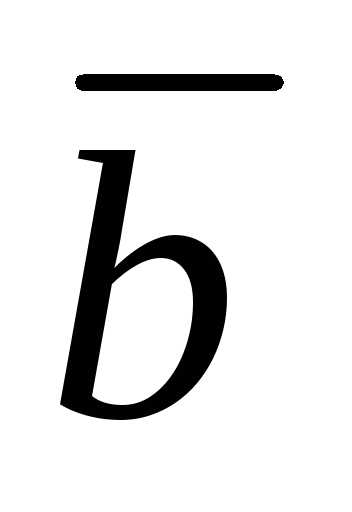 равен
равен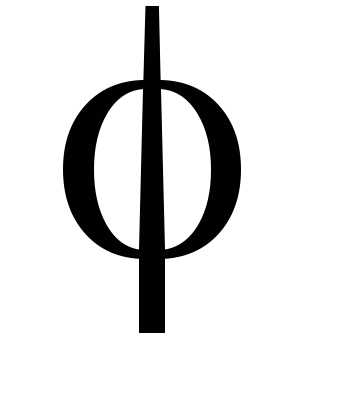 .
.
a) Докажем, что .
или 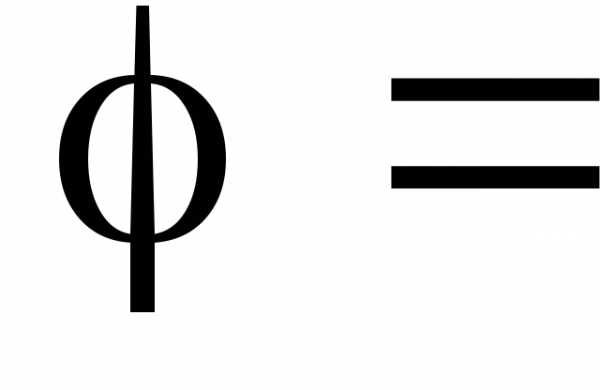 1800.
1800.
б) Докажем, что .
если
 .
.
Если
,
или.
Модуль векторного произведения
 равен площади параллелограмма,
построенного на этих векторах.
равен площади параллелограмма,
построенного на этих векторах.
Доказательство. Из курса геометрии
Из
свойства 2 следует, что
,
где – единичный вектор, перпендикулярный
векторам
– единичный вектор, перпендикулярный
векторам и
и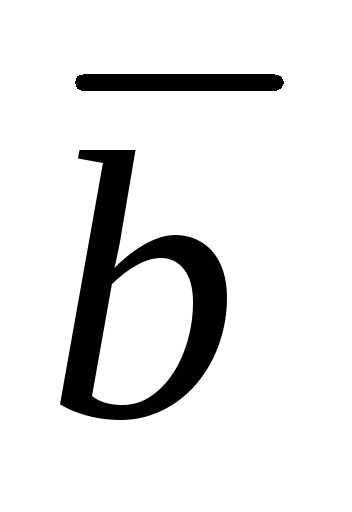 и
образующий с ними правую тройку:
и
образующий с ними правую тройку:
а)  =1,
=1,
б) 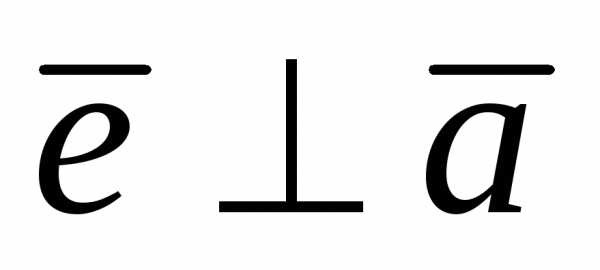 ,
, ,
,
в)  ,,
,, – правая тройка.
– правая тройка.
Алгебраические свойства
Антикоммутативность:
 =
= 
Доказательство.
Модули векторов  и
и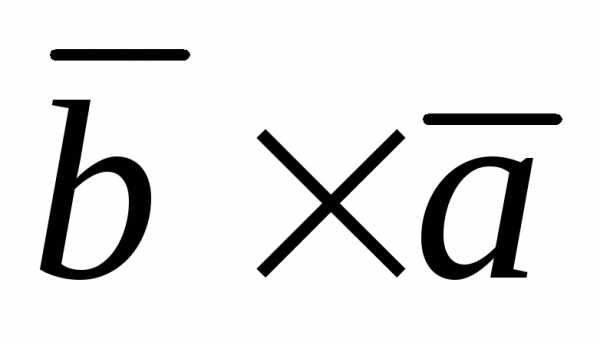 равны по определению векторного
произведения. Проверим их направление:
равны по определению векторного
произведения. Проверим их направление:
а)  ||
||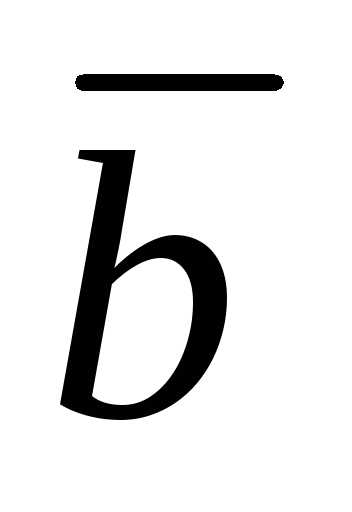 равенство выполняется;
равенство выполняется;
б)  и
и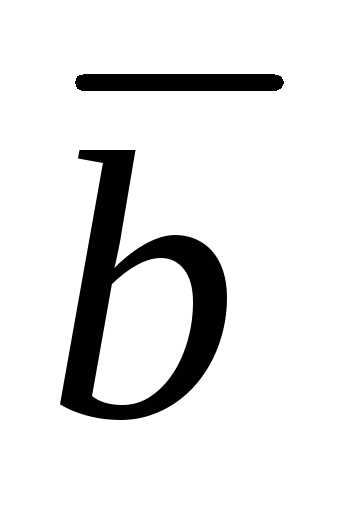 не
параллельны. Но
не
параллельны. Но ||
||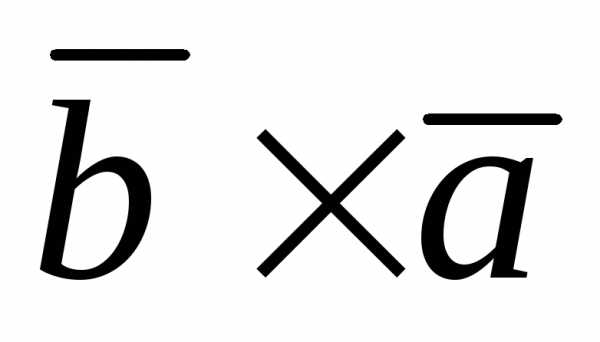 по определению векторного произведения,
тогда либо,
либо.
Пусть
по определению векторного произведения,
тогда либо,
либо.
Пусть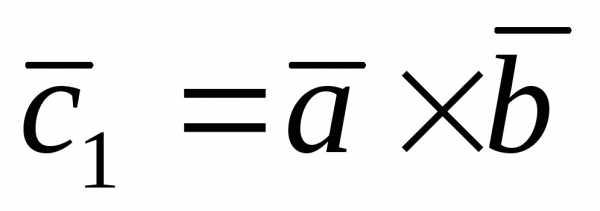 ,
а
,
а .
Тройка векторов
.
Тройка векторов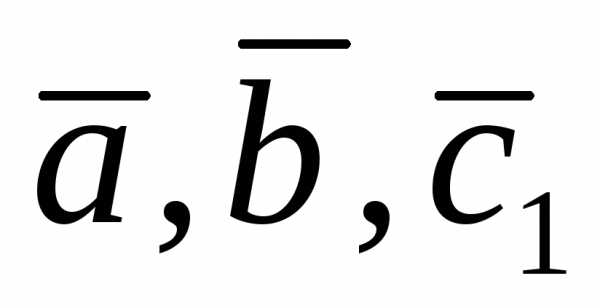 правая, а тройка
правая, а тройка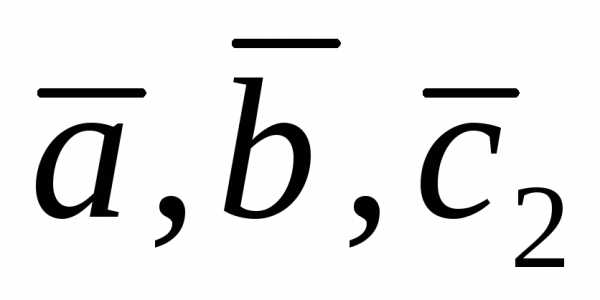 – левая. Следовательно,
– левая. Следовательно,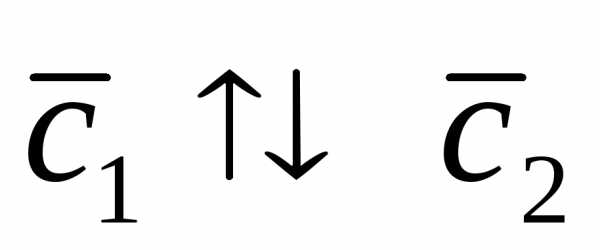 и
и 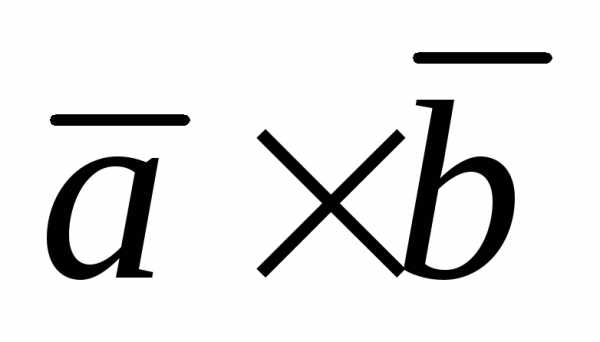 =
= 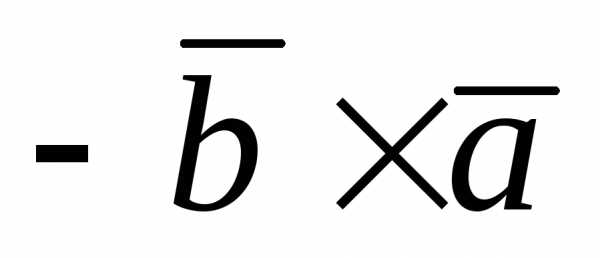 .
.
Ассоциативность относительно умножения на число.
проверяем модуль:
а),,
где  – угол между векторами
– угол между векторами и
и ,
а
,
а – угол между векторами
– угол между векторами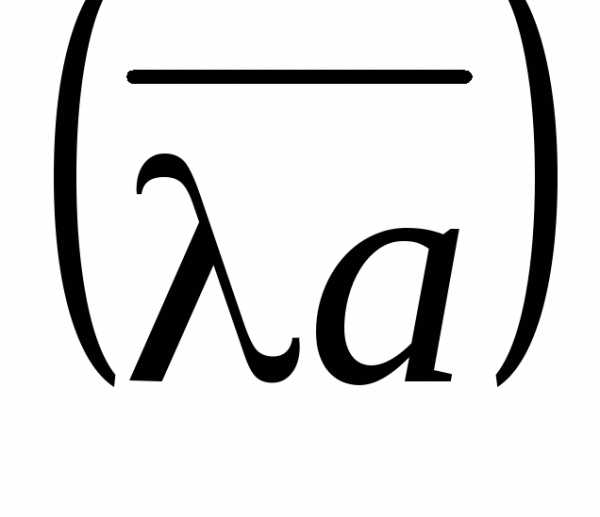 и
и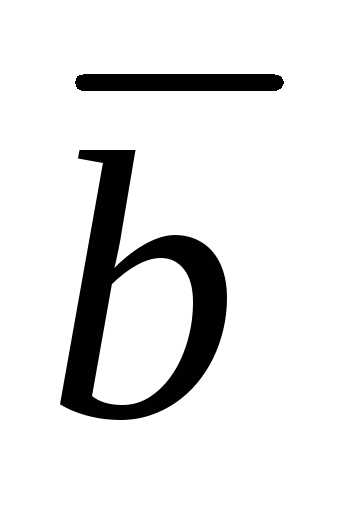 .
.
=>
поверяем направление:
б)
если 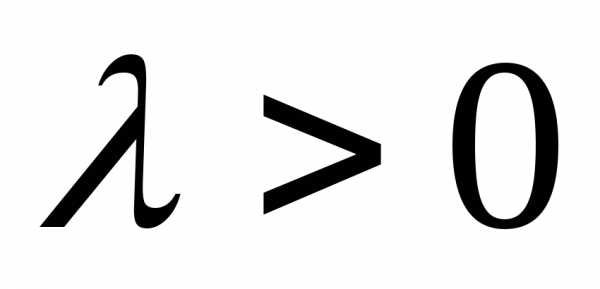
если  и
и  .
.
5. Дистрибутивность относительно сложения векторов
Выражение векторного произведения через координаты сомножителей
Теорема
1. Пусть
векторы  и
и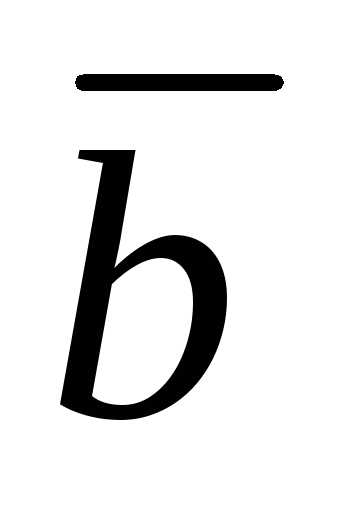 имеют координаты
имеют координаты
.
Векторное произведение этих векторов имеет координаты
. (16)
Можно расписать определители:
(16’)
или представить в виде
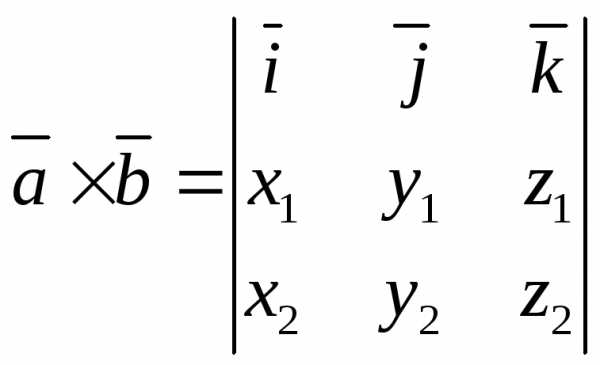 . (16’’)
. (16’’)
Доказательство. Рассмотрим векторные произведения базисных векторов:
(17)
.
Разложим
векторы  и
и по базису
по базису :
:

 .
.
На основании свойств векторного произведения мы можем перемножать правые части почленно:
с учетом формул (17).
Пример 1. Найти координаты векторного произведения векторов
.
Решение.
Пусть  .
.
.
Пример 2: Даны три точки: .
Найти
площадь треугольника АВС (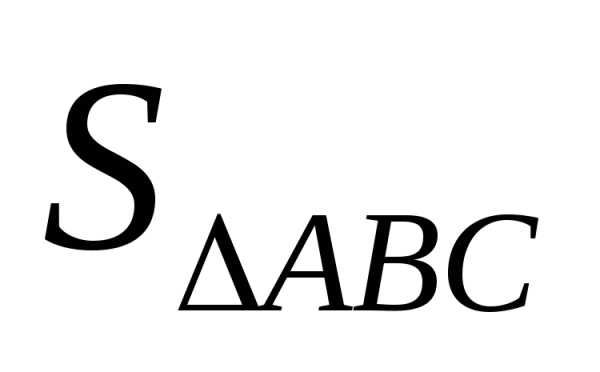 ).
).
Решение.
.
Найдем координаты векторов .
.
.
Смешанное произведение трёх векторов
Даны
при произвольных вектора 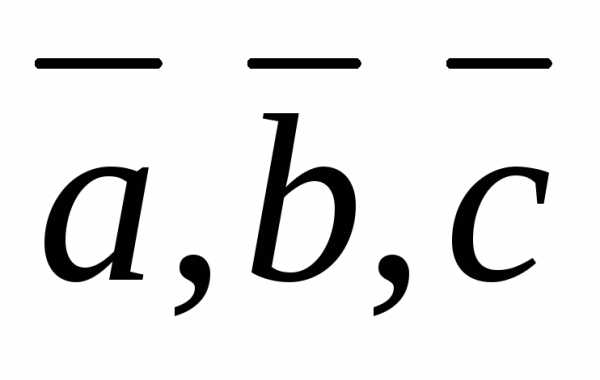 .
.
Определение.
Если результат векторного произведения 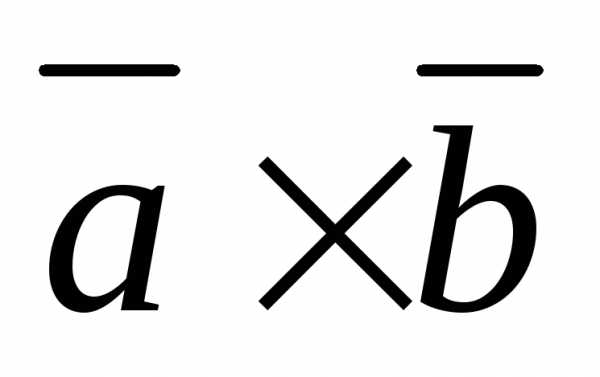 скалярно умножить на вектор
скалярно умножить на вектор  ,
то
,
то  – это смешанное произведение векторов
– это смешанное произведение векторов  .
.
Геометрический смысл смешанного произведения
Теорема
2. Смешанное
произведение  равно объему параллелепипеда, построенному
на приведённых к общему началу векторах,
взятому со знаком <+>, если
равно объему параллелепипеда, построенному
на приведённых к общему началу векторах,
взятому со знаком <+>, если  –
правая тройка векторов, и со знаком <->,
если тройка
–
правая тройка векторов, и со знаком <->,
если тройка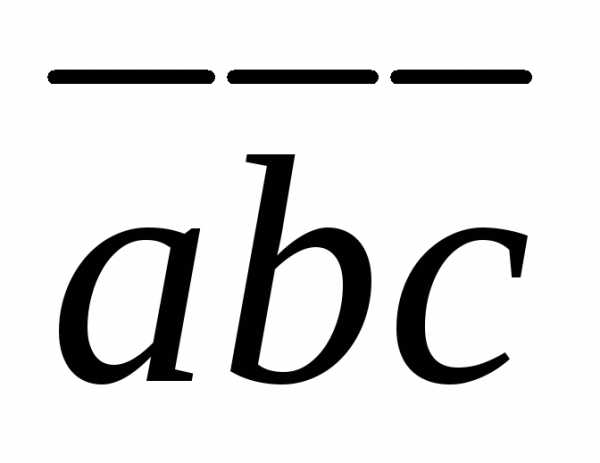 –
левая.
–
левая.
Если
векторы 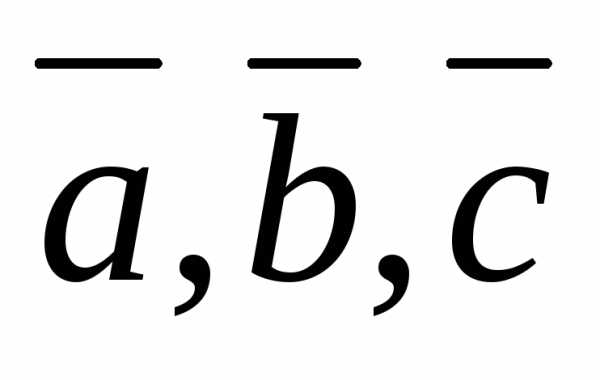 –
компланарны, то объем равен нулю, и
.
–
компланарны, то объем равен нулю, и
.
Доказательство.
Пусть S – площадь параллелограмма, построенного
на векторах 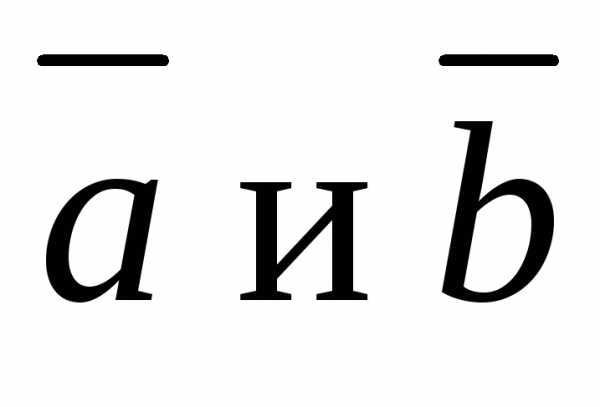 ,
,  – единичный вектор, перпендикулярный
к векторам
– единичный вектор, перпендикулярный
к векторам  и образующий с ними правую тройку.
(Вектор
и образующий с ними правую тройку.
(Вектор – орт векторного произведения
– орт векторного произведения  .)
.)
Из геометрического свойства 2 векторного произведения
(18)
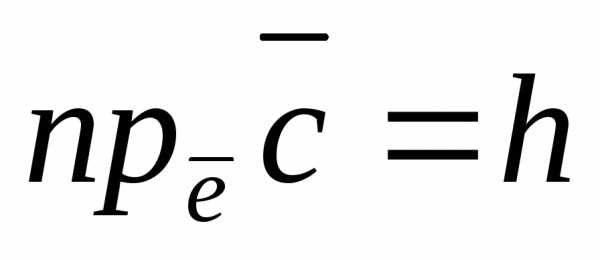 –высота
параллелепипеда, построенного на
векторах
–высота
параллелепипеда, построенного на
векторах 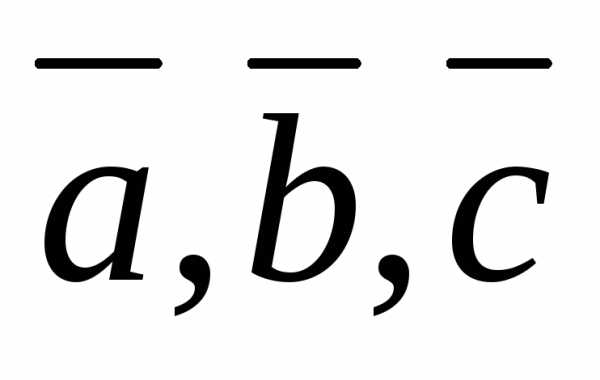 ,
с основанием S.
,
с основанием S.
,
а  ,
если
,
если  правая тройка, то есть той же ориентации,
что и
правая тройка, то есть той же ориентации,
что и 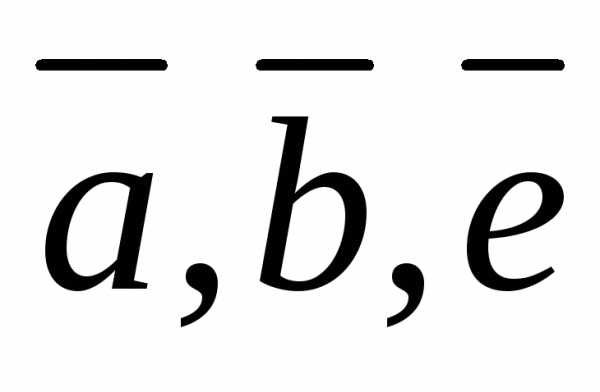 .
.
,
а 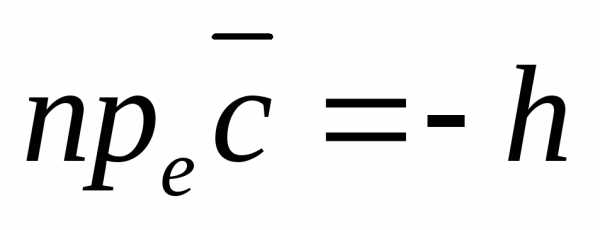 ,
если тройка
,
если тройка 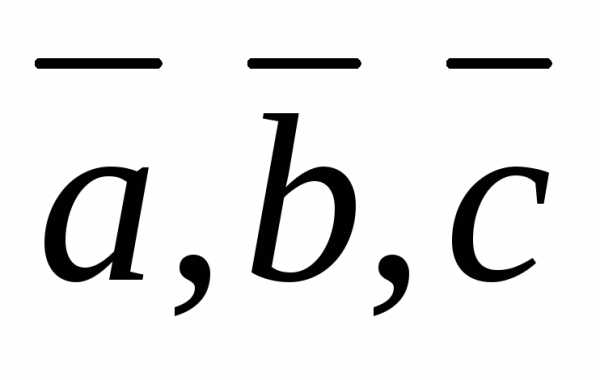 левая.
левая.
Если
векторы 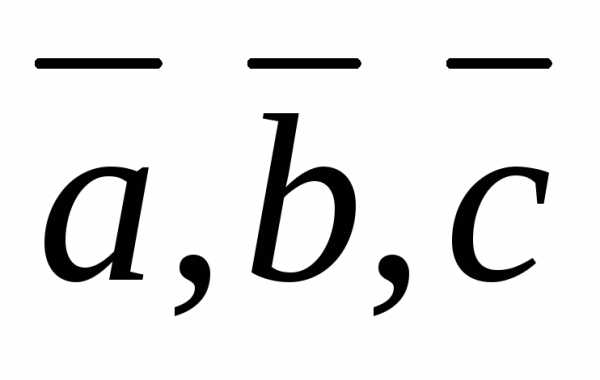 –
компланарны, то
.
–
компланарны, то
.
Следствие 1. .
Доказательство. Скалярное произведение векторов коммутативно, следовательно
.
По теореме 2: , .
Далее
будем обозначать смешанное произведение 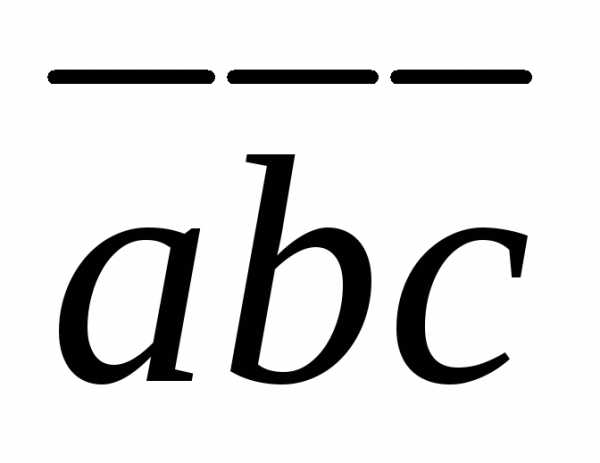 ,
так как
.
,
так как
.
Следствие 2. Смешанное произведение равно нулю тогда и только тогда, когда векторы компланарны.
Выражение смешанного произведения через координаты векторов
Теорема
3. Пусть векторы  имеют в ортонормированном базисе
координаты
.
Тогда смешанное произведение этих
векторов можно представить в виде
имеют в ортонормированном базисе
координаты
.
Тогда смешанное произведение этих
векторов можно представить в виде
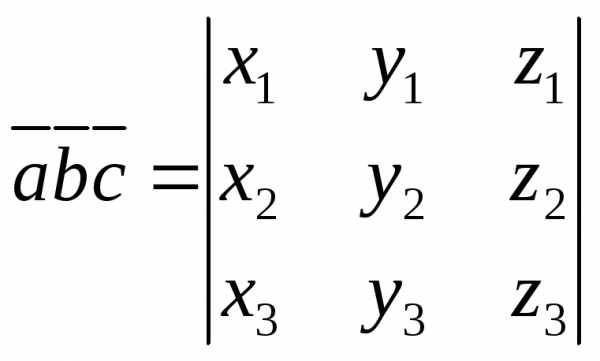 .
.
Доказательство. .
По теореме о векторном произведении:
.
Умножим
векторное произведение скалярно на
вектор  :
:
.
По следствию 2 необходимым и достаточным условием компланарности трех векторов является равенство нулю определителя, составленного из координат векторов:
 компланарны.
компланарны.
Пример 3. Даны четыре точки: . Найти объем тетраэдраАВСD.
Решение. Объем тетраэдра равен одной шестой объема параллелепипеда с теми же основанием и высотой:
.
Координаты векторов .
По теореме 3
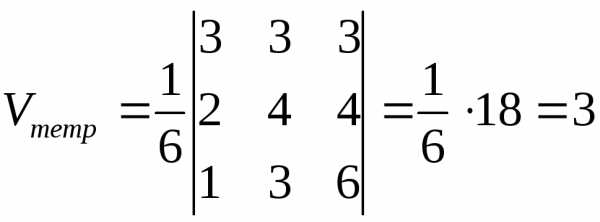 .
.
studfiles.net
1.4. Скалярное произведение двух векторов, его свойства и выражение через координаты сомножителей
Определение. Скалярным
произведением векторов  называется
число, равное произведению их модулей
на косинус угла между этими векторами.
Обозначается скалярное произведение
называется
число, равное произведению их модулей
на косинус угла между этими векторами.
Обозначается скалярное произведение 
= .
.
Отсюда, в частности, следует, что
,
где  —
орт вектора
—
орт вектора .
.
Непосредственно из определения следуют следующие свойства скалярного произведения:
1)
тогда и тольго тогда, когда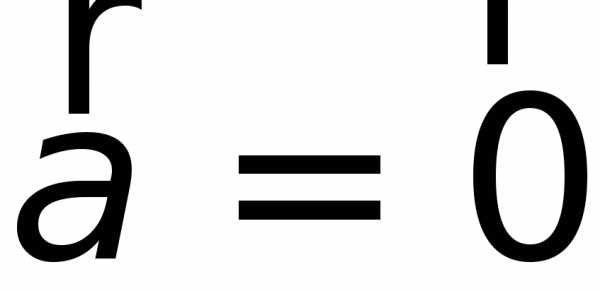 .
.
2) .
3) .
Из свойства линейности проекции следует:
4) .
Действительно, .
Выражение скалярного произведения в ортонормированном базисе.
Рассмотрим ортонормированный базис e1 , e2 , e3 и два вектора
x =x1 e1 + x2e2+ x3e3 , y =y1 e1 + y2e2 + y3e3 , или, кратко, x =(x1 , x2 , x3 ) , y =(y1 , y2 ,y3 ). Тогда скалярное произведение будет равно:
(x , y) =(x1 e1 + x2e2+ x3e3 ,y1 e1 + y2e2 + y3e3)= x1 y1 + x2y2 + x3y3 .
Для доказательства этого необходимо раскрыть скобки, используя свойства 2), 3) скалярного произведения и свойство ортонормированного базиса:
(ek, em)=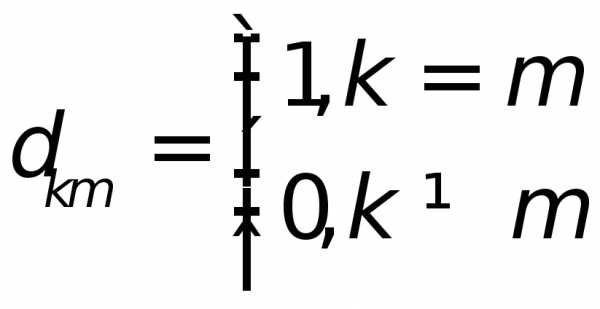 .
Символ
.
Символ называется символом Кронекера.
называется символом Кронекера.
Теорема. Для равенства двух векторов необходимо и достаточно, чтобы проекции этих векторов на любую ось совпадали.
Необходимость
следует из формулы Прe
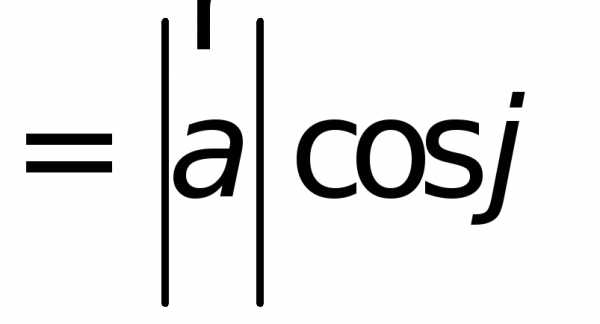 . Достаточност следует из равенств:
. Достаточност следует из равенств:
a = (Прi a) i +(Прj a) j +(Прk a) k = (Прi b) i +(Прj b) j +(Прk b) k=b .
1.5. Определители второго и третьего порядка. Решение систем. Правило Крамера. Векторное произведение двух векторов, его свойства и выражение через координаты сомножителей
1.5.1. Определители второго и третьего порядка.
Матрицей
типа
называется
прямоугольная таблица из чисел,
выстроенных в строк
и
строк
и столбцов.
столбцов.
Примеры
матриц 2×3,
3×1:  ,
, .
.
В общем случае матрицу записывают, используя индексы для нумерации строк и столбцов:
 .
.
Матрица

называется транспонированной матрицей для исходной матрицы.
Если , то матрица называется квадратной. Важной характеристикой квадратной матрицы является определитель. Здесь мы ограничимся рассмотрением определителей матриц втрого и третьего порядков.
Определитель
матрицы 2×2: | Определитель матрицы 3×3: . | |
Slide_1_15 «Определители 2-го и 3-го порядков»
Схема вычисления слагаемых для определителя третьего порядка (рис. 1.15).
Рис. 1.15. Вычисление определителя
Квадратная матрица называется вырожденной, если ее определитель равен нулю.
Разложение определителя по первой сторке.
Для вычисления определителя третьего порядка удобно пользоваться следующей формулой разложения:
.
Slide_1_15_2 «Разложение определителя по строке»
Для
элементов перовой строки 

 множителями служат
множителями служат
,
которые называются алгебраическими дополнениями соответствующих элементов первой строки.
1.5.2.Решение систем. Правило Крамера
Решение системы
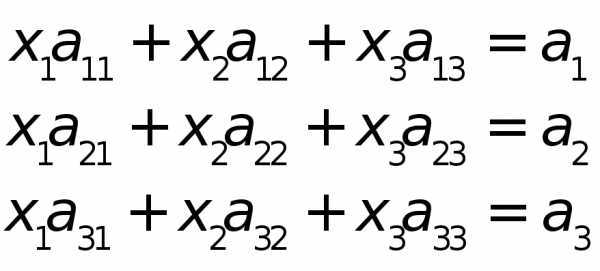
с
невырожденной матрицей коэффициентов  является единственным и находится по
правилу Крамера:
является единственным и находится по
правилу Крамера:
Slide_1_15_1 «Правило Крамера»
1.5.3. Векторное произведение
Тройка некомпланарных векторов a , b , c называется правой, если при приведении их к общему началу поворот от a к b по кратчайшему пути проводится против часовой стрелки, если смотреть из вершины вектора c. В противном случае, тройка векторов a , b , c называется левой.
Векторным произведением векторов a , b называется вектор c , удовлетворяющий условиям:
1) с=a b ,
-угол между векторами a , b ,
,
-угол между векторами a , b ,
2) с a , с
a , с b ,
b ,
3) тройка a , b , c — правая (см. рис. 1.16)
Рис. 1.16. Векторное произведение
Векторное произведение обозначается: с = [ a , b ] .
Slide_1_16 «Векторное произведение»
Из определения следуют простейшие свойства векторного произведения:
Условие коллинеарности двух векторов a , b можно записать в виде:
[ a , b ] = 0 .
Модуль векторного произведения [ a , b ] равен площади параллелограмма, построенного на векторах a , b (см. рис. 1.17).
Рис. 1.17. Модуль векторного произведения
Slide_1_17 «Модуль векторного произведения»
Докажем, что векторное произведение обладает следующими свойствами:
[ a , b ] = — [ b , a ] (см. Рис. 1.18),
[
 a , b ]
=
a , b ]
=  [a , b ],
[a , b ],[ a+с , b ] = [ a , b ]+ [ с , b ] (см. Рис. 1.19).
Первое свойство следует из определения (если тройка a , b , c — правая, то правой будет тройка b , a , —c . см. рисунок).
Рис. 1.18. Антикоммутативность
Slide_1_18 «Антикоммутативность векторного произведения»
Для
доказательства второго и третьего
свойств, обозначим через e единичный
вектор, лежащий в плоскости векторов a , b (a , b – приведены
к общему началу), перпендикулярный
вектору b и такой, что тройка векторов ebc правая, а через g – орт
вектора с
= [ a , b ], g = с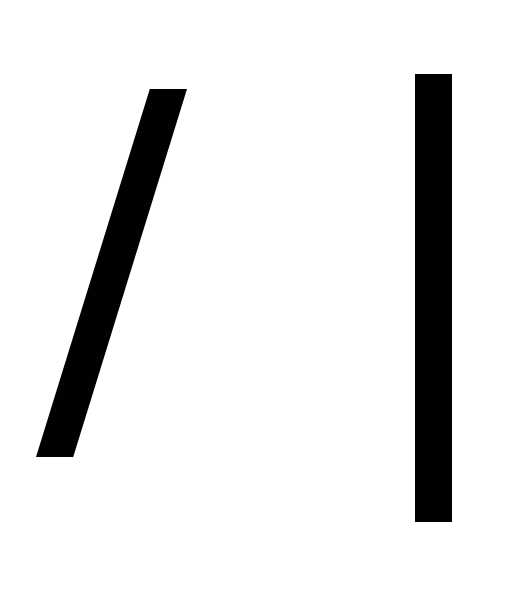 с (см. рисунок).
с (см. рисунок).
Рис. 1.19. Линейность
Тогда
[ a , b ]= b( Прe a ) g (3)
Действительно: [ a , b ]=
[a , b ] g =a b g=b( Прe a ) g .
g=b( Прe a ) g .
Из (3) получим свойство 2):
[  a , b ]= bПрe (
a , b ]= bПрe ( a) g =
a) g =  b( Прe a ) g =
b( Прe a ) g =  [ a , b ].
[ a , b ].
Аналогично выводится свойство 3):
[ a+с , b ] =bПрe (a+с) g=bПрe a g+bПрe с g = [ a , b ]+ [ с , b ].
Slide_1_19 «Линейность векторного произведения»
Выражение векторного произведения через координаты векторов сомножителей в декартовой системе координат.
Пусть в декартовом базисе (i,j,k) выполнены разложения векторов:
x =x1 i + x2j + x3k , y =y1 i + y2j +y3k .
Используя свойства 1)-3) векторного произведения и равенства
k = [ i , j ] , j = [k, i] , i = [j, k] , получим:
[x1 i + x2j + x3k , y1 i + y2j + y3k ] =
= [x1 i , y1 i + y2j + y3k ]+ [ x2j , y1 i + y2j + y3k ]+ [ x3k , y1 i + y2j + y3k ]=
= x1y2k + x1y3 (-j )+ x2 y1(-k)+ x2 y3 i + x3 y1 j + x3 y2(-i )=
=( x2 y3 – x3 y2 , x3 y1 – x1y3 , x1y2 – x2 y1) (см. Рис. 1.20).
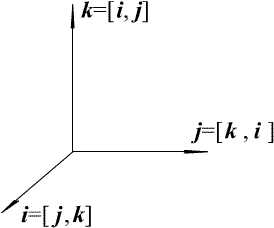
Рис. 1.20. Перемножение ортов осей
Для вычисления векторного произведения удобно использовать символический определитель:
[x1 i + x2j + x3k , y1 i + y2j + y3k ]
= .
.
studfiles.net
Геометрические свойства векторного произведения
1. Модуль векторного произведения численно равен площади параллелограмма, построенного на множителях (рис. 1.42,6).
2. Векторное произведение равняется нулевому вектору тогда и только тогда, когда множители коллинеарны, т.е.
, в частности, .
Первое свойство следует из определения. Докажем второе свойство. Равенство возможно в трех случаях: , или , или . В каждом из этих случаев векторы и коллинеарны (см. разд. 1.1).
Пример 1.19. Вычислить площади параллелограмма и треугольника, построенных на векторах , где , угол между векторами и равен (рис. 1.44).
Решение. Используя алгебраические свойства, найдем сначала векторное произведение
а затем его модуль .
По первому геометрическому свойству векторного произведения искомая площадь параллелограмма равна , а площадь треугольника в 2 раза меньше: .
Выражение векторного произведения через координаты векторов
Пусть в пространстве задан ортонормированный (стандартный) базис . Векторные произведения базисных векторов находятся по определению:
Формулы (1.14) можно получить, используя диаграмму (рис. 1.45): если на этой схеме кратчайший поворот от первого множителя ко второму совершается в положительном направлении (указанном стрелкой), то произведение равно третьему вектору, а если — в отрицательном направлении, то произведение равно третьему вектору, взятому со знаком минус (противоположному вектору).
Найдем выражение векторного произведения через координаты множителей. Пусть в стандартном базисе векторы и имеют координаты и соответственно. Тогда, используя линейность векторного произведения по любому множителю (см. пункт 2 замечаний 1.12) и формулы (1.14), получаем
Запишем это равенство при помощи определителей второго порядка:
Правую часть (1.15) можно представить как результат разложения символического определителя третьего порядка по первой строке
Формула вычисления векторного произведения
Теорема 1.8 (формула вычисления векторного произведения). Если векторы и в правом ортонормированием базисе имеют координаты и соответственно, то векторное произведение этих векторов находится по формуле (1.15), которую принято записывать в виде
Если и — координатные столбцы векторов и в стандартном базисе, то координатный столбец векторного произведения находится по формуле
В самом деле, выполняя умножение матрицы на столбец, получаем
Тогда , что совпадает с (1.15).
Пример 1.20. Параллелограмм построен на векторах (рис. 1.46). Найти:
а) векторные произведения и ; б) площадь параллелограмма ; в) направляющие косинусы такого вектора , перпендикулярного плоскости параллелограмма ,
для которого тройка , , — левая.
Решение. а) Векторное произведение находим по формуле (1.16):
Для нахождения векторного произведения можно использовать матричную запись формулы (1.15) (см. теорему 1.8). Векторам и соответствуют координатные столбцы .
По указанной формуле получаем координатный столбец вектора :
то есть . Результаты совпадают.
Векторное произведение находим, используя алгебраические свойства:
Следовательно, .
б) Площадь параллелограмма находим как модуль векторного произведения :
в) Вектор, противоположный вектору , удовлетворяет перечисленным в условии требованиям, поэтому
Разделив этот вектор на его длину , получим единичныи вектор:
Согласно его координатами служат направляющие косинусы
Мішаний добуток векторів, його властивості та геометричний зміст. Необхідна та достатня умова компланарності векторів. Обчислення мішаного добутку.
studfiles.net
Выражение смешанного произведения через координаты векторов.
а=ахi+ayj+azk, b= bхi+byj+bzk, c= cхi+cyj+czk
abc=(a×b)c=(cxi+cyj+czk)=
=(i-j+k) (cxi+cyj+czk) =cx—cy+cz
abc=
Т.о. объем параллелепипеда: V=±
Vпир.=Sосн. пир. Н= Sосн. парал.Н=±
Следствие. Критерий компланарности: три вектора a,b и c компланарны тогда и только тогда, когда abc==0 (в частности, любые два из них коллениарны).
Приложение смешанного произведения.
Определение ориентации тройки векторов. Если abc>0, то тройка векторов, которая его образует, является правой.
Если abc<0, то тройка векторов, которая его образует, является левой.
Определение компланарности векторов.
Вычисление объемов параллелепипеда и тетраэдра, построенного на векторах.
Пример. Определить ориентацию тройки векторов ijk.
ijk==1>0 – правая тройка векторов.
Двойное векторное произведение.
Пусть даны три произвольных вектора a, b и c. Если вектор b векторно умножается на вектор с, а вектор а также векторно умножается на векторное произведение bc, то полученный при этом вектор а(bc)=[a[bc]] называется двойным векторным произведением.
Теорема. (Док-во на с.79). Для любых векторов a, b и c справедлива формула:
а(bc)=[a[bc]]=b(ac)-c(ab) (13)
Из формулы (13) (аb)c=[[ab]c]=b(ac)-a(bc) (13)
(Т.е. средний вектор, умноженный на скалярное произведение двух остальных, минус другой вектор внутреннего произведения, умноженный на скалярное произведение двух остальных.)
studfiles.net

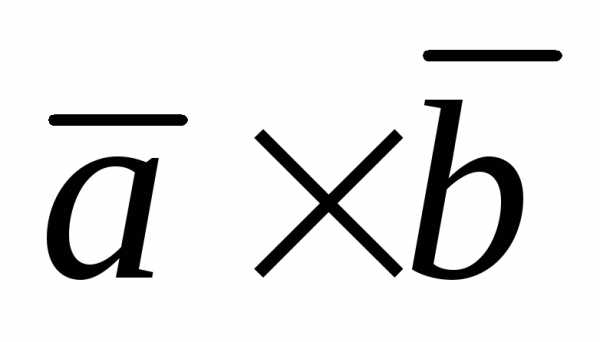 равно нулю тогда и только тогда, когда
эти векторы коллинеарны:
равно нулю тогда и только тогда, когда
эти векторы коллинеарны: равен площади параллелограмма,
построенного на этих векторах.
равен площади параллелограмма,
построенного на этих векторах.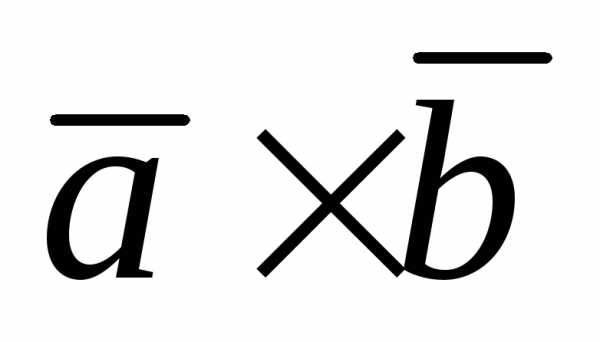 =
= 
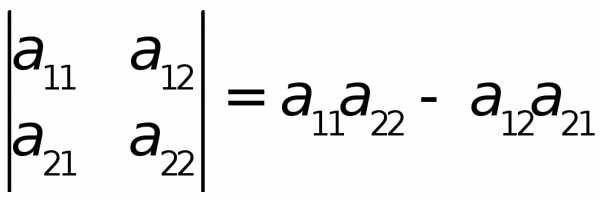 .
. a , b ]
=
a , b ]
=  [a , b ],
[a , b ],