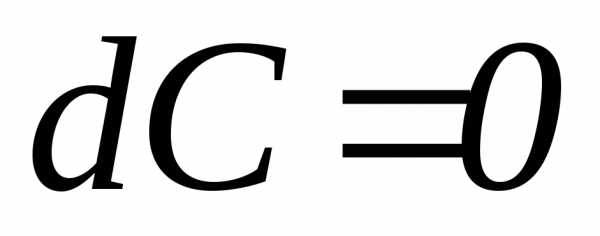21. Дифференцирование неявных и параметрически заданных функций
21.1. Неявно заданная функция
Если функция задана уравнением у=ƒ(х), разрешенным относительно у, то функция задана в явном виде (явная функция).
Под неявным заданием функции понимают задание функции в виде уравнения F(x;y)=0, не разрешенного относительно у.
Всякую явно заданную функцию у=ƒ (х) можно записать как неявно заданную уравнением ƒ(х)-у=0, но не наоборот.
Не всегда легко, а иногда и невозможно разрешить уравнение относительно у (например, у+2х+cosy-1=0 или 2у-х+у=0).
Если неявная функция задана уравнением F(x; у)=0, то для нахождения производной от у по х нет необходимости разрешать уравнение относительно у: достаточно продифференцировать это уравнение по x, рассматривая при этом у как функцию х, и полученное затем уравнение разрешить относительно у’.
Производная неявной функции выражается через аргумент х и функцию у.
<< Пример 21.1
Найти производную функции у, заданную уравнением х3+у3-3ху=0.
Решение: Функция у задана неявно. Дифференцируем по х равенство х3+у3-3ху=0. Из полученного соотношения
3х2+3у2 у’-3(1 у+х у’)=0
следует, что у2у’-ху’=у-х2, т. е. у’=(у-х2)/(у2-х).
21.2. Функция, заданная параметрически
Пусть зависимость между аргументом х и функцией у задана параметрически в виде двух уравнений
где t — вспомогательная переменная, называемая параметром.
Найдем производную у’х, считая, что функции (21.1) имеют производные и что функция х=x(t) имеет обратную t=φ(х). По правилу дифференцирования обратной функции
Функцию у=ƒ(х), определяемую параметрическими уравнениями (21.1), можно рассматривать как сложную функцию у=y(t), где t=φ(х). По правилу дифференцирования сложной функции имеем: у’ х=y’t•t’x. С учетом равенства (21.2) получаем
Полученная формула позволяет находить производную у’х от функции заданной параметрически, не находя непосредственной зависимости у от х.
<< Пример 21.2
Пусть
Найти у’х.
Решение: Имеем x’t=3t2, y’t=2t. Следовательно, у’х=2t/t2, т. е.
В этом можно убедиться, найдя непосредственно зависимость у от х.
Действительно, ТогдаОтсюдат. е.
50. Производные высших порядков. Формула Тейлора.
Производная от функциитоже представляет собой некоторую функцию. Ее можно дифференцировать и в результате получается производная второго порядка (вторая производная):. Следующее дифференцирование дает третью производную, четвертую, пятуюи т. д. Вообще (N–ой) производной называется производная от (N–1)производной: .
Аналогично вводятся дифференциалы второго, третьего и более высоких порядков: – это второй дифференциал (или дифференциал второго порядка). По определению он равен. Здесьрассматривается как константа, и.
Аналогично, и т. д. Найдем, например, производные и дифференциалы до 4го порядка включительно для:
, ,,.
, ,,.
Значение производных, как и значения дифференциалов, можно находить в конкретной точке. Например, найдем производные и дифференциалы до 3-го порядка включительно для рассмотренной функции в точке X = 0:
, ,,
, ,.
С помощью дифференциалов можно получить формулу для вычисления приращения функции более точную, чем (4). Эта формула называется формулой Тейлора:
(5)
Здесь использовано понятие факториала (!) для сокращенной записи произведения натуральных чисел: .
Обычно формулу Тейлора записывают иначе. Если считать, что ,, то. Тогда получается привычная запись формулы Тейлора:
Эта формула представляет дифференцируемую функцию в виде многочлена по степеням , а коэффициенты этого многочлена суть производные от функции при. Практическое применение этой формулы трудно переоценить.
Рассмотрим только один пример на применение формулы Тейлора. Пусть и нас интересует значениепри. Примем близкое число 1 в качестве. Тогдабудем считать равным. Таким образом,Приращение функциивычислим с помощью формулы Тейлора. Вычисляем производные и дифференциалы высших порядков, считая:
.
Все последующие производные равны нулю и, таким образом, формула Тейлора обрывается.
Наши результаты: .
Таким образом, . Естественно, значение функции с такой точностью редко используется. Обычно оставляют три – пять значащих цифр после запятой. Мы же на основании этого примера убеждаемся в следующем свойстве формулы Тейлора: начиная с некоторого номера слагаемые в формуле быстро убывают. В нашем случае второй дифференциал меньше первого в 80 раз, четвертый меньше третьего в двести раз и т. д. Это означает, что для вычисления значений функций в формуле Тейлора можно просто отбрасывать слагаемые, используя несколько первых. Это же правило имеет место, когда функцию заменяют формулой Тейлора, оставляя одно–два слагаемых. Например,мало отличается от нуля при. Мы использовали соотношение, если нужна большая точность, то, используя формулу Тейлора, получают:илии т. д.
studfiles.net
44. Дифференцирование функций, заданных неявно и параметрически.
44. ДИФФЕРЕНЦИРОВАНИЕ НЕЯВНЫХ И ПАРАМЕТРИЧЕСКИ ЗАДАННЫХ ФУНКЦИЙ
44.1. Неявно заданная функция
Если функция задана уравнением у=ƒ(х), разрешенным относительно у, то функция задана в явном виде (явная функция).
Под неявным заданием функции понимают задание функции в виде уравнения F(x;y)=0, не разрешенного относительно у.
Всякую явно заданную функцию у=ƒ (х) можно записать как неявно заданную уравнением ƒ(х)-у=0, но не наоборот.
Не всегда легко, а иногда и невозможно разрешить уравнение относительно у (например, у+2х+cosy-1=0 или 2у-х+у=0).
Если неявная функция задана уравнением F(x; у)=0, то для нахождения производной от у по х нет необходимости разрешать уравнение относительно у: достаточно продифференцировать это уравнение по x, рассматривая при этом у как функцию х, и полученное затем уравнение разрешить относительно у’.
Производная неявной функции выражается через аргумент х и функцию у.
<< Пример 21.1
Найти производную функции у, заданную уравнением х3+у3-3ху=0.
Решение: Функция у задана неявно. Дифференцируем по х равенство х
3х2+3у2· у’-3(1· у+х· у’)=0
следует, что у2у’-ху’=у-х2, т. е. у’=(у-х2)/(у2-х).
44.2. Функция, заданная параметрически
Пусть зависимость между аргументом х и функцией у задана параметрически в виде двух уравнений
где t — вспомогательная переменная, называемая параметром.
Найдем производную у’х, считая, что функции (21.1) имеют производные и что функция х=x(t) имеет обратную t=φ(х). По правилу дифференцирования обратной функции
Функцию у=ƒ(х), определяемую параметрическими уравнениями (21.1), можно рассматривать как сложную функцию у=y(t), где t=φ(х). По правилу дифференцирования сложной функции имеем: у’х=y’t•t’x. С учетом равенства (21.2) получаемПолученная формула позволяет находить производную у’х от функции заданной параметрически, не находя непосредственной зависимости у от х.
<< Пример 21.2
Пусть
Найти у’х.
Решение: Имеем x’t=3t2, y’t=2t. Следовательно, у’х=2t/t2, т. е.
В этом можно убедиться, найдя непосредственно зависимость у от х.
Действительно, Тогда Отсюда т. е.
3.1.8. Производные функций, заданных параметрически. Дифференцирование неявных функций
По правилу дифференцирования сложной функции
[y(x(t))]′t = y′x xt′,
а так как | xt′ dt = dx , то дифференциалdy | можно | записать в виде |
dy = y′x dx= | f ′(x) dx , то есть формула дифференциала сохраняет свой вид. | ||
Следствие |
| y = f(x) |
|
Из теоремы следует, что производную y′ функции | можно записывать в | ||
виде y′ = dydx , независимо от того, являетсяx простой переменной или функцией другой
переменной.
Иногда удобно вычислять дифференциал, не раскрывая до конца производные сложных функций, а пользуясь инвариантностью его формулы.
Производная функции, заданной параметрически
Если функция y = f (x) | x = ϕ(t) | , где |
задана параметрическими уравнениями | ||
| y = ψ(t) |
|
параметр и если функции ϕ(t) иψ(t) дифференцируемы в точкеt , то функцияy = также дифференцируема в точкеx(t) и ее производная вычисляется по правилу:
|
| y′x = | ψ′(t) | . |
|
|
| ||
|
|
| ϕ (t) | |
|
|
| ′ | |
Доказательство |
|
|
|
|
Было показано, | что производную y′x можно представить как отношение | |||
дифференциалов: y′x | = | dy . |
|
|
|
| dx |
|
|
Поскольку функции ϕ(t) иφ(t) дифференцируемы в точкеt , соответствующей точкеx , то, используя формулу дифференциала,dy иdx можно представить в виде:
|
| dy = ψ′(t) dt, | dx = ϕ′(t) dt. Тогда y′x | = | ψ′(t)dt | = | ψ′(t) | . | ||||
|
| ′ |
| |||||||||
|
|
|
|
|
|
|
|
|
| ′ | ||
|
|
|
|
|
|
|
|
| ϕ (t)dt |
| ϕ (t) | |
Задача 3.1.7 |
|
|
|
|
|
|
|
|
|
|
|
|
Вычислите |
| производную | y′x функцииy(x), |
| заданной | параметрическими | ||||||
|
|
|
| 1 |
|
|
|
|
|
|
| |
уравнениями: | x = |
|
| t . |
|
|
|
|
|
| ||
|
| 3 |
|
|
|
|
|
| ||||
|
|
| t |
|
|
|
|
|
| |||
| y = |
|
|
|
|
|
|
|
| |||
Решение
По теореме о производной функции, заданной параметрически, можно записать
| 3 |
| ′ |
|
| 1 |
|
| − | 2 |
|
|
|
|
|
|
| ||
|
|
|
|
|
| 3 |
| 5 |
| ||||||||||
y′x = | ( |
| t )t |
|
| 3 | t |
|
|
|
|
| 2 |
|
|
| |||
|
| = |
|
|
|
| = − | t 6 . | |||||||||||
| 1 |
| ′ | − | 1 | t | − | 3 |
| 3 | |||||||||
|
| 2 | |||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||
|
|
|
|
|
|
|
|
|
|
|
| ||||||||
|
|
|
|
|
|
|
|
|
|
|
| ||||||||
|
|
| t | t |
|
|
| 2 |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
| 20 |
|
|
|
|
|
|
|
|
|
|
|
|
Производная функции, заданной неявно | y = y(x) задана соотношением | |
Если дифференцируемая в точке | x функция | |
F (x, y)= 0 и если при этом функция | F(x, y(x))- | дифференцируема в точке x , то |
производную y′(x) можно определить из равенства
(F (x, y(x)))′x = 0 ,
так как функция F(x, y(x)) тождественно равна постоянной и, следовательно, ее производная равна нулю.
Задача 3.1.8
Вычислите производную y′x , если дифференцируемая функцияy = y(x) задана неявно равенством
x3 y+ x y3 −3×2 −3y2 + exy = 0 .
Решение
Согласно теореме 2 производную y′x следует определять из равенства
(x3 y+ x y3 −3×2 −3y2 +exy )′x = 0 .
Вычислим все производные в левой части этого соотношения, используя правила дифференцирования.
3×2 y+ x3 y′x + y3 + x3y2 y′x − 6x− 6 yy′x + exy (y+ xy′x )= 0 .
Из полученного равенства определим производную y′x .
(x3 +3x y2 −6y+ exy x) y′x = 6x−3×2 y− y3 −exy y.
y′x = | 6x−3×2 y− y3 | −exyy | . | |
x3 +3x y2 −6 y+ exy x | ||||
|
| |||
ЗАМЕЧАНИЕ
Аналогично вычисляется дифференциал функции, заданной неявно.
Задача 3.1.9
Найдите дифференциал функции y = y(x), заданной неявно равенством
x2 +y2 +xy =0 .
Решение
Поскольку переменная y является функциейx , то левая часть заданного уравненияx2 + y 2 + xy также является функциейx . Эта функция тождественно равна нулю. Следовательно, ее дифференциал тождественно равен нулю, то есть
d (x2 + y2 + xy)= 0 .
Вычислим дифференциал каждого слагаемого в левой части, используя правила дифференцирования
d (x2 )+ d(y2 )+ d( xy)= 0 , или 2x dx+ 2 y dy+ | x dy + y dx | = 0 . | |
2 xy | |||
|
| ||
Из полученного равенства определим дифференциал dy . |
|
| |
21 |
|
|
studfiles.net
Дифференцирование функций, заданных параметрически
Если зависимость функциии аргументазадана посредством параметра:, то, или. (2)
Пример 1. Найти , если,. Это параметрические уравнения окружностис центром в начале координат и радиуса.
Решение. Находим и.
Отсюда .
Пример 2. Найти от функции:,.
Решение: ,,теперь по формуле (2)
найдем .
Производная неявной функции
Пусть уравнение не разрешено относительно функции, т.е. функциязадана неявно. Чтобы найти производную, надо продифференцировать левую и правую часть уравнения, учитывая, чтоесть функция аргумента. Рассмотрим это правило на примерах.
Пример 1. Найти , если а), б).
Решение: а) , выразив, получим.;
б) дифференцируя обе части этого уравнения, получим уравнение относительно :,;найдем теперь.
Геометрический смысл производной
Здесь – угол наклона касательной к графику функциии точке. Через две точкиикривойпроведем секущую, ее угловой коэффициент. Двигая точкупо кривой к точке, мы будем поворачивать секущую вокруг точки, в результате секущая стремится занять положение касательной, проведенной к графику в точке, а уголстремится к углу– наклона касательной, т.е.,
где – угловой коэффициент касательной. Известное уравнение прямойиспользуем как уравнение касательной, проведенной к графику функциив точке, с угловым коэффициентом. Тогда уравнение касательной примет вид
(3)
Задача. Найти уравнение касательной к графику функции а) в точке, б),в точке.
Решение. а) Сначала вычислим ординату точки касания . Затем производную в точке,
. Это угловой коэффициент касательной.
Подставим найденные параметры в уравнение (3)
–искомая касательная;
б) кривая задана параметрически; найдем координаты точки касания, подставив значение параметра в уравнение кривой: ,. Для отыскания углового коэффициентавоспользуемся формулой,, теперь запишем уравнение касательной , или.
Дифференциал функции и формула приближенного вычисления
Определение. Дифференциалом функции называется величина, пропорциональная бесконечно малому приращению аргумента, отличающаяся от соответственного приращения функциина величину более высокого порядка.
По определению производной: , откуда следует, что, где– бесконечно малая при, т. е. , тогда, где первое слагаемое и есть дифференциал
, ,. (4)
Определение дифференциала позволяет использовать его в приближенных вычислениях, заменив вычисление функции ее дифференциалом. Рассмотрим приращение функции: , или, тогда
. (5)
Это и есть формула приближенного вычисления. Ошибка, получаемая при приближенных вычислениях, есть бесконечно малая высшего порядка, чем приращение аргумента, т. к.
.
Задача 1. Найти дифференциалы функций:
а) , б), в).
Решение: а) , найдем сначалаи затем;
б) ,;
в) ,.
Задача 2. Найти приращение и дифференциал функции прии. Вычислить абсолютную и относительную ошибки, которые получаются при замене приращения функции ее дифференциалом.
Решение ,
;
Абсолютная ошибка , относительная ошибка
.
Задача 3. Вычислить приближенно а) , б).
Решение. Чтобы воспользоваться формулой (5) надо составить функцию (по виду вычисляемого выражения) и выбрать начальные условия так, чтобыбыло мало, аможно было легко подсчитать. В случае а) выбираем,,
, .
, ,
;
б) чтобы было мало, необходимо извлечь целую часть корня, т. е.
, откуда ,,,
, ,,теперь вычислим приближенно:
.
Производные и дифференциалы высших порядков
Определение 1. Производной второго порядка от функции называется производная от производной первого порядка и обозначается символомили, или.
Пример. ,,.
Определение 2. Производной -го порядка называется производная первого порядка от производной-го порядка и обозначаетсяили, или.
Пример. . Найти.
, ,!,
!, используя метод математической индукции, запишем формулу производной-го порядка!
Определение 3. Дифференциалом высшего порядка функции называется дифференциал от дифференциала -го порядка:
, в частности , здесь.
Пример: . Найти.
, ;
Тогда .
Производная второго порядка от функции, заданной параметрически.
Если , то производные,, последовательно могут быть вычислены по формулам:
=,,и т. д.
Для производной второго порядка имеет место формула .
Пример. Найти от функции
Решение. Найдем сначала ,,
тогда ,.
Правило Лопиталя. Раскрытие неопределенностей при вычислении пределов
Теорема. Предел отношения двух бесконечно малых или двух бесконечно больших существует и равен пределу отношения их производных:
, если выполняются условия:
функции идифференцируемы в некоторой окрестности точкиив этой окрестности.
(или ).
существует конечный или бесконечный.
Здесь может быть числом или одним из символов:.
Задача 1. Вычислить пределы: а) , б).
Решение. а) Подставив предельное значение аргумента , получаем неопределенность, т.к.,и функции дифференцируемы.
Найдем .
б) При имеем неопределенность. Применим правило Лопиталя:. Полученный предел снова представляет неопределенность вида, применяя еще раз правило Лопиталя, найдем.
Другие виды неопределенностей ,,можно свести к видуили.
Задача 2. Найти предел .
Решение. Подставим предельное значение аргумента, получим неопределенность , которая легко сводится к частному:
=
=.
Возрастание, убывание функции. Точки экстремума
Определение 1. Функция называется возрастающей (убывающей) на некотором промежутке, если для любыхэтого промежутка().
Функция возрастающая (убывающая) называется монотонной.
Теорема 1. (Условие монотонности)
Если функция 1) определена на, 2) имеет конечную производнуюна, тогда, чтобыбыла возрастающей (убывающей) на, необходимо и достаточно, чтобы().
Задача 1. Найти интервалы монотонности функции .
Решение. Область определения функции дифференцируема всюду в области определения:.
Решим неравенство ,,
-это интервал возрастания функции.
Соответственно неравенство справедливо для всех– область убывания функции.
Определение 2. Точка называется точкой локального максимума (минимума), если в некоторой ее окрестностивыполняется неравенство() для всехэтой окрестности.
Теорема 2. (Необходимое условие существования экстремума)
Если 1) определена в окрестности точки, 2) дифференцируема в точкеи 3) имеет в ней локальный экстремум, то.
Точки, в которых производная называются критическими.
Замечание. Функция может иметь экстремум и в точках, где первая производная не существует. Например: Функция непрерывна в точке, но не дифференцируема т. к. односторонние пределы не равны, значит,не существует в точке, но функция имеет минимум.
Теорема 3. (Достаточное условие экстремума)
Если функция : 1) непрерывна в точке, 2) дифференцируема в некоторой области, 3)либо не существует и 4) при переходе через точкупроизводная меняет знак, то– точка экстремума, причем, если производная слева ототрицательна, а справа положительна, то– точка минимума; если слева отпроизводная положительна (функция возрастает) а справа отрицательна (функция убывает), то– точка максимума.
Замечание: в промежутке между критическими точками производная сохраняет знак, следовательно, это промежутки монотонности.
Теорема 4. (Исследование на экстремум с помощью второй производной или второе достаточное условие экстремума).
Если 1) в точке функциядифференцируема и,2) существует вторая производная, 3) в окрестности, то прифункция имеет минимум, а при– максимум.
Итак, при исследовании функции на экстремум необходимо пользоваться правилами:
Найти первую производную
Найти критические точки , решив уравненияи.
Проверить, меняет ли знак первая производная при переходе через точку или установить знак второй производной, классифицировать экстремум.
Найти значение функции в экстремальных точках.
Задача. Исследовать на экстремум функцию .
Решение. Область определения ,
, при. Это значениене принадлежит области определения функции. Значит,– единственная критическая точка. Проверим знак первой производной слева и справа от нее.
При ,, функция возрастает, при,функция убывает, значит– точка максимума,– максимальное значение функции.
Наибольшее и наименьшее значение функции.
Теорема Вейерштрасса. Если функция непрерывна на замкнутом промежутке , то она достигает на нем наибольшее и наименьшее значения. Эти значения находятся либо на концах промежутка, либо в экстремальных точках.
studfiles.net
ДИФФЕРЕНЦИРОВАНИЕ НЕЯВНЫХ И ПАРАМЕТРИЧЕСКИ ЗАДАННЫХ ФУНКЦИЙ
Неявно заданная функция
Если функция задана уравнением у=ƒ(х), разрешенным относительно у, то функция задана в явном виде (явная функция).
Под неявным заданием функции понимают задание функции в виде уравнения F(x;y)=0, не разрешенного относительно у.
Всякую явно заданную функцию у=ƒ (х) можно записать как неявно заданную уравнением ƒ(х)-у=0, но не наоборот.
Не всегда легко, а иногда и невозможно разрешить уравнение относительно у (например, у+2х+cosy-1=0 или 2у-х+у=0).
Если неявная функция задана уравнением F(x; у)=0, то для нахождения производной от у по х нет необходимости разрешать уравнение относительно у: достаточно продифференцировать это уравнение по x, рассматривая при этом у как функцию х, и полученное затем уравнение разрешить относительно у’.
Производная неявной функции выражается через аргумент х и функцию у.
<< Пример 21.1
Найти производную функции у, заданную уравнением х3+у3-3ху=0.
Решение: Функция у задана неявно. Дифференцируем по х равенство х3+у3-3ху=0. Из полученного соотношения
3х2+3у2· у’-3(1· у+х· у’)=0
следует, что у2у’-ху’=у-х2, т. е. у’=(у-х2)/(у2-х).
Функция, заданная параметрически
Пусть зависимость между аргументом х и функцией у задана параметрически в виде двух уравнений
где t — вспомогательная переменная, называемая параметром.
Найдем производную у’х, считая, что функции (21.1) имеют производные и что функция х=x(t) имеет обратную t=φ(х). По правилу дифференцирования обратной функции
Функцию у=ƒ(х), определяемую параметрическими уравнениями (21.1), можно рассматривать как сложную функцию у=y(t), где t=φ(х). По правилу дифференцирования сложной функции имеем: у’х=y’t•t’x. С учетом равенства (21.2) получаем
Полученная формула позволяет находить производную у’х от функции заданной параметрически, не находя непосредственной зависимости у от х.
<< Пример 21.2
Пусть
Найти у’х.
Решение: Имеем x’t=3t2, y’t=2t. Следовательно, у’х=2t/t2, т. е.
В этом можно убедиться, найдя непосредственно зависимость у от х.
Действительно, Тогда Отсюда т. е.
60)
Понятие дифференциала
Пусть функция y = f(x) дифференцируема при некотором значении переменной x. Следовательно, в точке xсуществует конечная производная
Тогда по определению предела функции разность
(1)
является бесконечно малой величиной при . Выразив из равенства (1) приращение функции, получим
(2)
(величина не зависит от , т. е. остаётся постоянной при ).
Если , то в правой части равенства (2) первое слагаемое линейно относительно . Поэтому при
оно является бесконечно малой того же порядка малости, что и . Второе слагаемое — бесконечно малая более высокого порядка малости, чем первое, так как их отношение стремится к нулю при
Поэтому говорят, что первое слагаемое формулы (2) является главной, линейной относительно частью приращения функции; чем меньше , тем большую долю приращения составляет эта часть. Поэтому при малых значениях (и при ) приращение функции можно приближенно заменить его главной частью , т.е.
(3)
Эту главную часть приращения функции называют дифференциалом данной функции в точке xи обозначают
или
Следовательно,
(4)
или
(5)
Итак, дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной.
Замечание. Нужно помнить, что если x – исходное значение аргумента,
— наращенное значение, то производная в выражении дифференциала берётся в исходной точке x; в формуле (5) это видно из записи, в формуле (4) – нет.
Дифференциал функции можно записать в другой форме:
(6)
или
Геометрический смысл дифференциала. Дифференциал функции y = f(x) равен приращению ординаты касательной, проведённой к графику этой функции в точке (x; y), при изменении xна величину .
61)
Инвариантность формы дифференциала первого порядка.
Следствие 2.4.1.
dz = F′(y0)dy = Φ′(x0)dx.
В зтой формуле dy = f′(x)dx является дифференциалом функции, а dx дифференциалом независимой переменной.
– 75 –Таким образом, дифференциал функции z имеет один и тот же вид (а именно, произведение производной функции на дифференциал переменной) независимо от того, считается ли эта переменная независимой (dz = Φ′(x0)dx) или она является функцией (dz = F′(y0)dy). В этом и заключается инвариантность формы дифференциала (первого порядка).
Замечание 2.4.2. Если приходится иметь дело со сложной функцией z =z(y), y = y(x), то для обозначения ее производной употребляется также индекс x или y, указывающий, по какой переменной берется производная, т.е. пишут z′x или z′y. В этих обозначениях формула для вычисления производной сложной функции имеет вид z′x = z′yy′x.
62)
infopedia.su
Производная параметрически заданной функции
В этой статье мы дадим определение параметрически заданной функции, покажем процесс нахождение ее производных и рассмотрим несколько примеров.
Определение. Пусть даны две функции переменной :
,
рассматриваемые при одних и тех же значениях . Тогда любому из этих значений соответствует некоторое определенное значение и , а значит, и определенная точка . Когда переменная пробегает все значения из области определения функций, точка описывает некоторую линию в плоскости . Данные уравнения называются параметрическими уравнениями этой линии, а переменная — параметром. В этом случае говорят, что функция задана параметрически.
То есть теперь у нас нет привычной зависимости . Но как же тогда будет находиться производная? Разберемся с этим вопросом.
Для каждого параметрического уравнения найдем дифференциал его левой и правой части:
Как известно, производная по есть . Таким образом, разделив второе уравнение на первое, получим:
С помощью данной формулы и находится первая производная функции, заданной параметрически.
Пример 2
Найти производную параметрически заданной функции
Решение:
Ответ:
[свернуть]
Пример 3
Найти производную параметрически заданной функции
Решение:
Ответ:
[свернуть]
Если поставлена задача нахождения производной высшего порядка, будем преобразовывать уже полученную формулу первой производной следующим образом:
И так далее. То есть, как и в случае с производными функции , для нахождения -ой производной нужно сначала последовательно найти с первой по производные.
Пример 4
Найти вторую производную параметрически заданной функции
Решение: Находим сначала первую производную :
Записываем найденную производную в параметрическом виде:
Для этой новой функции применяем формулу еще раз:
Ответ:
[свернуть]
Пример 5
Найти третью производную параметрически заданной функции
Решение: Находим сначала первую производную :
Записываем найденную производную в параметрическом виде:
Для этой новой функции применяем формулу еще раз:
И вторую производную пишем в параметрической форме:
Заключительный, третий раз применяем формулу:
Ответ:
[свернуть]
На этом всё. Мы познакомились с производной функции, заданной параметрически, а также рассмотрели процесс нахождения производных высшего порядка. Спасибо за внимание и удачи в дальнейшем изучении высшей математики!
higher-math.ru
Производная параметрически заданной функции
— Параметрически
заданная функция : 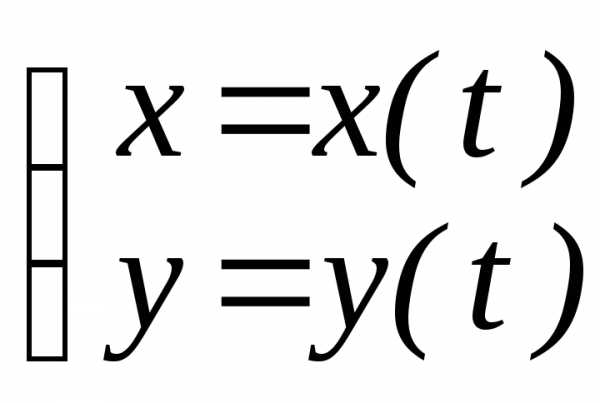 ,
то есть переменныех и у задаются
как функции третьей переменной t , которая называется параметром.
,
то есть переменныех и у задаются
как функции третьей переменной t , которая называется параметром.
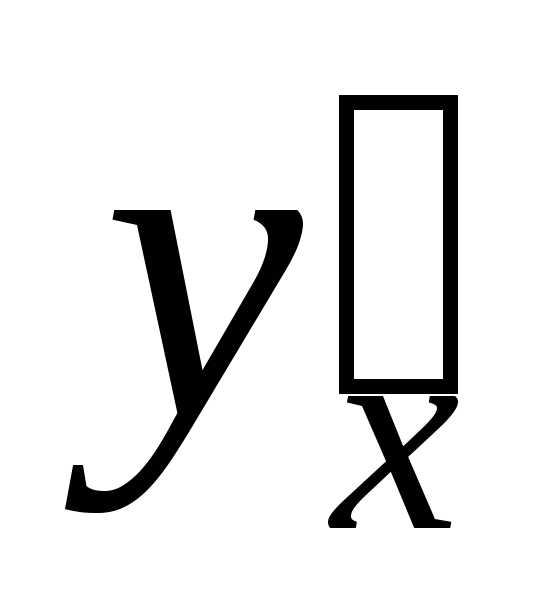
— Чтобы
найти производную параметрически
заданной функции, используют следующую
формулу: 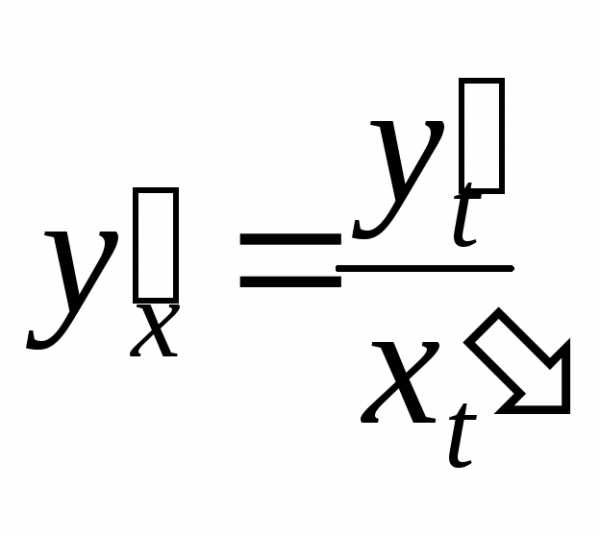 .
.
ПРИМЕР
Найти
производную 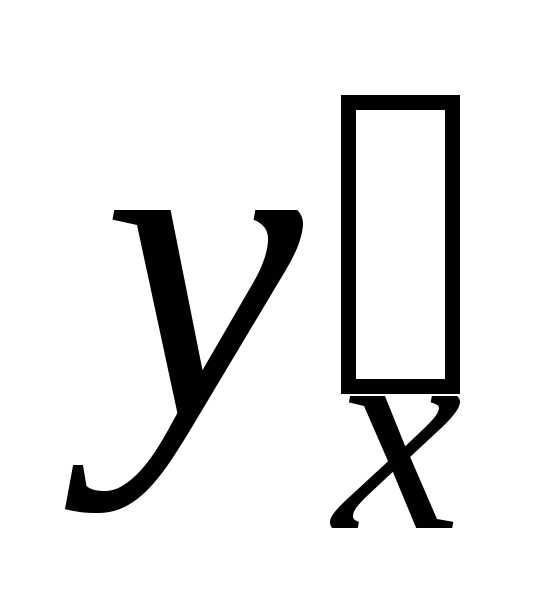 параметрически заданной функции:
параметрически заданной функции:
в точке М(0;а).
Найдем производные по параметру t от x и у.
Используем правила дифференцирования суммы и вынесения постоянной за знак производной (правила 3 и 5), а также дифференцирования сложной функции. | |
| По
формуле найдем производную |
| В заданной точке М: х=0; у=а; поэтому для определения значения параметра t, соответствующего точке М, следует решить систему. |
| Выбираем только те корни, которые удовлетворяют обоим уравнениям системы, и находим значение производной в точке М |
—
Если значение
производной функции в некоторой точке
,
то это означает, что график функции в
этой точке имеет касательную,
расположенную вертикально ( по
геометрическому смыслу: производная
функции в точке численно равна тангенсу
угла наклона касательной
; | |
Логарифмическое дифференцирование (логарифмическая производная)
К логарифмическому дифференцированию обращаются в двух случаях.
I случай | II случай |
Степенно-показательная функция: | Композиция (произведение/деление) более чем двух функций вида: . |
В обоих случаях перед дифференцированием соответствующие выражения логарифмируют по основанию е (натуральный логарифм), используя свойства логарифмов (см. справочный материал). Эти свойства позволяют преобразовать выражение I в произведение, а выражение II – в алгебраическую сумму функций.
; |
Затем находят производную, как производную неявно заданной функции, то есть, дифференцируя обе части полученных уравнений.
ПРИМЕР
Найти
производную 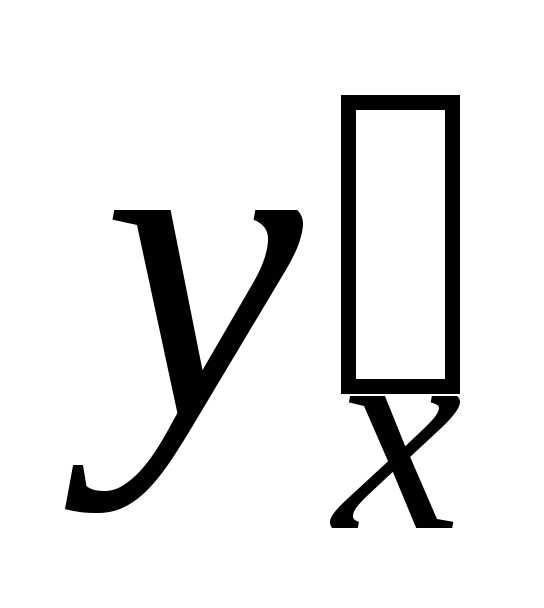 функции:
функции: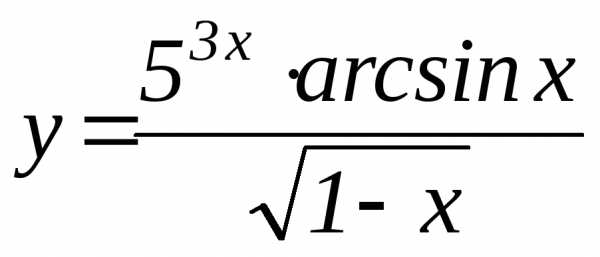 .
.
II случай.
Логарифмируем функцию. | |
Вычисляем производную, как от неявно заданной функции. | |
Из
полученного выражения найдем | |
. | |
Дифференциал функции и дифференциал аргумента
Пусть в некоторой точке функция дифференцируема, то есть имеет конечную производную: . Примем без доказательства, что в этом случае приращение функции можно представить в виде:
, где- бесконечно малые величины.
Очевидно, что при таких условиях приращение функции представляет собой БМ (бесконечно малую) величину, состоящую из суммы двух бесконечно малых величин. Выделим ее главную часть, сравнив слагаемые (см. тему 4, сравнение БМ величин).
Так как ,
то 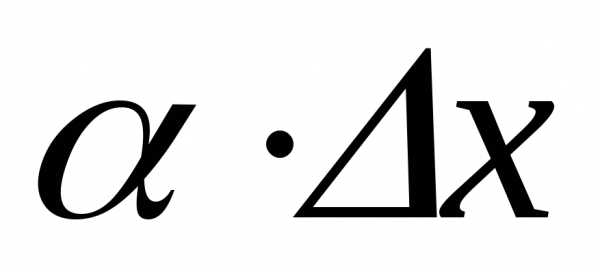 — БМ более высокого порядка малости, чем
— БМ более высокого порядка малости, чем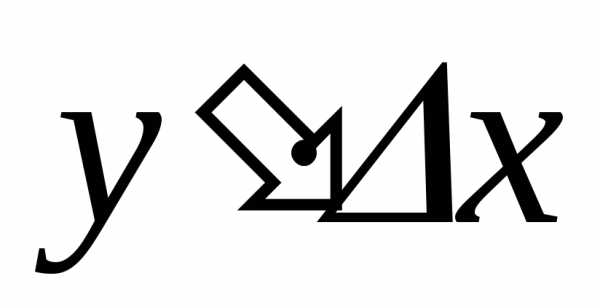 .
.
Главной частью БМ приращения функции будет (БМ величина эквивалентна своей главной части):
.
— Дифференциалом функции называют главную, линейную относительно приращения аргумента, часть бесконечно малого приращения функции.
Дифференциал
обозначается латинской буквой d.
Если учесть, что дифференциал аргумента
совпадает с его БМ приращением: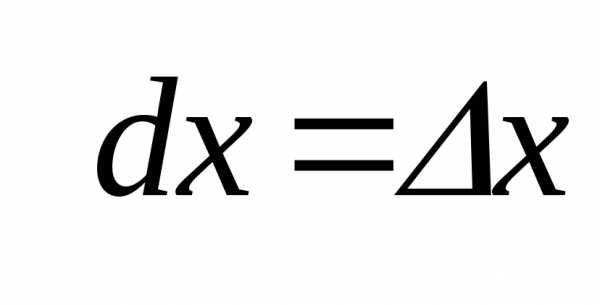 ,
то получим формулу для вычисления
дифференциала функции:
,
то получим формулу для вычисления
дифференциала функции:
— .
Из этого выражения 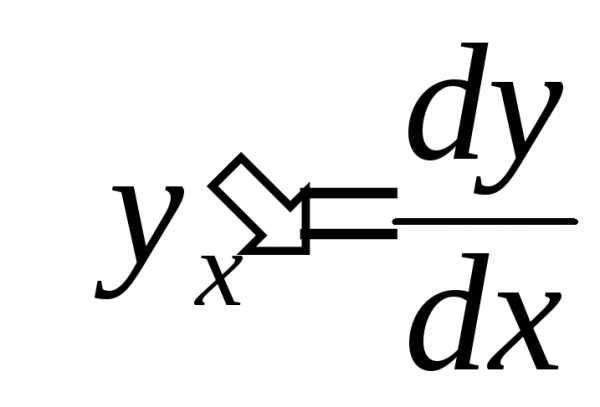 — производная в дифференциальном виде,
обозначение, введенное Лейбницем.
— производная в дифференциальном виде,
обозначение, введенное Лейбницем.
Для вычисления дифференциалов функций применяются все те же правила, что и для вычисления производной.
1 | | Дифференциал постоянной равен нулю: |
|
2 | | Дифференциал алгебраической суммы конечного числа дифференцируемых функций равен сумме дифференциалов этих функций: | |
3 | | Дифференциал произведения двух дифференцируемых функций: | |
4 | | Постоянный множитель можно выносить за знак дифференциала: | |
5 | | Дифференциал частного двух дифференцируемых функций (при условии, что V0): |
Главным
свойством дифференциала функции является инвариантность,
неизменность его формы. Пусть задана
функция y=f(x), где x=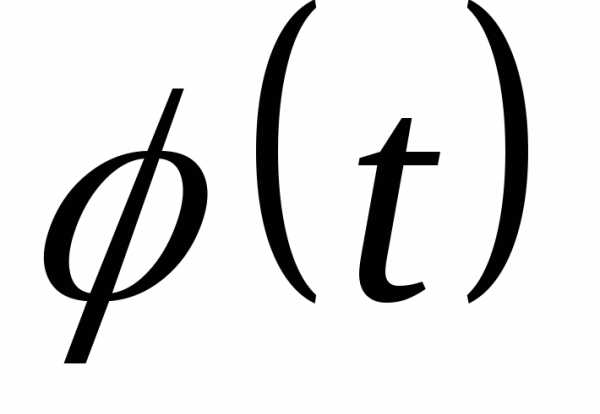 , т.е. y=f(
, т.е. y=f(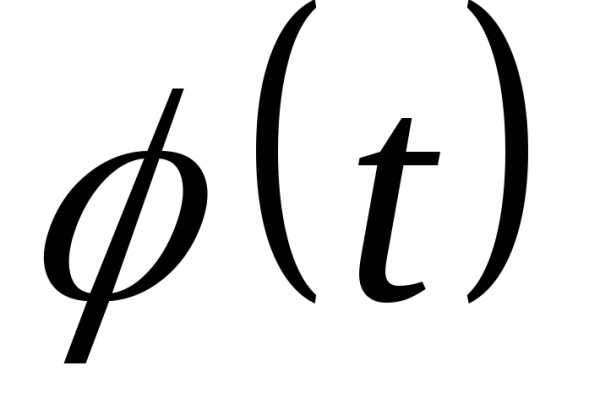 ) является сложной функцией. Предположим,
что f и
) является сложной функцией. Предположим,
что f и  — дифференцируемые функции. Вычислимdy:
— дифференцируемые функции. Вычислимdy:
.
Таким образом, дифференциал функции выражается одной и той же формулой как в случае функции от независимой переменной, так и в случае функции от функции. Именно это свойство дифференциала называют инвариантностью формулы (или формы) дифференциала.
Следует
обратить внимание на то, что инвариантна
(неизменна) именно форма дифференциала,
так как в содержании формулы дифференциала
функции от функции есть существенное
отличие от содержания формулы дифференциала
функции от независимой переменной. Так,
в формуле
,dx есть не только дифференциал, но и
приращение  аргументаx,
если x — независимая переменная, и dx есть дифференциал x,
но не приращение
аргументаx,
если x — независимая переменная, и dx есть дифференциал x,
но не приращение  ,
если аргументx есть в свою очередь функция некоторой
переменной t.
,
если аргументx есть в свою очередь функция некоторой
переменной t.
studfiles.net

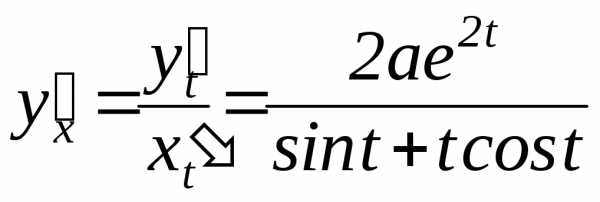 ;
; .
.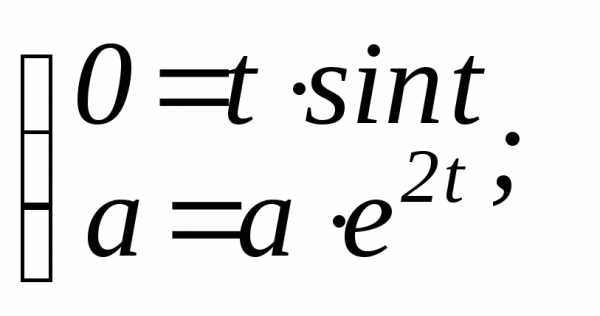
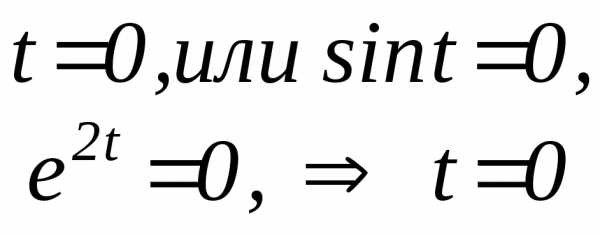
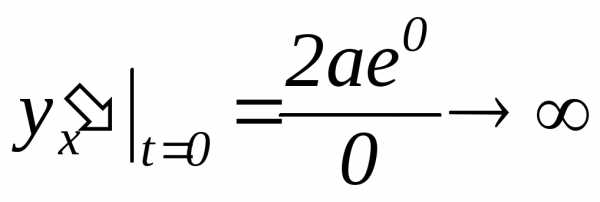
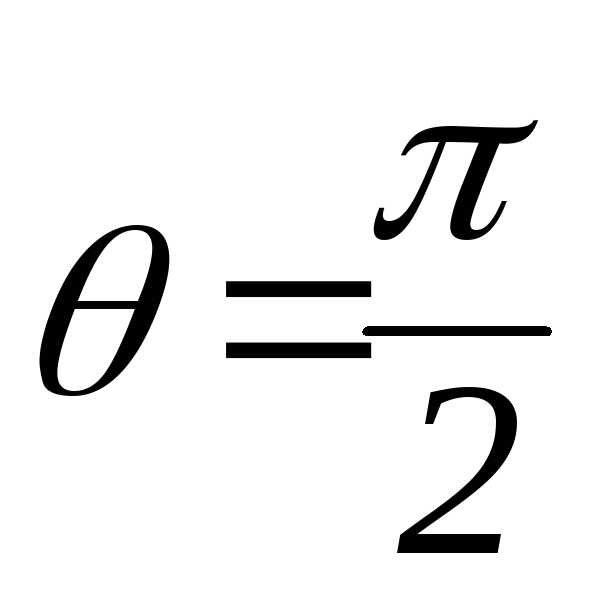 ).
).
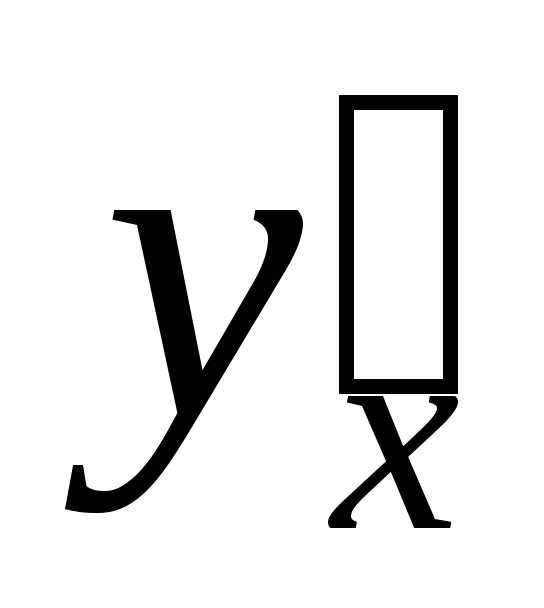 ,
учитывая задание функцииу.
,
учитывая задание функцииу.