Независимые испытания Бернулли. Формула Бернулли. Наивероятнейшее число успехов. Полиномиальная схема. Примеры.
Независимые испытания Бернулли.
При решении вероятностных задач часто приходится сталкиваться с ситуациями, в которых одно и тоже испытание повторяется многократно и исход каждого испытания независим от исходов других. Такой эксперимент еще называется схемой повторных независимых испытаний или схемой Бернулли.
Примеры повторных испытаний:
1) многократное извлечение из урны одного шара при условии, что вынутый шар после регистрации его цвета кладется обратно в урну;
2) повторение одним стрелком выстрелов по одной и той же мишени при условии, что вероятность удачного попадания при каждом выстреле принимается одинаковой (роль пристрелки не учитывается).
Итак, пусть в результате испытания возможны два исхода: либо появится событие А, либо противоположное ему событие. Проведем n испытаний Бернулли. Это означает, что все n испытаний независимы; вероятность появления события АА в каждом отдельно взятом или единичном испытании постоянна и от испытания к испытанию не изменяется (т.е. испытания проводятся в одинаковых условиях). Обозначим вероятность появления события АА в единичном испытании буквой рр, т.е. p=P(A)p=P(A), а вероятность противоположного события (событие АА не наступило) — буквой q=P(A¯¯¯¯)=1−pq=P(A¯)=1−p.
Формула Бернулли.
Распределение числа успехов (появлений события) носит название биномиального распределения.
Пример. В урне 20 белых и 10 черных шаров. Вынули 4 шара, причем каждый вынутый шар возвращают в урну перед извлечением следующего и шары в урне перемешивают. Найти вероятность того, что из четырех вынутых шаров окажется 2 белых.
Решение. Событие А – достали белый шар. Тогда вероятности, .
По формуле Бернулли требуемая вероятность равна
.
Наивероятнейшее число успехов.
Биномиальное распределение (распределение по схеме Бернулли) позволяет, в частности, установить, какое число появлений события А наиболее вероятно. Формула для наиболее вероятного числа успехов (появлений события) имеет вид:
Пример. При автоматической наводке орудия вероятность попадания по быстро движущейся цели равна 0,9. Найти наивероятнейшее число попаданий при 50 выстрелах.
Решение. Здесь . Поэтому имеем неравенства: Следовательно, .Полиномиальная схема.
Рассмотрим опыт, состоящий в n-кратном повторении одинаковых независимых испытаний, в каждом может произойти одно и только одно из m несовместных событий А1, А2, …, Аm, причем каждое событие Аi может произойти с вероятностью рi. Такой опыт называют полиномиальной (мультиноминальной) схемой.
Вероятность того, что в n испытаниях событие А1 произойдет равно k1 раз, событие А2 произойдет равно k2 раз, …, событие Аm произойдет равно k
Пример 1.66. В некотором государстве живут 60% блондинов, 25% брюнетов и 15% шатенов. Найдем вероятность того, что среди восьми наугад отобранных подданных этого государства окажутся четыре блондина, три брюнета и один шатен.
В данном случае мы имеем дело с полиномиальной схемой, в которой m=3; p1=0,6; p2=0,25; p3=0,15; n=8; k1=4; k2=3; k3=1.
Согласно формуле (1.38) искомая вероятность равна
studentmtuci.blogspot.com
Формула Бернулли. Примеры задач с решением. |
Пусть проводится n независимых испытаний, в каждом из которых событие А происходит с вероятностью p. При этом вероятность противоположного события равна
q=1-p.
В теории вероятностей особый интерес представляет случай, когда в n испытаниях событие А встречается k раз, тем самым не встречается (n-k) раз. Искомую вероятность Р n(k) можно вычислить по формуле Бернулли:
Пример 1
Монету подбрасывают шесть раз. Какова вероятность того, что герб выпадет только два раза.

Решение.
Для вычисления искомой вероятности применим формулу Бернулли. Число испытаний n=6, а число благоприятствующих исходов k=2. Вероятность события (выпадения герба)
p=1/2=0.5; q=1-p=0.5
Пример 2
Два равносильных противника играют в шахматы. Что вероятнее:
а) выиграть одну партию из двух или две партии из четырех?
б) выиграть не менее двух партий из четырех или не менее трех партий из пяти? Ничьи во внимание не принимаются.
Решение.
Так как играют равносильные шахматисты, то вероятность выигрыша р=1/2, вероятность проигрыша
q=1-p=0.5. Во всех партиях вероятность выигрыша постоянна и безразлично, в какой последовательности произойдут эти выигрыши, поэтому применима формула Бернулли:
а)
Так как P2(1) > Р4(2), то более вероятен выигрыш одной партии из двух, чем двух партий из четырех.
б) Пусть событие А — «выиграть не менее двух партий из четырех». Данное событие соответствует следующим независимым событиям:
• «выиграть две партии из четырех», вероятность этого события вычисляется как Р4(2);
• «выиграть три партии из четырех», вероятность этого события вычисляется как Р4(3);
• «выиграть четыре партии из четырех», вероятность этого события вычисляется как Р4(4).
Пусть событие В — «выигрыш не менее трех партий из пяти». Данное событие соответствует следующим независимым событиям:
• «выиграть три партии из пяти», вероятность этого события вычисляется как Р5(3);
• «выиграть четыре партии из пяти», вероятность этого события вычисляется как Р 5(4);
• «выиграть пять партий из пяти», вероятность этого события вычисляется как Р5(5).
Так как Р(А) > P(B), то выигрыш не менее двух партий из четырех более вероятен, чем выигрыш не менее трех партий из пяти.
www.matematicus.ru
Распределение Бернулли Википедия
| Распределение Бернулли | |
|---|---|
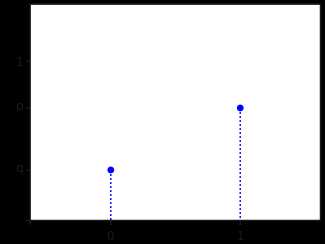 Функция вероятности Функция вероятности | |
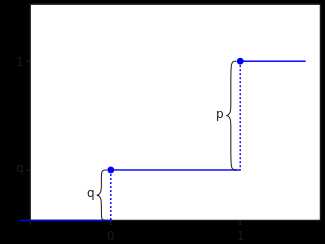 Функция распределения Функция распределения | |
| Параметры | p∈(0,1){\displaystyle p\in (0,1)} q≡1−p{\displaystyle q\equiv 1-p} |
| k={0,1}{\displaystyle k=\{0,1\}} | |
| Функция вероятности | qk=0p k=1{\displaystyle {\begin{matrix}q&k=0\\p~~&k=1\end{matrix}}} |
| Функция распределения | 0k<0q0≤k<11k≥1{\displaystyle {\begin{matrix}0&k<0\\q&0\leq k<1\\1&k\geq 1\end{matrix}}} |
| Математическое ожидание | p{\displaystyle p} |
| Мода | {0,q>p0,1,q=p1,q<p{\displaystyle {\begin{cases}0,&q>p\\0,1,&q=p\\1,&q<p\end{cases}}} |
| Дисперсия | pq{\displaystyle pq} |
| Коэффициент асимметрии | q−ppq{\displaystyle {\frac {q-p}{\sqrt {pq}}}} |
| Коэффициент эксцесса | 6p2−6p+1p(1−p){\displaystyle {\frac {6p^{2}-6p+1}{p(1-p)}}} |
| Дифференциальная энтропия | −qlnq−plnp{\displaystyle -q\ln q-p\ln p} |
| Производящая функция моментов | q+pet{\displaystyle q+pe^{t}} |
| Характеристическая функция | q+peit{\displaystyle q+pe^{it}} |
Распределе́ние Берну́лли в теории вероятностей и математической статистике — дискретное распределение вероятностей, моделирующее случайный эксперимент произвольной природы, при заранее известной вероятности успеха или неудачи.
Определение
Случайная величина X{\displaystyle X} имеет распределение Бернулли, если она принимает всего два значения: 1{\displaystyle 1} и 0{\displaystyle 0} с вероятностями p{\displaystyle p} и q≡1−p{\displaystyle q\equiv 1-p} соответственно. Таким образом:
- P(X=1)=p{\displaystyle \mathbb {P} (X=1)=p},
- P(X=0)=q{\displaystyle \mathbb {P} (X=0)=q}.
Принято говорить, что событие {X=1}{\displaystyle \{X=1\}} соответствует «успеху», а событие {X=0}{\displaystyle \{X=0\}} — «неудаче». Эти названия условные, и в зависимости от конкретной задачи могут быть заменены на противоположные.
Моменты распределения Бернулли
- E[X]=p{\displaystyle \mathbb {E} [X]=p},
- D[X]=p(1−p)=pq{\displaystyle \operatorname {D} [X]=p(1-p)=pq}, так как: E(X2)−E(X)2=p−p2=p⋅(1−p)=pq{\displaystyle \operatorname {E} \left(X^{2}\right)-\operatorname {E} (X)^{2}=p-p^{2}=p\cdot (1-p)=pq}.
Вообще, легко видеть, что
- E[Xn]=p,∀n∈N{\displaystyle \mathbb {E} \left[X^{n}\right]=p,\;\forall n\in \mathbb {N} }.
Замечание
Если независимые случайные величины X1,…,Xn{\displaystyle X_{1},\ldots ,X_{n}}, имеют распределение Бернулли с вероятностью успеха p{\displaystyle p}, то
- Y=∑i=1nXi{\displaystyle Y=\sum \limits _{i=1}^{n}X_{i}}
имеет биномиальное распределение с n{\displaystyle n} степенями свободы.
См. также
Литература
- Hazewinkel, Michiel, ed. (2001), «Binomial distribution», Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
wikiredia.ru
Формула Бернулли и следствие из нее.
*Событие – результат (исход) испытания.
*Вероятность события-число характеризующее степень объективной возможности появл-я событий в опыте.
Пусть производятся n независимых опытов,в кажд из кот событие А может появиться с вероятностью р. Тогда вероятность того,что в серии из n независ опытов событие А появится ровно m раз определиться по формуле.
Pn(m)=Сnm×Pm(1-p)n—m
Все из событий А появл ровно n раз
С-число сочетаний из n-опытов по m
С=n!:(m!(n-m)!)
m-число появлений события А
р-вероятность появл событий в одном опыте.
Пример:
1) По цели пороизв 5 независ выстрелов. Вероятность попад-я при кажд выстреле 0,8. Определить вероятность поражения цели 3 выстрелами.
n=5
h=0,8
P(3)=?
1. Сост расчет формулу:
Р5(3)=С53×р3(1-р)2
С53=5!:(3!(5×3)!)=10
Р5(3)=10×0,83(1-0,8)2=0,2048(20%)
Следствие 1
Вероятность появл-я события хотя бы 1 раз в серии из n испытаний определяется по формуле:
Pn(m>=1)=1-(1-p)n
Р-вероятность попадания при 1 выстреле
1-р-вероятность промаха -//-
Следствие 2
Кол-во испытаний, опытов n необходимых д/появления события А хотя бы 1 раз с задан вероятностью опред по формуле:
(1-p)n =1-Pn(m>=1)
Pn(m>=1)-надежность
n×lg(1-p)=lg(1-Pn(m>=1))
n=(lg(1-Pn(m>=1)): lg(1-p)
Дискретные СВ и законы их распределения.
cB-величина, кот в рез-те опыта может принимать то или иное значение неизвестно заранее какое именно(№:выпадание чисел при брос игральн карты)
Примеры случайных величин:
1. Число выпавших очков при подбрасывании игральной кости (значения: 0,1, 2, 3, 4, 5, 6).
2. Число попаданий в цель при n выстрелах (значения: 0, 1, 2,…, n).
3. Количество бракованных изделий в партии (значения: 0, 1, 2,…, n).
4. Ошибки при измерении физической величины.
Виды СВ:
1. Дискретные
2. Непрерывные
Дискретные-величина,кот в рез-те опыта может принимать только конечное или счетное число значений(№:выпад чисел при однократ бросании кости)
Примеры дискретных случайных величин:
— число попаданий при n выстрелах: Х={0,1,2…n};
— число очков при бросании игральной кости: Х={0,1,2,3,4,5,6}
Непрерывная-величина.кот может принимать любое знач-е в пределах некоторого промежутка(№:отклонение снаряда от цели при 1 выстреле)
Полной, исчерпывающей хар-кой CB явл закон распредел-я СВ
Закон распредел-я СВ-соотношение, устанавливающее связь м/д возможными значениями случ величины и отличающими их вероятностями.
Формы законов распределения СВ
Для дискретных СВ сущ формы:
Ряд распределения
| Х | х1 | Х2 | … | хn |
| pi | p1 | p2 | … | pn |
-возможные значения вероятностей
-событий
2. Многоугольник распределения-графическое изображение выражения ряда распределения.
3. Функция распределения-вероятность события сост в том, что случайная величина Х примет значение меньшее фиксируемого значения х.
*вероятность не м.б. >1
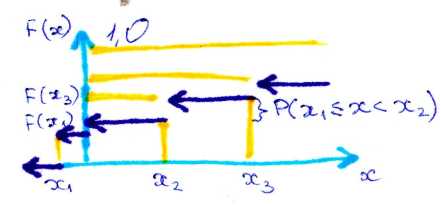
Свойства:
1. Возрастающая по своему физическому смыслу
2. F(-∞)=0
F(+∞)=1
3. F(x1)= P(Х<x1)=Р(-∞<X<х1)
F(x2)= P(Х<x2)=Р(-∞<X<х2)
Р(х1<=X<x2)= F(x2)-F(x1)
Законы распределения наиболее часто встречающихся на практике СВ.
Закон распределения дискретных СВ.
Биномиальный закон (Я.Бернулли)
Дискретная СВ X имеет биномиальное распределение, если ее возможные значения 0,1,2,n (конечно число значений) и отвечающие им вероятности рассчит по формуле:
Рm=P(X=m)=Cnmpmqn—m
P(X=m)-вероятность того,что СВ примет значение равное m
р-вероятность появления события А в одном опыте
q=(1-р)-вероятность не появл-я -//-
n-число проведенных опытов
*Р-не изм в каждом опыте. Все проводимые опыты должны провод в одинак условиях. №: на практике при контроле партии: выним из коробки,проверяют,записывают,кладут обратно в коробку. Затем берут др и тд. Если брак запис и возвр в контрол партию, тогда число подчин биномиальн закону.
Хар-ки закона:
M(x)=n*p-мат ожидание
Dx=h*p*q-дисперсия
σх=√ h*p*q-среднее квадратическое отклонение
Закон Пуассона
Распределение Пуассона-предельное распределение,к кот стремится биномиальное распределение. При увел числа n опытов и одновременном уменьшении вероятности появления события в одном опыте.
n→∞, p→0
закон Пуассона часто называют ЗАКОНОМ РЕДКИХ СОБЫТИЙ, т.к. вероятность столь мала.
СВ X имеет распределение Пуассона если ее возможные значения в серии из n испытаний: X 0,1,2,…m, … а соответствующие им вероятности: Рm= P(X=m)=(am:m!)×e—a
a-параметр закона Пуассона a=n*p
e-иррац число (2ой замечат предел) 2<e<3
n-число которое примет х
Хар-ки закона:
M(x)=a-мат ожидание
Dx=a-дисперсия
σч=√ a-среднее квадратическое отклонение
на практике данный закон применяется при многократном контроле продукции прибором высокой надежности (многокр контроль m→∞, p→0, вероятность отказа стрм к 0)
infopedia.su
Закон распределения Бернулли, его определение, свойства и примеры — ответы по терверу по 37
1 2 3 4 5 620. Закон распределения Бернулли, его определение, свойства и примеры.
Дискретная случайная величина X имеет биномиальное распределение (или распределена по биномиальному закону), если она принимает значения 0, 1, 2, …, n, с соответствующими вероятностями:
, где , , .
Математическое ожидание и дисперсия случайной величины X, имеющей биномиальное распределение, находятся по формулам:
.
Из формулы Бернулли следует, что случайная величина – число наступлений события в независимых испытаниях () – распределена по биномиальному закону.
21. Биномиальный закон распределения, его определение, свойства и примеры.
Пусть производится nнезависимых испытаний, в каждом из которых событие A может появиться или не появиться. Вероятность наступления события во всех испытаниях постоянна и равна p (следовательно, вероятность непоявления q = 1 — p).
Рассмотрим случайную величину X – число появлений события A в этих испытаниях. Случайная величина X принимает значения 0,1,2,…n с вероятностями, вычисленными по формуле Бернулли: , где k = 0,1,2,…n.
Определение: Биномиальным называют раcпределение вероятностей, определяемое формулой Бернулли.
Пример. По мишени производится три выстрела, причем вероятность попадания при каждом выстреле равна 0,8. Рассматривается случайная величина X – число попаданий в мишень. Найти ее ряд распределения.
Решение: Случайная величина X принимает значения 0,1,2,3 с вероятностями, вычисленными по формуле Бернулли, где n = 3, p = 0,8 (вероятность попадания), q = 1 — 0,8 = = 0,2 (вероятность непопадания).
Тогда
,
Таким образом, ряд распределения имеет следующий вид:
| 0 | 1 | 2 | 3 |
| 0,008 | 0,096 | 0,384 | 0,512 |
Пользоваться формулой Бернулли при больших значениях n достаточно трудно, поэтому для подсчета соответствующих вероятностей используют локальную теорему Лапласа, которая позволяет приближенно найти вероятность появления события ровно k раз в n испытаниях, если число испытаний достаточно велико.
22. Закон распределения Пуассона, его определение, свойства и примеры.
Определение. Будем говорить, что случайная величина ε распределена по закону Пуассона с параметром λ , если она принимает значения из множества { 0,1,…,n, …} с вероятностями P { ε=m} = (λm/m!)*e—λ.
Теорема. Если случайная величина ε распределена по закону Пуассона с параметром λ , то и математическое ожидание, и дисперсия этой случайной величины равны параметру λ.
Свойства распределения Пуассона:
1. .
Действительно:
2. .
3. если , то из биномиального распределения следует закон распределения Пуассона.
ПРИМЕР 1.Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равна 0,0002. Найти вероятность того, что на базу прибудут: а) три негодных изделия; б) не более трёх повреждённых изделия.
Решение: по условию n=5000, p=0,0002. Найдём .
а) k = 3. Искомая вероятность по формуле Пуассона приближённо равна
.
б) Пусть случайная величина Х – число изделий, повреждённых в пути, то есть . Очевидно, что данная случайная величина распределена по биномиальному закону. Следовательно, искомую вероятность можно вычислить по формуле
.
Но, так как , то по свойству 3о можем воспользоваться законом распределения Пуассона, то есть, можем записать:
.
Замечание.По формуле Пуассона можно вычислить вероятность того, что число событий, происшедших за время равно , если события образуют пуассоновский поток, причём – интенсивность потока, то есть среднее число событий, которые появляются в единицу времени:
.
ПРИМЕР 2. В течение часа коммутатор получает в среднем 60 вызовов. Какова вероятность того, что за время 30 сек, в течении которых телефонистка отлучилась, не будет ни одного вызова?
Решение: Найдём, прежде всего, – среднее число вызовов за 1 секунду:
.
Тогда, при , получим:
23.* Геометрическое распределение, его определение, свойства и примеры.
Пусть проводятся независимые испытания, каждое испытание может иметь два исхода: удача с вероятностью p и неудача с вероятностью q = 1 — p. Введем в рассмотрение случайную величину X — число испытаний до первого появления удачи. Эта случайная величина может принимать значения 1, 2, 3, 4 и так далее до бесконечности. Когда говорят, что случайная величина X имеет значение k, то это означает, что первые k — 1 испытание закончились неудачей, а k-ое испытание стало удачным. Вероятность того, что в серии независимых испытаний будет вначале k — 1 неудач, а в k-ое испытание — удача, равна . Таким образом мы получили закон распределения случайной величины X: значению k случайной величины соответствует вероятность . Этот закон распределения и называется геометрическим распределением. Название происходит из того, что величина представляет собой геометрическую прогрессию, с первым членом p и знаменателем q.Изучим теперь свойства этого распределения. С ростом k вероятности убывают. Используя формулу для суммы членов геометрической прогрессии, можем записать:, то есть условие, что сумма всех вероятностей в законе распределения равна единице, выполнено. Вычислим теперь математическое ожидание и дисперсию. По определению математического ожидания имеем:. Для вычисления суммы воспользуемся следующим приемом — заменим на и вынесем производную за знак суммы, в итоге получим:. Оставшаяся сумма представляет собой сумму членов геометрической прогрессии и равна . Вычисляя производную, запишем:. Аналогично можно получить выражение для :. Заменяя сумму на ее значение , вычисляем:. Таким образом, имеем выражение для дисперсии:. Если вероятность удачи равна единице, то математическое ожидание числа испытаний до первой удачи равно 1, а дисперсия — 0. Если, наоборот, вероятность удачи равна нулю, то математическое ожидание — бесконечность (то есть нужно произвести бесконечное число испытаний до появления удачи).Пример 30.1Вероятность попадания в мишень из винтовки равна 0,8. Найти математическое ожидание и дисперсию случайной величины — количества выстрелов до первого попадания.Математическое ожидание , дисперсия . Полученные результаты означают, что при вероятности попадания 0,8 попадание будет в среднем с 1—2 выстрела.
24.Равномерный закон распределения, его определение, свойства и примеры.
Законы распределения НСВ
Плотности распределения НСВ называют также законами распределения. Часто встречаются законы равномерного, нормального и показательного распределений.
Определение.1. Закон распределения НСВ называется равномерным, если ее плотность распределения задается в виде:
1. Зная плотность распределения, и используя формулу ,
можно найти функцию распределения:
2. Если НСВ имеет равномерное распределение, то ее числовые характеристики могут быть найдены по формулам:
.
3. Вероятность попадания равномерно-распределенной НСВ в интервал можно определить по формуле:
.
Пример 1. Автобусы подходят к остановке с интервалом в 5 минут. Считая, что НСВ — время ожидания автобуса — распределена равномерно, найти среднее время ожидания (математическое ожидание), среднее квадратическое отклонение. Какова вероятность того, случайно подошедший на остановку пассажир будет ожидать автобус не более 4 минут, но и не менее 2 минут.
Решение:
;
.
25. Нормальный (гауссовский) закон распределения.
Геометрический и вероятностный смысл параметров нормального закона распределения. Примеры.
26. Стандартный нормальный закон распределения. Функция Гаусса, ее свойства и график. Теорема о связи плотности нормального закона распределения и функции Гаусса.
27. Функция Лапласа, ее свойства, график и геометрический смысл. Теорема о связи функции распределения нормального закона и функции Лапласа. Примеры.
28.* Свойства случайной величины, распределенной по нормальному закону. Правило трех сигм. Примеры.
1) Вероятность попадания нормально распределенной случайной величины в интервал равна
.
2) Вероятность того, что отклонение нормально распределенной случайной величины от математического ожидания не превысит по абсолютному значению величину , равна:
..
3. «Правило трех сигм». Если случайная величина , то практически достоверно, что ее значения заключены в интервале (). (Вероятность выхода за эти границы составляет 0,0027.) Правило позволяет, зная параметры ( и ), ориентировочно определить интервал практических значений случайной величины.
topuch.ru
|
На этом уроке будем находить вероятность наступления события в независимых испытаниях при повторении испытаний. Испытания называются независимыми, если вероятность того или иного исхода каждого испытания не зависит от того, какие исходы имели другие испытания. Независимые испытания могут проводиться как в одинаковых условиях, так и в различных. В первом случае вероятность появления некоторого события во всех испытаниях одна и та же, во втором случае она меняется от испытания к испытанию. Примеры независимых повторных испытаний:
Эти события можно описать одной схемой. Каждое событие наступает в каждом испытании с одной и той же вероятностью, которая не изменяется, если становятся известными результаты предыдущих испытаний. Такие испытания называются независимыми, а схема называется схемой Бернулли. Предполагается, что такие испытания могут быть повторены как угодно большое количество раз. Если вероятность p наступления события A в каждом испытании постоянна, то вероятность того, что в n независимых испытаниях событие A наступит m раз, находится по формуле Бернулли: (где q = 1 – p — вероятность того, что событие не наступит) или Поставим задачу – найти вероятность того, что событие такого типа в n независимых испытаниях наступит m раз. Пример 1. Найти вероятность того, что среди взятых случайно пяти деталей две стандартные, если вероятность того, что каждая деталь окажется стандартной, равна 0,9. Решение. Вероятность события А, состоящего в том, что взятая случайно деталь стандартна, есть p=0,9, а вероятность того, что она нестандартна, есть q=1–p=0,1. Обозначенное в условии задачи событие (обозначим его через В) наступит, если, например, первые две детали окажутся стандартными, а следующие три – нестандартными. Но событие В также наступит, если первая и третья детали окажутся стандартными, а остальные – нестандартными, или если вторая и пятая детали будут стандартными, а остальные – нестандартными. Имеются и другие возможности наступления события В. Любая из них характеризуется тем, что из пяти взятых деталей две, занимающие любые места из пяти, окажутся стандартными. Следовательно, общее число различных возможностей наступления события В равно числу возможностей размещения на пяти местах двух стандартных деталей, т.е. равно числу сочетаний из пяти элементов по два, а . Вероятность каждой возможности по теореме умножения вероятностей равна произведению пяти множителей, из которых два, соответствующие появлению стандартных деталей, равны 0,9, а остальные три, соответствующие появлению нестандартных деталей, равны 0,1, т.е. эта вероятность составляет . Так как указанные десять возможностей являются несовместимыми событиями, по теореме сложения вероятность события В, которую обозначим Пример 2. Вероятность того, что станок в течение часа потребует внимания рабочего, равна 0,6. Предполагая, что неполадки на станках независимы, найти вероятность того, что в течение часа внимания рабочего потребует какой-либо один станок из четырёх обслуживаемых им. Решение. Используя формулу Бернулли при n=4, m=1, p=0,6 и q=1–p=0,4, получим
Пример 3. Для нормальной работы автобазы на линии должно быть не менее восьми автомашин, а их имеется десять. Вероятность невыхода каждой автомашины на линию равна 0,1. Найти вероятность нормальной работы автобазы в ближайший день. Решение. Автобаза будет работать нормально (событие F), если на линию выйдут или восемь (событие А), или девять (событие В), или все десять автомашин событие (событие C). По теореме сложения вероятностей, . Каждое слагаемое находим по формуле Бернулли. Здесь n=10, m=8; 9; 10, а p=1-0,1=0,9, так как p должно означать вероятность выхода автомашины на линию; тогда q=0,1. В результате получим Пример 4. Пусть вероятность того, что покупателю необходима мужская обувь 41-го размера, равна 0,25. Найти вероятность того, что из шести покупателей по крайней мере двум необходима обувь 41-го размера. Решение. Обозначенное в условии задачи событие (обозначим его через С) состоит в том, что из шести покупателей двум, трём, четырём, пяти или шести необходима обувь 41-го размера. Применив теорему сложения вероятностей, а затем формулу Бернулли, получим ответ. Однако задача решается проще, если сначала искать вероятность не требуемого в условии задачи, а противоположного ему события . Оно состоит в том, что менее чем двум покупателям необходима обувь 41-го размера, то есть или ни одному покупателю (событие А), или только одному (событие В). Таким образом, . По формуле Бернулли при n=6, p=0,25, q=0,75 и m=0; 1 получим (при подсчёте следует иметь в виду, что ). Тогда вероятность события С найдётся как вероятность события, противоположного найденному: . |
function-x.ru
Биномиальный закон (распределение Бернулли)
⇐ ПредыдущаяСтр 2 из 3Следующая ⇒
В общей форме биномиальный закон описывает осуществление признака в испытаниях с возвратом. Наглядной схемой таких испытаний является последовательный выбор с возвращением шаров из урны, содержащей белых и чёрных шаров. Если — число появления белых шаров в выборке из шаров, то
где — вероятность появления при одном извлечении соответственно белого и чёрного,
Производящая функция биномиального распределения задаётся формулой
Основные характеристики биномиального распределения (математическое ожидание и дисперсия):
Пример 1. Вероятность получения бракованного изделия равна 0,01. Какова вероятность того, что среди 100 изделий окажется не более 3 бракованных?
Решение. Пусть . Согласно биномиальному закону и закону сложения имеем
Билет 7. Непрерывные и дискретные случайные величины. Плотность вероятности. Нормальный закон распределения. Математическое распределение и дисперсия. Графическое представление. Примеры.
Случайная величина(далее СВ) – величина, которая принимает значение в зависимости от стечения случайных обстоятельств. (Пр.: число больных на приеме врача, число студентов в аудитории, номер бочонка, когда его вынимают из мешка, при игре в лото и т.п.)
СВ называется дискретной(далее – ДСВ), если она принимает счетное множество значений. (Пр.: число букв на произвольной странице книге, число волос на голове человека, число молекул в выделенном объеме газа и т.п.)
СВ называется непрерывной(далее – НСВ), если она принимает любые значения внутри некоторого интервала. (Пр.: температура тела, масса зерен в колосьях пшеницы и т.п.)
Вероятность
— предел, к которому стремится частота события при неограниченном увеличении числа испытаний. (статистическое определение)
P(A)=limn→∞(m/n)
— отношение благоприятствующих случаев к общему числу равновозможных случаев к общему числу равновозможных несовместимых событий. (классическое опредедение) P(A)=(m/n)
Распределение вероятностей — закон, описывающий область значений СВ и вероятности их принятия.
- Распределение ДСВ. Дискретная величина (Х) считается заданной, если указаны ее возможные значения (xn) соответствующие им вероятности Р(хn)=pn. Совокупность Х и Р называется распределением ДСВ.
- Распределение НСВ.
dP=f(x)dx
dP – вероятность того, что НСВ Х принимает значения между х и х+dх. Вероятность dP прямо пропорциональна интервалу dx.
f(x) – плотность вероятности (функция распределения вероятностей). Показывает, как изменяется вероятность, отнесенная к интервалу dx случайной величины, в зависимости от самой этой величины.
f(x)=dP/dx
x
F(x)=∫f(x)dx — функция распределения НСВ. Равна вероятности того, что СВ
-∞
принимает значения, меньшие х.
F(x)=(-∞<X<x)
Нормальный закон распределения (закон Гаусса).СВ распределена по этому закону, если плотность вероятности имеет вид
a=M(X) – мат.ожидание СВ, σ – среднее квадратическое отклонение, σ2— дисперсия СВ.
Дисперсия СВ – МО отклонения случайной величины от ее МО.
D(X)=M[X-M(X)]
Удобная формула: D(X)=M(X2)-[M(X)]2
Кривая закона носит колокообразную форму, симметричную относительно прямой х=а (центр рассеивания). В точке х=а функция достигает максимума.
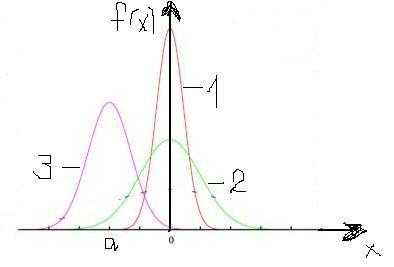
По мере возрастания |х-а| функция f(x) монотонно убывает, асимптотически приближаясь к нулю. С уменьшением σ кривая становится все более и более островершинной. Изменение а при постоянной σ не влияет на форму кривой, а лишь сдвигает ее вдоль оси абсцисс. Площадь, заключенной под кривой, согласно условию нормировки, равна единице. На рисунке изображены три кривые. Для кривых 1 и 2 а=0, но отличаются значением σ (σ1<σ2), кривая 3 имеет а≠0, σ=σ2.
Вычислим функцию распределения.
Обычно используют иное выражение. Введем новую переменную t=(x-a)/σ. Следовательно, dx=σdt. Подставляем это в формулу.
Значение функции Ф(t) обычно находят в составных таблицах, так как интеграл через элементарные функции не выражается. График:
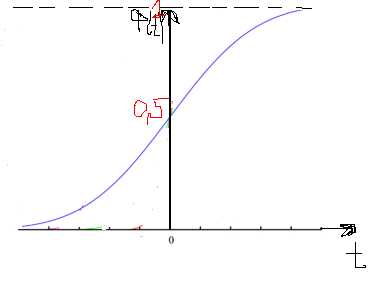
Случайная величина при нормальном распределении может находится в интервале (х1, х2). Вероятность этого равна
Р(х1<x<х2)=Ф((х2-а)/σ)-Ф((х1-а)/σ)
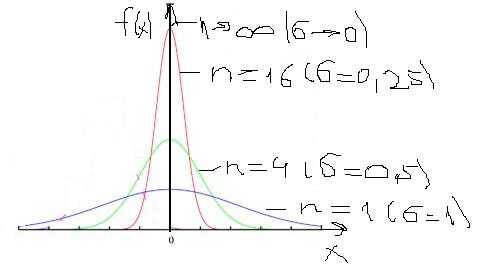
Допустим, что произвольно из нормальных распределений выбираются группы по n значений СВ. Для каждой группы можно найти средние значения (х1, х2, хi). Они сами образуют нормальное распределение (только среднему значению будет соответствовать не вероятность, а относительная частота). МО будет соответствовать исходному, дисперсия и среднее квадратическое отклонение – отличаться в n и в √n соответственно.
Dn=D/n и σn=σ/√n.
На рисунке представлены графики нормальных распределений, полученных для групп со значением n, равными 1, 4, 16 и n→∞. При n=1 – исходное распределение, σn=σ. При n→∞ σn→0, фактически «группа СВ» — все исходное распределение, среднее значение выражается одним числом и соответствует МО, к которому сводится все распределение.
Рекомендуемые страницы:
lektsia.com
