Сходящиеся и расходящиеся ряды
Пусть задана последовательность (an) действительных чисел
a1, a2, a3, …,an, … . (1.1)
Сопоставим этой последовательности чисел последовательность (Sn) конечных сумм вида:
S1=a1,
S2=a1+a2,
S3=a1+a2+a3, …,
Sn=a1+a2+…+an,…
Однако на практике часто приходят к задачам суммирования бесконечной последовательности чисел (1.1). В этом случае вместо слов последовательность (an) и последовательность (Sn) употребляют слово ряд. Для обозначения ряда используют символы:
a1+a2+…+an+…
или
Число называют n-й частичной суммой ряда , а число an– n-м (общим) членом этого ряда.
Так как каждому ряду соответствует последовательность (Sn) его частичных сумм, и, наоборот, каждой последовательности (Sn) соответствует ряд , где a1=S1, a2=S2-S1,…, an=Sn-Sn-1,…, то каждое свойство последовательностей можно переформулировать в некоторое свойство рядов заменой характеристики членов последовательности соответствующей характеристикой членов ряда.
Таким образом, фразы «последовательность (an)», «последовательность (Sn)», «совокупность последовательностей (an) и (Sn) », «ряд » суть математические синонимы.
При определении ряда естественно возникают вопросы:
1. Что такое «сумма» бесконечной последовательности чисел?
2. Если сумма существует, то каковы ее свойства?
Прежде чем ответить на эти вопросы, рассмотрим следующие примеры.
Пример 1. Отрезок [1,0] разобьем пополам (на два равных отрезка).
Правую половину отрезка, то есть отрезок [1/2, 1], снова разделим пополам, затем разобьем пополам отрезок [3/4, 1] и т. д. Продолжая этот процесс до бесконечности, получим разбиение отрезка [0, 1] на бесконечное множество отрезков: [0, 1/2], [1/2, 3/4], [3/4, 7/8], [7/8, 5/16],… Естественно считать, что «сумма» длин всех отрезков, на которые разбит отрезок [0, 1], равна длине отрезка, т.е. единице. Иными словами,
(1.3)
Это рассуждение было известно еще грекам, и философ Зенон (ок. 490 г. до н.э.), известный своими «парадоксами», оспаривал его законность. Один из парадоксов утверждал, что бегущий человек никогда не сможет достичь своей цели, поскольку он должен пробежать сначала половину требуемой дистанции, затем половину оставшейся части дистанции и т. д.; таким образом, он должен пробежать бесконечное множество расстояний, а это будет продолжаться вечно.
Если бы мы попытались вычислить сумму (1.3), последовательно выполняя все указанные в ней сложения, то это, конечно, никогда бы не окончилось.
И все-таки равенство (1.3) в некотором смысле верно. В чем же заключается точный его смысл?
Определим понятие суммы ряда. Прежде обратимся к примеру 1. Последовательности сопоставим последовательность частичных сумм (Sn), где
Ясно, что является длиной отрезка.
Определение. Если последовательность (Sn) частичных сумм ряда сходится, то ее предел называют суммой ряда, а сам ряд (1. 2) называют сходящимся или суммируемым. В этом случае пишут:
Если , или предел последовательности не существует, то ряд называют расходящимся.Если , то говорят, что ряд расходится к + , и пишут Аналогично в случае считаем, что
Пример 2. Рассмотрим ряд
Для этого ряда Данный ряд расходится к + .
Пример 3. Рассмотрим ряд Поскольку для этого ряда то последовательность не имеет предела при . Следовательно, ряд расходится. Заметим, что этот ряд не расходится ни к ни к
Пример 4. Рассмотрим последовательность
.
Ей соответствует ряд , где Так как последовательность сходится при и расходится при то и ряд сходится при и расходится при
Не существует каких-либо общих методов нахождения сумм сходящихся рядов. Эту задачу удается решить только в отдельных частных случаях.
Пример 5. Исследуем сходимость и найдем его сумму.
Так как то последовательность частичных сумм имеет . Итак, заданный ряд сходится и его сумма
Замечание. Для представления общего члена ряда в виде суммы простейших дробей полезно использовать метод неопределенных коэффициентов.
Пример 6. Исследуем на сходимость ряд
Представим общий член ряда в виде суммы простейших дробей:
Умножая обе части этого равенства на знаменатель левой части, приходим к тождеству: 1≡A(n+1)(n+2)+Bn(n+2)+Cn(n+1).
Последовательно полагая n=0, -1, -2, находим:
Таким образом,
Отсюда:
Ясно, что
следовательно, данный ряд сходится и его сумма
Пример 7. Исследуем на сходимость ряд
Преобразуем формулуn-го члена ряда, представив его в виде суммы простейших дробей: Выпишем последовательность частичных сумм данного ряда и найдем ее предел:
Следовательно, ряд сходится и его сумма
Пример 8. Выясним, сходится или расходится ряд
Частичные суммы ряда равны:
Имеем т.к. аргумент логарифма, а значит и сам логарифм при стремятся к бесконечности. Следовательно, исследуемый ряд расходится.
Пример 9. Пусть m–фиксированное натуральное число. Исследуем на сходимость ряд называемый рядом обратных факториалов.
Преобразуем общий член ряда по формуле
Выпишем последовательность частичных сумм данного ряда:
Так как то
Пример 10.Пусть члены ряда представимы в виде:
и пусть существует конечный предел:
Тогда исходный ряд сходится и его сумма равна т.е.
= (1. 4)
Действительно,
т.е.
Так как то отсюда получаем и поэтому справедлива формула (1. 4).
Применим данное свойство для ряда с общим членом:
Представим его в виде:
Обозначим Тогда причем По формуле (1. 4) находим:
Пример 11. Найдем сумму ряда
Так как то
Отсюда:
Рассмотрим так называемые эталонные ряды, которые часто используются при исследовании сходимости многих рядов.
Пример 12. Исследуем сходимость гармонического[1]ряда:
Его частичная сумма Пусть Тогда
Таким образом, Последовательность не ограничена сверху, а потому не может быть сходящейся, так как сходящаяся последовательность ограничена. Следовательно, ряд расходится.
Приведем еще одно доказательство того, что гармонический ряд расходится. Действительно, если бы он сходился, то, обозначив его сумму через S, мы бы имели:
(1.5)
Но т.е. что противоречит (1.5).
Заметим, что гармонический ряд расходится очень «медленно». Л.Эйлер, например, вычислил, что
(Леонард Эйлер (1707– 1783) – математик, физик, механик; родился в Швейцарии, большую часть жизни прожил в России и в Германии, активно участвовал во многих направлениях деятельности Петербургской и Берлинской академий.)
Пример 13. Ряд называется обобщенным гармоническим. При — это гармонический ряд, и его расходимость доказана. Покажем, что этот ряд расходится и при
Здесь и при любом . Следовательно, и поэтому при данный ряд расходится. Итак, обобщенный гармонический ряд расходится при Ниже будет доказано, что при этот ряд сходится.
Пример 14. Исследуем на сходимость ряд где
Преобразуем частичную сумму этого ряда следующим образом:
Отсюда Следовательно, ряд сходится и его
сумма равна
В частности, если то
1. 2. Число e как сумма ряда
Нам известно, что В этом пункте мы изучим ряд, с помощью которого можно указать достаточно хороший способ вычисления числа e.
По формуле бинома Ньютона:
Полагая и имеем
С другой стороны, при любом фиксированном k и любом из того же разложения имеем:
При левая часть последнего неравенства стремится к , а правая – к числу e, поэтому для любого Но тогда из двойного неравенства по известной теореме о пределе промежуточной последовательности получаем, что По определению суммы ряда теперь можно записать:
Оценим разность
Таким образом, чтобы абсолютная погрешность приближения числа e числом не превосходила, например, достаточно, чтобы имело место неравенство . Этому условию удовлетворяет уже
В заключение покажем, что число e иррационально.
Предположим, что где Тогда при любом число целое и положительное. Следовательно, при любом
С другой стороны, Противоречие!
В 1873 году Ш. Эрмит (Шарль Эрмит (1822-1901) – французский математик, член Парижской Академии наук) установил, что число e трансцендентно, т.е. не является корнем никакого алгебраического многочлена с целыми коэффициентами.
infopedia.su
Сходящийся ряд Википедия
Числовой ряд — одно из центральных понятий математического анализа. Ряд записывается как бесконечная сумма
- a1+a2+a3+…+an+…{\displaystyle a_{1}+a_{2}+a_{3}+\ldots +a_{n}+\ldots }; краткая запись: ∑n=1∞an{\displaystyle \sum _{n=1}^{\infty }a_{n}}
Здесь a1,a2,a3…{\displaystyle a_{1},a_{2},a_{3}\dots } — последовательность вещественных или комплексных чисел; эти числа называются членами ряда.
Чтобы присвоить такому ряду числовое значение, рассмотрим последовательность «частичных сумм», которые получаются, если оборвать бесконечную сумму на каком-то члене:
- S1=a1{\displaystyle S_{1}=a_{1}}
- S2=a1+a2{\displaystyle S_{2}=a_{1}+a_{2}}
- S3=a1+a2+a3{\displaystyle S_{3}=a_{1}+a_{2}+a_{3}}
- ⋯{\displaystyle \cdots }
- Sn=a1+a2+a3+⋯+an{\displaystyle S_{n}=a_{1}+a_{2}+a_{3}+\dots +a_{n}}
- ⋯{\displaystyle \cdots }
Если последовательность частичных сумм имеет предел S{\displaystyle S} (конечный или бесконечный), то говорят, что сумма ряда равна S.{\displaystyle S.} При этом, если предел конечен, то говорят, что ряд сходится. Если предел не существует или бесконечен, то говорят, что ряд расходится[1].
Ряды широко применяются в математике и других науках для вычислений, для анализа поведения разнообразных функций и т. п.
ru-wiki.ru
I. Числовые ряды
Ряды
§1. Основные понятия
1. Понятие числового ряда. Сходящиеся и расходящиеся ряды
Пусть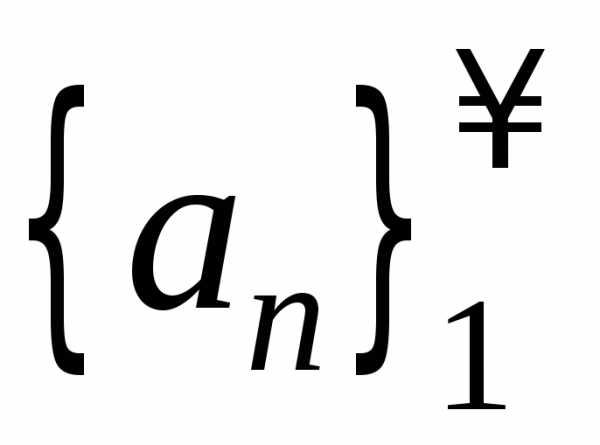 
— числовая последовательность. Образуем
из нее бесконечную сумму
, (1)
которая
называется числовым
рядом.
Числа
(члены последовательности) называютсячленами
ряда (1), a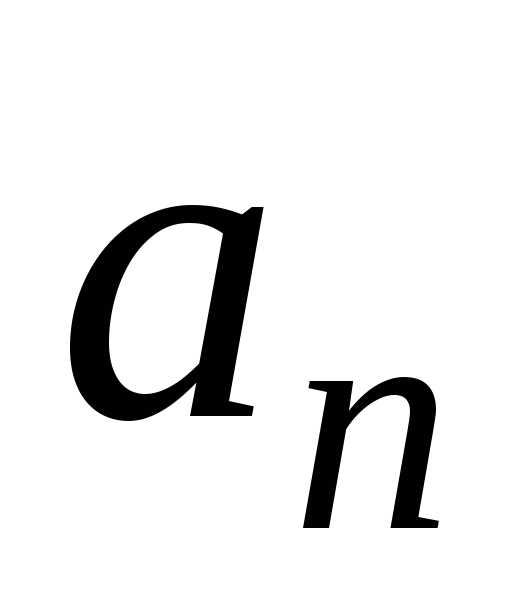 
— общим
членом ряда (1).
Суммы
S1=a1;- первая частичная сумма ряда (1)
S2=a1+a2;
S3=a1+a2+a3;
……………..
Sn=a1+a2+…+an — n-я частичная сумма
называют частичными суммами ряда (1).
Так как число слагаемых в ряде (1) бесконечно, то можно составить последовательность частичных сумм.
Определение. Ряд
(1) называется сходящимся,
если существует конечный предел
последовательности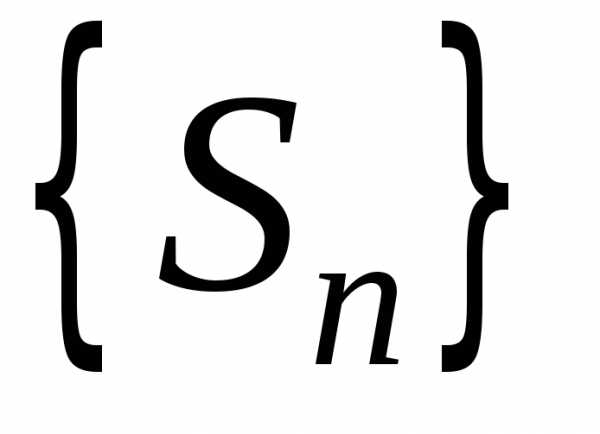 
его частичных сумм, то есть:
При этом число S называют суммой ряда (1) и
пишут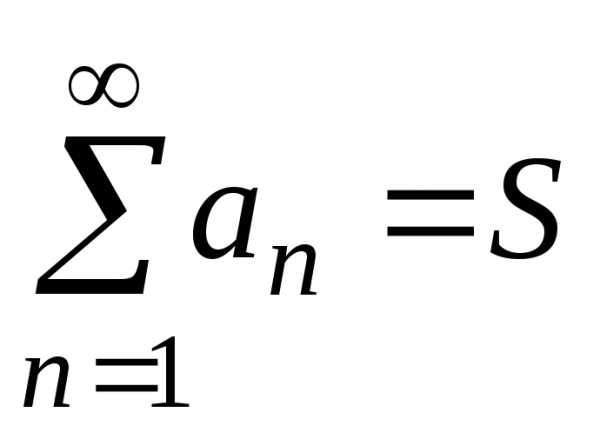 
.
В противном случае ряд (1) называетсярасходящимся. Для расходящегося ряда понятие суммы не определено.
Задача установления сходимости или расходимости ряда – одна из главных задач теории рядов.
Рассмотрим примеры исследования рядов на сходимость с помощью определения.
Пример 1. Исследовать на сходимость ряд
.
Δ Представим n-й член ряда в виде суммы простейших дробей
.
Приравнивая коэффициенты при одинаковых степенях n, получим
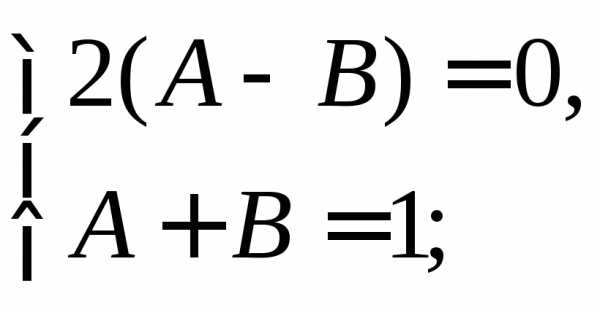
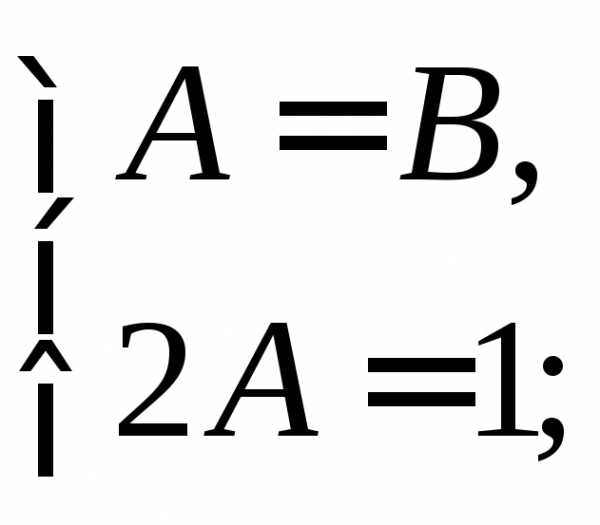
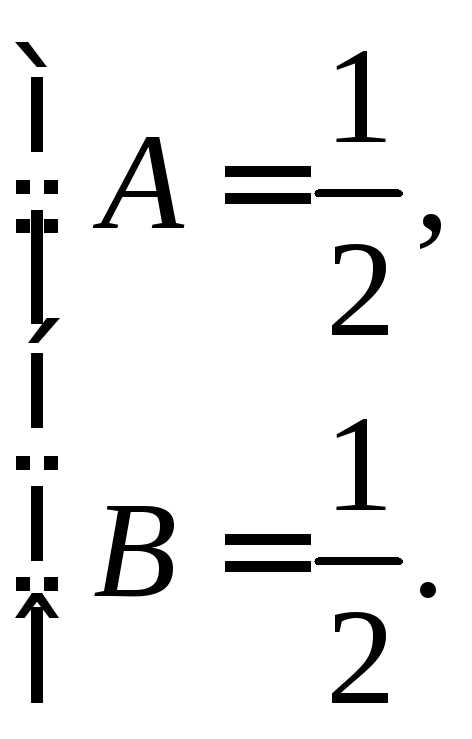
Значит,
.
Тогда n-я частичная сумма примет вид
.
Следовательно, .
Значит, согласно определению ряд сходится. Сумма ряда
Δ
Пример 2. Доказать,
что ряд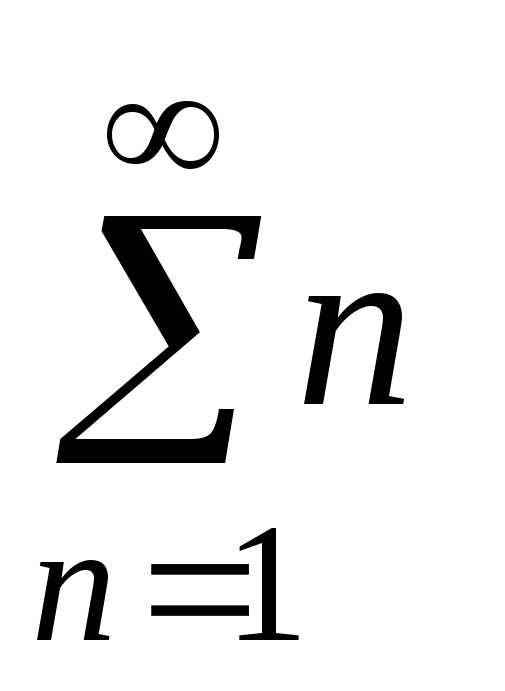 
расходится.
Δ
Значит, ряд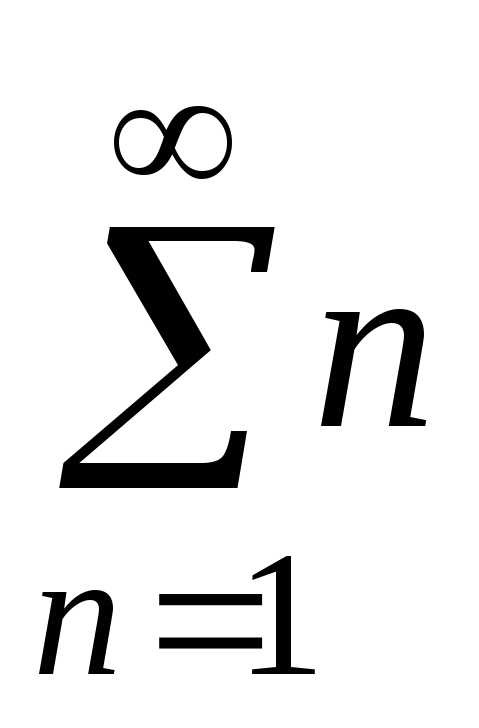 
расходящийся.
Δ
Пример 3. Исследовать
ряд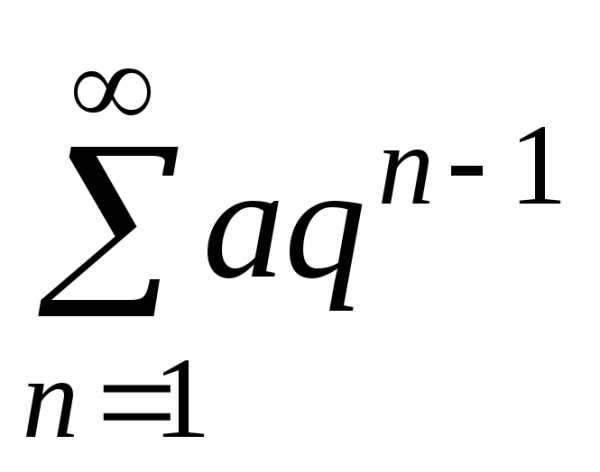 
на сходимость.
Δ Данный ряд
называется геометрическим. (
, 
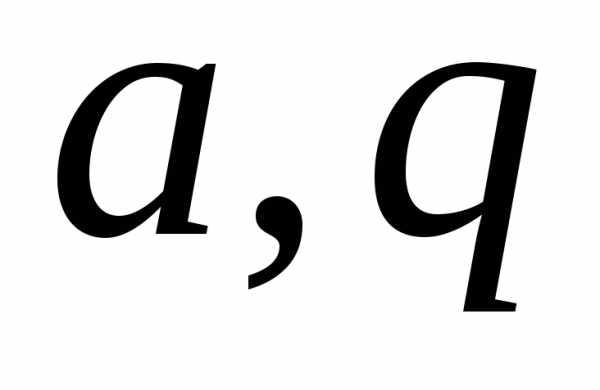– фиксированные числа). Геометрический
ряд является суммой членов геометрической
прогрессии. Как известно,
.
Рассмотрим 4 случая
1) 
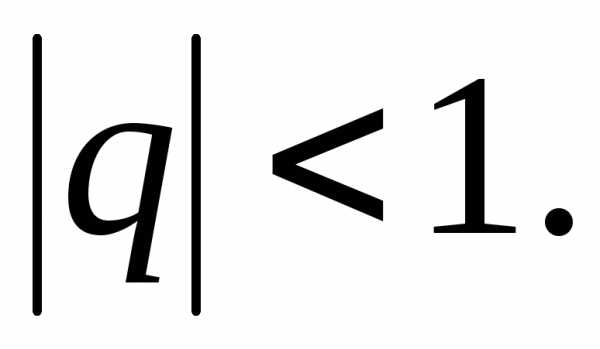Тогда
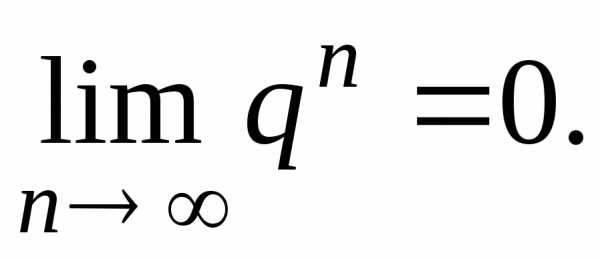Следовательно,
.
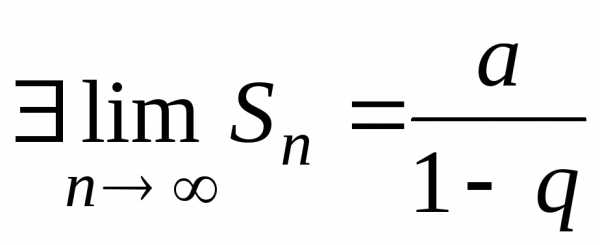Значит, при 
ряд
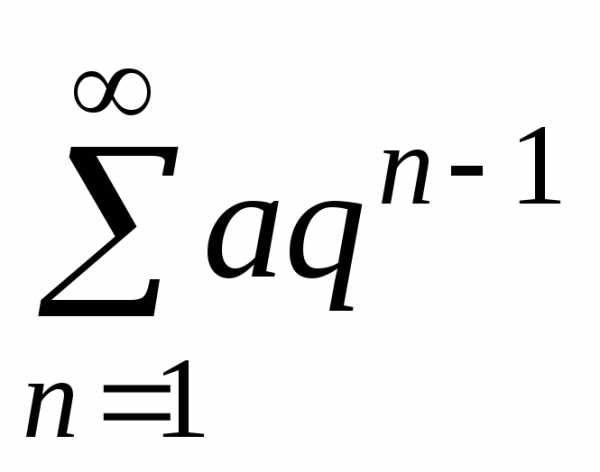сходится и его сумма
.
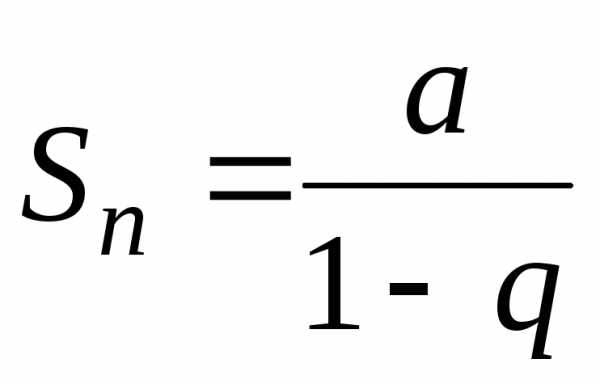2) 
.
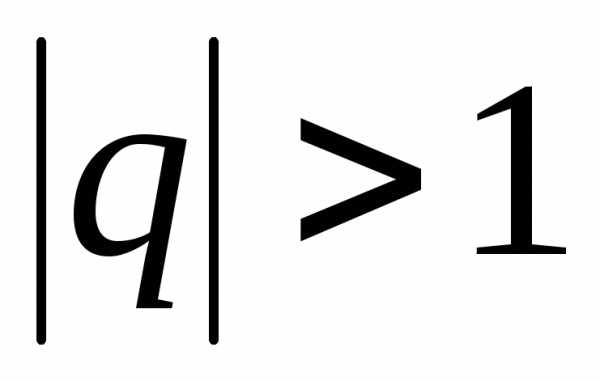Тогда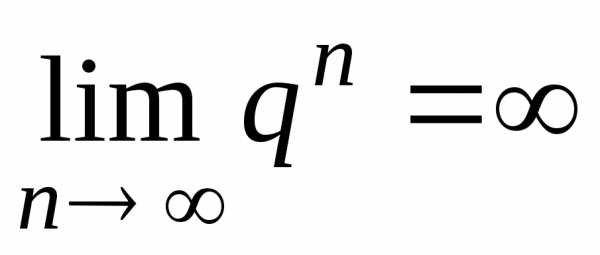
и, значит,
.
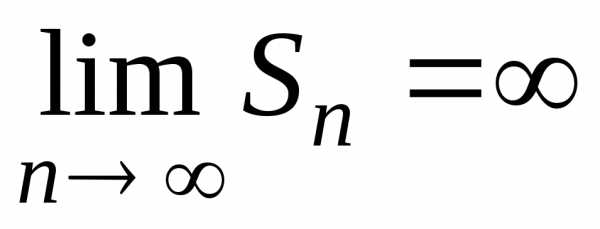Следовательно, ряд при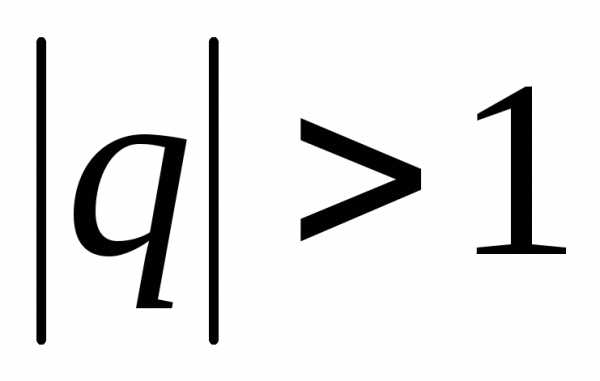
расходится.
3) q=1. Тогда данный ряд имеет вид
,
.
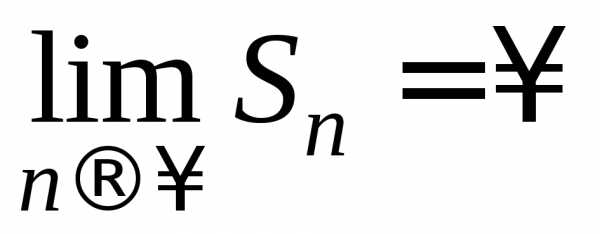Значит, ряд при 
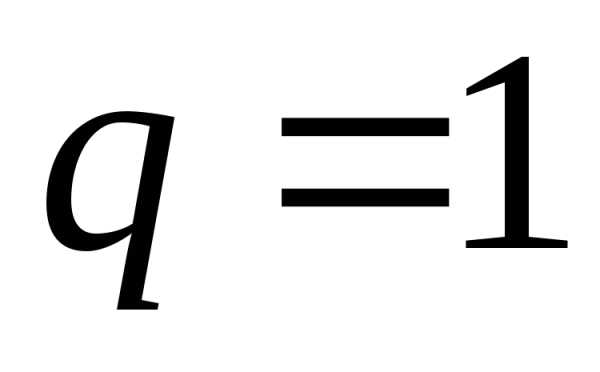расходится.
4) q=-1. Ряд примет вид
;
Значит,
{Sn}: a;0;a;0;…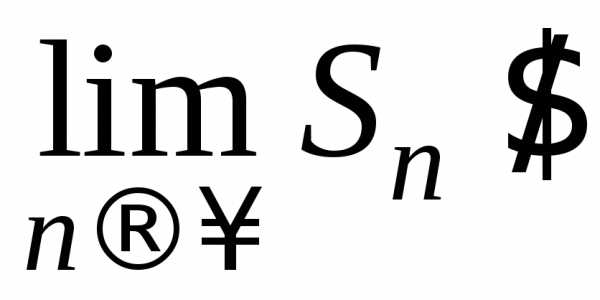 
.
Значит, и в этом случае ряд расходится.
Итак,
геометрический ряд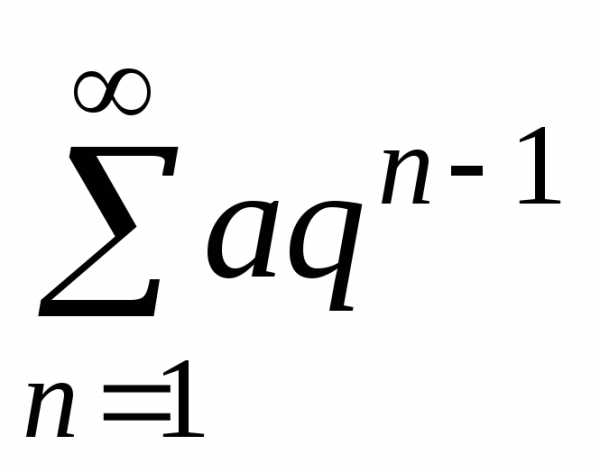 
(
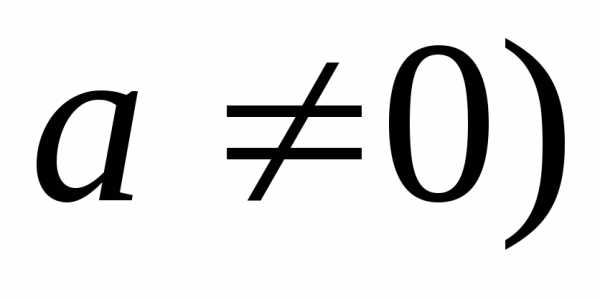сходится при
,
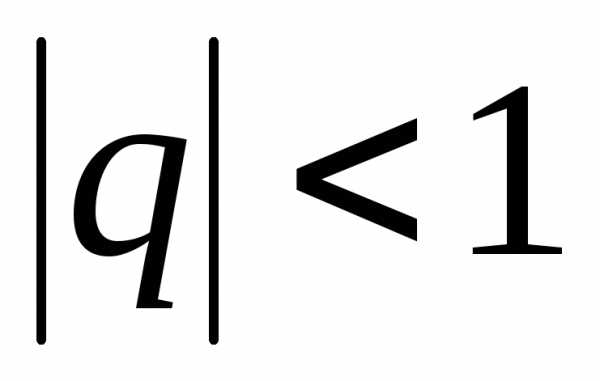расходится
при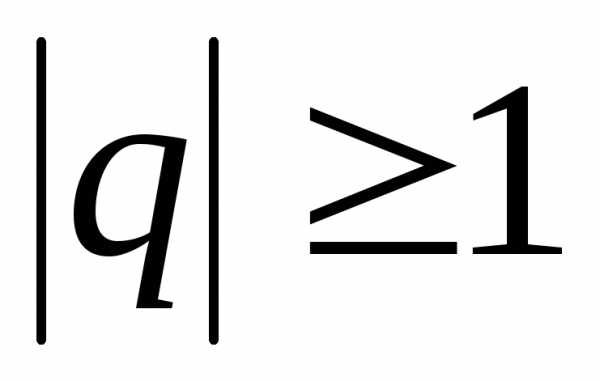 
. Δ
2. Остаток сходящегося ряда
Рассмотрим ряд (1):
(1)
Отбросим в этом ряде n членов подряд, начиная с первого. Получим ряд
(2)
Ряд (2) называется n-м остатком ряда (1).
Если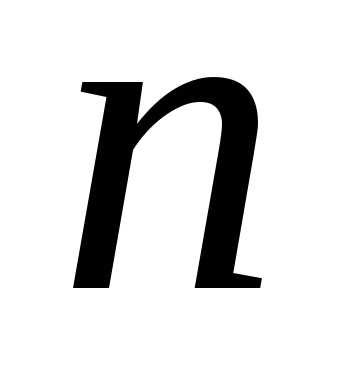 
-й
остаток (2) ряда (1) сходится, то его сумму
обозначают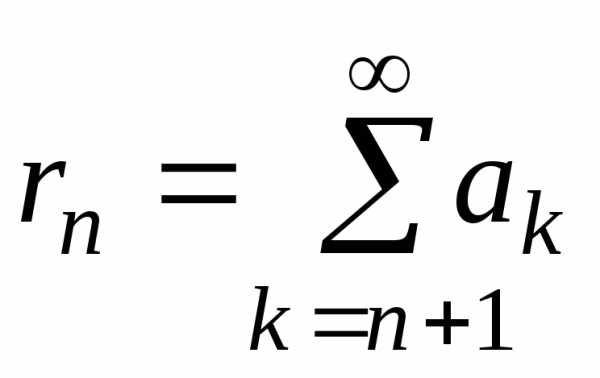
.
Теорема
1. Ряд
(1) 
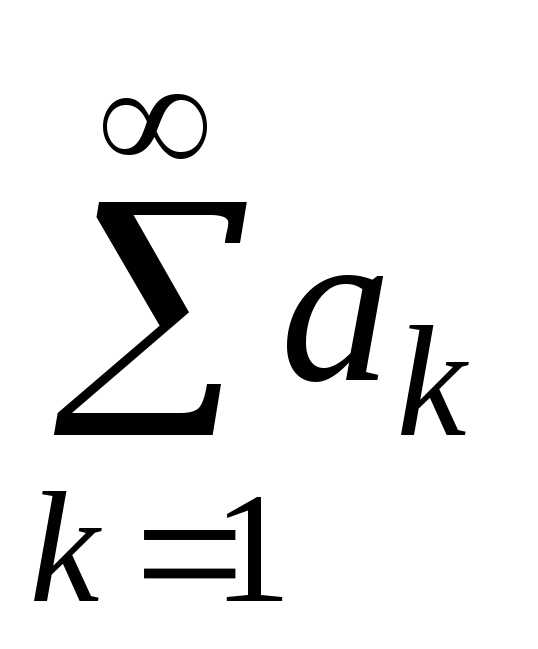сходится
тогда и только тогда, когда сходится
любой из его остатков (2)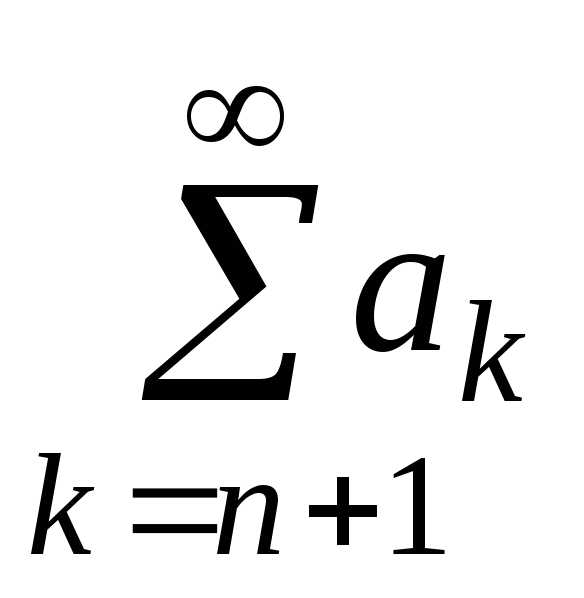
.
При этом если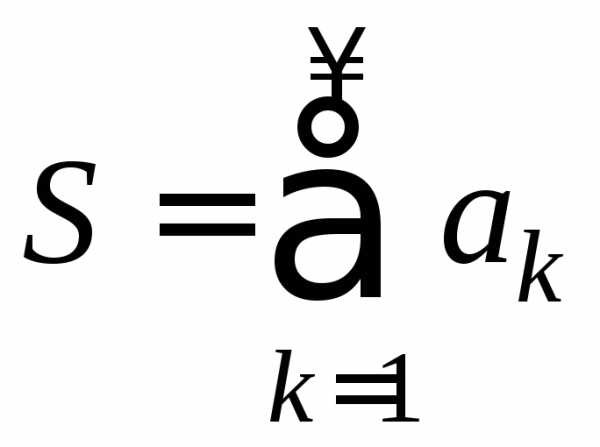
,
,
,
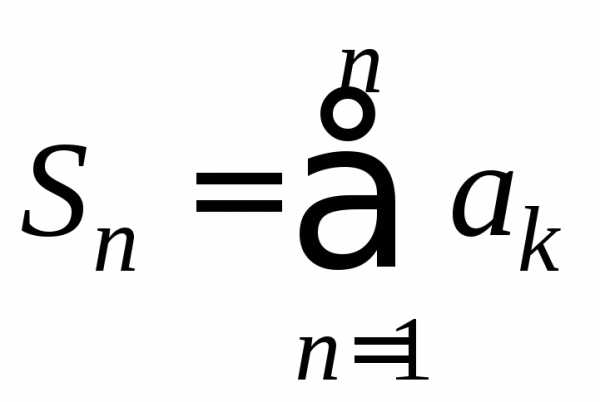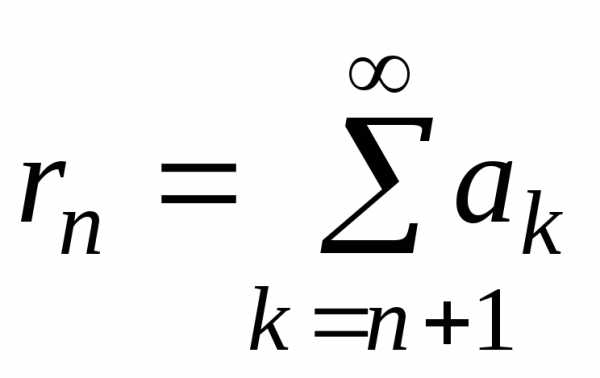то
. (3)
Из теоремы 1 следует, что отбрасывание или добавление любого конечного числа первых членов ряда не влияет на его сходимость или расходимость.
Теорема 2. Если
ряд (1) сходится, то его остаток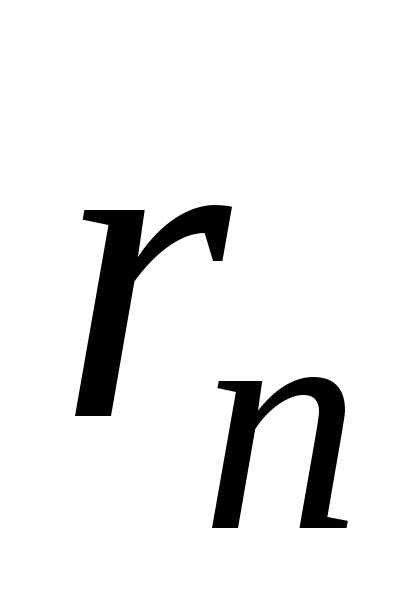 
имеет предел, равный 0:
.
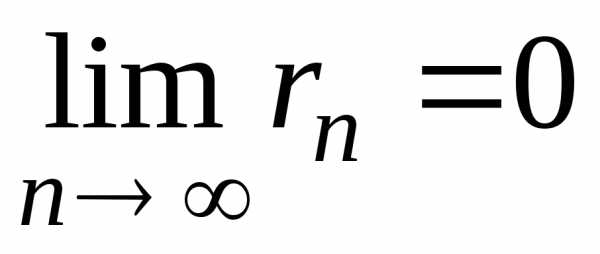Доказательство.
Пусть ряд (1)
сходится. Тогда, согласно теореме 1,
сходится его остаток (2) и имеет место
равенство (3):
.
Отсюда .
Переходя к 
,
получим:.
Из равенства
следует,
что абсолютная погрешность, допускаемая
при замене суммыS сходящегося ряда (1) его частичной суммой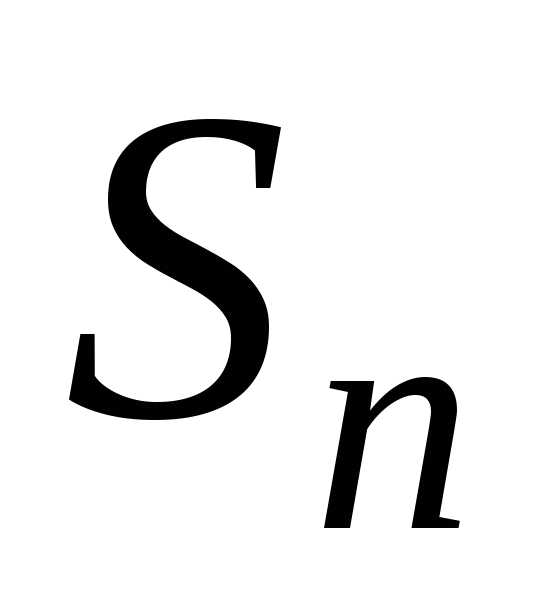 
,
равна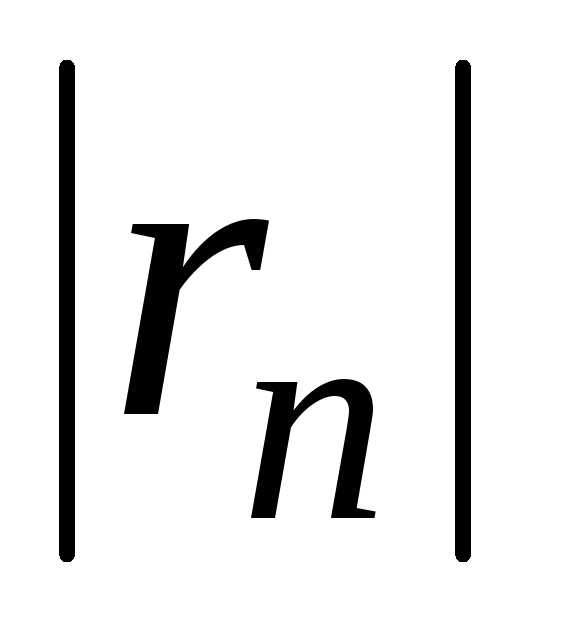
.
Т. о., для оценки этой погрешности
достаточно оценить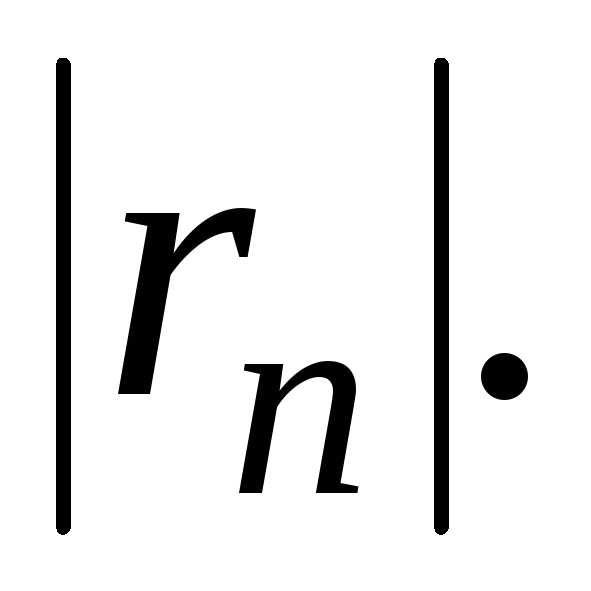
3. Свойства сходящихся рядов
Определение. Суммой рядов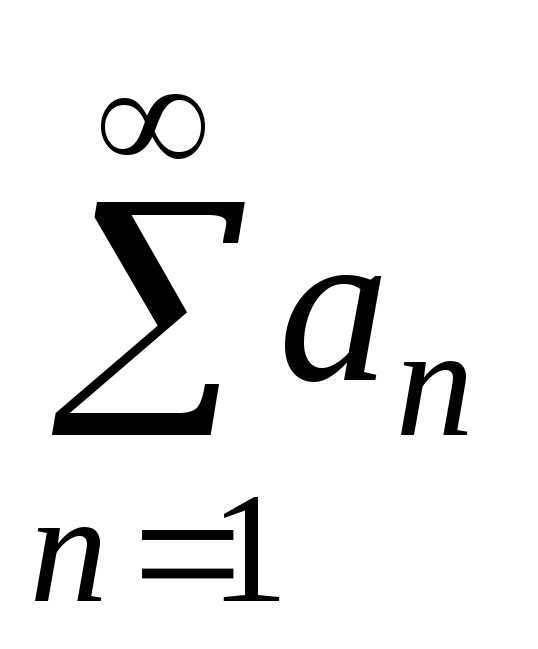 
(A)
и 
(B)
называется ряд 
(A+B).
Произведением ряда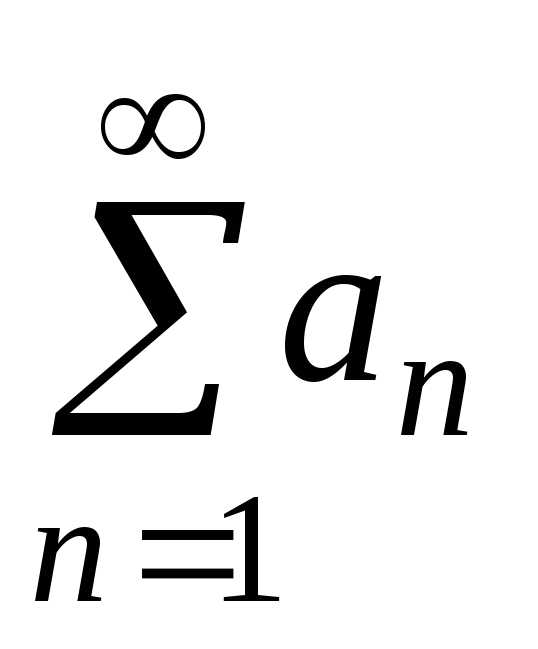 
на число
называется ряд
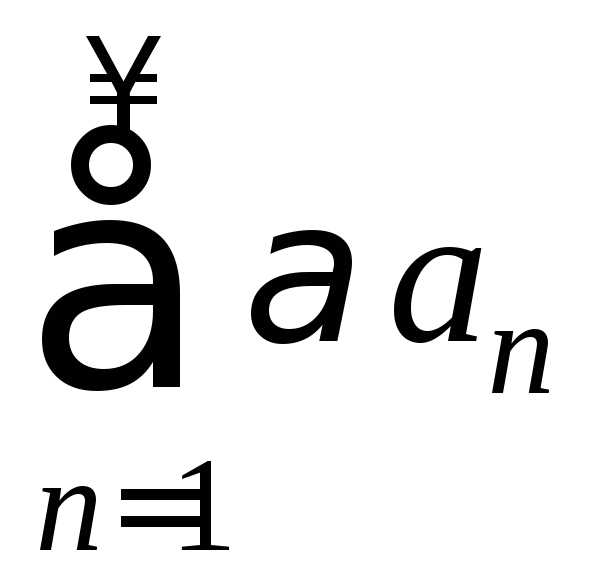(A).
Теорема 3. Если
ряды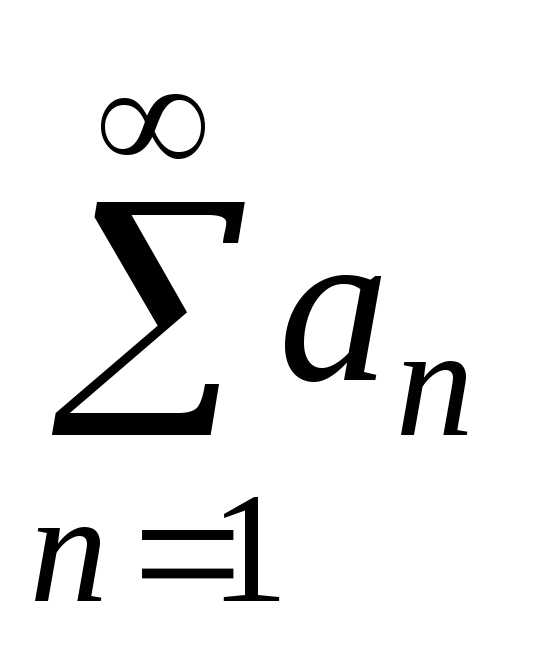 
и
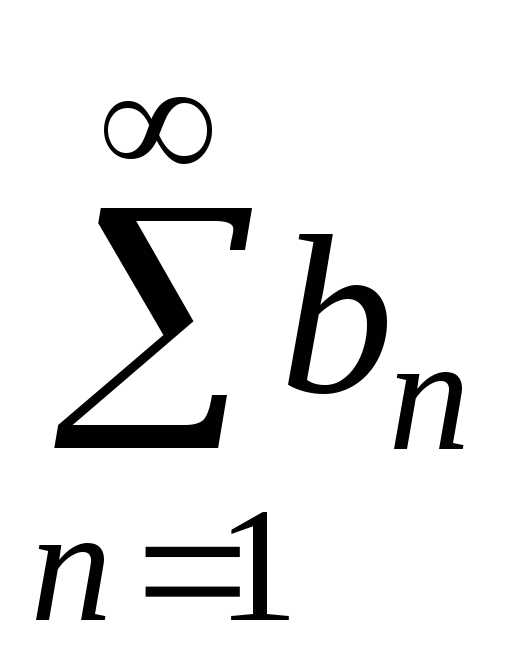сходятся, то сходится и их сумма, причем
.
Доказательство.
Так как ряды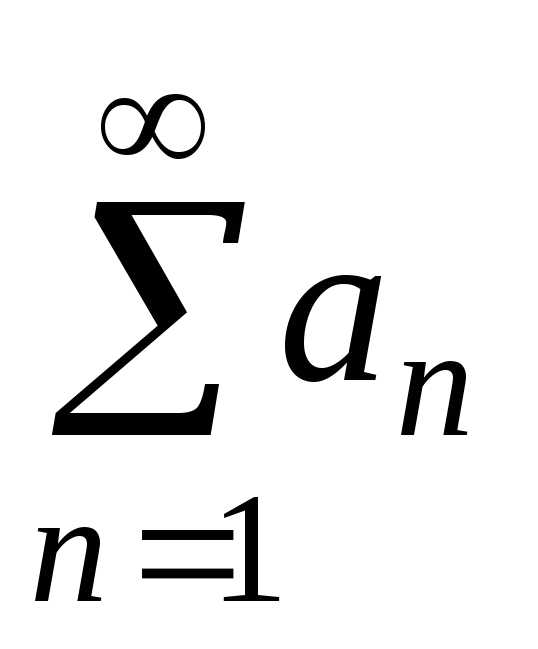 
и
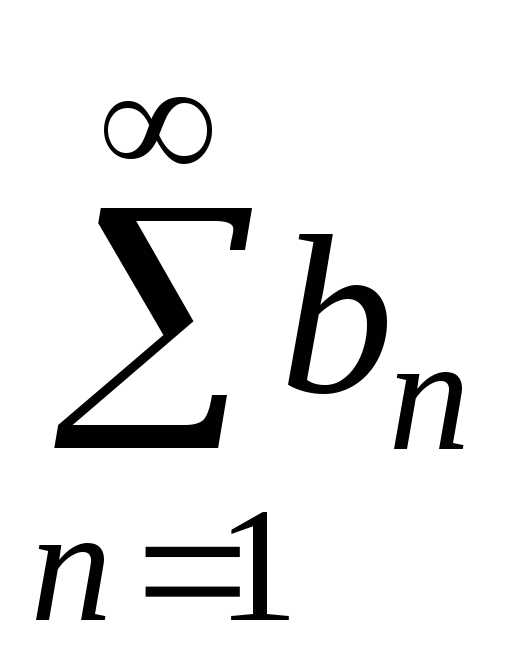сходятся, то
, .
Тогда .
следовательно,
ряд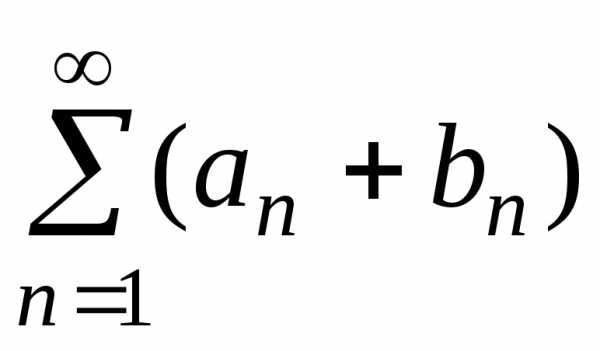 
сходится и.
Теорема 4. Если
ряд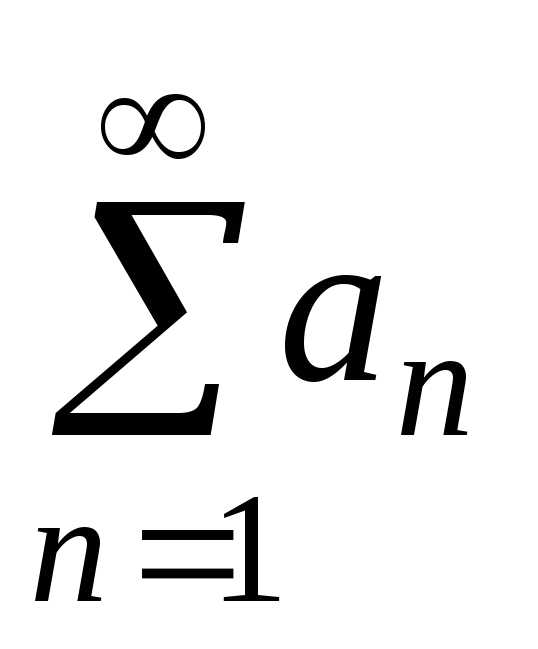 
,
сходится,
,
то ряд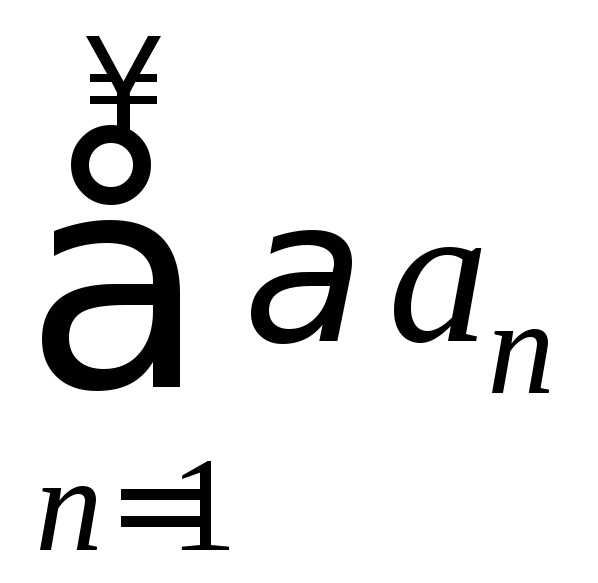
сходится
и
.
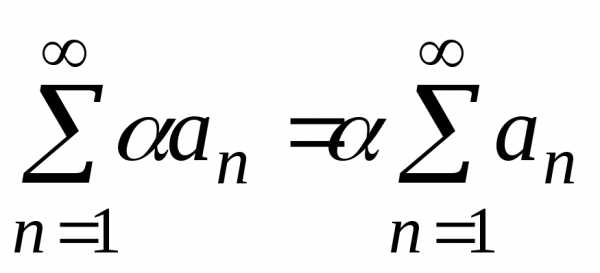Доказательство.
Так как ряд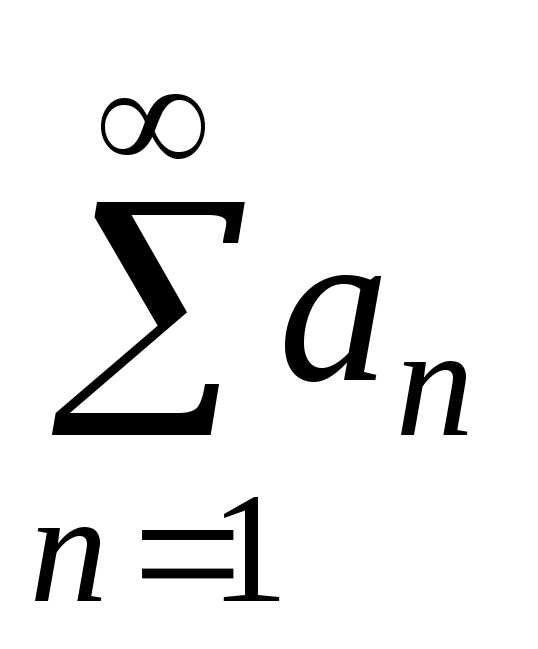 
сходится, то
.
тогда .
То есть ряд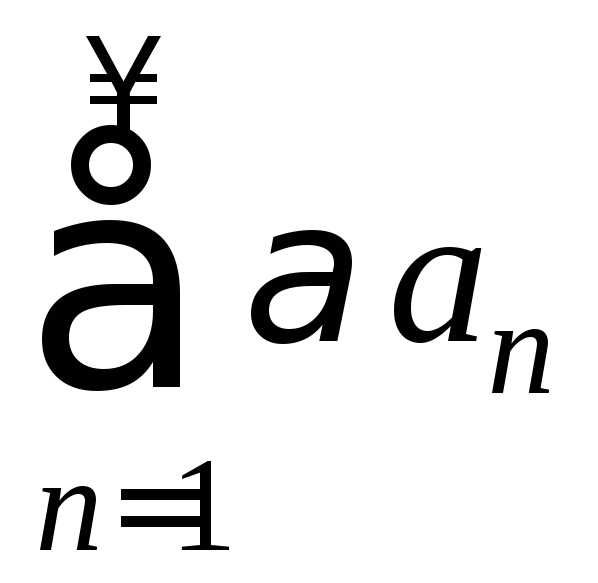 
сходится, и.
Пример 4. Исследовать
на сходимость ряд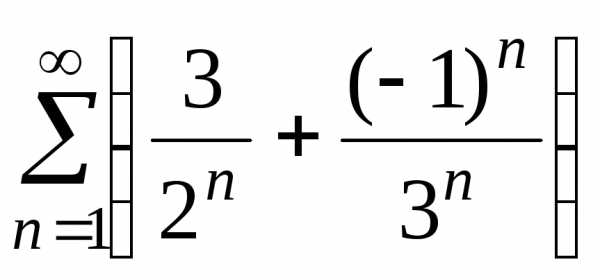 
.
В случае сходимости найти сумму ряда.
Δ По теореме 3 и теореме 4
.
Ряды в правой части – геометрические, сходятся. Следовательно данный ряд сходится. Найдем его сумму.
, 
.
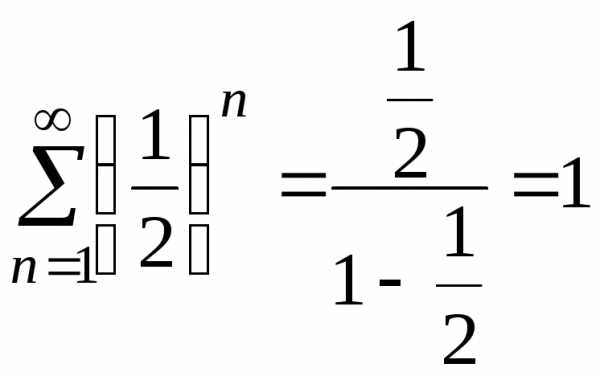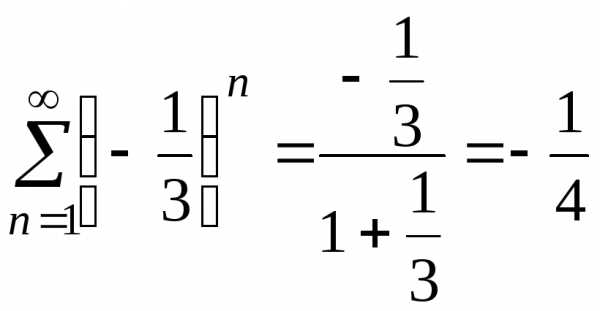тогда . Δ
Замечание. Сумма
двух расходящихся рядов не обязательно
является расходящимся рядом. Например,
ряды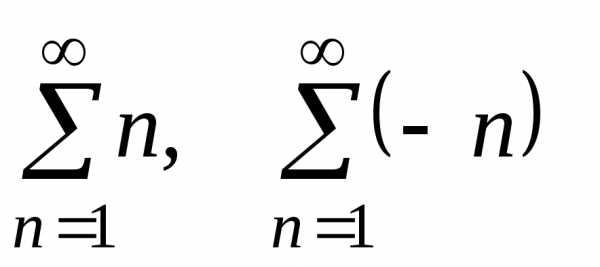 
расходятся,
а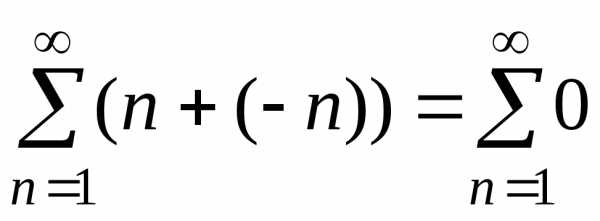
— сходится.
studfiles.net
Сходящиеся и расходящиеся числовые ряды. — КиберПедия
Простейшие свойства сходящихся рядов.
1. Если ряд сходится, то сходится любой из его остатков. Наоборот, из сходимости какого-то остатка вытекает сходимость всего ряда. Отсюда следует, что изменение или выбрасывание конечного числа членов ряда не изменяет его сходимости или расходимости.
2. Если ряд сходится, то .
3. Если ряд сходится, то сходится ряд и имеет место равенство .
4. Если ряды и сходятся, то сходится и ряд имеет место равенство .
5. Если ряд сходится, то .
Отсюда следует
Признак расходимости ряда. Если , то ряд расходится
Исследование ряда на сходимость.
| Сходимость рядов. Признаки сравнения |
| Необходимый признак сходимости, вообще говоря, не гарантирует сходимости ряда. Сходимость или расходимость ряда устанавливается с помощью достаточных признаков. Признаки сравнения, которые мы рассмотрим ниже, как раз и представляют собой достаточные признаки сходимости или расходимости рядов. Признаки сравнения рядов Даны два ряда и − такие, что для всех n. Тогда справедливы следующие признаки: Если сходится, то также сходится; Если расходится, то также расходится. Предельные признаки сравнения рядов Пусть даны два ряда и , у которых члены an и bn положительны для всех n. Тогда справедливы следующие предельные признаки: Если , то оба ряда и либо сходятся, либо расходятся; Если , то ряд сходится, если сходится ряд ; Если , то ряд расходится, если расходится ряд . Так называемый обобщенный гармонический ряд сходится при p > 1 и расходится при 0 < p ≤ 1. |
| Пример 1 |
| Определить, сходится или расходится ряд . Решение. Легко видеть, что для n > 1. Применяя далее признак сравнения, находим Поскольку ряд сходится как обобщенный гармонический ряд с показателем степени p = 2, то исходный ряд также сходится. |
Признак Даламбера.
Признак Даламбера — признак сходимости числовых рядов, установлен Жаном д’Аламбером в 1768 г.
Если для числового ряда
существует такое число , , что начиная с некоторого номера выполняется неравенство
то данный ряд абсолютно сходится; если же, начиная с некоторого номера
то ряд расходится.
Признак сходимости д’Аламбера в предельной форме
Если существует предел
то рассматриваемый ряд абсолютно сходится если , а если — расходится .
Замечание. Если , то признак д′Аламбера не даёт ответа на вопрос о сходимости ряда.
Примеры
Ряд
абсолютно сходится для всех комплексных , так как
Ряд
расходится при всех , так как
Если , то ряд может как сходиться, так и расходиться: оба ряда
и
удовлетворяют этому условию, причём первый ряд расходится, а второй сходится.
38. Признак Коши.
Радикальный признак Коши — признак сходимости числового ряда:
| Если для числового ряда с неотрицательными членами существует такое число , , что, начиная с некоторого номера, выполняется неравенство , то данный ряд сходится. |
Предельная форма
Условие радикального признака равносильно следующему:
То есть можно сформулировать радикальный признак сходимости знакоположительного ряда в предельной форме:
| Если для ряда , то если ряд сходится, если ряд расходится, если вопрос о сходимости ряда остается открытым. |
Доказательство
1. Пусть . Очевидно, что существует такое , что . Поскольку существует предел , то подставив в определение предела выбранное получим:
Раскрыв модуль, получаем:
Поскольку , то ряд сходится. Следовательно, по признаку сравнения ряд тоже сходится.
2. Пусть . Очевидно, что существует такое , что . Поскольку существует предел , то подставив в определение предела выбранное получим:
Раскрыв модуль, получаем:
Поскольку , то ряд расходится. Следовательно, по признаку сравнения ряд тоже расходится.
Примеры
1. Ряд
сходится, так как выполняется условие предельной формы радикального признака теоремы Коши
2. Рассмотрим ряд
ряд сходится.
cyberpedia.su
Числовой ряд — ПриМат
Пусть дана последовательность , где
Символ вида (*) называется числовым рядом и обозначается, при этом называется общим членом ряда. Ряд (*) называется сходящимся, если существует предел , где это n-ая частичная сумма ряда, .
При этом, число называется суммой ряда, и пишут .
Если же предел частичных сумм не существует или бесконечен, то говорят, что ряд (*) расходится и никакой суммы ряду не присваивается.
Пример:
Исследовать на сходимость ряд
Запишем n-ю частичную сумму и с упростим выражение с помощью формулы суммы геометрической прогрессии.
, , при , при . , при . не существует, при .Таким образом, при ряд сходится, а при — расходится.
Если ряд сходится, то необходимо .
Доказательство.
Если ряд сходится, то , следовательно .
Рассмотрим , где , — общий член ряда, . Теорема доказана.
Пример:
Исследовать на сходимость ряд
.Необходимое условие не выполняется: . Следовательно, ряд расходится.
Литература
Сходящиеся и расходящиеся ряды
Лимит времени: 0
Информация
Тест на проверку знаний о сходящихся и расходящихся рядах, а также необходимого условия сходимости.
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
| Место | Имя | Записано | Баллы | Результат |
|---|---|---|---|---|
| Таблица загружается | ||||
| Нет данных | ||||
- С ответом
- С отметкой о просмотре
Поделиться ссылкой:
ib.mazurok.com
Суммирование расходящихся рядов методами Абеля, Бореля, Чезаро и Дирихле
Перевод поста Давендра Кападия (Devendra Kapadia) «The ABCD of Divergent Series.»
Выражаю благодарность за помощь в переводе Андрею Дудину.
Какова сумма всех натуральных чисел? Интуиция подсказывает, что ответ — бесконечность. В математическом анализе сумма натуральных чисел является простым примером расходящегося ряда. Тем не менее, математики и физики сочли полезным придать дробные, отрицательные и даже нулевые значения суммам таких рядов. Цель моей статьи — желание отодвинуть завесу тайны, окружающую результаты суммирования расходящихся рядов. В частности, я буду использовать функцию Sum (функция поиска частичных сумм, рядов и т. п. в Mathematica), а так же другие функции в Wolfram Language для того, чтобы объяснить в каком смысле стоит рассматривать следующие утверждения:
Важность обозначений формул буквами A, B, C, и D вскоре станет вам понятна.
Начнем с того, что напомним понятие сходящегося ряда, используя следующую бесконечно убывающую геометрическую прогрессию.
Общий член ряда, начиная с n = 0, определяется по формуле:
In[1]:=
Теперь зададим сумму членов ряда от i = 0 до некоторого конечного значения i = n.
In[2]:=
Эта конечная сумма называется частичной суммой ряда.
График значений таких частичных сумм показывает, что их значения приближаются к числу 2 с ростом n:
In[3]:=
Out[3]=
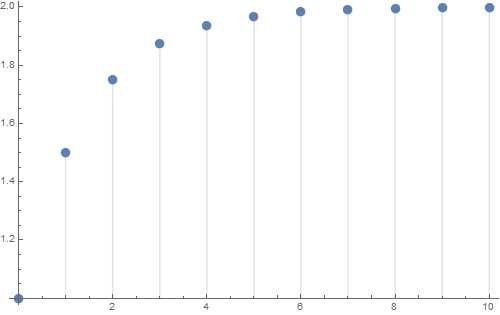
Применяя функцию Limit (поиск предела последовательности или функции в точке) найдем предел значения частичных сумм этого ряда при стремлении n к бесконечности, что подтвердит наши наблюдения.
In[4]:=
Out[4]=
Функция Sum даёт такой же результат, когда мы производим суммирование членов ряда в пределах от 0 до бесконечности.
In[5]:=
Out[5]=
Мы говорим, что данный ряд (сумма данной бесконечно убывающей геометрической прогрессии) сходится и что его сумма равна 2.
Вообще, бесконечный ряд сходится, если последовательность его частичных сумм стремится к некоторому значению при неограниченном увеличении номера частичной суммы. В этом случае, предельное значение частичных сумм называется суммой ряда.
Бесконечный ряд который не сходится называется расходящимся. По определению, сумма расходящегося ряда не может быть найдена с помощью рассмотренного выше метода частичных сумм. Тем не менее, математики разработали различные способы присваивания конечных числовых значений суммам этих рядов. Такая сумма называется регуляризованной суммой расходящегося ряда. Процесс вычисления регуляризованных сумм называется регуляризацией.
Теперь мы рассмотрим пример A из вступления.
“A” обозначает Абеля, знаменитого норвежского математика, который предложил одну из техник регуляризации расходящихся рядов. В ходе своей короткой жизни, он умер всего в 26 лет, Абель достиг впечатляющих результатов в решении одних из самых трудных математических задач. В частности, он показал, что решение алгебраического уравнения пятой степени не может быть найдено в радикалах, поставив тем самым точку в проблеме, которая оставалась нерешенной на протяжении 250 лет до него.
Для того чтобы применить метод Абеля, заметим, что общий член данного ряда имеет вид:
In[6]:=
Это можно легко проверить, найдя несколько первых значений a[n].
In[7]:=
Out[7]=
Как можно увидеть на графике ниже, частичные суммы ряда принимают значения, равные 1 или 0 в зависимости от того, четное n или нечетное.
In[8]:=
Out[8]=
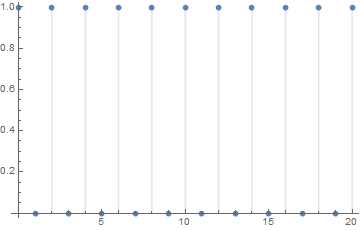
Естественно, что функция Sum выдает сообщение, о том что ряд расходится.
In[9]:=
Out[9]=
Регуляризация Абеля может быть применена к этому ряду в два шага. Сначала мы строим соответствующий степенной ряд.
In[10]:=
Out[10]=
Затем мы берем предел этой суммы при x стремящемся к 1, заметим при этом, что соответствующий ряд сходится для значений x меньших, но не равных 1.
In[11]:=
Out[11]=
Эти два шага можно объединить, сформировав, по сути, определение суммы расходящегося ряда по Абелю.
In[12]:=
Out[12]=
Мы можем получить тот же ответ используя опцию Regularization для функции Sum следующим образом.
In[13]:=
Out[13]=
Значение 1/2 представляется разумным, так как оно является средней величиной из двух значений, 1 и 0, принимаемых частичной суммой данного ряда. Кроме того, используемый в данном методе предельный переход интуитивно понятен, т. к. при x = 1 степенной ряд совпадает с нашим расходящимся рядом. Однако, Абель был сильно обеспокоен отсутствием строгости, которое было присуще математическому анализу того времени, и выражал свою обеспокоенность об этом:
«Расходящиеся ряды — изобретение дьявола, и это стыдно на них ссылаться при каких бы то ни было доказательствах. С их помощью, можно сделать любой вывод, какой ему будет угоден, и именно поэтому эти ряды производят столько ошибок и столько парадоксов.» (Н. Х. Абель в письме к своему бывшему учителю Берндту Хольмбою, Январь 1826)
Обратимся теперь к примеру B, в котором утверждается, что:
“B” обозначает Бореля, французского математика, который работал в таких областях как теория меры и теория вероятностей. В частности, Борель связан с так называемой “теоремой о бесконечных обезьянах”, которая утверждает, что если абстрактная обезьяна будет случайным образом ударять по клавиатуре пишущей машинки на протяжении бесконечного количества времени, то вероятность того, что она напечатает некоторый конкретный текст, например, полное собрание сочинений Уильяма Шекспира, отлична от нуля.
Для того чтобы применить метод Бореля заметим, что общий член данного ряда имеет вид:
In[14]:=
Регуляризация Бореля может быть применена к быстро расходящимся рядам в два шага. На первом шаге мы вычисляем экспоненциальную производящую функцию для последовательности членов данного ряда. Стоящий в знаменателе факториал обеспечивает сходимость данного ряд при всех значениях параметра t.
In[15]:=
Out[15]=
Затем мы производим преобразование Лапласа нашей экспоненциальной производящей функции и ищем его значение в точке s=1.
In[16]:=
Out[16]=
Out[17]=
Эти шаги можно объединить, в итоге мы получим, по сути, определение суммы расходящегося ряда по Борелю.
In[18]:=
Out[18]=
Также мы можем использовать специализированные функции Wolfram Language для поиска экспоненциальной производящей функции и преобразования Лапласа:
In[19]:=
Out[19]=
При этом, ответ можно получить непосредственно с помощью Sum следующим образом.
In[20]:=
Out[20]=
Определение суммы по Борелю разумно, т. к. оно даёт тот же самый результат, что и обычный метод частичных сумм, если его применить к сходящемуся ряду. В этом случае можно поменять местами суммирование и интегрирование, и затем определить Гамма-функцию, при этом мы получим, что соответствующий интеграл будет равен 1 и останется просто, по сути, исходная сумма ряда:
In[21]:=
Out[21]=
Однако в случае с расходящимися рядами поменять местами знаки суммы и интеграла нельзя, что приводит к интересным результатам, которые даёт данный метод регуляризации.
Суммирование по Борелю представляет собой универсальный метод суммирования расходящихся рядов, который применяется, скажем, в квантовой теории поля. О применении суммирования по Борелю существует огромная коллекция литературы.
Пример C утверждает что:
“C” обозначает Чезаро (на англ. языке его фамилия пишется как Cesaro), итальянского математика, который внес значительный вклад в дифференциальную геометрию, теорию чисел и математическую физику. Чезаро был очень продуктивным математиком и написал около 80 работ в период с 1884 по 1886 г., до того, как получил степень PhD в 1887!
Для начала заметим, что общий член ряда, начиная с n = 0, имеет вид:
In[22]:=
График показывает сильную осцилляцию частичных сумм данного ряда.
In[23]:=
Out[23]=
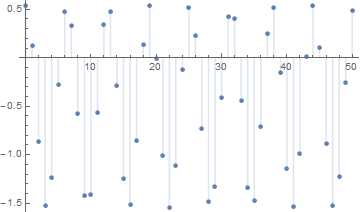
Метод Чезаро использует последовательность средних арифметических значений частичных сумм ряда для того, чтобы подавить осцилляции, что демонстрирует следующий график.
In[24]:=
Out[24]=
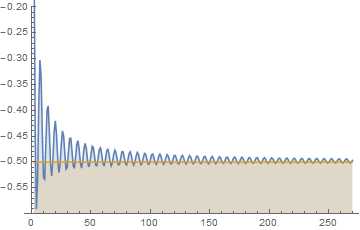
Формально говоря, суммирование по Чезаро определяется как предел последовательности средних арифметических значений частичных сумм ряда. Вычисляя данный предел для ряда из примера C, мы получим ожидаемый нами результат -1/2 (см. график выше).
In[25]:=
Out[25]=
Сумма по Чезаро может быть получена непосредственно, если мы в функции Sum используем данный тип регуляризации, указав соответствующее значение опции Regularization.
In[26]:=
Out[26]=
Метод суммирования по Чезаро играет важную роль в теории рядов Фурье, в которых ряды на основе тригонометрических функций используются для представления периодических функций. Ряд Фурье для непрерывной функции может и не сходится, но соответствующая сумма по Чезаро (или чезаровское среднее, как её обычно называют) всегда будет сходиться к функции. Этот красивый результат называется теоремой Фейера.
Наш последний пример утверждает, что сумма натурального ряда равна -1/12.
“D” означает Дирихле, немецкого математика, который совершил огромный вклад в теорию чисел и ряд других областей математики. О широте вкладов Дирихле можно судить, просто введя в Mathematica 10 следующий код.
In[27]:=
Out[27]//TableForm=
Регуляризация по Дирихле получила свое название от понятия “ряд Дирихле”, который определяется следующим образом:
Специальным случаем данного ряда является дзета-функция Римана, которую можно определить так:
In[28]:=
In[29]:=
Out[29]=
Функция SumConvergence говорит нам, что этот ряд сходится в том случае, если действительная часть параметра s будет больше 1.
In[30]:=
Out[30]=
Однако, сама по себе дзета-функция Римана может быть определена и для других значений параметра s с помощью процесса аналитического продолжения, известного из теории функций комплексного переменного. Например, при s = -1, мы получим:
In[31]:=
Out[31]=
Но при s = -1, ряд, задающий дзета-функцию Римана и есть натуральный ряд. Отсюда мы и получаем, что:
In[32]:=
Out[32]=
Еще один способ осознания этого результата заключается в том, чтобы ввести бесконечно малый параметр ε в выражение члена нашего расходящегося ряда, а затем найти разложение полученной функции в ряд Маклорена с помощью функции Series, как показано ниже.
In[33]:=
Out[33]=
Первое слагаемое в разложении выше стремится к бесконечности при приближении параметра ε к нулю, в то же время третий член и все следующие члены стремятся к нулю. Если отбросить все члены, зависящие от ε, то оставшееся число -1/12 как раз и будет суммой по Дирихле натурального ряда. Таким образом, сумма по Дирихле получается путем отбрасывания бесконечно малых и бесконечно больших членов разложения ряда, построенного описанным нами способом. Это находится в противоречии с тем, что принято отбрасывать лишь бесконечно малые величины в обычном математическом анализе, поэтому результат суммирования расходящихся рядов по Дирихле не столь интуитивно понятен.
Аналогично можно получить безумно странное значение 0 для расходящейся суммы квадратов натуральных чисел.
In[34]:=
Out[34]=
В этом случае в соответствующем разложении отсутствуют члены, не зависящие от параметра ε, в результате мы получаем 0.
In[35]:=
Out[35]=
Регуляризация Дирихле тесно связана с процессом дзета регуляризации, который используется в современной теоретической физике. В своей знаменитой работе, выдающийся британский физик Стивен Хокинг применил данный метод к задаче вычисления Фейнмановых интегралов в искривленном пространстве-времени. Статья Хокинга описывает процесс дзета-регуляризации очень системно и она приобрела большую популярность после публикации.
Наши знания о расходящихся рядах основаны на глубочайших теориях, разработанных одними из лучших мыслителей последних нескольких столетий. Тем не менее, я соглашусь со многими читателям, которые как и я, чувствуют некоторое непонимание, когда они видят их в современных физических теориях. Великий Абель, вероятно, был прав, когда назвал данные ряды “изобретением дьявола”. Не исключено, что какой-то будущий Эйнштейн, обладающий умом, свободным от всяческих устоев и авторитетов, отбросит преобладающие научные убеждения и переформулирует фундаментальную физику так, что в ней не не будет места для расходящихся рядов. Но даже если такая теория станет реальностью, расходящиеся ряды все равно будут давать нам богатый источник математических идей, освещая дорогу к более глубокому пониманию нашей Вселенной.
habr.com
Расходящийся ряд Википедия
Числовой ряд — одно из центральных понятий математического анализа. Ряд записывается как бесконечная сумма[1]:
- a1+a2+a3+…+an+…{\displaystyle a_{1}+a_{2}+a_{3}+\ldots +a_{n}+\ldots }; краткая запись: ∑n=1∞an{\displaystyle \sum _{n=1}^{\infty }a_{n}}
Здесь a1,a2,a3…{\displaystyle a_{1},a_{2},a_{3}\dots } — последовательность вещественных или комплексных чисел; эти числа называются членами ряда.
Чтобы присвоить такому ряду числовое значение, рассмотрим последовательность «частичных сумм», которые получаются, если оборвать бесконечную сумму на каком-то члене:
- S1=a1{\displaystyle S_{1}=a_{1}}
- S2=a1+a2{\displaystyle S_{2}=a_{1}+a_{2}}
- S3=a1+a2+a3{\displaystyle S_{3}=a_{1}+a_{2}+a_{3}}
- ⋯{\displaystyle \cdots }
- Sn=a1+a2+a3+⋯+an{\displaystyle S_{n}=a_{1}+a_{2}+a_{3}+\dots +a_{n}}
- ⋯{\displaystyle \cdots }
Если последовательность частичных сумм имеет предел S{\displaystyle S} (конечный или бесконечный), то говорят, что сумма ряда равна S.{\displaystyle S.} При этом, если предел конечен, то говорят, что ряд сходится. Если предел не существует или бесконечен, то говорят, что ряд расходится[1].
Ряды широко применяются в математике и других науках для вычислений, для анализа поведения разнообразных функций и т. п.
ru-wiki.ru