5.3 Разложение в ряд Фурье четных и нечетных функций
Если разлагаемая
на отрезке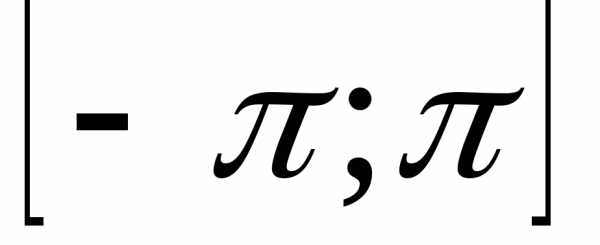 
в ряд Фурье функцияf(x)является четной или нечетной, то это
отражается на формулах коэффициентов
Фурье (вычисление их упрощается) и на
виде самого ряда (он становится неполным).
Приведем здесь несколько очевидных свойств четных и нечетных функций.
1. Произведение четной функции на четную функцию есть функция четная.
2. Произведение нечетной функции на нечетную функцию есть функция четная.
3. Произведение четной функции на нечетную функцию есть функция нечетная.
4. Если f(x)— четная функция, то.
5. Если f(x)— нечетная функция, то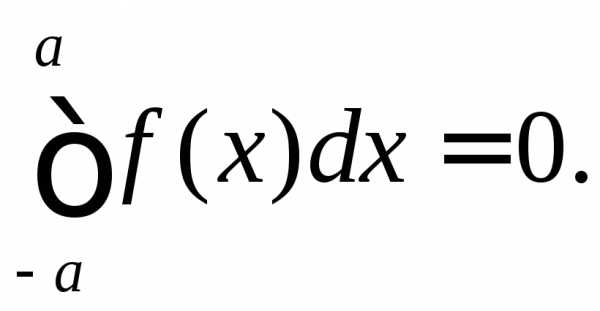
Используя указанные свойства, вычислим коэффициенты Фурье и построим ряды Фурье для четной и нечетной функций.
Если функция f(x)четная, то коэффициенты Фурье приобретают вид:
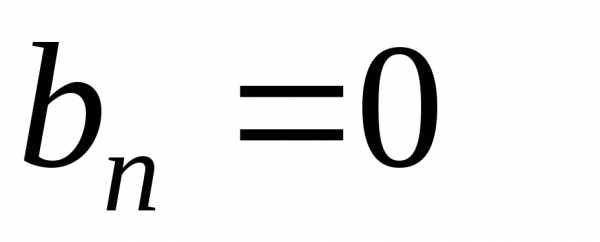
Ряд Фурье для четной функции: .
Если функция f(x)нечетная, то коэффициенты Фурье приобретают вид:
Ряд Фурье для
нечетной функции: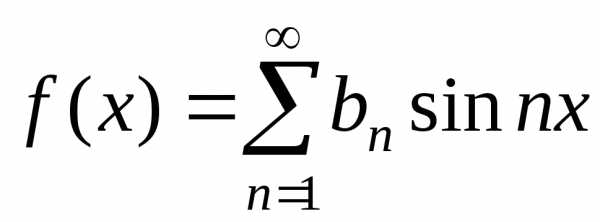 
.
Такие неполные тригонометрические ряды часто называют рядами по косинусам или рядами по синусам, а разложения функций разложение по синусам или разложение по косинусам.
Пример.
Разложить в ряд Фурье функцию периода 2π, заданную на интервале формулой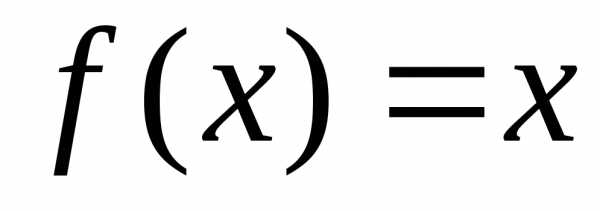
. Функция нечетная.
Следовательно
.
Находим коэффициенты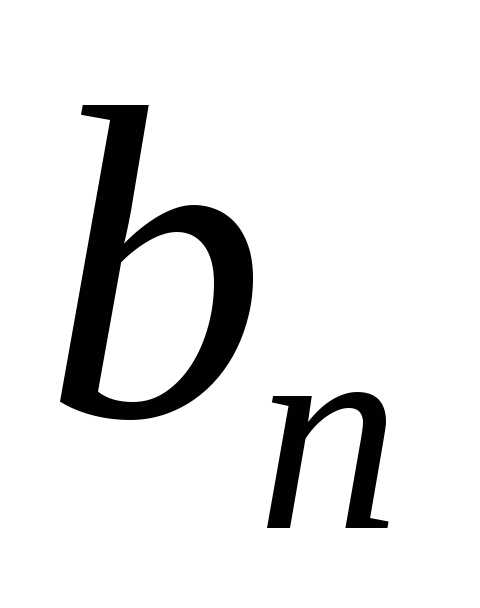
:
,
т.е. . Ряд Фурье содержит только синусы:
При этом
5.4 Разложение в ряд Фурье функций произвольного периода
Разлагать в ряд Фурье можно и периодические функции с периодом отличным от 2π.
Пусть функция f(x), определенная на отрезке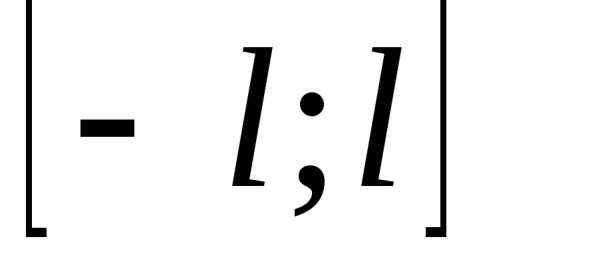
,
имеет период 2l и
удовлетворяет на этом отрезке условиям
Дирихле.
Сделав подстановку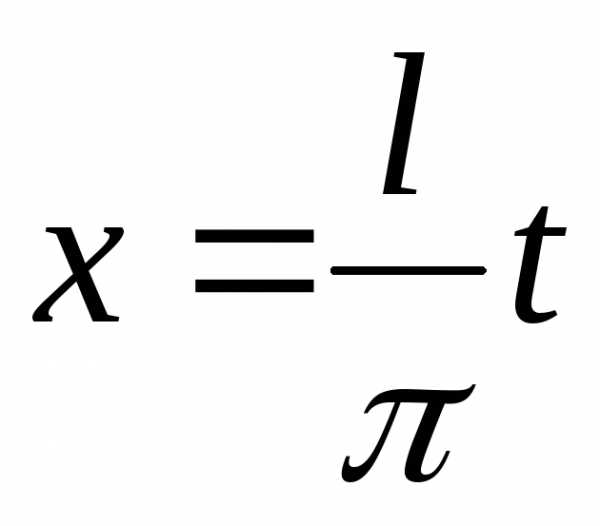 
,
данную функциюf(x)преобразуем в функцию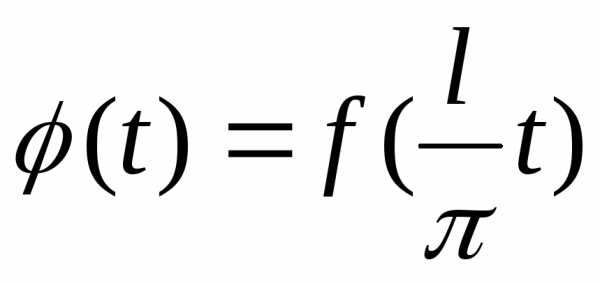
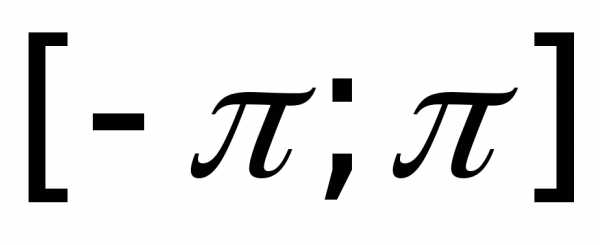и имеет периодТ=2π.Действительно, если t=-π, тоx=-l, еслиt=π, тоx=lи приимеем;
, т.е. .
Разложение функции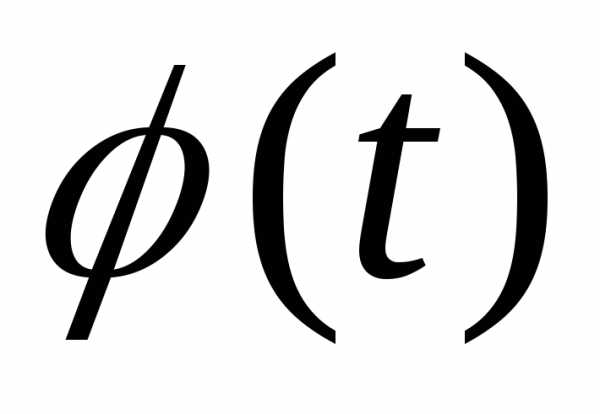 
в ряд Фурье на отрезке
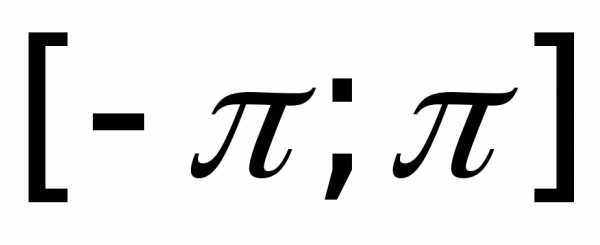имеет вид
,
где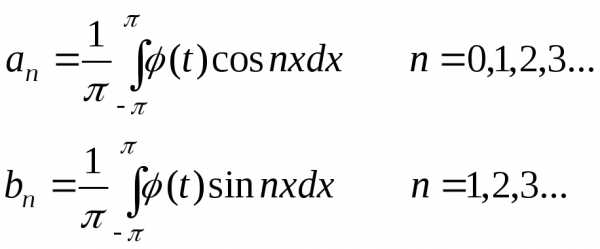 
Возвращаясь к
исходной переменной хи учитывая
, что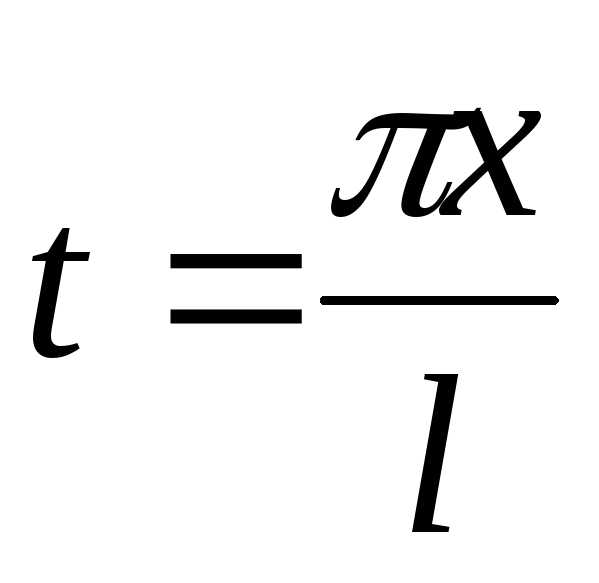
,
,
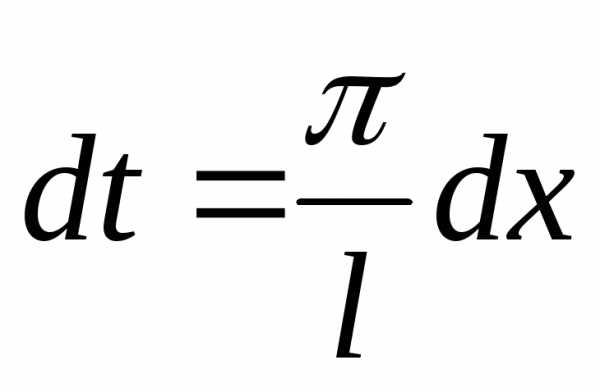получим
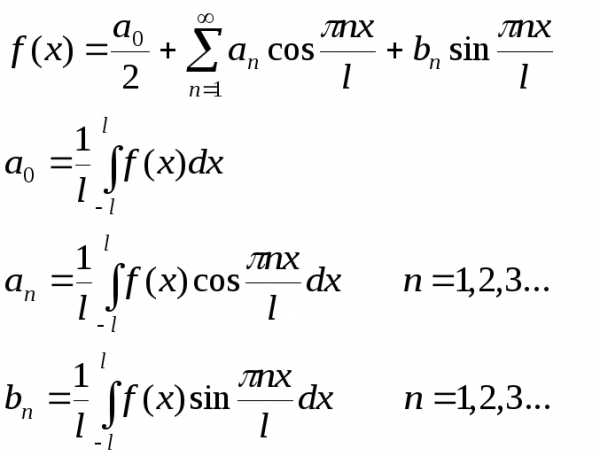
Полученный ряд называется рядом Фурье для функции f(x)с периодомТ=2l.
Правила разложения
четных и нечетных функций и здесь
остаются в силе. Если функция f(x)на отрезке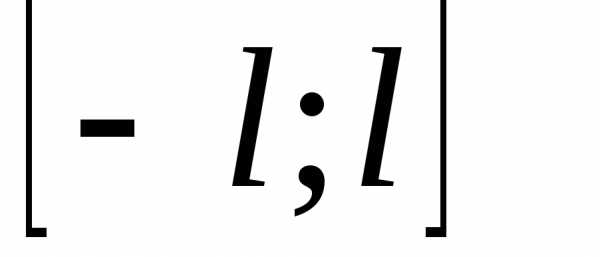
четная,
то ее ряд Фурье имеет вид,
где;
если функцияf(x)– нечетная, то
Пример.
Разложить в ряд
Фурье функцию, заданную в промежутке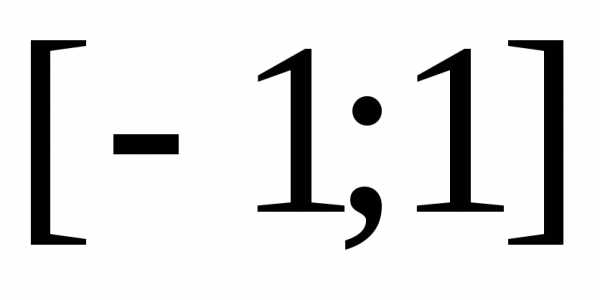 
уравнением
.
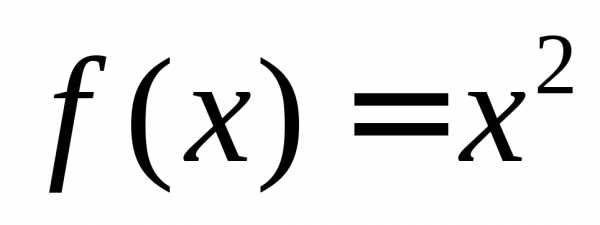Решение. Разложение
в ряд Фурье необходимо выполнить только
на интервале изменения аргумента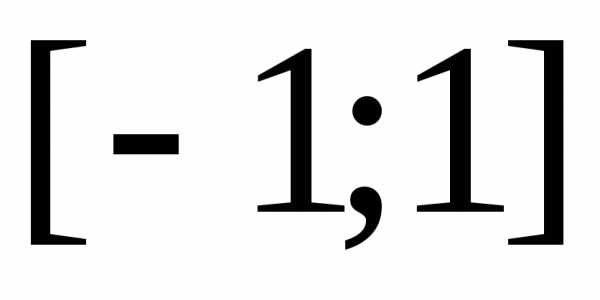 
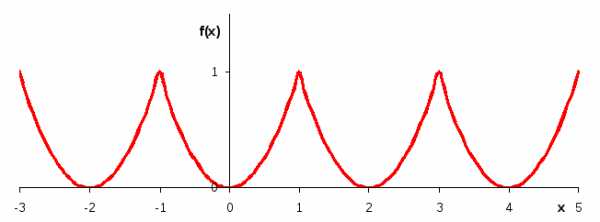
Рис. 34 График
функции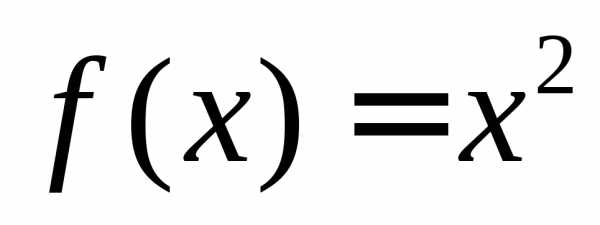 
в заданном интервале изменения аргумента
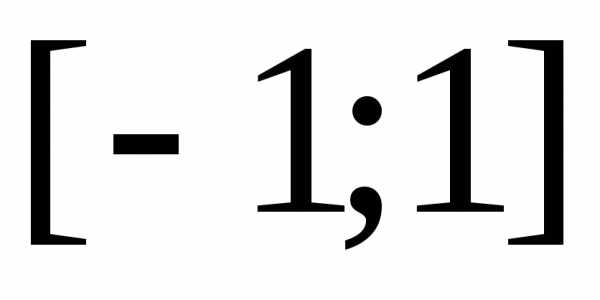с периодическим продолжением на оси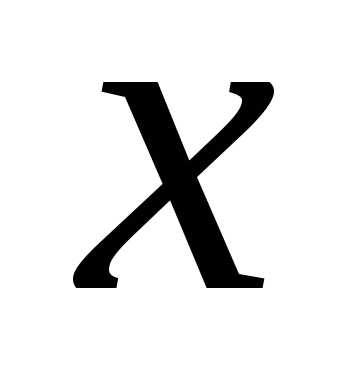
Заданная
функция является четной, определенной
в интервале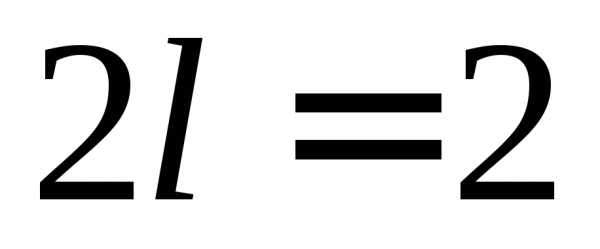 
(l=1), поэтому
коэффициенты ряда Фурье равны
В итоге получаем искомый ряд Фурье
.
5.5 Представление непериодической функции рядом Фурье
Пусть f(x)— непериодическая функция, заданная на всей числовой оси. Так как сумма тригонометрического ряда является периодической функцией, то, очевидно, что данная непериодическая функция не может быть разложена в ряд Фурье.
Однако непериодическая
функция f(x)может быть представлена в виде ряда
Фурье на любом конечном промежутке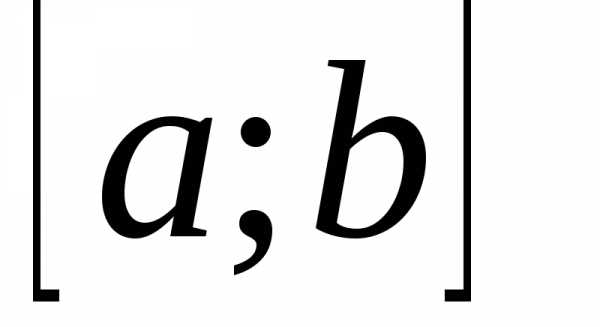
,
на котором она удовлетворяет условиям
Дирихле. Для этого можно поместить
начало координат в середину отрезка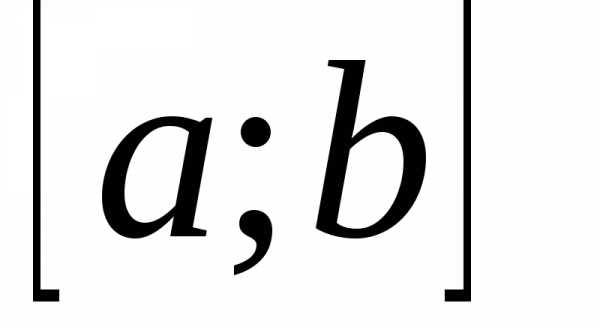
и
построить функциюf1(x) периодатакую, чтоf1(x)=f(x) при.
Разлагаем функцию f1(x) в ряд Фурье. Сумма этого ряда во всех
точках отрезка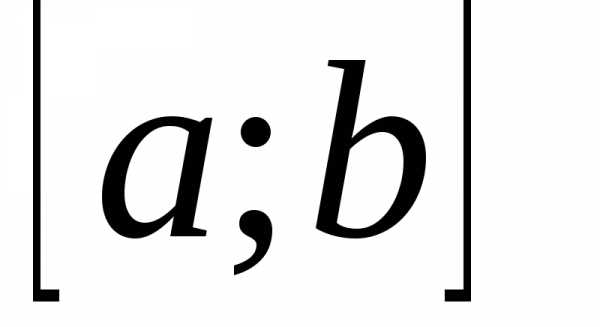
(кроме
точек разрыва) совпадает с заданной
функциейf(
Иногда приходится иметь дело с функциями, заданными только в интервале . В этом случае мы можем сначала продолжить (доопределить) по какому-либо закону функцию на интервал, а затем продолжить ее на всю числовую прямую периодически с периодом2l. Продолжить функцию из интервалана интервалможно произвольным образом.
Чаще всего продолжают четным или нечетным образом. Если функция продолжается четным образом (т.е. чтобы при былоf(x)= f(-x)), то ряд Фурье содержит только косинусы и свободный член. Если же функция продолжается нечетным образом, то ряд Фурье содержит только синусы.
Ряд
косинусов и ряд синусов для функции f(x), заданной на
отрезке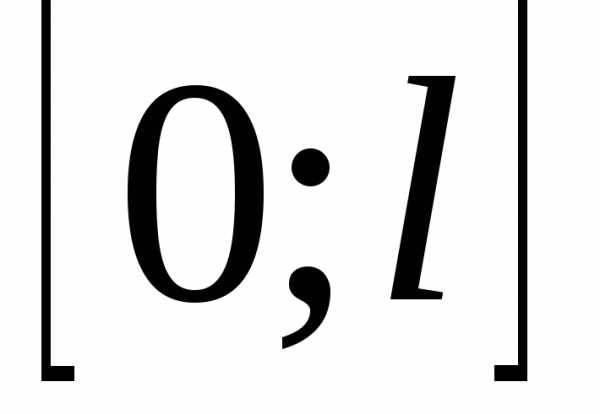 
Замечание.
Все выше сказанное справедливо для
функции f(x),
заданной на отрезке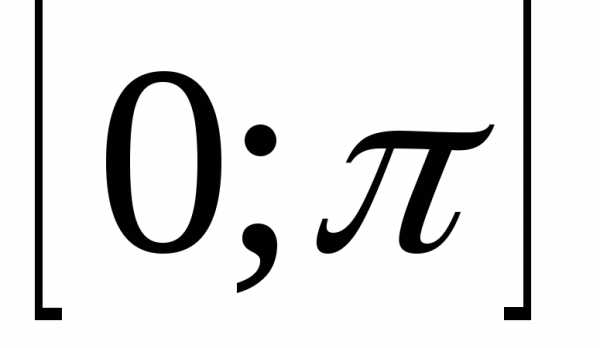 
.
Такую функцию можно разложить как в ряд
косинусов, так и вряд синусов.
Пример. Разложить
в ряд косинусов функцию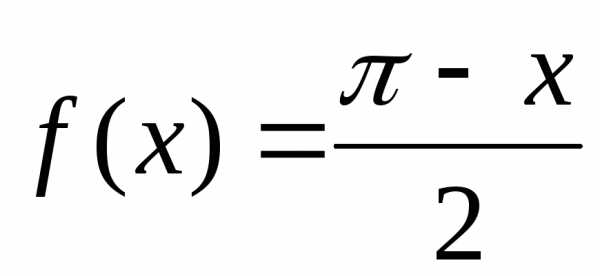
,.
Решение. Продолжим
функцию f(x)на отрезок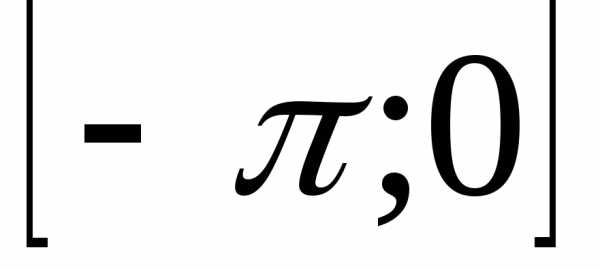
четным образом.
Разлагаем в ряд
функцию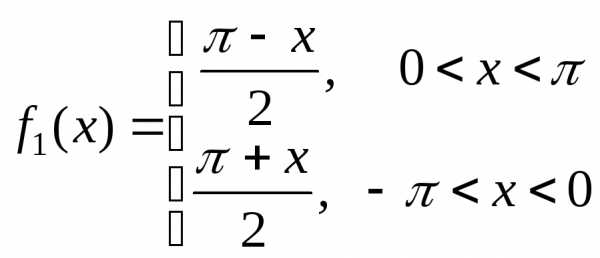 
с периодомТ=2π.
Функция
Таким образом ,
где .
Вопросы для самоконтроля.
Какие процессы называются периодическими? Привести пример периодических процессов.
Простейший периодический процесс. Функция простейшего периодического процесса.
Тригонометрический ряд Фурье.
Теорема Дирихле.
Разложение в ряд Фурье четных и нечетных функций.
Разложение в ряд Фурье функций произвольного периода.
Разложение непериодической функции в ряд Фурье на отрезке
.
.Литература: [5] стр. 328-343, [6] стр. 478-489, [7] стр. 400-410.
Примеры : [2] стр. 106-112, [3] стр. 190-235.
studfiles.net
6.2. Условия разложения функции в ряд Фурье
Что нужно для того, чтобы ряд Фурье сходился, и сумма полученного ряда равнялась значениям данной функции в соответствующих точках?
Определение 3. Функция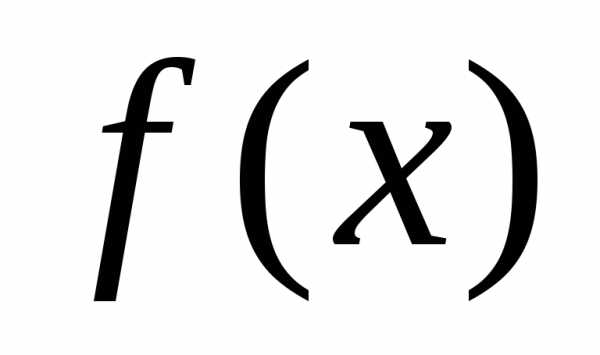 
называется кусочно–монотонной на
отрезке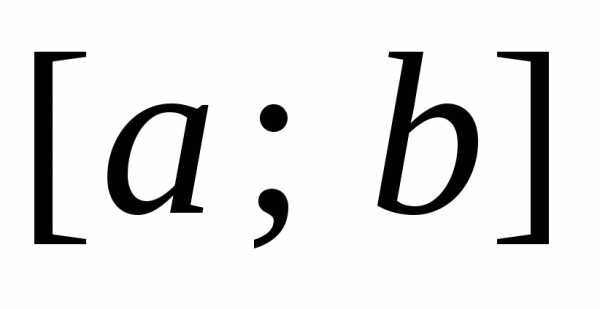
,
если этот отрезок можно разбить конечным
числом точекна интервалытак, что на каждом из этих интервалов
функция монотонна.
Вдальнейшем будем рассматривать
кусочно–монотонные функции, имеющие
разрывы только первого рода. Такие
условия принято называть
О а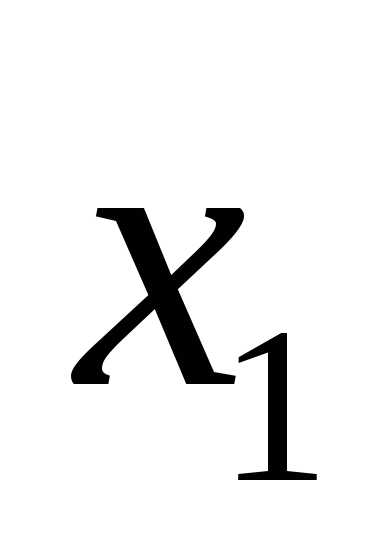 
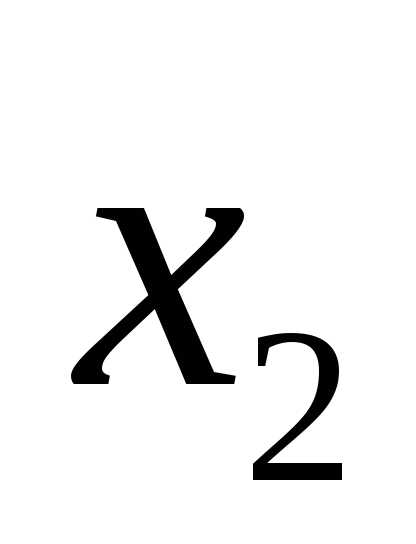
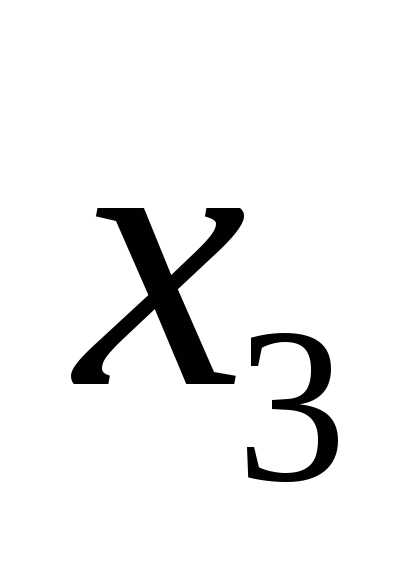
b x
Теорема Дирихле. Пусть функция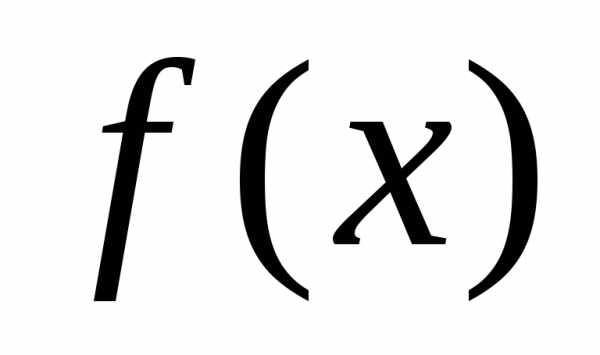 
с периодом
удовлет-воряет условиям Дирихле в
промежутке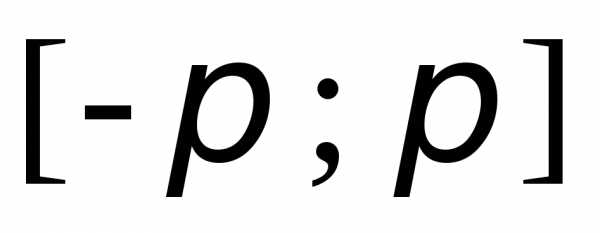
.
Тогда её ряд Фурье сходится в каждой
точкеи сумма этого ряда
равна:
1.
во всех точках непрерывности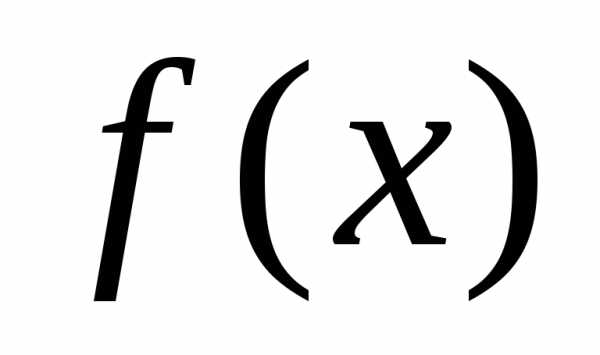
;
2. во всех точках разрыва;
3. на концах промежутка.
Замечание 2. Поэтому для разрывных функций иногда ряд Фурье пишут в виде .
Пример 1. Разложить в ряд Фурье периодическую функцию
при
с периодом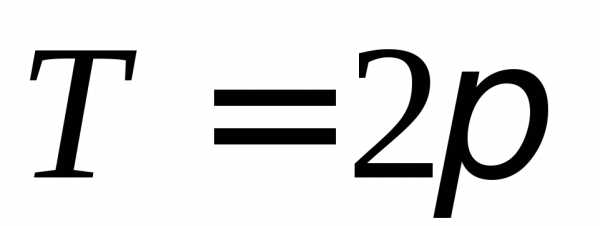
.у
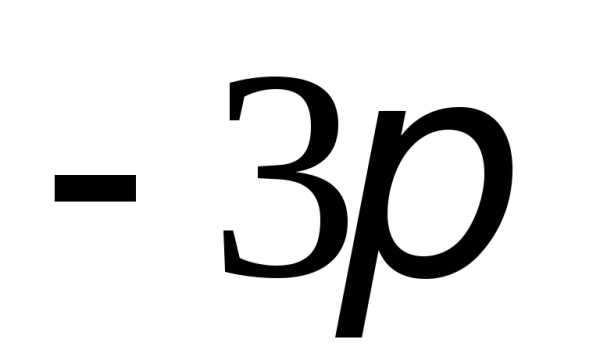
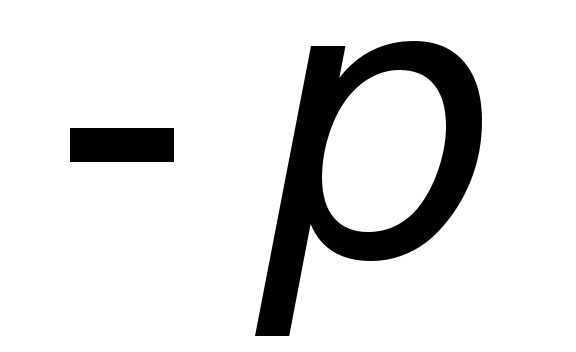
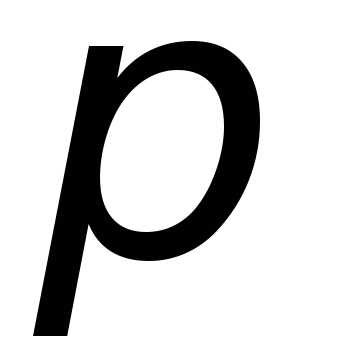
х
Вычислим коэффициенты Фурье:
.
Ряд Фурье для данной функции имеет вид
.
6.3. Ряд Фурье для функций с периодом T = 2 l
Пусть функция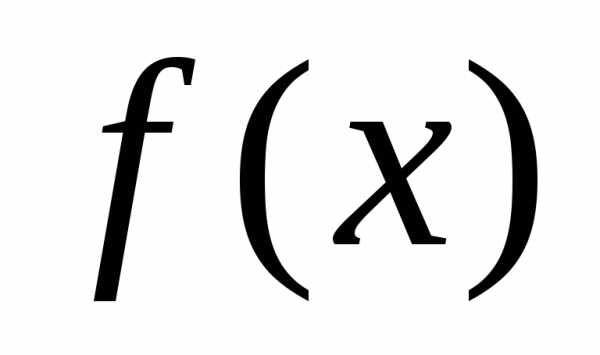 
,
заданная на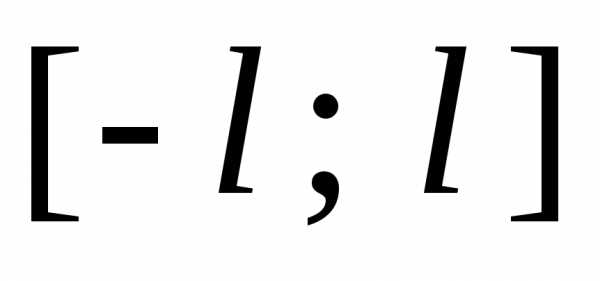
,
является периодической с периодомT = 2 l.
Введём новую переменную . Тогда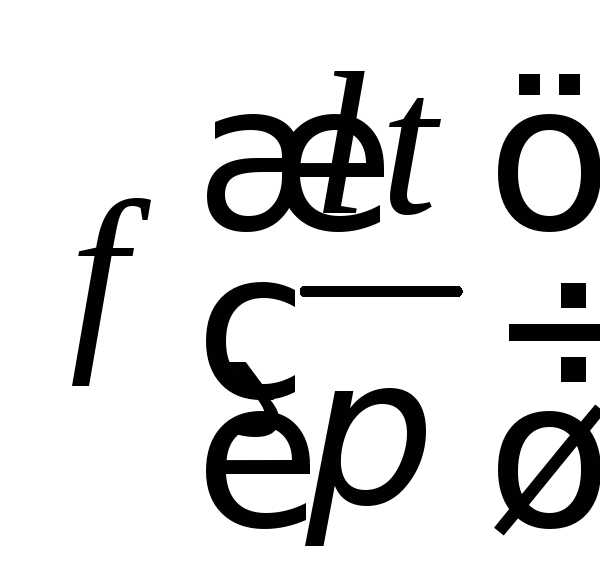 
будет функцией с
периодом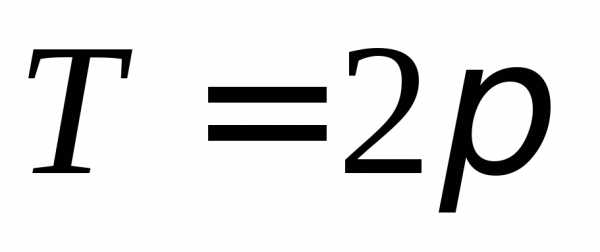 
и её можно разложить в ряд Фурье на
,
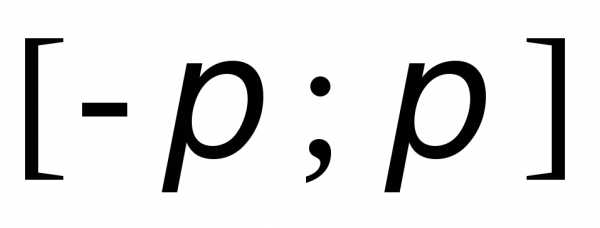т.е.
а, возвращаясь к
переменной x и учитывая, что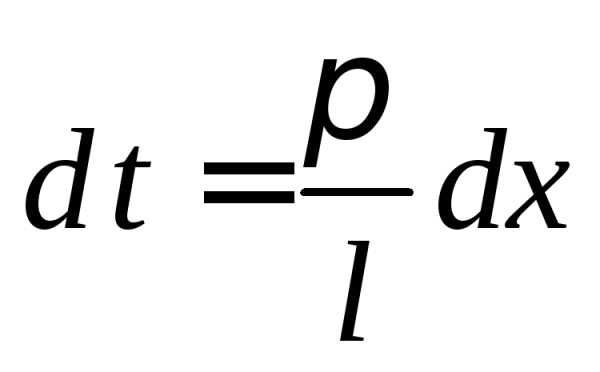 
,
получим
(8)
Тогда ряд Фурье для этого случая принимает вид
. (9)
Пример 2. Периодическую функцию с периодомразложить в ряд Фурье.
По формулам (8) вычислим коэффициенты:
.
При этом, если ,
а если ,
и тогда
.
Лекция № 50
6.4. Ряды Фурье для четных и нечетных функций
6.4.1. Рассмотрим случай разложения в ряд Фурье четной функции. Воспользуемся свойством интеграла в симметричных пределах от четных и нечетных функций. Тогда для четной функции получим
и ряд Фурье принимает вид
.
6.4.2. Рассмотрим случай разложения в ряд Фурье нечетной функции. Аналогично получаем
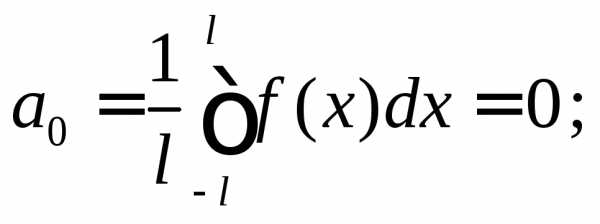
и ряд Фурье принимает вид
.
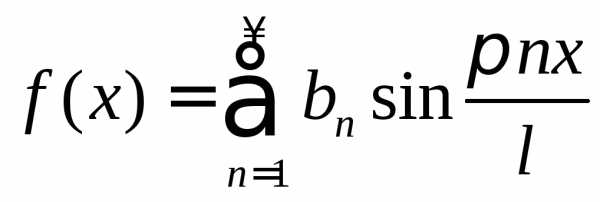Пример 1. Периодическую функцию
с периодомT = 2 l,
заданную на промежутке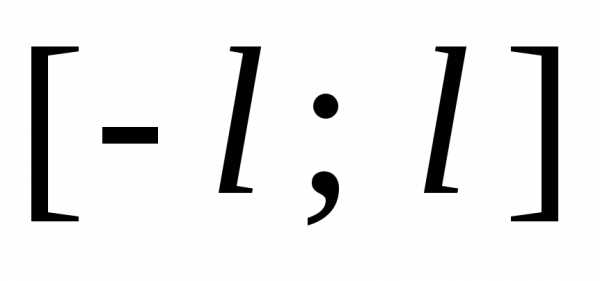 
,
разложить в ряд Фурье.
Так как функция четная, то ряд Фурье имеет вид
где
Тогда окончательно ряд Фурье этой функции примет вид
.
Из выражения для
этого ряда, если положить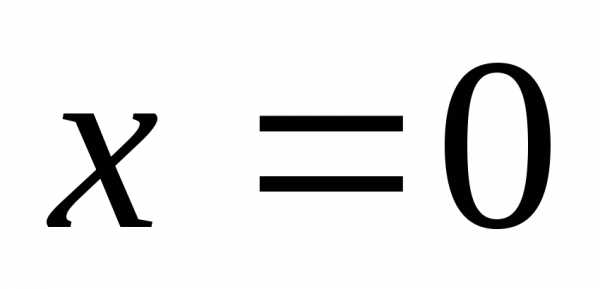 
,
можно получить интересную формулу для
приближенного вычисления числа
:
.
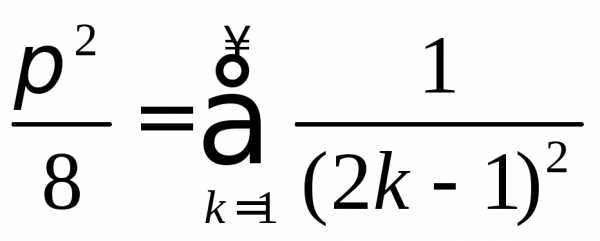6.5. Разложение непериодических функций в ряд Фурье
Часто возникает
задача о разложении в ряд Фурье функции,
удовлетворяющей условиям Дирихле на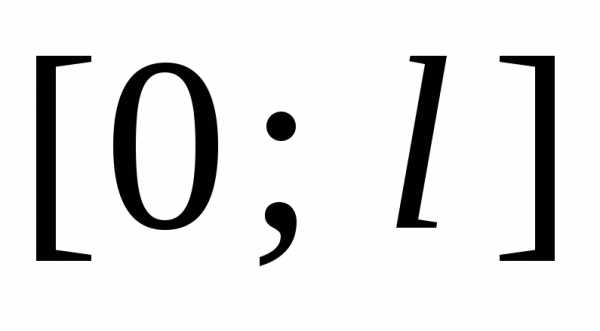 
,
только в ряд по косинусам или только
по синусам. В таких случаях поступают
следующим образом:
6.5.1. Если требуется
разложить в ряд Фурье по косинусам, то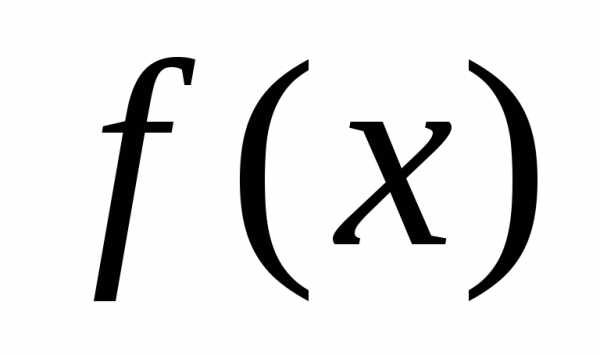 
доопределяют так чтобы прии периодически продолжают на всю числовую
ось. В этом случае говорят, что функция
продолжена “четным“ образом и для
неё
.
6.5.2. Если требуется
разложить в ряд Фурье по синусам, то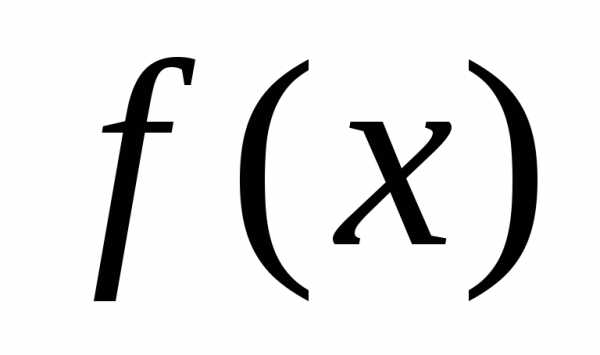 
доопределяют так чтобы прии периодически продолжают на всю числовую
ось. В этом случае говорят, что функция
продолжена “нечетным“ образом и для
неё
.
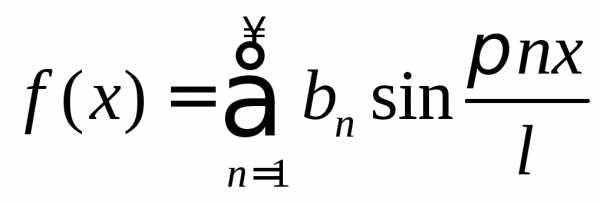Теперь рассмотрим общий случай.
6.5.3. Пусть функцию,
удовлетворяющую условиям Дирихле на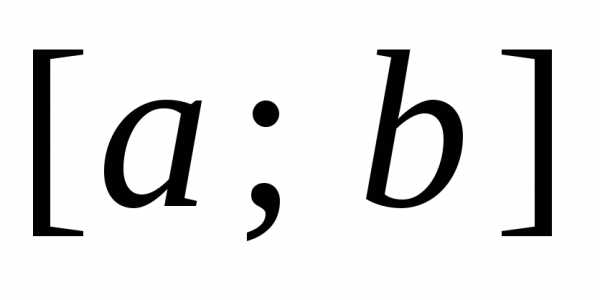 
,
требуется разложить в ряд Фурье. Для
этого функцию периодически с периодом
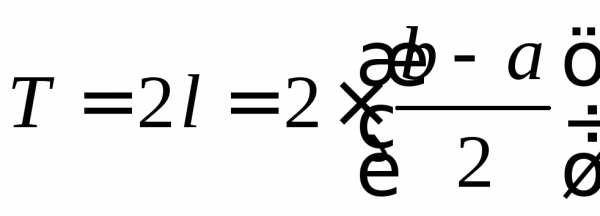продолжают на всё числовую ось, а затем
коэффициенты Фурье вычисляют по
формулам:
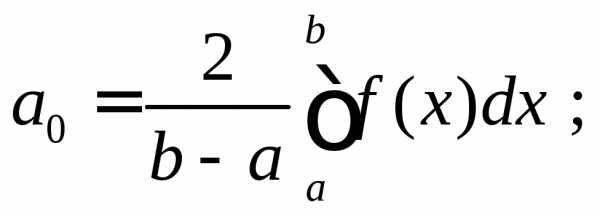
y
Пример 2. Функцию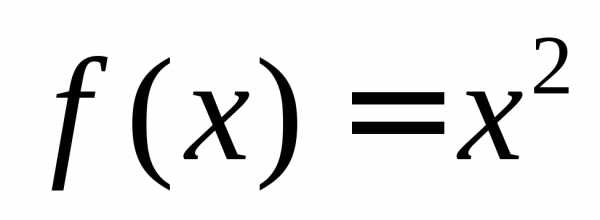 
,
заданную на
промежутке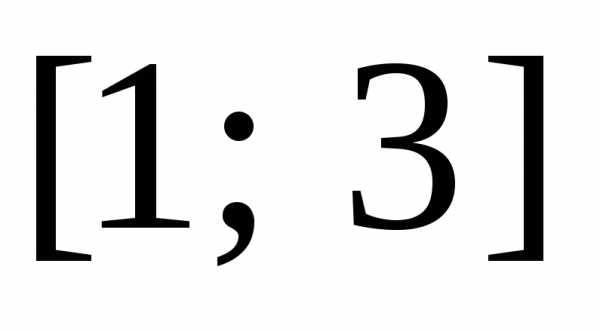 
,
разложить в ряд Фурье.
Вычислим коэффициенты Фурье
с учетом, что :
; O 1 3 x
;
Тогда ряд Фурье для данной функции примет вид
studfiles.net
Разложение в ряд Фурье непериодической функции.
Задача разложения непериодической функции в ряд Фурье в принципе не отличается от разложения в ряд Фурье периодической функции.
Допустим, функция f(x) задана на отрезке [a, b] и является на этом отрезке кусочно – монотонной. Рассмотрим произвольную периодическую кусочно – монотонную функцию f1(x) c периодом 2Т b-a, совпадающую с функцией f(x) на отрезке [a, b].
y
f(x)
— 2T a b +2T + 4T x
Таким образом, функция f(x) была дополнена. Теперь функция f1(x) разлагается в ряд Фурье. Сумма этого ряда во всех точках отрезка [a, b] совпадает с функцией f(x), т.е. можно считать, что функция f(x) разложена в ряд Фурье на отрезке [a, b].
Таким образом, если функция f(x) задана на отрезке, равном 2 ничем не отличается от разложения в ряд периодической функции. Если же отрезок, на котором задана функция, меньше, чем 2, то функция продолжается на интервал (b, a + 2) так, что условия разложимости в ряд Фурье сохранялись.
Вообще говоря, в этом случае продолжение заданной функции на отрезок (интервал) длиной 2 может быть произведено бесконечным количеством способов, поэтому суммы получившихся рядов будут различны, но они будут совпадать с заданной функцией f(x) на отрезке [a,b]
Свойства равномерно сходящихся рядов.
1) Теорема о непрерывности суммы ряда.
Если члены ряда — непрерывные на отрезке [a,b] функции и ряд сходится равномерно, то и его сумма S(x) есть непрерывная функция на отрезке [a,b].
2) Теорема о почленном интегрировании ряда.
Равномерно сходящийся на отрезке [a,b] ряд с непрерывными членами можно почленно интегрировать на этом отрезке, т.е. ряд, составленный из интегралов от его членов по отрезку [a,b] , сходится к интегралу от суммы ряда по этому отрезку.
3) Теорема о почленном дифференцировании ряда.
Если члены ряда сходящегося на отрезке [a,b] представляют собой непрерывные функции, имеющие непрерывные производные, и ряд, составленный из этих производных сходится на этом отрезке равномерно, то и данный ряд сходится равномерно и его можно дифференцировать почленно.
На основе того, что сумма ряда является некоторой функцией от переменной х, можно производить операцию представления какой – либо функции в виде ряда (разложения функции в ряд), что имеет широкое применение при интегрировании, дифференцировании и других действиях с функциями.
На практике часто применяется разложение функций в степенной ряд
Теорема. (Признак равномерной сходимости Вейерштрасса)
(Карл Теодор Вильгельм Вейерштрасс (1815 – 1897) – немецкий математик)
Ряд сходится равномерно и притом абсолютно на отрезке [a,b], если модули его членов на том же отрезке не превосходят соответствующих членов сходящегося числового ряда с положительными членами :
т.е. имеет место неравенство:
.
Еще говорят, что в этом случае функциональный ряд мажорируется числовым рядом
Ряды Фурье для функций любого периода.
Ряд Фурье для функции f(x) периода Т = 2l, непрерывной или имеющей конечное число точек разрыва первого рода на отрезке [-l, l] имеет вид:
Для четной функции произвольного периода разложение в ряд Фурье имеет вид:
Для нечетной функции:
Теорема. (Теорема Дирихле) Если функция f(x) имеет период 2 и на отрезке
[-;] непрерывна или имеет конечное число точек разрыва первого рода, и отрезок
[-;] можно разбить на конечное число отрезков так, что внутри каждого из них функция f(x) монотонна, то ряд Фурье для функции f(x) сходится при всех значениях х, причем в точках непрерывности функции f(x) его сумма равна f(x), а в точках разрыва его сумма равна , т.е. среднему арифметическому предельных значений слева и справа. При этом ряд Фурье функцииf(x) сходится равномерно на любом отрезке, который принадлежит интервалу непрерывности функции f(x).
studfiles.net
Разложение в ряд Фурье непериодической функции.
Задача разложения непериодической функции в ряд Фурье в принципе не отличается от разложения в ряд Фурье периодической функции.
Допустим, функция f(x) задана на отрезке [a, b] и является на этом отрезке кусочно – монотонной. Рассмотрим произвольную периодическую кусочно – монотонную функцию f1(x) c периодом 2Т b-a, совпадающую с функцией f(x) на отрезке [a, b].
y
f(x)
— 2T a b +2T + 4T x
Таким образом, функция f(x) была дополнена. Теперь функция f1(x) разлагается в ряд Фурье. Сумма этого ряда во всех точках отрезка [a, b] совпадает с функцией f(x), т.е. можно считать, что функция f(x) разложена в ряд Фурье на отрезке [a, b].
Таким образом, если функция f(x) задана на отрезке, равном 2 ничем не отличается от разложения в ряд периодической функции. Если же отрезок, на котором задана функция, меньше, чем 2, то функция продолжается на интервал (b, a + 2) так, что условия разложимости в ряд Фурье сохранялись.
Вообще говоря, в этом случае продолжение заданной функции на отрезок (интервал) длиной 2 может быть произведено бесконечным количеством способов, поэтому суммы получившихся рядов будут различны, но они будут совпадать с заданной функцией f(x) на отрезке [a,b]
Свойства равномерно сходящихся рядов.
1) Теорема о непрерывности суммы ряда.
Если члены ряда — непрерывные на отрезке [a,b] функции и ряд сходится равномерно, то и его сумма S(x) есть непрерывная функция на отрезке [a,b].
2) Теорема о почленном интегрировании ряда.
Равномерно сходящийся на отрезке [a,b] ряд с непрерывными членами можно почленно интегрировать на этом отрезке, т.е. ряд, составленный из интегралов от его членов по отрезку [a,b] , сходится к интегралу от суммы ряда по этому отрезку.
3) Теорема о почленном дифференцировании ряда.
Если члены ряда сходящегося на отрезке [a,b] представляют собой непрерывные функции, имеющие непрерывные производные, и ряд, составленный из этих производных сходится на этом отрезке равномерно, то и данный ряд сходится равномерно и его можно дифференцировать почленно.
На основе того, что сумма ряда является некоторой функцией от переменной х, можно производить операцию представления какой – либо функции в виде ряда (разложения функции в ряд), что имеет широкое применение при интегрировании, дифференцировании и других действиях с функциями.
На практике часто применяется разложение функций в степенной ряд
Теорема. (Признак равномерной сходимости Вейерштрасса)
(Карл Теодор Вильгельм Вейерштрасс (1815 – 1897) – немецкий математик)
Ряд сходится равномерно и притом абсолютно на отрезке [a,b], если модули его членов на том же отрезке не превосходят соответствующих членов сходящегося числового ряда с положительными членами :
т.е. имеет место неравенство:
.
Еще говорят, что в этом случае функциональный ряд мажорируется числовым рядом
Ряды Фурье для функций любого периода.
Ряд Фурье для функции f(x) периода Т = 2l, непрерывной или имеющей конечное число точек разрыва первого рода на отрезке [-l, l] имеет вид:
Для четной функции произвольного периода разложение в ряд Фурье имеет вид:
Для нечетной функции:
Теорема. (Теорема Дирихле) Если функция f(x) имеет период 2 и на отрезке
[-;] непрерывна или имеет конечное число точек разрыва первого рода, и отрезок
[-;] можно разбить на конечное число отрезков так, что внутри каждого из них функция f(x) монотонна, то ряд Фурье для функции f(x) сходится при всех значениях х, причем в точках непрерывности функции f(x) его сумма равна f(x), а в точках разрыва его сумма равна , т.е. среднему арифметическому предельных значений слева и справа. При этом ряд Фурье функцииf(x) сходится равномерно на любом отрезке, который принадлежит интервалу непрерывности функции f(x).
studfiles.net
Ряд Фурье. Разложение функции в ряд Фурье. Разложение функции в ряд синусов и косинусов.
Ряд Фурье. Разложение функции в ряд Фурье. Разложение функции в ряд синусов и косинусов.
Ряд Фурье периодических функций с периодом 2π.
Ряд Фурье позволяет изучать периодические (непериодические) функции, разлагая их на компоненты. Переменные токи и напряжения, смещения, скорость и ускорение кривошипно-шатунных механизмов и акустические волны — это типичные практические примеры применения периодических функций в инженерных расчетах.
Разложение в ряд Фурье основывается на предположении, что все имеющие практическое значение функции в интервале -π ≤x≤ π можно выразить в виде сходящихся тригонометрических рядов (ряд считается сходящимся, если сходится последовательность частичных сумм, составленных из его членов):
Стандартная (=обычная) запись через сумму sinx и cosx
f(x)=ao+ a1cosx+a2cos2x+a3cos3x+…+b1sinx+b2sin2x+b3sin3x+…,
где ao, a1,a2,…,b1,b2,.. — действительные константы, т.е.
(1)
Где для диапазона от -π до π коэффициенты ряда Фурье рассчитываются по формулам:
Коэффициенты ao,an и bn называются коэффициентами Фурье, и если их можно найти, то ряд (1) называется рядом Фурье, соответствующим функции f(x). Для ряда (1) член (a1cosx+b1sinx) называется первой или основной гармоникой,
Другой способ записи ряда — использование соотношения acosx+bsinx=csin(x+α)
f(x)=ao+c1sin(x+α1)+c2sin(2x+α2)+…+cnsin(nx+αn)
Где ao — константа, с 1=(a12+b12)1/2 , с n=(an2+bn2)1/2— амплитуды различных компонент, а фазовый угол равен an=arctg an/bn.
Для ряда (1) член (a1cosx+b1sinx) или c1sin(x+α1) называется первой или основной гармоникой, (a2cos2x+b2sin2x) или c2sin(2x+α2) называется второй гармоникой и так далее.
Для точного представления сложного сигнала обычно требуется бесконечное количество членов. Однако во многих практических задачах достаточно рассмотреть только несколько первых членов.
Ряд Фурье непериодических функций с периодом 2π.
Разложение непериодических функций.
Если функция f(x) непериодическая, значит, она не может быть разложена в ряд Фурье для всех значений х. Однако можно определить ряд Фурье, представляющий функцию в любом диапазоне шириной 2π.
Если задана непериодическая функция, можно составить новую функцию, выбирая значения f(x) в определенном диапазоне и повторяя их вне этого диапазона с интервалом 2π. Поскольку новая функция является периодической с периодом 2π, ее можно разложить в ряд Фурье для всех значений х. Например, функция f(x)=x не является периодической. Однако, если необходимо разложить ее в ряд Фурье на интервале от о до 2π, тогда вне этого интервала строится периодическая функция с периодом 2π (как показано на рис. ниже) .
Для непериодических функций, таких как f(x)=х, сумма ряда Фурье равна значению f(x) во всех точках заданного диапазона, но она не равна f(x) для точек вне диапазона. Для нахождения ряда Фурье непериодической функции в диапазоне 2π используется все таже формула коэффициентов Фурье.
Четные и нечетные функции.
Говорят, функция y=f(x) четная, если f(-x)=f(x) для всех значений х. Графики четных функций всегда симметричны относительно оси у (т.е. являются зеркально отраженными). Два примера четных функций: у=х2 и у=cosx.
Говорят, что функция y=f(x) нечетная, если f(-x)=-f(x) для всех значений х. Графики нечетных функций всегда симметричны относительно начала координат.
Многие функции не являются ни четными, ни нечетными.
Разложение в ряд Фурье по косинусам.
Ряд Фурье четной периодической функции f(x) с периодом 2π содержит только члены с косинусами (т.е. не содержит членов с синусами) и может включать постоянный член. Следовательно,
где коэффициенты ряда Фурье,
Разложение в ряд Фурье по синусам.
Ряд Фурье нечетной периодической функции f(x) с периодом 2π содержит только члены с синусами (т.е. не содержит членов с косинусами).
Следовательно,
где коэффициенты ряда Фурье,
Ряд Фурье на полупериоде.
Если функция определена для диапазона, скажем от 0 до π, а не только от 0 до 2π, ее можно разложить в ряд только по синусам или тольо по косинусам. Полученный ряд Фурье называется рядом Фурье на полупериоде.
Если требуется получить разложение Фурье на полупериоде по косинусам функции f(x) в диапазоне от 0 до π, то необходимо составить четную периодическую функцию. На рис. ниже показана функция f(x)=х, построенная на интервале от х=0 до х=π. Поскольку четная функция симметрична относительно оси f(x), проводим линию АВ, как показано на рис. ниже. Если предположить, что за пределами рассмотренного интервала полученная треугольная форма является периодической с периодом 2π, то итоговый график имеет вид, показ. на рис. ниже. Поскольку требуется получить разложение Фурье по косинусам, как и ранее, вычисляем коэффициенты Фурье ao и an
Если требуется получить разложение Фурье на полупериоде по синусам функции f(x) в диапазоне от 0 до π, то необходимо составить нечетную периодическую функцию. На рис. ниже показана функция f(x)=x, построенная на интервале от от х=0 до х=π. Поскольку нечетная функция симметрична относительно начала координат, строим линию CD, как показано на рис. Если предположить, что за пределами рассмотренного интервала полученный пилообразный сигнал является периодическим с периодом 2π, то итоговый график имеет вид, показанный на рис. Поскольку требуется получить разложение Фурие на полупериоде по синусам, как и ранее, вычисляем коэффициент Фурье. b
Ряд Фурье для произвольного интервала.
Разложение периодической функции с периодом L.
Периодическая функция f(x) повторяется при увеличении х на L, т.е. f(x+L)=f(x). Переход от рассмотренных ранее функций с периодом 2π к функциям с периодом L довольно прост, поскольку его можно осуществить с помощью замены переменной.
Чтобы найти ряд Фурье функции f(x) в диапазоне -L/2≤x≤L/2, введем новую переменную u таким образом, чтобы функция f(x) имела период 2π относительно u. Если u=2πх/L, то х=-L/2 при u=-π и х=L/2 при u=π. Также пусть f(x)=f(Lu/2π)=F(u). Ряд Фурье F(u) имеет вид
Где коэффициенты ряда Фурье,
Однако чаще приведенную выше формулу приводят к зависимости от х. Поскольку u=2πх/L, значит, du=(2π/L)dx, а пределы интегрирования — от -L/2 до L/2 вместо — π до π. Следовательно, ряд Фурье для зависимости от х имеет вид
где в диапазоне от -L/2 до L/2 коэффициенты ряда Фурье,
(Пределы интегрирования могут быть заменены на любой интервал длиной L, например, от 0 до L)
Ряд Фурье на полупериоде для функций, заданных в интервале L≠2π.
Для подстановки u=πх/L интервал от х=0 до х=L соответствует интервалу от u=0 до u=π. Следовательно, функцию можно разложить в ряд только по косинусам или только по синусам, т.е. в ряд Фурье на полупериоде.
Разложение по косинусам в диапазоне от 0 до L имеет вид
Оценка статьи:
e4-cem.ru
Разложение в ряд Фурье функции продолженной произвольным способом — КиберПедия
Достроим функцию на участке [-π;0).
Тогда получим
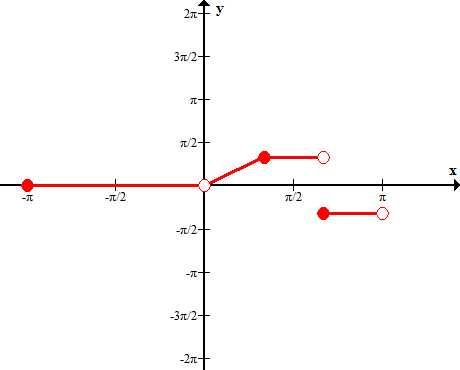
Функция непериодическая, кусочно-гладкая, задана на интервале [-π;π]. Функция имеет на промежутке [-π;π] конечное число точек разрыва первого рода.
Сумма ряда в точках разрыва функции сходится к значению самой функции, а в точках разрыва к величине f(x0), где x0 – точка разрыва.
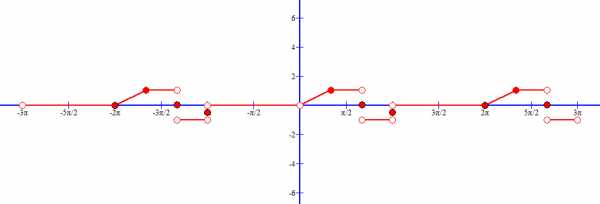
Производная так же непрерывна везде, кроме конечного числа точек разрыва первого рода.
Вывод: функция удовлетворяет условиям Дирихле.
Так как отсутствует симметрия относительно оси OY, а также центральная симметрия, то рассматриваемая функция произвольна.
Представление функции рядом Фурье:
Построим первые три гармоники и одну бесконечно большую гармонику для найденного ряда.
1-ая гармоника
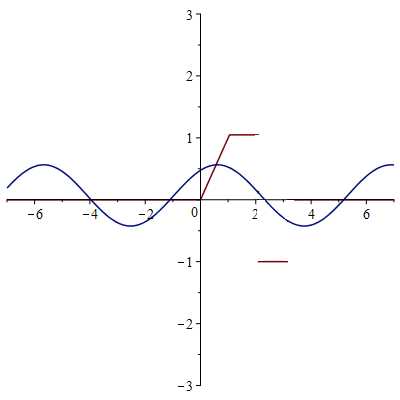
2-ая гармоника
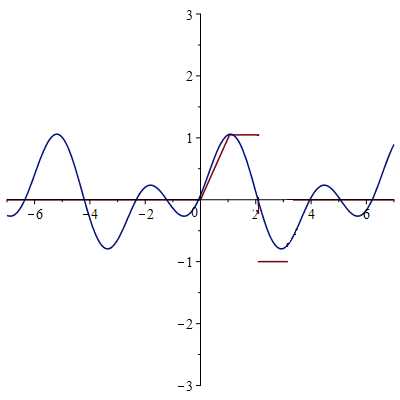
3-я гармоника
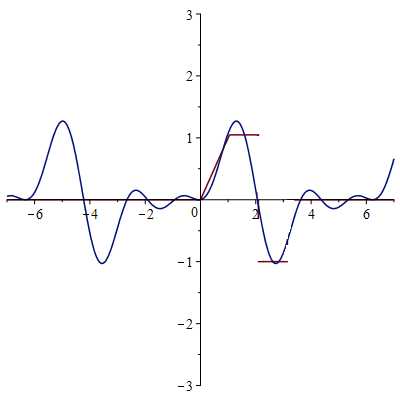
Сумма 100 гармоник
Построим амплитудный и фазовый спектры функции по формулам:
Амплитудный спектр для данной функции:
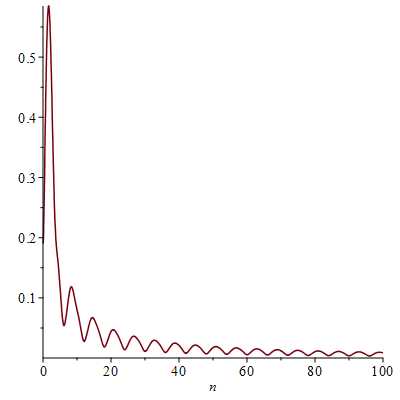
Рассчитаем фазовый спектр для данной функции:
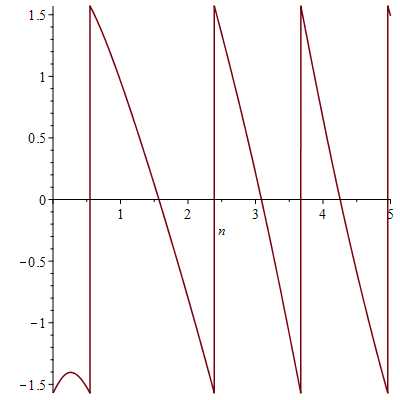
Вычислим среднеквадратическую ошибку между исходной функцией f(t) и частичной суммой Фурье для t, принадлежащих промежутку задания f(t).
Среднеквадратическую ошибку вычисляем по формуле:
Разложение в ряд Фурье функции продолженной четным способом
Достроим функцию на участке (-π;0):
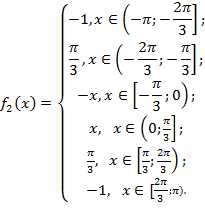
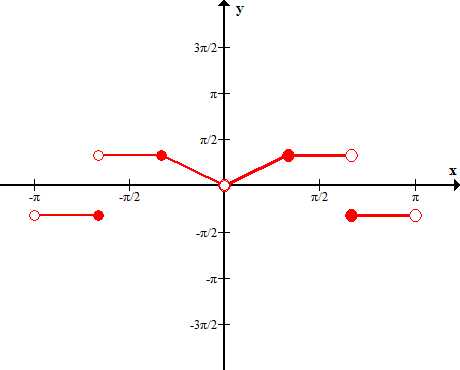
Функция непериодическая, задана на интервале (- , имеет конечное число точек разрыва первого рода. Производная непрерывна везде, кроме конечного числа точек разрыва первого рода.
Вывод: функция удовлетворяет условию разложения в ряд Фурье.
Так как функция симметрична относительно оси ОУ, четная, то:
1-ая гармоника
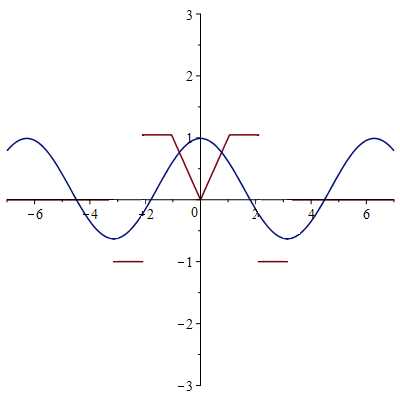
2-ая гармоника
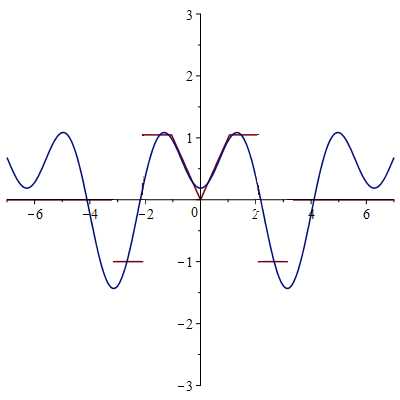
3-я гармоника
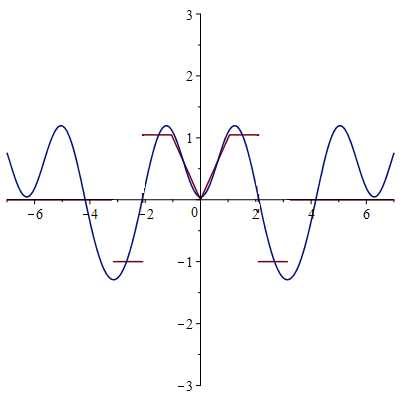
Сумма 100 гармоник
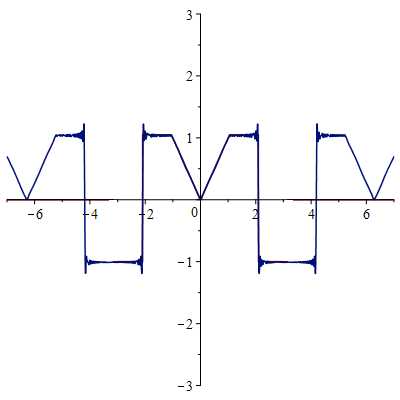
Сумма ряда в точках функции сходится к значению самой функции, в точках разрыва к величине , где х0-точка разрыва.
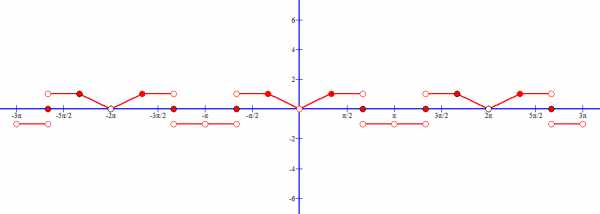
Построим амплитудный спектр:
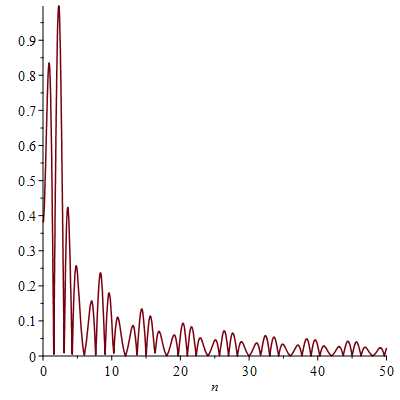
Вычислим среднеквадратическую ошибку:
Разложение в ряд Фурье функции продолженной нечетным способом
Достроим функцию на участке (-π;0):
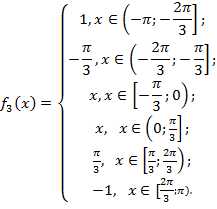
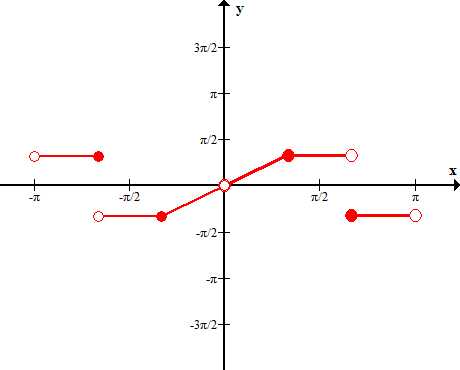
Функция непериодическая, задана на интервале (- , имеет конечное число точек разрыва первого рода. Производная непрерывна везде, кроме конечного числа точек разрыва первого рода.
Вывод: функция удовлетворяет условию разложения в ряд Фурье.
Сумма ряда в точках разрыва функции сходится к значению самой функции, а в точках разрыва к величине , где x0 – точка разрыва.
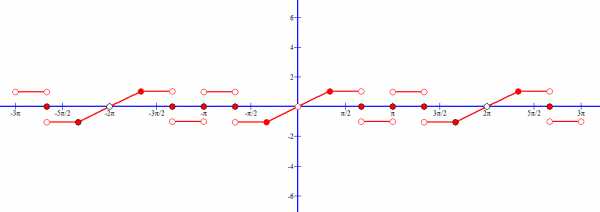
Так как присутствует симметрия относительно начала координат, то рассматриваемая функция нечетная.
1-ая гармоника
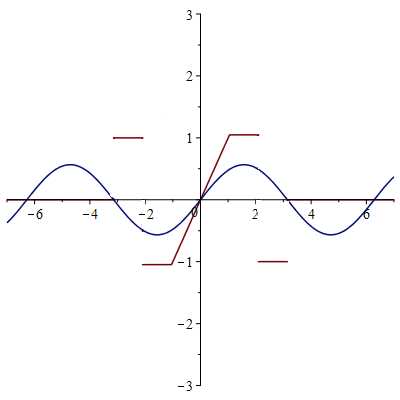
2-ая гармоника
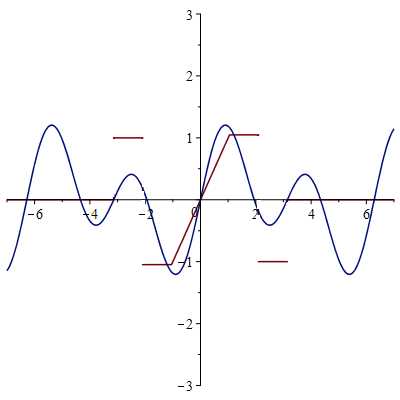
3-я гармоника
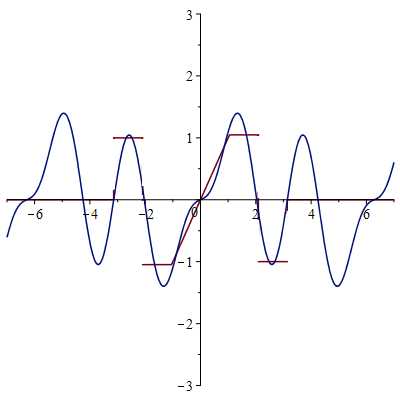
Сумма 100 гармоник
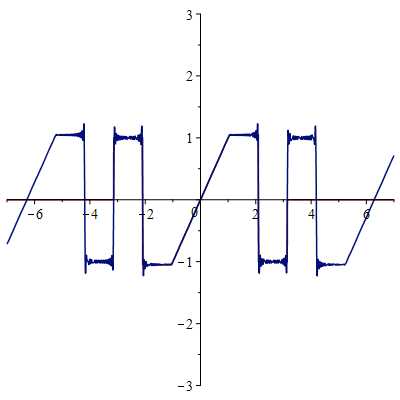
Амплитудный спектр:
Вычислим среднеквадратическую ошибку:
Вывод
Таким образом, разложение в ряд Фурье упрощает вычисление значения функции, а в некоторых случаях, это единственный способ решения.
Исходя из выполненной нами курсовой работы, видно, что при увеличении количества сумм гармоник, ряд Фурье все больше, и больше приближается к исходной функции, а в точках разрыва первого рода значение функции численно равно среднему арифметическому между левым и правым пределом.
Погрешности вычислений в каждом из способов разложения функции в ряд Фурье указывают на то, что наиболее точный график получается при разложении по косинусам, так как 0.0363972441, 0.0914397582, 0.0286996531.
Список литературы
1. Власова Е.А. Ряды. М. : МГТУ им. Н. Э. Баумана, 2000. – 612 с.
2. Демидович Б.П., Кудрявцев В.А. Краткий курс высшей математики. М.:АСТ: Астрель, 2005. – 654 с.
3. Пискунов Н.С. Дифференциальное и интегральное исчисления. Том 2. М.: Наука, 1985. – 560 с.
4. Письменный Д.Т. Конспект лекций по высшей математике. Полный курс. М.: Айрис-пресс, 2011. – 608 с.
5. http://www.mathprofi.ru/
6. http://ru.wikipedia.org
7. http://www.math34.ru/definition-of-fourier-series.html
cyberpedia.su
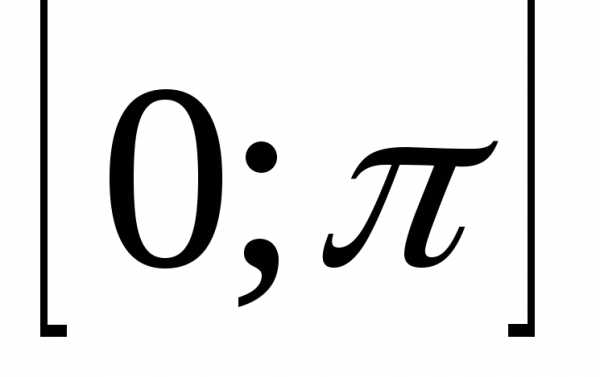