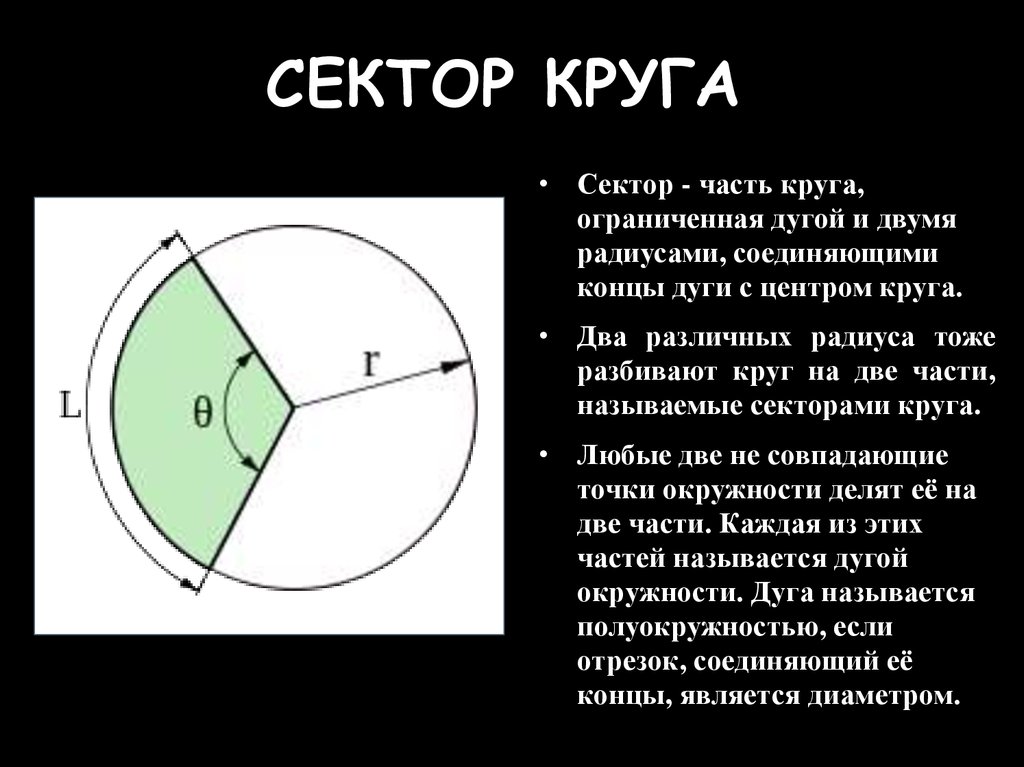
Круг: сектор, сегмент. Площадь круга, сектора и сегмента
- Площадь круга
- Сектор круга. Площадь сектора
- Сегмент. Площадь сегмента
Круг — это часть плоскости, ограниченная окружностью. Центр данной окружности называется центром круга, а расстояние от центра до любой точки окружности — радиусом круга:
O — центр круга, OA — радиус круга.
Площадь круга
Площадь круга равна произведению числа π на квадрат радиуса. Формула нахождения площади круга:
S = πr2,
где S — площадь круга, а r — радиус круга.
Так как диаметр круга равен удвоенному радиусу, то радиус равен диаметру, разделённому на 2:
| D = 2r, значит r = | D | . |
| 2 |
Следовательно, формула нахождения площади круга через диаметр будет выглядеть так:
| S = π( | D | )2 = π | D2 | = π | D2 | . |
| 2 | 22 | 4 |
Сектор круга. Площадь сектора
Сектор — это часть круга, ограниченная двумя радиусами и дугой. Два радиуса разделяют круг на два сектора:
Чтобы найти площадь сектора, дуга которого содержит n°, надо площадь круга разделить на 360 и полученный результат умножить на n.
Формула площади сектора:
| S = | πr2 | · n = | πr2n | , |
| 360 | 360 |
где S — площадь сектора. Выражение
| πr2n |
| 360 |
можно представить в виде произведения
| πr2n | = n · | πr | · | r | , |
| 360 | 180 | 2 |
| где | nπr | — это длина дуги сектора. |
| 180 |
Следовательно, площадь сектора равна длине дуги сектора, умноженной на половину радиуса:
| S = | sr | , |
| 2 |
где S — это площадь сектора, s — длина дуги данного сектора, r — радиус круга.
Сегмент. Площадь сегмента
Сегмент — это часть круга, ограниченная дугой и стягивающей её хордой. Любая хорда делит круг на два сегмента:
Площадь сегмента равна половине радиуса, умноженной на разность между дугой сегмента и половиной хорды двойной дуги.
Площадь сегмента AMB будет вычисляться по формуле:
| S = | r | (s — BC), |
| 2 |
где S — это площадь сегмента, r — радиус круга, s — длина дуги AB, а BC — длина половины хорды двойной дуги.
Площадь кругового сектора / Длина окружности и площадь круга / Справочник по геометрии 7-9 класс
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Длина окружности и площадь круга
- Площадь кругового сектора
Проведем два радиуса ОА и ОВ окружности с центром в точке О:
Мы видим, что данные радиусы делят круг на две части. Каждую из этих частей вместе с радиусами называют круговым сектором или сектором
Пусть — площадь кругового сектора радиуса , который ограничен дугой с градусной мерой . Нам известно, что площадь круга равна , значит, площадь кругового, сектора ограниченного дугой в 10, равна . Следовательно, площадь выражается формулой
Круговой сегмент (сегмент) — это часть круга, ограниченная дугой окружности и хордой, которая соединяет концы этой дуги:
В том случае когда градусная мера дуги меньше 180 0, площадь сегмента равна разности площади сектора и площади равнобедренного треугольника, сторонами которого являются два радиуса и хорда сегмента.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Правильный многоугольник
Окружность, описанная около правильного многоугольника
Окружность, вписанная в правильный многоугольник
Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности
Построение правильных многоугольников
Длина окружности
Площадь круга
Длина окружности и площадь круга
Правило встречается в следующих упражнениях:
7 класс
Задание 1126, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1127, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1128, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 12, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 13, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 21, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 22, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1250, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1290, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Сектор круга – определение, формулы, примеры
Вы, должно быть, заметили кусок круглой пиццы.
Его форма выглядит так, что в математике называется сектором круга. Например, если пиццу радиусом 10 дюймов разрезать на 6 частей, каждая часть представляет собой сектор.
Что такое сектор окружности
Сектор окружности – это часть, заключенная между двумя радиусами и дугой окружности. Обозначается символом ⌔.
Сектор кругаТипы секторов круга
Существует 2 типа секторов: малый и большой сектор. Малая дуга меньше сектора полукруга и поэтому имеет центральный угол меньше 180, а большой сектор больше полукруга и поэтому имеет центральный угол больше 180.
Типы секторов в кругеФормулы
Площадь сектора круга
Существуют три формулы для расчета площади сектора круга. Все три формулы дают один и тот же результат, но используются на основе информации, предоставленной о секторе.
Как найти площадь сектора по центральному углу в градусах
Если известен радиус и центральный угол сектора задан в градусах, формула для нахождения площади сектора приведена ниже.
Давайте решим несколько примеров, чтобы лучше понять концепцию.
Найдите площадь сектора с центральным углом 60° и радиусом 16 см. Выразите свой ответ с точностью до десятых.
Решение:
Как известно,
Площадь (A) сектора = (θ/360°) × πr 2 , здесь θ = 60°, r = 16 см, π = 3,141
= (60° /360°) × 3.141 × (16) 2
= 3.141 × 16 × 16/60
= (50.25 × 0.26) cm 2
= 13.06 cm 2
Calculate the area of сектор радиусом 20 ярдов и углом 90 градусов.
Решение:
Как мы знаем,
Площадь (A) сектора = (θ/360°) × πr 2 , здесь θ = 90°, r = 20 ярдов, π = 3,141
= (90°/360°) × 3,141 × (20) 2
= (1256,4/4) ярдов 2 = 9304,5 ярдов 2
Найдите радиус полукруга площадью 24 квадратных дюйма.
Решение:
Полукруг есть половина круга; следовательно, угол θ = 180 градусов.
Как известно,
Площадь (A) сектора = (θ/360°) × πr 2 , A = 24 квадратных дюйма, здесь θ = 180°, π = 3,141
24 = (180°/360°) × 3,141 × r 2
24 = 3,141 × r 2 /2
r 2 = 48/3,141 = 15,28 дюйма Как найти площадь сектора 0
9 Учитывая центральный угол в радианах
Если радиус известен, а центральный угол сектора задан в радианах, формула для нахождения площади сектора приведена ниже.
Площадь сектора круга ФормулаДавайте решим несколько примеров, чтобы лучше понять концепцию.
Найдите площадь сектора радиусом 8 м и центральным углом 0,62 радиана.
Решение:
Как известно,
Площадь (A) сектора = (θr 2 )/2, здесь θ = 0,62 радиан, r = 8 м
= 0,62 × 8 × 8/2
= 19,84 м 2
Площадь сектора 225 м 2 .
Если радиус сектора равен 8 м, найдите центральный угол сектора в радианах.
Решение:
Как известно,
Площадь (A) сектора = (θr 2 )/2, здесь A = 225,r = 8 м
225 = θ × 8 × 8/2
θ =225 × 2/64
θ = 7,031 радиан
Как найти площадь сектора по длине дуги
Если радиус и длина дуги известны, формула для нахождения площади сектора приведена ниже.
Сектор круга ФормулаДавайте решим несколько примеров, чтобы лучше понять концепцию.
Длина дуги 64 мм. Найдите площадь сектора, образованного дугой, если радиус окружности равен 15 мм.
Решение:
Как известно,
Площадь (А) сектора = r × L/2, здесь r = 15 мм, L = 64 мм
= (15 × 64/2) мм 2
= 480 мм 2
Найдите площадь сектора, длина дуги которого равна 10 дюймам, а радиус — 6 дюймам.
Решение:
Как мы знаем,
Площадь (A) сектора = r × L/2, здесь r = 6 дюймов, L = 10 дюймов
= (6 × 10/2) дюймов 2
= 30 дюймов 2
Периметр сектора круга
Периметр сектора круга представляет собой общую длину двух радиусов и дуги, образующей сектор.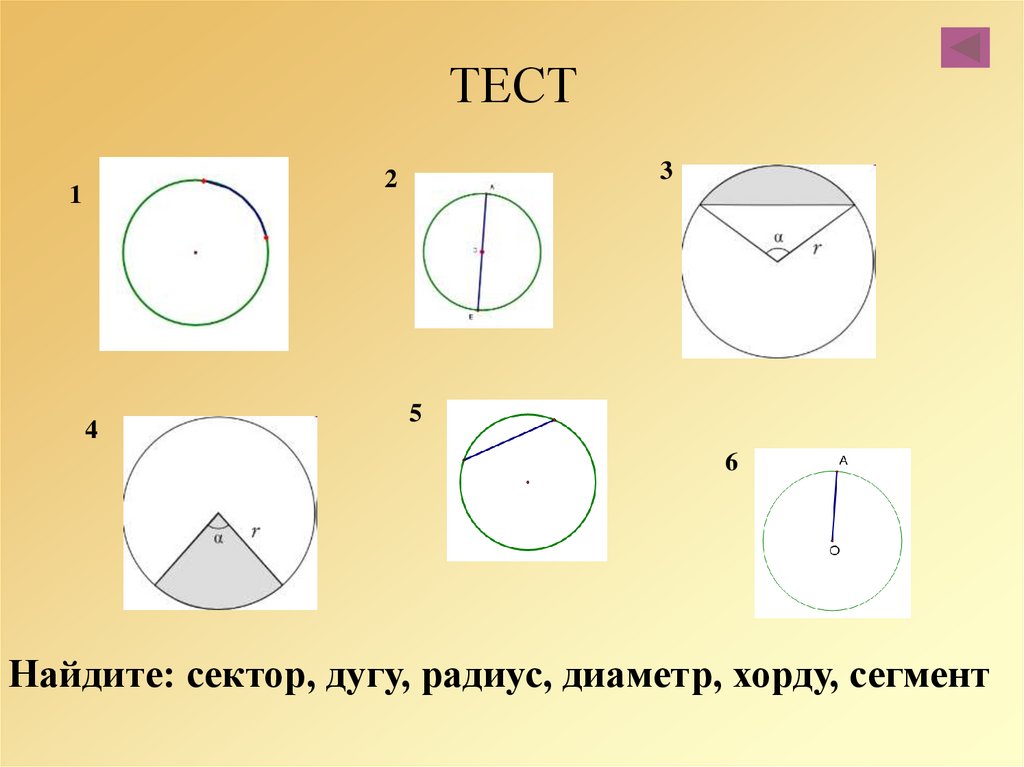
Формула для расчета периметра сектора приведена ниже.
Вывод
Периметр (P) сектора = радиус (r) + радиус (r) + длина дуги (L)
= 2 радиуса (r) + длина дуги (L)
= 2r + L
Периметр сектора окружностиПоскольку длина дуги рассчитывается по соотношению
Длина дуги (L) = (θ/360) × 2πr
Таким образом, приведенную выше формулу также можно записать в виде:
Периметр (P) сектора = 2r + [(θ/360) × 2πr] , здесь r = радиус, θ = центральный угол в радианах, π = 3,141 = 22/7
Давайте решим несколько примеров, чтобы лучше понять концепцию.
Дуга окружности радиусом 14 см образует дугу длиной 6 см. Найдите периметр образовавшегося сектора.
Решение:
Как известно,
Периметр (P) сектора = 2r + L, здесь r = 14 см, L = 6 см
= (2 × 14) + 6
= 34 см периметр сектора круга радиусом 22 см и углом 30° в центре.
Решение:
Как известно,
Периметр (P) сектора = 2r + [(θ/360) × 2πr], здесь r = 22 см, θ =30°, π = 3,141
= ( 2 × 22) + [(30/360) × 2 × 3,141 × 22]
= (44 + 11,51) см
= 55,51 см
Площадь сектора — тригонометрия
Все ресурсы по тригонометрии
6 Диагностические тесты 155 практических тестов Вопрос дня Карточки Learn by ConceptПомощь по тригонометрии » Угловые приложения » Площадь сектора
Что из следующего является определением сектора круга?
Возможные ответы:
Любое сечение окружности
Сечение окружности, ограниченное хордой и дугой хорды
Любая часть круга треугольной формы
Часть круга, окруженная двумя радиусами, соединенными в центре круга, и дугой между двумя радиусами
Правильный ответ:
Часть круга, окруженная двумя радиусами, соединенными в центре круга, и дугой между двумя радиусами
Пояснение:
Ниже приведено изображение сектора круга.
Сообщить об ошибке
Какая из следующих формул является формулой площади сектора?
Возможные ответы:
Правильный ответ:
Пояснение:
Думая о том, как вывести формулу для сектора, мы должны учитывать угол всего круга. Угол всего круга, 360 градусов, и мы знаем, что площадь круга равна .
При рассмотрении сектора это только часть всего круга, поэтому он является отдельным из всего . Мы можем подключить это к нашей площади круга, и она упростится до площади сектора.
Сообщить об ошибке
Если в круге есть сектор с углом и диаметром 4, какова площадь сектора?
Возможные ответы:
Правильный ответ:
Объяснение:
Всегда лучше нарисовать картинку, чтобы визуализировать проблему, которую вы пытаетесь решить.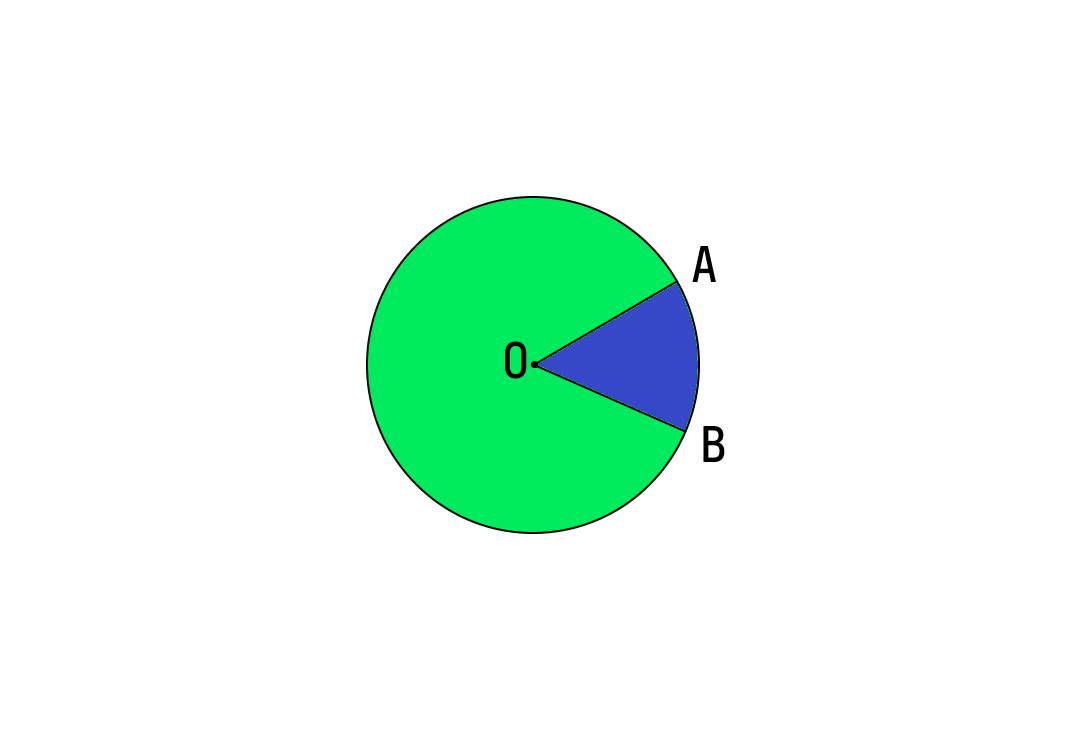
На рисунке ниже показан сектор, площадь которого мы пытаемся найти.
Мы знаем, что формула для нахождения площади сектора . Из приведенной выше информации мы знаем, что диаметр равен 4. Поскольку для нашей формулы нам нужен только радиус, мы делим диаметр на 2, чтобы получить длину радиуса. Радиус имеет длину 2. Мы также знаем, что у нас есть мера угла в градусах, и мы должны преобразовать его в радианы. Воспользуемся формулой преобразования.
Теперь мы можем подставить все в нашу формулу и решить.
Сообщить об ошибке
Возможные ответы:
Верно
Неверно
Правильный ответ:
Верно
Объяснение:
Это неправда.
Конвертирование 330 градусов в радиан:
Теперь мы можем подключить это к нашей формуле
9024. сектора, образованного
площадь остатка, образованная острым углом 30 градусов. Для этого сначала найдем общую
площадь круга, а затем вычтем площадь сектора, образованного острым углом. Это должно быть равно площади большего вектора, если наша формула работает для всех углов, потому что сумма обоих секторов должна быть общей площадью круга.
Чтобы найти площадь круга:
Чтобы найти площадь меньшего сектора (обратите внимание, 30 градусов в радианах:
Ясно, что общая площадь круга за вычетом площади малого сектора равна площади
большего круга, поэтому эта формула работает для всех углов, меньших2
9000
Сообщить об ошибке
Зная, что длина дуги сектора и мера угла равны , какова площадь сектора?
Возможные ответы:
Правильный ответ:
Пояснение:
Чтобы решить эту задачу, мы должны знать формулу для нахождения длины дуги сектора.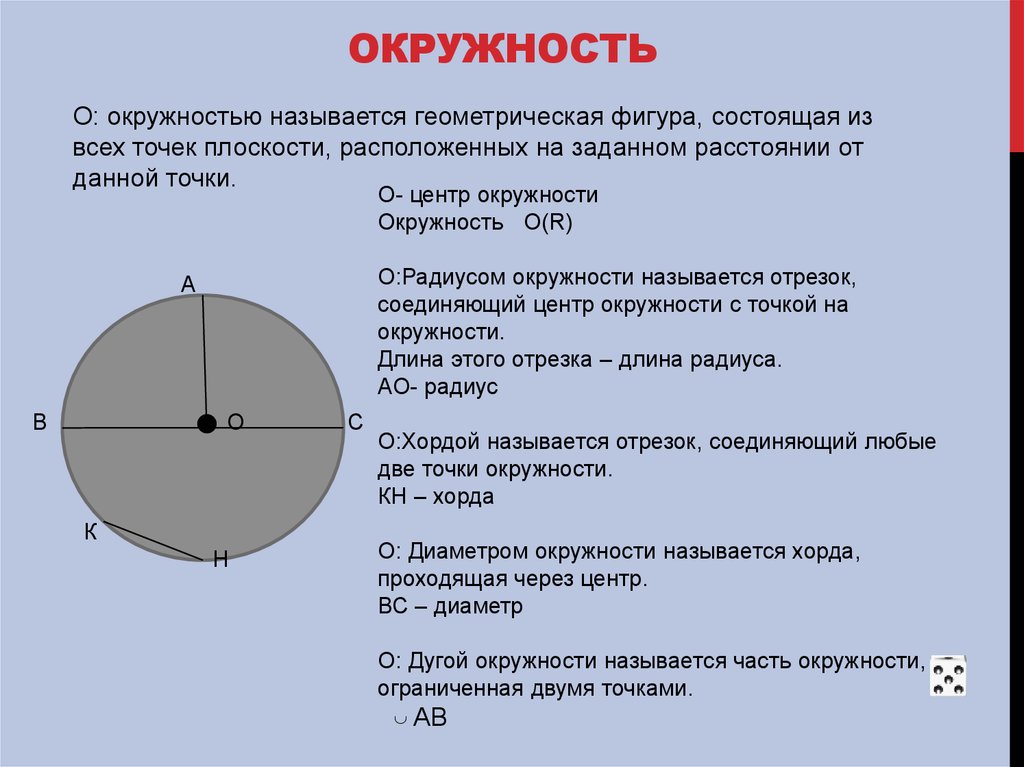
Эта формула есть. Имея данную информацию, мы можем определить радиус, который затем можно использовать для определения площади самого сектора.
Теперь мы можем подставить этот радиус в формулу для определения площади сектора.
Сообщить об ошибке
Верно или неверно: у вас есть сектор круга, радиус круга и общая площадь круга. Вы можете найти площадь сектора.
Возможные ответы:
Верно
Неверно
Правильный ответ:
Неверно
Объяснение:
Формула для нахождения площади круга . Если мы знаем радиус и площадь всей окружности, мы все равно не знаем ни угла, образующего сектор, ни длины дуги. Поэтому у нас недостаточно информации для определения площади сектора.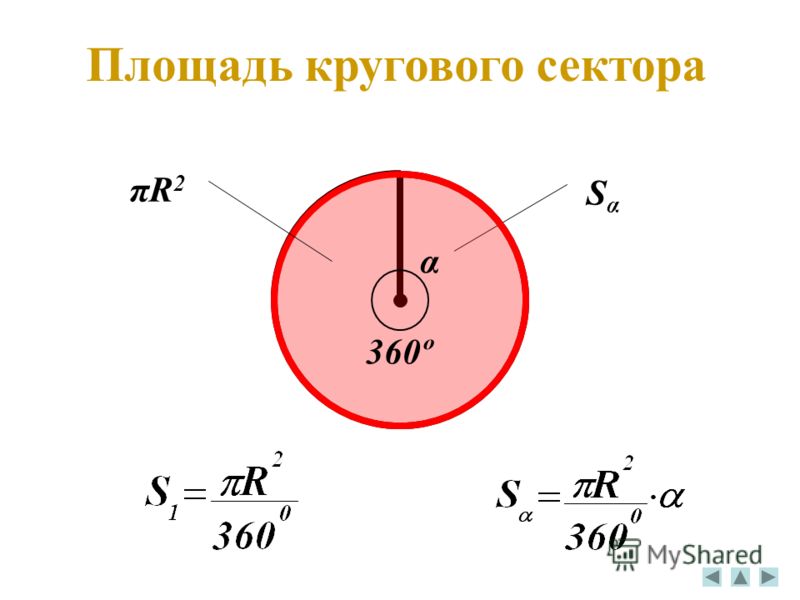
Чтобы найти площадь сектора, нам нужно либо знать угол сектора и радиус, либо иметь какие-то средства для решения этой информации.
Сообщить об ошибке
Круг имеет сектор, образованный радиусами длиной 3 и углом . Какова площадь сектора?
Возможные ответы:
Правильный ответ:
Объяснение:
Формула для определения площади сектора: . У нас есть вся информация, необходимая для того, чтобы подставить значения прямо в формулу и найти площадь.
Сообщить об ошибке
Вам дан круг с сектором, образованным дугой длиной . Круг имеет диаметр 20. Какова площадь сектора?
Возможные ответы:
Правильный ответ:
Объяснение:
Во-первых, если у нас есть диаметр 20, мы знаем, что радиус должен быть половиной диаметра.