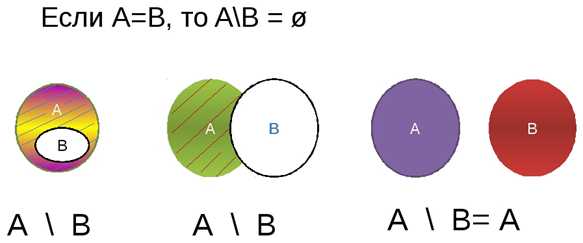
Разность множеств. Дополнение множества.
Множества и его элементы
УРОК 7 РАЗНОСТЬ МНОЖЕСТВ. ДОПОЛНЕНИЕ МНОЖЕСТВА.
Цель: Ввести понятие «разности» множеств и соответствующие им графические модели в виде кругов Эйлера. Ввести обозначение разности множеств. Знакомство с универсальным множеством и дополнением множества.
Повторение, проверка д/з:
Что обозначает слово «множество»?
Что мы называем элементом множества?
Что бывает элементами множества?
Как различают множества по числу элементов?
Какими способами можно задать множество? (перечисление элементов, характеристическое свойство)
Какое свойство называется характеристическим свойством?
Какие множества называются равными?
Какие математические «иероглифы» мы используем для сокращенной записи?
Что такое подмножество?
Что такое круги Эйлера? Зачем они? (Круги Эйлера – геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления)
Что такое объединение множеств? Знак объединения.
Что такое пересечение множеств? Знак пересечения.
Решить упражнение 1, 2, 3, 4. Проверить упражнения 1, 2 из д/з.
Проверить упражнение 3 из д/з (все предложенные детьми варианты решений)
Проверить упражнения из домашнего задания:
Даны множества: А = {a; b; c; d}, В = {c; d; e; f} и С = {c; e; q; k}.
Найти: (А ∪ В) ∪ С.
А – множество четных натуральных чисел, В – множество двузначных чисел. Составьте характеристическое свойство пересечения этих множеств. Приведите примеры элементов этого множества.
Решение: А ∩ В — множество четных натуральных чисел и двузначных чисел. Примеры 42, 86, 12, 32, 50 и т.д.

Каждый учащийся в классе изучает английский или французский язык. Английский язык изучают 25 учащихся, французский — 27 учащихся, а два языка — 18 учащихся. Сколько учащихся в классе?
Решение:

Упражнение 1: Составить рассказ по рисунку:

Упражнение 2: Даны множества А = {1; 2; 3}, В = {3; 4; 5} и С = {3; 6; 7}. Найти объединение и пересечение этих множеств. Изобразите решение с помощью кругов Эйлера.
Решение: А ∪ В ∪ С = {1; 2; 3; 4; 5; 6; 7}, А ∩ В ∩ С = {3}.
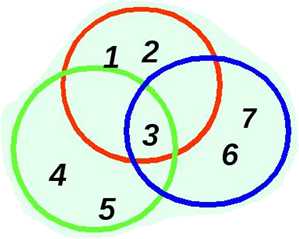
Упражнение 3: Показать фигуру, которая является пересечением геометрических фигур на рисунке:
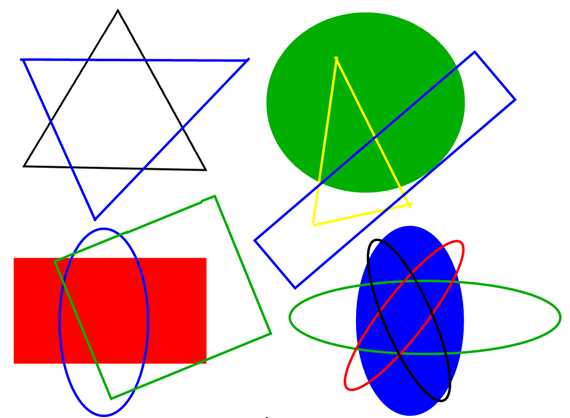
Упражнение 4: Расположи 4 элемента в двух множествах так, чтобы в каждом из них было по три элемента.(круги Эйлера)
Решение:
Открытие нового знания: РАЗНОСТЬ МНОЖЕСТВ. ДОПОЛНЕНИЕ МНОЖЕСТВА.
Если заданы два множества, то можно не только найти их пересечение и объединение, но и вычесть из одного множества другое. Результат вычитания, как вам известно, называют разностью.
Попытаемся найти разность двух множеств.
Упражнение 1: Даны два множества: A = {1,2,3,4,5} и B = {4,5,8,9}. Найти разность множества А и множества В.
Ответ: {1,2,3}.
Из всех ваших ответов выберем правильный — {1,2,3}.
Проанализируйте множества А и В и разность А и В. Попытайтесь дать определение разности двух множеств.
Разностью множеств А и В называют множество, состоящее из тех и только тех элементов множества
А, которые не принадлежат множеству В.Или:
Разностью двух множеств является третье множество, которое содержит элементы 1-го множества, не входящие во 2-е множество.
Или:
Разностью двух множеств называют третье множество, в которое входят все элементы одного из двух множеств и не входят элементы принадлежащие обоим множествам.
Обозначают: А \ В или А – В.
Вернемся к упражнению 1: А \ В = {1,2,3}.
Как составить множество – разность? Можно пользоваться терминами «уменьшаемое», «вычитаемое».
Чтобы составить множество-разность надо записать множество, содержащее все элементы множества-уменьшаемого, которые не содержатся в множестве-вычитаемом, т.е. из множества-вычитаемого изъять все элементы, входящие в множество-вычитаемое.
Используя данные упражнения 1, найдем теперь разность множеств В и А: В / А = {8; 9}.
Сравниваем разности: А \ В = {1,2,3} и В / А = {8; 9}. Вывод?
Совершенно верно: Если результат пересечения и объединения двух множеств не меняется от перестановки множеств при выполнении операции, то результат разности зависит от того, какое множество из какого «вычитают». Поэтому: А \ В ≠ В / А.
Вывод: Операция разности определяется только для двух множеств. Эта операция двухместная и не коммутативная.
Изображение с помощью кругов Эйлера:
Найди ошибку на рисунке:
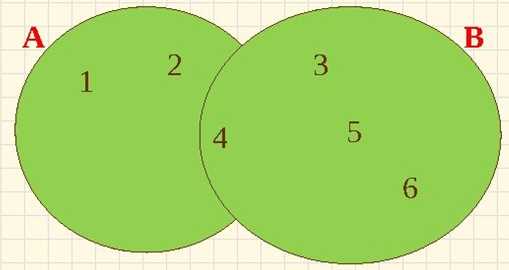
(Число 3 должно стоять в части пересечения множеств, т.к. принадлежит обоим множествам)
Упражнение 2: Даны два множества: A = {1,2,5} и B = {3, 4}. Найти разность множества А и множества В.
Ответ: А – В = {1,2,5} = А.
Проанализируйте разность и данные множества и сделайте вывод.
Правильно, у данных множеств нет одинаковых элементов (т.е. множества не пересекаются). Их разностью является множество-уменьшаемое.
Таким образом, если у множеств нет общих элементов, то их разность будет равна «уменьшаемому», т. е. первому множеству.
А / В = А
Упражнение 3: Даны два множества: A = {1,2} и B = {1, 2, 3, 4}. Найти разность множества А и множества В.
Ответ: А – В = .
Проанализируйте разность и данные множества и сделайте вывод.
Действительно, если элементы множества-уменьшаемого полностью совпадают с элементами множества-вычитаемого, то их разностью будет пустое множество.
Упражнение 4: Даны два множества: A = {1,2, 3, 4, 5} и B = {1, 2, 3}. Найти разность множества А и множества В.
Ответ: А / В = {4, 5}.
Проанализируйте разность и данные множества и сделайте вывод.
Верно: множество В является подмножеством множества А.
Если все элементы «вычитаемого» множества B входят в состав «уменьшаемого» A (A \ B), то B называют дополнением некоторого множества C (на рисунке оно желтого цвета) до A.
Если множество В – подмножество множества А (В ⊂ А), то разность А / В называется дополнением множества В до множества А.
Обозначают: (на рисунке оно желтого цвета)
Свойства дополнения:
Как мы уже видели, роль нуля в алгебре множеств играет пустое множество. Определим множество, которое будет играть роль единицы в алгебре множеств – УНИВЕРСАЛЬНОЕ МНОЖЕСТВО.
Что же это такое?
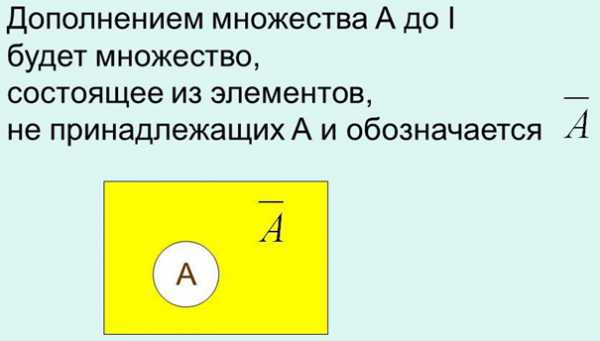
Множество U, такое, что все рассматриваемые множества являются его подмножествами, называется универсальным.
U
То есть это множество, которое по предположению содержит все используемые нами множества. Обозначается не кругом, а прямоугольником .
Пример: Множества: {звездные скопления}, {черные дыры}, {планеты} являются подмножествами универсального множества {вселенная}.
Множество U \ A называется дополнением множества A (до универсального множества) и обозначается через .
Дополнением множества А называется разность между универсальным множеством и множеством А:
= U \ A
На кругах Эйлера это определение представлено на предыдущем рисунке.
Также можно сказать, что универсальным множеством U (основным множеством) называется множество, для которого все множества, рассматриваемые в данный момент, являются подмножествами.
Например, для N универсальным считается множество Z.
Вычитание множеств обладает рядом свойств:
1. (А \ В) \ С = (А \ С) \ В.
2. (А U В) \ С = (А \ С) U (В \ С).
3. (А \ В) ∩ С = (А ∩ С) \ (В ∩С).
4. А \ (В U С) = (А \ В) ∩ (А \ С).
5. А \ (В ∩ С) = (А \ В) U (А \ С).
Подведение итогов урока, рефлексия
Мне больше всего удалось…
Для меня было открытием то, что …
За что ты можешь себя похвалить?
Что на ваш взгляд не удалось? Почему? Что учесть на будущее?
Мои достижения на уроке.

Домашнее задание: конспект, упражнения:
Найти разность множеств: К = {1; 2; 3; 7; 8; 9} и М = {0; 2; 8}. Решение: К \ М = {1; 3; 7; 9}.
Даны множества: А = {a; b; c; d}, В = {c; d;} .
Найти: а) А \ В; б) В \ А; в) (А \ В) ∪ (В \ А). Решение: а) А \ В = {a; b}; б) В \ А = ; в) (А \ В) ∪ (В \ А) = {a; b} ∪ = {a; b}.
Каждая семья, живущая в нашем доме выписывает или газету, или журнал, или и то и другое вместе. 75 семей выписывают газету, а 27 семей выписывают и газету, и журнал. Сколько семей живет в нашем доме?
vseosvita.ua
разность множеств — ПриМат
Операции на множествах
1. Объединение
Объединение двух множеств:
Пусть даны два множества и тогда их объединением называется множество содержащее в себе все элементы
исходных множеств:
Объединение более чем двух множеств:
Пусть дано семейство множеств тогда его
Пересечение
Пусть даны два множества и , тогда их пересечением называется множество , которому принадлежат те и только те элементы, которые одновременно принадлежат двум множествам:
3.Разность
Пусть даны два множества и , тогда их разностью называется множество , содержащее в себе элементы , но не :
4.Симметрическая разность
Пусть даны два множества и тогда их симметрической разностью называется множество , куда входят все те элементы первого множества, которые не входят во второе множество, а, также те элементы второго множества, которые не входят в первое множество:
5.Дополнение
Пусть дано множество его дополнением называется семейство элементов, не принадлежащие данному множеству:
Свойства операций
Пусть — произвольные множества, тогда:
1. Операция объединение множеств коммутативна:
2. Операция объединение множеств ассоциативна:
3. Операция пересечение множеств коммутативна:
4. Операция пересечения множеств ассоциативна:
5.
6.
7.
8.
9.
10.
11. Симметрическая разность коммутативна:
12. Симметрическая разность ассоциативна:
Примеры
1. Пусть тогда
2. Пусть , тогда
3. Пусть тогда
4. Пусть тогда
Литература:
Операции на множествах. Свойства операций.
Лимит времени: 0
Информация
Тестовые вопросы по выше изложенному материалу
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
Правильных ответов: 0 из 7
Ваше время:
Время вышло
Вы набрали 0 из 0 баллов (0)
| Средний результат |
|
| Ваш результат |
|
| Место | Имя | Записано | Баллы | Результат |
|---|---|---|---|---|
| Таблица загружается | ||||
| Нет данных | ||||
- С ответом
- С отметкой о просмотре
Задание 1 из 7
Поставьте в соответствие:
- $$ \left\{ x\,|\,x \in A \vee x \in B \right\} $$
- $$ \left\{ x\,|\,x \in A \wedge x \in B \right\} $$
- $$ \left\{\,x\, \in A\,|\,x\,\not\in B \right\} $$
- $$ (A \setminus B) \cup (B \setminus A) $$
Симметрическая разность
Задание 2 из 7
Укажите ошибочную формулировку:
Задание 3 из 7
Пусть , , . Расположить в порядке возрастания по количеству элементов в получившемся множестве:
$$ A\Delta B \Delta C $$
$$ A\setminus B $$
$$ A\cup B $$
Задание 4 из 7
Вставьте пропущенные слова:
Задание 5 из 7
Пусть , ,
, тогда =
- $$ \left\{ 1, 3, 6, 8, 12 \right\} $$
- $$ \left\{ 2, 4, 5, 9 \right\} $$
- $$ \left\{ 1, 2, 3, 5, 6, 8 \right\} $$
- $$ \left\{ 1, 2, 5, 6, \right\} $$
Задание 6 из 7
Пусть , ,
, тогда
- $$ \left\{ 1, 2, 3, 5, 6 \right\} $$
- $$ \left\{ 3, 4, 5, 8 \right\} $$
- $$ \left\{ 5, 6, 8, 9 \right\} $$
- $$ \left\{ 1, 2, 4, 7 \right\} $$
Задание 7 из 7
Пусть дано множество , семейство элементов, не принадлежащему данному множеству, называется его
Поделиться ссылкой:
ib.mazurok.com
Тема 2.3 Операции над множествами.
1 ВОПРОС:Множеством называется совокупность некоторых элементов, объединенных каким-либо общим признаком. Элементами множества могут быть числа, фигуры, предметы, понятия и т.п.
Множества обозначаются прописными буквами, а элементы множество строчными буквами. Элементы множеств заключаются в фигурные скобки.
Если элемент x принадлежит множеству X, то записывают x ∈ Х (∈ — принадлежит). Если множество А является частью множества В, то записывают А ⊂ В (⊂ — содержится).
Определение 1 (определение равенства множеств). Множества А и B равны, если они состоят из одних и тех же элементов, то есть, если из x A следует x B и обратно, из x B следует x A.
Формально равенство двух множеств записывается следующим образом:
(А=В):= x((x A) (x B)),
это означает, что для любого объекта x соотношения x A и x B равносильны.
Здесь – квантор всеобщности ( x читается как «для каждого x«).
Подмножество
Определение: Множество Х является подмножеством Y, если любой элемент множества Х принадлежит множеству Y. Это еще называется нестрогим включением.Некоторые свойства подмножества:
1. ХХ — рефлективность
2. X Y & YZ X Z — транзитивность
3. X т.е. пустое множество является подмножеством любого множества.Универсальное множествоОпределение: Универсальное множество — это такое множество, которое состоит из всех элементов, а так же подмножеств множества объектов исследуемой области, т.е.
1. Если М I , то М I
2. Если М I , то Ώ(М) I , где под Ώ(М) — понимаются все возможные подмножества М, или Булеан М.
Универсальное множество обычно обозначается I.
Универсальное множество может выбираться самостоятельно, в зависимости от рассматриваемого множества, и решаемых задач.
Способы задания множеств:
1. путем перечисления его элементов. Обычно перечислением задают конечные множества.
2. путем описания свойств, общих для всех элементов этого множества, и только этого множества. Это свойство называетсяхарактеристическим свойством, а такой способ задания множества описанием. Таким образом, можно задавать как конечные, так и бесконечные множества. Если мы задаем множество каким-либо свойством, потом может оказаться, что этим свойством обладает всего лишь один объект или вообще такого объекта нет. Данный факт может быть совсем не очевиден.
Теперь определим операции над множествами.
1. Пересечение множеств.
Определение: Пересечением множеств Х и У называется множество, состоящее из всех тех, и только тех элементов, которые принадлежат и множеству Х и множеству У.
Например: Х={1,2,3,4} У={2,4,6} пересечением {2,4}
Определение: Множества называются непересекающимися, если не имеют общих элементов, т.е. их пересечение равно пустому множеству.
Например: непересекающимися множествами являются множества отличников группы и неуспевающих.
Данную операцию можно распространить и на большее чем два число множеств. В этом случае это будет множество элементов, принадлежащих одновременно всем множествам.
Свойства пересечения:
1. X∩Y = Y∩X — коммутативности
2. (X∩Y) ∩Z =X∩ (Y∩Z)=X∩Y∩Z — ассоциативности
3. X∩ =
4. X∩I = Х
2. Объединение множеств
Определение: Объединением двух множеств называется множество, состоящее из всех и только тех элементов, которые принадлежат хотя бы одному из множеств Х или У.
Например: Х={1,2,3,4} У={2,4,6} объединением {1,2,3,4,6}
Данную операцию можно распространить и на большее чем два число множеств. В этом случае это будет множество элементов, принадлежащих хотя бы одному из этих множеств.
Свойства объединения:
1. XUY= YUY- коммутативности
2. (X UY)UZ =XU (YUZ)=XUYUZ — ассоциативности
3. XU = X
4. XUI = I
Из свойств операций пересечения и объединения видно, что пустое множество аналогично нулю в алгебре чисел.
3. Разность множеств
Определение: Данная операция, в отличие от операций пересечения и объединения определена только для двух множеств. Разностью множеств Х и У называется множество, состоящее их всех тех и только тех элементов, которые принадлежат Х и не принадлежат У.
Например: Х={1,2,3,4} У={2,4,6} разность {1,3}
Как мы уже видели, роль нуля в алгебре множеств играет пустое множество. Определим множество, которое будет играть роль единицы в алгебре множеств
4. Дополнение множества
Дополнением множества Х называется разность I и Х.
Свойства дополнения:
1. Множество Х и его дополнение не имеют общих элементов
2.Любой элемент I принадлежит или множеству Х или его дополнению.
2 ВОПРОС Множества чисел
Натуральные числа − числа, используемые при счете (перечислении) предметов: N={1,2,3,…}
Натуральные числа с включенным нулем − числа, используемые для обозначения количества предметов: N0={0,1,2,3,…}
Целые числа − включают в себя натуральные числа, числа противоположные натуральным(т.е. с отрицательным знаком) и ноль. Целые положительные числа: Z+=N={1,2,3,…} Целые отрицательные числа: Z−={…,−3,−2,−1} Z=Z−∪{0}∪Z+={…,−3,−2,−1,0,1,2,3,…}
Рациональные числа − числа, представляемые в виде обыкновенной дроби a/b, где a и b − целые числа и b≠0. Q={x∣x=a/b,a∈Z,b∈Z,b≠0} При переводе в десятичную дробь рациональное число представляется конечной или бесконечной периодической дробью.
Иррациональные числа − числа, которые представляются в виде бесконечной непериодической десятичной дроби.
Действительные (вещественные) числа − объединение рациональных и иррациональных чисел: R
Комплексные числа C={x+iy∣x∈Rиy∈R}, где i − мнимая единица.
Модуль действительного числа и свойства
Модуль действительного числа — это абсолютная величина этого числа.
Попросту говоря, при взятии модуля нужно отбросить от числа его знак.
Модуль числа a обозначается |a|. Обратите внимание: модуль числа всегда неотрицателен: |a|≥ 0.
|6| = 6, |-3| = 3, |-10,45| = 10,45
studfiles.net
Разность множеств
Не следует путать с Симметрической разностью.Разность двух множеств — теоретико-множественная операция, результатом которой является множество, в которое входят все элементы первого множества, не входящие во второе множество.Обычно разность множеств A{\displaystyle A} и B{\displaystyle B} обозначается как A∖B{\displaystyle A\setminus B},но иногда можно встретить обозначение A−B{\displaystyle A-B} и A∼B{\displaystyle A\sim B}.
Пусть A{\displaystyle A} и B{\displaystyle B} — два указанных в определении множества, тогда их разность определяется (на теоретико-множественном языке):
- A
www.wikiplanet.click
1.1.4 Операции над множествами
В результате операций над множествами из одних множеств могут получаться другие множества. Основные из этих операций – объединение, пересечение и дополнение множеств. Кроме того, часто применяются операции разности и симметрической разности множеств.
Объединение множеств. Пусть заданы множества A и В. Объединение этих множеств – множество, состоящее из всех тех и только тех элементов, которые принадлежат или множеству A, или множеству B (т.е. хотя бы одному из них). Объединение двух множеств обозначают как .
Аналогично
определяется объединение нескольких
множеств. Пусть даны множества
.
Их объединение — множество, состоящее
из всех тех и только тех элементов,
которые принадлежат хотя бы одному из
этих множеств. Операция объединения в
этом случае обозначается как,
или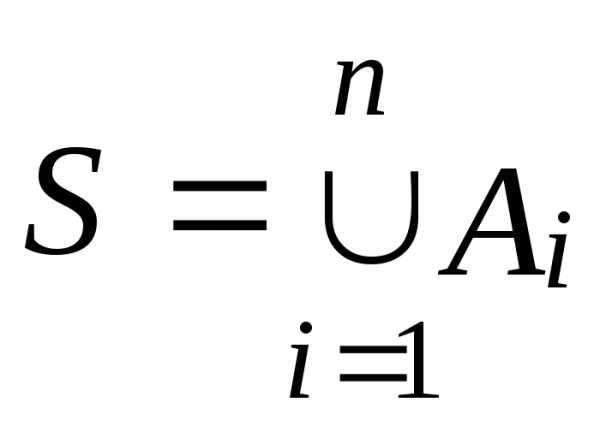 .
.
Пересечение множеств. Пусть заданы множества A и В. Пересечение этих множеств – множество, состоящее из всех тех и только тех элементов, которые принадлежат и множеству A, и множеству B (т.е. обоим множествам сразу). Пересечение двух множеств обозначают как .
Аналогично
определяется пересечение нескольких
множеств. Пусть даны множества
.
Их пересечение — множество, состоящее
из всех тех и только тех элементов,
которые принадлежат всем этим множествам
сразу. Операция пересечения в этом
случае обозначается как,
или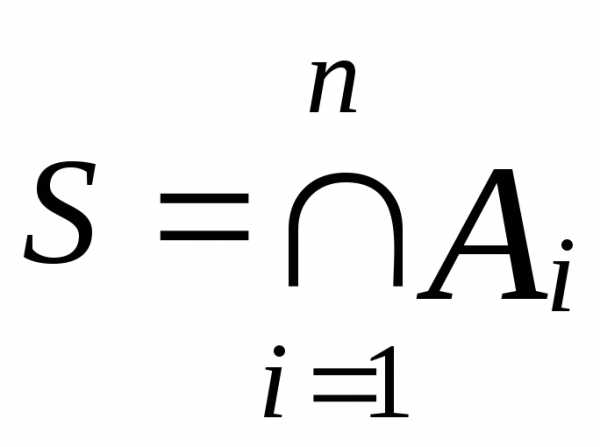 .
.
Дополнение
множества.
Пусть задано множество A.
Дополнение этого множества – множество,
состоящее из всех тех и только тех
элементов, которые не принадлежат
множеству A.
Дополнение множества обозначают как  .
.
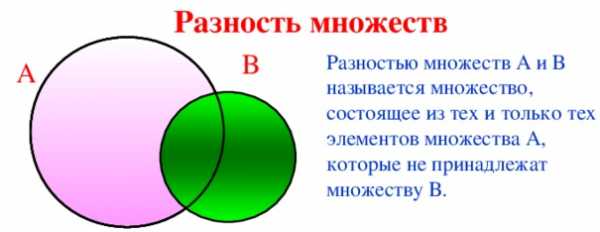
Разность множеств. Пусть заданы множества A и В. Разность этих множеств – множество, состоящее из всех тех и только тех элементов, которые принадлежат множеству A, но не принадлежат множеству B. Разность множеств обозначают как S = A \ B.
Симметрическая разность множеств. Пусть заданы множества A и В. Симметрическая разность этих множеств – множество, состоящее из всех тех и только тех элементов, которые принадлежат или множеству A, или множеству B, но не им обоим сразу. Симметрическую разность множеств обозначают как S = A B.
Следует обратить внимание, что операции пересечения и объединения выполняются с несколькими множествами (двумя или более), а операция дополнения – с одним множеством. Операции разности и симметрической разности выполняются с двумя множествами.
Операции разности и симметрической разности можно выразить через операции пересечения, объединения и дополнения:
, (1.1)
. (1.2)
Эти равенства можно доказать на основе определений операций над множествами.
Пример 1.1 – Даны множества: A = {2, 7, 9, 12}, B = {3, 6, 7, 12, 15}. Выполнить над этими множествами операции, рассмотренные выше.
A B = {7, 12}
A B = {2, 3, 6, 7, 9, 12, 15}
A \ B = {2, 9}
B \ A = {3, 6, 15}
A B = {2, 3, 9, 15}.
Чтобы найти
дополнения множеств A и B,
необходимо уточнить, что в данной задаче
имеется в виду под универсальным
множеством. Пусть под ним имеется в виду
все множество целых чисел (обозначим
его как Z).
Тогда дополнение множества A можно записать как  = {a | a Z, a A}.
Аналогично записывается дополнение
множества B:
= {a | a Z, a A}.
Аналогично записывается дополнение
множества B:  = {b | b Z, b B}.
= {b | b Z, b B}.
Примечания
1Числа во множествах записаны по возрастанию только для удобства. На самом деле, порядок элементов во множествах безразличен. Поэтому, например, пересечение множествAиBможно записать и как {7, 12}, и как {12, 7}.
2Следует обратить внимание, что в операциях пересечения, объединения, а также симметрической разности порядок множеств, с которыми выполняется операция, безразличен:,,AB=BA. Говорят, что эти операции обладают свойством коммутативности. В то же времяA\BB\A.
Пример 1.2 – Даны множества: A = {a | 5 a < 20}, B = {b | b 17}, C = {c | 10 < c 12}. Приведем некоторые примеры операций над этими множествами:
X = AB = {x | 5 x 17}
X = AB = {x | x < 20}
X = A \ B = {x | 17 < x < 20}
X = B \ A = {x | x < 5}
X = AC = {x | 10 < x 12}
X = AC = {x | 5 x < 20}
X = A \ C = {x | 5 x 10 или 12 < x < 20}
X = C \ A =
X =  = {x | x < 5 или x
20}
= {x | x < 5 или x
20}
X =  = {x | x
17}.
= {x | x
17}.
studfiles.net
Разность множеств Википедия
Разность двух множеств — теоретико-множественная операция, результатом которой является множество, в которое входят все элементы первого множества, не входящие во второе множество. Обычно разность множеств A{\displaystyle A} и B{\displaystyle B} обозначается как A∖B{\displaystyle A\setminus B}, но иногда можно встретить обозначение A−B{\displaystyle A-B} и A∼B{\displaystyle A\sim B}.
Пусть A{\displaystyle A} и B{\displaystyle B} — два указанных в определении множества, тогда их разность определяется (на теоретико-множественном языке):
- A∖B={x∈A∣x∉B}.{\displaystyle A\setminus B=\{x\in A\mid x\not \in B\}.}
Это множество часто называют дополнением множества B{\displaystyle B} до множества A{\displaystyle A}. (только когда множество В полностью принадлежит множеству А)
Обычно предполагается, что рассматриваются подмножества одного и того же множества, которое, в этом случае называют универсумом, скажем, X{\displaystyle X}. Тогда можно рассматривать вместе с каждым множеством A⊂X{\displaystyle A\subset X} и его относительное дополнение X∖A{\displaystyle X\setminus A}, при обозначении которого часто опускается значок универсума: ∖A{\displaystyle \setminus A}[источник не указан 1071 день]; при этом говорится, что
ruwikiorg.ru
Разность множеств — WiKi
Разность двух множеств — теоретико-множественная операция, результатом которой является множество, в которое входят все элементы первого множества, не входящие во второе множество. Обычно разность множеств A{\displaystyle A} и B{\displaystyle B} обозначается как A∖B{\displaystyle A\setminus B}, но иногда можно встретить обозначение A−B{\displaystyle A-B} и A∼B{\displaystyle A\sim B}.
Пусть A{\displaystyle A} и B{\displaystyle B} — два указанных в определении множества, тогда их разность определяется (на теоретико-множественном языке):
- A∖B={x∈A∣x∉B}.{\displaystyle A\setminus B=\{x\in A\mid x\not \in B\}.}
Это множество часто называют дополнением множества B{\displaystyle B} до множества A{\displaystyle A}. (только когда множество В полностью принадлежит множеству А)
Обычно предполагается, что рассматриваются подмножества одного и того же множества, которое, в этом случае называют универсумом, скажем, X{\displaystyle X}. Тогда можно рассматривать вместе с каждым множеством A⊂X{\displaystyle A\subset X} и его относительное дополнение X∖A{\displaystyle X\setminus A}, при обозначении которого часто опускается значок универсума: ∖A{\displaystyle \setminus A}[источник не указан 1071 день]; при этом говорится, что ∖A{\displaystyle \setminus A} — (просто) дополнение множества (без указания, дополнением до чего является данное множество).
С учётом данного замечания, оказывается, что A∖B=A∩(∖B){\displaystyle A\setminus B=A\cap (\setminus B)}, то есть дополнение множества B{\displaystyle B} до множества A{\displaystyle A} есть пересечение множества A{\displaystyle A} и дополнения множества B{\displaystyle B}.
Также применяется и операторная запись вида A∁{\displaystyle A^{\complement }}, ∁XA{\displaystyle \complement _{X}A} или (если опустить универсальное множество) ∁A{\displaystyle \complement A}.
Операция разности множеств не является по определению симметричной по отношению ко входящим в неё множествам. Симметричный вариант теоретико-множественной разности двух множеств описывается понятием симметрической разности.
В пакете Mathematica операция реализована с помощью функции Complement. В пакете MATLAB она же реализована с помощью функции setdiff.
В языке программирования Pascal (а также в его объектном расширении Object Pascal) операция разности множеств представлена оператором «−», обоими операндами и результатом выполнения которого являются значения типа set.
www.ru-wiki.org
