Решение биквадратных уравнений
В этой статье мы будем учиться решать биквадратные уравнения.
Итак, уравнения какого вида называются биквадратными?
Все уравнения вида ах4 + bx2 + c = 0, гдеа ≠ 0, являющиеся квадратными относительно х2, и называются биквадратными уравнениями. Как видите, эта запись очень похожа на запись квадратного уравнения, поэтому и решать биквадратные уравнения будем используя формулы, которые мы применяли при решении квадратного уравнения.
Только нам необходимо будет ввести новую переменную, то есть обозначим х2 другой переменной, например, у или t
Например, решим уравнение х4 + 4х2 ‒ 5 = 0.
Обозначим х2через у (х2 = у) и получим уравнение у2 + 4у – 5 = 0.
Как видите, такие уравнения вы уже умеете решать.
Решаем полученное уравнение:
D = 42 – 4 (‒ 5) = 16 + 20 = 36, √D = √36 = 6.
у1 = ( ‒ 4 – 6)/2= ‒ 10 /2 = ‒ 5,
у2 = ( ‒ 4 + 6)/2= 2 /2 = 1.
Вернемся к нашей переменной х.
Получили, что х2 = ‒ 5 и х2 = 1.
Замечаем, что первое уравнение решений не имеет, а второе дает два решения: х1 = 1 и х2 = ‒1. Будьте внимательны, не потеряйте отрицательный корень (чаще всего получают ответ х = 1, а это не правильно).
Ответ: — 1 и 1.
Для лучшего усвоения темы разберем несколько примеров.
Пример 1. Решите уравнение 2х4 ‒ 5 х2 + 3 = 0.
Пусть х2 = у, тогда 2у2 ‒ 5у + 3 =0.
D = (‒ 5)2 – 4· 2 · 3 = 25 ‒ 24 = 1, √D = √1 = 1.
у1 = (5 – 1)/(2· 2) = 4 /4 =1, у2 = (5 + 1)/(2· 2) = 6 /4 =1,5.
Тогда х2 = 1 и х2 = 1,5.
Получаем х1 = ‒1, х2 = 1, х3 = ‒ √1,5 , х4 = √1,5.
Ответ: ‒1; 1; ‒ √1,5; √1,5.
Пример 2.Решите уравнение 2х4 + 5 х2 + 2 = 0.
х2 = у
2у2 + 5у + 2 =0.
D = 52 – 4 · 2 · 2 = 25 ‒ 16 = 9, √D = √9 = 3.
у1 = (‒ 5 – 3)/(2 · 2) = ‒ 8 /4 = ‒2, у2 = (‒5 + 3)/(2 · 2) = ‒ 2 /4 = ‒ 0,5.
Тогда х2 = ‒ 2 и х2
Ответ: решений нет.
Неполные биквадратные уравнения — это когда b = 0 (ах4 + c = 0) или же c = 0
(ах4 + bx2 = 0) решают как и неполные квадратные уравнения.
Пример 3. Решить уравнение х4 ‒ 25х2 = 0
Разложим на множители, вынесем х2 за скобки и тогда х2 (х2 ‒ 25) = 0.
Получим х2 = 0 или х2 ‒ 25 = 0, х2 = 25.
Тогда имеем корни 0; 5 и – 5.
Ответ: 0; 5; – 5.
Пример 4. Решить уравнение 5х4 ‒ 45 = 0.
5х4 = 45
х4 = 45 / 5
х4 = 9
х2 = ‒ √9 (решений не имеет)
х2 = √9, х1 = ‒ 3, х2 = 3.
Как видите, умея решать квадратные уравнения, вы сможете справиться и с биквадратными.
Если же у вас остались вопросы, записывайтесь на мои уроки. Репетиор Валентина Галиневская.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
blog.tutoronline.ru
Решение биквадратных уравнений
Пример 1. Решить уравнение x4 — 17x2 + 16 = 0.Решение.
Исходное уравнение является биквадратным. Сделав замену переменной t = x2 => x4 = t2, перейдем к эквивалентному исходному квадратному уравнению:
x4 — 17x2 + 16 = 0 t2 — 17t + 16 = 0
Вычислим дискриминант квадратного трехчлена: a = 1, b = -17, c = 16,
D = b2 — 4ac = (-17)2 — 4*1*16 = 289-64 = 225 > 0, следовательно, уравнение имеет два действительных корня.
По найденным значениям t, решая уравнения x2 = t, найдем корни исходного биквадратного уравнения:
Таким образом, исходное уравнение имеет 4 действительных корня.
Ответ: ±1, ±4.
Пример 2. Решить уравнение 9x4 + 32x2 — 16 = 0.
Решение.
Исходное уравнение является биквадратным. Сделав замену переменной t = x2 => x4 = t2, перейдем к эквивалентному исходному квадратному уравнению:
9x4 + 32x2 — 16 = 0 9t2 + 32t — 16 = 0
Вычислим дискриминант квадратного трехчлена. У нас a = 9, b = 32, c = -16.
Так как b = 32, то есть b делится на 2 (
= 16), вычислим дискриминант D1:. Cледовательно, уравнение имеет два действительных корня.
По найденным значениям t, решая уравнения x2 = t, найдем корни исходного биквадратного уравнения:
Первое уравнение x2 = -4 корней не имеет, а второе, а значит, и исходное, имеет два действительных корня x =
.Ответ:
.Пример 3. Решить уравнение x4 + 3x2 — 10 = 0.
Решение.
Исходное уравнение является биквадратным. Сделав замену переменной t = x2 => x4 = t2, перейдем к эквивалентному исходному квадратному уравнению:
x4 + 3x2 — 10 = 0 t2 + 3t — 10 = 0
Вычислим дискриминант полученного квадратного трехчлена: a = 1, b = 3, c = -10,
D = b2 — 4ac = 32 — 4*1*(-10) = 9+40 = 49 > 0, следовательно, уравнение имеет два действительных корня.
По найденным значениям t, решая уравнения x2 = t, найдем корни исходного биквадратного уравнения:
Первое уравнение x2 = -5 корней не имеет, а второе, а значит, и исходное, имеет два действительных корня .
Ответ: .
ru.intemodino.com
| | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Решение уравнений и неравенств. Системы уравнений. Формулы. Методы. / / Биквадратные уравнения. Решение биквадратных уравнений. Нахождение корней биквадратных уравнений.
| |||||
dpva.ru
Уравнения приводимые к квадратным. Биквадратные уравнения
УРАВНЕНИЯ, ПРИВОДИМЫЕ К КВАДРАТНЫМ.
БИКВАДРАТНЫЕ УРАВНЕНИЯ. (СЛАЙД 1)
Предварительная подготовка к уроку: учащиеся должны уметь решать биквадратные уравнения и уравнения, приводимые к квадратным, владеть методом введения новой переменной; учащиеся заранее готовят сообщения о великих итальянских ученых-математиках.
Цели урока:
а) образовательная: рассмотрение способов решения уравнений, приводимых к квадратным уравнениям;
б) воспитательная: воспитание навыков групповой работы, сознательной деятельности учащихся;
в) развивающая: развитие мыслительной деятельности учащихся, навыков взаимодействия между учащимися, умения обобщать изучаемые факты.
Оборудование: сетка кроссворда на карточках, карточки, плакат-план путешествия, записи на доске, проектор, компьютер.
Тип урока: урок-путешествие по стране «Математика».
ХОД УРОКА:
Организационный момент
(План путешествия, в котором перечислены названия станций, записан на доске или плакате.)
Сегодня мы отправимся в путешествие по стране «Математика». Остановимся в городе Уравнений третьей и четвертой степени, продолжим знакомство с биквадратными уравнениями, услышим новое о математиках.
Каждый этап урока (станция) будет оценена, поэтому у Вас на столе лежат Листы успеха! Не забываем ставить оценки!
Путешествие по стране «Математика»
СТАНЦИЯ ЛЮБИТЕЛЕЙ КРОССВОРДОВ
Я предлагаю вашему вниманию – ответить на вопросы кроссворда. У каждого из вас есть карточки с сеткой кроссворда и вопросами. Ответы записывайте только в именительном падеже. Разгадайте кроссворд, на который вам достаточно будет 5 минут, а по истечению времени (5 минут) вы обменяетесь листочками с соседом по парте и выполните проверку.
(СЛАЙД 2)
По горизонтали:
4.Чем является выражение 
для квадратного уравнения? (дискриминант)
6.Значение переменной, при которой уравнение обращается в верное равенство. (корень)
8.Уравнение вида , где 
. (биквадратное)
9.Французский математик, имеющий отношение к квадратным уравнениям. (Виет)
10.Уравнение, в котором левая и правая части являются целыми выражениями. (целое)
11. Уравнения с одной переменной, имеющие одинаковое множество корней. (равносильные)
По вертикали:
1.Множество корней уравнения. (решение)
2.Решение уравнения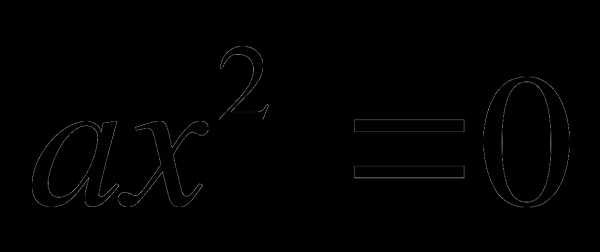 
. (ноль)
3.Равенство, содержащее переменную. (уравнение)
5.Квадратное уравнение, в котором один из коэффициентов b или с равен 0. (неполное)
7. Квадратное уравнение, в котором первый коэффициент равен единице. (приведенное)
СТАНЦИЯ «ИСТОРИЧЕСКАЯ»
Ученик: В проблему уравнений 3-й и 4-й степеней большой вклад внесли итальянские математики 16 века Н.Тарталья, А.Фиоре, Д.Кардано и др. В 1535 г. между А.Фиоре и Н.Тартальей состоялся научный поединок, на котором последний одержал победу. Он за 2 часа решил 30 задач, предложенных Фиоре, а сам Фиоре не смог решить ни одной, заданной ему Тартальей.
Учитель: Кто еще подготовил сообщения? (заслушиваются сообщения, подготовленные учащимися. На каждое 2-3 минуты.)
История развития квадратных уравнений
Выступления учащихся
ГОРОД УРАВНЕНИЙ (устная часть)
Это не просто город Уравнений, а уравнений 3-й и 4-й степеней. Вам предстоит ответить на все вопросы. Только ответив на них, вы сможете отправиться дальше.
ЗАДАНИЕ 1. Каким способом вы решали бы уравнения каждой из групп?
(Уравнения к заданиям 1-3 высвечиваются на экран) (СЛАЙД 3)
ОТВЕТЫ: Примеры группы 1) лучше решать разложением на множители с помощью вынесения общего множителя за скобки или с помощью формул сокращенного умножения.
Примеры группы 2) лучше решать способом группировки и разложения на множители.
Примеры группы 3) лучше решать введением новой переменной и переходом к квадратному уравнению.
ЗАДАНИЕ 2. Какой множитель вы вынесли бы за скобки в примерах группы 1) задания 1? (СЛАЙД 3)
ОТВЕТЫ:
ЗАДАНИЕ 3. Как вы сгруппировали бы слагаемые в примерах группы 2) задания 1? (СЛАЙД 3)
ОТВЕТЫ:
ЗАДАНИЕ 4. Что бы вы обозначили через новую переменную в примерах группы 3) задания 1? (СЛАЙД 3)
ОТВЕТЫ:
ЗАДАНИЕ 5. Как можно разложить на множители многочлен ?
ОТВЕТЫ: .
Оцените свои знания на листе успеха!
Переулок отдыхай!
ГОРОД УРАВНЕНИЙ (практическая часть)
Вы справились с устной работой, и мы отправляемся дальше.
ЗАДАНИЕ 6. Решите уравнение. (См. приложение.)
(задание у доски одновременно решают 2 ученика.)
а) (Первый ученик решает у доски с объяснением.)
б) (Второй учащийся решает уравнение молча, затем объясняет решение, класс слушает и задает вопросы, если что-то непонятно.)
ЗАДАНИЕ 7. Решите уравнение. (См. приложение.)
(Задание выполняется самостоятельно по вариантам, предварительно оговорив замену для введения новой переменной. Проверяется устно.) (СЛАЙД 4)
Вариант 1 Замена: .
Вариант 2 Замена: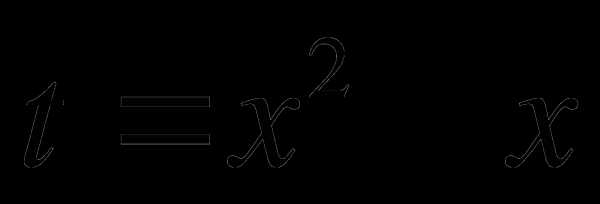 
.
ЗАДАНИЕ 8. Решите уравнение. (См. приложение.)
(Дополнительно для тех, кто раньше справился с предыдущими уравнениями).
. (СЛАЙД 5)
ЗАДАНИЕ 9. Решите уравнение. (См. приложение.)
(Тот, кто верно решит больше биквадратных уравнений за 10 минут, получит «5». Учащиеся работают самостоятельно с последующей взаимопроверкой). (СЛАЙД 8)
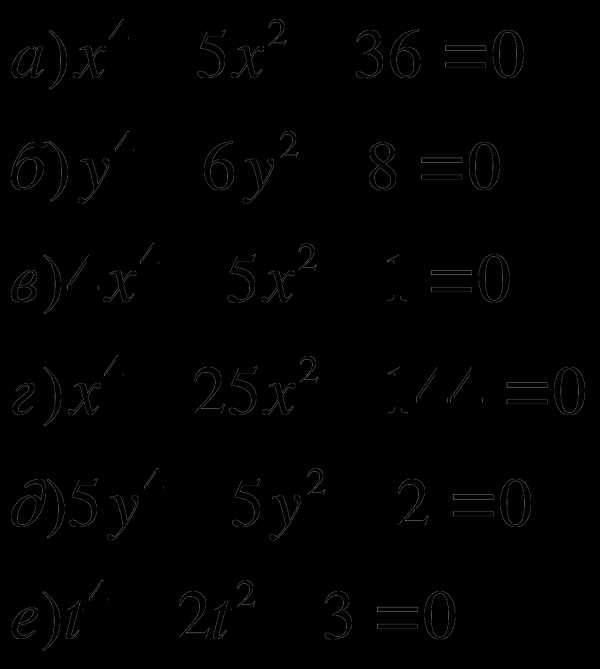
ЗАДАНИЕ 10. При каких значениях а уравнение не имеет корней? (См. приложение.) (СЛАЙД 9)
(Пример на повторение.)
СТАНЦИЯ «ДОМАШНЯЯ»
Вы прибыли на станцию «Домашняя». Получите домашнее задание:
№279 (в, г), №276 (а, в),
Разобрать пример 2 на стр. 74 и решите уравнение итальянских математиков:
. (См. приложение.) (СЛАЙД 10)
Подведение итогов урока.
Наше путешествие завершено.
Попрошу вас поставить итоговую оценку за урок учитывая все станции!
Итак, подсчитайте, сколько каждый из вас решил уравнений.
За урок весь 9 класс решил 11 уравнений. Оценки за урок….
Если вам понравилось путешествовать по стране «знаний», то поднимите «Смайлик»,
если были затруднения в городе уравнений –«Квадрат»,
а если было трудно – «Треугольник».
infourok.ru
Биквадратные уравнения решение задач онлайн
Биквадратным уравнением называется уравнение следующего вида:
где — любые действительные числа, но , x – неизвестная искомая переменная.
Коэффициенты имеют соответственно названия: — старший коэффициент (коэффициент при ), — второй коэффициент (коэффициент при ), — свободный член.
Корнем биквадратного уравнения называется такое значение переменной , при подстановке которого трехчлен обращается в ноль.
Решить биквадратное уравнение – это значит найти все его корни или установить, что корней нет.
При решении биквадратного уравнения необходимо придерживаться следующей схемы:
1) Подстановкой свести заданное биквадратное уравнение к квадратному уравнению вида
2) Найти корни полученного квадратного уравнения. (См. схему решения квадратных уравнений).
3) Приравнять полученные значения корней квадратного уравнения к введенной переменной подстановки . То есть провести обратную замену.
4) Найти корни биквадратного уравнения, решив уравнения обратной замены.
Пример 1: Решить уравнение
Данное уравнение является биквадратным.
Введем замену переменных:
Тогда заданное уравнение перепишется в следующем виде:
Полученное уравнение является полным неприведенным и имеет следующие коэффициенты:
Найдем дискриминант:
Так как , то квадратное уравнение имеет два корня.
Найдем их:
Таким образом, решением квадратного уравнения будут корни
Введем обратную замену и . И решим полученные уравнения:
Ответ:
Пример 2: Решить уравнение
Данное уравнение является биквадратным.
Введем замену переменных:
Тогда заданное уравнение перепишется в следующем виде:
Полученное уравнение является полным приведенным и имеет следующие коэффициенты:
Найдем дискриминант:
Так как , то квадратное уравнение имеет два корня.
Найдем их:
Таким образом, решением квадратного уравнения будут корни
Введем обратную замену и . И решим полученные уравнения:
Уравнение же решения не имеет.
Таким образом, решением биквадратного уравнения будут корни
Ответ:
Примечание: Из решенного выше примера видно, что при получении отрицательного значения корня квадратного уравнения , можно сразу исключать его из рассмотрения как неудовлетворяющего условию
Пример 3: Решить уравнение
Данное уравнение является биквадратным.
Введем замену переменных:
Тогда заданное уравнение перепишется в следующем виде:
Данное квадратное уравнение является полным неприведенным и имеет следующие коэффициенты: .
Найдем дискриминант: .
Так как , то квадратное уравнение не имеет корней.
Таким образом, биквадратное уравнение тоже не имеет корней.
Ответ: Корней нет.
Пример 4: Решить уравнение
Данное уравнение является биквадратным.
Введем замену переменных:
Тогда заданное уравнение перепишется в следующем виде:
Полученное уравнение является полным приведенным и имеет следующие коэффициенты:
Найдем дискриминант:
Так как , то квадратное уравнение имеет два корня.
Найдем их:
Таким образом, решением квадратного уравнения будут корни
Так как оба полученных корня квадратного уравнения отрицательны , то биквадратное уравнение иметь решений не будет. (Смотри примечание данной главы)
Ответ: Корней нет.
Автор статьи: Каташева Г.Г.
ktoreshit.ru
Как решать биквадратное уравнение 🚩 решение биквадратного уравнения онлайн 🚩 Математика
Автор КакПросто!
Биквадратное уравнение представляет собой уравнение четвертой степени, общий вид которого представляется выражением ax^4 + bx^2 + c = 0. Его решение основано на применении метода подстановки неизвестных. В данном случае х^2 заменяется другой переменной. Таким образом, в итоге получается обычное квадратное уравнение, которое и требуется решить.
Статьи по теме:
Инструкция
Запишите заданное биквадратное уравнение. Произведите замену х^2 на переменную k. В итоге получится ak^2 – bk + c = 0. Решите квадратное уравнение, получившееся в результате замены. Для этого сначала посчитаем значение дискриминанта в соответствии с формулой: D = b^2 ? 4ac. При этом переменные a, b, c являются коэффициентами нашего уравнения. Если дискриминант получился отрицательным, то наше уравнение не имеет решения, как и заданное биквадратное уравнение. Если дискриминант равен нулю, то единственное решение определяется так: k = -b/2а.Если дискриминант больше нуля, существуют два решения. Для их нахождения возьмите корень квадратный из дискриминанта D. Запишите значение в виде переменной QD.
Решите квадратное уравнение. Для этого подставьте в формулы известные значения. Для первого решения формула k1 = (-b+QD)/2а, для второго — k2 = (-b-QD)/2а.
Найдите корни биквадратного уравнения. Для этого возьмите корень квадратный из полученных решений квадратного уравнения. Если решение было одно, то корней будет два – положительное и отрицательное значение корня квадратного. Если решений было два, у биквадратного уравнения будет четыре корня.
Видео по теме
Совет полезен?
Статьи по теме:
Не получили ответ на свой вопрос?
Спросите нашего эксперта:
www.kakprosto.ru
Биквадратное уравнение, решение биквадратных уравнений
Всем еще со школы известно такое понятие, как уравнения. Уравнение – это равенство, содержащее одну или несколько переменных. Зная то, что одна из частей данного равенства равна другой, можно вычленять отдельные части уравнения, перенося те или иные его составляющие за знак равенства по четко оговоренным правилам. Можно упростить уравнение до необходимого логического завершения в виде х=n, где n – это любое число.
С начальной школы все дети проходят курс изучения линейных уравнений различной сложности. Позже в программе появляются более сложные линейные уравнения – квадратные, затем идут кубические уравнения. Каждый последующий вид уравнений имеет новые методики решения, становится труднее в изучении и повторении.
Однако после этого возникает вопрос о решении такого вида уравнений, как биквадратные уравнения. Данный вид, несмотря на кажущуюся сложность, решается достаточно просто: главное – уметь привести такие уравнения в должный вид. Их решение изучается за один-два урока вместе с практическими заданиями, если у учащихся имеются базовые знания о решении квадратных уравнений.
Что необходимо знать человеку, столкнувшемуся с этим типом уравнений? Для начала то, что они включают в себя только четные степени переменной «икс»: четвертая и, соответственно, вторая. Чтобы биквадратное уравнение было решаемо, необходимо привести его к виду квадратного уравнения. Как это сделать? Достаточно просто! Нужно всего лишь заменить «икс» в квадрате на «игрек». Тогда устрашающий для многих школьников «икс» в четвертой степени превратится в «игрек» в квадрате, а уравнение примет вид обычного квадратного.
Далее оно решается как обычное квадратное уравнение: раскладывается на множители, после чего находится значение таинственного «игрека». Чтобы решить биквадратное уравнение до конца, нужно найти квадратный корень из числа «игрек» – это и будет искомая величина «икс», после нахождения значений которого можно будет поздравить себя с успешным завершением расчетов.
Что же следует помнить, решая уравнения данного вида? Первое и самое главное: игрек не может быть отрицательным числом! Само условие, что игрек – это квадрат числа икс, исключает подобный вариант решения. Поэтому если при первичном решении биквадратного уравнения одно из значений «игрек» получается у вас положительным, а второе – отрицательным, необходимо взять только его положительный вариант, иначе биквадратное уравнение будет решено неверно. Лучше сразу ввести правило, что переменная «игрек» больше либо равна нулю.
Второй немаловажный нюанс: число «икс», являясь квадратным корнем числа «игрек», может быть как положительным, так и отрицательным. Допустим, если «игрек» равен четырем, то биквадратное уравнение будет иметь два решения: два и минус два. Это происходит по той причине, что отрицательное число, возведенное в четную степень, равно числу того же модуля, но отличного знака, возведенному в ту же степень. Поэтому всегда стоит помнить об этом немаловажном моменте, иначе можно попросту потерять один или несколько ответов уравнения. Лучше всего сразу писать, что «икс» равен плюс-минус квадратному корню от «игрек».
В общем и целом, решение биквадратных уравнений – это достаточно просто и не требует больших временных затрат. На изучение этой темы в школьной программе хватает двух академических часов – не считая, конечно, повторений и контрольных работ. Биквадратные уравнения стандартного вида решаются очень легко, если соблюдать перечисленные выше правила. Их решение не составит для вас никакого труда, потому что оно подробно расписано в учебниках математики. Удачной вам учебы и успехов в решении любых, не только математических, задач!
fb.ru