Кто придумал параболу
Парабола известна математикам уже очень давно, а название этой функции дал древнегреческий математик Аполлоний Пергский в III в. до н.э., изучавший свойства сечений конуса.
Также изучением параболы занимались Архимед и Папп Александрийский.
В дальнейшем разные учёные показали, что многие явления можно описать параболой, так, например, была открыта траектория движения снаряда.
Основные определения и строение параболы
Вершина параболы — это точка, находящаяся на минимальном расстоянии от директрисы параболы $d$.
Фокус $F$ параболы — это точка, через которую проходит ось симметрии параболы, перпендикулярная прямой, находящаяся на расстоянии $d$. Фокус расположен на расстоянии $\frac{p}{2}$ от вершины. Координаты фокуса классической параболы можно определить из её уравнения.
Фокус и вершина являются основными точками, характеризующими параболу.
Параметр $p$ параболы иначе называется фокальным параметром и является расстоянием между фокусом и директрисой. 2$. Если он отрицательный, то парабола перевёрнутая по отношению к обычной и её ветви смотрят вниз, а если положительный – то её ветви смотрят вверх.
Также модуль коэффициента $a$ влияет на степень пологости (ширину) параболы, чем меньше модуль $a$, тем парабола более широкая (пологая), и чем больше модуль $a$, тем она более узкая (крутая).
2$. Если он отрицательный, то парабола перевёрнутая по отношению к обычной и её ветви смотрят вниз, а если положительный – то её ветви смотрят вверх.
Также модуль коэффициента $a$ влияет на степень пологости (ширину) параболы, чем меньше модуль $a$, тем парабола более широкая (пологая), и чем больше модуль $a$, тем она более узкая (крутая).
Далее необходимо посмотреть на коэффициент $c$. Коэффициент $c$ обозначает смещение по оси $OY$ относительно пересечения осей координат. Это легко проверить, если приравнять $x$ к нулю в имеющемся уравнении. Если коэффициент $c$ — положительный, то парабола смещена вверх относительно точки $(0;0)$, а если отрицательный – то вниз. В случае если $c=0$ — парабола проходит через точку начала координат.
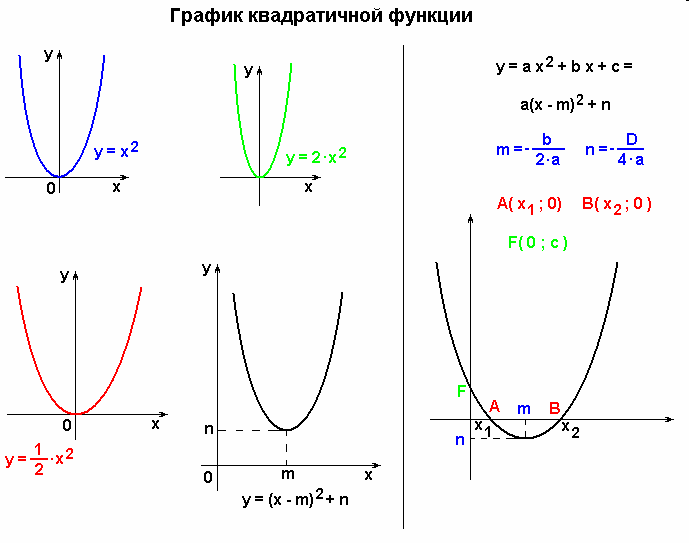
Теперь можно найти вершину параболы, её координаты вычисляются по формуле:
$x = — \frac{b}{2a}$ (1).
Чтобы найти $y$, нужно подставить полученный по формуле $x$ в уравнение. {2}+y_{0}}
{2}+y_{0}}
Парабола
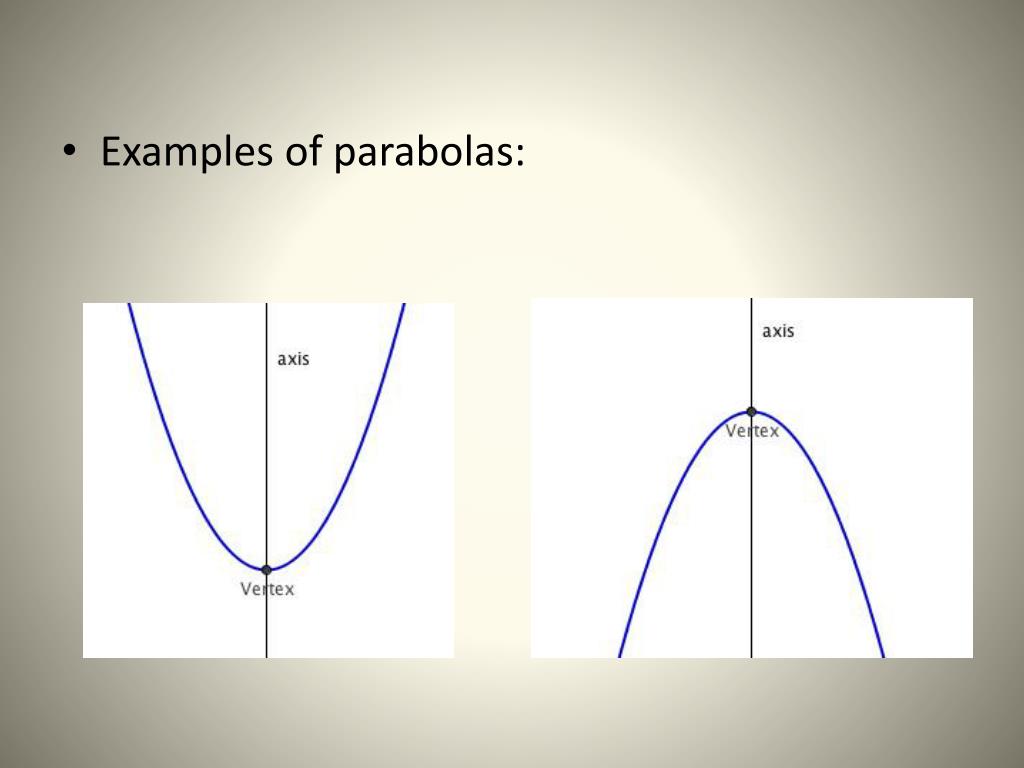
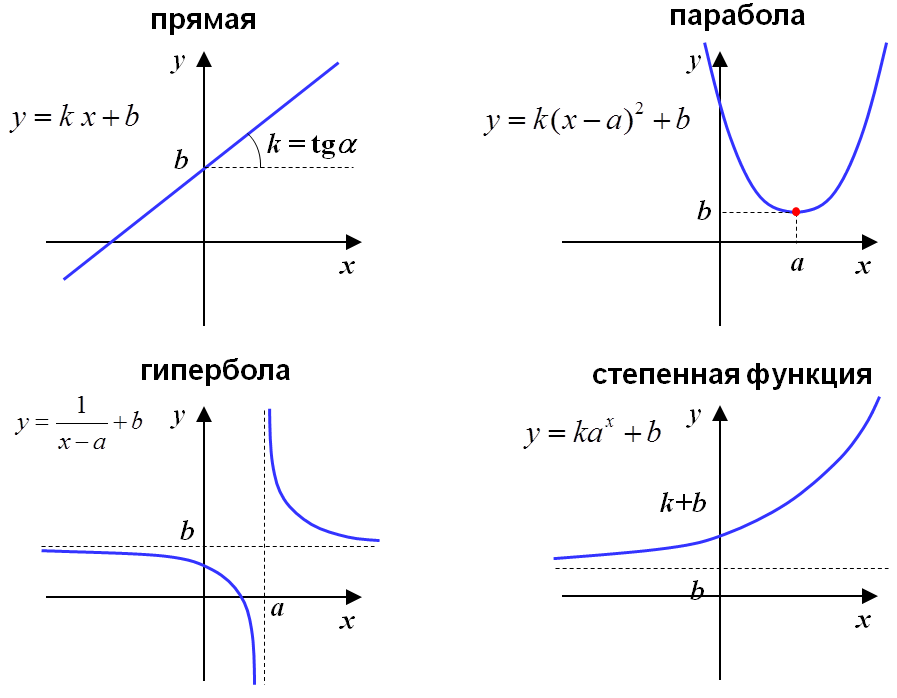
Парабола определяется как набор точек, расстояние до фиксированной точки (фокуса) и фиксированной прямой линии (директрисы) равны. Но, вероятно, его легче запомнить как U-образную изогнутую линию, созданную при построении квадратичного уравнения.
Многие объекты реального мира движутся по параболе. Когда вы бросаете баскетбольный мяч, траектория мяча образует параболу.
Пример
Парабола, которая направлена вверх, имеет форму буквы «U», а парабола, направленная вниз, имеет форму перевернутой буквы U.
|
|
Парабола не обязательно должна быть вертикальной, но горизонтальные параболы не являются функциями (они не проходят тест вертикальной линии). Некоторые функции, которые вы видите, будут горизонтальными параболами с ограниченными областями (). Вы узнаете больше об этом, когда будете изучать коники.
Некоторые функции, которые вы видите, будут горизонтальными параболами с ограниченными областями (). Вы узнаете больше об этом, когда будете изучать коники.
Пример
|
|
Вершина параболы — это точка, в которой парабола меняет направление и где график наиболее изогнут. На графиках квадратичных чисел он находится в самом верху или в самом низу квадратичного уравнения. Вершина — это точка параболы на оси симметрии.
Для квадратичных уравнений стандартной формы ax 2 + bx + c ось симметрии можно найти с помощью уравнения x = . Чтобы найти координату y вершины, найдите ось симметрии и подставьте это значение x в исходное уравнение.
Пример
f(x) = x 2 + 6x + 11
a = 1; б = 6; c = 11
x = = -3
f(-3) = (-3) 2 + 6(-3) + 11
f(-3) = 9 — 18 + 11 = 2
Вершина в (-3,2)
Расчет фокуса и директрисы
Ниже приведен пример расчета фокуса и директрисы, который поможет лучше понять математическое определение параболы, приведенное выше:
Пример
Фокус — это точка, расположенная на той же прямой, что и ось симметрии, а директриса — это прямая, перпендикулярная оси симметрии. Для парабол фокус всегда находится внутри параболы, а директриса никогда не касается параболы. Поскольку вершина находится на одинаковом расстоянии от фокуса и директрисы, директриса находится прямо напротив фокуса.
Для парабол фокус всегда находится внутри параболы, а директриса никогда не касается параболы. Поскольку вершина находится на одинаковом расстоянии от фокуса и директрисы, директриса находится прямо напротив фокуса.
Для параболы в форме вершины y = a(x — h) 2 + k фокус расположен в точке (h, k + ), а направляющая расположена в точке y = k — .
Пример
y = (x — 3) 2 + 2
h = 3 ; к = 2; a =
Фокус: (3,2 + ) = (3,4)
Директриса: y = 2 — = 0
Для горизонтальных парабол вершина x = a(y — k) 2 + h , где (h,k) — вершина. Фокусы парабол в этой форме имеют фокус, расположенный в точке (h + , k), и направляющую в точке x = h — . Ось симметрии расположена в точке y = k.
Вершинная форма параболы
Вершинная форма параболы – это другая форма квадратичной функции f(x) = ax 2 + bx + c. Вершинная форма параболы:
Вершинная форма параболы:
f(x) = a(x — h) 2 + k
А в вершинной форме параболы соответствует а в стандартной форме. Если a положительно, парабола направлена вверх. Если а отрицательно, парабола направлена вниз.
В вершинной форме (h,k) описывает вершину параболы, а парабола имеет линию симметрии x = h.
Форма вершины очень похожа на общее выражение для преобразования функций. Форма вершины значительно упрощает построение параболы, потому что она упрощает построение вершины.
Пример
f(x) = -(x — 1) 2 + 4
Из этого уравнения уже можно сказать, что вершина параболы находится в точке (1,4), а ось симметрии находится в точке x = 1. Теперь все, что нужно сделать, это подставить точки вокруг вершины, а затем построить график.
Вы можете использовать завершение квадрата для преобразования квадратного числа в стандартной форме в вершинную форму. Вы также можете преобразовать форму вершины, зная, что вершина лежит на оси симметрии.
Значение x вершины равно x = — , поэтому значение y равно y = f (-). Подставьте эти значения для h и k в уравнение формы вершины. Затем a одинаково в обеих формах, так что просто скопируйте это в уравнение вершинной формы.
Пример
f(x) = x 2 — x — 20
a = 1; б = -1; c = -20
x = h = — = — =
f() = () 2 — — 20 = — — 20 = -20
f(x) = (x — ) 2 — 20
Чтобы преобразовать параболу в вершинной форме в стандартную форму, разверните уравнение и упростите его.
Пример
f(x) = 5(x + 3) 2 — 6
f(x) = 5(x 2 + 6x + 9) — 6
f(x) = 5x 2 + 30x + 45 — 6
f(x) = 5x 2 + 30x + 39
12.3: Парабола — Математика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 3289
- OpenStax
- OpenStax
Цели обучения
- Графические параболы с вершинами в начале координат.

- Запишите уравнения парабол в стандартной форме.
- Параболы графа с вершинами не в начале координат.
- Решение прикладных задач на параболах.
А вы знали, что олимпийский огонь зажигают за несколько месяцев до начала игр? Церемониальный метод зажжения пламени такой же, как и в древние времена. Церемония проходит в храме Геры в Олимпии, Греция, и уходит своими корнями в греческую мифологию, отдавая дань уважения Прометею, который украл огонь у Зевса, чтобы раздать его всем людям. Одна из одиннадцати действующих жриц помещает факел в фокус параболического зеркала (рис. \(\PageIndex{1}\)), которое фокусирует солнечные лучи и зажигает пламя.
Параболические зеркала (или отражатели) способны улавливать энергию и фокусировать ее в одной точке. О преимуществах этого свойства свидетельствует обширный список параболических объектов, которые мы используем каждый день: спутниковые антенны, подвесные мосты, телескопы, микрофоны, прожекторы и автомобильные фары, и это лишь некоторые из них. Параболические отражатели также используются в устройствах альтернативной энергии, таких как солнечные плиты и водонагреватели, потому что они недороги в производстве и не требуют особого обслуживания. В этом разделе мы рассмотрим параболу и ее использование, в том числе недорогие и энергоэффективные солнечные конструкции.
О преимуществах этого свойства свидетельствует обширный список параболических объектов, которые мы используем каждый день: спутниковые антенны, подвесные мосты, телескопы, микрофоны, прожекторы и автомобильные фары, и это лишь некоторые из них. Параболические отражатели также используются в устройствах альтернативной энергии, таких как солнечные плиты и водонагреватели, потому что они недороги в производстве и не требуют особого обслуживания. В этом разделе мы рассмотрим параболу и ее использование, в том числе недорогие и энергоэффективные солнечные конструкции.
Графическое изображение парабол с вершинами в начале координат
Ранее мы видели, что эллипс образуется, когда плоскость пересекает прямой круговой конус. Если плоскость параллельна ребру конуса, образуется неограниченная кривая. Эта кривая представляет собой параболу (рис. \(\PageIndex{2}\)).
Рисунок \(\PageIndex{2}\): Парабола Подобно эллипсу и гиперболе, парабола также может быть определена набором точек на координатной плоскости. Парабола — это множество всех точек \((x,y)\) на плоскости, которые находятся на одинаковом расстоянии от фиксированной линии, называемой директриса , а фиксированная точка ( фокус ) не на директрисе.
Парабола — это множество всех точек \((x,y)\) на плоскости, которые находятся на одинаковом расстоянии от фиксированной линии, называемой директриса , а фиксированная точка ( фокус ) не на директрисе.
Ранее мы узнали о вершине параболы и оси симметрии. Теперь мы расширим обсуждение, включив в него другие ключевые свойства параболы (рис. \(\PageIndex{3}\)). Обратите внимание, что ось симметрии проходит через фокус и вершину и перпендикулярна директрисе. Вершина — это середина между директрисой и фокусом. Отрезок, проходящий через фокус и параллельный директрисе, называется 9-м.0243 широкая прямая кишка . Концы широкой прямой кишки лежат на кривой. По определению расстояние d от фокуса до любой точки \(P\) на параболе равно расстоянию от \(P\) до директрисы.
Рисунок \(\PageIndex{3}\): Основные характеристики параболы Для работы с параболами в координатной плоскости мы рассмотрим два случая: с вершиной в начале координат и с вершиной в точке . точку, отличную от исходной. Начнем с первого.
точку, отличную от исходной. Начнем с первого.
СТАНДАРТНЫЕ ФОРМЫ ПАРАБОЛ С ВЕРШИНОЙ \((0,0)\)
Таблица \(\PageIndex{1}\) и рисунок \(\PageIndex{5}\) суммируют стандартные характеристики парабол с вершиной в Происхождение.
| Ось симметрии | 2=4py\)\((0, р)\) | \(у=-р\) | \((\pm 2p, p)\) |
|---|
Ключевыми характеристиками параболы являются ее вершина, ось симметрии, фокус, директриса и широкая прямая кишка (рис. \(\PageIndex{5}\)). Получив стандартное уравнение для параболы с центром в начале координат, мы можем легко определить ключевые особенности для построения графика параболы. Прямая называется касательной к кривой, если она пересекает кривую ровно в одной точке. Если мы нарисуем линии, касающиеся параболы в конечных точках прямой кишки , эти линии пересекутся на оси симметрии, как показано на рисунке \(\PageIndex{6}\). 92=4px\), тогда
- осью симметрии является ось \(x\), \(y=0\)
- набор \(4p\) равный коэффициенту \(x\) в данном уравнении, которое нужно решить для \(p\). Если \(p>0\), парабола открывается вправо. Если \(p<0\), парабола открывается влево.

- используйте \(p\) для нахождения координат фокуса, \((p,0)\)
- используйте \(p\) для нахождения уравнения направляющей, \(x=−p\)
- используйте \(p\) для нахождения концов широкой прямой кишки, \((p,\pm 2p)\). В качестве альтернативы подставьте \(x=p\) в исходное уравнение. 92=4py\), тогда
- осью симметрии является ось \(y\), \(x=0\)
- набор \(4p\) равный коэффициенту \(y\) в данном уравнении, которое нужно решить для \(p\). Если \(p>0\), парабола раскрывается. Если \(p<0\), парабола раскрывается вниз.
- используйте \(p\) для нахождения координат фокуса, \((0,p)\)
- используйте \(p\) для нахождения уравнения направляющей, \(y=−p\)
- используйте \(p\) для нахождения концов широкой прямой кишки, \((\pm 2p,p)\) 92=4px\). Таким образом, осью симметрии является ось x . Отсюда следует, что:
- \(24=4p\), значит \(p=6\).
 Так как \(p>0\), парабола выходит вправо
Так как \(p>0\), парабола выходит вправо - координаты фокуса \((p,0)=(6,0)\)
- уравнение направляющей \(x=−p=−6\)
- конечные точки широкой прямой кишки имеют одинаковые координаты x в фокусе. Чтобы найти конечные точки, подставьте \(x=6\) в исходное уравнение: \((6,\pm 12)\)
- \(−6=4p\), поэтому \(p=−\dfrac{3}{2}\). Так как \(p<0\), парабола направлена вниз.
- координаты фокуса \((0,p)=(0,−\dfrac{3}{2})\)
- уравнение направляющей \(y=−p=\dfrac{3}{2}\)
- концы широкой прямой кишки можно найти, подставив \(y=\dfrac{3}{2}\) в исходное уравнение, \((\pm 3,−\dfrac{3}{2})\)
Далее наносим фокус, директрису и 92=8у\). Определите и обозначьте фокус, направляющую и конечные точки прямой кишки latus .
- Ответить
- Фокус: \((0,2)\)
- Директриса: \(y=−2\)
- Конечные точки широкой прямой кишки: \((\pm 4,2)\).
 2=4p(y−k)\) для парабол, у которых ось симметрии параллельна оси \( у\)-ось. Эти стандартные формы приведены ниже вместе с их общими графиками и ключевыми характеристиками.
2=4p(y−k)\) для парабол, у которых ось симметрии параллельна оси \( у\)-ось. Эти стандартные формы приведены ниже вместе с их общими графиками и ключевыми характеристиками.СТАНДАРТНЫЕ ФОРМЫ ПАРАБОЛ С ВЕРШИНОЙ \((H, K)\)
Таблица \(\PageIndex{2}\) и рисунок \(\PageIndex{11}\) суммируют стандартные характеристики парабол с вершиной в точка \((h,k)\).
Рисунок \(\PageIndex{11}\): (a) Когда \(p>0\), парабола открывается вправо.Таблица \(\PageIndex{2}\) Ось симметрии Уравнение Фокус Директриса Конечные точки широкой прямой кишки 92=4р(у-к)\) \((ч, к+р)\) \(у=к-р\) \((ч\пм 2р, к+р)\)  2=4p(y−k)\). 92=4p(x−h)\), тогда:
2=4p(y−k)\). 92=4p(x−h)\), тогда:- использовать данное уравнение для определения \(h\) и \(k\) для вершины, \((h,k)\)
- использовать значение \(k\) для определения оси симметрии, \(y=k\)
- набор \(4p\) равный коэффициенту \((x−h)\) в данном уравнении для решения \(p\). Если \(p>0\), парабола выходит вправо. Если \(p<0\), парабола открывается влево.
- используйте \(h\), \(k\) и \(p\) , чтобы найти координаты фокуса, \((h+p, k)\) 92=4p(y−k)\), тогда:
- использовать данное уравнение для определения \(h\) и \(k\) для вершины, \((h,k)\)
- использовать значение \(h\) для определения оси симметрии, \(x=h\)
- набор \(4p\) равный коэффициенту \((y−k)\) в данном уравнении для решения \(p\). Если \(p>0\), парабола раскрывается. Если \(p<0\), парабола раскрывается вниз.
- используйте \(h\), \(k\) и \(p\) , чтобы найти координаты фокуса, \((h, k+p)\)
- используйте \(k\) и \(p\) для нахождения уравнения направляющей, \(y=k−p\)
- используйте \(h\), \(k\) и \(p\) , чтобы найти концы широкой прямой кишки, \((h\pm 2p, k+p)\)
- Постройте вершину, ось симметрии, фокус, директрису и прямую кишку, а затем нарисуйте плавную кривую, чтобы сформировать параболу.

- вершина равна \((h,k)=(−3,1)\)
- ось симметрии \(y=k=1\)
- \(−16=4p\), поэтому \(p=−4\). Так как \(p<0\), парабола открывается влево.
- координаты фокуса равны \((h+p,k)=(−3+(−4),1)=(−7,1)\)
- уравнение направляющей \(x=h−p=−3−(−4)=1\)
- концы широкой прямой кишки равны \((h+p,k\pm 2p)=(−3+(−4),1\pm 2(−4))\), или \((−7,− 7)\) и \((−7,92=4(х-8)\). Определите и обозначьте вершину, ось симметрии, фокус, направляющую и конечные точки прямой кишки latus .
- Ответить
- Вершина: \((8,−1)\)
- Ось симметрии: \(y=−1\)
- Фокус: \((9,−1)\)
- Директриса: \(x=7\)
- Концы широкой прямой кишки : \((9,−3)\) и \((9,1)\).

92&= 4⋅7⋅(y+8) \end{align*}\]- вершина \((h,k)=(4,−8)\)
- ось симметрии \(x=h=4\)
- так как \(p=7\), \(p>0\) и таким образом парабола раскрывается
- координаты фокуса равны \((h,k+p)=(4,−8+7)=(4,−1)\)
- уравнение направляющей имеет вид \(y=k−p=−8−7=−15\)
- концы широкой прямой кишки равны \((h\pm 2p,k+p)=(4\pm 2(7),−8+7)\) или \((−10,−1)\) и \((18,−1)\) 92=−20(y−3)\). Определите и обозначьте вершину, ось симметрии, фокус, направляющую и конечные точки прямой кишки latus .
- Ответить
- Вершина: \((−2,3)\)
- Ось симметрии: \(x=−2\)
- Фокус: \((−2,−2)\)
- Директриса: \(y=8\)
- Конечные точки широкой прямой кишки : \((−12,−2)\) и \((8,−2)\).
Решение прикладных задач с использованием парабол
Как мы упоминали в начале раздела, параболы используются для проектирования многих объектов, которые мы используем каждый день, таких как телескопы, подвесные мосты, микрофоны и радиолокационное оборудование.
Рисунок \(\PageIndex{16}\): Отражающее свойство парабол Параболические зеркала, такие как то, которое использовалось для зажигания олимпийского огня, обладают уникальными отражающими свойствами. Когда лучи света, параллельные оси симметрии параболы, направляются на любую поверхность зеркала, свет отражается прямо в фокус (рис. \(\PageIndex{16}\)). Вот почему олимпийский факел зажигается, когда его держат в фокусе параболического зеркала.
Параболические зеркала, такие как то, которое использовалось для зажигания олимпийского огня, обладают уникальными отражающими свойствами. Когда лучи света, параллельные оси симметрии параболы, направляются на любую поверхность зеркала, свет отражается прямо в фокус (рис. \(\PageIndex{16}\)). Вот почему олимпийский факел зажигается, когда его держат в фокусе параболического зеркала.Параболические зеркала способны фокусировать солнечную энергию в одной точке, повышая температуру на сотни градусов за считанные секунды. Таким образом, параболические зеркала используются во многих недорогих, энергоэффективных солнечных продуктах, таких как солнечные плиты, солнечные обогреватели и даже дорожные разжигатели огня.
Пример \(\PageIndex{6}\): решение прикладных задач, связанных с параболами
На рисунке \(\PageIndex{17}\) показано поперечное сечение конструкции переносного солнечного пожарного пускателя. Солнечные лучи отражаются от параболического зеркала к объекту, прикрепленному к воспламенителю.
 2=4py\), где \(p>0\). Воспламенитель, который является фокусом, находится на \(1,7\) дюймах выше вершины тарелки. Таким образом, мы имеем \(p=1,7\). 92&=6.8y\qquad \text{Подставить } 2.25 \text{ вместо } x\\ y&\ приблизительно 0.74\qquad \text{Решить для } y \end{align*}\]
2=4py\), где \(p>0\). Воспламенитель, который является фокусом, находится на \(1,7\) дюймах выше вершины тарелки. Таким образом, мы имеем \(p=1,7\). 92&=6.8y\qquad \text{Подставить } 2.25 \text{ вместо } x\\ y&\ приблизительно 0.74\qquad \text{Решить для } y \end{align*}\]Блюдо примерно \(0.74 \) дюймов глубиной.
Упражнение \(\PageIndex{6}\)
Солнечные плиты размером с балкон были разработаны для семей, живущих в Индии. Верх блюда имеет диаметр \(1600\) мм. Солнечные лучи отражаются от параболического зеркала в сторону «варки», расположенной \(320\) мм от основания.
- Найдите уравнение, моделирующее поперечное сечение солнечной плиты. Предположим, что вершина параболического зеркала является началом координатной плоскости и что парабола выходит вправо (т. е. имеет 92=4р(у-к)\)
Ключевые понятия
- Парабола — это множество всех точек \((x,y)\) на плоскости, находящихся на одинаковом расстоянии от фиксированной прямой, называемой направляющей, и фиксированной точки (директрисы).
 фокус) не на директрисе.
фокус) не на директрисе. - Для построения графика параболы можно использовать стандартную форму параболы с вершиной \((0,0)\) и осью x в качестве оси симметрии. Если \(p>0\), парабола открывается вправо. Если \(p<0\), парабола открывается влево. См. пример \(\PageIndex{1}\).
- Стандартная форма параболы с вершиной \((0,0)\) и осью y в качестве оси симметрии может быть использована для построения графика параболы. Если \(p>0\), парабола раскрывается. Если \(p<0\), парабола раскрывается вниз. См. пример \(\PageIndex{2}\).
- Зная фокус и направляющую параболы, мы можем записать ее уравнение в стандартной форме. См. пример \(\PageIndex{3}\).
- Для построения параболы можно использовать стандартную форму параболы с вершиной \((h,k)\) и осью симметрии, параллельной оси \(x\). Если \(p>0\), парабола открывается вправо. Если \(p<0\), парабола открывается влево. См. пример \(\PageIndex{4}\).
- Для построения параболы можно использовать стандартную форму параболы с вершиной \((h,k)\) и осью симметрии, параллельной оси \(y\) .

- Парабола — это множество всех точек \((x,y)\) на плоскости, находящихся на одинаковом расстоянии от фиксированной прямой, называемой направляющей, и фиксированной точки (директрисы).
Отсюда следует, что:
Пример \(\PageIndex{4}\): построение параболы с вершиной \((h, k)\) и осью симметрии, параллельной оси \(x\) 92=4p(x−h)\). Таким образом, ось симметрии параллельна оси \(х\). Отсюда следует, что:
- \(24=4p\), значит \(p=6\).

 Так как \(p>0\), парабола выходит вправо
Так как \(p>0\), парабола выходит вправо 2=4p(y−k)\) для парабол, у которых ось симметрии параллельна оси \( у\)-ось. Эти стандартные формы приведены ниже вместе с их общими графиками и ключевыми характеристиками.
2=4p(y−k)\) для парабол, у которых ось симметрии параллельна оси \( у\)-ось. Эти стандартные формы приведены ниже вместе с их общими графиками и ключевыми характеристиками. 2=4p(y−k)\). 92=4p(x−h)\), тогда:
2=4p(y−k)\). 92=4p(x−h)\), тогда: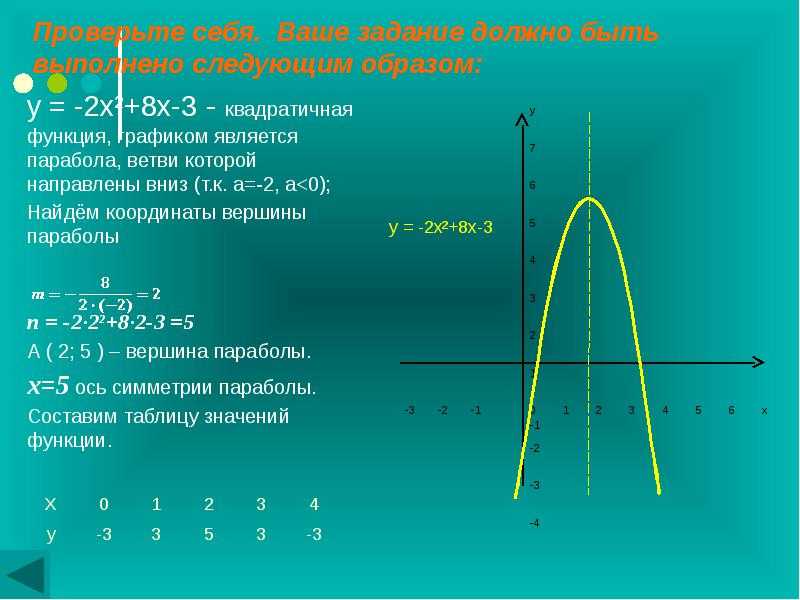
 Параболические зеркала, такие как то, которое использовалось для зажигания олимпийского огня, обладают уникальными отражающими свойствами. Когда лучи света, параллельные оси симметрии параболы, направляются на любую поверхность зеркала, свет отражается прямо в фокус (рис. \(\PageIndex{16}\)). Вот почему олимпийский факел зажигается, когда его держат в фокусе параболического зеркала.
Параболические зеркала, такие как то, которое использовалось для зажигания олимпийского огня, обладают уникальными отражающими свойствами. Когда лучи света, параллельные оси симметрии параболы, направляются на любую поверхность зеркала, свет отражается прямо в фокус (рис. \(\PageIndex{16}\)). Вот почему олимпийский факел зажигается, когда его держат в фокусе параболического зеркала. 2=4py\), где \(p>0\). Воспламенитель, который является фокусом, находится на \(1,7\) дюймах выше вершины тарелки. Таким образом, мы имеем \(p=1,7\). 92&=6.8y\qquad \text{Подставить } 2.25 \text{ вместо } x\\ y&\ приблизительно 0.74\qquad \text{Решить для } y \end{align*}\]
2=4py\), где \(p>0\). Воспламенитель, который является фокусом, находится на \(1,7\) дюймах выше вершины тарелки. Таким образом, мы имеем \(p=1,7\). 92&=6.8y\qquad \text{Подставить } 2.25 \text{ вместо } x\\ y&\ приблизительно 0.74\qquad \text{Решить для } y \end{align*}\]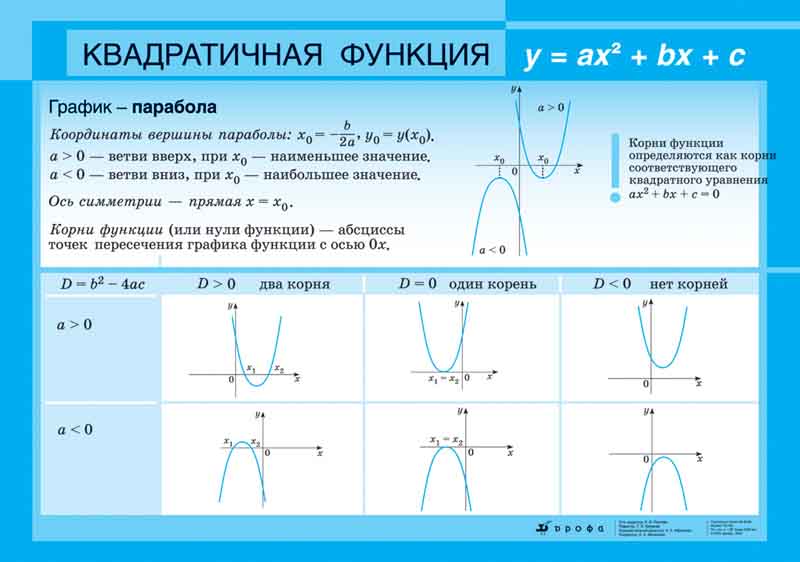 фокус) не на директрисе.
фокус) не на директрисе.