8. Формулы Крамера решения систем линейных алгебраических уравнений.
Метод Крамера состоит в том, что мы последовательно находим главный определитель системы (5.3), т.е. определитель матрицы А
= det (aij)
и n вспомогательных определителей i (i=), которые получаются из определителя заменой i-го столбца столбцом свободных членов.
Формулы Крамера имеют вид:
xi= i( i = ). (5.4)
Из (5.4) следует правило Крамера, которое дает исчерпывающий ответ на вопрос о совместности системы (5.3): если главный определитель системы отличен от нуля, то система имеет единственное решение, определяемое по формулам:
x i= i/ .
Если главный определитель системы и все вспомогательные определители i = 0 (i= ), то система имеет бесчисленное множество решений. Если главный определитель системы = 0, а хотя бы один вспомогательный определитель отличен от нуля, то система несовместна.
Пример 2.14. Решить методом Крамера систему уравнений:
x1 + x2 + x3 + x4 = 5,
x1 + 2x2 — x3 + 4x4 = -2,
2x1 — 3x2 — x3 — 5x4 = -2,
3x1 + x 2 +2x3 + 11 x4 = 0.
Решение. Главный определитель этой системы
значит, система имеет единственное решение. Вычислим вспомогательные определители i ( i = ), получающиеся из определителя путем замены в нем столбца, состоящего из коэффициентов при xi, столбцом из свободных членов:
Отсюда x1 = 1/ = 1, x2 = 2/ = 2, x3 = 3/ = 3, x4 = 4/ = -1, решение системы — вектор С=(1, 2, 3, -1)T.
9. Метод Гаусса решения систем линейных алгебраических уравнений.
Наиболее распространенным методом решения систем линейных уравнений является метод Гаусса, или метод последовательного исключения неизвестных. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной. При практическом решении системы линейных уравнений методом Гаусса удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу этой системы, выполняя элементарные преобразования над ее строками. Последовательно получающиеся в ходе преобразования матрицы обычно соединяют знаком эквивалентности.
Пример 2.13. Решить систему уравнений методом Гаусса:
x + y — 3z = 2,
3x — 2y + z = — 1,
2x + y — 2z = 0.
Решение. Выпишем расширенную матрицу данной системы
и произведем следующие элементарные преобразования над ее строками:
а) из ее второй и третьей строк вычтем первую, умноженную соответственно на 3 и 2:
~ ;
б) третью строку умножим на (-5) и прибавим к ней вторую:
.
В результате всех этих преобразований данная система приводится к треугольному виду:
x + y — 3z = 2,
-5y + 10z = -7,
— 10z = 13.
Из последнего уравнения находим z = -1,3. Подставляя это значение во второе уравнение, имеем y = -1,2. Далее из первого уравнения получим x = — 0,7.
studfiles.net
6.Решение линейных систем по формулам Крамера
Дана система, в которой число уравнений совпадает с числом неизвестных
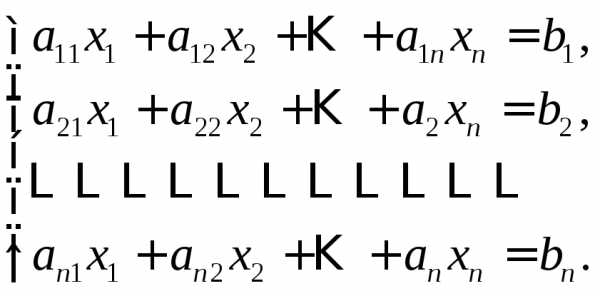 (10)
(10)
Определитель, составленный из коэффициентов системы
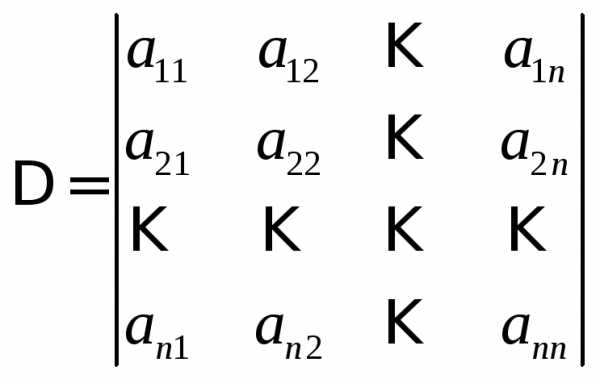 ,
,
называется главным определителем системы.
Если главный
определитель системы не равен нулю, то
система имеет единственное решение и  ,
где
,
где
Определители , получены из главного определителя заменой соответствующего столбца на столбец свободных членов.
►Пример 8. По
формулам Крамера найти решение системы
уравнений 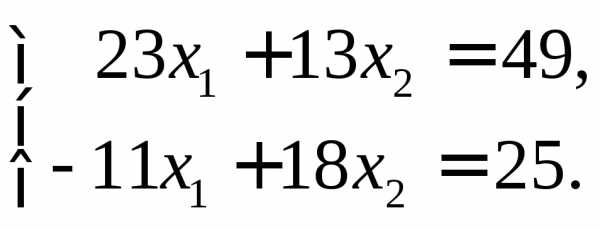
Решение.
Вычислим определители и найдем решение
Ответ: 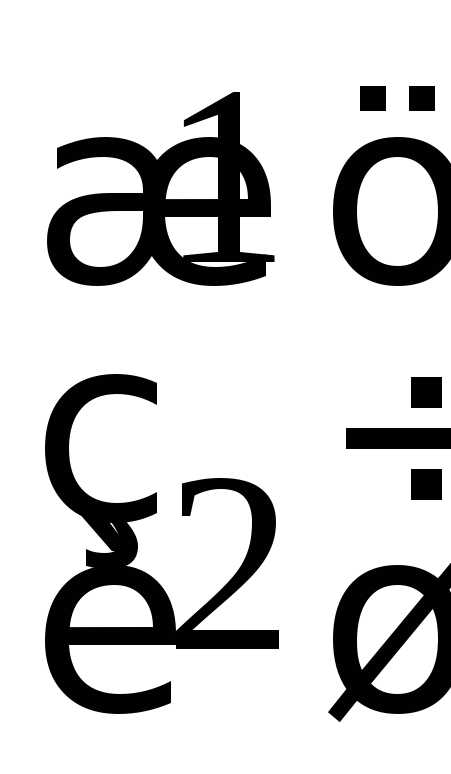 .◄
.◄
Упражнения.
Решить системы по формулам Крамера.
1)  2)
2)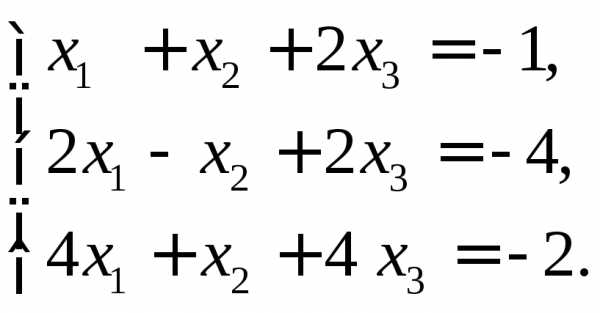 3)
3)
 ,
2)
,
2)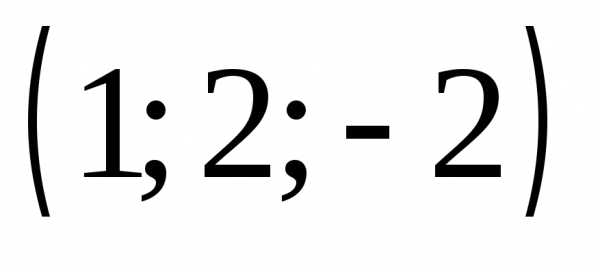 ,
3)
,
3)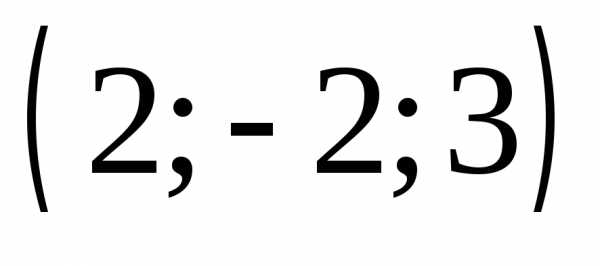 .
.
7. Решение систем с помощью обратной матрицы
Система из  уравнений с
уравнений с неизвестными (10) в матричной форме
имеет вид (5)
неизвестными (10) в матричной форме
имеет вид (5)
,
где 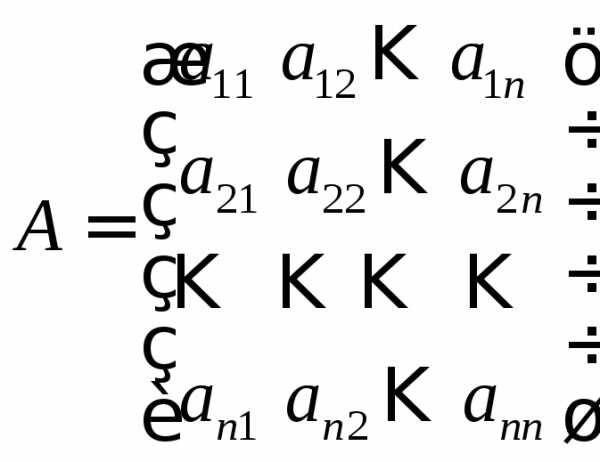 ,
,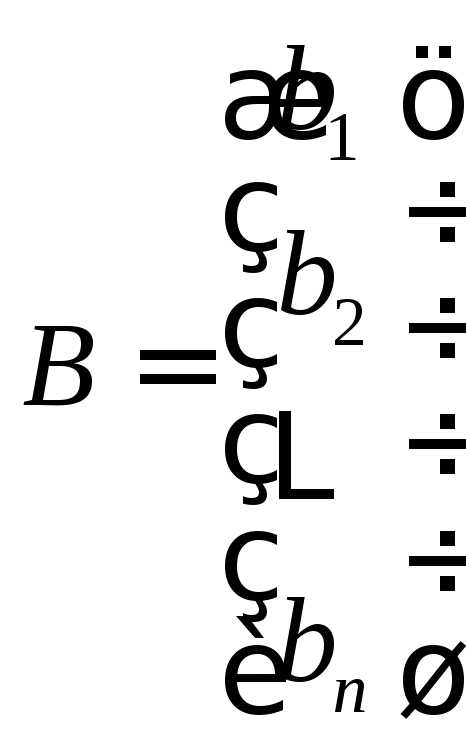 ,
, .
.
Если матрица  невырожденная, то система имеет
единственное решение, которое вычисляется
по формуле.
невырожденная, то система имеет
единственное решение, которое вычисляется
по формуле.
►Пример 9. С помощью обратной матрицы найти решение системы
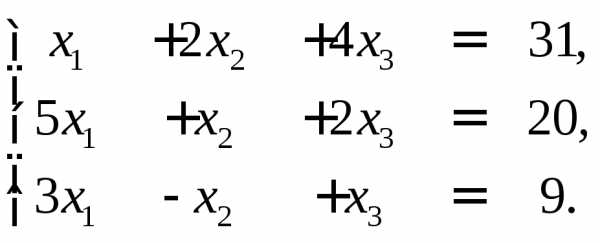
Решение.
Проведем необходимые вычисления
.
Ответ: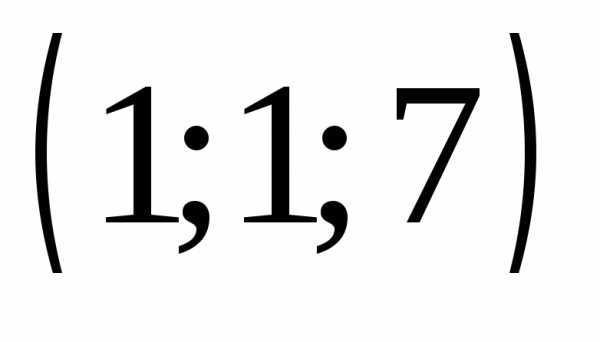 .
◄
.
◄
Упражнения.
Найти решение систем с помощью обратной матрицы.
а) 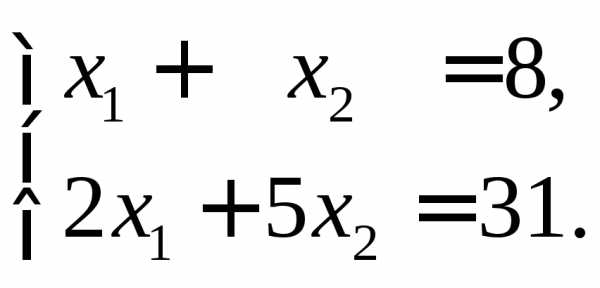 б)
б)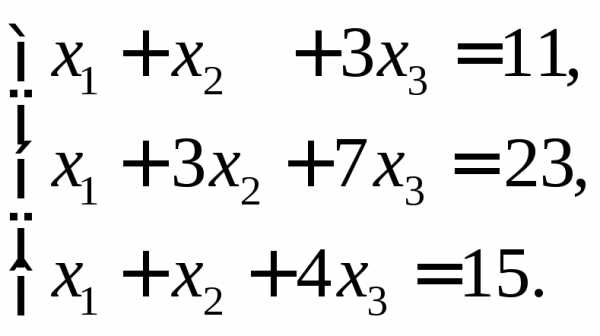 в)
в)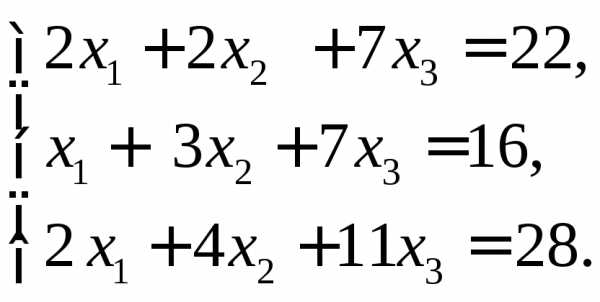
г) 
 ;
б)
;
б)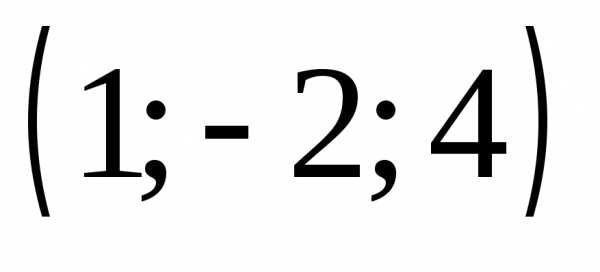 ;
в)
;
в)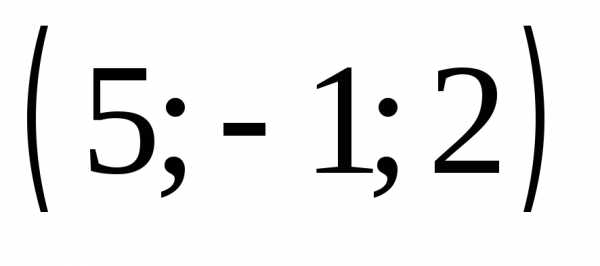 4
г)
4
г) .
.8. Исследование систем линейных уравнений. Метод Гаусса.
Рассмотрим линейную систему общего вида:
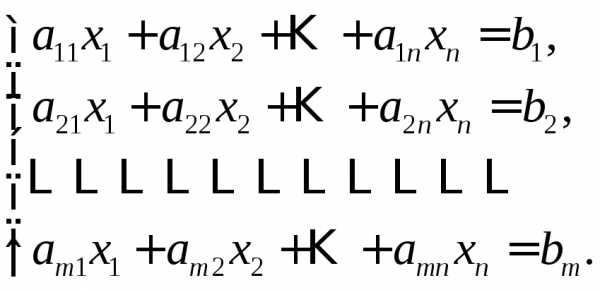
Теорема (Кронекера-Капелли).
Для совместности
системы линейных уравнений необходимо
и достаточно, чтобы ранг ее основной
матрицы (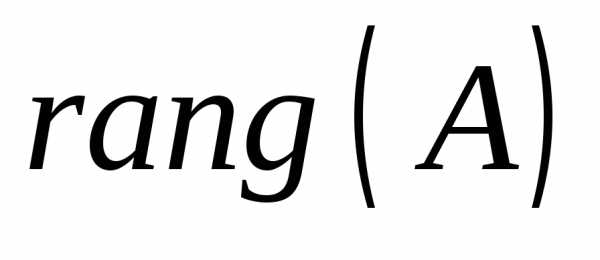 )
был равен рангу расширенной матрицы
(
)
был равен рангу расширенной матрицы
(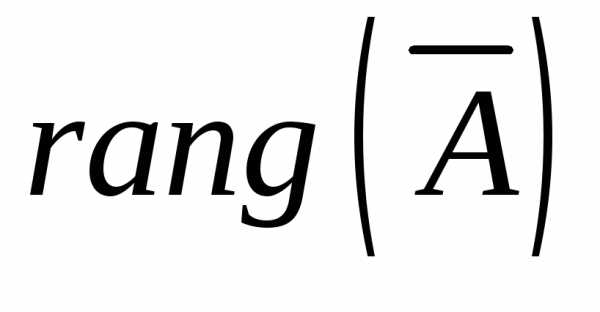 ).
).
Пусть 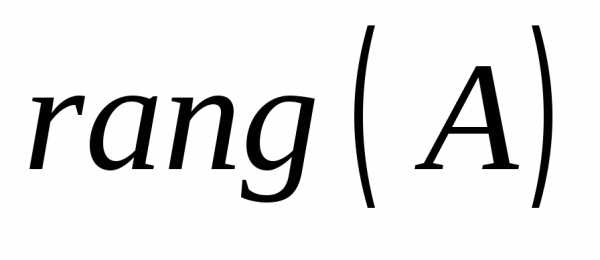
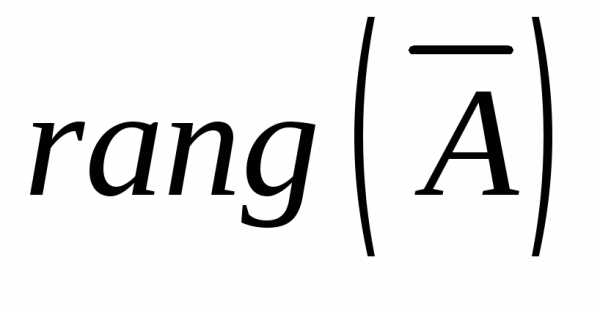 =
=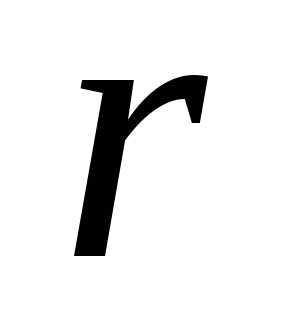 .
Тогда верны следующие утверждения.
.
Тогда верны следующие утверждения. Следствие
1. Если ранг
матрицы 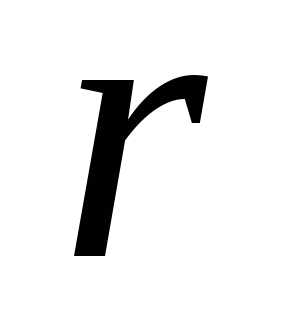 равен числу неизвестных
равен числу неизвестных ,
то система имеет единственное решение.
,
то система имеет единственное решение.
Следствие
2. Если ранг
матрицы 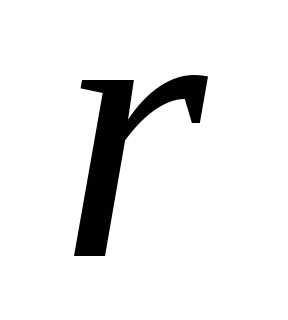 меньше числа неизвестных, то система
имеет бесконечное множество решений.
При этом
меньше числа неизвестных, то система
имеет бесконечное множество решений.
При этом неизвестных, которые называются
свободными, принимают произвольные
значения. Говорят, что система имеет
неизвестных, которые называются
свободными, принимают произвольные
значения. Говорят, что система имеет степеней свободы.
степеней свободы.
Метод Гаусса
Составим расширенную матрицу систему и отделим для удобства свободные члены вертикальной линией. С помощью элементарных преобразований приводим матрицу к треугольному виду. Элементарные преобразования матрицы проводим только для строк.
Умножая первую строку на соответствующие коэффициенты и прибавляя к лежащим ниже строкам, получим нули в первом столбце. Затем проделываем такую же процедуру со второй строкой, третьей и т.д., до предпоследней строки. В результате преобразований получаем матрицу, по которой можно записать систему, равносильную исходной.
Рассмотрим три ситуации, возникающие при исследовании линейных систем.
1) .Система несовместна.
►Пример 10.
Решить систему уравнений методом Гаусса.
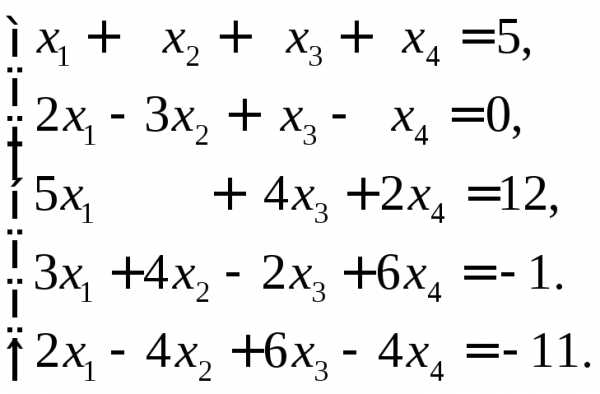
Решение.
Составим расширенную матрицу и преобразуем ее
.
Для удобства вычислений переставим четвертую строку на место второй и за счет второй строки получим нули во втором столбце во всех строках ниже второй, а затем за счет третьей строки — в третьем столбце.
В четвертой строке легко было получить нули, умножив третью строку на минус единицу и прибавив ее к четвертой. Мы не упрощали вычислений, чтобы сохранить алгоритм получения нулей в нижележащих строках за один шаг.
По преобразованной матрице определяем ранги: ,, следовательно, данная система уравнений несовместна.
.
Ответ: система не имеет решений. ◄
2) .Система совместна и имеет единственное решение. В результате преобразований приходим к ступенчатой системе, решение которой легко находится.
►Пример 11. Решить систему уравнений методом Гаусса
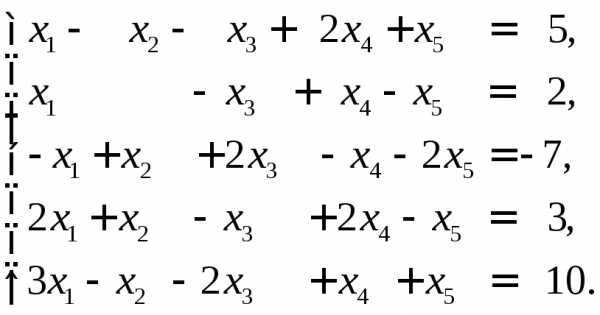
Решение.

Ранг основной матрицы равен рангу расширенной матрицы и равен числу неизвестных. Следовательно, система совместна и имеет единственное решение. По преобразованной матрице составляем систему, равносильную исходной

Полученная система имеет ступенчатый вид и легко решается.
Ответ: .◄
3) .Система совместна, но имеет бесконечное множество решений. Это множество решений находим, перенося члены со свободными неизвестными в правую часть уравнений.
Рассмотрим запись решения таких систем в матричной форме.
Пусть дана система
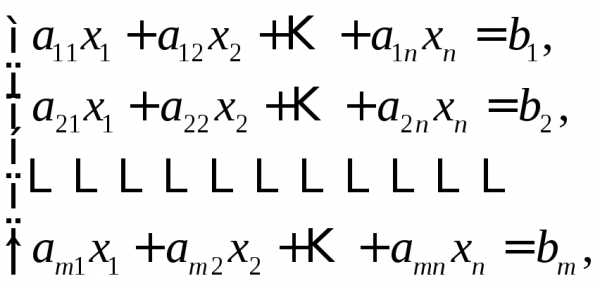
и известно, что
.
Тогда система имеет степеней свободы, т.е.
степеней свободы, т.е. неизвестных принимают произвольные
значения, а
неизвестных принимают произвольные
значения, а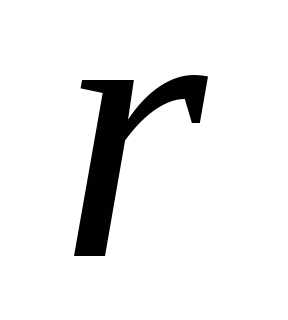 неизвестных выражаются через них.
Минор, не равный нулю, напоминаем,
называетсябазисным.
Не уменьшая общности, будем считать,
что базисный минор системы занимает в
ней верхний левый угол. Обозначим этот
минор
неизвестных выражаются через них.
Минор, не равный нулю, напоминаем,
называетсябазисным.
Не уменьшая общности, будем считать,
что базисный минор системы занимает в
ней верхний левый угол. Обозначим этот
минор 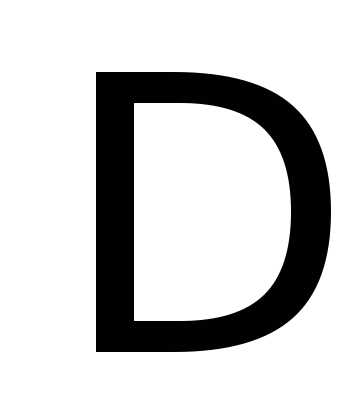 :
:
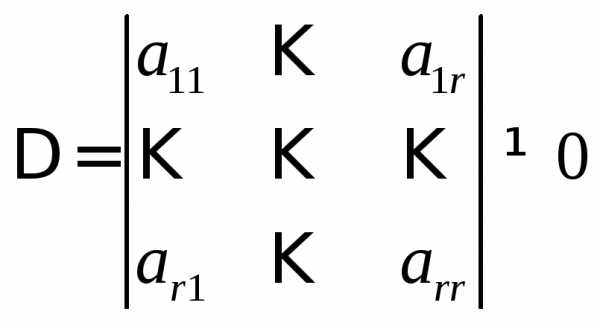 .
.
Минор 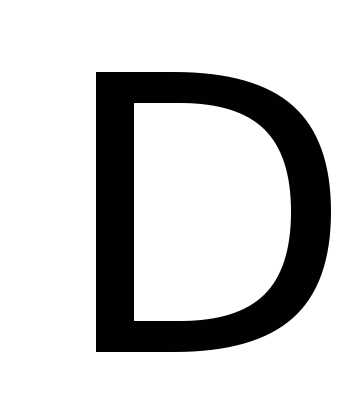 является базисным и для матрицы
является базисным и для матрицы ,
поэтому строки с номерами
,
поэтому строки с номерами являются линейными комбинациями первых
являются линейными комбинациями первых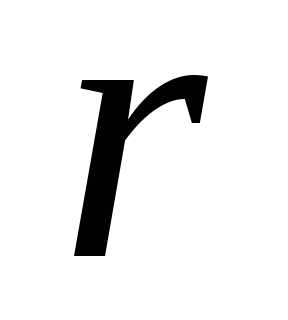 строк и система эквивалентна системе
из
строк и система эквивалентна системе
из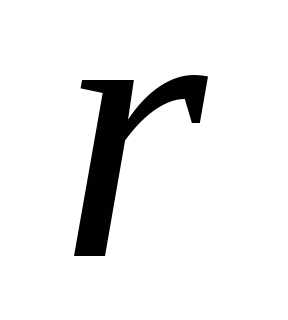 уравнений (свободные неизвестные
перенесены в правую часть)
уравнений (свободные неизвестные
перенесены в правую часть)
Решая эту систему по методу Крамера, имеем
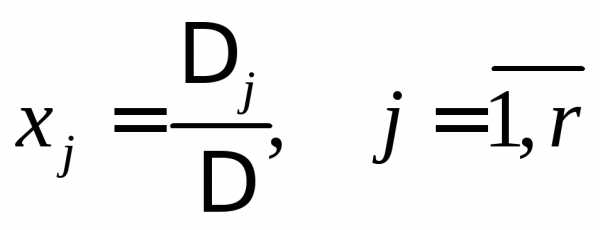 ,
,
где
— определитель,
полученный из базисного заменой 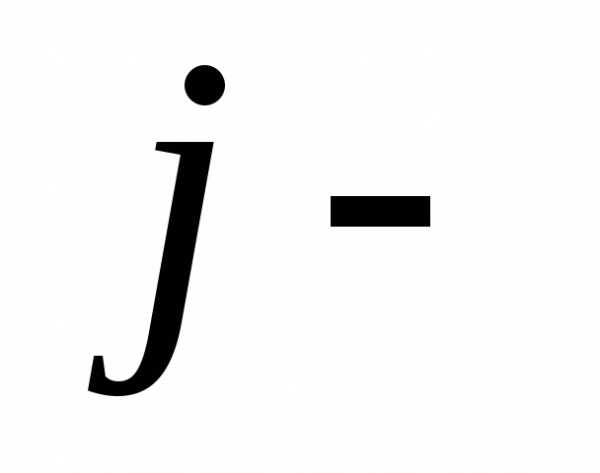 го
столбца на столбец правой части системы.
Пользуясь свойствами определителей,
имеем
го
столбца на столбец правой части системы.
Пользуясь свойствами определителей,
имеем
. (11)
Символ:  ,-
означает, что
,-
означает, что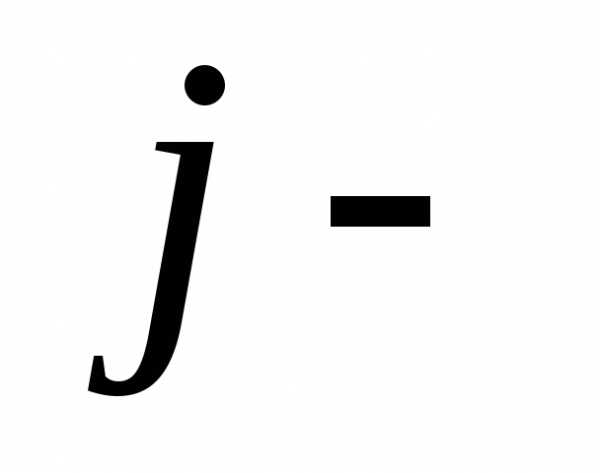 й
столбец базисного минора заменен на
столбец коэффициентов при неизвестном
й
столбец базисного минора заменен на
столбец коэффициентов при неизвестном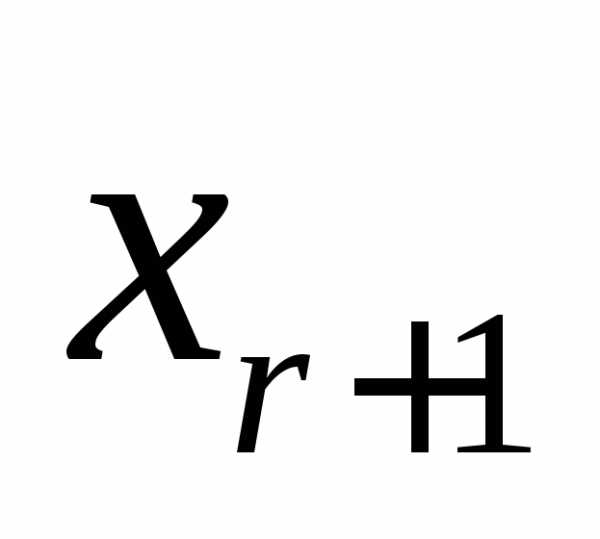 .
Вектор,
является решением системы, Главный
определитель системы совпадает с
базисным минором, а свободные члены
равны коэффициентам при неизвестном
.
Вектор,
является решением системы, Главный
определитель системы совпадает с
базисным минором, а свободные члены
равны коэффициентам при неизвестном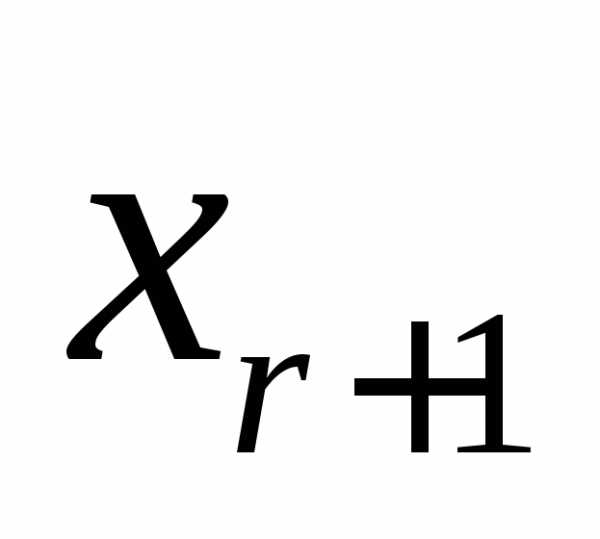 .
Введем обозначения
.
Введем обозначения
.
Тогда множество решений системы можно записать в виде
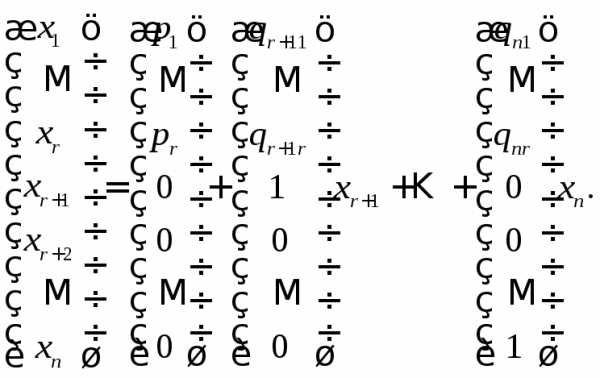 (12)
(12)
Для вычисления
полагаем свободные неизвестные равными
нулю. Для вычисленияполагаем свободные члены равными нулю,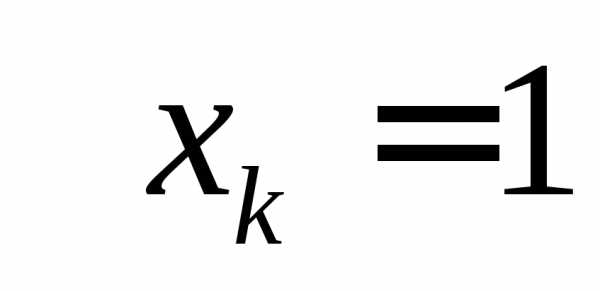 ,
а остальные свободные неизвестные
равными нулю.
,
а остальные свободные неизвестные
равными нулю.
. Выбор свободных
неизвестных, вообще говоря, можно делать
по-разному. Однако не всякие  неизвестных можно принять за свободные.
Необходимо, чтобы коэффициенты при
остальных
неизвестных можно принять за свободные.
Необходимо, чтобы коэффициенты при
остальных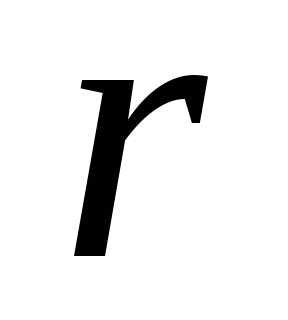 неизвестных составили базисный минор.
неизвестных составили базисный минор.
►Пример 12. Решить систему уравнений

Решение.
Преобразуем расширенную матрицу системы
.
Ранг основной
матрицы равен рангу расширенной матрицы
,
но меньше числа неизвестных. Следовательно,
система совместна, но имеет бесконечное
множество решений. Число степеней
свободы равно двум. Выберем свободными
неизвестными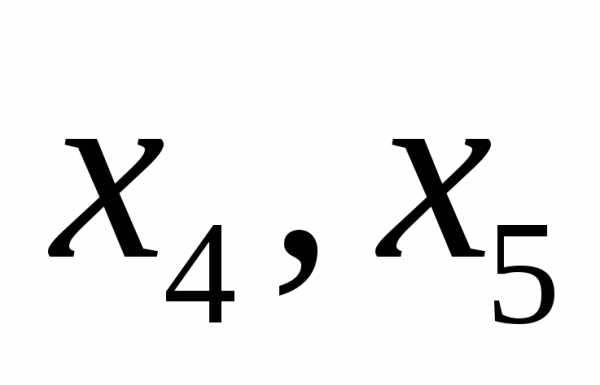 и выразим
и выразим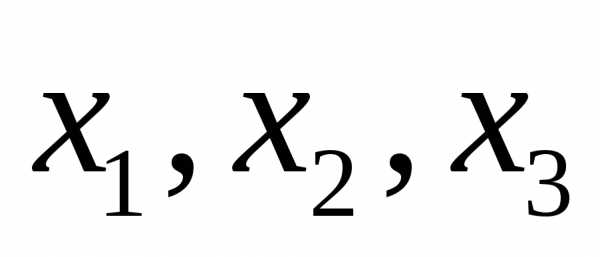 через них.
через них.

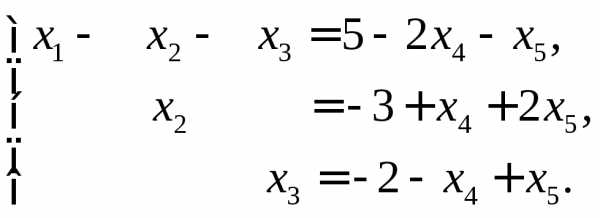 отсюда получаем
отсюда получаем 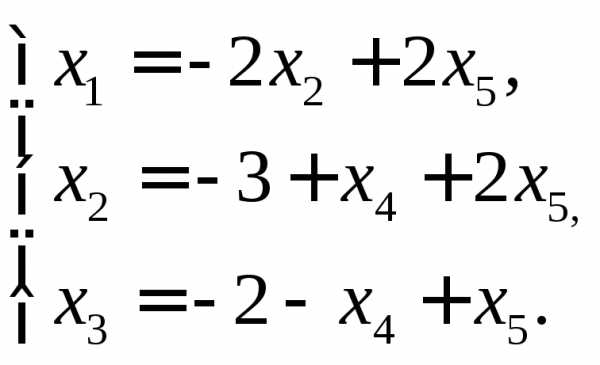
Ответ запишем в виде вектора-столбца.
Ответ: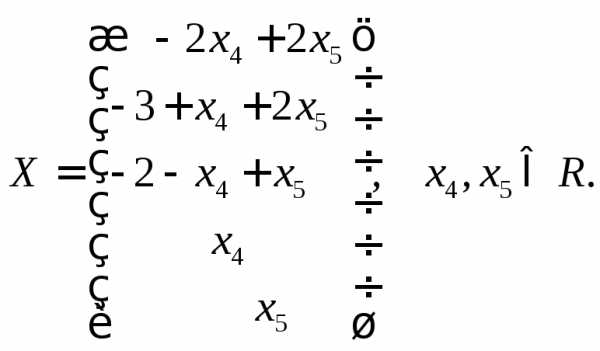 .
◄
.
◄
Получим также
решение заданной системы, используя
формулу (11). Положим
.
 Получаем вектор
Получаем вектор 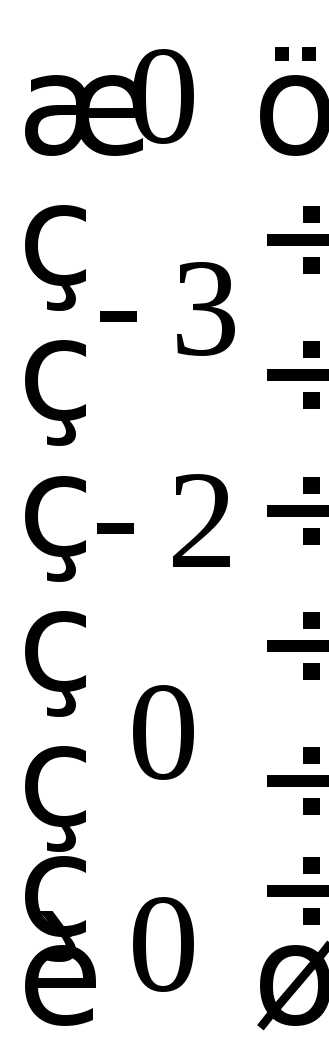 .
.
Положим .
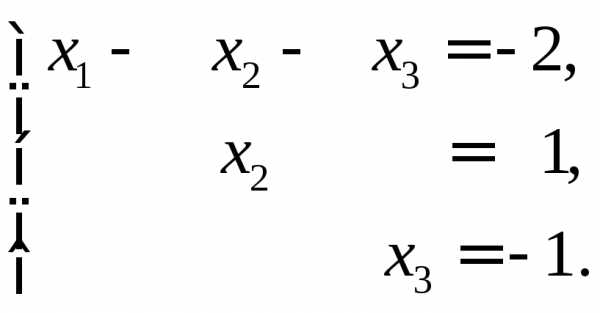 Получаем вектор
Получаем вектор 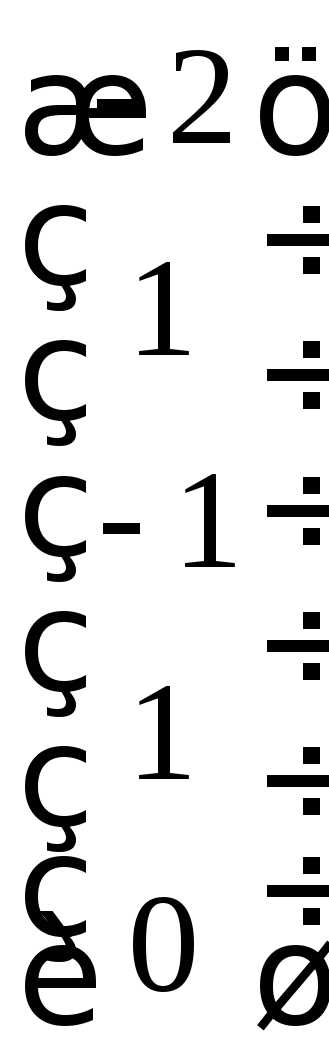 .
.
Положим .
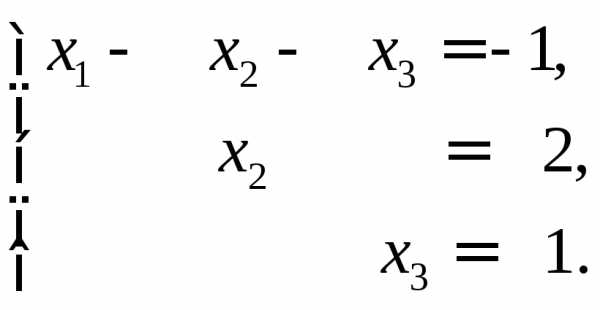 Получаем вектор
Получаем вектор 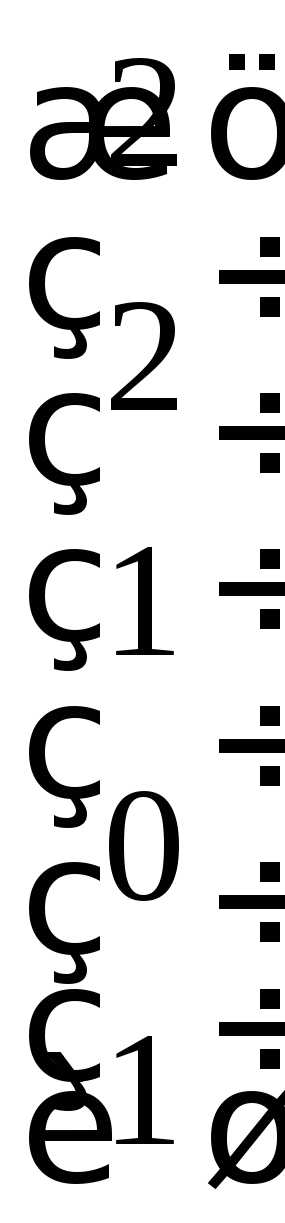 .
.
Окончательное
решение: 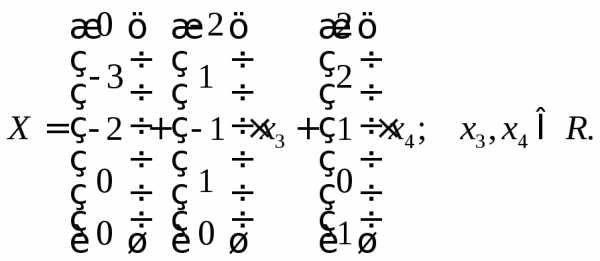 ◄
◄
Упражнения.
Исследовать и решить системы уравнений.
1. 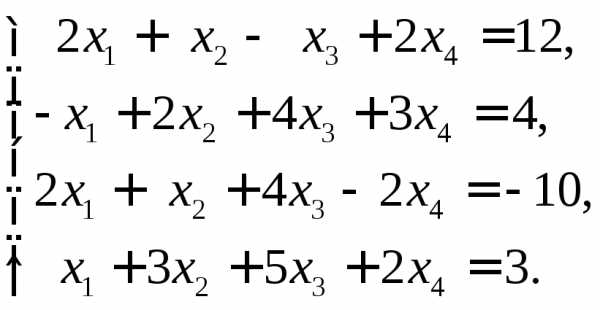 Ответ:
Ответ: 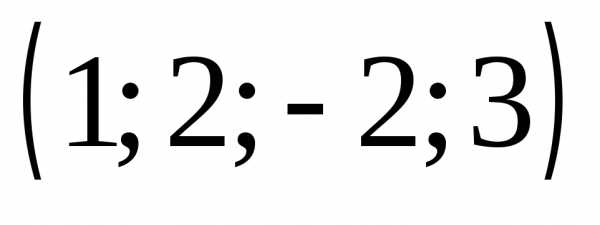 .
.
2.  Ответ:
Ответ: 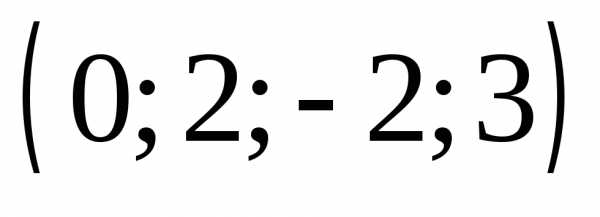 .
.
3. 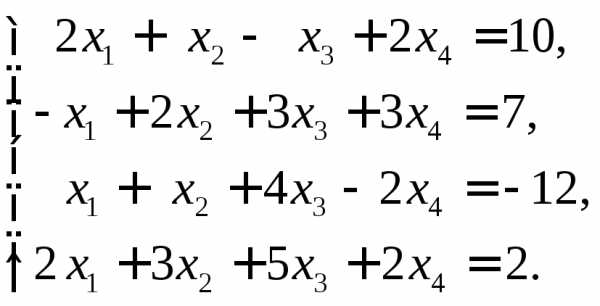 Ответ:
Ответ: 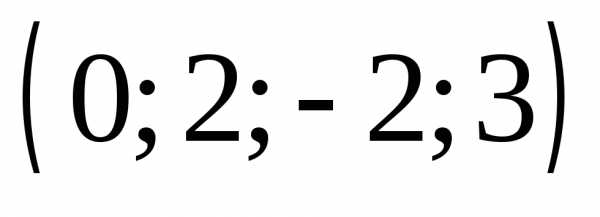 .
.
4.  Ответ: .
Ответ: .
5. 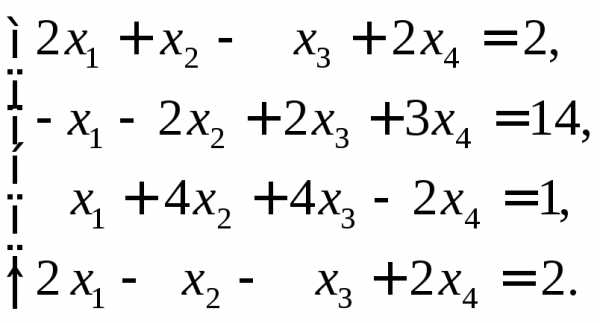 Ответ:
Ответ: 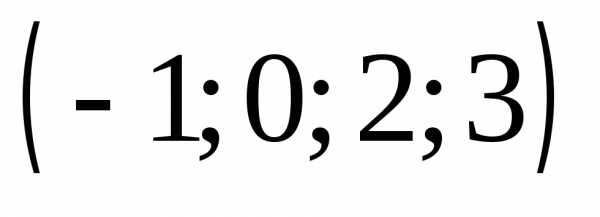 .
.
6. 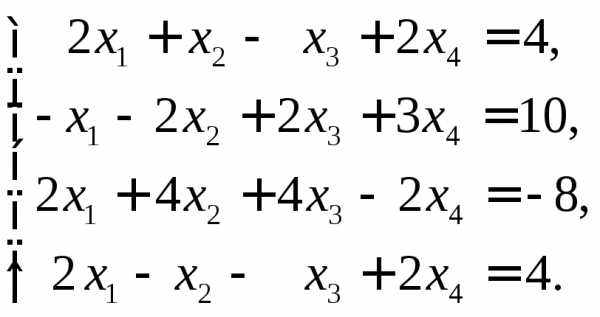 Ответ:
Ответ:  .
.
7. 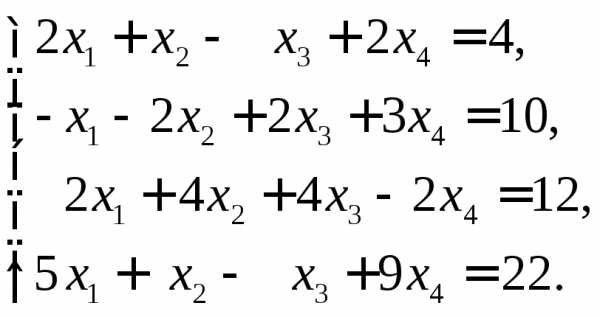 Ответ:
Ответ: 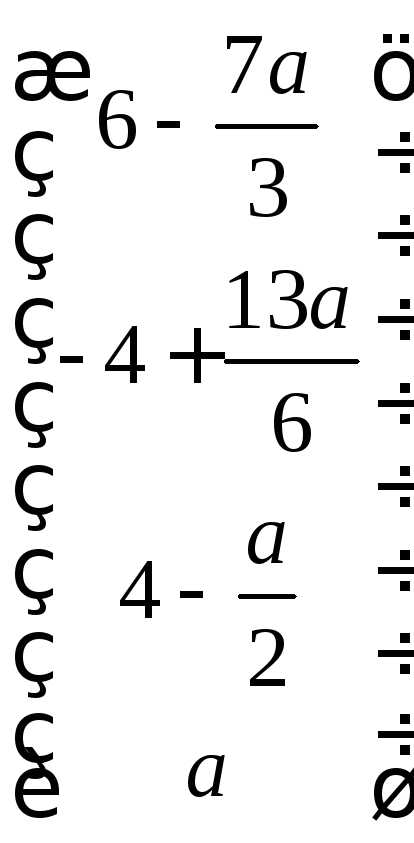 .
.
8. 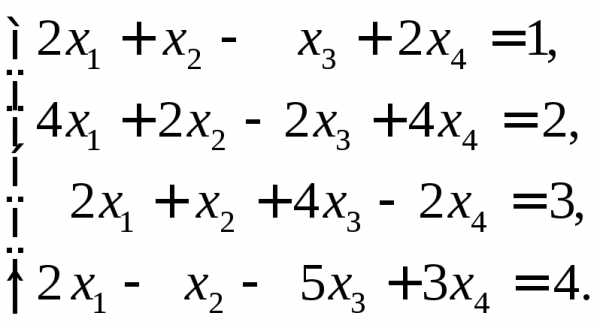 Ответ:
Ответ:  .
.
9. 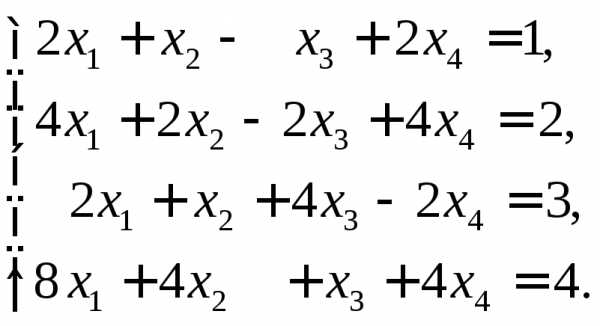 Ответ:
Ответ:  .
.
10. 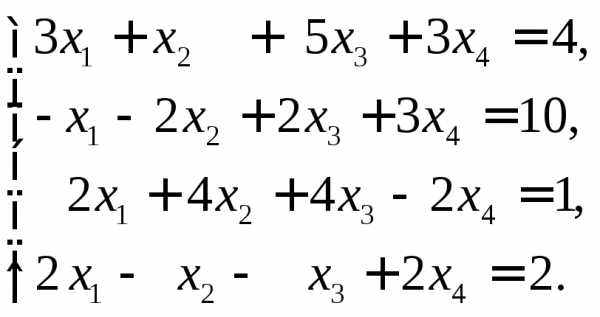 Ответ:
Ответ: 
studfiles.net
Решение систем линейных уравнений методом Крамера онлайн
Одним из способов решения системы линейных алгебраических уравнений (СЛАУ) является метод Крамера . Предположим, нам дана СЛАУ вида:
Требуется её решить, т.е. найти такие значения переменных x1, x2, x3 чтобы при подстановке их в исходную СЛАУ, последняя обращалась в верное тождество. Чтобы проиллюстрировать метод Крамера, запишем исходную СЛАУ в матричной форме:
Первым шагом метода Крамера, является нахождение определителя матрицы СЛАУ:
Если полученный определитель отличен от нуля, тогда исходная СЛАУ имеет единственное решение, которое может быть найдено методом Крамера. Если полученный определитель равен нулю, тогда исходная СЛАУ может не иметь решений или иметь бесконечное множество решений которые не могут быть найдены методом Крамера.
Предположим, что полученный определитель не равен нулю:
тогда, по методу Крамера, решения находятся по формулам:
причем ∆x, ∆y и ∆z — определители полученные из определителя ∆ путем замены соответствующего столбца на вектор свободных коэффициентов. Например, определитель ∆x получается из определителя ∆ путем замены 1-ого столбца на вектор свободных коэффициентов:
аналогичным образом нужно сформировать определители ∆y и ∆z. Стоит отметить, что метод Крамера применим к СЛАУ в которых число уравнений равно числу неизвестных.
Данный онлайн калькулятор решает СЛАУ методом Крамера с описанием пошагового хода решения на русском языке. Коэффициенты СЛАУ могут быть не только числами или дробями, но также и параметрами. Для работы калькулятора необходимо ввести уравнения и выбрать переменные СЛАУ, которые необходимо найти.
www.mathforyou.net
