Неполные квадратные уравнения 🐲 СПАДИЛО.РУ
ОпределениеКвадратным уравнением называется уравнение вида ax2+bx+c=0, где х – переменная, a, b, c некоторые числа, причем a≠0. Обычно его называют полным квадратным уравнением.
Если в таком уравнении один из коэффициентов b или c равен нулю, либо оба одновременно равны нулю, то такое уравнение называется неполным квадратным уравнением.
Неполное квадратное уравнение при b=0: ax2+c=0
Для решения такого вида уравнения надо выполнить перенос коэффициента с в правую часть, затем найти квадрат переменной (делим обе части на одно и то же число), найти два корня уравнения, либо доказать, что корней нет (если х2 равен отрицательному коэффициенту; знаем, что квадрат любого числа равен только положительному числу).
Пример №1. Решить уравнение:
5х2–45=0
Выполним перенос числа –45 в правую часть, изменяя знак на противоположный: 5х2=45; найдем переменную в квадрате, поделив обе части уравнения на 5: х2=9. Видим, что квадрат переменной равен положительному числу, поэтому уравнение имеет два корня, находим их устно, извлекая квадратный корень из числа 9, получим –3 и 3. Оформляем решение уравнения обычным способом:
5х2–45=0
5х2=45
х2=9
Ответ: х=±3 или можно записать ответ так: х1=–3, х2=3 (обычно меньший корень записывают первым).
Пример №2. Решить уравнение:
–6х2–90=0
Выполним решение уже известным способом: –6х2=90. х2=–15 Здесь видим, что квадрат переменной равен отрицательному числу, а это значит, что уравнение не имеет корней. Ответ: нет корней.
Пример №3. Решить уравнение:
х2–100=0
Здесь мы видим в левой части уравнения формулу сокращенного умножения (разность квадратов двух выражений). Поэтому, можем разложить данное выражение на множители, и найти корни уравнения: (х–10)(х+10)=0. Соответственно, вспомним, что произведение двух множителей равно нулю тогда, когда хотя бы один из множителей равен нулю, то есть х–10=0 или х+10=0. Откуда имеем два корня х1=10, х2=–10.
Неполное квадратное уравнение при с=0: ax2+bx=0
Данного вида уравнение решается способом разложения на множители – вынесением за скобки переменной. Данное уравнение всегда имеет два корня, один из которых равен нулю. Рассмотрим данный способ на примерах.
Пример №4. Решить уравнение:
х2+8х=0
Выносим переменную х за скобки: х(х+8)=0. Получаем два уравнения х=0 или х+8=0. Отсюда данное уравнение имеет два корня – это 0 и –8.
Пример №5. Решить уравнение:
3х2–12х=0
Здесь кроме переменной можно вынести за скобки еще и коэффициент 3, который является общим множителем для данных в уравнении коэффициентов. Получим: 3х(х–4)=0. Получаем два уравнения 3х=0 и х–4=0. Соответственно и два корня – нуль и 4.
Неполное квадратное уравнение с коэффициентами b и с равными нулю: ax2=0
Данное уравнение при любых значениях коэффициента а будет иметь один корень, равный нулю.
Пример №6. Решить уравнение:
–14х2=0
Обе части уравнения делим на (–14) и получаем х2=0, откуда соответственно и единственный корень – нуль.
Пример №6. Решить уравнение:
23х2=0
Также делим обе части на 23 и получаем х2=0. Значит, корень уравнения – нуль.
Неполные квадратные уравнения. Примеры и решение
Неполное квадратное уравнение – это уравнение вида
ax2 + bx + c = 0,
в котором хотя бы один из коэффициентов b или c равен нулю. Следовательно, неполное квадратное уравнение может иметь вид:
| ax2 + bx = 0, | если c = 0; |
| ax2 + c = 0, | если b = 0; |
| ax2 = 0, | если b = 0 и c = 0. |
Решение неполных квадратных уравнений
Чтобы решить уравнение вида ax2 + bx = 0, надо разложить левую часть уравнения на множители, вынеся x за скобки:
x(ax + b) = 0.
Произведение может быть равно нулю только в том случае, если один из множителей равен нулю, значит:
Чтобы ax + b было равно нулю, нужно, чтобы
Следовательно, уравнение ax2 + bx = 0 имеет два корня:
| x1 = 0 и x2 = — | b | . |
| a |
Неполные квадратные уравнения вида ax2 + bx = 0, где b ≠ 0, решаются разложением левой части на множители. Такие уравнения всегда имеют два корня, один из которых равен нулю.
Пример 1. Решите уравнение:
a2 — 12a = 0.
Решение:
| a2 — 12a = 0 | |
| a(a — 12) = 0 | |
| a1 = 0 | a — 12 = 0 |
| a2 = 12 | |
Пример 2. Решите уравнение:
7x2 = x.
Решение:
| 7x2 = x | |
| 7x2 — x = 0 | |
| x(7x — 1) = 0 |
| x1 = 0 | 7x — 1 = 0 |
| 7x = 1 | |
Чтобы решить уравнение вида ax2 + c = 0, надо перенести свободный член уравнения c в правую часть:
| ax2 = —c, следовательно, | c | . |
| a |
В этом случае уравнение не будет иметь корней, так как квадратный корень нельзя извлечь из отрицательного числа.
Если данное неполное уравнение будет иметь вид x2 — c = 0, то сначала опять переносим свободный член в правую часть и получаем:
x2 = c.
В этом случае уравнение будет иметь два противоположных корня:
x1 = +√c , x2 = -√c .
Неполное квадратное уравнение вида ax2 + c = 0, где c ≠ 0, либо не имеет корней, либо имеет два корня, которые являются противоположными числами.
Пример 1. Решите уравнение:
24 = 2y2.
Решение:
| 24 = 2y2 | |
| 24 — 2y2 = 0 | |
| -2y2 = -24 | |
| y2 = 12 | |
| y1 = +√12 | y2 = -√12 |
Пример 2. Решите уравнение:
b2 — 16 = 0.
Решение:
| b2 — 16 = 0 | |
| b2 = 16 | |
| b1 = 4 | b2 = -4 |
Уравнение вида ax2 = 0 всегда имеет только один корень: x = 0. Так как a ≠ 0, то из ax2 = 0 следует, что x2 = 0, значит, и
Неполные квадратные уравнения | Алгебра
Как решать неполные квадратные уравнения? Решение и количество корней зависят от вида уравнения.
Неполные квадратные уравнения бывают трёх видов.
Повторим теорию и рассмотрим примеры решения неполных квадратных уравнений каждого вида.
I. Неполные квадратные уравнения, к которых коэффициент c=0, то есть уравнение имеет вид ax²+bx=0.
Такие уравнения решаются разложением левой части уравнения на множители.
Общий множитель x выносим за скобки:
Это уравнение — типа «произведение равно нулю«. Произведение равно нулю, если хотя бы один из множителей равен нулю. Приравниваем к нулю каждый из множителей:
Второе уравнение — линейное. Решаем его:
Таким образом, неполное квадратное уравнение вида ax²+bx=0 имеет 2 корня,один из которых равен нулю, а второй — -b/a.
Примеры.
Общий множитель x выносим за скобки:
Это уравнение типа «произведение равно нулю». Произведение равно нулю, если хотя бы один из множителей равен нулю. Приравниваем к нулю каждый из множителей:
Ответ: 0; -18.
Общий множитель 5x выносим за скобки:
Приравниваем к нулю каждый множитель:
Ответ: 0; 3.
II. Неполные квадратные уравнения, к которых коэффициент b=0, то есть уравнение имеет вид ax²+c=0 (или ax²-c=0).
Неполное квадратное уравнение такого вида либо имеет два корня, которые отличаются только знаками (являются противоположными числами), либо не имеет корней.
1. Если знаки a и c — разные, уравнение имеет два корня.
В курсе алгебры 7 класса такие уравнения решают разложением левой части на множители по формуле разности квадратов (поскольку квадратные корни начинают учить только в курсе 8 класса, коэффициенты a и c в 7 классе обычно являются квадратами некоторых рациональных чисел):
Уравнение типа «произведение равно нулю». Приравниваем к нулю каждый из множителей:
Раскладываем левую часть уравнения по формуле разности квадратов:
Это уравнение — типа «произведение равно нулю». приравниваем к нулю каждый множитель:
Ответ: 7; -7.
Ответ: 2,25; -2,25.
2. Если знаки a и c — одинаковые, уравнение не имеет корней.
Корней нет, так как сумма положительных чисел не может равняться нулю.
Ответ: нет корней.
Корней нет, так как сумма отрицательных чисел не может равняться нулю.
Ответ: нет корней.
В курсе алгебры 8 класса, после изучения квадратных корней, эти уравнения обычно решают приводя к виду x²=d:
Примеры.
Ответ:±2.
Чтобы избавиться от иррациональности в знаменателе, умножаем и числитель, и знаменатель на √11:
Ответ:
Корней нет, так как квадратный корень не может равняться отрицательному числу.
Ответ: нет корней.
Нет корней, так как квадратный корень не может быть равным отрицательному числу.
Ответ: нет корней.
III. Неполные уравнения, в которых коэффициенты b=0 и c=0, то есть уравнение имеет вид ax²=0.
Уравнение такого рода имеет единственный корень x=0
В некоторых учебниках считается, что уравнение имеет два одинаковых корня, каждый из которых равен нулю:
Примеры.
Ответ: 0.
Ответ: 0.
Ответ: 0.
В следующий раз рассмотрим примеры решения полных квадратных уравнений.
Как решить квадратное уравнение?
Как выглядит формула квадратного уравнения?
Какие бывают квадратные уравнения?
Что такое полное квадратное уравнение?
Что такое неполное квадратное уравнение?
Что такое дискриминант?
Сколько корней имеет квадратное уравнение?
Эти вопросы вас больше не будут мучить, после изучения материала.
Формула квадратного уравнения:
ax2+bx+c=0,где a≠0
где x — переменная,
a,b,c — числовые коэффициенты.
 Виды квадратного уравнения
Виды квадратного уравненияПример полного квадратного уравнения:
3x2-3x+2=0
x2-16x+64=0
Решение полных квадратных уравнений сводится к нахождению дискриминанта:
Формула дискриминанта:
D=b2-4aс
Если D>0, то уравнение имеет два корня и находим эти корни по формуле:
 Корни квадратного уравнения
Корни квадратного уравненияЕсли D=0, уравнение имеет один корень
 корень уравнения
корень уравненияЕсли D<0, уравнение не имеет вещественных корней.
Рассмотрим пример №1:
x2-x-6=0
Записываем сначала, чему равны числовые коэффициенты a, b и c.
Коэффициент a всегда стоит перед x2, коэффициент b всегда перед переменной x, а коэффициент c – это свободный член.
a=1,b=-1,c=-6
Находим дискриминант:
D=b2-4ac=(-1)2-4∙1∙(-6)=1+24=25
Дискриминант больше нуля, следовательно, у нас два корня, найдем их:
 Нахождения корней по дискриминанту
Нахождения корней по дискриминантуОтвет: x1=3; x2=-2
Пример №2:
x2+2x+1=0
Записываем, чему равны числовые коэффициенты a,b и c.
a=1,b=2,c=1
Далее находи дискриминант.
D=b2-4ac=(2)2-4∙1∙1=4-4=0
Дискриминант равен нулю, следовательно, один корень:
x=-b/2a=-2/(2∙1)=-1
Ответ: x=-1
Пример №3:
7x2-x+2=0
Записываем, чему равны числовые коэффициенты a,b и c.
a=7,b=-1,c=2
Далее находи дискриминант.
D=b2-4ac=(-1)2-4∙7∙2=1-56=-55
Дискриминант меньше нуля, следовательно, корней нет.
Рассмотрим неполное квадратное уравнение:
ax2+bx=0, где числовой коэффициент c=0.
Пример как выглядят такие уравнения:
x2-8x=0
5x2+4x=0
Чтобы решить такое уравнение необходимо переменную x вынести за скобки. А потом каждый множитель приравнять к нулю и решить уже простые уравнения.
ax2+bx=0
x(ax+b)=0
x1=0 x2=-b/a
Пример №1:
3x2+6x=0
Выносим переменную x за скобку,
x(3x+6)=0
Приравниваем каждый множитель к нулю,
x1=0
3x+6=0
3x=-6
Делим все уравнение на 3, чтобы получить у переменной x коэффициент равный 1.
x=(-6)/3
x2=-2
Ответ: x1=0; x2=-2
Пример №2:
x2-x=0
Выносим переменную x за скобку,
x(x-1)=0
Приравниваем каждый множитель к нулю,
x1=0
x-1=0
x2=1
Ответ: x1=0; x2=1
Рассмотрим неполное квадратное уравнение:
ax2+c=0, где числовой коэффициент b=0.
Чтобы решить это уравнение, нужно записать так:
x2=c/a , если число c/a будет отрицательным числом, то уравнение не имеет решения.
А если c/a положительное число, то решение выглядит таким образом:
 корень квадратного уравнения
корень квадратного уравненияПример №1:
x2+5=0
x2=-5, видно, что -5<0, значит нет решения.
Ответ: нет решения
Пример №2:
3x2-12=0
3x2=12
x2=12/3
x2=4
4>0 следовательно, есть решение,
x1=√4
x1=2
x2=-√4
x2=-2
Ответ: x1=2; x2=-2
Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.
Научившись решать уравнения первой степени, хочется научиться работать с более сложными уравнениями, например, с квадратными. Многим известно, как решаются стандартные квадратные уравнения, но есть особый вид таких выражений, которые называют квадратные уравнения в краткой записи. Рассмотрим подробнее, как решать неполные квадратные уравнения.
Алгоритм нахождения решений
На сегодняшний день существует три вида таких выражений. В зависимости от этого каждое решение имеет свои особенности, от которых зависит решение конкретного примера, будь оно целым или в виде иррационального числа.
Уравнение вида ax2+bx=0 при отсутствии c
Это наиболее распространенное выражение в укороченном типе с квадратными корнями. Как решить нечто похожее в этом случае? Для этого надо разложить левую часть на множители. Алгоритм решения следующий, и обычно не меняется:
- Раскладываем выражение как x*(ax+b), равное нулю.
- Так как выражение равно нулю, если хотя бы один из множителей равен ему, то запишем следующую систему уравнений в виде x и ax+b=0.
- Первое решение так и пишется x=0. Второе равенство линейное и решается как равное -b/a.
В качестве примера приведем следующее равенство: x2+18x=0. Раскладываем его в виде x*(x+18)=0. Получаем x=0 и -18. Оба решения являются правильными и подойдут под результат. Также решаются и остальные выражения, относящиеся к неполным квадратным уравнениям такого вида.
ax2+c=0 при b равном нулю
Не такой частый, но встречающийся тип квадратного выражения. Здесь имеются два корня, отличающиеся лишь знаками, в крайнем случае корней не имеется вообще.
План действий для решения такого выражения разберем на следующем примере:
- Имеем уравнение x2−49=0 или аналогичное ему.
- Раскладываем его как (x-7)*(x+7)=0.
- Получаем решение типа x=7 и -7.
- Записываем ответ в виде двух корней.
А вот при одинаковых знаках в записи решения не будет в принципе. Например, для выражения 25×2+1=0 не имеется ответа, потому что сумма положительных чисел никогда не может равняться нулю.
В школьном курсе алгебры эти равенства стараются решить так, чтобы прийти к формату x2=d. То есть 9×2−2 равно нулю. Тогда x2=2/9, а ответом послужат два одинаковых корня с разными знаками.
Особый вид уравнения
Имеется также один особый тип укороченного выражения. Он имеет следующий вид ax2, которое равно нулю. У таких уравнений имеется решение в виде единственного корня. В учебниках есть указание, что решение состоит в виде двух корней, каждый из которых равен нулю.

Другие способы решения неполных уравнений
Любое подобное выражение в квадрате можно решить, не применяя формулу квадратных корней. К таким видам решения называют формулу сокращенного умножения и правило деления на число.
Допустим, выражение 5×2=0. В этом выражении только умножение на ноль даст результат, а значит, единственный ответ здесь x=0.
Теперь возьмем выражение вида 5×2=125. Делим обе части уравнения на 5. Получим следующий промежуточный результат: x2=25. Переносим все в левую часть и получится x2−25=0. Затем используем формулу разности квадратов в виде (x-5)*(x+5)=0. Получаем итоговый результат в виде x=5 или x=-5.
Далее разберем, как решить вышеописанными способами равенство 16*x2-x=0. Выносится общий множитель за скобки x*(16x-1)=0. Получается два варианта ответа: x=0 и 16x=1. После этого делим каждую часть на 16, в итоге получаем x=1/16. Записываем итоговый ответ в виде x1=0 и x2=1/16.
Стоит отметить, что если вы не знаете, как применить формулы сокращенного умножения или деления на число, то лучше применить способ решения такого выражения согласно стандартным правилам решения квадратного уравнения. Каким именно методом решить данные квадратные выражения, выбирает сам человек. Иногда самые очевидные способы решения не подойдут для определенного примера, может и вовсе не оказаться конкретных ответов. Также не является обязательным такой вариант, как стандартные целые числа.
Здесь могут быть и иррациональные числа, а также дробные. Все будет зависеть от конкретного выражения.
Не являющиеся полными примеры по типу квадрата, несмотря на свое название, решаются достаточно просто. Можно применить как стандартные методы нахождения ответа, например, квадратные корни, так и формулы сокращенного умножения, а также деления на число.

При этом нельзя сказать, что какой-либо из вышеописанных способов является универсальным. Под каждое конкретное уравнение подбирается свой способ нахождения ответа. Не забывайте также о том, что не все такие квадратные равенства имеют ответ, иногда у них нет корней вовсе. Это верно, если оба числа являются положительными, а их сумма не может равняться нулю.
Видео
Из видео вы узнаете способы решения неполных квадратных уравнений.
Неполное квадратное уравнение. Примеры решения
Неполное квадратное уравнение отличаются от классических (полных) уравнений тем, что его множители или свободный член равны нулю. Графиком таких функций являются параболы. В зависимости от общего вида их делят на 3 группы. Принципы решения для всех типов уравнений одинаковы.
Разновидности неполных уравнений
Ничего сложного в определении типа неполного многочлена нет. Рассмотреть основные отличия лучше всего на наглядных примерах:
- Если b = 0, то уравнение имеет вид ax2 + c = 0.
- Если c = 0, то решать следует выражение ax2 + bx = 0.
- Если b = 0 и c = 0, то многочлен превращается в равенство типа ax2 = 0.
Последний случай является скорее теоретической возможностью и никогда не встречается в заданиях для проверки знаний, так как единственно верное значение переменной x в выражении – это ноль. В дальнейшем будет рассмотрены способы и примеры решения неполных квадратных уравнений 1) и 2) видов.
Общий алгоритм поиска переменных и примеры с решением
Не зависимо от разновидности уравнения алгоритм решения сводится к следующим шагам:
- Привести выражение к удобному для поиска корней виду.
- Произвести вычисления.
- Записать ответ.
Решать неполные уравнения проще всего, разложив на множители левую часть и оставив ноль в правой. Таким образом, формула неполного квадратного уравнения для поиска корней сводится к вычислению значения x для каждого из множителей.
Научиться способам решения можно только лишь на практике, поэтому рассмотрим конкретный пример нахождения корней неполного уравнения:
4x2 – 1 = 0.
Как видно, в данном случае b = 0. Разложим левую часть на множители и получим выражение:
4(x – 0,5) ⋅ (x + 0,5) = 0.
Очевидно, что произведение равно нулю, когда хотя бы один из множителей равен нулю. Подобным требованиям отвечают значения переменной x1 = 0,5 и (или) x2 = -0,5.
Для того, чтобы легко и быстро справляться с задачей разложения квадратного трехчлена на множители, следует запомнить следующую формулу:

Если в выражении отсутствует свободный член, задача многократно упрощается. Достаточно будет всего лишь найти и вынести за скобки общий знаменатель. Для наглядности рассмотрим пример, как решать неполные квадратные уравнения вида ax2 + bx = 0.
x2 + 3x = 0
Вынесем переменную x за скобки и получим следующее выражение:
x ⋅ (x + 3) = 0.
Руководствуясь логикой, приходим к выводу, что x1 = 0, а x2 = -3.
Традиционный способ решения и неполные квадратные уравнения
Что же будет, если применить формулу дискриминанта и попытаться найти корни многочлена, при коэффициентах равных нулю? Возьмем пример из сборника типовых заданий для ЕГЭ по математики 2017 года, решим его с помощью стандартных формул и методом разложения на множители.
-7x2 – 3x = 0.
Рассчитаем значение дискриминант: D = (-3)2 – 4 ⋅ (-7) ⋅ 0 = 9. Получается, многочлен имеет два корня:

Теперь, решим уравнение разложением на множители и сравним результаты.
-x ⋅ (7x + 3) = 0,
1) –x1 = 0,
2) 7x + 3 = 0,
7x = -3,
x = -.
Как видно, оба метода дают одинаковый результат, но решить уравнение вторым способ получилось гораздо проще и быстрее.
Теорема Виета
А что же делать с полюбившейся теоремой Виета? Можно ли применять данный метод при неполном трехчлене? Попробуем разобраться в аспектах приведения неполных уравнений к классическому виду ax2 + bx + c = 0.
На самом деле применять теорему Виета в данном случае возможно. Необходимо лишь привести выражение к общему виду, заменив недостающие члены нулем.
Например, при b = 0 и a = 1, дабы исключить вероятность путаницы следует записать задание в виде: ax2 + 0 + c = 0. Тогда отношение суммы и произведения корней и множителей многочлена можно выразить следующим образом:

Теоретические выкладки помогают ознакомиться с сутью вопроса, и всегда требуют отработки навыка при решении конкретных задач. Снова обратимся к справочнику типовых заданий для ЕГЭ и найдем подходящий пример:
x2 – 16 = 0.
Запишем выражение в удобном для применения теоремы Виета виде:
x2 + 0 – 16 = 0.
Следующим шагом составим систему условий:

Очевидно, что корнями квадратного многочлена будут x1 = 4 и x2 = -4.
Теперь, потренируемся приводить уравнение к общему виду. Возьмем следующий пример: 1/4× x2 – 1 = 0
Для того, чтобы применить к выражению теорему Виета необходимо избавиться от дроби. Перемножим левую и правую части на 4, и посмотрим на результат: x2– 4 = 0. Полученное равенство готово для решения теоремой Виета, но гораздо проще и быстрее получить ответ просто перенеся с = 4 в правую часть уравнения: x2 = 4.
Подводя итог, следует сказать, что лучшим способом решения неполных уравнений является разложения на множители, является самым простым и быстрым методом. При возникновении затруднений в процессе поиска корней можно обратиться к традиционному методу нахождения корней через дискриминант.
Похожие статьи
Рекомендуем почитать:
Квадратное уравнение – уравнение вида , где
Числа называются коэффициентами квадратного уравнения.
Квадратное уравнение может иметь два действительных корня, один действительный корень или ни одного.
Количество корней квадратного уравнения зависит от знака выражения, которое называется дискриминант.
Дискриминант квадратного уравнения: .
Если > 0, квадратное уравнение имеет два корня: и .
Если = 0, квадратное уравнение имеет единственный корень .
Если < 0, квадратное уравнение не имеет действительных корней.
Запишем несколько квадратных уравнений и проверим, сколько корней они имеют.
1)
В этом уравнении , , .
Дискриминант уравнения равен > 0. Уравнение имеет два корня.
2)
В этом уравнении .
Дискриминант уравнения равен . Уравнение имеет единственный корень.
Заметим, что в левой части уравнения находится выражение, которое называют полным квадратом. В самом деле, . Мы применили формулу сокращенного умножения.
Уравнение имеет единственный корень .
3) .
В этом уравнении .
Дискриминант уравнения равен < 0. Корней нет.
4) Решим уравнение .
Дискриминант уравнения равен > 0.
Уравнение имеет два корня.
Корни уравнения
Теорема Виета
Полезная теорема для решения квадратных уравнений – теорема Виета.
Если и – корни уравнения , то , .
Например, в нашем уравнении сумма корней равна , а произведение корней равно .
Квадратное уравнение можно решить несколькими способами. Можно вычислять дискриминант, или воспользоваться теоремой Виета, а иногда можно просто угадать один из корней. Или оба корня.
Неполные квадратные уравнения
Квадратное уравнение, в котором один из коэффициентов b или с (или они оба) равны нулю, называется неполным. В таких случаях искать дискриминант не обязательно. Можно решить проще.
1) Рассмотрим уравнение .
В этом уравнении и . Очевидно, – единственный корень уравнения.
2) Рассмотрим уравнение . Здесь , а другие коэффициенты нулю не равны.
Проще всего разложить левую часть уравнения на множители по формуле разности квадратов. Получим:
Произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.
Значит, или .
3) Вот похожее уравнение:
.
Поскольку , уравнение можно записать в виде:
Отсюда или
.
4) Пусть теперь не равно нулю и .
Рассмотрим уравнение
.
Его левую часть можно разложить на множители, вынеся за скобки. Получим:
.
Произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.
Значит, или .
Разложение квадратного трехчлена на множители
.
Здесь и – корни квадратного уравнения .
Запомните эту формулу. Она необходима для решения квадратичных и дробно-рациональных неравенств.
Например, наше уравнение
.
Его корни
,
.
.
Полезные лайфхаки для решения квадратных уравнений.
1) Намного проще решать квадратное уравнение, если коэффициент а, который умножается на х², положителен. Кажется, что это мелочь, да? Но сколько ошибок на ЕГЭ возникает из-за того, что старшеклассник игнорирует эту «мелочь».
Например, уравнение
.
Намного проще умножить его на – 1, чтобы коэффициент а стал положительным. Получим:
.
Дискриминант этого уравнения равен
.
Корни уравнения .
2)Прежде чем решать квадратное уравнение, посмотрите на него внимательно. Может быть, можно сократить обе его части на какое-нибудь не равное нулю число?
Вот, например, уравнение
.
Можно сразу посчитать дискриминант и корни. А можно заметить, что все коэффициенты и делятся на 17. Поделив обе части уравнения на 17, получим:
.
Здесь можно и не считать дискриминант, а сразу угадать первый корень: . А второй корень легко находится по теореме Виета.
3)Работать с дробными коэффициентами неудобно. Например, уравнение
.
Вы уже догадались, что надо сделать. Умножить обе части уравнения на 100! Получим:
.
Корни этого уравнения равны 1 и -6.
Смотри также: Квадратичная функция
Шаг 1: Введите квадратичную функцию в терминах х.
Шаг 2: Выберите команду, относящуюся к функции f (x), которую вы ввели выше.
| Решить f (x) = 0 с помощью: | |
| (i) Факторинг квадратичный. | Идти |
| (ii) Используя квадратную формулу. | Идти |
| (iii) Завершение квадрата. | Идти |
| Перепишите f (x) в виде а (х ± б) 2 ± с завершив квадрат. | Идти |
| Для параболы у = ф (х), рассчитать следующее: | |
| (i) Вогнутость | Идти |
| (ii) x-перехватов | Идти |
| (iii) y-перехват | Идти |
| (iv) Ось симметрии | Идти |
| (v) Vertex | Идти |
| Сюжет о параболе у = ф (х). | Идти |
| Рассчитать дискриминант f (x) = 0. | Идти |
| Рассчитать количество корней f (x) = 0. | Идти |
Решение уравнений является центральной темой алгебры.Все полученные навыки в конечном итоге приводят к способности решать уравнения и упрощать решения. В предыдущих главах мы решили уравнения первой степени. Теперь у вас есть необходимые навыки для решения уравнений второй степени, которые известны как квадратные уравнения .
КВАДРАТИКА, РЕШЕННАЯ ФАКТОРИНГОМ
ЦЕЛИ
По завершении этого раздела вы сможете:
- Определите квадратное уравнение.
- Поместите квадратное уравнение в стандартную форму.
- Решите квадратное уравнение с помощью факторинга.
Квадратичное уравнение — это полиномиальное уравнение, которое содержит вторую, но не более высокую степень переменной.
Стандартной формой квадратного уравнения является ax 2 + bx + c = 0, когда a ≠ 0 и a, b и c являются действительными числами.
Все квадратные уравнения могут быть представлены в стандартной форме, и любое уравнение, которое может быть представлено в стандартной форме, является квадратным уравнением. Другими словами, стандартная форма представляет все квадратные уравнения.
Решение уравнения уравнения иногда называют корнем уравнения .
| Эта теорема доказана в большинстве книг по алгебре колледжей. |
Важная теорема, которая не может быть доказана на уровне этого текста, гласит: «Каждое полиномиальное уравнение степени n имеет ровно n корней». Использование этого факта говорит нам, что квадратные уравнения всегда будут иметь два решения. Возможно, что оба решения равны.
| У квадратного уравнения будет два решения, потому что оно имеет степень два. |
Простейший метод решения квадратиков — это факторинг. Этот метод не всегда можно использовать, потому что не все многочлены являются факториальными, но он используется всякий раз, когда возможен факторинг.
Метод решения с помощью факторинга основан на простой теореме.
Если AB = 0, то либо A = 0, либо B = 0.
| Другими словами, если произведение двух факторов равно нулю, то хотя бы один из факторов равен нулю. |
Мы не будем пытаться доказать эту теорему, а внимательно отметим ее формулировку. Мы никогда не можем умножить два числа и получить ответ ноль, если хотя бы одно из чисел не равно нулю. Конечно, оба числа могут быть нулевыми, поскольку (0) (0) = 0.
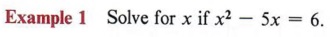
Решение Шаг 1 Приведите уравнение в стандартную форму.
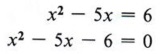
| Мы должны вычесть 6 с обеих сторон. |
Шаг 2 Фактор полностью.
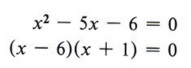
| Вспомните, как вычислять триномы. |
Шаг 3 Установите каждый фактор равным нулю и решите для х. Поскольку мы имеем (x — 6) (x + 1) = 0, мы знаем, что x — 6 = 0 или x + 1 = 0, и в этом случае x = 6 или x = — 1.
| Это применимо вышеупомянутой теореме, которая говорит, что по крайней мере один из факторов должен иметь значение ноль. |
Шаг 4 Проверьте решение в исходном уравнении.Если x = 6, то x 2 — 5x = 6 становится
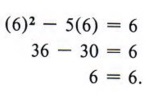
| Проверка ваших решений — верный способ определить, правильно ли вы решили уравнение. |
Следовательно, x = 6 является решением. Если x = — 1, то x 2 — 5x = 6 становится
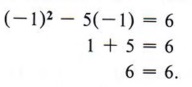
Следовательно, — 1 является решением.
Решения могут быть обозначены либо написанием x = 6 и x = — 1, либо с помощью набора обозначений и написания {6, — 1}, что мы читаем «набор решений для x равен 6 и — 1.«В этом тексте мы будем использовать набор обозначений.
| В этом примере 6 и -1 называются элементами набора. |
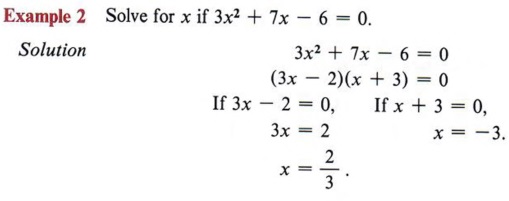
| Обратите внимание, что в этом примере уравнение уже находится в стандартной форме. |

Опять же, проверка решений гарантирует, что вы не допустили ошибку при решении уравнения. 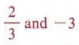 также называют корнями уравнения. также называют корнями уравнения. |

| (x + 1) — наименьший общий знаменатель из всех дробей в уравнении. Помните, что каждый член уравнения должен быть умножен на (x + 1). |
Проверьте решения в исходном уравнении.

| Проверьте в исходном уравнении, чтобы убедиться, что вы не получите знаменатель со значением ноль. |

| Обратите внимание, что здесь два решения равны.Это происходит только тогда, когда трином является идеальным квадратом. |
НЕПОЛНАЯ КВАДРАТИКА
ЦЕЛИ
По завершении этого раздела вы сможете:
- Определите неполное квадратное уравнение.
- Решить неполное квадратное уравнение.
Если, когда уравнение помещено в стандартную форму ax 2 + bx + c = 0, либо b = 0, либо c = 0, уравнение представляет собой неполный квадратичный .
Пример 1
5x 2 — 10 = 0 — неполный квадратик, так как средний член отсутствует и, следовательно, b = 0.
Когда вы встречаете неполный квадратик с c — 0 (третий член отсутствует), он все еще может быть решен с помощью факторинга.

| х является общим фактором. Произведение двух факторов равно нулю. Поэтому мы используем теорему из предыдущего раздела. Проверьте эти решения. |
Обратите внимание, что если термин c отсутствует, вы всегда можете выделить x из других терминов.Это означает, что во всех таких уравнениях ноль будет одним из решений.
Неполная квадратика с отсутствующим термином b должна быть решена другим методом, поскольку факторинг будет возможен только в особых случаях.
Пример 3 Решите для х, если х 2 — 12 = 0.
Решение Поскольку x 2 — 12 не имеет общего множителя и не является разностью квадратов, его нельзя разложить на рациональные факторы. Но из предыдущих наблюдений мы имеем следующую теорему.

| Обратите внимание, что есть два значения, которые в квадрате будут равны A. |
Используя эту теорему, мы имеем

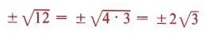 Проверьте эти решения. |
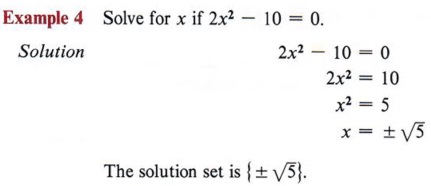
| Добавьте 10 с каждой стороны. Проверьте эти решения. |
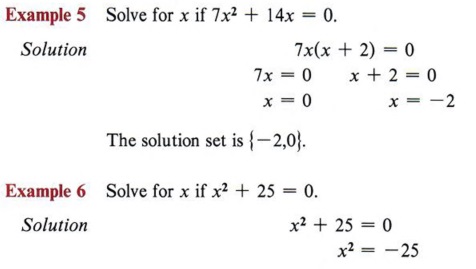
| Здесь 7x является общим фактором. Проверьте эти решения. |
Обратите внимание, что в этом примере мы имеем квадрат числа, равного отрицательному числу. Это никогда не может быть правдой в реальной системе счисления, и поэтому у нас нет реального решения.
ЗАПОЛНЕНИЕ ПЛОЩАДИ
ЦЕЛИ
По завершении этого раздела вы сможете:
- Определите идеальный квадратный трином.
- Завершите третий член, чтобы сделать идеальный квадратный трином.
- Решите квадратное уравнение, заполнив квадрат.
Из вашего опыта в факторинге вы уже понимаете, что не все многочлены являются факториальными. Следовательно, нам нужен метод решения квадратиков, который не является факторизованным. Необходимый метод называется «завершение квадрата».
Сначала давайте рассмотрим значение «идеального квадратного тринома». Когда мы возводим в квадрат бином, мы получаем идеальный квадратный трином. Общая форма (a + b) 2 = 2 + 2ab + b 2 .
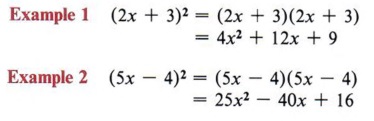
| Помните, возведение в квадрат бинома означает умножение его на себя. |
Из общего вида и этих примеров можно сделать следующие наблюдения относительно идеального квадратного тринома.
- Два из трех слагаемых являются идеальными квадратами. 4x 2 и 9 в первом примере, 25x 2 и 16 во втором примере и 2 и b 2 в общем виде.
Другими словами, первое и третье слагаемые являются идеальными квадратами. - Другой термин — это либо плюс, либо минус в два раза больше, чем произведение квадратных корней двух других терминов.

Термин -7 сразу говорит, что это не может быть идеальный квадратный трином. Задача при заполнении квадрата состоит в том, чтобы найти число, заменяющее -7 так, чтобы был идеальный квадрат.
Рассмотрим эту проблему: заполните пробел, чтобы «x 2 + 6x + _______» было идеальным квадратным триномом. Из двух условий для идеального квадратного тринома мы знаем, что бланк должен содержать идеальный квадрат, и что 6x должно быть в два раза больше квадратного корня из x 2 и числа в бланке.Поскольку x уже присутствует в 6x и является квадратным корнем из x 2 , то число 6 должно быть в два раза больше квадратного корня из числа, которое мы помещаем в пробел. Другими словами, если мы сначала возьмем половину 6, а затем возведем в квадрат этот результат, мы получим необходимое число для пробела.
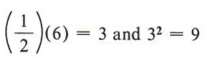
Следовательно, x 2 + 6x + 9 — идеальный квадратный трином.
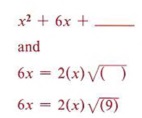


Теперь давайте рассмотрим, как мы можем использовать завершение квадрата для решения квадратных уравнений.
Пример 5 Решите x 2 + 6x — 7 = 0, заполнив квадрат.
| Напомним, что вместо -7, +9 сделает выражение идеальным квадратом. |
Решение Сначала мы заметим, что термин -7 должен быть заменен, если мы хотим получить идеальный квадратный трином, поэтому мы перепишем уравнение, оставив пробел для нужного числа.
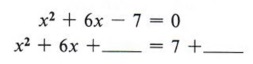
На этом этапе будьте осторожны, чтобы не нарушать какие-либо правила алгебры.Например, обратите внимание, что вторая форма пришла от добавления +7 к обеим сторонам уравнения. Никогда не добавляйте что-либо в одну сторону, не добавляя то же самое в другую.
Теперь мы найдем половину 6 = 3 и 3 2 = 9, чтобы дать нам номер для пробела. Опять же, если мы поместим 9 в пробел, мы также должны добавить 9 с правой стороны.
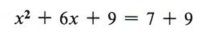
| Помните, что если 9 добавлено к левой части уравнения, оно также должно быть добавлено к правой стороне. |
Теперь вычислим идеальный квадратный трином, который дает

| Теперь x 2 + 6x + 9 можно записать как (x + 3) 2 . |

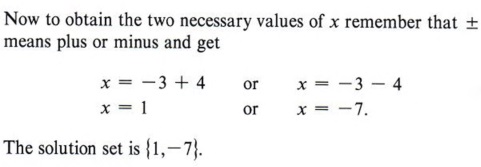
| Таким образом, 1 и -7 являются решениями или корнями уравнения. |
Пример 6 Решите 2x 2 + 12x — 4 = 0, заполнив квадрат.
Решение Эта проблема приносит еще одну трудность.Первый член, 2x , 2 , не является идеальным квадратом.
Мы исправим это, разделив все члены уравнения на 2 и получим

| Другими словами, получите коэффициент 1 для члена x 2 . |
Теперь мы добавим 2 к обеим сторонам, давая
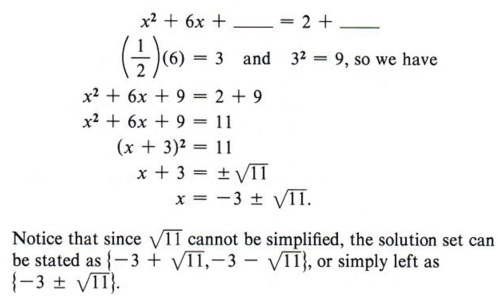
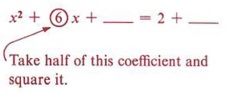 Опять же, это более кратко. |
Пример 7 Решите 3x 2 + 7x — 9 = 0, заполнив квадрат.
Solution Шаг 1 Разделите все условия на 3.
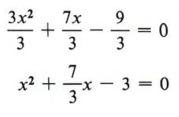
| Снова, получите коэффициент 1 для x 2 , разделив на 3. |
Шаг 2 Перепишите уравнение, оставив пробел для термина, необходимого для завершения квадрата.
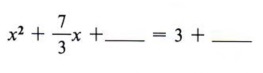

Шаг 3 Найдите квадрат половины коэффициента x и добавьте к обеим сторонам.
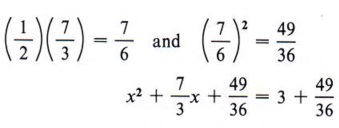
| Это выглядит сложно, но мы следуем тем же точным правилам, что и раньше. |
Шаг 4 Фактор завершенного квадрата.
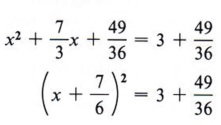
Факторинг никогда не должен быть проблемой, так как мы знаем, что у нас есть идеальный квадратный трином, что означает, что мы находим квадратные корни первого и третьего членов и используем знак среднего.

Если вы столкнулись с какими-либо трудностями, вам следует ознакомиться с арифметикой, связанной с добавлением чисел справа.
Теперь у нас 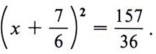
Шаг 5 Возьмите квадратный корень с каждой стороны уравнения.
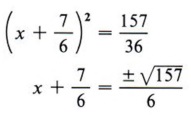
Шаг 6 Решите для х (два значения).
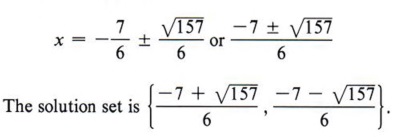
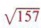 нельзя упростить. Мы могли бы также написать решение этой проблемы в более сжатой форме как нельзя упростить. Мы могли бы также написать решение этой проблемы в более сжатой форме как 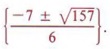 |
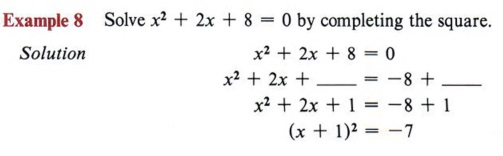

Выполните шаги в предыдущем вычислении, а затем обратите внимание на последний ин. Какой вывод, когда квадрат величины равен отрицательному числу? «Нет реального решения.»
| Какое действительное число мы можем вывести в квадрат и получить -7? |
В итоге, чтобы решить квадратное уравнение, заполнив квадрат, следуйте этому пошаговому методу.
Шаг 1 Если коэффициент x2 не равен 1, разделите все члены на этот коэффициент.
Шаг 2 Перепишите уравнение в виде x2 + bx + _______ = c + _______.
Шаг 3 Найдите квадрат половины коэффициента x и добавьте эту величину к обеим сторонам уравнения.
Шаг 4 Разложите полученный квадрат и сложите числа в правой части уравнения.
Шаг 5 Найдите квадратный корень с каждой стороны уравнения.
Шаг 6 Решите для х и упростить.
Если шаг 5 невозможен, то уравнение не имеет реального решения.
| Эти шаги помогут в решении уравнений в следующем упражнении. |
КВАДРАТИЧНАЯ ФОРМУЛА
ЦЕЛИ
По завершении этого раздела вы сможете:
- Решите общее квадратное уравнение, заполнив квадрат.
- Решите любое квадратное уравнение, используя квадратную формулу.
- Решите квадратное уравнение, заполнив квадрат.
Стандартной формой квадратного уравнения является ax 2 + bx + c = 0. Это означает, что каждое квадратное уравнение может быть представлено в этой форме. В некотором смысле, то топор 2 + bx + c = 0 представляет все квадратичные значения. Если вы можете решить это уравнение, у вас будет решение для всех квадратных уравнений.
Решим общее квадратное уравнение методом заполнения квадрата.
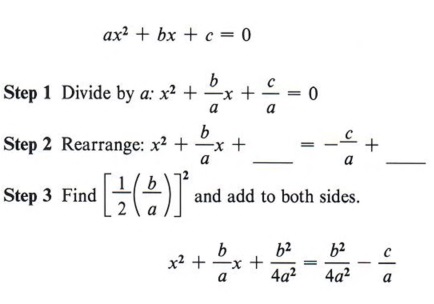
| Чтобы получить член x 2 с коэффициентом 1. Это мы делали в предыдущем разделе много раз. |

Мы должны добавить  с каждой стороны. с каждой стороны. |
Эта форма  называется квадратичной формулой и представляет собой решение всех квадратных уравнений.
называется квадратичной формулой и представляет собой решение всех квадратных уравнений.
| Запомните это выражение. |
Чтобы использовать квадратную формулу, вы должны указать a, b и c.Для этого данное уравнение всегда должно быть в стандартной форме.

| Осторожно подставьте значения a, b и c в формулу. |

Не каждое квадратное уравнение будет иметь
.Завершение площади
« Завершение квадрата » — вот где мы …
| … возьмите квадратное уравнение , например: | и превратить это в это: | |
| топор 2 + bx + c = 0 | a (x + d ) 2 + e = 0 |
Для тех из вас, кто торопится, я могу сказать вам, что: d = b 2a
и: e = c — b 2 4a
Но если у вас есть время, позвольте мне показать вам, как « завершить квадрат » самостоятельно.
Завершение площади
Скажем, у нас есть простое выражение, например x 2 + bx. Наличие x в одном выражении может усложнить жизнь. Что мы можем сделать?
Хорошо, с небольшим вдохновением от Geometry мы можем преобразовать это, как это:
Как видите, x 2 + bx можно переставить почти в квадрат …
.. и мы можем завершить квадрат с (б / 2) 2
В алгебре это выглядит так:
| x 2 + bx | + (б / 2) 2 | = | (х + б / 2) 2 |
| «Завершить площадь» |
Итак, добавив (b / 2) 2 , мы можем завершить квадрат.
А (х + b / 2) 2 имеет х только на , что проще в использовании .
Сохранение баланса
Теперь … мы не можем просто добавить (b / 2) 2 без вычитая это тоже! В противном случае вся стоимость меняется.
Итак, давайте посмотрим, как это сделать правильно на примере:
| Начать с: | |
| (в данном случае «b» равно 6) | |
| Завершить площадь: | |
Также вычитают новый срок | |
Упростите это, и мы сделали. | |
Результат:
x 2 + 6x + 7 = (x + 3) 2 — 2
И теперь х появляется только один раз, и наша работа выполнена!
Быстрый подход
Вот быстрый способ получить ответ. Вам может понравиться этот метод.
Сначала подумайте о желаемом результате: (x + d) 2 + e
После расширения (x + d) 2 получаем: x 2 + 2dx + d 2 + e
Теперь посмотрим, сможем ли мы превратить наш пример в эту форму, чтобы обнаружить д и е
Пример: попробуйте вписать x 2 + 6x + 7 в x 2 + 2dx + d 2 + e
Теперь мы можем «форсировать» ответ:
- Мы знаем, что 6x должно закончиться как 2dx, поэтому d должно быть 3
- Далее мы видим, что 7 должно стать d 2 + e = 9 + e, поэтому e должно быть -2
И мы получаем тот же результат (х + 3) 2 — 2, что и выше!
Теперь давайте рассмотрим полезное приложение: решение квадратичных уравнений…
Решение общих квадратичных уравнений путем заполнения квадрата
Мы можем заполнить квадрат до , решить с помощью квадратичного уравнения (найти, где оно равно нулю).
Но общее квадратное уравнение может иметь коэффициент a перед x 2 :
топор 2 + bx + c = 0
Но с этим легко справиться … сначала разделите все уравнение на «а», а затем продолжайте:
x 2 + (б / у) х + с / а = 0
Шаги
Теперь мы можем решить квадратное уравнение в 5 шагов:
- Шаг 1 Разделите все члены на и (коэффициент x 2 ).
- Шаг 2 Переместите числовой член ( c / a ) в правую часть уравнения.
- Шаг 3 Заполните квадрат в левой части уравнения и уравновесите его, добавив то же значение в правую часть уравнения.
Теперь у нас есть нечто, похожее на (x + p) 2 = q, которое можно решить довольно легко:
- Шаг 4 Возьмите квадратный корень с обеих сторон уравнения.
- Шаг 5 Вычтите число, которое остается в левой части уравнения, чтобы найти x .
Примеры
ОК, некоторые примеры помогут!
Пример 1: Решить x 2 + 4x + 1 = 0
Шаг 1 В этом примере можно пропустить , поскольку коэффициент x 2 равен 1
Шаг 2 Переместите числовой член в правую часть уравнения:
x 2 + 4x = -1
Шаг 3 Заполните квадрат в левой части уравнения и выровняйте его, добавив то же число в правую часть уравнения.
(б / 2) 2 = (4/2) 2 = 2 2 = 4
x 2 + 4x + 4 = -1 + 4
(х + 2) 2 = 3
Шаг 4 Возьмите квадратный корень с обеих сторон уравнения:
x + 2 = ± √3 = ± 1,73 (до 2 десятичных знаков)
Шаг 5 Вычтите 2 с обеих сторон:
х = ± 1,73 — 2 = -3.73 или -0,27
А вот интересная и полезная вещь. В конце шага 3 мы получили уравнение: (х + 2) 2 = 3 Это дает нам вершину (точку поворота) x 2 + 4x + 1: (-2, -3) |
Пример 2: Решить 5x 2 — 4x — 2 = 0
Шаг 1 Разделите все условия на 5
x 2 — 0.8x — 0,4 = 0
Шаг 2 Переместите числовой член в правую часть уравнения:
x 2 — 0,8x = 0,4
Шаг 3 Заполните квадрат в левой части уравнения и выровняйте его, добавив то же число в правую часть уравнения:
(б / 2) 2 = (0,8 / 2) 2 = 0,4 2 = 0,16
x 2 — 0.8x + 0,16 = 0,4 + 0,16
(х — 0,4) 2 = 0,56
Шаг 4 Возьмите квадратный корень с обеих сторон уравнения:
x — 0,4 = ± √0,56 = ± 0,748 (до 3 десятичных знаков)
Шаг 5 Вычтите (-0,4) с обеих сторон (другими словами, добавьте 0,4):
х = ± 0,748 + 0,4 = -0,348 или 1,148
Почему «Завершить площадь»?
Зачем заполнять квадрат, если мы можем просто использовать квадратную формулу для решения квадратного уравнения?
Хорошо, одна из причин приведена выше, когда новая форма не только показывает нам вершину, но и облегчает ее решение.
Бывают также случаи, когда форма топор 2 + bx + c может быть частью вопроса большего размера , и перестановка его в a (x + d ) 2 + e дает решение проще, потому что x появляется только один раз.
Например, «x» может быть функцией (например, cos (z) ), и перестановка может открыть путь к лучшему решению.
Кроме того, завершение квадрата — это первый шаг в выводе квадратичной формулы
Просто подумайте об этом как о другом инструменте в вашем наборе математики.
Сноска: Значения «d» и «e»
Как я получил значения d и e из верхней части страницы?
И вы заметите, что у нас есть:
a (x + d) 2 + e = 0
где: d = b 2а
и: е = с — b 2 4а
Так же, как в верхней части страницы!
,Purplemath
Некоторые квадратики довольно просто решить, потому что они имеют форму «что-то с квадратом x равно некоторому числу», и затем вы берете квадратный корень с обеих сторон.
Примером может быть:
MathHelp.ком
К сожалению, большинство квадратиков не имеют такого квадратного сечения. Для вашего среднего ежедневного квадратика вы сначала должны использовать технику «завершения квадрата», чтобы переставить квадратик в аккуратный (квадратная часть) равный (число) формат, показанный выше.Например:
Найти x -цепи y = 4 x 2 — 2 x — 5.
Прежде всего, помните, что обнаружение x-перехватов означает установку y равной нулю и решение для значений x , поэтому этот вопрос действительно просит вас: «Решить 4 x 2 — 2 x — 5 = 0 «.
Теперь давайте начнем процесс завершения квадрата. Для начала у нас есть исходное уравнение (или, если нам нужно было сначала решить для «= 0» форму уравнения «равно нулю»). В этом случае нас попросили перехватить x квадратичной функции, что означало, что мы установили функцию равной нулю. Так что мы в порядке. Наша отправная точка — это уравнение:
Теперь, вопреки всему, что мы узнали раньше, мы собираемся переместить константу (то есть число , а не с переменной) на другую сторону знака «равно»:
При решении путем заполнения квадрата мы хотим, чтобы x 2 были сами по себе, поэтому нам нужно разделить на то, что умножается на этот термин.В этом случае у нас есть 4, умноженное на x 2 , поэтому нам нужно разделить на 4, чтобы избавиться от этого. Наш результат:
Теперь мы собираемся поработать на стороне. Если посмотреть на квадратик выше, у нас есть член x 2 и член x с левой стороны. Мы собираемся работать с коэффициентом члена x . В нашем настоящем случае это значение вместе со знаком равно
.числовой коэффициент: –1/2.
Чтобы создать наш законченный квадрат, нам нужно разделить этот числовой коэффициент на 2 (или, что то же самое, умножить его на половину). В нашем случае мы получаем:
производное значение: (1/2) (- 1/2) = –1/4
Теперь возведем это производное значение в квадрат. (Конечно, это даст нам положительное число в результате.)
квадрат производного значения: (-1/4) 2 = 1/16
Хорошо; Теперь мы вернемся к последнему шагу перед нашей диверсией:
… и мы добавим, что «+1/16» по обе стороны уравнения:
x 2 — (1/2) x + 1/16 = 5/4 + 1/16
Мы можем упростить строго числовые данные с правой стороны:
x 2 — (1/2) x + 1/16 = 21/16
На данный момент мы готовы перейти к форме завершенного квадрата, потому что, добавив +1/16 к каждой из сторон, мы переставили левую сторону в квадрат, который является идеальным квадратом.Другими словами, мы можем преобразовать эту левую часть в хороший, аккуратный бином в квадрате. Но как?
Самый простой способ — вернуться к значению, которое мы получили после деления на два (или, что то же самое, умножения на половину), и использовать это значение, вместе со знаком , для формирования квадратного бинома. Другими словами, в этом случае мы получаем:
ууу! Завершено-квадратная форма! Теперь мы можем получить квадратный корень с любой стороны (помня «плюс-минус» на строго числовой стороне):
кв.м. [( x — (1/4)) 2 ] = ± кв.м. [21/16]
x — (1/4) = ± sqrt [21/16]
Теперь мы можем решить для значений переменной:
«плюс-минус» означает, что у нас есть два решения :
Решения также могут быть записаны в округленной форме или округлено до некоторого разумного числа десятичных знаков (например, двух).
Возможно, вам понадобятся округленные формы для «реальных» ответов на словесные задачи и для построения графиков. Например, для вышеупомянутого упражнения намного проще построить график перехвата при x = -0,9, чем попытаться построить график в форме квадратного корня с «минусом» в середине. Но (предупреждение!) В большинстве других случаев вы должны считать , что ответ должен быть в «точной» форме, со всеми квадратными корнями.
Когда вы заполняете квадрат, будьте внимательны со знаком числового коэффициента на x , когда вы умножаете этот коэффициент на половину. Если вы потеряете знак этого термина, вы можете получить неправильный ответ в конце концов, потому что вы забудете, какой знак идет в скобках в форме заполненного квадрата.
Кроме того, не будьте неряшливыми и подождите, пока знак плюс / минус не дойдет до самого конца. На ваших тестах у вас не будет ответов в ответ, чтобы «напомнить» вам, что вы «имели в виду» использовать плюс-минус, и вы, скорее всего, забудете поставить плюс-минус в ответе.Кроме того, нет никаких причин, чтобы ставить галочку на своего инструктора, делая что-то не так, когда это так просто сделать правильно.
На той же ноте, убедитесь, что вы рисуете знак квадратного корня, если необходимо, когда вы квадратный корень обе стороны. Не ждите, пока ответ в конце книги «напомнит» вам, что вы «хотели» поместить туда символ квадратного корня.
Если вы привыкнете быть неряшливым, вы только навредите себе!
Решите x 2 + 6 x — 7 = 0, заполнив квадрат.
Я сделаю ту же процедуру, что и в первом упражнении, в том же порядке. (Учебный совет: всегда работая с этими проблемами одинаково, вы сможете запомнить шаги при прохождении тестов.)
Сначала я запишу уравнение, которое они мне дали.
Я перемещаю постоянное слагаемое (свободное число) на другую сторону от «равно».
Первый член уже умножен только на 1, поэтому мне не нужно делить что-либо. Итак, этот шаг сделан.
Теперь я возьму бумажку и проведу вычисления. Во-первых, коэффициент «линейного» члена (т. Е. Члена с x , а не члена x 2 ), со знаком , равен:
числовой коэффициент: +6
Я умножу это на 1/2:
производное значение: (+6) (1/2) = +3
Мой следующий шаг — возвести в квадрат это производное значение:
квадрат производного значения: (+3) 2 = 9
Теперь я возвращаюсь к своему уравнению и добавляю это квадратное значение к любой из сторон:
Я упросту строго числовые данные с правой стороны:
А теперь я преобразую левую часть в форму готового квадрата, используя производное значение (которое я обвел в своей работе, чтобы не потерять его), а также его знак:
Теперь, когда левая часть имеет форму завершенного квадрата, я могу квадратный корень с каждой стороны, помня поставить знак «плюс-минус» на строго числовой стороне:
кв.м. [( x + 3) 2 ] = ± кв.м. [16]
x + 3 = ± 4
..и тогда я решу для моих двух решений:
x = –3 ± 4
= –3 — 4, –3 + 4
= –7, 1
Тогда мой ответ:
Пожалуйста, найдите время, чтобы проработать два вышеупомянутых упражнения для себя, убедившись, что вы четко понимаете каждый шаг, как эти шаги работают вместе и как я пришел к перечисленным ответам.А затем найдите время, чтобы практиковать дополнительные упражнения из вашей книги. С практикой этот процесс может стать довольно простым, особенно если вы будете осторожны, выполняя одни и те же шаги в одном и том же порядке. Да, «в реальной жизни» вы бы использовали Квадратичную формулу или свой калькулятор, но вы должны ожидать, по крайней мере, один вопрос в следующем тесте (и, возможно, в финале), где вам необходимо показать шаги для завершения квадрата.
Партнерская

Примечание: поскольку решения для второго упражнения выше были целыми числами, это говорит о том, что мы могли бы решить это с помощью факторинга.
x 2 + 6 x — 7 = 0
( x -1) ( x + 7) = 0
x — 1 = 0, x + 7 = 0
x = 1, x = — 7
Предупреждение. Если вы не согласны с тем, что не помните, что нужно ставить плюс / минус, как только вы получите квадратный корень с обеих сторон, то это пример типа упражнения, в котором вы столкнетесь с проблемами.Вы напишете свой ответ для второго упражнения выше как « x = –3 + 4 = 1» и не будете знать, как они получили « x = –7», потому что у вас не будет квадратного корня символ «напоминать» вам, что вы «имели в виду» поставить плюс / минус. Другими словами, если вы неаккуратны, эти более простых проблем с смущают вас!
На следующей странице мы сделаем еще один пример, а затем покажем, как квадратичная формула может быть получена из процедуры завершения квадрата…
URL: https://www.purplemath.com/modules/sqrquad.htm
,