Рисунок смежных углов – . .

Конспект «Угол. Смежные и вертикальные углы»

«Угол. Смежные и вертикальные углы»

Ключевые слова конспекта: углы, биссектриса, виды углов, измерение углов, смежные и вертикальные углы, свойства смежных и вертикальных углов, углы при пересечении двух прямых секущей.

---

---

Угол — фигура, образованная двумя лучами, которые выходят из одной точки (вершины).
Биссектриса — луч, который выходит из вершины угла и делит его пополам.

Виды углов. Измерение углов

• Развернутый угол — угoл, стороны которого лежат на одной прямой.
• Прямой угoл — угoл, который равен половине развернутого угла.
• Острый угол — угoл меньше прямого угла.
• Тупой угoл — угoл больше прямого, но меньше развернутого.

Единицы измерения углов:
Градус — величина (градусная мера) угла, равная части развернутого угла.
Минута

— часть градуса.
Секунда — часть минуты.

Смежные и вертикальные углы

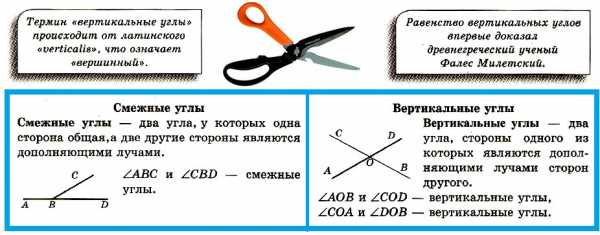
Смежные углы — два угла, у которых одна сторона общая,а две другие стороны являются дополняющими лучами.
Вертикальные углы — два угла, стороны одного из которых являются дополняющими лучами сторон другого.

Теорема. Сумма смежных углов равна 180°.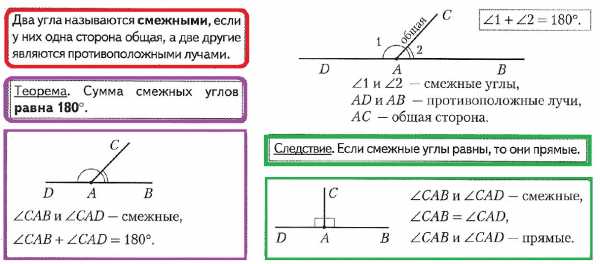

Теорема. Вертикальные углы равны.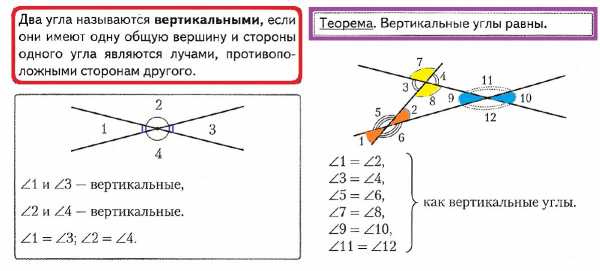

---

Свойства смежных и вертикальных углов

 

Углы при пересечении двух прямых секущей

---

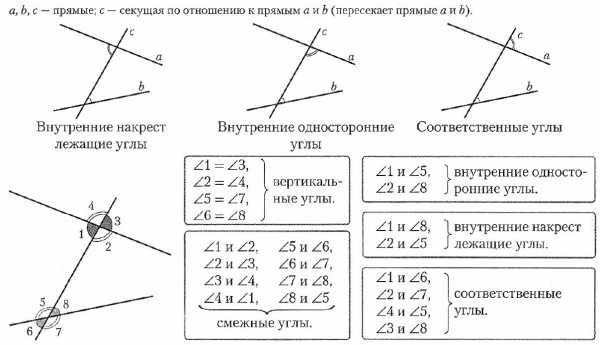
Это конспект по теме «Смежные и вертикальные углы». Выберите дальнейшие действия:

Угол. Смежные и вертикальные углы

5 (100%) 3 vote[s]

uchitel.pro

Смежные и вертикальные углы

Смежные

и

вертикальные

Углы

Учитель математике Дедова Ольга Андреевна

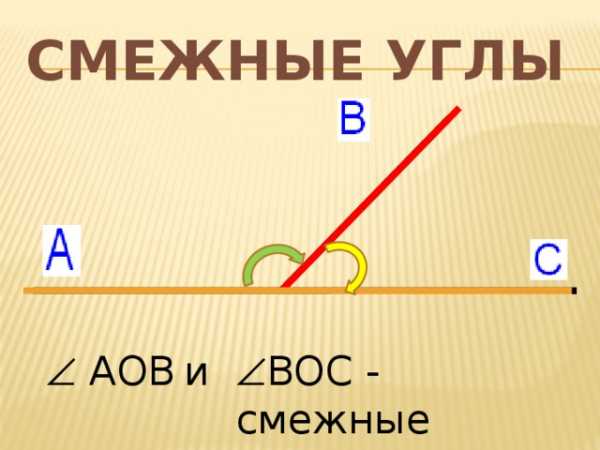
Смежные углы

 АОВ

и

 ВОС — смежные

Запомни !!!

Два угла, у которых одна сторона общая, а две другие являются продолжением одна другой, называются

смежными.

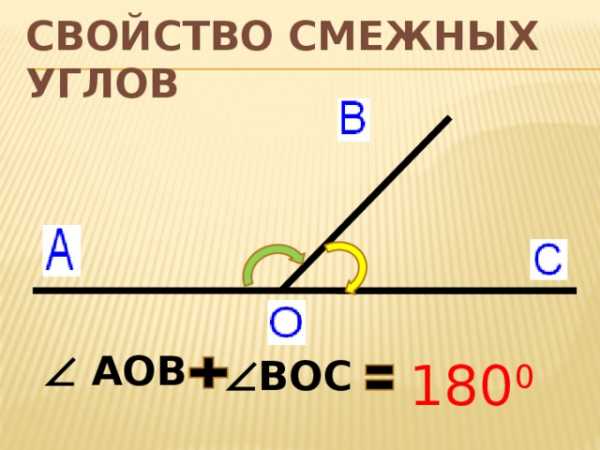
Свойство смежных углов

 АОВ

 ВОС

180 0

Запомни!!!

Сумма смежных уг лов равна

180 0

Вертикальные углы

2

1

3

4

• 1 и  3 ;  2 и  4
• 1 и  3 ;  2 и  4
• 1 и  3 ;  2 и  4
• 1 и  3 ;  2 и  4
• 1 и  3 ;  2 и  4
• 1 и  3 ;  2 и  4
• 1 и  3 ;  2 и  4
• 1 и  3 ;  2 и  4
• 1 и  3 ;  2 и  4

– вертикальные углы.

Запомни!!!

Два угла,

стороны одного из них являются продолжением

сторон другого, называются

вертикальными.

Свойство вертикальных углов

2

1

3

4

 1 =  3

 2 =  4

Запомни!!!

Вертикальные углы

равны

videouroki.net

Смежные углы

СМЕЖНЫЕ УГЛЫ

• Определение,
• Свойства
• Учитель Козина Н.А.

СМЕЖНЫЕ УГЛЫ

Учебник. Стр. 22.

• Два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой, называются смежными

СМЕЖНЫЕ УГЛЫ

Учебник. Стр. 22.

•  ACB и
   BCD – смежные

• CB — сторона общая
• CA и CD — являются продолжениями одна другой.

B

A

D

C

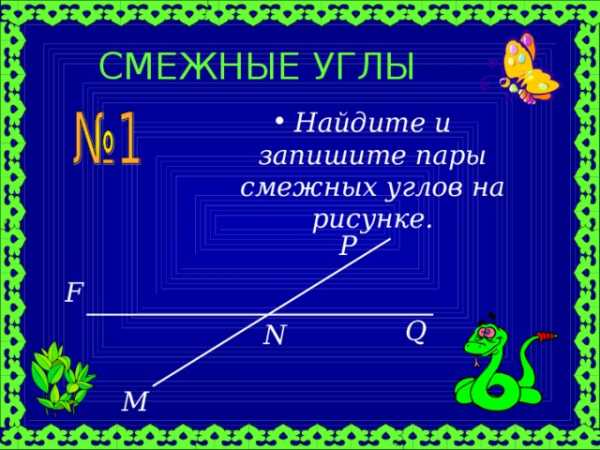
СМЕЖНЫЕ УГЛЫ

• Найдите и запишите пары смежных углов на рисунке.

P

F

Q

N

M

СМЕЖНЫЕ УГЛЫ

• Найдите и запишите пары смежных углов на рисунке.

B

C

A

D

O

•  AOB и  BOD;
•  AOC и  COD.

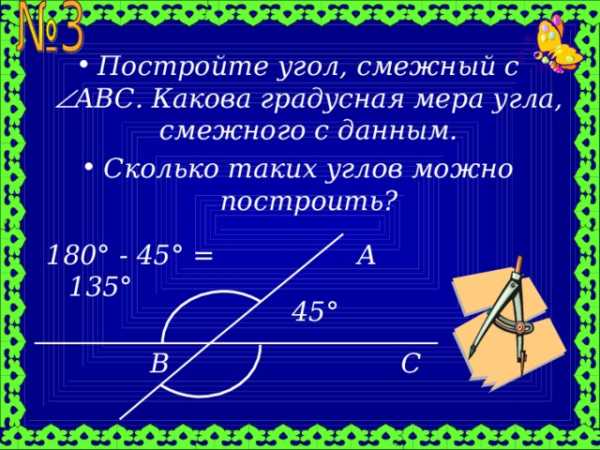
• Постройте угол, смежный с 
  ABC . Какова градусная мера угла, смежного с данным.
• Сколько таких углов можно построить?

180 ° — 45 ° = 135 °

A

45 °

B

С

ТЕОРЕМА 2.1

• Сумма смежных углов равна 180 °

• Дано:  AOC и  COB – смежные ;
• Доказать:

•  AOC +  COB = 180°.

C

O

A

B

• Доказательство.

• Дано:  AOC и  COB – смежные ;
• Доказать:

•  AOC +  COB = 180°.

C

A

O

B

• Доказательство.

• OA и OB – являются продолжениями одна другой;
• Значит,  AOB — развернутый, по определению развернутого угла.

C

• Доказательство.

• Значит,  AOB — развернутый, по определению развернутого угла.

A

O

B

•  AOB = 180° по аксиоме измерения углов;

• Луч OC проходит между сторонами  AOB , т.к. он выходит из вершины и отличен от OA и OB .

C

• Доказательство.

• Луч OC проходит между сторонами  AOB , т.к. он выходит из вершины и отличен от OA и OB .

A

O

B

• Значит, по аксиоме измерения углов, имеем  AOC +  COB =  AOB = 180°
• Теорема доказана.

• Один из смежных углов 30 °
• Найди другой угол.
• 150 ° .

C

O

A

B

• Один из смежных углов 112 °
• Найди другой угол.
• 68 ° .

C

N

• Найдите градусные меры

70°

K

25°

P

L

M

•  KLN = 180° — 25° = 155°;
•  LPN = 180° — 70° = 110°.

C

ЗАДАЧА №5

• Найдите смежные углы, если градусная мера одного из них на 40% больше градусной мера другого.

O

A

B

• Дано:  AOC и  COB – смежные ;

•  AOC на 40% больше
•  COB

1,4x°

x°

180°

• Ответ:  AOC = 105°,  COB = 75°.

ДОМАШНЕЕ ЗАДАНИЕ

• Учебник.П14. Вопросы 1 – 5. Стр. 30.
• Задачи №3, №4(1). Стр. 30.
• Принести транспортир.
• Рабочая тетрадь
• № 77, 78, 79(выучить устно),
• 82, 83, 84.

СМЕЖНЫЕ УГЛЫ

Следствия.

Решение

задач.

МАТЕМАТИЧЕСКИЙ ДИКТАНТ

• Начертите угол AOB .
• Начертите угол с ним смежный.
• Обозначьте его.
• Измерьте эти углы.
• Сделайте записи.

МАТЕМАТИЧЕСКИЙ ДИКТАНТ

• Один из смежных углов равен 123 ° . Найдите второй угол.

• Острым, тупым или прямым будет угол, смежный с углом в 30 ° .

МАТЕМАТИЧЕСКИЙ ДИКТАНТ

• Являются ли смежными углы AOC и COB ?

С

A

B

O

• Найдите смежные углы, если один из них на 30 ° больше другого (без оформления).

СМЕЖНЫЕ УГЛЫ

Следствия.

Следствием из данной теоремы называют такое утверждение, которое доказывается со ссылкой только на данную теорему.

СМЕЖНЫЕ УГЛЫ

Следствия.

Учебник. Стр.25.

• Если два угла равны, то смежные с ними углы равны.
• Если угол не развернутый, то его градусная мера меньше 180 ° .
• Угол, смежный с прямым углом, есть прямой угол.

СМЕЖНЫЕ УГЛЫ

Следствия.

Учебник. Стр.25.

• Если два угла равны, то смежные с ними углы равны.

• Доказательство в рабочей тетради стр. 17.

СМЕЖНЫЕ УГЛЫ

Следствия.

Учебник. Стр.25.

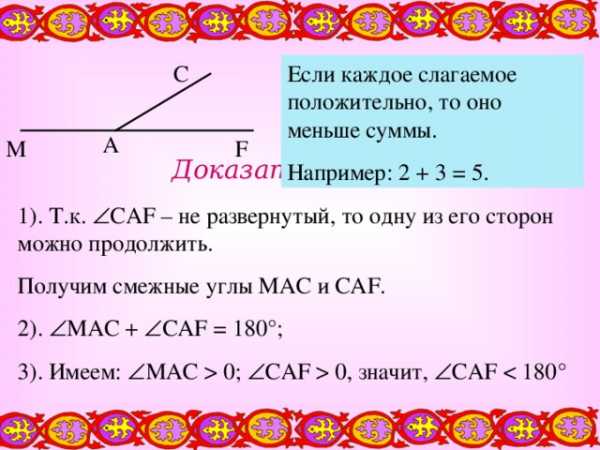
• Если угол не развернутый, то его градусная мера меньше 180 ° .

С

Дано:  CAF – не

развернутый.

Доказать:  CAF

A

F

0;  CAF 0, значит,  CAF «

С

Дано:  CAF – не

развернутый.

Если каждое слагаемое положительно, то оно меньше суммы.

Например: 2 + 3 = 5.

Доказать:  CAF

A

F

M

Доказательство.

1). Т.к.  CAF – не развернутый, то одну из его сторон можно продолжить.

Получим смежные углы MAC и CAF .

2).  MAC +  CAF = 180 °;

3). Имеем:  MAC 0;  CAF 0, значит,  CAF

СМЕЖНЫЕ УГЛЫ

Следствия.

Учебник. Стр.25.

• Угол, смежный с прямым углом, есть прямой угол.

F

Дано:  F BD = 90 ° ,  F BD и  KBF – смежные.

K

B

D

Доказать:  KBF = 90 ° .

Устно, самостоятельно.

ЗАДАЧА №1

Найдите смежные углы, если одна третья часть одного из них равна 0,2 другого.

Дано:  AOC и  COB – смежные.

C

B

A

O

Найти:  AOC и  COB.

Решение.

•  AOC +  COB = 180 ° по свойству смежных углов.

• Пусть  AOC = x °, тогда  COB = (180 – x) °;

Дано:  AOC и  COB – смежные.

C

B

A

O

Найти:  AOC и  COB.

Решение.

•  AOC +  COB = 180 ° по свойству смежных углов.

• Пусть  AOC = x °, тогда  COB = (180 – x) °;

Решение.

•  AOC +  COB = 180 ° по свойству смежных углов.

• Пусть  AOC = x °, тогда  COB = (180 – x) °;

• 180 ° — 67,5° = 112,5°;

Ответ:  AOC = 67,5 °;

 COB = 112,5 ° .

ДОМАШНЕЕ ЗАДАНИЕ

• Учебник.
• Вопросы 1 – 5.
• Задачи:
• № 4(2), №6(1).
• Рабочая тетрадь
• № 88, №89.

videouroki.net

Смежные и вертикальные углы

Тема урока: Смежные и вертикальные углы.
Цели урока:

Ознакомить учащихся с понятиями смежных и вертикальных углов, рассмотреть их свойства;

• 
  Научить строить угол, смежный с данным углом, изображать вертикальные углы, находить на рисунке вертикальные и смежные углы.
  

Ход урока

1. 
   Организационный момент
   

2. 
   Давай вспомним!
   

Что такое угол? (слайд1)

• 
  Как обозначаются углы?(слайд2)
  

Что называется биссектрисой угла? (слайд3)

Назовите единицы измерения углов (слайд4)

Какие виды углов вам известны? (слайд5)

Какой угол образует клюв вороны, когда: «Ворона сыр во рту держала?»

А когда «Ворона каркнула во все воронье горло?» (слайд6)

Острый Тупой(слайд7)

В сказке об углах квадрата брат-круг отрубил ему углы. Какими они стали после этого? (слайд8)
2.Изучение нового материала

К вашим знаниям об углах сегодня добавится еще два вида:

вертикальные и смежные углы. (слайд10)

Построить развернутый угол АОС. Провести луч ОВ. Сколько при этом получилось углов? Укажите получившиеся углы и общую сторону. Что можно сказать про две другие стороны ОА и ОС? (слайд11)

Определение. Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми (слайд12)

Являются ли смежными углы (слайд13)

ÐAOD и ÐBOD
ÐAOС и ÐDOС
ÐAOС и ÐDOВ
ÐAOС, ÐDOС и ÐBOD?

Построение смежных углов. (слайд14)

1.Одну из сторон угла продолжить за его вершину.

2.Получившийся угол АОС является смежным с углом АОВ. (слайд15)

Угол смежный для острого угла является тупым.

Угол смежный для тупого угла является острым. (слайд16)

Угол смежный с прямым углом является прямым (слайд17)

Cвойство смежных углов(слайд18)

1. Сколько углов изображено на рисунке? Какие это углы?

2. Существует ли какая-нибудь взаимосвязь между этими углами? (Вспомните свойство сложения углов).

Сумма смежных углов равна 180

Дано: ÐAOC и ÐBOC – смежные.

Доказать: ÐAOC + ÐBOC = 180°.

Доказательство. 1) Так как ÐAOC и ÐBOC – смежные, то лучи ОА и ОВ – противоположные, то есть, ÐAOB – развернутый, следовательно, ÐAOB = 180°.

2) Луч OC проходит между сторонами ÐAOB, значит, ÐAOC + ÐBOC = ÐAOB = 180°

Решите задачу по чертежу(слайд19)

Решение:

Слайд 20

Начертите произвольный ÐAOB. Постройте лучи OC и OD, противоположные к его сторонам.

Определение. Два угла называются вертикальными, если стороны одного угла являются противоположными лучами к сторонам другого.

Слайд 21

Найдите вертикальные углы.

Слайд 22 Построение вертикальных углов

Слайд 23

1.Построить угол.

2.Продлить каждую сторону угла за его вершину.

Свойство вертикальных углов Слайд 24

Теорема. Вертикальные углы равны.

Дано: ÐAOD и ÐCOB – вертикальные.

Доказать: ÐAOD=ÐCOB

Доказательство. ÐAOD и ÐCOB – смежные с углом ÐAOB. По свойству смежных углов: ÐAOB + ÐAOD = 180°

и ÐCOВ + ÐAOD = 180°. Имеем: ÐAOB = 180° – ÐAOD и ÐCOD = 180° – ÐAOD, значит, ÐAOB = ÐCOD

Решите задачу по чертежу Слайд 25

Решение:

(по свойству вертикальных углов)

Закончи предложение Слайд 26

Если один из смежных углов равен 50°, то другой равен…

Угол, смежный с прямым, всегда…

Если один из вертикальных углов прямой, то второй…

Угол смежный с острым…

Если один из вертикальных углов равен 25°, то второй угол равен…

Задания для самопроверки Слайд 27-28 Определите по рисункам:

Найдите Ð1 и Ð2

ОС- биссектриса

Дано: a = 3 b. Найти: a и b Найти ÐBOC

.

Найти ÐBOC

.

Тест по теме смежные и вертикальные углы Слайды 29-38

1. Сумма смежных углов равна…

3600 900 1800

2. Как называется угол меньше 1800, но больше 900

Острый тупой прямой

3. Чему равен угол, если смежный с ним равен 470?

1330 470 430

4. Какой угол образуют часовая и минутная стрелки часов, когда они показывают 6 часов?

тупой развернутый прямой

5. Найдите

770 1030 30

6. Найдите

540 1260 360

7. Найдите смежные углы, если один из них в два раза больше другого.

900 и 1000 600 и 1200 400 и 800

8. Угол равен 720. Чему равен вертикальный ему угол?

180 1080 720

9. Какой угол образуют часовая и минутная стрелки часов, когда они показывают три часа?

Острый тупой прямой

Проверь себя. Слайды 39

1. C 2. B 3. A 4. B 5. B 6. B 7. B 8. C 9. C

Образец оформления решения задачи Слайды 40

При пересечении двух прямых образовалось четыре угла. Один из них равен 430. Найдите величины остальных углов.

Дано:

МК Ç PF = О

ÐМОF = 43°

Найти:ÐFOK, ÐKOP, ÐPOM

Решение:

ÐМОF и ÐKOP вертикальные, значит, по свойству вертикальных углов, ÐМОF = ÐKOP , ÐKOP = 43°

ÐМОF + ÐFOK = 180°, так как они смежные. Отсюда ÐFOK = 180°- 43°=137°

ÐFOK и ÐPOM вертикальные, значит ÐFOK = ÐPOM ,

ÐPOM =137°

Ответ: 137, 43, 137

Слайды 41

Задача 1. Найдите углы, полученные при пересечении двух прямых, если один из углов равен 102

Задача 2. Найдите величины смежных углов, если один из них в 5 раз меньше другого.

Задача 3. Чему равны смежные углы, если один из них на 300 больше другого?

Задача 4. Найдите величину каждого из двух вертикальных углов, если их сумма равна 980.

Обучающая самостоятельная работа Слайд 42

На рисунке изображены прямые АС и ВD, пересекающиеся в точке О. Дополните записи:

ÐВОС и Ð . . . — вертикальные,

ÐВОС и Ð . . . — смежные,

ÐСОD и Ð . . . — вертикальные,

ÐСОD и Ð . . . — смежные.

2. Начертите угол МОК. Постройте смежный с ним: а) угол КОN; б) угол MOR.

3. Запишите пары смежных углов, имеющиеся на рисунке:

4. Запишите пары вертикальных углов, имеющиеся на рисунке:

ru.convdocs.org