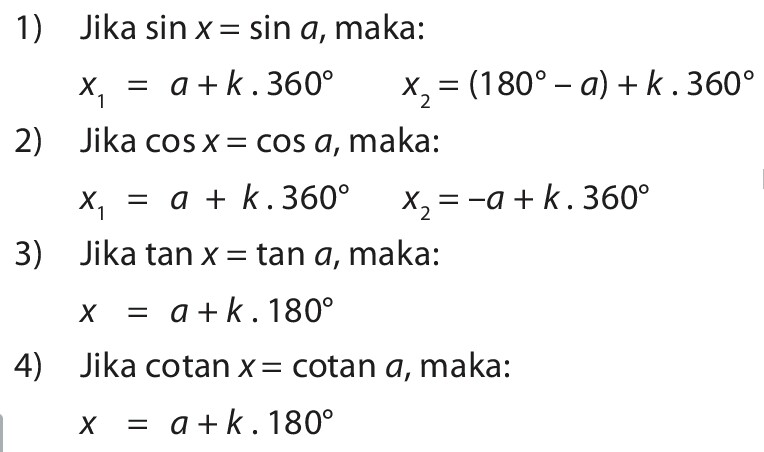Синус умножить на 2 косинус: Синус умножить на косинус, формула и примеры

тригонометрия — косинус и синус угла, умноженные на скаляр

спросил 7 лет, 1 месяц назад

Изменено 7 лет, 1 месяц назад

Просмотрено 3к раз

$\begingroup$

Можете ли вы записать $\cos \alpha x$ через $\cos x$ ? аналогично для $\sin\alpha x$. где $\alpha$ — скаляр в $\mathbb{R}$. (не обязательно целое число).

• тригонометрия

$\endgroup$

$\begingroup$

Для целого числа $\alpha=n$ выполняется соотношение $$ \cos{nx} = T_n(\cos{x}), $$ где $T_n$ — $n$-й полином Чебышева. Это работает для каждого реального $x$.

Для $-\pi \leqslant x \leqslant \pi$ мы также имеем формулу половинного угла $$ \cos{\tfrac{1}{2}x} = \sqrt{\frac{1+\cos{x}}{2}}, $$ из которого мы можем вывести полуцелые формулы типа $$ \cos{\tfrac{3}{2}x} = \sqrt{\frac{1+\cos{x}}{2}}(2\cos{x}-1), $$ и мы могли бы также итерировать «уполовинивание», чтобы выразить двоично-рациональные числа над $[-\pi,\pi]$.

Следовательно, мы можем составить последовательность функций от $\cos{x}$, аппроксимирующих $\cos{\alpha x}$ для любого действительного $\alpha$. 92)} \cos{kx}, $$ и опять же, это работает для $x \in [-\pi,\pi]$. В случае, если вы хотите, вы можете заменить $\cos{kx}$s на $T_k(\cos{x})$, чтобы получить функцию полностью в терминах $\cos{x}$. Таким же образом можно составить аналогичные выражения для более длинных конечных интервалов, хотя их длина должна быть кратна $\pi$.

$\endgroup$

3

$\begingroup$

В общем случае нет, потому что $\cos x=\cos (x+2\pi)$, а $\cos(\alpha x)\neq \cos(\alpha(x+2\pi))$, когда $ \alpha$ не является целым числом. Итак, если бы вы могли написать:

$$g(x)=\cos(\alpha x)=f(\cos x)$$ для некоторой функции $f$, то $$\cos(\alpha(x+2) \pi))=g(x+2\pi)=g(x)=\cos(\alpha x)$$ для всех $x$.

Это верно только для $\alpha$ целого числа.

Теперь вы можете определить $\left|\cos(\alpha x)\right|$ через $\cos x$, когда $\alpha$ является полуцелым числом. Это потому, что $\left|\cos x\right|$ имеет период $\pi$.

$\endgroup$

0

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Math Scene — Правила тригонометрии

Math Scene — Правила тригонометрии — Урок 1

2008 Расмус Эф    и Джанн Сак

Правила тригонометрии

Урок 1    Пифагор правило для косинуса и синуса

---

В математике есть много правил, которые помогают нам упрощать и тем самым решать более сложные триггерные уравнения.

Сейчас мы найдем и воспользуемся одним из них, пожалуй, самый полезный из всех.

Это правило часто называют правилом Пифагора для синусы и косинусы. На диаграмме показано прямоугольный треугольник, нарисованный в единичной окружности. Правило Пифагора верно для всех точек P включен единичный круг. Это означает, что (sin v) 2 +(cosv) 2 =1. Это правило обычно записывается в виде:

sin 2 v + cos 2 v = 1

Можно переписать двумя способами:

sin 2 v = 1 − cos 2 v

и

cos 2 v = 1 — sin 2 v

Пример 1

Найдите sin x, если cos x = ⅓ и 0 х <

(x — угол между 0 и 90).

Мы можем решить эту проблему с помощью калькулятора,
cos ⁻¹ (⅓) ≈ 70,53 и, следовательно, грех 70,53 ≈ 0,94. Если мы хотим получить точный ответ мы можем сделать этот пример без калькулятора, используя правило Пифагора.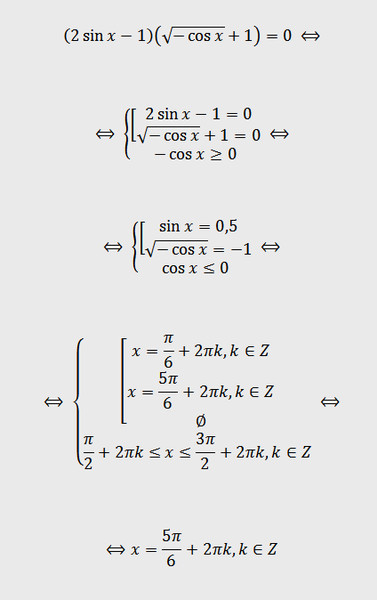

Пример 2

Используйте правило sin ² v + cos ² v = от 1 до найти другие способы записи выражения 1/ cos ² v.

Один из способов — переместить sin ² v над знаком равенства, чтобы получить cos ² v = 1 − sin ² v, а затем инвертировать обе части уравнения. Это дает нам

Есть и другой, не столь очевидный путь, ведущий к выражению, которое часто может быть полезным. Посмотрите, что произойдет, если мы разделим исходное уравнение sin ² v + cos ² v = 1 на cos ² v

.

Теперь мы доказали правило:

Пример 3

Теперь мы будем использовать Pythagoras для триггерных функций, чтобы найти значение первого sin ² v тогда соз ² v, заданный sin

2 v = cos ² v.

Сначала заменим cos ² v по правилу cos ² v = 1 − sin ² v.