Ряд Маклорена (=Макларена) это ряд Тейлора в окрестности точки а=0.
Ряд Маклорена (=Макларена) это ряд Тейлора в окрестности точки а=0.
Оказывается, большинство практически встречающихся математических функций могут быть с любой точностью представлены в окрестностях некоторой точки в виде степенных рядов, содержащих степени переменной в порядке возрастания. Например, в окрестности точки х=0:
При использовании рядов, называемых рядами Маклорена (=Макларена), смешанные функции, содержащие, скажем, алгебраические, тригонометрические и экспоненциальные функции, могут быть выражены в виде чисто алгебраических функций. С помощью рядов зачастую можно быстро осуществить дифференцирование и интегрирование.
Теорема Маклорена (ряд Маклорена (=Макларена)) имеет вид:
1) , где f(x) — функция, имеющая при а=0 производные всех порядков. Rn — остаточный член в ряде Маклорена (=Макларена) (Тейлора при а=0)определяется выражением
2)
k-тый коэффициент (при хk) ряда определяется формулой
Ряды Маклорена являются частным случаем рядов Тейлора.
Условия применния рядов Маклорена (=Макларена).
1) Для того, чтобы функция f(x) могла быть разложена в ряд Маклорена (=Макларена) на интервале (-R;R) необходимо и достаточно, чтобы остаточный член в формуле Маклорена (=Макларена) для данной функции стремился к нулю при k→∞ на указанном интервале (-R;R).
2) Необходимо чтобы существовали производные для данной функции в точке а=0, в окрестности которой мы собираемся строить ряд Маклорена (=Макларена).
Численное интегрирование с использованием рядов Маклорена (=Макларена).
Значения многих интегралов нельзя найти с помощью каких-либо аналитических методов. Мы уже рассказывали о вычислении таких интегралов с помощью формулы трапеций, формулы Симпсона. Другой метод нахождения числового значения определенного интеграла — выражение функции в виде ряда Маклорена (=Макларена) с последующим поочередным интегрированием каждого члена.
tehtab.ru
§6. Ряды Маклорена и Тейлора
Предположим, что функция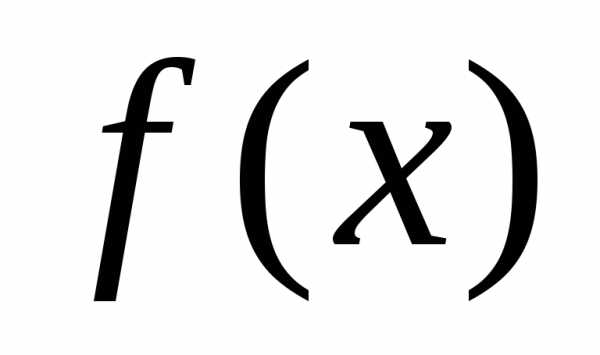 
,
определенная и бесконечно дифференцируемая
в окрестности точки
,
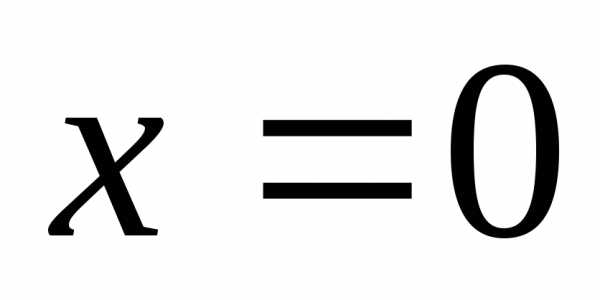может быть представлена в виде суммы
степенного ряда или, другими словами,
может быть разложена в степенной ряд
Выразим коэффициенты ряда через 
.
Найдем производные функции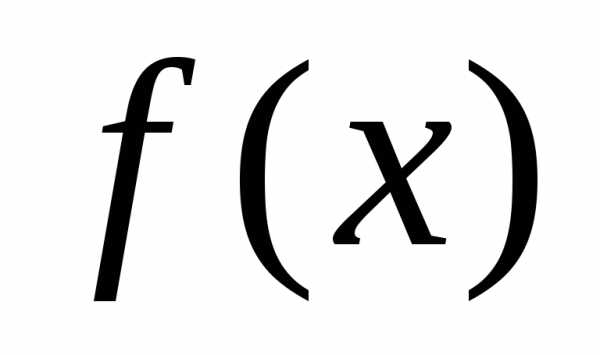
,
почленно дифференцируя ряд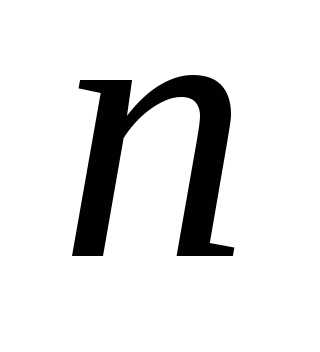
…………………………………………………………….
Полагая в полученных равенствах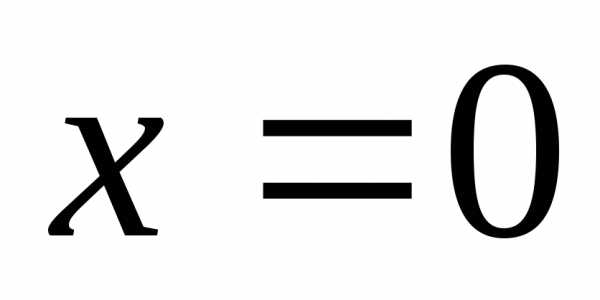 
,
получим
,,,,
…,,
откуда
,,
,
,…,
,…
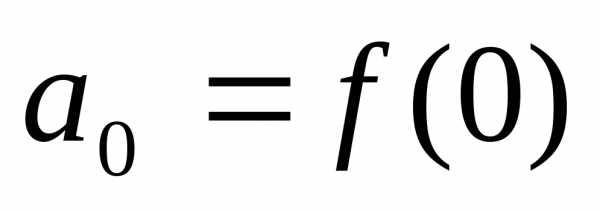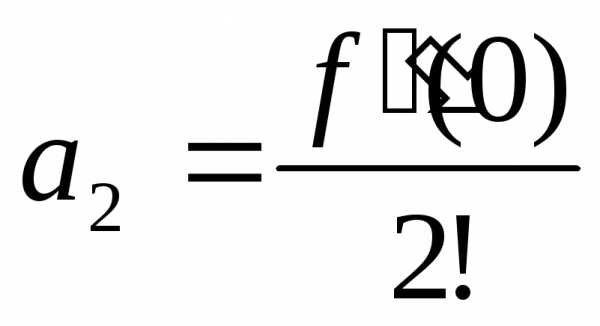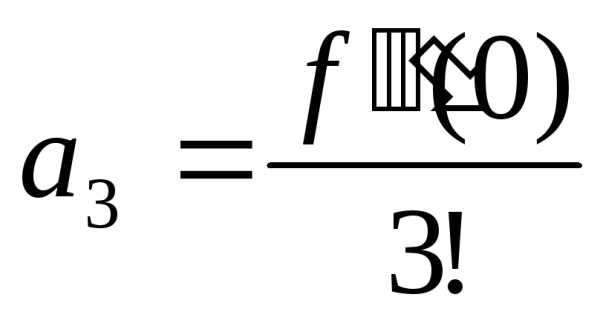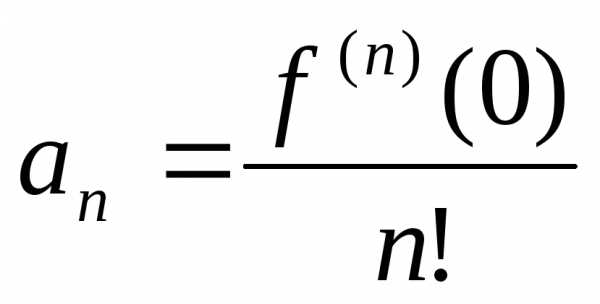Подставляя значения коэффициентов , получим ряд:
(1)
называемый рядом Маклорена.
Отметим, что не все функции могут быть
разложены в ряд Маклорена. Может
оказаться, что ряд Маклорена, составленный
формально для функции 
,
является расходящимся или сходящимся
не к функции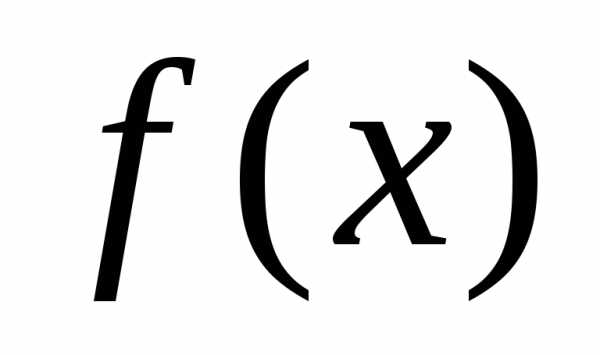
Если представить ряд Маклорена в виде
,
где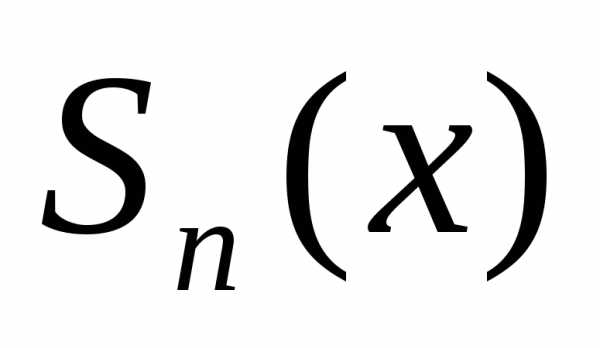
– 
—я
частичная сумма ряда,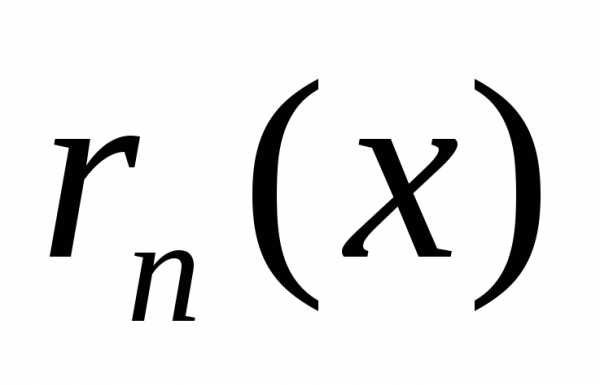
–
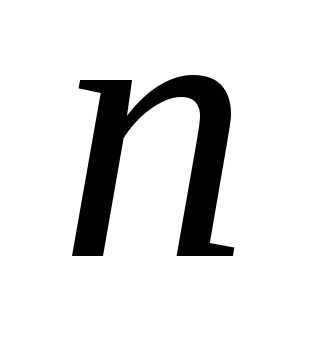—й
остатокряда, то можно сформулировать
следующую теорему:
Теорема. Для того чтобы ряд Маклорена
сходился к функции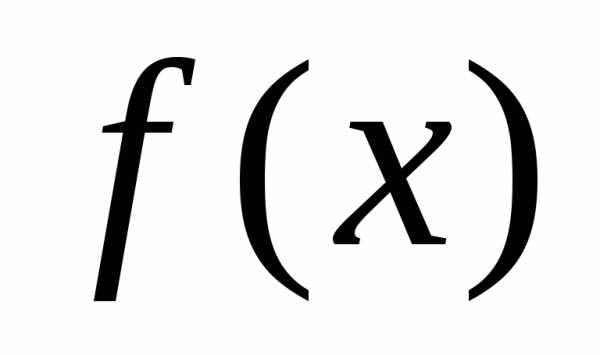
,
необходимо и достаточно, чтобы приостаток ряда стремился к нулю, т.е.
для всех значенийиз интервала сходимости ряда.
Можно доказать, что если функция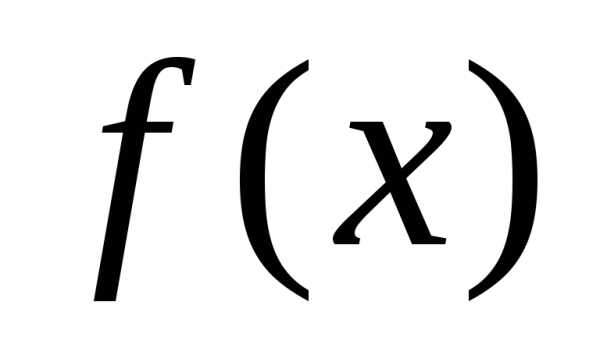 
разложима в ряд Маклорена, то это
разложение единственное.
Замечание. Ряд Маклорена является
частным случаем
при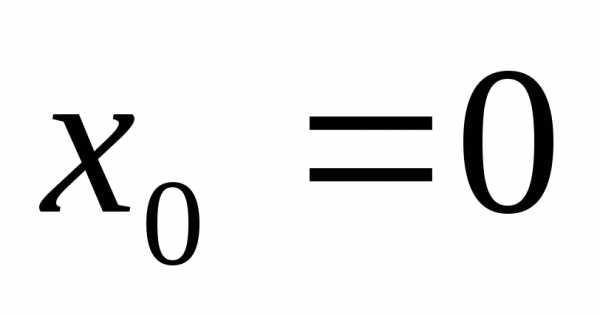
Ряд Тейлора тесно связан с формулой Тейлора:
,
где
– остаточный член формулы Тейлора,
который можно записатьв форме Лагранжа:
,.
§7. Разложение в ряд Маклорена некоторых функций
1. 
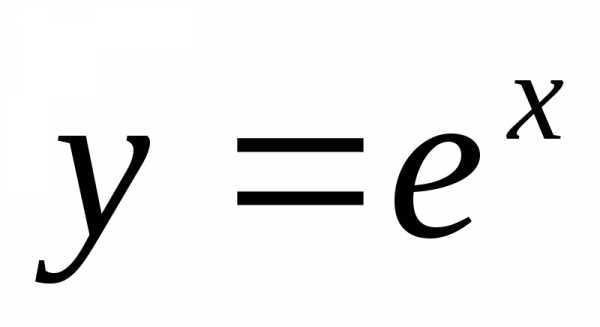
Имеем ;
, и по формуле (1) получаем
. (2)
Областью сходимости этого степенного
ряда является интервал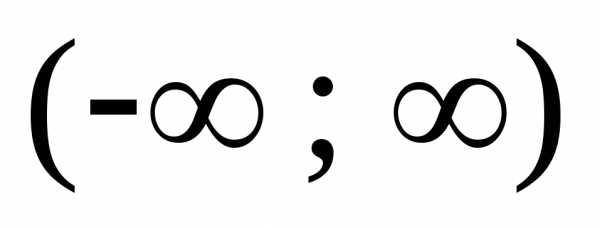 
.
2. 
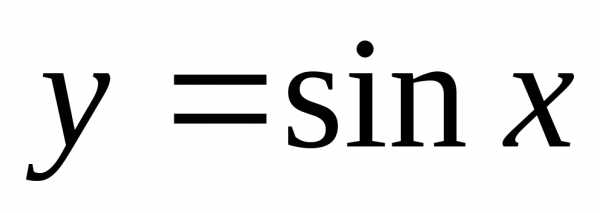
Имеем: ,,,,, откуда
,
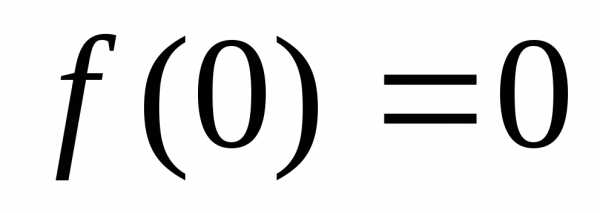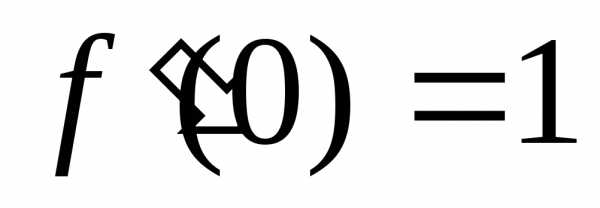,,,и т.д.
Очевидно, что производные четного порядка , а нечетного порядка,, и по формуле (1)
(?)(3)
Область сходимости ряда 
3. .
Рассматривая аналогично функции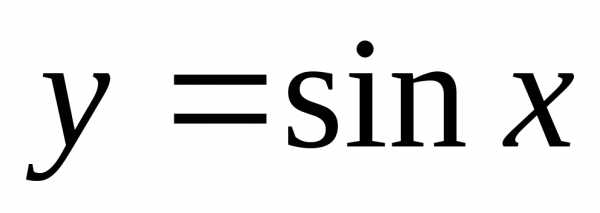 
,
получим:
(4)
Область сходимости ряда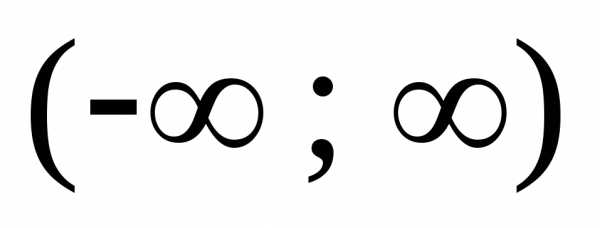 
.
4.
,
где
– любое действительное число.
Имеем ,,
,, …,
, …
При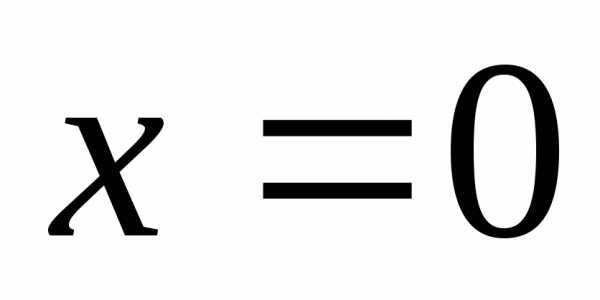 
:
,,,
, …,и по формуле (1) получаем
(5)
Найдем интервал сходимости ряда:
Ряд, составленный из модулей , исследуем с помощью признака Даламбера:
.
Следовательно, интервал сходимости
ряда 
.
На концах интервала при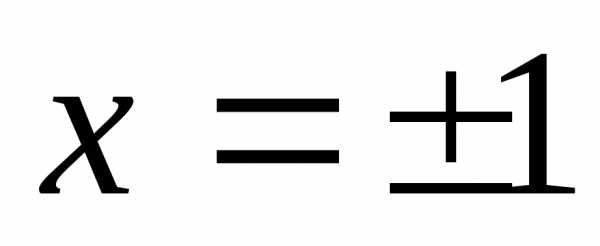
сходимость ряда зависит от конкретных
значений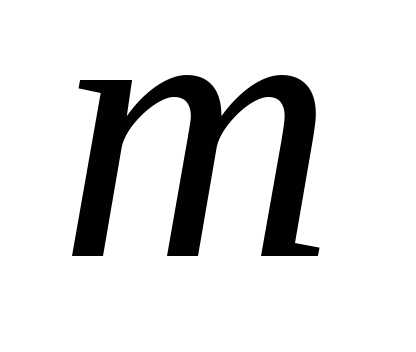
Ряд (5) называется биномиальным. Если
– целое положительное число, то
биномиальный ряд представляет формулубинома Ньютона, так как присомножительравен нулю, следовательно,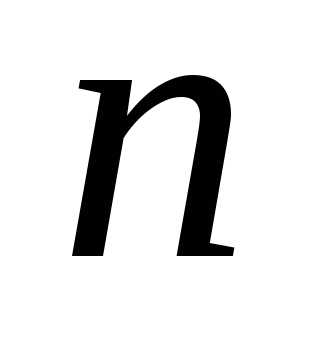
-й член ряда и все последующие равны
нулю, т.е. ряд обрывается, и вместо
бесконечного разложения получается
конечная сумма.
Выпишем некоторые разложения функции
при различных
.
:
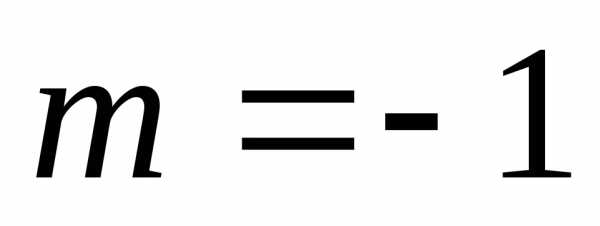,(6)
если в это разложение подставить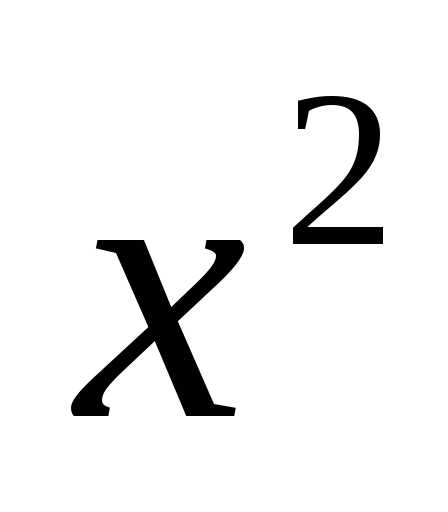 
вместо
,
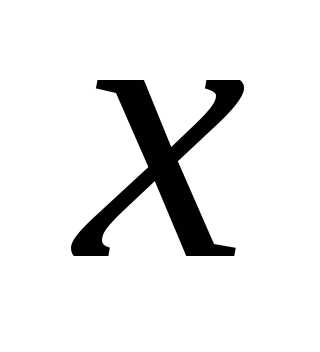получим:
(7)
:
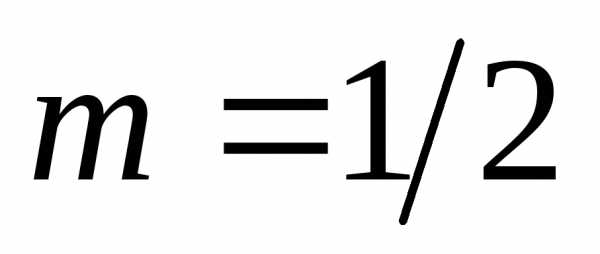,(8)
:
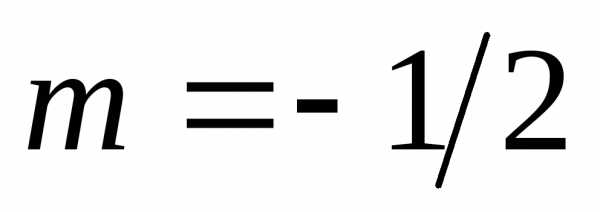,(9)
5. .
Получить разложение для этой функции,
непосредственно вычисляя коэффициенты
с помощью производных, не очень просто,
поэтому мы воспользуемся разложением
(6) и свойством 2) степенных рядов.
Интегрируя почленно равенство (6) в
интервале 
,
где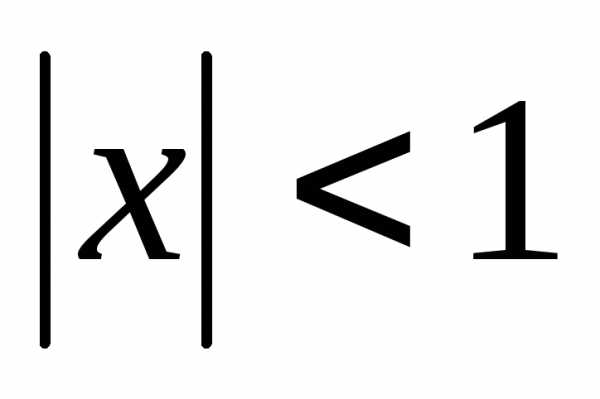
,
с учетом того, что,
получим
(10)
Область сходимости ряда (после выяснения
сходимости на концах интервала) есть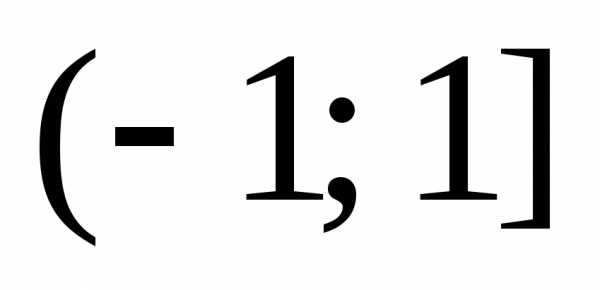 
.
6.
Проделаем то же самое, что и в предыдущем случае, воспользовавшись разложением (7):
(11)
Область сходимости ряда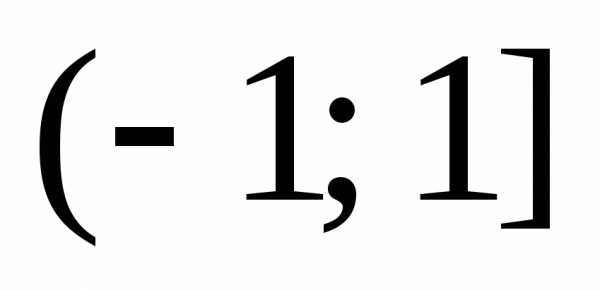 
.
7.
Воспользуемся разложением (9), подставив
в него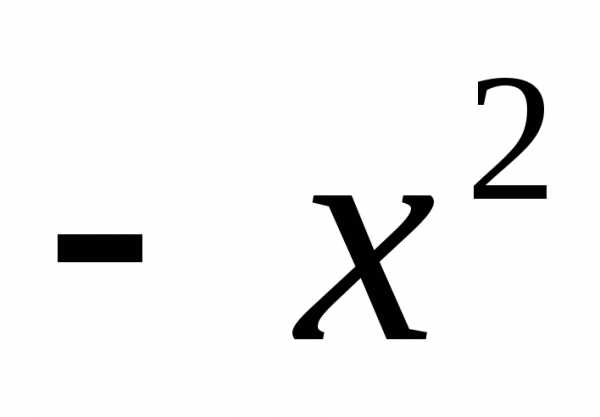 
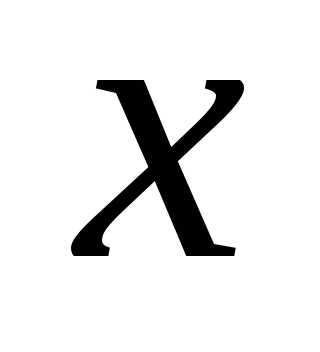: Интегрируя в интервал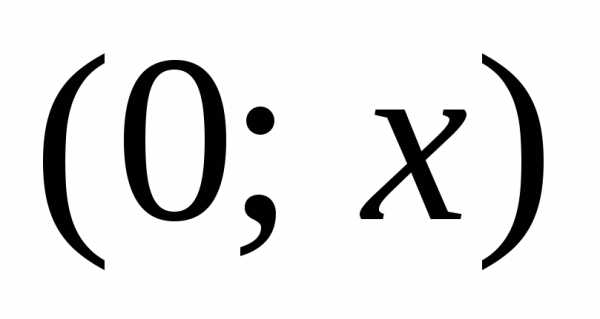е 
,
где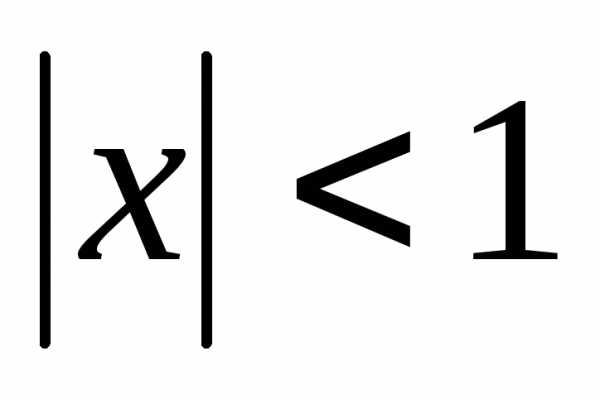
,
получаем:
(12)
Область сходимости ряда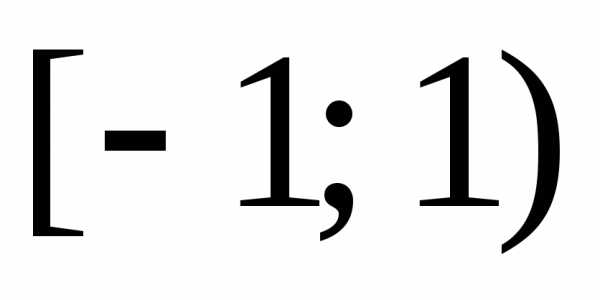 
Можно доказать, что ряды, приведенные в формулах (2) –(12), сходятся к функциям, для которых они составлены.
При разложении более сложных функций часто используют готовые разложения (2) – (12).
Примеры.
1) Разложить в ряд Маклорена функцию
Решение. Воспользуемся известной тригонометрической формулой
Разложим в ряд Маклорена функцию 
,
заменяя в разложении (4)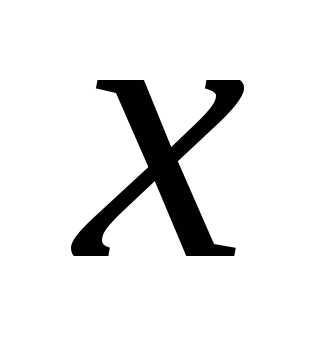
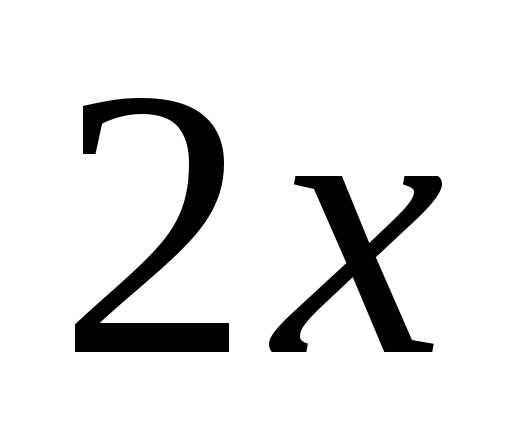:Тогда
Это и есть разложение в ряд Маклорена
функции
.
Очевидно, что оно справедливо при любом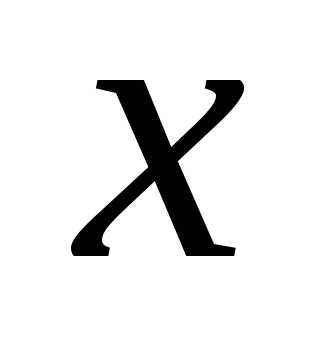
.
2) Разложить в ряд Тейлора по степеням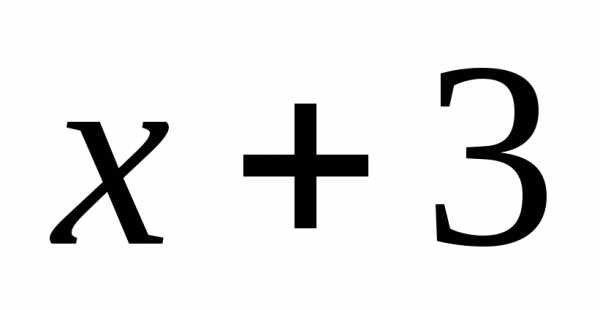 
функцию
Решение.Преобразуем данную функцию так, чтобы можно было воспользоваться разложением (6):
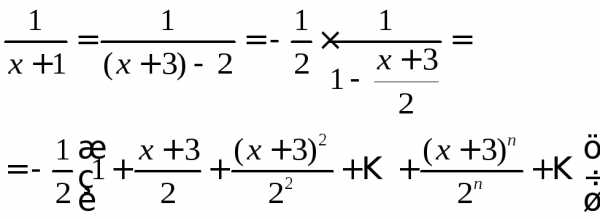
Полученное разложение справедливо,
когда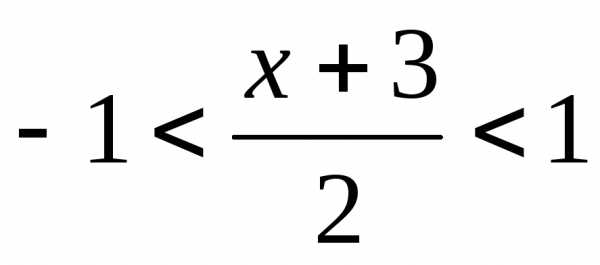 
.
Отсюда получаемили.
studfiles.net
§6. Ряд Тейлора. Ряд Маклорена. Использование степенных рядов в приближенных вычислениях.
Пусть задана функция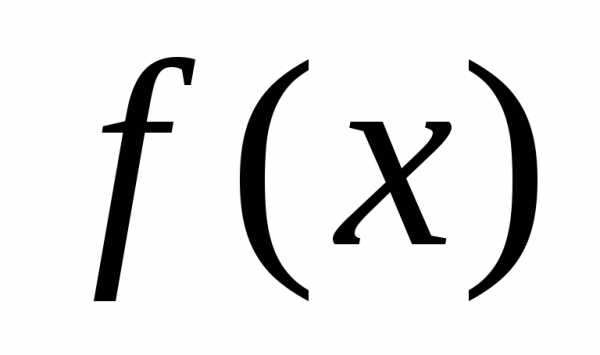
,
имеющая на некотором отрезке производные
всех порядков, тогда она разлагается
на этом отрезке в ряд вида
,
который называется рядом Тейлора.Здесь
—
заданное число.
Формально ряд Тейлора можно написать
для всякой функции, которая в окрестности
точки 
имеет производные любого порядка. Однако
этот ряд будет сходиться к породившей
ее функции только при тех значениях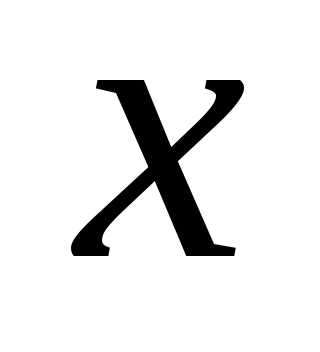
,
при которых остаток ряда стремиться к
нулю:
.
Остаток ряда Тейлора записывается в форме Лагранжа следующим образом:
,
где 
заключено между
и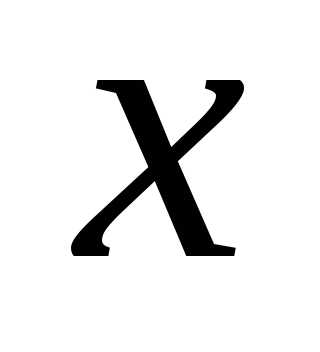
.
Если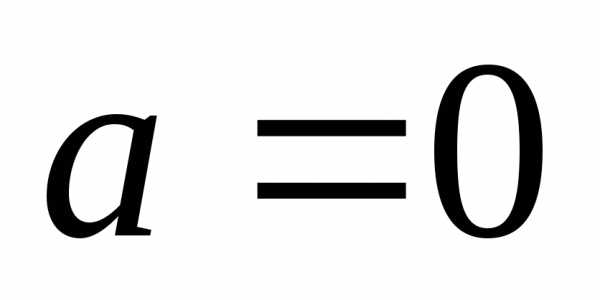 
,
то получаем частный случай ряда Тейлора,
который называетсярядом Маклорена:
.
Рассмотрим ряды Маклорена для некоторых элементарных функций.
—
данный ряд называется биномиальным,
поскольку при натуральном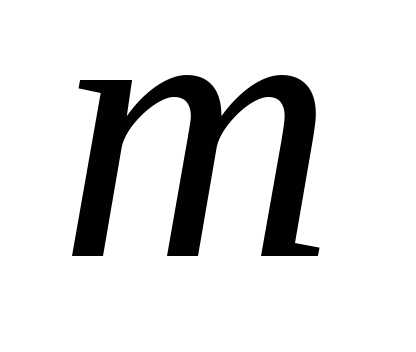 
из
него получается бином Ньютона.
Подчеркнем, что степенные ряды для
функций
сходятся к соответствующим функциям
при,
а степенные ряды для функцийисходятся лишь при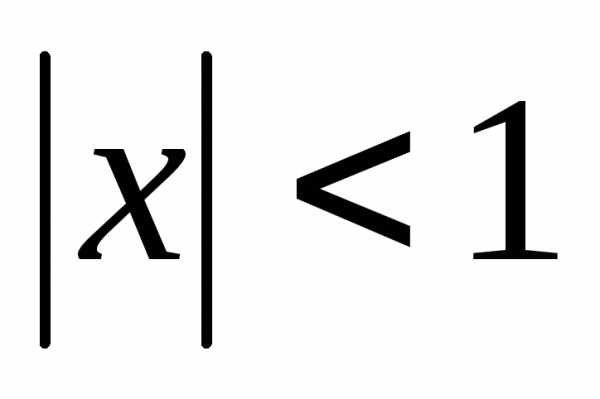
.
Задача №1. Написать разложение в
степенной ряд функции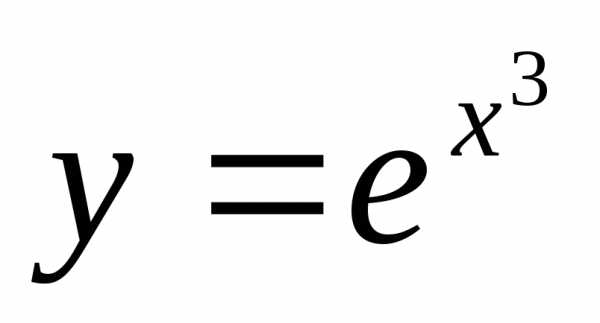
.
Решение.В качестве исходной формулы возьмем разложение в ряд Маклорена
функции 
:
.
Заменим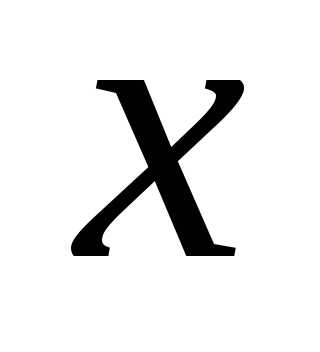 
на
:
Ответ:
Задача №2. Написать разложение в
степенной ряд функции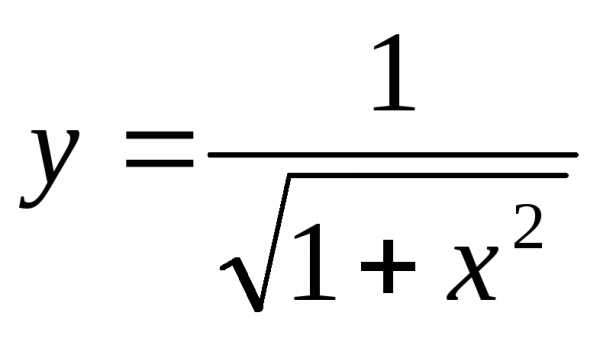
.
Решение. Запишем биномиальный ряд
и сделаем в нем замену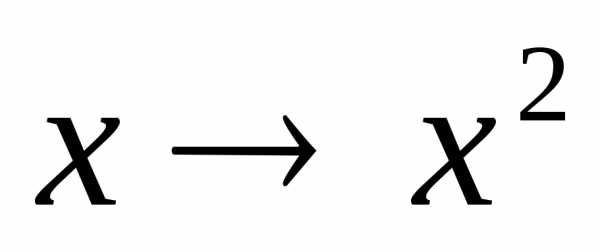 
:
.
По условию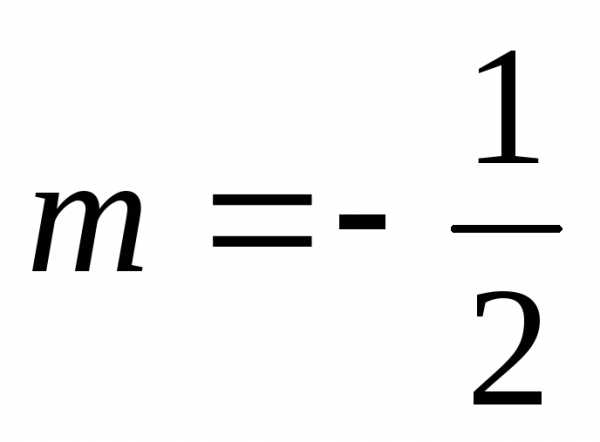 
,
подставим это значение в предыдущую
формулу:
Ответ: .
Степенные ряды широко используются в приближенных вычислениях. Рассмотрим применение рядов Тейлора для приближенного вычисления значений функций, значений определенных интегралов и приближенного решения дифференциальных уравнений.
Задача №3. Вычислить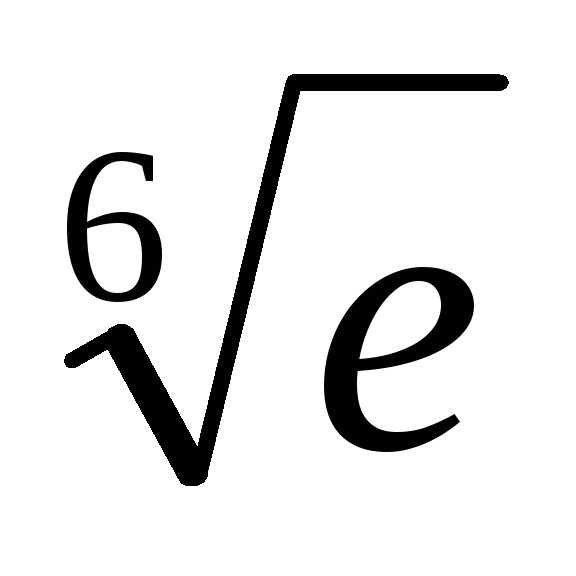
приближенно с точностью 0,0001.
Решение. Для любого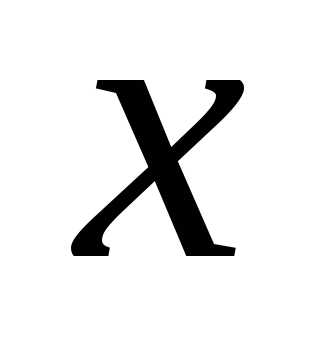
имеет место формула:
.
При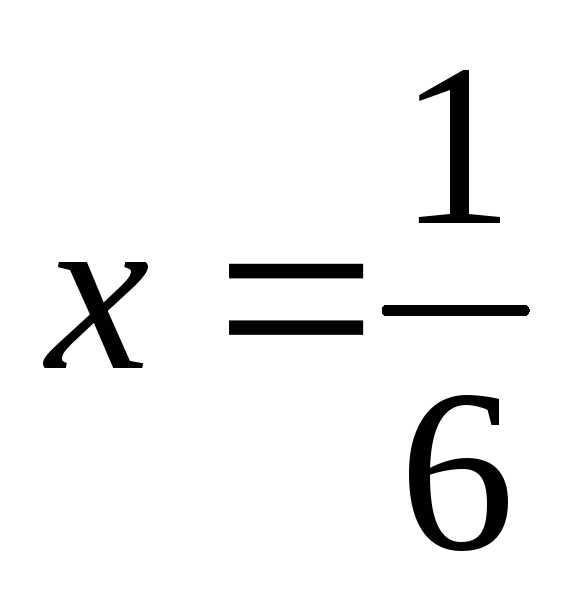 
получим
.
Оценим погрешность вычислений с помощью остаточного члена в форме Лагранжа:
.
Так как
, то
,
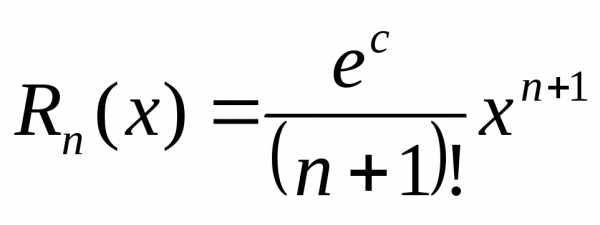где 
лежит между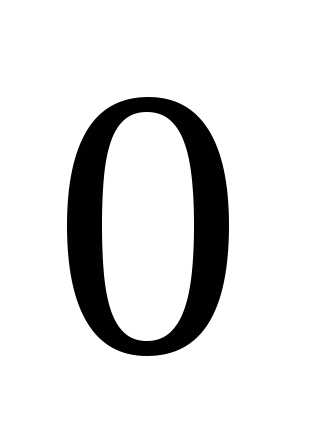
и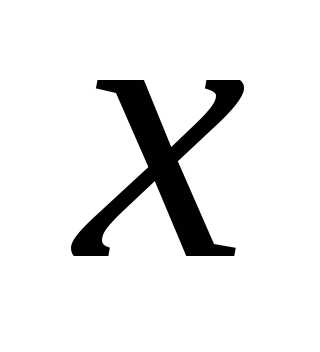
.
При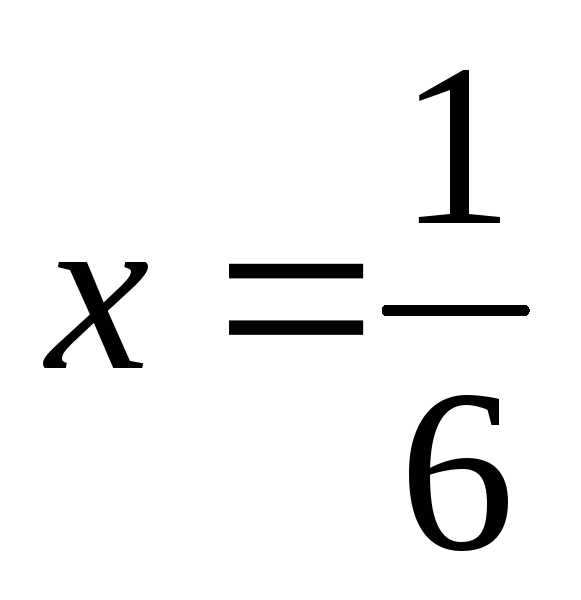 
имеем
,
где 
.
Учитывая, что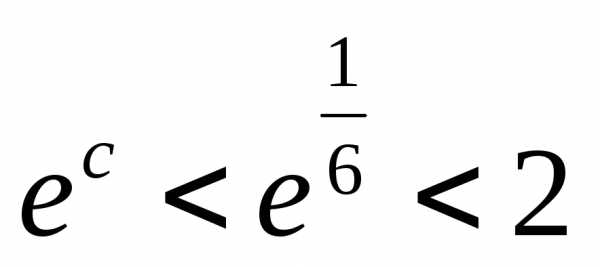 
,
получим
.
При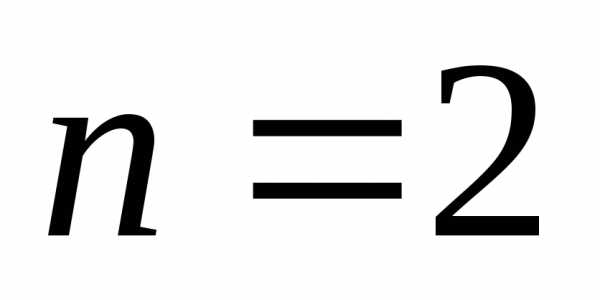 
.
При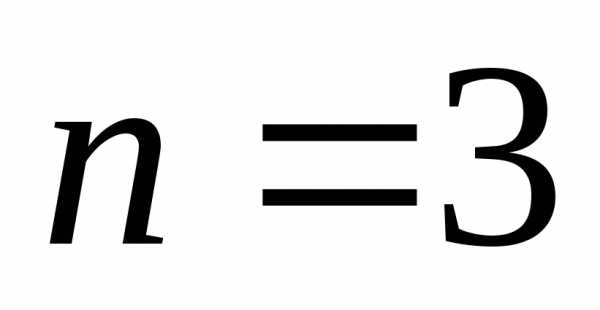 
.
Таким образом, для достижения требуемой
точности достаточно взять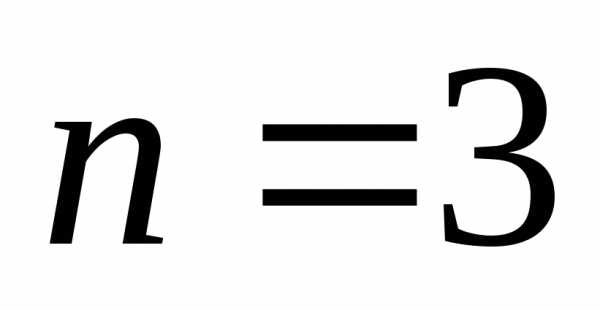 
(или
более):
.
Каждое слагаемое вычислим с одним дополнительным знаком после запятой, чтобы к нашей ошибке не добавлялись ошибки от округления:
.
Ответ: с точностью 0,0001 .
Задача №4. Вычислить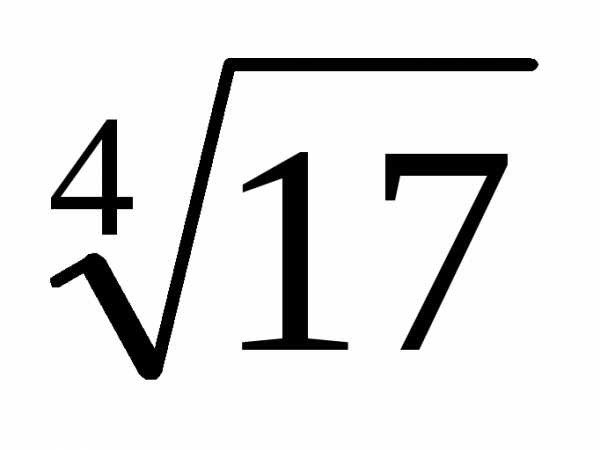
приближенно с точностью 0,0001.
Решение.Для вычисления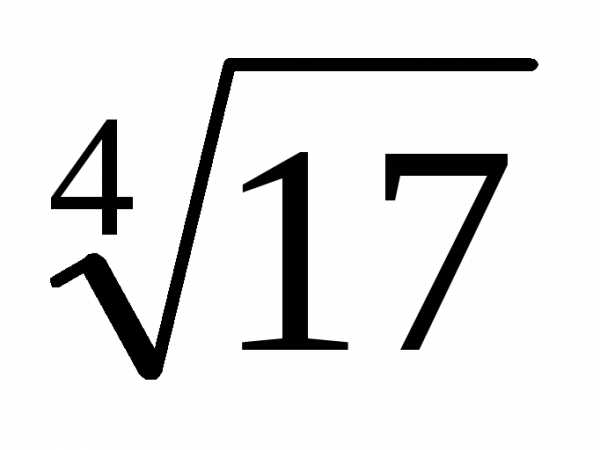
будем использовать биномиальный ряд,
который сходится только при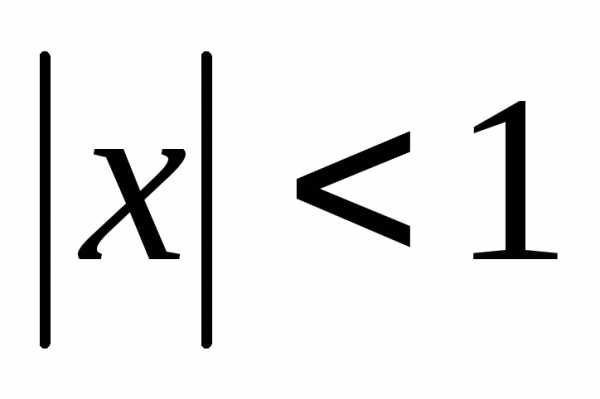
,
поэтому сначала преобразуем данный
корень:
.
В биномиальном ряде положим 
:
.
Данный знакочередующийся числовой ряд
является рядом Лейбница. Чтобы определить,
сколько взять первых членов ряда для
вычисления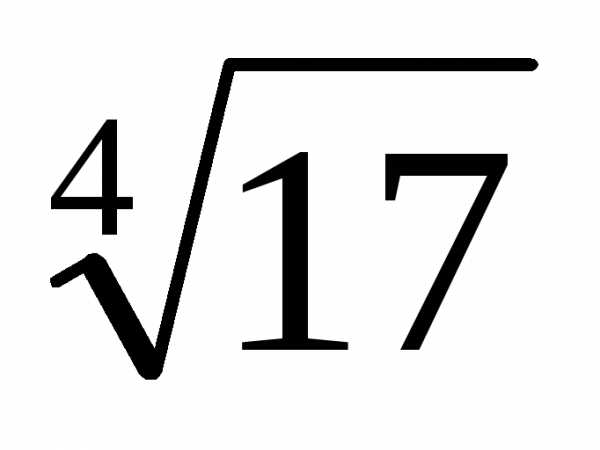 
с
точностью 0,0001, вычислим последовательно
несколько первых членов ряда:
.
Согласно свойству ряда Лейбница, если
оставить первые три слагаемые, то ошибка
искомого приближенного значения корня
будет меньше 
:
,
следовательно,
.
Ответ: с точностью 0,0001
Пусть необходимо посчитать определенный интеграл
от некоторой функции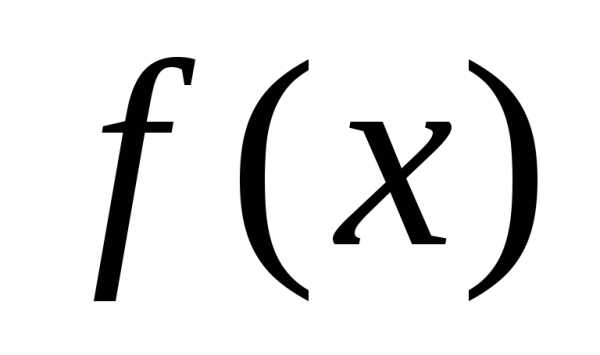
,
первообразная которой не вычисляется
в элементарных функциях. Следовательно,
формулу Ньютона-Лейбница применить не
удается. Если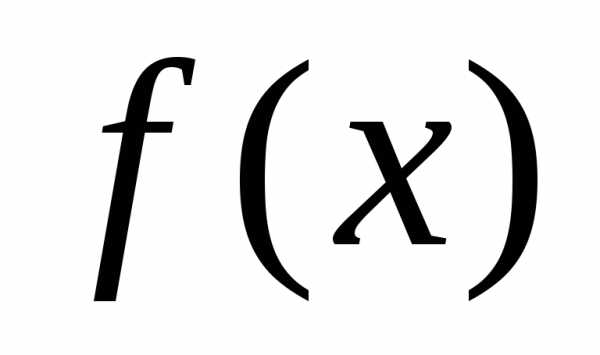
разложима в степенной ряд на отрезке
,
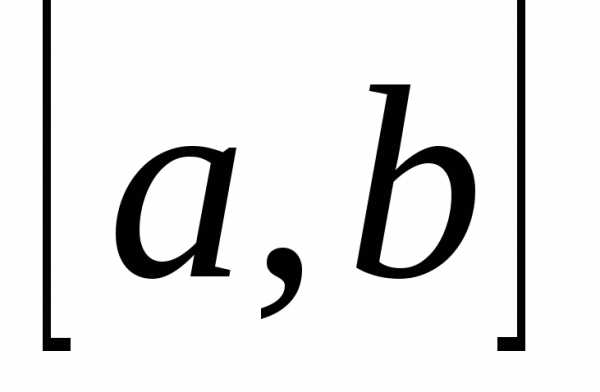принадлежащем области сходимости ряда,
то интеграл может быть вычислен
приближенно. Иногда приближенного
вычисления бывает достаточно и при
наличии первообразной функции. Для
решения такой задачи используются
ряды Тейлора. Рассмотрим примеры.
Задача №5. Вычислить определенный
интеграл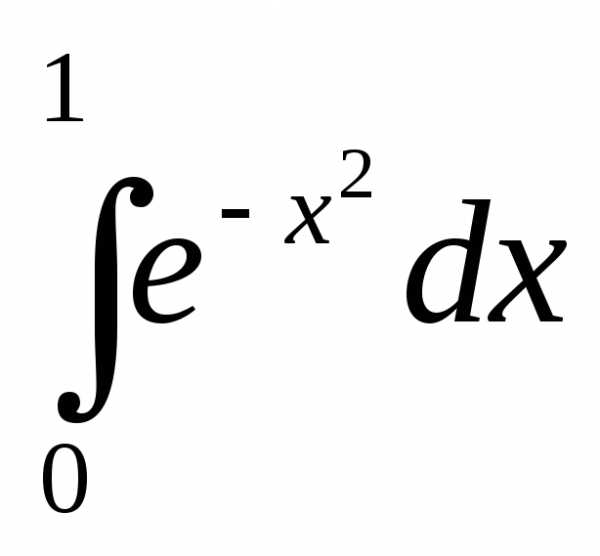
с точностью 0,01.
Решение.Заметим, что этот широко используемый интеграл не выражается в элементарных функциях.
В ряде Маклорена для функции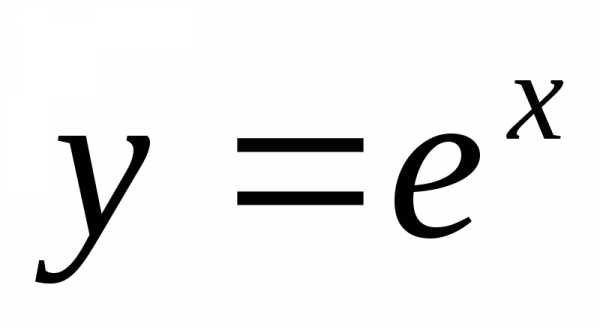 
сделаем
замену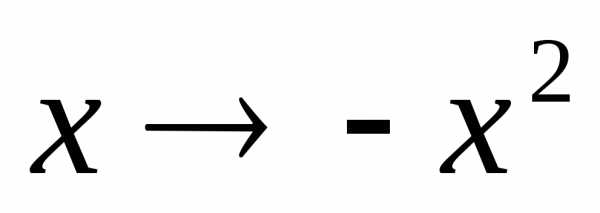
:
.
Теперь воспользуемся теоремой о том,
что степенной ряд можно почленно
интегрировать по любому отрезку,
принадлежащему интервалу сходимости.
Данный ряд сходится на всей числовой
прямой, следовательно, его можно
интегрировать по любому отрезку, в том
числе по отрезку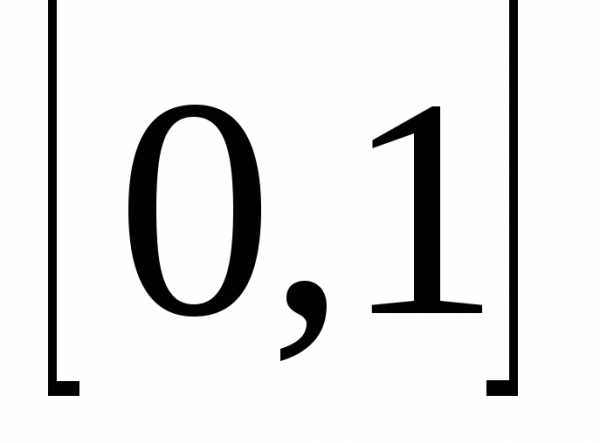 
:
Мы получили числовой ряд, который равен значению определенного интеграла.
Оценим погрешность вычислений. Данный ряд – это ряд Лейбница, следовательно, погрешность вычислений не превосходит по модулю первого отброшенного члена ряда. Поэтому, вычисляя по порядку члены ряда, первым отбросим тот, который окажется по модулю меньше заданной точности:
,
.
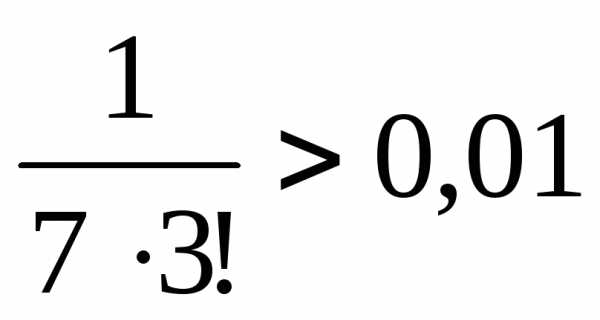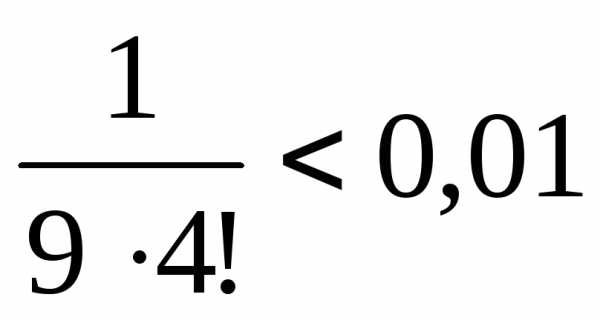Тогда 
024=0,743.
Ответ: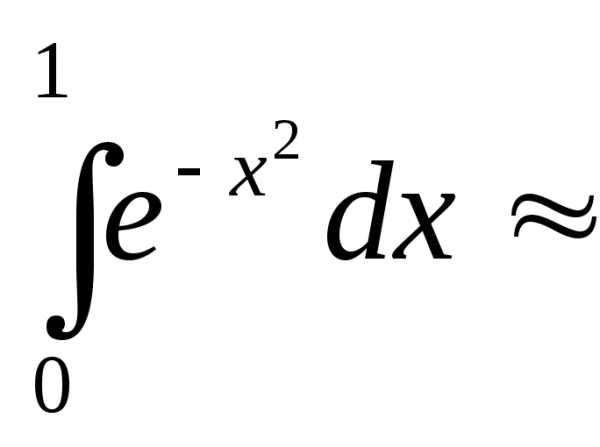
0,743.
Задача №6. Вычислить определенный
интеграл
с точностью 0,001.
Решение.Вычислить этот интеграл по формуле Ньютона-Лейбница нельзя, поскольку первообразная функциине выражается в элементарных функциях. Используем для решения задачи степенной ряд. Запишем разложение в ряд Маклорена функции:
.
Сделаем в этой формуле замену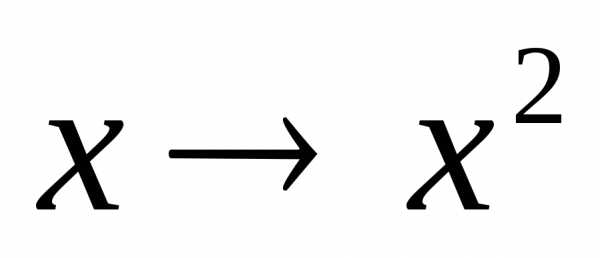
:
Данный ряд можно почленно проинтегрировать
по отрезку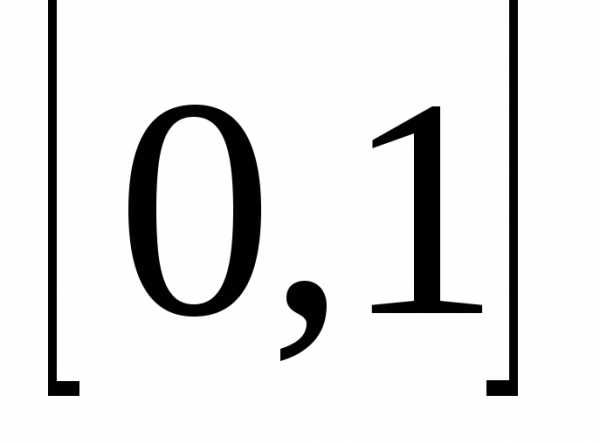 
:
Таким образом, вычисляемый определенный интеграл равен сумме знакочередующегося числового ряда, который удовлетворяет условиям признака Лейбница, следовательно, погрешность вычислений не превосходит модуля первого из отброшенных членов ряда.
,
.
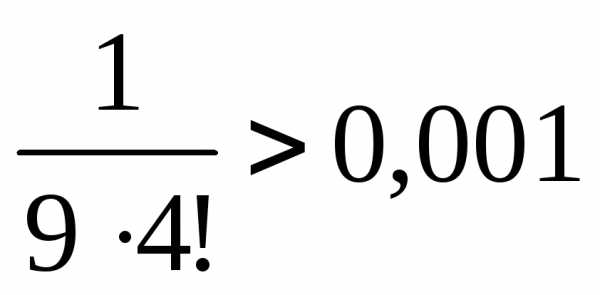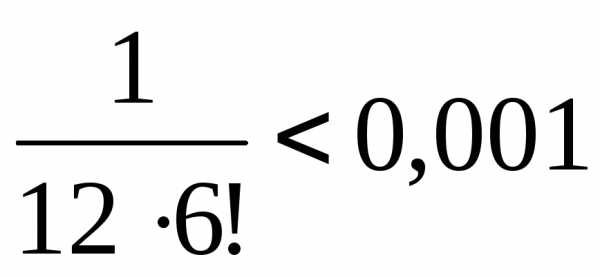Поэтому для достижения заданной точности необходимо оставить первые 3 слагаемые.
.
Ответ: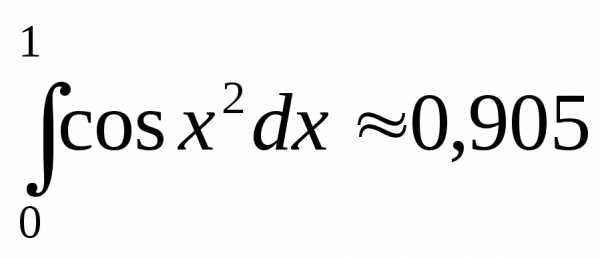 
.
Задача №7. . Вычислить определенный
интеграл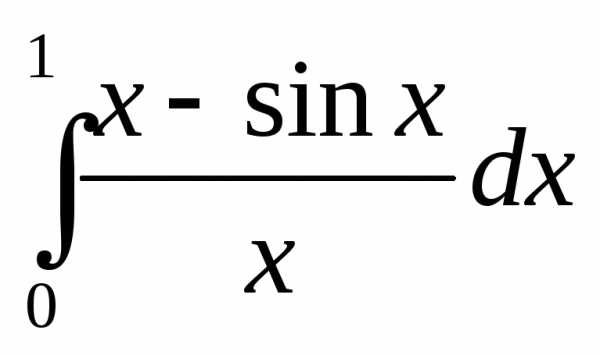
с точностью 0,001.
Решение.Распишем ряд Маклорена для функции.
.
Тогда
.
Поделим левую и правую часть формулы
на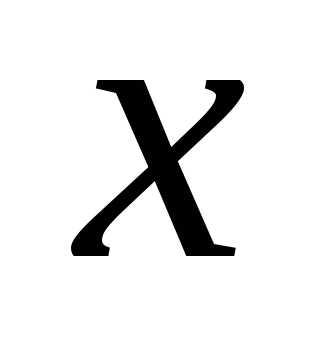 
:
.
Полученный степенной ряд можно
почленно проинтегрировать по отрезку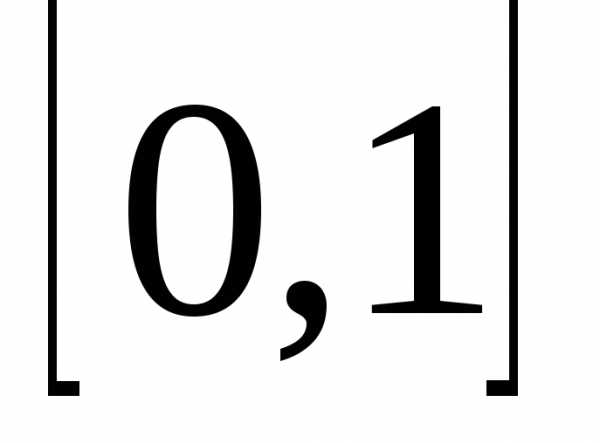
.
.
Получившийся числовой ряд сходится по признаку Лейбница, поэтому отбрасываем первым слагаемое, которое меньше объявленной точности:
,
.
.
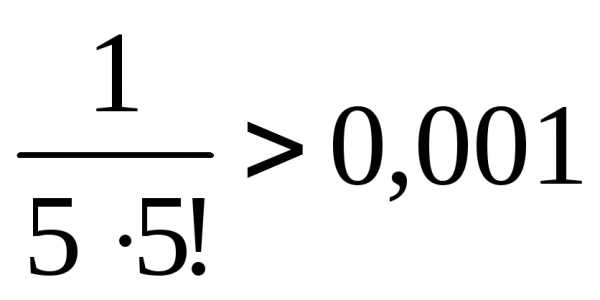Ответ: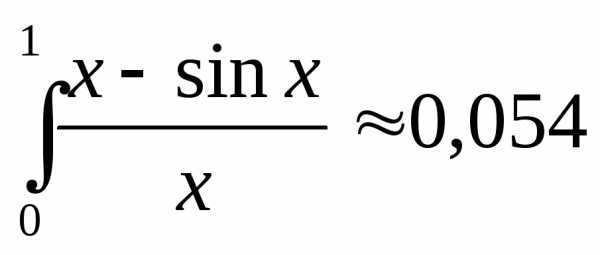 
.
Рассмотрим еще одно приложение степенных рядов, к приближенному решению дифференциальных уравнений. Решение дифференциального уравнения не всегда можно выразить в элементарных функциях. Интегралы многих дифференциальных уравнений могут быть представлены в виде степенного ряда, сходящегося в некотором интервале значений независимой переменной. В таком случае ряд, являющийся решением дифференциального уравнения можно найти с помощью рядов Тейлора.
Пусть необходимо найти частное решение дифференциального уравнения с заданными начальными условиями, т.е. решить задачу Коши.
Проиллюстрируем решение на примере.
Задача №8. Найти первые пять членов
разложения в степенной ряд решения
дифференциального уравнения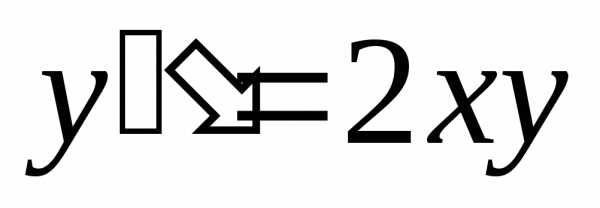
,
удовлетворяющего начальным условиям
.
Решение.Будем искать частное решение дифференциального уравнения в виде ряда
.
Мы выбрали разложение в ряд Маклорена,
поскольку в условии задачи нам даны
значения искомой функции и ее первой
производной в точке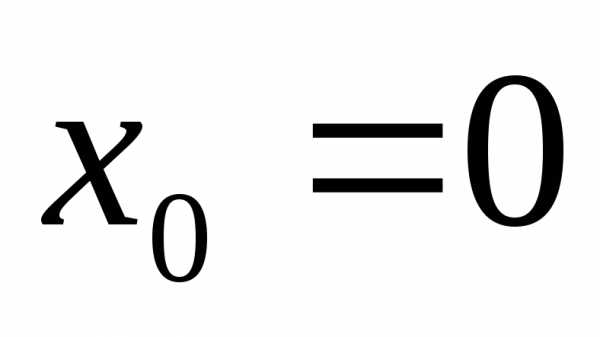 
.
Для того, чтобы найти приближенное
значение функции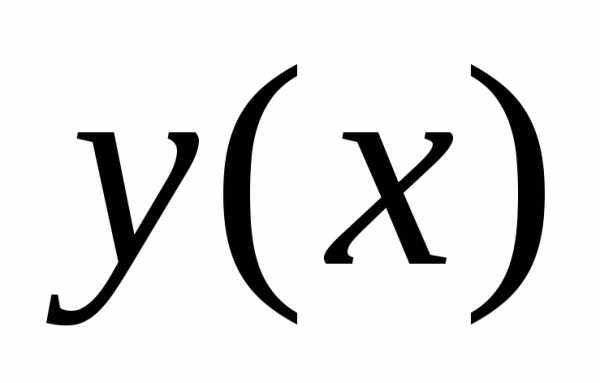
,
нам необходимо знать значения ее второй,
третьей и четвертой производных в точке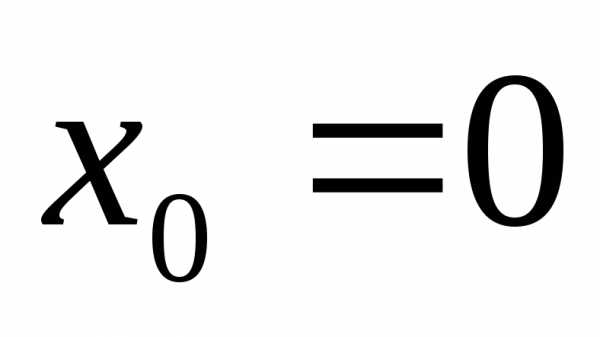
.
Значения самой функции и первой
производной в нуле даны по условию.
Значение второй производной при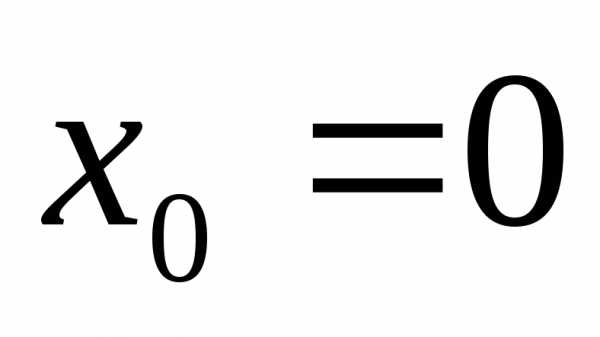 
найдем из дифференциального уравнения,
подставив начальные условия:
.
Для нахождения третьей производной продифференцируем данное дифференциальное уравнение:
.
При этом необходимо учесть, что 
—
это функция, а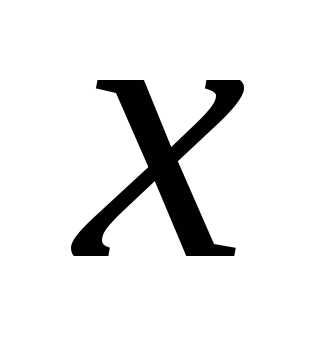
—
независимая переменная:
.
Теперь можно вычислить значение третьей
производной в точке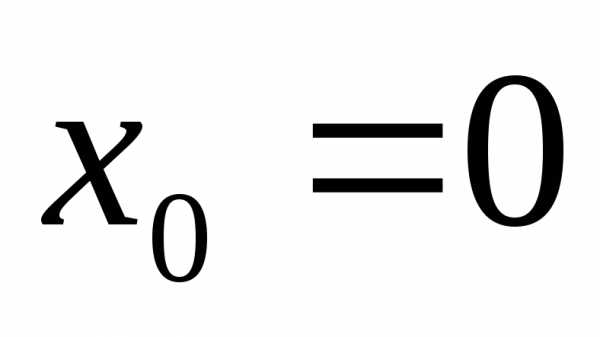 
:
.
Аналогично вычислим значение четвертой производной:
, или
.
Подставив в найденное равенство значения
получим:
.
Осталось подставить вычисленные в заданной точке значения производных в ряд Маклорена:
.
Ответ: .
Задача №9. Найти первые четыре члена
разложения в степенной ряд решения
дифференциального уравнения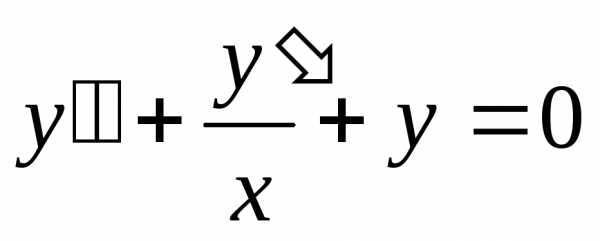
,
удовлетворяющего начальным условиям
.
Решение.Начальные условия заданы в точке, поэтому решение будем искать в виде ряда Тейлора:
.
Значения самой функции и ее первой
производной даны в условии задачи.
Вторую производную в точке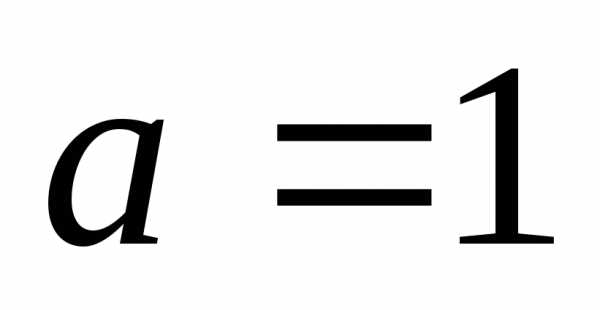 
найдем
из дифференциального уравнения:
.
Вычислим третью производную, продифференцировав дифференциальное уравнение:
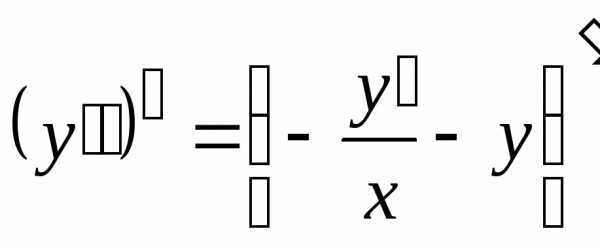или
.
Тогда значение третьей производной равно
.
Осталось записать искомый ряд:
Ответ:
studfiles.net
| Техническая информация тут | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Степенные ряды Тейлора, Маклорена (=Макларена) и периодический ряд Фурье. Разложение функций в ряды. / / Примеры некоторых распространенных разложений степенных функций в ряды Маклорена (=Макларена,Тейлора в окрестностях точки 0) и Тейлора в окрестностях точки 1.
|
dpva.ru
| Техническая информация тут | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Степенные ряды Тейлора, Маклорена (=Макларена) и периодический ряд Фурье. Разложение функций в ряды.
|
dpva.ru
Ряд Маклорена | C++ для приматов
Задача
Вычислите с точностью [latex]\varepsilon[/latex] значение функции [latex]f\left( x \right) = \ln \left( 1-x^2 \right)[/latex] . При вычислениях допустимо использовать только арифметические операции.
Входные данные
В одной строке заданы значение переменной [latex]x[/latex] и точность вычислений [latex]\varepsilon[/latex].
[latex]\left | x \right |< 1[/latex]
Выходные данные
Значение функции в точке [latex]x[/latex] .
Тесты
| [latex]\varepsilon[/latex] | [latex]x[/latex] | [latex]ln(1-x^2)[/latex] | Результат |
| 0.001 | 0.5 | [latex]ln(0.75)[/latex] | -0.287435 |
| 0.0001 | 0.5 | [latex]ln(0.75)[/latex] | -0.287671 |
| 0.01 | 0.1 | [latex]ln(0.99)[/latex] | -0.01005 |
| 0.001 | -0.1 | [latex]ln(0.99)[/latex] | -0.01005 |
| 0.1 | 0 | [latex]ln(1.00)[/latex] | 0 |
| 0.01 | 0 | [latex]ln(1.00)[/latex] | 0 |
Код программы
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
#include <iostream> #include <cmath> using namespace std;
int main() { double E, logarithm = 0, ai = 1, p = 1, x; int i = 1; cin >> x >> E; while(ai > E){ p *= x*x; // вычисление числителя члена ряда ai = p / i; // вычисление члена ряда logarithm -= ai; i++; } cout << logarithm; return 0; } |
ideone.com
Решение
Функцию [latex]f\left( x \right) = \ln \left( 1-x^2 \right)[/latex] можно представить в виде:
[latex]ln\left ( 1-x^2 \right )= ln\left ( 1-x \right )\left ( 1+x \right ) = ln\left ( 1-x \right )+ln\left ( 1+x \right )[/latex] (по свойствам логарифма).
Для решения задачи необходимо воспользоваться формулой Тейлора для натурального логарифма с опорной точкой [latex]x_{0}=0[/latex] (ряд Маклорена). Для функции [latex]ln\left (1+x\right )[/latex] она имеет следующий вид:
[latex]ln\left (1+x\right )=x-\frac{x^{2}}{2}+\frac{x^{3}}{3}-\cdots+\frac{\left ( -1 \right )^{n-1}}{n}x^{n}=\sum_{n=1}^{\infty}\frac{\left (-1\right )^{n-1}}{n}x^{n}[/latex]
Подставив в формулу [latex]-x[/latex] вместо [latex]x[/latex] , получим:
[latex]ln\left (1-x\right )=-x-\frac{x^{2}}{2}-\frac{x^{3}}{3}-\cdots -\frac{x^{n}}{n}=-\sum_{n=1}^{\infty}\frac{x^{n}}{n}[/latex]
Тогда,
[latex]ln\left (1+x\right )+ln\left (1-x\right )=\sum_{n=1}^{\infty}\frac{\left (-1\right )^{n-1}}{n}x^{n}-\sum_{n=1}^{\infty}\frac{x^{n}}{n}=[/latex]
[latex]=\sum_{n=1}^{\infty }\left[\frac{\left (-1\right )^{n-1}}{n}x^{n}-\frac{x^{n}}{n}\right]=\sum_{n=1}^{\infty }\frac{x^{n}\left (\left (-1\right )^{n-1}-1\right )}{n}=[/latex][latex]=-x^{2}+0-\frac{x^{4}}{2}+0-\frac{x^{6}}{3}+0-\cdots[/latex]
Так как при нечетном [latex]n[/latex] члены данного ряда обращаются в ноль, его можно записать в виде:
[latex]-\sum_{0}^{\infty}\frac{x^{2n+2}}{n+1}=-x^{2}-\frac{x^{4}}{2}-\frac{x^{6}}{3}-\cdots-\frac{x^{2n+2}}{n+1}[/latex]
Далее необходимо найти рекуррентную формулу для членов данного ряда.
[latex]\frac{a_{n}}{a_{n-1}}=\frac{x^{2n+2}}{n+1}\cdot\frac{n-1+1}{x^{2\left ( n-1 \right )+2}}=\frac{x^{2}\cdot n }{n+1}[/latex]
Затем необходимо суммировать до тех пор пока очередное слагаемое не будет меньше заданной точности.
cpp.mazurok.com
Ряды Тейлора и Маклорена. Разложение функций на практике
Задачи на разложение функций в ряды Тейлора и Маклорена очень важны в курсе высшей математики при приближенном вычислении значений функций в определенных точках, приближении производных в точках, сложных пределах. Поэтому внимательно разберитесь с приведенным ниже материалом. Начнем с основных определений.
Рядом Тейлора для функции f(x) при условии, что она определена в окрестности точки a, а также ее конечные производные любого порядка называется ряд вида
Пусть сумма ряда задана формулой
тогда формула Тейлора имеет вид
называют остаточным членом формулы Тейлора.
Бесконечно дифференцируема функция f(x) на интервале разлагается в ряд Тейлора только в случаях, когда на этом интервале выполняется условие
При нулевом значении формула Тейлора превращается в ряд Маклорена:
РАСПИСАНИЕ В РЯД МАКЛОРЕНА ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
———————————————
Пример 1. Развить в ряд Тейлора функцию (9.293)
по степеням
Решение. Разложение по степенях множителя следует понимать, как расписание в точке Вычислим значения функции и ее производных в этой точке
Подставляем полученные значения в ряд Тейлора
Упрощенно ряд можно записать в виде суммы
Исследуем сходимость полученного ряда по признаку Деламбера
Из условия находим область сходимости
Исследуем границы интервала. При значении ряд
превращается в гармоничный со знаком минус. Этот ряд расходится. При получим знакопочережний ряд вида
который убывает.
Таким образом, областью сходимости ряда является . Исследуя остаточный член ряда
формулы Тейлора для данной функции, убеждаемся, что в заданном интервале ряд совпадает и остаточный член ряда существенного вклада при больших не вносит.
———————————————
Пример 2. Развить в ряд Маклорена функцию (9.305)
Решение. Воспользовавшись первой из формул расписания элементарных функций, получим
Умножая на , получим расписание заданной функции в виде такого ряда
или в упрощенной форме
По признаку Деламбера найдем область сходимости ряда
То есть, радиусом сходимости будет интервал .
На этом знакомство с темой подходит к концу. Больше материалов Вы найдете в категории «Ряды».
yukhym.com