Википедия круги эйлера – Круги Эйлера — Википедия

Круги Эйлера — Википедия

Пример кругов Эйлера. Буквами обозначены, например, свойства:  — живое существо,  — человек,  — неживая вещь

Круги́ Э́йлера^[1] — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Изобретены Леонардом Эйлером. Используется в математике, логике, менеджменте и других прикладных направлениях.

Важный частный случай кругов Эйлера — диаграммы Эйлера — Венна, изображающие все комбинаций свойств, то есть конечную булеву алгебру. При диаграмма Эйлера — Венна обычно изображается в виде трёх кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приблизительно равным длине стороны треугольника.

При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов. Однако этим методом ещё до Эйлера пользовался выдающийся немецкий философ и математик Готфрид Вильгельм Лейбниц. Лейбниц использовал их для геометрической интерпретации логических связей между понятиями, но при этом всё же предпочитал использовать линейные схемы.

[2]

Пример получения произвольных кругов Эйлера из диаграмм Венна с пустыми (чёрными) множествами

Но достаточно основательно развил этот метод сам Л. Эйлер. Методом кругов Эйлера пользовались и немецкие математики Алекс ван Сивцео и Эрнст Шрёдер в книге «Алгебра логики». Особенного расцвета графические методы достигли в сочинениях английского логика Джона Венна, подробно изложившего их в книге «Символическая логика», изданной в Лондоне в 1881 году. Поэтому такие схемы иногда называют Диаграммы Эйлера — Венна.

1. ↑ «Круги…» — это условный термин, вместо кругов могут быть любые многомерные фигуры, иерархически расположенные в пространстве, то есть одни фигуры поглощают либо часть других фигур, либо полностью.
2. ↑ Leibniz G. W. Opuscules et fragments inédits de Leibniz. — Paris, 1903. — p. 293—321.

Логика
Формальная	Логические операции с понятиями Изменение содержания понятия: отрицание • ограничение • обобщение • деление Изменение объёма понятия: сложение • умножение • вычитание Типы: Многозначная логика • Бинарная логика Логическая константа Законы: Закон обратного отношения между содержанием и объёмом понятия
Математическая (теоретическая, символическая)	Логические связки (операции) над высказываниями Высказывание — построение над множеством {B, , , , 0, 1} В — непустое множество, над элементами которого определены три базовые операции: конъюнкция ( или &,бинарная) • дизъюнкция (,бинарная) • отрицание (,унарная) 2 константы: 0 • 1
См. также	импликация () • Круги Эйлера/Диаграмма Венна • Теория множеств

wp.wiki-wiki.ru

Круги Эйлера — Википедия (с комментариями)

Материал из Википедии — свободной энциклопедии

Круги́ Э́йлера^[1] — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Изобретены Леонардом Эйлером. Используется в математике, логике, менеджменте и других прикладных направлениях.

Важный частный случай кругов Эйлера — диаграммы Эйлера — Венна, изображающие все <math>2^n</math> комбинаций <math>n</math> свойств, то есть конечную булеву алгебру. При <math>n=3</math> диаграмма Эйлера — Венна обычно изображается в виде трёх кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приблизительно равным длине стороны треугольника.

При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов. Однако этим методом ещё до Эйлера пользовался выдающийся немецкий философ и математик Готфрид Вильгельм Лейбниц. Лейбниц использовал их для геометрической интерпретации логических связей между понятиями, но при этом всё же предпочитал использовать линейные схемы.^[2]

Но достаточно основательно развил этот метод сам Л. Эйлер. Методом кругов Эйлера пользовался и немецкий математик Эрнст Шрёдер в книге «Алгебра логики». Особенного расцвета графические методы достигли в сочинениях английского логика Джона Венна, подробно изложившего их в книге «Символическая логика», изданной в Лондоне в 1881 году. Поэтому такие схемы иногда называют Диаграммы Эйлера — Венна.

См. также

Напишите отзыв о статье «Круги Эйлера»

Примечания

1. ↑ «Круги…» — это условный термин, вместо кругов могут быть любые многомерные фигуры, иерархически расположенные в пространстве, то есть одни фигуры поглощают либо часть других фигур, либо полностью.
2. ↑ Leibniz G. W. Opuscules et fragments inédits de Leibniz. — Paris, 1903. — p. 293—321.

Формальная Математическая (теоретическая, символическая) См. также

Отрывок, характеризующий Круги Эйлера

В такие минуты в душе княжны Марьи собиралось чувство, похожее на гордость жертвы. И вдруг в такие то минуты, при ней, этот отец, которого она осуждала, или искал очки, ощупывая подле них и не видя, или забывал то, что сейчас было, или делал слабевшими ногами неверный шаг и оглядывался, не видал ли кто его слабости, или, что было хуже всего, он за обедом, когда не было гостей, возбуждавших его, вдруг задремывал, выпуская салфетку, и склонялся над тарелкой, трясущейся головой. «Он стар и слаб, а я смею осуждать его!» думала она с отвращением к самой себе в такие минуты.

В 1811 м году в Москве жил быстро вошедший в моду французский доктор, огромный ростом, красавец, любезный, как француз и, как говорили все в Москве, врач необыкновенного искусства – Метивье. Он был принят в домах высшего общества не как доктор, а как равный.
Князь Николай Андреич, смеявшийся над медициной, последнее время, по совету m lle Bourienne, допустил к себе этого доктора и привык к нему. Метивье раза два в неделю бывал у князя.
В Николин день, в именины князя, вся Москва была у подъезда его дома, но он никого не велел принимать; а только немногих, список которых он передал княжне Марье, велел звать к обеду.
Метивье, приехавший утром с поздравлением, в качестве доктора, нашел приличным de forcer la consigne [нарушить запрет], как он сказал княжне Марье, и вошел к князю. Случилось так, что в это именинное утро старый князь был в одном из своих самых дурных расположений духа. Он целое утро ходил по дому, придираясь ко всем и делая вид, что он не понимает того, что ему говорят, и что его не понимают. Княжна Марья твердо знала это состояние духа тихой и озабоченной ворчливости, которая обыкновенно разрешалась взрывом бешенства, и как перед заряженным, с взведенными курками, ружьем, ходила всё это утро, ожидая неизбежного выстрела. Утро до приезда доктора прошло благополучно. Пропустив доктора, княжна Марья села с книгой в гостиной у двери, от которой она могла слышать всё то, что происходило в кабинете.
Сначала она слышала один голос Метивье, потом голос отца, потом оба голоса заговорили вместе, дверь распахнулась и на пороге показалась испуганная, красивая фигура Метивье с его черным хохлом, и фигура князя в колпаке и халате с изуродованным бешенством лицом и опущенными зрачками глаз.

wiki-org.ru

Диаграмма Эйлера — Википедия. Что такое Диаграмма Эйлера

Пример кругов Эйлера. Буквами обозначены, например, свойства: B{\displaystyle B} — живое существо, A{\displaystyle A} — человек, C{\displaystyle C} — неживая вещь

Диагра́ммы Э́йлера (круги́ Э́йлера) — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Первое их использование приписывают Леонарду Эйлеру (подробней см. ниже). Используется в математике, логике, менеджменте и других прикладных направлениях. Не следует их путать с диаграммами Эйлера — Венна (о различии между ними см. ниже).

Диаграммы Эйлера также называют кругами Эйлера. При этом «круги» — это условный термин, вместо кругов могут быть любые фигуры.

На диаграммах Эйлера множества изображаются кругами (или другими фигурами). Причём непересекающиеся множества изображены непересекающимися кругами, а подмножества изображены вложенными кругами. Например, диаграмма на рисунке показывает, что множество A является подмножеством B, а B не пересекается с C.

История

При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов. Однако этим методом ещё до Эйлера пользовался выдающийся немецкий философ и математик Готфрид Вильгельм Лейбниц. Лейбниц использовал их для геометрической интерпретации логических связей между понятиями, но при этом всё же предпочитал использовать линейные схемы.^[1]

Но достаточно основательно развил этот метод сам Л. Эйлер. Методом кругов Эйлера пользовался и немецкий математик Эрнст Шрёдер в книге «Алгебра логики». Особенного расцвета графические методы достигли в сочинениях английского логика Джона Венна, подробно изложившего их в книге «Символическая логика», изданной в Лондоне в 1881 году. Венн предложил свою схему изображения отношения между множествами, которая теперь называется диаграммами Эйлера — Венна. Первоначально круги Эйлера возникли на основе идей силлогистики Аристотеля. Диаграммы Венна были созданы для решения задач математической логики. Их основная идея разложения на конституенты возникла на основе алгебры логики

[2].

Связь диаграмм Эйлера и Венна

Пример получения произвольных кругов Эйлера из диаграмм Венна с пустыми (чёрными) множествами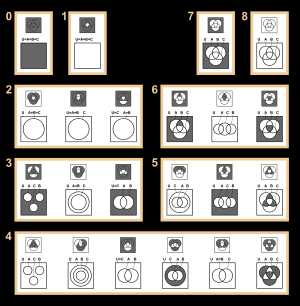 22 (из 256) существенно различных диаграмм Венна с 3 кругами (сверху) и соответствующие им диаграммы Эйлера (снизу)

Диаграммы Эйлера — Венна в отличие от диаграмм Эйлера изображают все 2n{\displaystyle 2^{n}} комбинаций n{\displaystyle n} свойств, то есть конечную булеву алгебру. При n=3{\displaystyle n=3} диаграмма Эйлера — Венна обычно изображается в виде трёх кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приблизительно равным длине стороны треугольника.

На рис. ниже даны диаграммы Венна и Эйлера для 3 множеств однозначных натуральных чисел:

• A={1,2,5}{\displaystyle A=\{1,\,2,\,5\}}
• B={1,6}{\displaystyle B=\{1,\,6\}}
• C={4,7}{\displaystyle C=\{4,\,7\}}

• диаграмма Эйлера

• диаграмма Венна

Иногда, если какая-то комбинация свойств соответствует пустому множеству, то эту комбинацию закрашивают. На рисунке справа даны 22 существенно различных диаграмм Венна с 3 кругами (сверху) и соответствующие им диаграммы Эйлера (снизу). Некоторые из диаграмм Эйлера не типичны, а некоторые даже эквивалентны диаграммам Венна. Черные области указывают на то, что в них нет элементов (пустые множества).

Примеры

На рисунке внизу дана Диаграмма Эйлера, иллюстрирующая тот факт, что множество существ с 4 конечностями является подмножеством животных, которое не пересекается с множеством минералов.

Диаграмма Эйлера

См. также

Примечания

1. ↑ Leibniz G. W. Opuscules et fragments inédits de Leibniz. — Paris, 1903. — p. 293—321.
2. ↑ Кузичев, 1968, с. 25.

Литература

• Кузичев А. С. Диаграммы Венна. История и применения. — М.: Наука, 1968. — 249 с.

wiki.sc

Круги Эйлера Википедия

Пример кругов Эйлера. Буквами обозначены, например, свойства: B{\displaystyle B} — живое существо, A{\displaystyle A} — человек, C{\displaystyle C} — неживая вещь

Диагра́ммы Э́йлера (круги́ Э́йлера) — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Первое их использование приписывают Леонарду Эйлеру (подробней см. ниже). Используется в математике, логике, менеджменте и других прикладных направлениях. Не следует их путать с диаграммами Эйлера — Венна (о различии между ними см. ниже).

Диаграммы Эйлера также называют кругами Эйлера. При этом «круги» — это условный термин, вместо кругов могут быть любые фигуры.

На диаграммах Эйлера множества изображаются кругами (или другими фигурами). Причём непересекающиеся множества изображены непересекающимися кругами, а подмножества изображены вложенными кругами. Например, диаграмма на рисунке показывает, что множество A является подмножеством B, а B не пересекается с C.

История[ | ]

При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов. Однако этим методом ещё до Эйлера пользовался выдающийся немецкий философ и математик Готфрид Вильгельм Лейбниц. Лейбниц использовал их для геометрической интерпретации логических связей между понятиями, но при этом всё же предпочитал использовать линейные схемы.^[1]

Но достаточно основательно развил этот метод сам Л. Эйлер. Методом кругов Эйлера пользовался и немецкий математик Эрнст Шрёдер в книге «Алгебра логики». Особенного расцвета графические методы достигли в сочинениях английского логика Джона Венна, подробно изложившего их в книге «Символическая логика», изданной в Лондоне в 1881 году. Венн предложил свою схему изображения отношения между множествами, которая теперь называется диаграммами Эйлера — Венна. Первоначально круги Эйлера возникли на основе идей силлогистики Аристотеля. Диаграммы Венна были созданы для решения задач математической логики. Их основная идея разложения на конституенты возникла на основе алгебры логики^[2].

Связь диаграмм Эйлера и Венна[ | ]

Пример получения произвольных кругов Эйлера из диаграмм Венна с пустыми (чёрными) множествами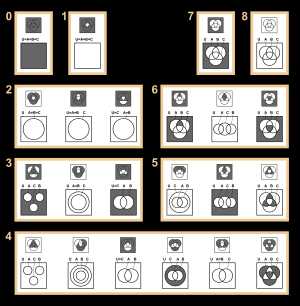

ru-wiki.ru

Круги Эйлера Википедия

Пример кругов Эйлера. Буквами обозначены, например, свойства: B{\displaystyle B} — живое существо, A{\displaystyle A} — человек, C{\displaystyle C} — неживая вещь

Диагра́ммы Э́йлера (круги́ Э́йлера) — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Первое их использование приписывают Леонарду Эйлеру (подробней см. ниже). Используется в математике, логике, менеджменте и других прикладных направлениях. Не следует их путать с диаграммами Эйлера — Венна (о различии между ними см. ниже).

Диаграммы Эйлера также называют кругами Эйлера. При этом «круги» — это условный термин, вместо кругов могут быть любые фигуры.

На диаграммах Эйлера множества изображаются кругами (или другими фигурами). Причём непересекающиеся множества изображены непересекающимися кругами, а подмножества изображены вложенными кругами. Например, диаграмма на рисунке показывает, что множество A является подмножеством B, а B не пересекается с C.

История

При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов. Однако этим методом ещё до Эйлера пользовался выдающийся немецкий философ и математик Готфрид Вильгельм Лейбниц. Лейбниц использовал их для геометрической интерпретации логических связей между понятиями, но при этом всё же предпочитал использовать линейные схемы.^[1]

Но достаточно основательно развил этот метод сам Л. Эйлер. Методом кругов Эйлера пользовался и немецкий математик Эрнст Шрёдер в книге «Алгебра логики». Особенного расцвета графические методы достигли в сочинениях английского логика Джона Венна, подробно изложившего их в книге «Символическая логика», изданной в Лондоне в 1881 году. Венн предложил свою схему изображения отношения между множествами, которая теперь называется диаграммами Эйлера — Венна. Первоначально круги Эйлера возникли на основе идей силлогистики Аристотеля. Диаграммы Венна были созданы для решения задач математической логики. Их основная идея разложения на конституенты возникла на основе алгебры логики^[2].

Связь диаграмм Эйлера и Венна

Пример получения произвольных кругов Эйлера из диаграмм Венна с пустыми (чёрными) множествами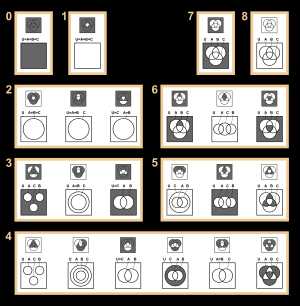 22 (из 256) существенно различных диаграмм Венна с 3 кругами (сверху) и соответствующие им диаграммы Эйлера (снизу)

Диаграммы Эйлера — Венна в отличие от диаграмм Эйлера изображают все 2n{\displaystyle 2^{n}} комбинаций n{\displaystyle n} свойств, то есть конечную булеву алгебру. При n=3{\displaystyle n=3} диаграмма Эйлера — Венна обычно изображается в виде трёх кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приблизительно равным длине стороны треугольника.

На рис. ниже даны диаграммы Венна и Эйлера для 3 множеств однозначных натуральных чисел:

• A={1,2,5}{\displaystyle A=\{1,\,2,\,5\}}
• B={1,6}{\displaystyle B=\{1,\,6\}}
• C={4,7}{\displaystyle C=\{4,\,7\}}

• диаграмма Эйлера

• диаграмма Венна

Иногда, если какая-то комбинация свойств соответствует пустому множеству, то эту комбинацию закрашивают. На рисунке справа даны 22 существенно различных диаграмм Венна с 3 кругами (сверху) и соответствующие им диаграммы Эйлера (снизу). Некоторые из диаграмм Эйлера не типичны, а некоторые даже эквивалентны диаграммам Венна. Черные области указывают на то, что в них нет элементов (пустые множества).

Примеры

На рисунке внизу дана Диаграмма Эйлера, иллюстрирующая тот факт, что множество существ с 4 конечностями является подмножеством животных, которое не пересекается с множеством минералов.

Диаграмма Эйлера

См. также

Примечания

1. ↑ Leibniz G. W. Opuscules et fragments inédits de Leibniz. — Paris, 1903. — p. 293—321.
2. ↑ Кузичев, 1968, с. 25.

Литература

• Кузичев А. С. Диаграммы Венна. История и применения. — М.: Наука, 1968. — 249 с.

wikiredia.ru

Диаграмма Эйлера — Википедия

Материал из Википедии — свободной энциклопедии

Пример кругов Эйлера. Буквами обозначены, например, свойства: B{\displaystyle B} — живое существо, A{\displaystyle A} — человек, C{\displaystyle C} — неживая вещь

Диагра́ммы Э́йлера (круги́ Э́йлера) — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Первое их использование приписывают Леонарду Эйлеру (подробней см. ниже). Используется в математике, логике, менеджменте и других прикладных направлениях. Не следует их путать с диаграммами Эйлера — Венна (о различии между ними см. ниже).

Диаграммы Эйлера также называют кругами Эйлера. При этом «круги» — это условный термин, вместо кругов могут быть любые фигуры.

На диаграммах Эйлера множества изображаются кругами (или другими фигурами). Причём непересекающиеся множества изображены непересекающимися кругами, а подмножества изображены вложенными кругами. Например, диаграмма на рисунке показывает, что множество A является подмножеством B, а B не пересекается с C.

История

При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов. Однако этим методом ещё до Эйлера пользовался выдающийся немецкий философ и математик Готфрид Вильгельм Лейбниц. Лейбниц использовал их для геометрической интерпретации логических связей между понятиями, но при этом всё же предпочитал использовать линейные схемы.^[1]

Но достаточно основательно развил этот метод сам Л. Эйлер. Методом кругов Эйлера пользовался и немецкий математик Эрнст Шрёдер в книге «Алгебра логики». Особенного расцвета графические методы достигли в сочинениях английского логика Джона Венна, подробно изложившего их в книге «Символическая логика», изданной в Лондоне в 1881 году. Венн предложил свою схему изображения отношения между множествами, которая теперь называется диаграммами Эйлера — Венна. Первоначально круги Эйлера возникли на основе идей силлогистики Аристотеля. Диаграммы Венна были созданы для решения задач математической логики. Их основная идея разложения на конституенты возникла на основе алгебры логики^[2].

Видео по теме

Связь диаграмм Эйлера и Венна

Пример получения произвольных кругов Эйлера из диаграмм Венна с пустыми (чёрными) множествами 22 (из 256) существенно различных диаграмм Венна с 3 кругами (сверху) и соответствующие им диаграммы Эйлера (снизу)

Диаграммы Эйлера — Венна в отличие от диаграмм Эйлера изображают все 2n{\displaystyle 2^{n}} комбинаций n{\displaystyle n} свойств, то есть конечную булеву алгебру. При n=3{\displaystyle n=3} диаграмма Эйлера — Венна обычно изображается в виде трёх кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приблизительно равным длине стороны треугольника.

На рис. ниже даны диаграммы Венна и Эйлера для 3 множеств однозначных натуральных чисел:

• A={1,2,5}{\displaystyle A=\{1,\,2,\,5\}}
• B={1,6}{\displaystyle B=\{1,\,6\}}
• C={4,7}{\displaystyle C=\{4,\,7\}}

• диаграмма Эйлера

• диаграмма Венна

Иногда, если какая-то комбинация свойств соответствует пустому множеству, то эту комбинацию закрашивают. На рисунке справа даны 22 существенно различных диаграмм Венна с 3 кругами (сверху) и соответствующие им диаграммы Эйлера (снизу). Некоторые из диаграмм Эйлера не типичны, а некоторые даже эквивалентны диаграммам Венна. Черные области указывают на то, что в них нет элементов (пустые множества).

Примеры

На рисунке внизу дана Диаграмма Эйлера, иллюстрирующая тот факт, что множество существ с 4 конечностями является подмножеством животных, которое не пересекается с множеством минералов.

Диаграмма Эйлера

См. также

Примечания

1. ↑ Leibniz G. W. Opuscules et fragments inédits de Leibniz. — Paris, 1903. — p. 293—321.
2. ↑ Кузичев, 1968, с. 25.

Литература

• Кузичев А. С. Диаграммы Венна. История и применения. — М.: Наука, 1968. — 249 с.

wiki2.red

Диаграмма Эйлера Википедия

Пример кругов Эйлера. Буквами обозначены, например, свойства: B{\displaystyle B} — живое существо, A{\displaystyle A} — человек, C{\displaystyle C} — неживая вещь

Диагра́ммы Э́йлера (круги́ Э́йлера) — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Первое их использование приписывают Леонарду Эйлеру (подробней см. ниже). Используется в математике, логике, менеджменте и других прикладных направлениях. Не следует их путать с диаграммами Эйлера — Венна (о различии между ними см. ниже).

Диаграммы Эйлера также называют кругами Эйлера. При этом «круги» — это условный термин, вместо кругов могут быть любые фигуры.

На диаграммах Эйлера множества изображаются кругами (или другими фигурами). Причём непересекающиеся множества изображены непересекающимися кругами, а подмножества изображены вложенными кругами. Например, диаграмма на рисунке показывает, что множество A является подмножеством B, а B не пересекается с C.

История[ | ]

При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов. Однако этим методом ещё до Эйлера пользовался выдающийся немецкий философ и математик Готфрид Вильгельм Лейбниц. Лейбниц использовал их для геометрической интерпретации логических связей между понятиями, но при этом всё же предпочитал использовать линейные схемы.^[1]

Но достаточно основательно развил этот метод сам Л. Эйлер. Методом кругов Эйлера пользовался и немецкий математик Эрнст Шрёдер в книге «Алгебра логики». Особенного расцвета графические методы достигли в сочинениях английского логика Джона Венна, подробно изложившего их в книге «Символическая логика», изданной в Лондоне в 1881 году. Венн предложил свою схему изображения отношения между множествами, которая теперь называется диаграммами Эйлера — Венна. Первоначально круги Эйлера возникли на основе идей силлогистики Аристотеля. Диаграммы Венна были созданы для решения задач математической логики. Их основная идея разложения на конституенты возникла на основе алгебры логики^[2].

Связь диаграмм Эйлера и Венна[ | ]

ru-wiki.ru

No related posts.