Задачи на применение теоремы Пифагора
Когда вы только начинали изучать квадратные корни и способы решения иррациональных уравнений (равенств, содержащих неизвестную под знаком корня), вы, вероятно, получили первое представление об их практическом использовании. Умение извлекать квадратный корень из чисел также необходимо для решения задач на применение теоремы Пифагора. Эта теорема связывает длины сторон любого прямоугольного треугольника.
Пусть длины катетов прямоугольного треугольника (тех двух сторон, которые сходятся под прямым углом) будут обозначены буквами и , а длина гипотенузы (самой длинной стороны треугольника, расположенной напротив прямого угла) будет обозначена буквой . Тогда соответствующие длины связаны следующим соотношением:
| (сумма квадратов длин катетов прямоугольного треугольника равна квадрату длины его гипотенузы). |
Данное уравнение позволяет найти длину стороны прямоугольного треугольника в том случае, когда известна длина двух других его сторон. Кроме того, оно позволяет определить, является ли рассматриваемый треугольник прямоугольным, при условии, что длины всех трёх сторон заранее известны.
Решение задач с использованием теоремы Пифагора
Для закрепления материала решим следующие задачи на применение теоремы Пифагора.
| Задача 1. Используя приведённые ниже данные о длинах сторон прямоугольных треугольников, вычислите длины других сторон. |

Итак, дано:
- Длина одного из катетов равняется 48, гипотенузы – 80.
- Длина катета равняется 84, гипотенузы – 91.
Приступим к решению:
a) Подстановка данных в приведённое выше уравнение даёт следующие результаты:
482+ b2 = 802
2304 + b2 = 6400
b2 = 4096
b = 64 или b = -64
Поскольку длина стороны треугольника не может быть выражена отрицательным числом, второй вариант автоматически отбрасывается.
Ответ к первому рисунку: b = 64.
b) Длина катета второго треугольника находится тем же способом:
842+ b2 = 912
7056 + b2 = 8281
b2 = 1225
b = 35 или b = -35
Как и в предыдущем случае, отрицательное решение отбрасывается.
Ответ ко второму рисунку: b = 35
| Задача 2. Используя приведённые ниже данные о длинах сторон треугольников, определите, являются ли они прямоугольными. |
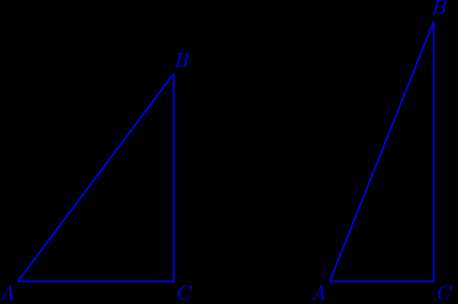
Нам дано:
- Длины меньших сторон треугольника равны 45 и 55 соответственно, большей – 75.
- Длины меньших сторон треугольника равны 28 и 45 соответственно, большей – 53.
Решаем задачу:
a) Необходимо проверить, равна ли сумма квадратов длин меньших сторон данного треугольника квадрату длины большей:
752= 5625
452+ 552 = 2025 + 3025 = 5050
5625 ≠ 5050
Следовательно, первый треугольник не является прямоугольным.
b) Выполняется та же самая операция:
532= 2809
282+ 452 = 784 + 2025 = 2809
2809 = 2809
Следовательно, второй треугольник является прямоугольным.
| Задача 3. Даны точки (-2, -3), (2, 1), (5, -2) в прямоугольной системе координат на плоскости. Выясните, являются ли они вершинами прямоугольного треугольника. |
Сперва найдем длину наибольшего отрезк
yourtutor.info
Задачи с фантазией — 18: теорема Пифагора.
Вы думаете, что теорема Пифагора – это совсем несложно? Ну, в общем, да. Но интересные задачи все же иногда можно встретить. В основном мы столкнемся здесь с отношениями и сравнением чисел.Задача 1. Один из катетов прямоугольного треугольника на 10 больше другого и на 10 меньше гипотенузы. Найдите гипотенузу этого треугольника.
Решение. Показать
Запишем для этого треугольника теорему Пифагора. Для этого обозначим катеты и , а гипотенузу . Тогда
Откуда . Тогда гипотенуза на 10 больше – 50.
Ответ: 50.
Задача 2. В треугольнике ABC угол BAC прямой, длины сторон AB и BC равны соответственно 1 и 3. Точка K делит сторону AC в отношении 7:1, считая от точки A. Что больше: длина AC или длина BK?
Решение. Показать
Задача 3. В прямоугольнике ABCD длины отрезков AB и BD равны соответственно 2 и . Точка M делит отрезок CD в отношении 1:2, считая от точки C, K – середина AD. Что больше: длина BK или длина AM?
Решение. Показать
Задача 4. В треугольнике ABC угол BAC прямой, длины сторон AB и BC равны соответственно 5 и 6. Точка K делит сторону AC в отношении 3:1, считая от точки A, AH – высота треугольника ABC. Что больше: 2 или отношение длины BK к длине AH?
Решение. Показать
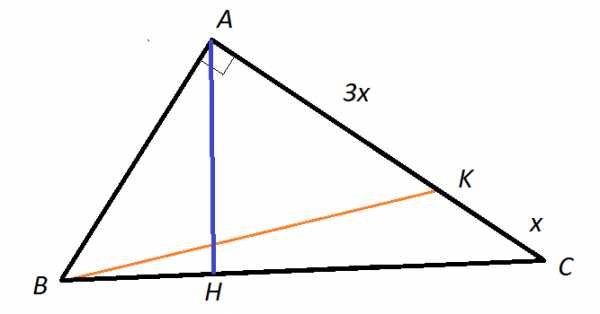
Рисунок 3
Чтобы найти высоту треугольника , определим его удвоенную площадь, так как
определим по теореме Пифагора:
Теперь найдем , чтобы найти :
Тогда
Отношение
Сравним теперь и .
Таким образом, .
Задача 5. В равнобедренном треугольнике ABC длина основания AC равна 2, длина боковой стороны равна 8. Точка K делит высоту BD треугольника в отношении 2:3, считая от точки B. Что больше: длина CK или длина AC?
Решение. Показать

Рисунок 4
Длина высоты :
Длина отрезка :
По теореме Пифагора определяем :
Таким образом, .
Задача 6. Найдите радиусы вписанной и вневписанных окружностей треугольника со сторонами 3, 4, 5.
Решение. Показать
Треугольник подчиняется теореме Пифагора, он прямоугольный. Гипотенуза его . Пусть катеты , .
Сначала вписанная окружность.
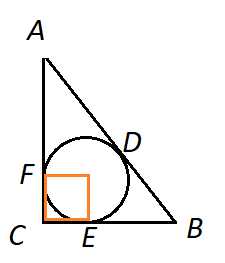
Рисунок 5
Пусть – точки касания окружности. Тогда по теореме об отрезках касательных, проведенных из одной точки, . Но длины этих отрезков равны радиусу . Тогда
Откуда
Теперь вневписанные окружности: рассмотрим сначала зеленую.
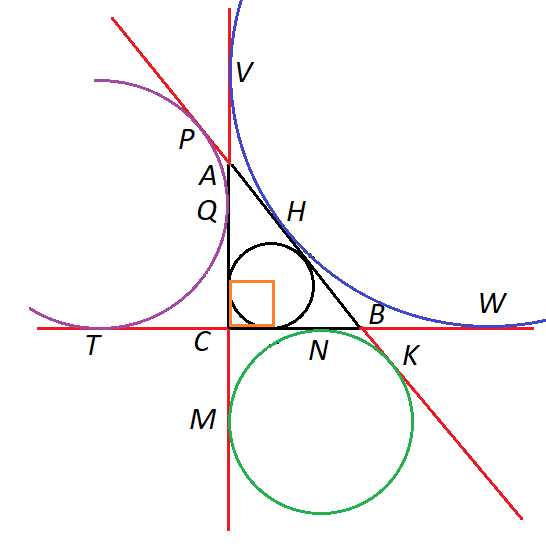
Рисунок 6
По теореме об отрезках касательных, проведенных из одной точки, , .
Но . Тогда (периметру треугольника ). Но , опять же, по свойству касательных. Тогда .
Так как , то
Теперь рассмотрим фиолетовую окружность.
, .
Но . Тогда (периметру треугольника ). Но , опять же, по свойству касательных. Тогда .
Так как , то
Наконец, последняя, самая большая.
Ответ: , , , .
Задача 7. Из одной точки проведены к данной прямой перпендикуляр и две наклонные. Найдите длину перпендикуляра, если наклонные равны 41 и 50, а их проекции на данную прямую относятся как 3 : 10.
Решение. Показать
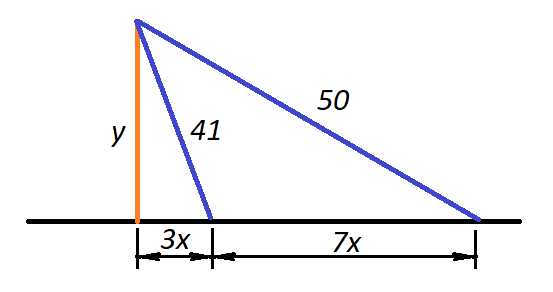
Рисунок 7
По теореме Пифагора
Тогда
Откуда , , следовательно, .
Ответ: 40.
Задача 8. В прямоугольном треугольнике медианы, проведённые из вершин острых углов, равны и . Найдите гипотенузу треугольника.
Решение. Показать
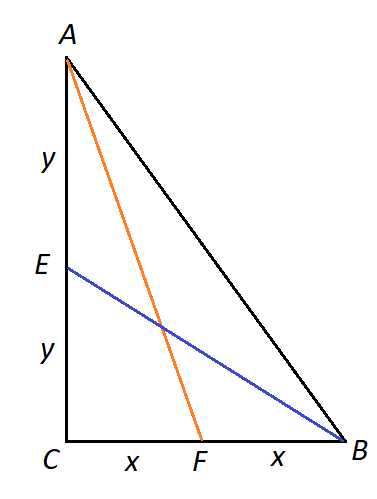
Рисунок 8
Составим теорему Пифагора для треугольников и . Пусть , тогда
Если , то
Первое уравнение умножаем на 4, чтобы уравнять коэффициенты:
Вычитаем из него второе уравнение:
Следовательно, , катеты треугольника 6 и 8, гипотенуза, следовательно, 10.
Ответ: 10.
Задача 9. В прямоугольном треугольнике точка касания вписанной окружности делит гипотенузу на отрезки, равные 5 и 12. Найдите катеты треугольника.
Решение. Показать
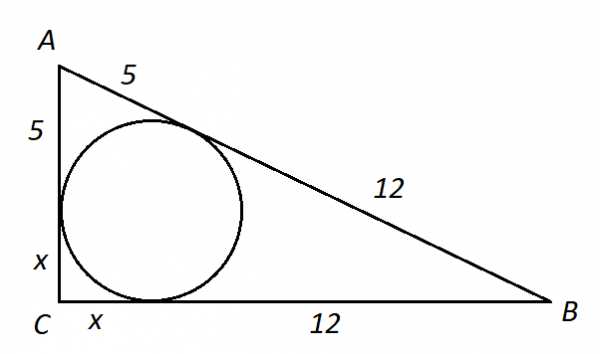
Рисунок 9
По свойству касательных, проведенных к окружности из одной точки, имеем: , , . Тогда
По теореме Виета получаем корни: 3 и (-20). По условию устраивает положительный корень. Катеты равны тогда 8 и 15.
Ответ: 8 и 15.
easy-physic.ru
Решение задач по теорема Пифагора
План- конспект урока геометрии в 8 классе
по теме:
Решение задач по теме «Теорема Пифагора»
УМК : Погорелов А.В. Геометрия : Учебник для 7 – 9 классов общеобразовательных учреждений. – М.: Просвещение, 2013 г.
Цели урока:
Обучающая: формировать умения и навыки применения теоретических знаний при решении задач, в изменившейся ситуации;
Развивающая: развивать сознательное восприятие учебного материала, логическое мышление;
Воспитывающая: способствовать воспитанию познавательной активности, культуры общения
Задачи урока:
Повторить теорему Пифагора,
Рассмотреть применение теоремы Пифагора при решении различного типа задач, в том числе практического содержания.
Метод: исследование с применением теоретических знаний.
Оборудование: раздаточный материал (задачи для работы в группах), мультимедийный проектор, презентация
Ход урока.
Организационный момент.
Вступительное слово учителя.
Природа формулирует свои законы
языком математики.
Г. Галилей.
Геометрия – это не просто наука о свойствах геометрических фигур.
Геометрия – это целый мир, который окружает нас с самого рождения.
Ведь все, что мы видим вокруг, так или иначе относится к геометрии, ничто не ускользает от ее внимательного взгляда. Геометрия помогает человеку идти по миру с широко открытыми глазами, учит внимательно смотреть вокруг и
видеть красоту обычных вещей, смотреть и думать, думать и делать выводы.
Одна из заповедей Пифагора гласит: «Не делай никогда того, что не знаешь, но научись всему, что следует знать».
Как именно помогает знание геометрии в жизни, покажет наш урок
Фронтальный опрос:
а) Как называются стороны прямоугольного треугольника?
б) Назовите гипотенузу и катеты прямоугольного треугольника (слайд 3)
в) Как найти третью сторону треугольника (слайд 4)
г) сформулируйте теорему Пифагора (слайд 5)
Решение задач (с записью в тетрадях)
Учитель: Теорема Пифагора – одна из самых известных и важных в математике теорем. В шутку, хотя и не совсем безосновательно, было решено передать обитателям Марса сигнал в виде теоремы Пифагора. Неизвестно, как это сделать; но для всех очевидно, что математический факт, выражаемый теоремой Пифагора, имеет место всюду, и обитатели другого мира должны понять такой сигнал
Задача 1: (слайд 7)
Образуют ли «пифагорову тройку» длины сторон прямоугольного треугольника АВС, если ВС= 5, АС=12,⦟ С = 90º?
Задача 2:(слайд 8) нВелосипедист проехал из М в N по улицам ( см. рис.) Какое расстояние он проехал? На сколько короче оказался бы его путь, если можно было бы проехать напрямик?
Задача 3. (слайд 9) На какой высоте находится воздушный змей?
Задача 4 (слайд 10)
Устно составьте план решения задачи. Какие факты, определения, свойства, теоремы необходимо знать для её решения?
Работа в группах (разбиваются на три группы, каждой группе выдается одна задача — из задач 4,5,6 из презентации). Работают в течение 5-7 мин, представитель от каждой группы выходит с решением, сообщает его всему классу
Домашнее задание (см. слайд 14) Провести исследование и ответить на вопрос, как построить отрезок длины √8 (задание заранее распечатать)
Итог урока (рефлексия) Что нового вы узнали? Чем понравился урок? Что осталось непонятным? Какие формы урока наиболее эффективны?
Заключительные слова:
Пребудет вечной истина, как скоро
Ее познает слабый человек!
И ныне теорема Пифагора
Верна, как и в его далекий век.
Обильно было жертвоприношенье
Богам от Пифагора. Сто быков
Он отдал на закланье и сожженье
За света луч, пришедший с облаков.
Поэтому всегда с тех самых пор,
Чуть истина рождается на свет,
Быки ревут, ее почуяв, вслед.
Они не в силах свету помешать.
А могут лишь, закрыв глаза, дрожать
От страха, что вселил в них Пифагор.
66666666666Задачае знаешь, но научись всему, что следует знать».
infourok.ru
| 1. |
Гипотенуза прямоугольного треугольника
Сложность: лёгкое |
2 |
| 2. |
Площадь прямоугольного треугольника
Сложность: лёгкое |
3 |
| 3. |
Боковая сторона прямоугольной трапеции
Сложность: лёгкое |
3 |
| 4. |
Диагональ прямоугольника
Сложность: лёгкое |
3 |
| 5. |
Сторона ромба
Сложность: среднее |
3 |
| 6. |
Диагональ квадрата
Сложность: среднее |
3 |
| 7. |
Высота равнобедренного треугольника
Сложность: среднее |
3 |
| 8. |
Катет прямоугольного треугольника
Сложность: среднее |
1 |
| 9. |
Признак прямоугольного треугольника
Сложность: среднее |
2 |
| 10. |
Периметр равнобедренной трапеции (подобные треугольники)
Сложность: среднее |
3 |
| 11. |
Прикладная задача на составление уравнения
Сложность: среднее |
5 |
| 12. |
Старинная китайская задача
Сложность: среднее |
5 |
| 13. |
Прикладная задача на вычисление расстояния
Сложность: среднее |
4 |
| 14. |
Текстовая задача на использование теоремы Пифагора
Сложность: сложное |
3 |
| 15. |
Стороны прямоугольного треугольника, дана сумма катета и гипотенузы
Сложность: сложное |
3 |
| 16. |
Расстояние между вершинами тупых углов параллелограмма
Сложность: сложное |
5 |
| 17. |
Прикладная задача на вычисление стороны квадрата
Сложность: сложное |
2 |
| 18. |
Общая хорда двух равных окружностей
Сложность: сложное |
4 |
www.yaklass.ru
Теорема Пифагора в решении задач
Разделы: Математика
Как символ вечного союза
Как вечной дружбы знак простой
Связала ты, гипотенуза,
Навеки катеты с собой.
Скрывала тайну ты,
Не скоро явился некий мудрый грек
И теоремой Пифагора
Тебя прославил он навек.
Цели:
- систематизировать, обобщить знания и умения по применению теоремы Пифагора при решении задач, показать их практическое применение;
- содействовать развитию математического мышления;
- воспитывать познавательный интерес.
Оборудование: потрет Пифагора, рисунок и макет телевизионной башни, таблицы для устного счета.
ХОД УРОКА
1. Организационный момент
2. Работа по готовым чертежам
– Можно ли по этим условиям найти площадь
треугольника?
– Какой еще вопрос можно поставить к данным
задачам?
– Найдите площади треугольников.
– Какую теорему вы применяли для нахождения
сторон треугольников?
– Как называются треугольники 1, 4 и 3? (Пифагоровые)
– Приведите еще примеры таких треугольников.
– Является ли прямоугольным треугольник со
сторонами 6, 29 и 25? Какую теорему вы использовали
для доказательства?
В это время 4 ученика работают самостоятельно.
1. Найдите площадь прямоугольника, если его диагональ 10 см и образует со стороной угол равный 30о. (25√3 см2)
2. В прямоугольной трапеции основания равны 22 см и 6 см, большая боковая сторона – 20 см. Найдите площадь трапеции. (224 см2)
3. Самостоятельная работа 3-х уровней по готовым чертежам.
1 вариант
| 1) а = 3 см |
2) с = 10 см |
3) а =10 см |
2 вариант
1)
|
2)
|
3)
|
3 вариант
1)
|
2) АВ = 6 см |
3) АС = 6 √2 см |
Таблица ответов
| 1 | 2 | 3 | |
| 1 вариант | 5 см | 6 см | 25 см2 |
| 2 вариант | 0,4 см | 3 2 см | 48 м2 |
| 3 вариант | 48 м2 | 12 см2 | 6 см |
Самопроверка работ с помощью таблицы ответов.
4. Решение задач
№ 493.
Найдите сторону и площадь ромба, если его диагонали равны 10 см и 24 см.
Дано: АВСD – ромб, ВD = 10 cм, АС = 24 см
Найти: АВ и S ромба
Решение:
1. ВD перпендикулярна АС по свойству диагоналей
ромба.
2. Рассмотрим треугольник АВО: О = 90, ВО = 5 см,
АО = 12 см. По теореме Пифагора АВ = ВО2 + АО2
АВ = 13 см
3. S = 1/2 * 10 * 24 = 120 см2.
Ответ: АВ = 13 см, S = 120 см2
№ 495.
Найдите площадь трапеции АВСD с основаниями АВ и СD, если АВ = 10 см, ВС = DА = 13 см, СD = 20 см.
Дано: АВСD – трапеция, АВ и СD основания, АВ = 10
СD = 20 см, ВС = DA = 13 см
Найти: S?
Решение:
1. Проведем высоту АН и рассмотрим треугольник
АDН : Н = 90, АD = 13 cм,
DН = (20 – 10) : 2 = 5 см.
АН = 132 – 52 = 12 см
2. S = (20 + 10) : 2 * 12 = 180 см2
Ответ: S = 180cм2.
– Какие формулы вы использовали при решении задач? А какие формулы для вычисления площади треугольника вы знаете?
Сегодня Маша Л. познакомит вас с формулой для вычисления площади равностороннего треугольника по его стороне. (Ученица самостоятельно готовила задание дом.)
S = а2 * √3/4, где а – сторона треугольника.
Решение задачи на применение данной формулы.
Треугольник состоит из 4-х треугольников со стороной 1см. Сколько равносторонних треугольников вы видите? Чему равна площадь данного треугольника?
Решение задачи: 5 равносторонних треугольников, а = 2 см, тогда S = √3 кв.ед.
5. Практическое задание
Отчет учеников о проделанной работе: В нашем поселке есть телевышка, высота которой 124 м. Чтобы она стояла вертикально, требуются растяжки, они несколько уровневые. Нам была поставлена задача выяснить, сколько метров троса потребуется для 4 нижних растяжек.
Так как растяжки одинаковой длины, то задача свелась к нахождению длины одной растяжки. Для этого мы выделили прямоугольный треугольник, катетами которого являются расстояния АС и СВ. Мы узнали, что трос крепится на высоте 40 м (АС = 40 м) и измерили расстояние от основания вышки до крепления троса на поверхности (СВ = 24 м). По теореме Пифагора АВ = 46,7 м, значит троса потребуется не менее 186,8 м.
Во время отчета демонстрируется макет телевышки и ее рисунок.
6. Итог урока
7. Домашнее задание
Закончить урок словами: Говорят, что наука отличается от искусства тем ,что в то время как создания искусства вечны, великие творения науки безнадежно стареют. К счастью это не так, теорема Пифагора этому пример, мы применяли и будем применять ее при решении задач.
6.02.2012
Поделиться страницей:xn--i1abbnckbmcl9fb.xn--p1ai
Решение задач по теме «Теорема Пифагора»
Разделы: Математика
Цель: применение теоремы Пифагора при решении задач.
Задачи. Систематизировать знания по теме при решении задач с историческим и практическим содержанием. Создавать атмосферу заинтересованности каждого ученика. Учить выслушивать мнение одноклассников и высказывать свое при работе в парах и группе. Применить полученные знания при самостоятельном выполнении заданий.
1. Организационный момент. (Проверка готовности обучающихся к уроку. Создание эмоционального настроя. Приветствие.)
2. Мотивация. Иоганн Кеплер немецкий астроном, один из творцов астрономии нового времени говорил так: “Геометрия владеет двумя сокровищами: одно из них — теорема Пифагора, а другое — деление отрезка в крайнем и среднем отношении. Первое можно сравнить с мерой золота, второе же больше напоминает драгоценный камень”
Без преувеличения можно сказать, что теорема Пифагора самая известная теорема геометрии, т.к. о ней знает подавляющее большинство населения планеты, хотя доказать ее способна лишь незначительная его часть.
Выяснением истории возникновения названия занимались два учащихся. Предоставляем им слово. (3 мин.)
Презентация уч-ся. (5-7 мин.) (Индивидуальная работа)
Презентация 1
Презентация 2
Слайды 1-4. Древнегреческий философ и математик (VI в до н.э.) Пифагор – едва ли не самый популярный ученый за всю историю человечества. Вокруг личности Пифагора образовалась множество легенд. Одни называли его математиком, пророком, философом, другие шарлатаном. Судить о правдивости высказываний сложно. Пифагор много путешествовал, после возвращения на родину- в Кротон, начинается самый славный период его биографии. Пифагор основывает школу – пифагорейский союз, состоявший из молодых представителей аристократии, куда принимались с большими церемониями после долгих испытаний. Каждый вступающий отрекался от своего имущества и давал клятву хранить в тайне учения основателя. Пифагорейцы занимались математикой, философией, естественными науками, сделали много важных открытий в арифметике и геометрии. Но в школе существовал Декрет, по которому авторство всех математических работ приписывалось Пифагору. На основе преданий, распространенных известными математиками (Проклом, Плутархом и др.), длительное время считали, что до Пифагора эта теорема не была известна, отсюда и название – теорема Пифагора.
Слайды 5-7. Различные формулировки теоремы Пифагора:
“В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов (общепризнанная) Евклид (дословный перевод): «В прямоугольном треугольнике квадрат стороны, натянутой над прямым углом, равен квадратам на сторонах, заключающих прямой угол». “Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на катетах”. (Во времена Пифагора)
В первом русском переводе евклидовых «Начал», сделанном Ф.И. Петрушевским: «В прямоугольных треугольниках квадрат из стороны, противолежащей прямому углу, равен сумме квадратов из сторон, содержащих прямой угол».
Латинский перевод арабского текста Аннаирици (около 900 г. до н. э.): «Во всяком прямоугольном треугольнике квадрат, образованный на стороне, натянутой над прямым углом, равен сумме двух квадратов, образованных на двух сторонах, заключающих прямой угол». К теореме Пифагора его ученики составляли стишки и рисовали шаржи.
“Пифагоровы штаны во все стороны равны”.
Доказательство теоремы называли “мостом ослов”, так как слабые ученики, заучивающие теоремы наизусть, без понимания, и прозванные поэтому “ослами”, были не в состоянии преодолеть теорему Пифагора, служившую для них вроде непреодолимого моста. Или “бегство убогих”, так как некоторые “убогие” ученики, не имевшие серьезной математической подготовки, бежали от геометрии. Саму теорему называли “ветряной мельницей”, “теоремой – бабочкой” или “теоремой невесты” Известно около 150, а по некоторым источникам около 500 различных доказательств теоремы Пифагора, поэтому она занесена в книгу рекордов Гиннеса.
Слайды 8- 10. Однако эту теорему знали за много лет до Пифагора. Так, за 1500 лет до Пифагора древние египтяне знали о том, что треугольник со сторонами 3, 4 и 5 является прямоугольным и применяли этот способ для строительства пирамид. В самом древнем индийском геометрическом сборнике “Сульвасутра” (“Правила веревки”, 600 год до н.э.), даются правила построения прямых углов при помощи веревки с узлами, расстояния между которыми равны 15, 36 и 39 падас (мера длины). В Древнем Китае уже около 2200 года до н.э. для треугольника со сторонами 3, 4, 5 было найдено правило “гоу-гу”, с помощью которого можно было по известным гипотенузе и одному из катетов находить другой неизвестный катет, а также гипотенузу, если известны оба катета.
Слайды 11-12. Большая часть доказательств теоремы Пифагора выполнена геометрическими методами, один из них метод разложения, который заключается в том, что квадрат, построенный на гипотенузе, с одной стороны, и квадраты, построенные на катетах, с другой, складываются из равных частей. На рисунке доказательство для равнобедренного треугольника. Из рисунка все так понятно, что комментировать его не требуется. Как писал в подобных случаях индийский математик XII века Бхаскара: “Смотри!”. Среди методов разложения есть два таких доказательства, что их можно назвать шедеврами: иранского математика ан-Найризи (конец IX — начало Х века), лондонского биржевого маклера и астронома-любителя Генри Перигэлу (1873 год).
3. Несколько уроков мы рассматривали свойства прямоугольного треугольника. Зачем? (Например ответ: решать задачи). Как можем сформулировать тему урока?
Тема сегодняшнего урока: Решение задач по теме “Теорема Пифагора”.
Какую цель поставим на урок? Какие задачи должны выполнить для ее достижения? (2 мин.)
4. Применение знаний и умений.
1) Разминка-блиц опрос
Слайды. Устное решение по готовым чертежам. (7 мин.) (Фронтальная работа)
2) Письменное выполнение упражнений. Старинные задачи с практической направленностью. (4 мин.)
Старинная задача из учебника Магницкого: Случися некоему человеку к стене лествицу прибрати, длиною 125 стоп, у стены же тоя высота есть 117 стоп. И ведати хощет, колико стоп сея лествицы нижний конец от стены отстояти имать? (Ответ: 44 стопы)
Задача Бхаскары
На берегу реки рос тополь одинокий.
Вдруг ветра порыв его ствол надломал.
Бедный тополь упал. И угол прямой,
С теченьем реки его ствол составлял.
Запомни теперь, что в том месте река
В четыре лишь фута была широка.
Верхушка склонилась у края реки.
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота? (Ответ: 8 футов)
Задачи с практическим содержанием. С решением у доски.
3) Выход к ГИА
Большое количество задач на свойства прямоугольного треугольника и теорему Пифагора вынесено на ГИА. Рассмотрим несколько.
На расстоянии 20 метров друг от друга растут две сосны высотой 8 и 23 метра. Определите расстояние между их вершинами. (Ответ: 25 м)
С решением у доски. (2 мин.)
Слайд-карточки. У гол. Найти значения sin, cos, tq, ctq угла, изображенного на рисунке. (5 мин.) (Работа в парах по нахождению решения данной задачи)
Обсуждение решения: исправление ошибок, если они есть; нахождению решения, если не нашли.
4) Выход к ЕГЭ
Знания, которые получили при изучении данной темы, будут использоваться и в старших классах.
Слайд-Карточки. Найти диагональ прямоугольного параллелепипеда по его измерениям. (5 мин.) (Работа в группах)
5) Дифференцированная самостоятельная работа.
Карточки. (5-7 мин.) Обучающимся предлагается выбрать для решения любые 2-4 задания. Проверка при наличии времени по готовым ответам на уроке, либо работы сдают на проверку.
Ответы
| № задачи | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Ответ | 10 | 5 | 2V2 | 16 | 16 | V2 | V3 |
5) Контроль усвоения, обсуждение допущенных ошибок и их коррекция
Наш урок подходит к концу. Давайте обсудим: какие задачи вызвали у вас затруднения и почему?
6) Рефлексия
Подведение итога урока, в соответствии с целью и задачами. Качественная оценка работы класса и отдельных учащихся. Оценка учащихся. Учащиеся подводят итоги своей работы, продолжая незаконченное предложение. (У меня получилось…, Я попробую…и т.д.)
7) Домашнее задание (на карточке).
№16,18 всем; по желанию: вывести формулу диагонали прямоугольного параллелепипеда; мини сообщения (биография Пифагора, пифагорейская школа, история таблицы Пифагора).
28.01.2015
xn--i1abbnckbmcl9fb.xn--p1ai
Задачи на теорему Пифагора
Задача 1 Расстояние по прямой линии от Испериха в Тутракан и Дулово равно 40 км и 28 км соответственно. Соединяя три города, получаем прямой угол в Исперихе. Найдите расстояние от Дулово до Тутракана.
Решение Если искомое расстояние обозначить как x, тогда x2 = 402 + 282 = 1600 + 784 = 2384, x2 = 2384 => x = √2384 ≈ 50 kм.
Задача 2 Докажите, что треугольник со сторонами 3 см, 4 см и 5 см является прямоугольным треугольником.
Решение 32 + 42 = 9 + 16 = 25 = 52. Так как 32 + 42 = 52, то треугольник с такими длинами сторон есть прямоугольным (с гипотенузой 5 cм).
Задача 3 В таблице внизу мы имеем расстояние между точками A, B и C. Проверьте, являются ли эти точки вершинами прямоугольного треугольника.
| AB | BC | AC | |
| a) | 9 | 12 | 15 |
| b) | 5 | 11 | 12 |
| c) | 8,8 | 11,7 | 14,8 |
| d) | 5 | 9 | 8 |
| e) | 41 | 9 | 40 |
| f) | 6 | 4,5 | 7,5 |
Ответ:a) — да;
b) — нет;
c) — да;
d) — нет;
e) — да;
f) — да.
Задача 4 Являются ли треугольники с длиной сторон, указанной ниже, прямоугольными?
a) √2, 4, 3√2;
b) √3, 3, 2√3;
c) √3, √5, √8.
Ответ: a) — да;
b) — да;
c) — да.
Задача 5 Найдите длину гипотенузы прямоугольного треугольника, если длины двух других сторон равны:
a)√2 и √3;
b) √5 и √7;
c) √9 и √11.
Ответ: a) — √5;
b) — √12;
c) — √20.
Задача 6 В параллелограмме ABCD АВ = 33см, BC = 56 см и АС = 65 см. Проверьте, является ли этот параллелограмм прямоугольником.
Ответ: да.
Задача 7 Медианы сторон ромба являются вершинами прямоугольника. Если длины сторон прямоугольника есть a и b, какая длина стороны ромба?
Ответ:√a2 + b2.
Задача 8 Стороны прямоугольника равны 10 см и 24 см. Найти радиус окружности, описанной вокруг прямоугольника.
Ответ: 13 cм.
Задача 9 Гипотенуза прямоугольного треугольника равна 10 cм, а одна из его сторон — 8 cм. Найдите периметр треугольника.
Ответ: 24 см2.
Задача 10 Одна из сторон прямоугольника равна 12 м, а его диагональ — 13 м. Найдите периметр прямоугольника.
Ответ: 60 м2.
Задача 11 Диагонали ромба 10 см и 4 см. Найдите стороны ромба.
Ответ: √29 ≈ 5,4 cм.
www.math10.com
