Решение типового варианта контрольной работы. Ряды
Пример 1. Исследовать на сходимость числовые ряды:
А)
Б)
В)
Г)
Д)
Е)
Ж)
З)
Решение.
А) В данном случае
Вычислим
Следовательно, ряд расходится.
Б) Поскольку в записи общего члена ряда есть показательная функция , то используем признак Даламбера.
Для рассматриваемого ряда
;
Вычислим
Следовательно, по признаку Даламбера, исходный ряд сходится.
В) Так как в записи общего члена ряда есть факториал (), то используем признак Даламбера. Для исследуемого ряда
Вычислим
В пределе получили бесконечность, следовательно, исследуемый ряд расходится.
Г) Воспользуемся радикальным признаком Коши. Здесь
Вычислим
Полученное значение больше 1, следовательно, ряд расходится.
Исследуем данный ряд с помощью интегрального признака Коши. Составим соответствующий интеграл и вычислим его
Интеграл сходится, следовательно, исследуемый ряд сходится.
Составим ряд, эквивалентный исходному, оставив в числителе и знаменателе лишь старшие степени n:
Полученный ряд эквивалентен исходному, так как
Таким образом, исходный ряд и ряд сходятся и расходятся одновременно. Т. к. ряд сходится, следовательно, исходный ряд также сходится.
Д) Так как , то
.
Ряд расходится , следовательно, исходный ряд также расходится.
Оценим общий член ряда:
.
Ряд
Ряд сходится , следовательно, эквивалентный ряд также сходится. Т. к. из сходимости большего ряда следует сходимость меньшего, то исходный ряд сходится.
Пример2. Найти область сходимости ряда .
Решение. Воспользуемся признаком Даламбера:
Ряд сходится, если
или ;
или ,
.
Ряд расходится, если .
Неопределенный случай: т. е. или ,
Пусть : ‑ сходится.
Ряд сходится как эквивалентный сходящемуся ряду.
Пусть : .
Этот ряд – знакочередующийся. Исследуя его на абсолютную сходимость (рассматриваем ряд, состоящий из абсолютных величин), получим ряд как и при , а он сходится. Т. к. ряд, состоящий из абсолютных величин, сходится, то данный ряд сходится абсолютно.
Получили, что ‑ область сходимости ряда.
Пример 3. Вычислить с точностью интеграл .
Решение. Запишем разложение функции в ряд Маклорена:
+…
Вычислим интеграл
.
Заметим, что при вычислении интеграла получаем знакочередующийся ряд. Мы отбрасываем при вычислении все слагаемые, начиная со слагаемого, меньшего по абсолютной величине заданной точности .
Пример 4. Найти три первые (отличные от 0) члена разложения в степенной ряд решения задачи Коши .
Решение.
Для представления решения в виде ряда Маклорена необходимо найти первые три отличные от нуля значения . По условию задачи Выразим из уравнения :
Найдем , продифференцировав обе части равенства по :
Окончательно получим:
.
Пример 5. Разложить данную функцию в ряд Фурье
А) в интервале (-2, 2):
Б) по синусам на интервале .
Решение.
Разложение периодической (период ) функции имеет вид:
А) В нашем примере L=2.
Где
Вычислим значения интегралов-слагаемых по отдельности.
;
Используя формулу интегрирования по частям, получаем
.
Вычислим значения интегралов-слагаемых по отдельности.
Аналогично предыдущему
И окончательно получим:
Подставляя полученные значения в разложение , получим:
Б) Продолжим функцию на отрезок нечетным образом (рис. 1).
Рис. 1
Тогда получим нечетную функцию, ряд Фурье которой содержит только синусы, т. е. .
Найдем коэффициенты , используя формулу:
Для вычисления первого и третьего интегралов используем метод интегрирования по частям:
.
Таким образом, .
| < Предыдущая | Следующая > |
|---|
matica.org.ua
РЯДЫ
Смех без причины – признак Даламбера
Вот и пробил час функциональных рядов. Для успешного освоения темы, и, в частности, этого урока, нужно хорошо разбираться в обычных числовых рядах. Следует хорошо понимать, что такое ряд, уметь применять признаки сравнения для исследования ряда на сходимость. Таким образом, если Вы только-только приступили к изучению темы или являетесь чайником в высшей математике, необходимо последовательно проработать три урока: Ряды для чайников, Признак Даламбера. Признаки Коши и Знакочередующиеся ряды. Признак Лейбница. Обязательно все три! Если есть элементарные знания и навыки решения задач с числовыми рядами, то справиться с функциональными рядами будет довольно просто, поскольку нового материала не очень и много.
На данном уроке мы рассмотрим понятие функционального ряда (что это вообще такое), познакомимся со степенными рядами, которые встречаются в 99%-ах практических заданий, и научимся решать распространенную типовую задачу на нахождение радиуса сходимости, интервала сходимости и области сходимости степенного ряда. Далее можно будет рассмотреть материал о сумме степенного ряда и разложении функций в степенные ряды.
Понятие функционального ряда и степенного ряда
Обычный числовой ряд, вспоминаем, состоит из чисел:
Все члены ряда – этоЧИСЛА.
Функциональный
же ряд состоит из
В общий член ряда помимо многочленов, факториалов и других подарковнепременновходит буковка «икс». Выглядит это, например, так: . Как и числовой ряд, любой функциональный ряд можно расписать в развернутом виде:
Как видите, все члены функционального ряда – этофункции.
Наиболее популярной разновидностью функционального ряда является степенной ряд.
Определение:
Степенной ряд – это ряд, в общий член которого входятцелые положительные степени независимой переменной . Упрощенно степенной ряд во многих учебниках записывают так:, где– это старая знакомая «начинка» числовых рядов (многочлены, степени, факториалы, зависящиетолько от «эн»). Простейший пример:
Посмотрим на это разложение и еще раз осмыслим определение: члены степенного ряда содержат «иксы» в целых положительных (натуральных) степенях. Очень часто степенной ряд можно встретить в следующих «модификациях»: или, где– константа. Например:
Строго говоря, упрощенные записи степенного ряда ,илине совсем корректны. В показателе степени вместо одинокой буквы «эн» может располагаться более сложное выражение, например:
Или такой степенной ряд:
Лишь бы показатели степеней при «иксАх» были натуральными.
Сходимость степенного ряда. Интервал сходимости, радиус сходимости и область сходимости
Не нужно пугаться такого обилия терминов, они идут «рядом друг с другом» и не представляют особых сложностей для понимания. Лучше выберем какой-нибудь простой подопытный ряд и сразу начнём разбираться.
Прошу любить и жаловать степенной ряд .
Переменная может приниматьлюбое действительное значение от «минус бесконечности» до «плюс бесконечности». Подставим в общий член ряда несколько произвольных значений «икс»: Если , тоЕсли, тоЕсли, тоЕсли, тоИ так далее.
Очевидно, что, подставляя в то или иное значение «икс», мы получаем различные числовые ряды. Некоторые числовые ряды будут сходиться, а некоторые расходиться. И наша задача
Для любого степенного ряда (временно отвлекаемся от конкретного примера) возможны три случая:
1) Степенной ряд сходится абсолютно на некотором интервале . Иными словами, если мы выбираем любое значение «икс» из интервалаи подставляем его в общий член степенного ряда, то у нас получаетсяабсолютно сходящийся числовой ряд. Такой интервал и называетсяинтервалом сходимости степенного ряда.
Радиус сходимости, если совсем просто, это половина длины интервала сходимости:
Геометрически ситуация выглядит так:
В данном случае, интервал сходимости ряда: , радиус сходимости ряда:
Широко распространен тривиальный случай, когда интервал сходимости симметричен относительно нуля:
>
Здесь интервал сходимости ряда: , радиус сходимости ряда:
А что будет происходить на концах интервала ? В точках,степенной рядможет, как сходиться, так и расходится, и для выяснения этого необходимо проводить дополнительное исследование. После такого исследования речь идёт уже об области сходимости ряда:
– Если установлено, что степенной ряд расходится на обоих концах интервала, то область сходимости ряда совпадает с интервалом сходимости:
– Если установлено, что степенной ряд сходится на одном конце интервала и расходится на другом, то область сходимости ряда представляет собой полуинтервал: или.
– Если установлено, что степенной ряд сходится на обоих концах интервала, то область сходимости ряда представляет собой отрезок:
Термины очень похожи, область сходимости ряда – это чуть более детализированныйинтервал сходимости ряда.
С двумя оставшимися случаями всё короче и проще:
2) Степенной ряд сходится абсолютно при любом значении . То есть, какое бы значение «икс» мы не подставили в общий член степенного ряда – в любом случае у нас получитсяабсолютно сходящийся числовой ряд. Интервал сходимости и область сходимости в данном случае совпадают: . Радиус сходимости:. Рисунок приводить не буду, думаю, нет необходимости.
3) Степенной ряд сходится в единственной точке. Если ряд имеет вид , то он будет сходиться в единственной точке. В этом случае интервал сходимости и область сходимости ряда тоже совпадают и равны единственному числу – нулю:. Если ряд имеет вид, то он будет сходиться в единственной точке, если ряд имеет вид, то, понятно, – в точке «минус а». Радиус сходимости ряда во всех случаях, естественно, нулевой:.
Других вариантов нет. Область сходимости степенного ряда – это всегда либо единственная точка, либо любое «икс», либо интервал (возможно полуинтервал, отрезок). Подчеркиваю, чтоданная классификация справедлива для степенных рядов. Для произвольного функционального ряда она в общем случае является неверной.
Исследование степенного ряда на сходимость
После небольшой порции теоретического материала переходим к рассмотрению типового задания, которое практически всегда встречается на зачетах и экзаменах по высшей математике.
Пример 1
Найти область сходимости степенного ряда
Задание часто формулируют эквивалентно: Найти интервал сходимости степенного ряда и исследовать его сходимость на концах найденного интервала.
Алгоритм решения довольно прозрачен и трафаретен.
На первом этапе находим интервал сходимости ряда. Почти всегда необходимо использовать признак Даламбера и находить предел . Технология применения признака Даламбера точно такая же, как и для числовых рядов, с ней можно ознакомиться на урокеПризнак Даламбера. Признаки Коши. Единственное отличие – все дела у нас происходят под знаком модуля.
Итак, решаем наш предел:
(1) Составляем отношение следующего члена ряда к предыдущему.
(2) Избавляемся от четырехэтажности дроби.
(3) В числителе по правилу действий со степенями «отщипываем» один «икс». В знаменателе возводим двучлен в квадрат.
(4) Выносим оставшийся «икс» за знак предела, причем, выносим его вместе со знаком модуля. Почему со знаком модуля? Дело в том, что наш предел и так будет неотрицательным, а вот «икс» вполне может принимать отрицательные значения. Поэтому модуль относится именно к нему.
Кстати, почему можно вообще вынести за знак предела? Потому-что «динамической» переменной в пределе у нас является «эн», и от этого нашему «иксу» ни жарко ни холодно.
(5) Устраняем неопределенность стандартным способом.
После того, как предел найден, нужно проанализировать, что у нас получилось.
Если в пределе получается ноль, то алгоритм решения заканчивает свою работу, и мы даём окончательный ответ задания: «Область сходимости степенного ряда: » (любое действительное число – случай №2 предыдущего параграфа). То есть, степенной ряд сходится при любом значении «икс». Ответ можно записать эквивалентно: «Ряд сходится при» (значокв математике обозначает принадлежность).
Если в пределе получается бесконечность, то алгоритм решения также заканчивает свою работу, и мы даём окончательный ответ задания: «Ряд сходится при » (или прилибо»). Смотрите случай №3 предыдущего параграфа.
Если в пределе получается не ноль и не бесконечность, то у нас самый распространенный на практике случае №1 – ряд сходится на некотором интервале.
В данном случае предел равен . Как найти интервал сходимости ряда? Составляем неравенство:
В ЛЮБОМ задании данного типа в левой части неравенства должен находиться результат вычисления предела, а в правой части неравенства – строго единица. Не буду объяснять, почему именно такое неравенство и почему справа единица. Уроки носят практическую направленность, и уже очень хорошо, что от моих рассказов не повесился профессорско-преподавательский состав стали понятнее некоторые теоремы.
Техника работы с модулем и решения двойных неравенств подробно рассматривалась на первом курсе в статье Область определения функции, но для удобства я постараюсь максимально подробно закомментировать все действия. Раскрываем неравенство с модулем по школьному правилу . В данном случае:
– интервал сходимости исследуемого степенного ряда.
Половина пути позади.
На втором этапе необходимо исследовать сходимость ряда на концах найденного интервала.
Сначала берём левый конец интервала и подставляем его в наш степенной ряд:
При
Получен числовой ряд, и нам нужно исследовать его на сходимость (уже знакомая из предыдущих уроков задача).
Используем признак Лейбница: 1) Ряд является знакочередующимся. 2) – члены ряда убывают по модулю. Каждый следующий член ряда по модулю меньше, чем предыдущий, значит, убывание монотонно.
Вывод: ряд сходится.
Исследуем ряд на абсолютную сходимость: – сходится (случай обобщенного гармонического ряда).
Таким образом, полученный числовой ряд сходится абсолютно.
Далее рассматриваем правый конец интервала , подставляем это значение в наш степенной ряд:
При – сходится.
Таким образом, степенной ряд сходится на обоих концах найденного интервала.
Ответ: Область сходимости исследуемого степенного ряда:
Имеет право на жизнь и другое оформление ответа: Ряд сходится, если
Иногда в условии задачи требуют указать радиус сходимости. Очевидно, что в рассмотренном примере .
Пример 2
Найти область сходимости степенного ряда
Решение: Найдем интервал сходимости данного ряда. Используем признак Даламбера:
Составляем стандартное неравенство: Ряд сходится при
Слева нам нужно оставить только , поэтому умножаем обе части неравенства на 3:
И раскрываем неравенство с модулем по правилу :– интервал сходимости исследуемого степенного ряда.
Исследуем сходимость степенного ряда на концах найденного интервала. 1) При
Обратите внимание, что при подстановке значения в степенной ряду нас сократилась степень. Это верный признак того, что мы правильно нашли интервал сходимости ряда.
Исследуем полученный числовой ряд на сходимость.
Используем признак Лейбница. – Ряд является знакочередующимся. – – члены ряда убывают по модулю. Каждый следующий член ряда по модулю меньше, чем предыдущий, значит, убывание монотонно. Вывод: Ряд сходится.
Исследуем ряд на абсолютную сходимость: Сравним данный ряд с расходящимся рядом. Используем предельный признак сравнения:Получено конечное число, отличное от нуля, значит, рядрасходится вместе с рядом.
Таким образом, ряд сходится только условно.
2) При – расходится (по доказанному).
Ответ: Область сходимости исследуемого степенного ряда: . Приряд сходится только условно.
В рассмотренном примере областью сходимости степенного ряда является полуинтервал, причем во всех точках интервала степенной рядсходится абсолютно (см. предыдущий параграф), а в точке , как выяснилось –сходится только условно.
Пример 3
Найти интервал сходимости степенного ряда и исследовать его сходимость на концах найденного интервала
Это пример для самостоятельного решения.
Рассмотрим пару примеров, которые встречаются редко, но встречаются.
Пример 4
Найти область сходимости ряда:
Решение: Найдем
интервал сходимости данного ряда.
Используем признак Даламбера: 
(1) Составляем отношение следующего члена ряда к предыдущему.
(2) Избавляемся от четырехэтажности дроби.
(3) Кубы ипо правилу действий со степенями подводим под единую степень. В числителе хитро раскладываем степень, т.е. раскладываем таким образом, чтобы на следующем шаге сократить дробь на. Факториалы расписываем подробно.
(4) Под кубом почленно делим числитель на знаменатель, указывая, что . В дроби сокращаем всё, что можно сократить. Множительвыносим за знак предела, его можно вынести, поскольку в нём нет ничего, зависящего от «динамической» переменной «эн». Обратите внимание, что знак модуля не нарисован – по той причине, чтопринимает неотрицательные значения при любом «икс».
В пределе получен ноль, а значит, можно давать окончательный ответ:
Ответ: Ряд сходится при
А сначала-то казалось, что этот ряд со «страшной начинкой» будет трудно решить. Ноль или бесконечность в пределе – почти подарок, ведь решение заметно сокращается!
Пример 5
Найти область сходимости ряда
Это пример для самостоятельного решения. Будьте внимательны 😉 Полное решение ответ в конце урока.
Рассмотрим еще несколько примеров, содержащих элемент новизны в плане использования технических приемов.
Пример 6
Найти интервал сходимости ряда и исследовать его сходимость на концах найденного интервала
Решение: В общий член степенного ряда входит множитель , обеспечивающий знакочередование. Алгоритм решения полностью сохраняется, но при составлении пределамы игнорируем (не пишем) этот множитель, поскольку модуль уничтожает все «минусы».
Найдем интервал сходимости данного ряда. Используем признак Даламбера:
Составляем стандартное неравенство: Ряд сходится при Слева нам нужно оставить только модуль, поэтому умножаем обе части неравенства на 5: Теперь раскрываем модуль уже знакомым способом:
В середине двойного неравенства нужно оставить только «икс», в этих целях из каждой части неравенства вычитаем 2:
– интервал сходимости исследуемого степенного ряда.
Исследуем сходимость ряда на концах найденного интервала:
1) Подставляем значение в наш степенной ряд:
Будьте предельно внимательны, множитель не обеспечивает знакочередование, при любом натуральном «эн». Полученный минус выносим за пределы ряда и забываем про него, поскольку он (как и любая константа-множитель) никак не влияет на сходимость или расходимость числового ряда.
Еще раз заметьте, что в ходе подстановки значения в общий член степенного ряда у нас сократился множитель. Если бы этого не произошло, то это бы значило, что мы либо неверно вычислили предел, либо неправильно раскрыли модуль.
Итак, требуется исследовать на сходимость числовой ряд . Здесь проще всего использовать предельный признак сравнения и сравнить данный ряд с расходящимся гармоническим рядом. Но, если честно, предельный признак сравнения до ужаса мне надоел, поэтому внесу некоторое разнообразие в решение.
Используем интегральный признак. Подынтегральная функция непрерывна на.Таким образом, полученный числовой ряд расходится вместе с соответствующим несобственным интегралом.
2) Исследуем второй конец интервала сходимости. При
Используем признак Лейбница: – Ряд является знакочередующимся. – – члены ряда убывают по модулю. Каждый следующий член ряда по модулю меньше, чем предыдущий, значит, убывание монотонно. Вывод: ряд сходится
Рассматриваемый числовой ряд не является абсолютно сходящимся поскольку – расходится (по доказанному).
Ответ: – область сходимости исследуемого степенного ряда, приряд сходится только условно.
studfiles.net
1. Числовые ряды
Понятие числового ряда
Даны члены числовой
последовательности u1, u2,
…, un,
… . Выражение u1+u2+…+un+… называется числовым
рядом. Числа u1, u2,
…, un,
… называются членами ряда.
un – общий член ряда. Сокращенно ряд
записывают 
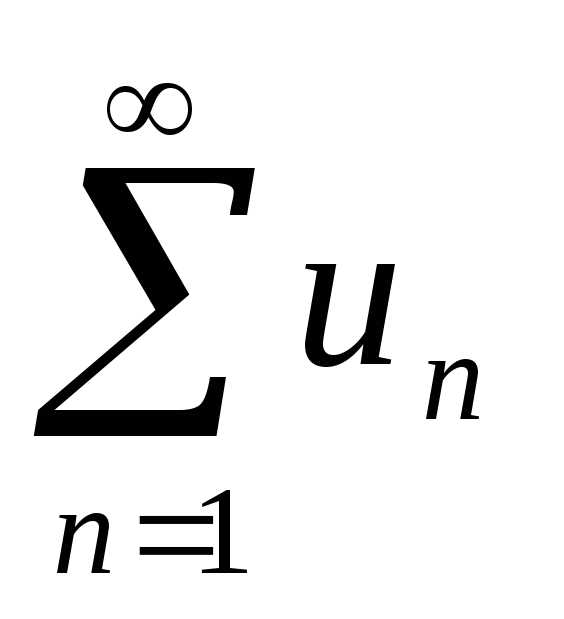 .
.
Запишем суммы S1 = u1, S2 = u1+u2, S3 = u1+u2+u3, … , Sn = u1+u2+…+un, … Их называют частными или частичными суммами ряда. Частные суммы образуют бесконечную числовую последовательность S1, S2, S3, …, Sn, … .
Если существует
конечный предел последовательности
частных сумм 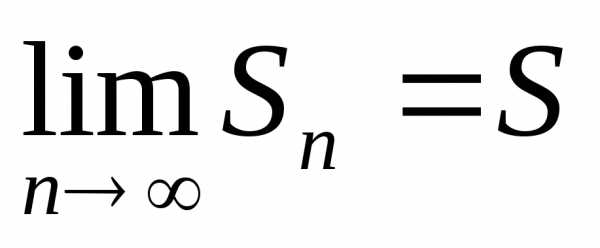 ,
то ряд называютсходящимся. Число S
называют суммой
ряда и
записывают
,
то ряд называютсходящимся. Число S
называют суммой
ряда и
записывают 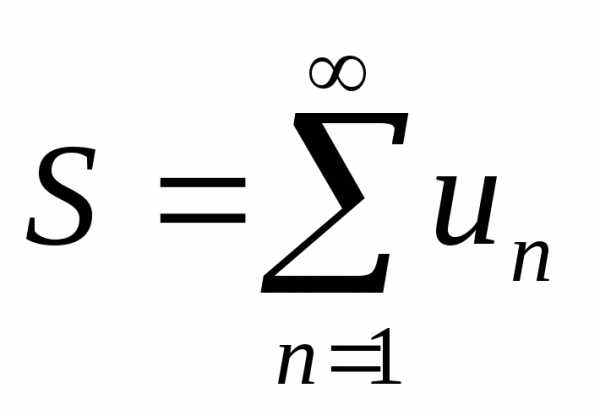 .
.
Если предел последовательности частных сумм не существует или равен бесконечности, то ряд называется расходящимся.
Пример1.
Задан ряд:
Запишем частную сумму ряда:
Члены ряда представим следующим образом:
Ряд сходится, и его сумма равна 1.
Пример 2.
Ряд
называется рядом геометрической
прогрессии со знаменателемq.
Этот ряд сходится только при |q|
< 1 и его сумма равна 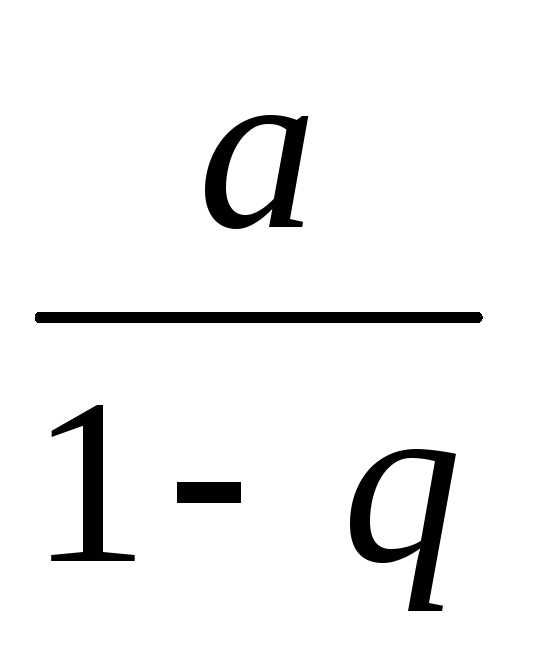 .
.
Пример 3.
Ряд называется гармоническим. Он является расходящимся.
1.2. Ряды с положительными членами
Ряд u1 + u2 + … + un + … называется рядом с положительными членами, если при всех значениях n выполняется неравенство un > 0.
Пусть даны два ряда с положительными членами
, (1)
. (2)
Если при всех
значениях n
выполняется неравенство 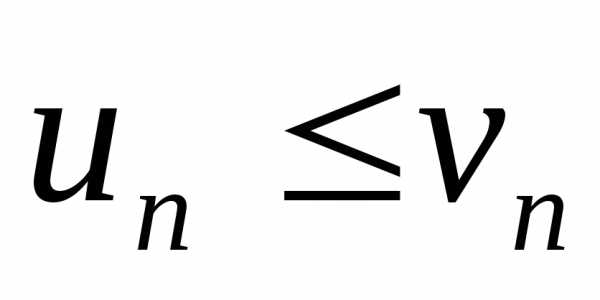 ,
то ряд (2) называетсямажорантным по отношению к ряду (1), а ряд (1) называется минорантным (т. е. рядом с меньшими членами).
,
то ряд (2) называетсямажорантным по отношению к ряду (1), а ряд (1) называется минорантным (т. е. рядом с меньшими членами).
Теорема (признак сравнения). Из сходимости ряда (2) следует сходимость ряда (1). Из расходимости ряда (1) следует расходимость ряда (2).
Пример 1.
Исследовать сходимость ряда: .
Данный ряд можно
сравнить с гармоническим рядом 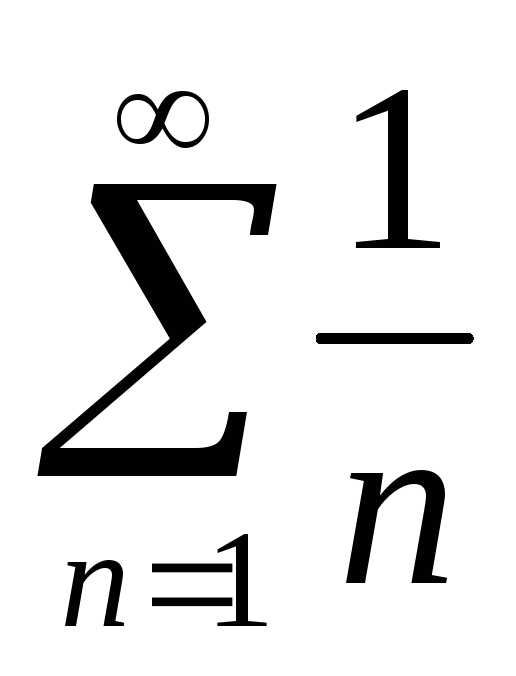 ,
т. к.
,
т. к.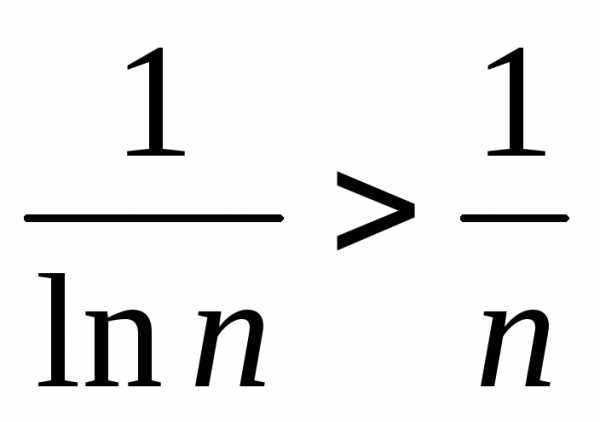 .
Гармонический ряд расходится, значит,
данный ряд расходится.
.
Гармонический ряд расходится, значит,
данный ряд расходится.
Пример 2.
Исследовать
сходимость ряда: 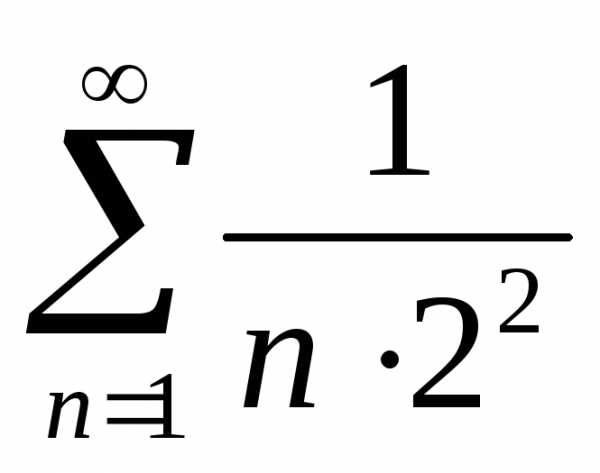 .
.
Члены данного ряда не больше соответствующих членов ряда
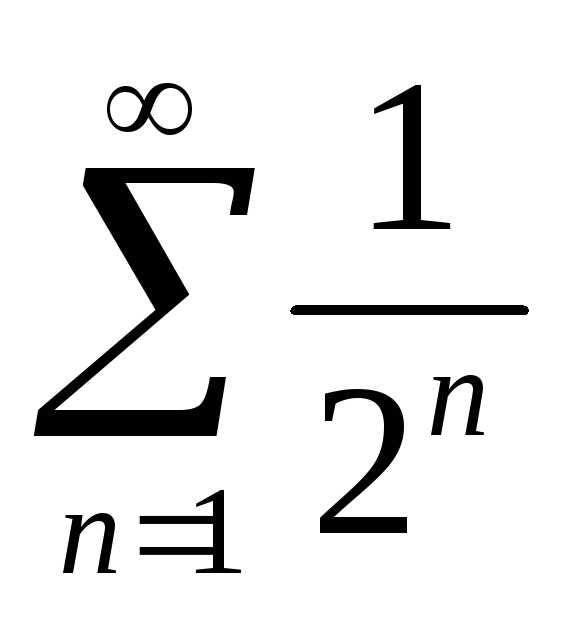 ,
т. к.
,
т. к. 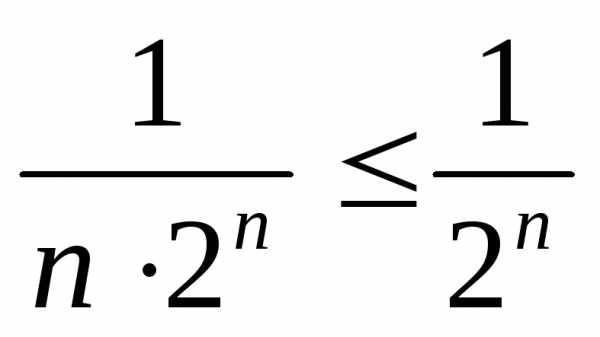 .
Ряд
.
Ряд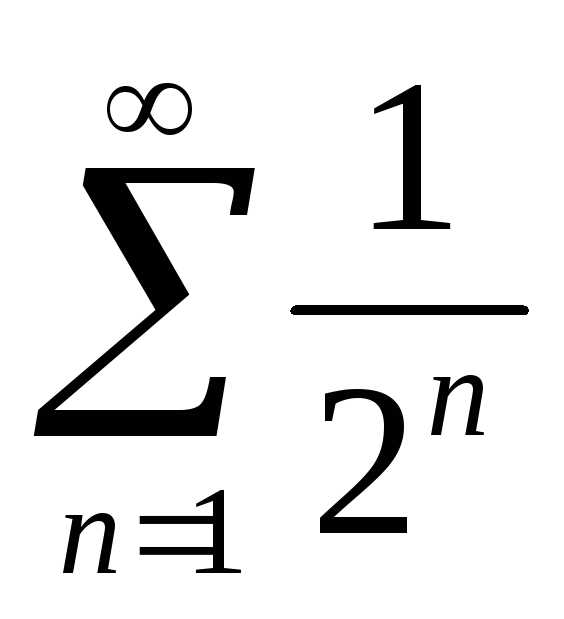 является рядом геометрической прогрессии
со знаменателем
является рядом геометрической прогрессии
со знаменателем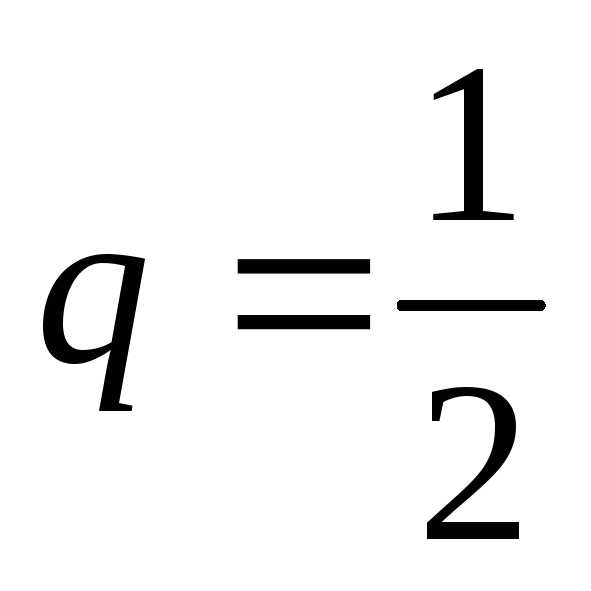 <1.
Такой ряд сходится, следовательно, ряд
<1.
Такой ряд сходится, следовательно, ряд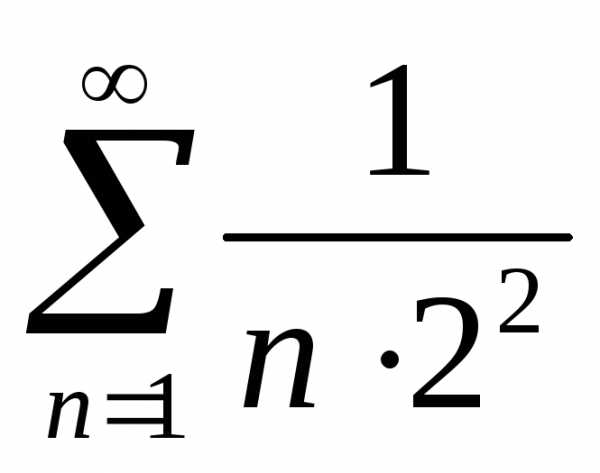 сходится.
сходится.
Пример 3.
Исследовать сходимость ряда: .
Члены данного ряда
не меньше соответствующих членов
гармонического ряда 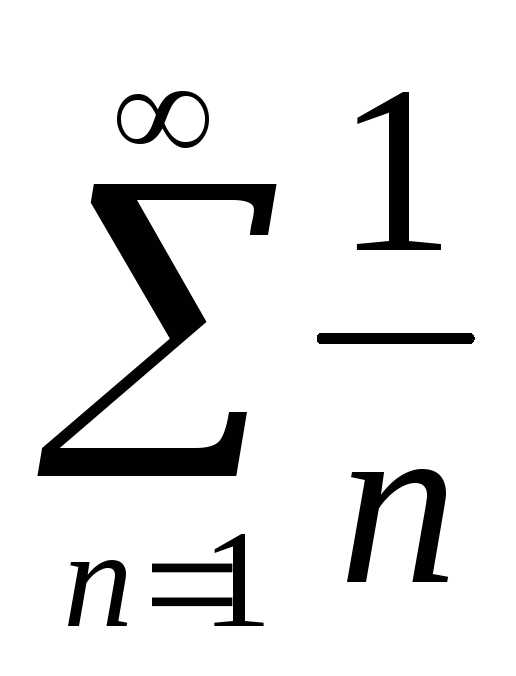 ,
т. к.
,
т. к.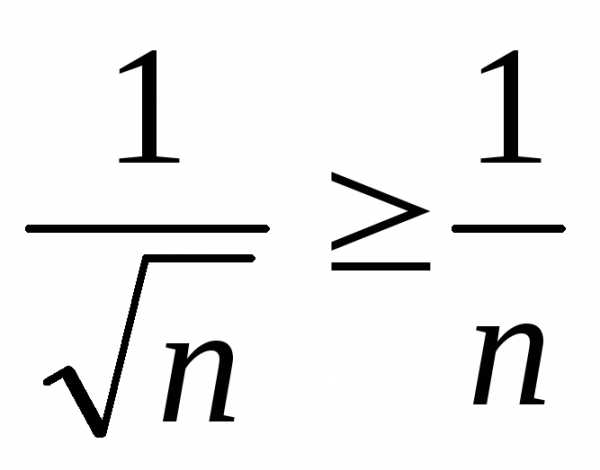 .
Гармонический ряд расходится, значит,
по признаку сравнения рядов данный ряд
расходится.
.
Гармонический ряд расходится, значит,
по признаку сравнения рядов данный ряд
расходится.
1.3. Признак Даламбера
Дан ряд с положительными членами u1 + u2 + … + un + … .
Пусть 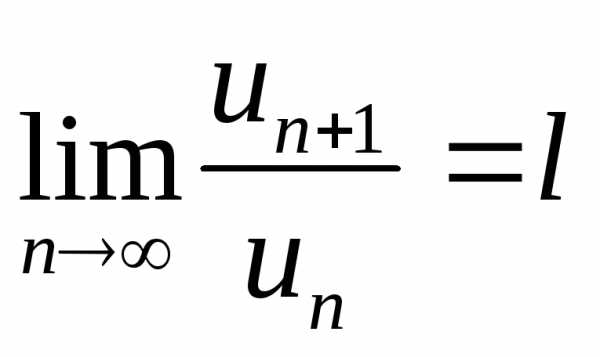 .
.
Если l < 1, то ряд сходится.
Если l > 1, то ряд расходится.
Если l = 1, то признак вопроса не решает.
Пример 1.
Исследовать
сходимость ряда: 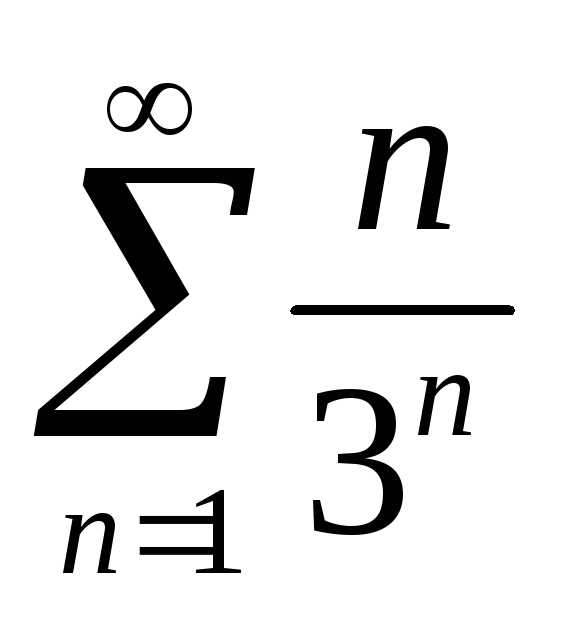 ,
,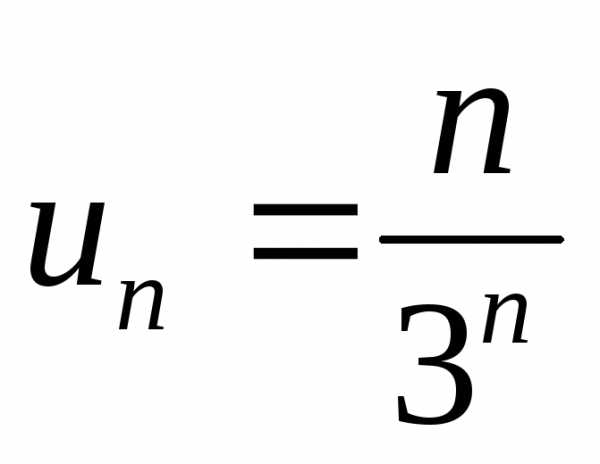 ,
,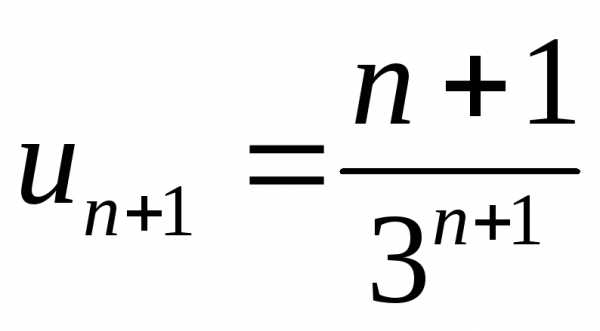 .
.
<1. Ряд сходится.
Пример 2.
Исследовать
сходимость ряда: 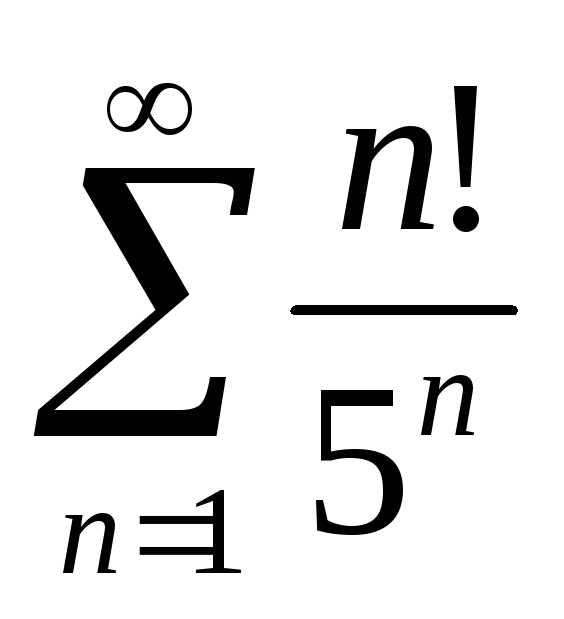 ,
,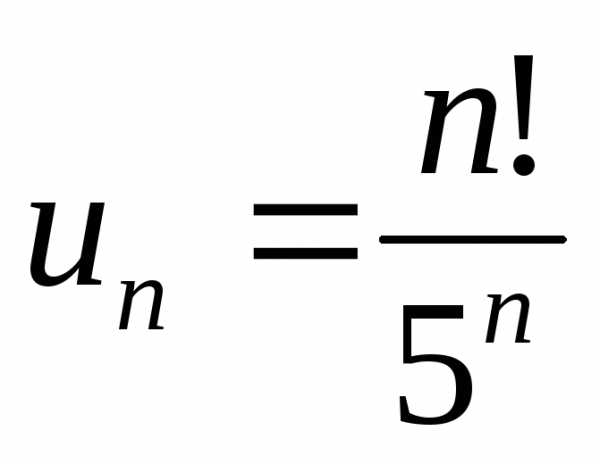 ,
,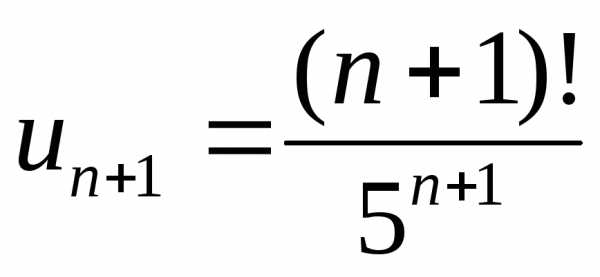 .
.
. Ряд расходится.
Пример 3.
Исследовать
сходимость ряда: 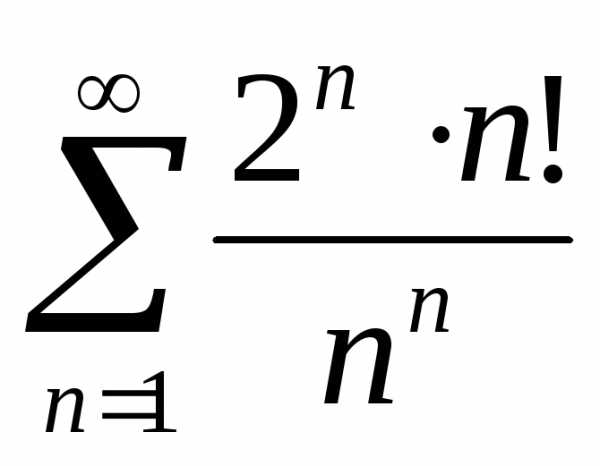 ,
,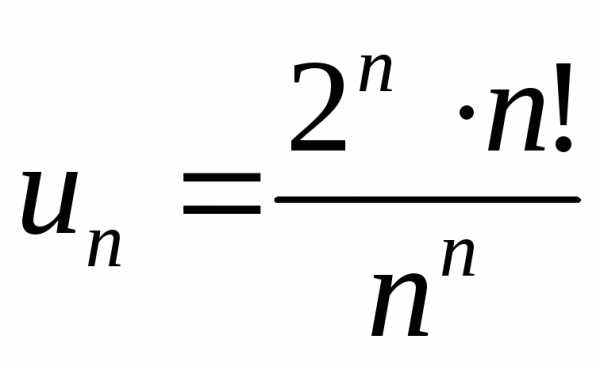 ,
,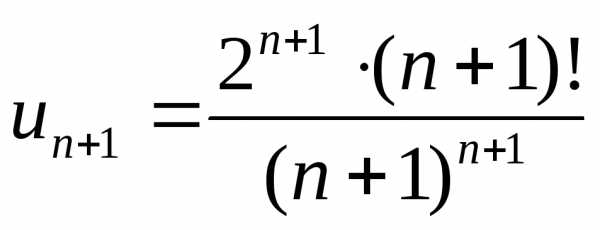 .
.
Ряд сходится.
Пример 4.
Исследовать
сходимость ряда: 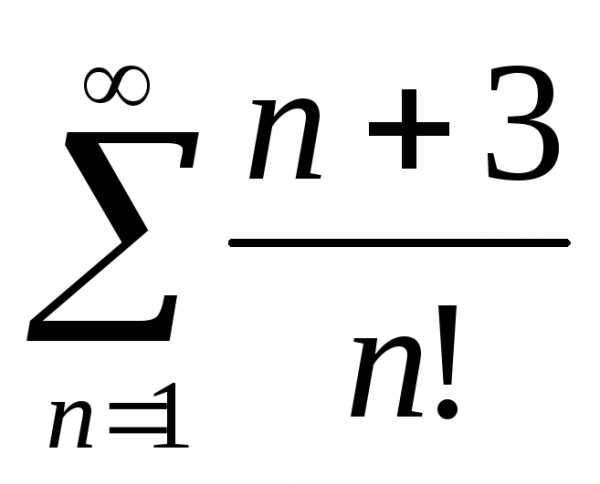 ,
,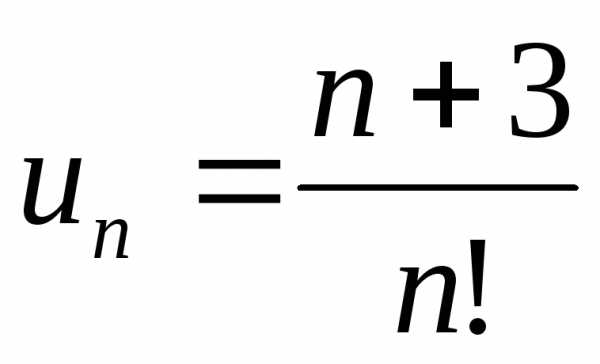 ,
,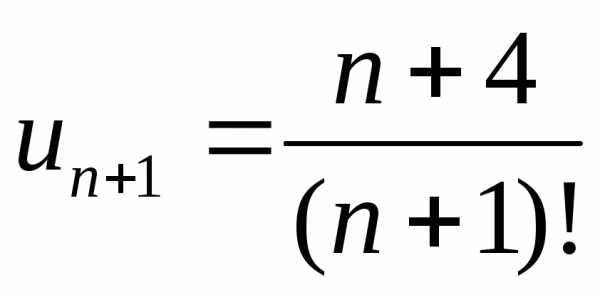 .
.
Ряд сходится.
1.4. Интегральный признак Коши сходимости ряда
Дан ряд с положительными членами u1+u2+…+un+… , члены которого монотонно убывают, т.е. un+1 < un.
Составим непрерывную
невозрастающую положительную функцию f(x), заданную на 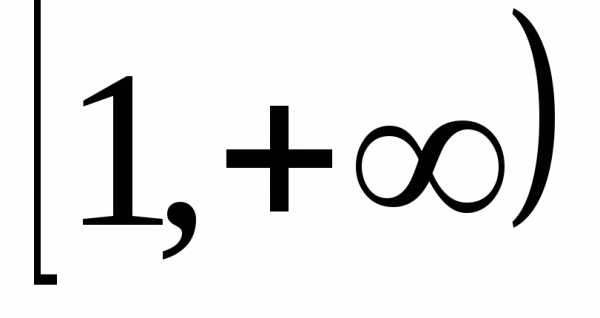 такую, что приx = 1,2,3,…,n,… значение функции равно соответствующему
члену ряда. Функция f(x) называется производящей
функцией данного ряда.
такую, что приx = 1,2,3,…,n,… значение функции равно соответствующему
члену ряда. Функция f(x) называется производящей
функцией данного ряда.
Теорема. Если члены данного ряда монотонно
убывают (un+1 < 0 un , n = 1,2, 3, …) и
если функция y = f(x) при 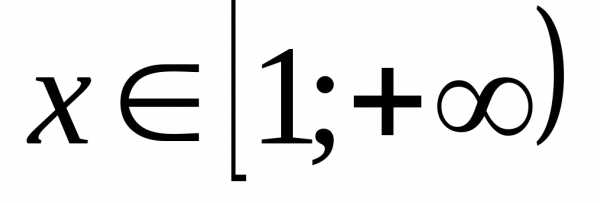 непрерывна, положительна и монотонно
убывает, иf(n)=un,
тогда
непрерывна, положительна и монотонно
убывает, иf(n)=un,
тогда
если
 сходится, то сходится и данный ряд;
сходится, то сходится и данный ряд;если
 расходится, то расходится и данный ряд.
расходится, то расходится и данный ряд.
Пример 1.
Исследовать на
сходимость ряд: 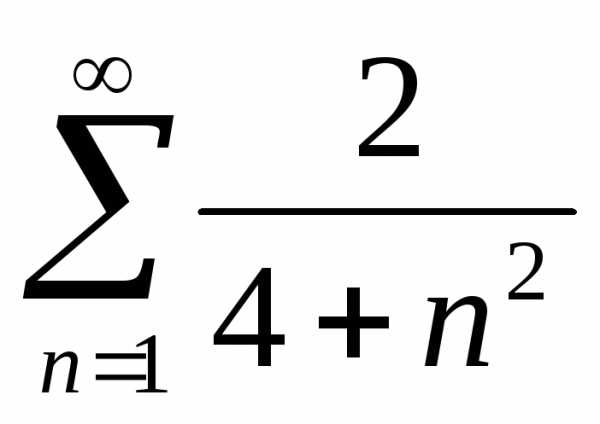 .
.
Составим
производящую функцию ряда 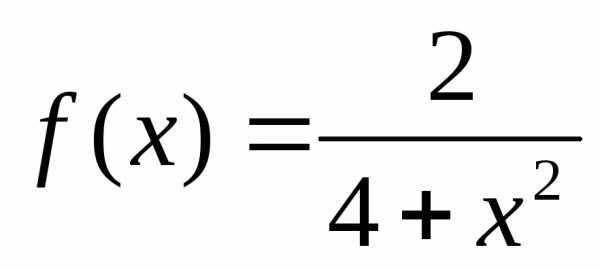 .
Вычислим несобственный интеграл этой
функции:
.
Вычислим несобственный интеграл этой
функции:
.
Несобственный интеграл сходится, сходится и данный ряд.
Пример 2.
Исследовать
сходимость числового ряда: 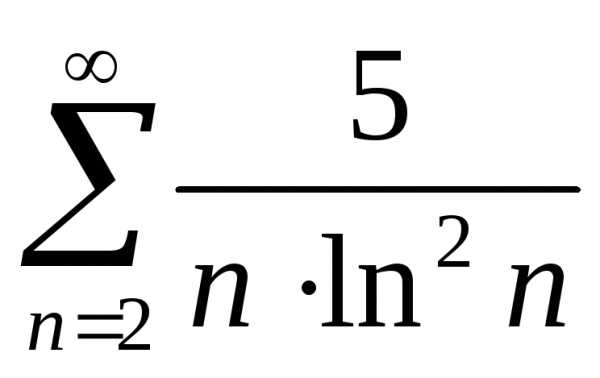 .
.
Составим
производящую функцию ряда 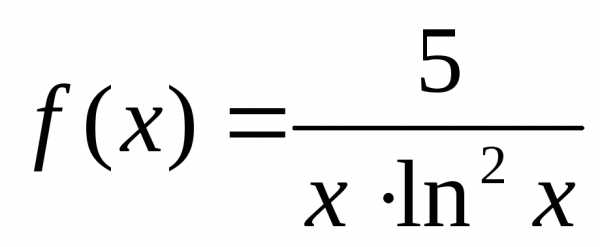 .
Вычислим:
.
Вычислим:
Несобственный интеграл сходится, сходится и данный ряд.
Пример 3.
Исследовать
сходимость ряда: 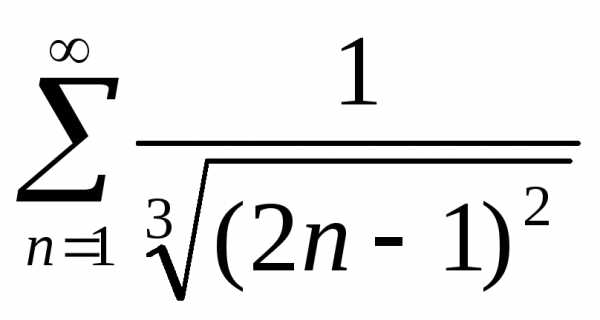 .
.
Составим производящую
функцию ряда 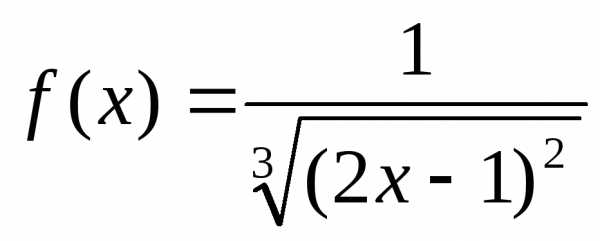 .
Вычислим:
.
Вычислим:
Несобственный интеграл расходится, расходится и данный ряд.
studfiles.net
Исследование степенного ряда на сходимость — Мегаобучалка
После небольшой порции теоретического материала переходим к рассмотрению типового задания, которое практически всегда встречается на зачетах и экзаменах по высшей математике.
Пример 1
Найти область сходимости степенного ряда
Задание часто формулируют эквивалентно: Найти интервал сходимости степенного ряда и исследовать его сходимость на концах найденного интервала.
Алгоритм решения довольно прозрачен и трафаретен.
На первом этапе находим интервал сходимости ряда. Почти всегда необходимо использовать признак Даламбера и находить предел . Технология применения признака Даламбера точно такая же, как и для числовых рядов, с ней можно ознакомиться на урокеПризнак Даламбера. Признаки Коши. Единственное отличие – все дела у нас происходят под знаком модуля.
Итак, решаем наш предел:
(1) Составляем отношение следующего члена ряда к предыдущему.
(2) Избавляемся от четырехэтажности дроби.
(3) В числителе по правилу действий со степенями «отщипываем» один «икс». В знаменателе возводим двучлен в квадрат.
(4) Выносим оставшийся «икс» за знак предела, причем, выносим его вместе со знаком модуля. Почему со знаком модуля? Дело в том, что наш предел и так будет неотрицательным, а вот «икс» вполне может принимать отрицательные значения. Поэтому модуль относится именно к нему.
Кстати, почему можно вообще вынести за знак предела? Потому-что «динамической» переменной в пределе у нас является «эн», и от этого нашему «иксу» ни жарко ни холодно.
(5) Устраняем неопределенность стандартным способом.
После того, как предел найден, нужно проанализировать, что у нас получилось.
Если в пределе получается ноль, то алгоритм решения заканчивает свою работу, и мы даём окончательный ответ задания: «Область сходимости степенного ряда: » (любое действительное число – случай №2 предыдущего параграфа). То есть, степенной ряд сходится при любом значении «икс». Ответ можно записать эквивалентно: «Ряд сходится при » (значок в математике обозначает принадлежность).
Если в пределе получается бесконечность, то алгоритм решения также заканчивает свою работу, и мы даём окончательный ответ задания: «Ряд сходится при » (или при либо »). Смотрите случай №3 предыдущего параграфа.
Если в пределе получается не ноль и не бесконечность, то у нас самый распространенный на практике случае №1 – ряд сходится на некотором интервале.
В данном случае предел равен . Как найти интервал сходимости ряда? Составляем неравенство:
В ЛЮБОМ задании данного типа в левой части неравенства должен находиться результат вычисления предела, а в правой части неравенства – строго единица. Я не буду объяснять, почему именно такое неравенство и почему справа единица. Уроки носят практическую направленность, и уже достаточно того, что я пересказал своими словами несколько теорем.
Теперь раскрываем модуль по школьному правилу: .
В данном случае:
– интервал сходимости исследуемого степенного ряда.
Половина пути позади.
На втором этапе необходимо исследовать сходимость ряда на концах найденного интервала.
Сначала берём левый конец интервала и подставляем его в наш степенной ряд :
При
Получен числовой ряд, и нам нужно исследовать его на сходимость (уже знакомая из предыдущих уроков задача).
Используем признак Лейбница:
1) Ряд является знакочередующимся.
2) – члены ряда убывают по модулю.
Вывод: ряд сходится.
Исследуем ряд на абсолютную сходимость:
– сходится (случай обобщенного гармонического ряда).
Таким образом, полученный числовой ряд сходится абсолютно.
Далее рассматриваем правый конец интервала , подставляем это значение в наш степенной ряд :
При – сходится.
Таким образом, степенной ряд сходится на обоих концах найденного интервала.
Ответ: Область сходимости исследуемого степенного ряда:
Имеет право на жизнь и другое оформление ответа: Ряд сходится, если
Иногда в условии задачи требуют указать радиус сходимости. Очевидно, что в рассмотренном примере .
Пример 2
Найти область сходимости степенного ряда
Решение: Найдем интервал сходимости данного ряда. Используем признак Даламбера:
Составляем стандартное неравенство:
Ряд сходится при
Слева нам нужно оставить только , поэтому умножаем обе части неравенства на 3:
И раскрываем модуль по школьному правилу :
– интервал сходимости исследуемого степенного ряда.
Исследуем сходимость степенного ряда на концах найденного интервала.
1) При
Обратите внимание, что при подстановке значения в степенной ряд у нас сократилась степень . Это верный признак того, что мы правильно нашли интервал сходимости ряда.
Исследуем полученный числовой ряд на сходимость.
Используем признак Лейбница.
– Ряд является знакочередующимся.
– – члены ряда убывают по модулю.
Вывод: Ряд сходится.
Исследуем ряд на абсолютную сходимость:
Сравним данный ряд с расходящимся рядом .
Используем предельный признак сравнения:
Получено конечное число, отличное от нуля, значит, ряд расходится вместе с рядом .
Таким образом, ряд сходится только условно.
2) При – расходится (по доказанному).
Ответ: Область сходимости исследуемого степенного ряда: . При ряд сходится только условно.
В рассмотренном примере областью сходимости степенного ряда является полуинтервал, причем во всех точках интервала степенной ряд сходится абсолютно (см. предыдущий параграф), а в точке , как выяснилось – сходится только условно.
Пример 3
Найти интервал сходимости степенного ряда и исследовать его сходимость на концах найденного интервала
Это пример для самостоятельного решения.
Рассмотрим пару примеров, которые встречаются редко, но встречаются.
Пример 4
Найти область сходимости ряда:
Решение: Найдем интервал сходимости данного ряда. Используем признак Даламбера:
(1) Составляем отношение следующего члена ряда к предыдущему.
(2) Избавляемся от четырехэтажности дроби.
(3) Кубы и по правилу действий со степенями подводим под единую степень. В числителе хитро раскладываем степень , т.е. раскладываем таким образом, чтобы на следующем шаге сократить дробь на . Факториалы расписываем подробно.
(4) Под кубом почленно делим числитель на знаменатель, указывая, что . В дроби сокращаем всё, что можно сократить. Множитель выносим за знак предела, его можно вынести, поскольку в нём нет ничего, зависящего от «динамической» переменной «эн». Обратите внимание, что знак модуля не нарисован – по той причине, что принимает неотрицательные значения при любом «икс».
В пределе получен ноль, а значит, можно давать окончательный ответ:
Ответ: Ряд сходится при
А сначала-то казалось, что этот ряд со «страшной начинкой» будет трудно решить. Ноль или бесконечность в пределе – почти подарок, ведь решение заметно сокращается!
Пример 5
Найти область сходимости ряда
Это пример для самостоятельного решения. Будьте внимательны 😉 Полное решение ответ в конце урока.
Рассмотрим еще несколько примеров, содержащих элемент новизны в плане использования технических приемов.
Пример 6
Найти интервал сходимости ряда и исследовать его сходимость на концах найденного интервала
Решение: В общий член степенного ряда входит множитель , обеспечивающий знакочередование. Алгоритм решения полностью сохраняется, но при составлении предела мы игнорируем (не пишем) этот множитель, поскольку модуль уничтожает все «минусы».
Найдем интервал сходимости данного ряда. Используем признак Даламбера:
Составляем стандартное неравенство:
Ряд сходится при
Слева нам нужно оставить только модуль, поэтому умножаем обе части неравенства на 5:
Теперь раскрываем модуль уже знакомым способом:
В середине двойного неравенства нужно оставить только «икс», в этих целях из каждой части неравенства вычитаем 2:
– интервал сходимости исследуемого степенного ряда.
Исследуем сходимость ряда на концах найденного интервала:
1) Подставляем значение в наш степенной ряд :
Будьте предельно внимательны, множитель не обеспечивает знакочередование, при любом натуральном «эн» . Полученный минус выносим за пределы ряда и забываем про него, поскольку он (как и любая константа-множитель) никак не влияет на сходимость или расходимость числового ряда.
Еще раз заметьте, что в ходе подстановки значения в общий член степенного ряда у нас сократился множитель . Если бы этого не произошло, то это бы значило, что мы либо неверно вычислили предел, либо неправильно раскрыли модуль.
Итак, требуется исследовать на сходимость числовой ряд . Здесь проще всего использовать предельный признак сравнения и сравнить данный ряд с расходящимся гармоническим рядом. Но, если честно, предельный признак сравнения до ужаса мне надоел, поэтому внесу некоторое разнообразие в решение.
Используем интегральный признак.
Подынтегральная функция непрерывна на .
Таким образом, полученный числовой ряд расходится вместе с соответствующим несобственным интегралом.
2) Исследуем второй конец интервала сходимости.
При
Используем признак Лейбница:
– Ряд является знакочередующимся.
– – члены ряда убывают по модулю.
Вывод: ряд сходится
Рассматриваемый числовой ряд не является абсолютно сходящимся поскольку – расходится (по доказанному).
Ответ: – область сходимости исследуемого степенного ряда, при ряд сходится только условно.
Пример 7
Найти интервал сходимости ряда и исследовать его сходимость на концах найденного интервала
Это пример для самостоятельного решения.
Кто утомился, может сходить покурить, а мы рассмотрим еще два примера.
Пример 8
Найти интервал сходимости ряда и исследовать его сходимость на концах найденного интервала
Решение: Найдем интервал сходимости данного ряда. Используем признак Даламбера:
Предел по той причине, что числитель и знаменатель одного порядка роста. Более подробно об этом моменте и «турбо»-методе решения читайте в статьеПризнак Даламбера. Признаки Коши.
Итак, ряд сходится при
Умножаем обе части неравенства на 9:
Извлекаем из обеих частей корень, при этом помним старый школьный прикол :
Раскрываем модуль:
И прибавляем ко всем частям единицу:
– интервал сходимости исследуемого степенного ряда.
Исследуем сходимость степенного ряда на концах найденного интервала:
1) Если , то получается следующий числовой ряд:
Множитель бесследно пропал, поскольку при любом натуральном значении «эн» .
И в третий раз обращаю внимание на то, что в результате подстановки сократились степени , а значит, интервал сходимости найден правильно.
По всем признакам для полученного числового ряда следует применить предельный признак сравнения. Какой ряд подобрать для сравнения? Об этой методике я уже рассказывал на урокеРяды для чайников. Повторим.
Определяем старшую степень знаменателя, для этого мысленно или на черновике отбрасываем под корнем всё, кроме самого старшего слагаемого: . Таким образом, старшая степень знаменателя равна . Старшая степень числителя, очевидно, равна 1. Из старшей степени знаменателя вычитаем старшую степень числителя: .
Таким образом, наш ряд нужно сходить со сходящимся рядом .
Используем предельный признак сравнения:
Получено конечное, отличное от нуля число, значит, ряд сходится вместе с рядом .
2) Что происходит на другом конце интервала?
При – сходится.
А вот и вознаграждение за мучения в предыдущем пункте! Получился точно такой же числовой ряд, сходимость которого мы только что доказали.
Ответ: область сходимости исследуемого степенного ряда:
Чуть менее сложный пример для самостоятельного решения:
Пример 9
Найти область сходимости ряда
Достаточно для начала =)
В заключение остановлюсь на одном моменте. Во всех примерах мы использовали признак Даламбера и составляли предел . Всегда ли при решении заданий такого типа нужно применять признак Даламбера? Почти всегда. Однако в редких случаях невероятно выгодно использовать радикальный признак Коши и составлять предел , при этом техника и алгоритм решения задачи остаются точно такими же! Что это за случаи? Это те случаи, когда из общего члена степенного ряда «хорошо» (полностью) извлекается корень «энной» степени.
Следующий урок по теме – Разложение функций в степенные ряды. Примеры решений.
Желаю успехов!
Решения и ответы:
Пример 3: Решение: Найдем интервал сходимости данного ряда. Используем признак Даламбера:
Ряд сходится при
Слева нужно оставить только модуль, поэтому умножаем обе части неравенства на 7
– интервал сходимости исследуемого степенного ряда.
Исследуем сходимость ряда на концах найденного интервала.
1) При
Используем признак Лейбница.
– Ряд является знакочередующимся.
– члены ряда не убывают по модулю.
Вывод: Ряд расходится
2) При
Ряд расходится, так как не выполнен необходимый признак сходимости ряда.
Ответ: – область сходимости исследуемого степенного ряда
Пример 5: Решение: Найдем интервал сходимости данного ряда. Используем признак Даламбера:
Ответ: Ряд сходится при
Почему получилась двойка, а не ноль? Перечитайте классификацию области сходимости степенного ряда. Хотя, наверное, многие уже понимают, почему.
Пример 7: Решение: Найдем интервал сходимости данного ряда. Используем признак Даламбера:
Ряд сходится при
Слева нужно оставить только модуль, умножаем обе части неравенства на :
В середине нужно оставить только «икс», вычитаем из каждой части неравенства 3:
– интервал сходимости исследуемого степенного ряда.
Исследуем сходимость ряда на концах найденного интервала:
1) При
Степень сократилась, значит, мы на верном пути.
Используем признак Лейбница.
Ряд является знакочередующимся.
– члены ряда убывают по модулю.
Ряд сходится по признаку Лейбница.
Исследуем ряд на абсолютную сходимость:
Используем интегральный признак.
Подынтегральная функция непрерывна на .
Таким образом, ряд расходится вместе с соответствующим несобственным интегралом. Ряд сходится только условно.
2) При – расходится (по доказанному).
Ответ: Область сходимости исследуемого степенного ряда: , при ряд сходится только условно.
Область сходимости окончательно можно записать так: , или даже так: .
Примечание: Ряд можно было исследовать на сходимость с помощью предельного признака сравнения.
Пример 9: Решение: Найдем интервал сходимости данного ряда. Используем признак Даламбера:
Ряд сходится при
– интервал сходимости исследуемого степенного ряда.
Исследуем сходимость ряда на концах найденного интервала.
1) При
Сравним данный ряд с расходящимся гармоническим рядом . Используем предельный признак сравнения.
Получено конечное число, отличное от нуля, значит, полученный числовой ряд расходится вместе с гармоническим рядом.
2) При – расходится (по доказанному).
Ответ: область сходимости исследуемого степенного ряда:
Автор: Емелин Александр
megaobuchalka.ru
Числовые ряды
ВЫСШАЯ МАТЕМАТИКА
Числовые ряды
Содержание
Лекция. Числовые ряды
1. Определение числового ряда. Сходимость
2. Основные свойства числовых рядов
3. Ряды с положительными членами. Признаки сходимости
4. Знакочередующиеся ряды. Признак сходимости Лейбница
5. Знакопеременные ряды
Вопросы для самопроверки
Литература
Лекция. ЧИСЛОВЫЕ РЯДЫ
1. Определение числового ряда. Сходимость.
2. Основные свойства числовых рядов.
3. Ряды с положительными членами. Признаки сходимости.
4. Знакочередующиеся ряды. Признак сходимости Лейбница.
5. Знакопеременные ряды.
1. Определение числового ряда. Сходимость
В математических приложениях, а также при решении некоторых задач в экономике, статистике и других областях рассматриваются суммы с бесконечным числом слагаемых. Здесь мы дадим определение того, что понимается под такими суммами.
Пусть задана бесконечная числовая последовательность
, , …, , …Определение 1.1 . Числовым рядом или просто рядом называется выражение (сумма) вида
. (1.1)Числа
называются членами ряда , – общим или n – м членом ряда.Чтобы задать ряд (1.1) достаточно задать функцию натурального аргумента
вычисления -го члена ряда по его номеруПример 1.1 . Пусть
. Ряд (1.2)называется гармоническим рядом .
Пример 1.2 . Пусть
, Ряд (1.3)называется обобщенным гармоническим рядом . В частном случае при
получается гармонический ряд.Пример 1.3 . Пусть
=. Ряд (1.4)называется рядом геометрической прогрессии .
Из членов ряда (1.1) образуем числовую последовательность частичных сумм где
– сумма первых членов ряда, которая называется n —й частичной суммой , т. е. , , ,…………………………….
, (1.5)…………………………….
Числовая последовательность
при неограниченном возрастании номера может:1) иметь конечный предел;
2) не иметь конечного предела (предел не существует или равен бесконечности).
Определение 1.2 . Ряд (1.1) называется сходящимся, если последовательность его частичных сумм (1.5) имеет конечный предел, т. е.
В этом случае число
называется суммой ряда (1.1) и пишется .Определение 1.3. Ряд (1.1) называется расходящимся, если последовательность его частичных сумм не имеет конечного предела .
Расходящемуся ряду не приписывают никакой суммы.
Таким образом, задача нахождения суммы сходящегося ряда (1.1) равносильна вычислению предела последовательности его частичных сумм.
Рассмотрим несколько примеров.
Пример 1.4. Доказать, что ряд
сходится, и найти его сумму.
Найдем n — ю частичную сумму данного ряда
.Общий член
ряда представим в виде .Тогда
Отсюда имеем:
. Следовательно, данный ряд сходится и его сумма равна 1:Пример 1.5 . Исследовать на сходимость ряд
(1.6)Для этого ряда
. Следовательно, данный ряд расходится.Замечание. При
ряд (1.6) представляет собой сумму бесконечного числа нулей и является, очевидно, сходящимся.Пример 1.6. Исследовать на сходимость ряд
(1.7)Для этого ряда
В этом случае предел последовательности частичных сумм
не существует, и ряд расходится.Пример 1.7. Исследовать на сходимость ряд геометрической прогрессии (1.4):
Нетрудно показать, что n -я частичная сумма ряда геометрической прогрессии при
задается формулой .Рассмотрим случаи:
1)
Тогда и .Следовательно, ряд сходится и его сумма равна
2)
.Тогда
и .Следовательно, ряд расходится.
3)
или Тогда исходный ряд имеет вид (1.6) или (1.7) соответственно, которые расходятся. Окончательно имеем (1.8)Пример 1.8. Найти сумму ряда
Очевидно, что данный ряд является рядом геометрической прогрессии. В нашем случае
. Тогда из формулы (1.8) следует .Исследование на сходимость гармонического ряда (1.2) и обобщенного гармонического ряда (1.3) будет проведено в следующем разделе.
2. Основные свойства числовых рядов
Свойства суммы конечного числа слагаемых отличаются от свойств ряда, т. е. суммы бесконечного числа слагаемых. Так, в случае конечного числа слагаемых их можно группировать в каком угодно порядке, от этого сумма не изменится. Существуют сходящиеся ряды (условно сходящиеся, которые будут рассмотрены в разделе 5), для которых, как показал Риман* , меняя надлежащим образом порядок следования их членов, можно сделать сумму ряда равной какому угодно числу, и даже расходящийся ряд.
Пример 2.1. Рассмотрим расходящийся ряд вида (1.7)
Сгруппировав его члены попарно, получим сходящийся числовой ряд с суммой, равной нулю:
mirznanii.com

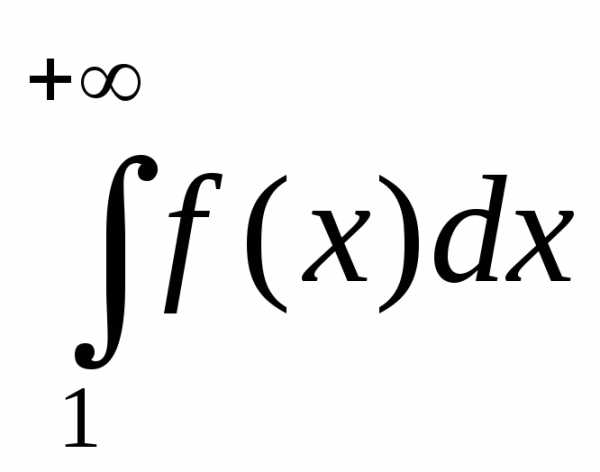 сходится, то сходится и данный ряд;
сходится, то сходится и данный ряд;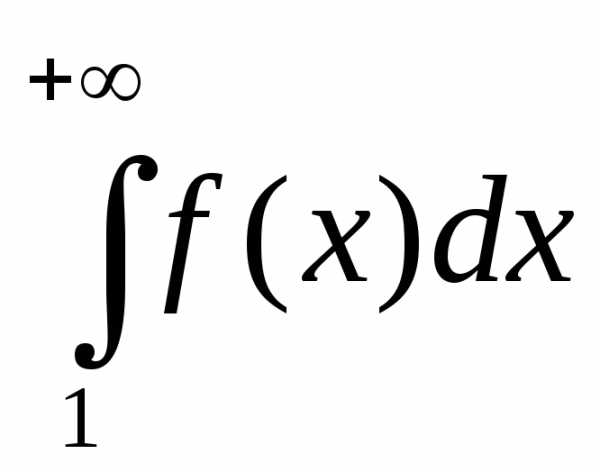 расходится, то расходится и данный ряд.
расходится, то расходится и данный ряд.