Алгоритм штрассена для умножения матриц – Divide&Conquer над алгоритмом Штрассена / Habr

Алгоритм Штрассена

стоит умножать по Штрассену. Этот существенный минус легко объяснить большим количесвом сложений и вычитаний. Но для целочисленных матриц, конечно, проблемы не возникает.

Рекурсивный алгоритм Штрассена умножает две матрицы за время (n2:81) [1], тогда как простое умножение справляется с этой задачей за (n3). Для матриц большого размера(начиная примерно с 2000) эта разница существенна.

3Умножение матриц по определению, встроенная функция matmul и оптимизация

В этом разделе пойдет речь об умножении матриц без помощи алгоритма Штрассена. Прежде чем приступать непосредственно к алгоритму, нужно выяснить, нельзя ли ускорить процесс умножения с помощью других возможностей фортрана. Также в фортране есть специальная встроенная функция matmul, которая возвращает результат умножения двух матриц. Каким образом эта функция производит умножение, неизвестно. Попробуем написать код для умножения матриц по опредлению. Пусть A и B — умножаемые матрицы, а C — их произведение.

do i = 1, N

do j = 1, N C (i , j) = 0

do k = 1, N

C(i , j) = C(i , j) + A(i , k )* B(k , j)

end do

end do

end do

Назовем такой вариант def mul. Посмотрим, как быстро умножает матрицы matmul и как медленно происходит умножение по определению. В первой строке таблицы указан размер умножаемых матриц, во второй — время, за которое умножает matmul, а втретьей — время умножения по определению. Время указано в секундах, т.о. матрицы размера 2048 умножаются в первом случае — за 13 секунд, а во втором — за 15 минут!

	size	128	256	512	1024	2048
	matmul	4.00000019E-03	2.00009998E-02	0.21601403	1.7041068	13.596855
	def mul	2.80019976E-02	0.28801799	6.7804241	98.874176	900.42432

Откуда возникает такая разница? В фортране обращение к элементам массива происходит по столбцам [4]. Т.е., к примеру, чтобы обратиться к первому элементу пятого столбца, компилятор сначала просчитает все впереди стоящие элементы по столбцам. Значит, имеет смысл попробовать переписать умножение так, чтобы индекс столбца менялся быстрее,

studfiles.net

Алгоритм Штрассена — это… Что такое Алгоритм Штрассена?

MODULE STRASSEN_MUL
 
CONTAINS
! X = A * B
! V - dimension of matrices
RECURSIVE SUBROUTINE MUL(A, B, V, C)
 
INTEGER, INTENT(IN) :: V
DOUBLE PRECISION, INTENT(IN) :: A( : , : ), B( : , : )
INTEGER :: H ! H = V/2 (see below)
DOUBLE PRECISION, INTENT(OUT) :: C(V, V)
DOUBLE PRECISION, DIMENSION(:,:), ALLOCATABLE :: P1, P2, P3, P4, P5, P6, P7
DOUBLE PRECISION, DIMENSION(:,:), ALLOCATABLE :: A11, A12, A21, A22, B11, B12, B21, B22
 
IF (V <= 64) THEN ! if dimension equals 64 use MUL2
CALL MUL2 (A, B, V, C)
RETURN
ENDIF
 
H = V/2
 
ALLOCATE (P1(H,H), P2(H,H), P3(H,H), P4(H,H), P5(H,H), P6(H,H), P7(H,H))
ALLOCATE (A11(H,H), A12(H,H), A21(H,H), A22(H,H), B11(H,H), B12(H,H), B21(H,H), B22(H,H))
 
A11 (1:H, 1:H) = A (1:H, 1:H)
A12 (1:H, 1:H) = A (1:H, H+1:V)
A21 (1:H, 1:H) = A (H+1:V, 1:H)
A22 (1:H, 1:H) = A (H+1:V, H+1:V)
 
B11 (1:H, 1:H) = B (1:H, 1:H)
B12 (1:H, 1:H) = B (1:H, H+1:V)
B21 (1:H, 1:H) = B (H+1:V, 1:H)
B22 (1:H, 1:H) = B (H+1:V, H+1:V)
 
!$OMP PARALLEL
CALL MUL(A11 + A22, B11 + B22, H, P1) ! P1 = (A11 + A22) * (B11 + B22)
CALL MUL(A21 + A22, B11, H, P2) ! etc. ...
CALL MUL(A11, B12 - B22, H, P3)
CALL MUL(A22, B21 - B11, H, P4)
CALL MUL(A11 + A12, B22, H, P5)
CALL MUL(A21 - A11, B11 + B12, H, P6)
CALL MUL(A12 - A22, B21 + B22, H, P7)
!$OMP END PARALLEL
 
DEALLOCATE (B11, B12, B21, B22)
DEALLOCATE (A11, A12, A21, A22)
 
C (1:H, 1:H) = P1 + P4 + P7 - P5
C (1:H, H+1:V) = P3 + P5
C (H+1:V, 1:H) = P2 + P4
C (H+1:V, H+1:V) = P1 - P2 + P3 + P6
 
DEALLOCATE (P1, P2, P3, P4, P5, P6, P7)
 
RETURN
END SUBROUTINE MUL
 
! X = A * B using standard method
SUBROUTINE MUL2 (A, B, V, X)
IMPLICIT NONE
INTEGER, INTENT(IN) :: V
DOUBLE PRECISION, INTENT(IN) :: A( : , : ), B( : , : )
DOUBLE PRECISION, INTENT(OUT), DIMENSION (:,:) :: X
INTEGER :: I, J, K
DO I = 1, V
DO J = 1, V
X (I, J) = 0
DO K = 1, V
X (I, J) = X (I, J) + A (I, K) * B (K, J)
ENDDO
ENDDO
ENDDO
RETURN
END SUBROUTINE MUL2
 
END MODULE STRASSEN_MUL

dic.academic.ru

Как у Штрассена появился метод умножения матриц?

Мне только что было поручено сделать это для домашней работы, и я подумал, что у меня есть аккуратное прозрение: алгоритм Штрассена жертвует «широтой» своих компонентов предварительного суммирования, чтобы использовать меньше операций в обмен на » более глубокие компоненты предварительного суммирования, которые все еще можно использовать для извлечения окончательного ответа.

(это не лучший способ сказать это, но мне трудно объяснить это). Р>

Я собираюсь использовать пример умножения двух комплексных чисел для иллюстрации баланса между « операциями и компонентами »:

Обратитевнимание,чтомыиспользуем4умножения,врезультатечего4компонентапродукта:

Обратитевнимание,что2конечныхкомпонента,которыемыхотим:действительнаяимнимаячастикомплексногочисла,насамомделеявляютсялинейнымиуравнениями:этосуммымасштабированныхпроизведений.Такимобразом,мыимеемделосдвумяоперациями:сложениеиумножение.

Деловтом,чтонаши4компонентапродуктамогутпредставлятьнаши2конечныхкомпонента,еслимыпростодобавимиливычтемнашикомпоненты:

Нонашипоследние2компонентамогутбытьпредставленыввидесуммпродуктов.Вотчтояпридумал:

Есливывидите,намнужнытолько

3отдельныхкомпонентапродукта,чтобысделатьнашипоследниедва:

Ноподожди!Каждаяиззаглавныхбукв-самапосебепродукция!Новыгодавтом,чтомызнаем,чтомыможемгенерировать(A+B+C+D)из(a+b)(c+d),чтоявляетсятолько1умножением.

Такимобразом,вконечномитогенашалгоритмоптимизировандляиспользованияменьших,но»более толстых» компонентов, где мы обмениваем количество умножений на более сложную операцию.

Частью того, что позволяет это, является свойство распределения, которое позволяет A (B + C) быть эквивалентным (AB + AC). Обратите внимание, как первое можно вычислить, используя операции 1 сложения и 1 умножения, в то время как второе требует 2 умножения и 1 суммы.

Алгоритм Штрассена является расширением оптимизации, которую мы применили к продуктам с комплексным числом, за исключением того, что есть больше целевых терминов продукта и возможно больше компонентов продукта, которые мы можем использовать для получения этих терминов. Для матрицы 2×2 алгоритм Штрассена трансформирует алгоритм, которому требуется 8 умножений, в алгоритм, которому требуется 7 умножений, и использует свойство распределения для «объединения» двух умножений в одну операцию, а вместо этого убирает из нового узла «более толстый» для извлечения одного термин продукта или другой, и т. д.

Хороший пример: чтобы получить (-1) и (2) и (5), вы можете думать об этом как о (-1), (2), (5), или вы можете думать об этом как ( 2-3), (2), (2 + 3). Вторые операции используют менее четкие числа, хотя. Суть в том, что число различных чисел эквивалентно количеству компонентов продукта, которое необходимо вычислить для умножения матриц. Мы просто оптимизируем это, чтобы найти определенное представление об основных операциях, которое использует изоморфные выходные данные, используя другое изменение через свойство распределения.

Возможно, это как-то связано с топологией? Это просто способ моего непрофессионала понять это.

Изменить . Вот фотография моих заметок, которые я нарисовал в процессе объяснения комплексного числа:

    

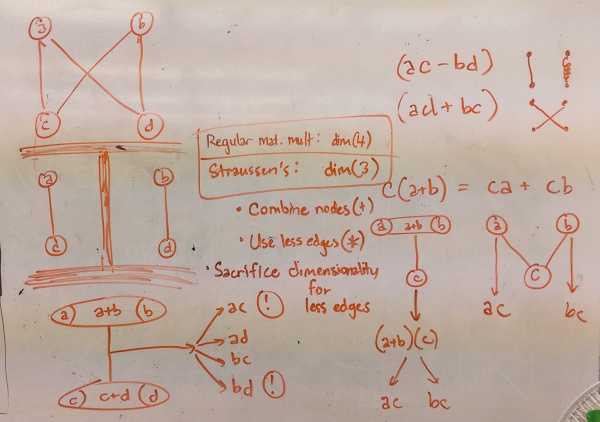
ubuntugeeks.com

Умножение двух матриц

Национальный Исследовательский Университет

МОСКОВСКИЙ ЭНЕРГЕТИЧЕСКИЙ ИНСТИТУТ

Институт автоматики и вычислительной техники

Кафедра прикладной математики

Лабораторная работа № 1

методом статического разделения на полосы

Курс «Параллельные системы и параллельные вычисления»

Выполнил

студент 5 курса группы А-13-08

Захаров Антон

Преподаватель

Панков Николай Александрович

Постановка задачи

Пусть даны две прямоугольные матрицы иразмерностиисоответственно:

Требуется найти матрицу (произведением) размерности:

Для нахождения произведения матриц методом статического разделения на полосы необходимо составить последовательно-параллельную программу на языке C/C++ с применением интерфейса передачи сообщений (MPI,MessagePassingInterface), а также исследовать характеристики разработанной программы в зависимости от числа исполнителей.

Последовательный алгоритм решения

Умножение матриц по определению

В соответствии с определением, произведение матриц состоит из всех возможных комбинаций скалярных произведений строк матрицыи столбцов матрицы. Элемент матрицыс индексами (i, j) есть скалярное произведение i-ой строки матрицыи j-го столбца матрицы.

1. for (i = 0; i < m; i++) {

2. for (j = 0; j < q; j++) {

3. C[i][j] = 0;

4. for (k = 0; k < n; k++)

5. C[i][j] += A[i][k] * B[k][j];

6. }

7. }

На первый взгляд это минимальный объем работы, необходимый для перемножения двух матриц. Однако исследователям не удалось доказать минимальность, и в результате они обнаружили другие алгоритмы, умножающие матрицы более эффективно.

Алгоритм Штрассена

Первый алгоритм быстрого умножения матриц был разработан В. Штрассеном в 1969. В основе алгоритма лежит рекурсивное разбиение матриц на блоки. Недостатком данного метода является большая сложность программирования по сравнению со стандартным алгоритмом, численная неустойчивость и большой объём используемой памяти.

Разработано большое количество алгоритмов на основе метода Штрассена, которые улучшают его численную устойчивость и уменьшают объём используемой памяти.

Алгоритм Копперсмита-Винограда

В 1990 Копперсмит и Виноград опубликовали алгоритм, умножающий матрицы со сложностью . Этот алгоритм использует идеи, схожие с алгоритмом Штрассена. На сегодняшний день алгоритм Копперсмита-Винограда является наиболее асимптотически быстрым, но он эффективен только на очень больших матрицах и поэтому не применяется.

В 2003 Кох и др. рассмотрели в своих работах алгоритмы Штрассена и Копперсмита-Винограда в контексте теории групп. Они показали возможность существования алгоритмов умножения матриц со сложностью .

Параллельный алгоритм решения

В предлагаемой реализации метода статического разделения на полосы исходные матрицы разбиваются на горизонтальные полосы. Получаемые полосы распределяются по процессорам: все полосы одной матрицы, например , распределяются между процессорами, а полосы другой – по мере необходимости передаются на все процессоры. При этом на каждом из имеющегося набора процессоров в каждый конкретный момент времени располагается только по одной полосе матрици. Перемножение полос (а данная операция может быть выполнена процессорами параллельно) приводит к получению частей (полос) результирующей матрицы, которые затем в совокупности и дадут искомую матрицу.

– полоса матрицы;

– полоса матрицы;

– число процессоров.

studfiles.net

2.4.2. Быстрое умножение матриц

Оценим трудоемкость обычного умножения двух матриц n×n. Трудоемкость будет иметь порядок n³, т.к. в матрице-результате перемножения будет n×n = n² элементов и каждый из них вычисляется за n операций попарного умножения и сложения.

Попробуем применить ту же идею, что и быстрого умножения чисел, при перемножении двух матриц n×n. Разделим каждую из них на 4 матрицы вдвое меньшего размера:

Итак, при применении обычных формул блочного произведения матриц получаем рекуррентную формулу:

трудоемкость перемножения матриц вдвое меньшего размера.

трудоемкость сложений.

Соответственно по Теореме 2.2 получаем T(n) = , то есть трудоемкость такая же, как и при обычном умножении.

Однако существуют формулы Штрассена для блочного умножения матриц. В этих формулах будет не 8, а 7 попарных умножений матриц размера .

Формула Штрассена:

M₁ = (A₂ – A₄)(B₃ + B₄)

M₂ = (A₁ + A₄)(B₁ + B₄)

M₃ = (A₁ – A₃)(B₁ + B₂)

M₄ = (A₁ + A₂)B₄

M₅ = A₁(B₂ – B₄)

(2.11)

M₆ = A₄ (B₃ – B₁)

M₇ = (A₃ + A₄)B₁

C₁ = M₁ +M₂ – M₄ + M₆

C₂ = M₄ + M₅

C₃ = M₆ +M₇

C₄ = M₂ – M₃ + M₅ – M₇

7 умножений и 18 сложений и вычитаний в этих формулах.

Следовательно, по Теореме 2.2 получаем

2.4.3. Очень быстрое умножение числе (алгоритм Шенхаге – Штрассена)

Как уже было замечено, умножение многоразрядных чисел есть сверка двух массивов с переносом в старшие разряды. Если делать свертку с применением БПФ, то трудоемкость подобного алгоритма T(n) = n logn. Однако в таком случае на вход свертки подаются целочисленные массивы, а на выходе получается массив вещественных чисел, которые нужно округлить до ближайшего целого.

Замечание. При большой погрешности вычислений существует опасность округлить не в ту сторону. Следовательно, для уменьшения вероятности ошибки нужно увеличивать разрядность вычислений.

Тогда трудоемкость алгоритма составит:

T(n) = nlog₂n · log₂(log₂n).

т.к. мы увеличиваем разрядность чисел, с которыми работаем

трудоемкость быстрого перемножения

Домашнее задание №3. Найти произведение 3871 и 9211 по формуле быстрого умножения чисел.

Домашнее задание №4. Найти произведение 8329 и 5631 по формуле быстрого умножения чисел.

3. Задачи на графах

3.1. Справочный материал

Кратко напомним определения, известные из курса дискретной математики.

Определения. Граф – пара G(V,E), где V = {V₁,V₂, …,V_n} – множество вершин графа G, E – множество ребёр (дуг) графа: Е={ (V_1i, V_2i) }.

Рёбра можно задавать разными способами, например матрицей инцидентности или списком ребёр.

Неориентированный граф – граф, удовлетворяющий условию, что если (a, b) E, то и (b, a) E, т.е. порядок расположения концов дуг графа не существенен.

Матрица инцидентности такого графа симметрична.

Взвешенный граф – граф, каждой дуге которого приписан её вес.

Цикл в графе – маршрут, заданный последовательностью вершин, каждая вершина посещается по одному разу, и начальная вершина совпадает с конечной.

Граф без цикла – куст.

Связный граф – граф, из любой вершины которого можно дойти до любой другой.

Связный куст – дерево.

Компонента связности – совокупность вершин, для каждой из которых существует пусть в любую другую вершину этой совокупности.

studfiles.net

2.4.2. Быстрое умножение матриц

Оценим трудоемкость обычного умножения двух матриц n×n. Трудоемкость будет иметь порядок n³, т.к. в матрице-результате перемножения будет n×n = n² элементов и каждый из них вычисляется за n операций попарного умножения и сложения.

Попробуем применить ту же идею, что и быстрого умножения чисел, при перемножении двух матриц n×n. Разделим каждую из них на 4 матрицы вдвое меньшего размера:

Итак, при применении обычных формул блочного произведения матриц получаем рекуррентную формулу:

трудоемкость перемножения матриц вдвое меньшего размера.

трудоемкость сложений.

Соответственно по Теореме 2.2 получаем T(n) = , то есть трудоемкость такая же, как и при обычном умножении.

Однако существуют формулы Штрассена для блочного умножения матриц. В этих формулах будет не 8, а 7 попарных умножений матриц размера .

Формула Штрассена:

M₁ = (A₂ – A₄)(B₃ + B₄)

M₂ = (A₁ + A₄)(B₁ + B₄)

M₃ = (A₁ – A₃)(B₁ + B₂)

M₄ = (A₁ + A₂)B₄

M₅ = A₁(B₂ – B₄)

(2.11)

M₆ = A₄ (B₃ – B₁)

M₇ = (A₃ + A₄)B₁

C₁ = M₁ +M₂ – M₄ + M₆

C₂ = M₄ + M₅

C₃ = M₆ +M₇

C₄ = M₂ – M₃ + M₅ – M₇

7 умножений и 18 сложений и вычитаний в этих формулах.

Следовательно, по Теореме 2.2 получаем

2.4.3. Очень быстрое умножение числе (алгоритм Шенхаге – Штрассена)

Как уже было замечено, умножение многоразрядных чисел есть сверка двух массивов с переносом в старшие разряды. Если делать свертку с применением БПФ, то трудоемкость подобного алгоритма T(n) = n logn. Однако в таком случае на вход свертки подаются целочисленные массивы, а на выходе получается массив вещественных чисел, которые нужно округлить до ближайшего целого.

Замечание. При большой погрешности вычислений существует опасность округлить не в ту сторону. Следовательно, для уменьшения вероятности ошибки нужно увеличивать разрядность вычислений.

Тогда трудоемкость алгоритма составит:

T(n) = nlog₂n · log₂(log₂n).

т.к. мы увеличиваем разрядность чисел, с которыми работаем

трудоемкость быстрого перемножения

Домашнее задание №3. Найти произведение 3871 и 9211 по формуле быстрого умножения чисел.

Домашнее задание №4. Найти произведение 8329 и 5631 по формуле быстрого умножения чисел.

3. Задачи на графах

3.1. Справочный материал

Кратко напомним определения, известные из курса дискретной математики.

Определения. Граф – пара G(V,E), где V = {V₁,V₂, …,V_n} – множество вершин графа G, E – множество ребёр (дуг) графа: Е={ (V_1i, V_2i) }.

Рёбра можно задавать разными способами, например матрицей инцидентности или списком ребёр.

Неориентированный граф – граф, удовлетворяющий условию, что если (a, b) E, то и (b, a) E, т.е. порядок расположения концов дуг графа не существенен.

Матрица инцидентности такого графа симметрична.

Взвешенный граф – граф, каждой дуге которого приписан её вес.

Цикл в графе – маршрут, заданный последовательностью вершин, каждая вершина посещается по одному разу, и начальная вершина совпадает с конечной.

Граф без цикла – куст.

Связный граф – граф, из любой вершины которого можно дойти до любой другой.

Связный куст – дерево.

Компонента связности – совокупность вершин, для каждой из которых существует пусть в любую другую вершину этой совокупности.

studfiles.net

Алгоритм Штрассена — WiKi

Приведён пример реализации алгоритма Штрассена на Фортране. Предполагается, что все матрицы квадратные, их размер является степенью 2.

MODULE STRASSEN_MUL

CONTAINS
! X = A * B
! V - dimension of matrices
RECURSIVE SUBROUTINE MUL(A, B, V, C)

INTEGER, INTENT(IN) :: V
DOUBLE PRECISION, INTENT(IN) :: A( : , : ), B( : , : )
INTEGER :: H ! H = V/2 (see below)
DOUBLE PRECISION, INTENT(OUT) :: C(V, V)
DOUBLE PRECISION, DIMENSION(:,:), ALLOCATABLE :: P1, P2, P3, P4, P5, P6, P7
DOUBLE PRECISION, DIMENSION(:,:), ALLOCATABLE :: A11, A12, A21, A22, B11, B12, B21, B22

IF (V <= 64) THEN ! if dimension equals 64 use MUL2
CALL MUL2 (A, B, V, C)
RETURN
ENDIF

H = V/2

ALLOCATE (P1(H,H), P2(H,H), P3(H,H), P4(H,H), P5(H,H), P6(H,H), P7(H,H))
ALLOCATE (A11(H,H), A12(H,H), A21(H,H), A22(H,H), B11(H,H), B12(H,H), B21(H,H), B22(H,H))

A11 (1:H, 1:H) = A (1:H, 1:H)
A12 (1:H, 1:H) = A (1:H, H+1:V)
A21 (1:H, 1:H) = A (H+1:V, 1:H)
A22 (1:H, 1:H) = A (H+1:V, H+1:V)

B11 (1:H, 1:H) = B (1:H, 1:H)
B12 (1:H, 1:H) = B (1:H, H+1:V)
B21 (1:H, 1:H) = B (H+1:V, 1:H)
B22 (1:H, 1:H) = B (H+1:V, H+1:V)

!$OMP PARALLEL
CALL MUL(A11 + A22, B11 + B22, H, P1) ! P1 = (A11 + A22) * (B11 + B22)
CALL MUL(A21 + A22, B11, H, P2) ! etc. ...
CALL MUL(A11, B12 - B22, H, P3)
CALL MUL(A22, B21 - B11, H, P4)
CALL MUL(A11 + A12, B22, H, P5)
CALL MUL(A21 - A11, B11 + B12, H, P6)
CALL MUL(A12 - A22, B21 + B22, H, P7)
!$OMP END PARALLEL

DEALLOCATE (B11, B12, B21, B22)
DEALLOCATE (A11, A12, A21, A22)

C (1:H, 1:H) = P1 + P4 + P7 - P5
C (1:H, H+1:V) = P3 + P5
C (H+1:V, 1:H) = P2 + P4
C (H+1:V, H+1:V) = P1 - P2 + P3 + P6

DEALLOCATE (P1, P2, P3, P4, P5, P6, P7)

RETURN
END SUBROUTINE MUL

! X = A * B using standard method
SUBROUTINE MUL2 (A, B, V, X)
IMPLICIT NONE
INTEGER, INTENT(IN) :: V
DOUBLE PRECISION, INTENT(IN) :: A( : , : ), B( : , : )
DOUBLE PRECISION, INTENT(OUT), DIMENSION (:,:) :: X
INTEGER :: I, J, K
DO I = 1, V
DO J = 1, V
X (I, J) = 0
DO K = 1, V
X (I, J) = X (I, J) + A (I, K) * B (K, J)
ENDDO
ENDDO
ENDDO
RETURN
END SUBROUTINE MUL2

END MODULE STRASSEN_MUL

Вычисления промежуточных матриц P1 — P7 можно проводить параллельно при использовании таких библиотек как OpenMP или MPI, что позволяет значительно повысить скорость работы алгоритма на многопроцессорных машинах.

ru-wiki.org