Упростите выражение дроби – Преобразование выражений. Подробная теория.

С1 ГИА по математике — упрощение выражений. Сокращение дробей

В этой статье рассмотрим упрощение выражений, а также и сокращение дробей, числители и знаменатели которых состоят из буквенных выражений. Как правило, в таких выражениях нужно поискать формулы сокращенного умножения – они сильно облегчают жизнь. Тем не менее, встречаются и такие задания, где подстановка значения неизвестной без предварительного упрощения делает решение даже проще. Рассмотрим несколько примеров.

1. Найдите значение выражения при :

Имеем сумму дробей, и очевидно, что необходимо все привести к общему знаменателю, который равен :

Можем произвести подстановку:

Ответ: 18

2. Найдите значение выражения при  :

В знаменателе второй дроби – разность квадратов, а в знаменателе первой можно вынести за скобки общий множитель:

Приводим к общему знаменателю:

Теперь пришло время сделать подстановку:

Ответ: 0,4

3. Найдите значение выражения при  :

Здесь как раз тот случай, когда вычислительные затраты меньше при непосредственной подстановке без предварительного упрощения выражения:

Ответ: -0,2

4. Найдите значение выражения при  :

Упростим выражение:

Сделаем подстановку:

Ответ: -1,4

5. Сократите дробь:

В числителе присутствуют как разность квадратов, так и квадрат разности. В знаменателе – разность кубов и разность квадратов. Разложим на “простые кирпичики” каждую из “сборок”:

6. Выполните умножение:

Приведем к общему знаменателю (uv) выражение в первой скобке:

7. Найдите значение выражения:

при

Приведем к общему знаменателю каждую из скобок:

Сделаем подстановку:

Ответ: -4

easy-physic.ru

Что значит «упростите выражение»(алгебраические дроби)? Как это сделать???? и что нужно делать, я не понимаю помогите!!

Это значит, сделать его более простым: сократить, прибавить, умножить, вычесть и т. д.

Упростить выражение — сократить до минимума выражение, сделать его проще, для этого существуют разные там формулы сокращенного умножения, различные распределительные, сочетательные свойства и т. д.

Упростить выражение, -это убрать лишнее, для этого нужно что то сократить. (одинаковые члены). Было бы лучше если бы саму дробь кинула… Но если там квадратные уравнения в числители и в знаменатели, то реши их и разложи по формуле К (х-х1)(х-х2),скорее всего после этого все должно сократиться…

Упростить выражение это значит, раскрыть скобки если это возможно, Зделать все возможные действия с выражением, короче говоря что бы из большого выражения получилось маленькое при этом можно пользоваться различными формулами!

touch.otvet.mail.ru

Упрощение дроби | Математика

§ 15. Упрощение дроби, числитель и знаменатель
которой являются алгебраическими суммами дробей

Глава V. ПРЕОБРАЗОВАНИЕ ДРОБНЫХ АЛГЕБРАИЧЕСКИХ ВЫРАЖЕНИЙ.

На главную страницу Алгебра. Д.К. Фаддев, И.С. Соминский.

Скачать оригинал Алгебра. Д.К. Фадеев, И.С. Соминский на странице Сборники Математики.
Ниже можете посмотреть тексты для быстрого ознакомления (формулы отображаются не корректно).

Похожие статьи: Алгебра в школе. ВЕКТОРЫ. Библиотека учителя. Школьная математика.

Д. К. ФАДДЕЕВ и И. С. СОМИНСКИЙ
АЛГЕБРА

Упрощение дроби

Для упрощения дроби, числитель и знаменатель которой
являются алгебраическими суммами дробей, следует умножить
числитель и знаменатель на общее кратное знаменателей всех
дробей, находящихся в числителе и знаменателе.

ЧП в семье Порошенко — сын попал в ДТП

§ 16. Общие выводы

В § 12—14 мы убедились в том, что сумму, разность, произведение
и частное двух алгебраических дробей можно снова представить
в виде алгебраической дроби или, в отдельных частных случаях,
в виде многочлена. Отсюда следует, что любое дробное алгебраическое

выражение может быть преобразовано к виду алгебраической
дроби (или многочлена). Действительно, всякое дробное алгебраическое
выражение есть запись результата действий сложения, вычитания,
умножения и деления над числами и буквами. В результате первых
по порядку действий сложения, вычитания и умножения мы придем
к многочленам. В результате первого деления мы получим алгебраическую
дробь. Результаты дальнейших действий над алгебраическими
дробями будут представлять собой алгебраические дроби, и окончательный
результат также будет алгебраической дробью. При этом
возможно, что многочлен, находящийся в числителе дроби, поделится
на многочлен, находящийся в знаменателе, и тогда окончательный
результат преобразуется к виду многочлена

133 Алгебра Упрощение дроби, ПРЕОБРАЗОВАНИЕ ДРОБНЫХ АЛГЕБРАИЧЕСКИХ ВЫРАЖЕНИЙ

Как уже говорилось в гл. III, цепочка тождественных преобразований
алгебраического выражения называется алгебраической выкладкой*.

В результате изложенного в гд. Ill, IV, V мы видим, что алгебраическая
выкладка может вестись в различных направлениях. При
преобразовании целых алгебраических выражений** можно раскрывать
скобки, можно, наоборот, производить вынесение за скобку, при
выполнении Сложения многочлена и дроби можно сумму представить
в виде одной дроби, а иногда бывает полезно выделение из данной
дро^и целой части, что приводит к разложению данной дроби на
сумму многочлена и дроби и т, д.
Само собой разумеется, что алгебраическая выкладка должна? проводиться
верно. Но этого недостаточно для полного овладения искусством
алгебраической выкладки. Приведем: один очень грубый пример:
(a — f b f = а* + 2 ab + й* = (а + Ь)\
Выкладка проведена верно, но бессмысленность ее бросается в глаза,
Зачем было производить какие-то преобразования, чтобы вернуться
к исходному выражению?
Алгебраическая выкладка всегда должна быть направлена к определенной
цели. В упражнениях цель бывает обычно указана в условии,
например «разложить на множители», «сложить дроби» и т, д.
Часто целью является упрощение данного алгебраического выражения.
Но в применениях алгебры к решению практических задач нужно
уметь найти цель в проведении выкладки.
П р и м е р. При решении некоторой задачи в общем виде ответ
получен в виде формулы .у = а* 4- Ь* . -Требуется вычислить х с точностью
до ОД при а=?51, 62, 53, 54, 55 и при £ = 3, 4, 5.
Решение . Здесь целесообразно сделать следующее преобразование:
а* — Ь* + 2Ь* . . . 2Ь*
По внешнему виду мы даже несколько усложнили ответ, но считать
после преобразования становится много легче, так как мы
избавились от необходимости возводить большое число а ^ квадрат,
а затем делить большое число на й — Ь. Например, при
а = 51, Ь = 3 по исходной формуле

134 Алгебра Упрощение дроби, ПРЕОБРАЗОВАНИЕ ДРОБНЫХ АЛГЕБРАИЧЕСКИХ ВЫРАЖЕНИЙ

Упрощение дроби

matematika.advandcash.biz

упростить алгебраическое выражение

Записи с меткой «упростить алгебраическое выражение»

1. Чтобы упростить данное выражение, разложим на множители числители и знаменатели данных дробей.

 2. Вынесем у за скобки, а выражение в скобках разложим на множители по формуле разности квадратов двух выражений.

 3. Проволоку длиной 135 м разрезали на две части так, что одна из частей в 2 раза длиннее другой. Требуется найти длину каждой части. Решаем. Обозначим меньшую часть через х. Тогда другая часть будет равна 2х. Зная, что сумма этих двух частей равна 135 м, составим уравнение: х+2х=135. Отсюда 3х=135, а х=135:3=45 (м) — длина меньшей части. Другая часть составит 45·2=90 (м).

4.  Дробь отрицательна, если ее числитель и знаменатель имеют разные знаки. Так как знаменатель данной дроби 3x²+1>0 при любом действительном значении х, то числитель должен быть меньше нуля.

x²-5x+4<0. По теореме Виета найдем корни квадратного трехчлена x₁=1 и x₂=4 и разложим его на множители. Получаем: (x-1)(x-4)<0. Методом интервалов находим решение неравенства:  1<x<4. Ответ: (1; 4).

5. Упростить выражение: sin(90°-α)-cos(180°-α)+tg(180°-α)-ctg(270°+α). Применяем правило для формул приведения: 1) перед приведенной функцией ставят знак приводимой; 2) если в записи аргумента π/2 взято нечетное число раз, то функцию меняют на кофункцию. Решаем. sin(90°-α)-cos(180°-α)+tg(180°-α)-ctg(270°+α)=cosα+cosα-tgα+tgα=2cosα.

6. Применим формулу для решения простейшего уравнения sint=a:

t=(-1)ⁿ∙arcsina+πn, nєZ.  

7. Известен четвертый член геометрической прогрессии  c₄=24  и знаменатель геометрической прогрессии  q=-2. Требуется найти первый член этой геометрической прогрессии. Решаем. Применим формулу общего члена геометрической прогрессии: c_n=c₁∙q^n-1. У нас: c₄=c₁∙q³. подставляем свои данные: 24=c₁∙(-2)³; 24=c₁∙(-8) → c₁=-3.

8. Так как график данной линейной функции проходит через точку (-2; -3), то координаты этой точки удовлетворяют данному равенству: подставляем х=-2, у=-3 и находим b=-6.

9. Углы треугольника относятся, как 1:1:2. Такое возможно только в прямоугольном треугольнике (45°, 45° и 90°). Здесь частный случай треугольника. В общем случае нужно обозначить одну часть через х, выразить через х все углы, и, зная, что сумма внутренних углов треугольника равна 180°, составить уравнение. В нашем примере можно было записать:

х+х+2х=180°. Отсюда 4х=180°, х=45°. Углы: 45°, 45° и 90°.

10. Дано уравнение с модулем: x²-6x+|x-4|+8=0. Решаем. Нужно освободиться от знака модуля. Возможны 2 случая:

1) Если х≤4, то x²-6x-x+4+8=0 → x²-7x+12=0  → x₁=3  и x₂=4. Оба значения подходят, так как удовлетворяют условию 1): х≤4

2) Если х>4, то x²-6x+x-4+8=0 → x²-5x+4=0  → x₁=1 и x₂=4. Значение х=4 мы уже взяли, а х=1 не подходит, так как не удовлетворяет условию 2): х>4. Ответ: 3 и 4. 

11. Подставляем предложенные пары чисел вместо х и у в каждое уравнение системы. Начинаем с ответа В), так как под знаком логарифма не должно быть отрицательных чисел. Проверяем пару чисел (2; 5):

2+5=7 и lg2+lg5=lg(2·5)=lg10=1. Пара (5; 2) также подходит.

12. Решаем логарифмическое уравнение:

13. Решаем иррациональное уравнение:

14. Чтобы найти функцию, обратную данной функции y=x²,  где х≥0, нужно выразить х через у, а затем, в полученном равенстве вместо х написать у, а вместо у написать х.

15. Дана функция: y=sin3x cos5x-cos3x sin5x. Преобразуем правую часть по формуле синуса разности двух углов:

sin(α-β)=sinα cosβ-cosα sinβ. Получаем у=sin(3x-5x)=sin(-2x)=-sin2x. Найдем производную y’(x)=(-sin2x)’=-2cos2x.

16. Катеты прямоугольного треугольника относятся как 3:4. Периметр треугольника равен 24 см. Найдите радиус описанной окружности.

Смотрите видео: решение задачи 16.

17. Радиус шара равен 8 см, через его середину в шаре проведено сечение. Найдите разность площадей большего и отсеченного кругов. Решаем. Находим площадь большого круга:  S=πR²=π∙8²=64π см². Радиус r отсеченного круга – катет в прямоугольном треугольнике с гипотенузой 8 см (радиус шара) и вторым катетом 4 см (половина радиуса шара). По теореме Пифагора r²=8²-4²=64-16=48 см². Тогда площадь отсеченного круга s=πr²=48π см². Тогда искомая разность площадей большого и отсеченного кругов равна 64π-48π=16π (см²).

Смотрите видео: решение задачи 17.

18. Задача на призму.

19. Определить точки пересечения двух окружностей, если уравнение одной из них x²+y²=9, а центр другой, с радиусом, равным 5 см, находится в точке (4; 0). Решаем. Уравнение окружности с центром в точке (a; b) и радиусом R имеет вид: (x-a)²+(y-b)²=R². Запишем уравнение второй окружности по этой формуле: (х-4)²+(у-0)²=5². Упростим: (х-4)²+у²=25. Так как окружности пересекаются, то нужно решить систему уравнений: x²+y²=9 и (х-4)²+у²=25. Вычтем первое уравнение из второго: (х-4)²-х²=25-9. Раскроем скобки и приведем подобные слагаемые: х²-8х+16-х²=16, отсюда -8х=0, тогда х=0. Подставим значение х=0 в любое уравнение системы, например, в первое: x²+y²=9. Получаем: y²=9. Отсюда у=±3. Координаты точек пересечения: (0; -3) и (0; 3).

20. Освободимся от иррациональности в знаменателе, умножив числитель и знаменатель дроби на выражение, сопряженное  знаменателю. Упростим полученное выражение и опять умножим числитель и знаменатель дроби на выражение, сопряженное знаменателю.

Дважды примененная при этом формула разности квадратов двух выражений (a-b)(a+b)=a²-b² позволяет освободиться от знака радикала в знаменателе дроби.

21. Найти значение выражения:

22. Решаем каждое неравенство системы. 1) заменим логарифм числа х по основанию 2 через у. Получаем неравенство:

y²-3y+2≤0. Корни трехчлена  y₁=1, y₂=2. Неравенство можно записать в виде: (y-1)(y-2)≤0. Решение можно найти методом интервалов:  yє[1; 2]. Возвращаемся к переменной х.

23. Решаем тригонометрическое неравенство. Представим числитель дроби в виде разности синусов, а знаменатель дроби в виде суммы синусов. Представим числитель и знаменатель дроби в виде произведения по формулам преобразования разности и суммы синусов в произведение. Упрощаем полученную дробь и получаем простейшее неравенство с тангенсом.

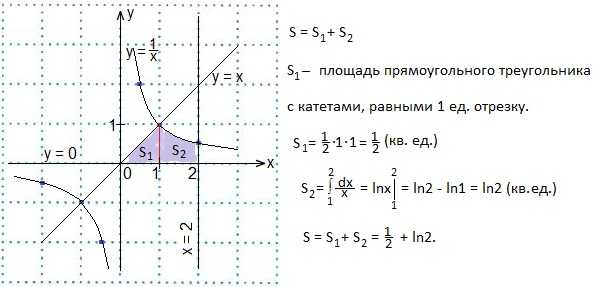
24. Начертим фигуру, ограниченную данными линиями.

25. Иными словами, вас спрашивают, какие из данных чисел 30, 33 и 36 являются составными. Конечно, 30 и 36. Составным называют число, имеющее более двух делителей. Простое число имеет только два делителя: единицу и само это число.

test-training.ru