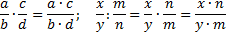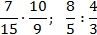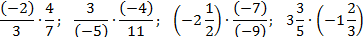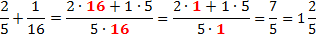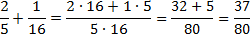Примеры с дробями на сложение вычитание деление умножение 5 класс: «Сложение и вычитание, деление и умножение обыкновенных дробей» (стр. 1 из 2)

«Сложение и вычитание, деление и умножение обыкновенных дробей» (стр. 1 из 2)

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ КАЗАХСТАН

КОСТАНАЙСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ ИНСТИТУТ

Реферат

На тему: «Сложение и вычитание, деление и умножение обыкновенных дробей».

Костанай

2011 год

СОДЕРЖАНИЕ

1. Из истории обыкновенных дробей ………………………………………..3

2. Действия с обыкновенными дробями …………..…………………………..5

2.1. Сложение и вычитание обыкновенных дробей …………………………..5

2.2. Умножение и деление обыкновенных дробей ………………………….7

3. Примеры на сложение, вычитание, умножение и деление дробей ……. 10

4. Список литературы ……………………………………………………………11

1. Из истории возникновения обыкновенных дробей.

Дроби появились в глубокой древности. При разделе добычи, при измерениях величин, да и в других похожих случаях люди встретились с необходимостью ввести дроби.

Древние египтяне уже знали, как поделить 2 предмета на троих, для этого числа –2/3- у них был специальный значок. Между прочим, это была единственная дробь в обиходе египетских писцов, у которой в числителе не стояла единица – все остальные дроби непременно имели в числителе единицу (так называемые основные дроби): 1/2; 1/3; 1/28; … . Если египтянину нужно было использовать другие дроби, он представлял их в виде суммы основных дробей. Например, вместо 8/15 писали 1/3+1/5. Иногда это бывало удобно. В папирусе Ахмеса есть задача :

«Разделить 7 хлебов между 8 людьми». Если резать каждый хлеб на 8 частей, придётся провести 49 разрезов.

А по-египетски эта задача решалась так: Дробь 7/8 записывали в виде долей: 1/2+1/4+1/8. Значит каждому человеку надо дать полхлеба, четверть хлеба и восьмушку хлеба; поэтому четыре хлеба разрезали пополам, два хлеба- на 4 части и один хлеб на 8 долей, после чего каждому дали его часть.

Но складывать такие дроби было неудобно. Ведь в оба слагаемых могут входить одинаковые доли, и тогда при сложении появится дробь вида 2/n. А таких дробей египтяне не допускали. Поэтому, папирус Ахмеса начинается с таблицы, в которой все дроби такого вида от 2/5 до 2/99 записаны в виде суммы долей. С помощью этой таблицы выполняли и деление чисел. Вот, например, как 5 делили на 21: 5/21

Умели египтяне также умножать и делить дроби. Но для умножения приходилось умножать доли на доли, а потом, быть может, снова использовать таблицу. Ещё сложнее обстояло с делением.

В древнем Вавилоне предпочитали наоборот, — постоянный знаменатель, равный 60-ти. Шестидесятеричными дробями, унаследованными от Вавилона, пользовались греческие и арабские математики и астрономы. Но было неудобно работать над натуральными числами, записанными по десятичной системе, и дробями, записанными по шестидесятеричной. А работать с обыкновенными дробями было уже совсем трудно. Поэтому голландский математик Симон Стевин предложил перейти к десятичным дробям.

Интересная система дробей была в Древнем Риме. Она основывалась на делении на 12 долей единицы веса, которая называлась асс. Двенадцатую долю асса называли унцией. А путь, время и другие величины сравнивали с наглядной вещью- весом. Например, римлянин мог сказать, что он прошел семь унций пути или прочел пять унций книги. При этом, конечно, речь шла не о взвешивании пути или книги. Имелось в виду, что пройдено 7/12 пути или прочтено 5/12 книги. А для дробей, получающихся сокращением дробей со знаменателем 12 или раздроблением двенадцатых долей на более мелкие, были особые названия.

Даже сейчас иногда говорят:”Он скрупулёзно изучил этот вопрос.” Это значит, что вопрос изучендо конца, что не одной самой малой неясности не осталось. А происходит странное слово “скрупулёзно” от римского названия 1/288 асса — “скрупулус”. В ходу были и такие названия: ”семис”- половина асса, “секстанс”- шестая его доля, “семиунция”- половина унции, т.е. 1/24 асса и т.д. Всего применялось 18 различных названий дробей. Чтобы работать с дробями, надо было помнить для этих дробей таблицу сложения и таблицу умножения. Поэтому римские купцы твёрдо знали, что при сложении триенса (1/3 асса) и секстанса получается семис, а при умножении беса (2/3 асса) на сескунцию( 2/3 унции, т.е.1/8 асса) получается унция. Для облегчения работы составлялись специальные таблицы, некоторые из которых дошли до нас.

Современную систему записи дробей с числителем и знаменателем создали в Индии. Только там писали знаменатель сверху, а числитель — снизу, и не писали дробной черты. А записывать дроби в точности, как сейчас, стали арабы.

Обыкновенная дробь – это число вида

, где m и n – натуральные числа, например . Число m называется числителем дроби, n – знаменателем. Среди обыкновенных дробей различают правильные и неправильные дроби. Дробь называется правильной, если ее числитель меньше знаменателя, и неправильной, если ее числитель больше знаменателя или равен ему.

2. Действия с обыкновенными дробями.

2.1. Сложение и вычитание обыкновенных дробей.

Сложение обыкновенных дробей выполняется так:

а) если знаменатели дробей одинаковы, то к числителю первой дроби прибавляют числитель второй дроби и оставляют тот же знаменатель, т.е.

;

б) если знаменатели дробей различны, то дроби сначала приводят к общему знаменателю, предпочтительнее к наименьшему, а затем к числителю первой дроби прибавляют числитель второй дроби, т.е.

Вычитание обыкновенных дробей выполняют следующим образом:

а) если знаменатели дробей одинаковы, то от числителя первой дроби вычитают числитель второй дроби и оставляют тот же знаменатель, т.е.

б) если знаменатели различны, то сначала дроби приводят к общему знаменателю, а затем от числителя первой дроби вычитают числитель второй дроби, т.е.

Сложение и вычитание дробей. Если знаменатели дробей одинаковы, то для того, чтобы сложить дроби, надо сложить их числители, а для того, чтобы вычесть дроби, надо вычесть их числители (в том же порядке). Полученная сумма или разность будет числителем результата; знаменатель останется тем же.

Например:

Если знаменатели дробей различны, необходимо сначала привести дроби к общему знаменателю. При сложении смешанных чисел их целые и дробные части складываются отдельно. При вычитании смешанных чисел мы рекомендуем сначала преобразовать их к виду неправильных дробей, затем вычесть из одной другую, а после этого вновь привести результат, если требуется, к виду смешанного числа.

Например:

2.2. Умножение и деление обыкновенных дробей.

Умножение обыкновенных дробей выполняется следующим образом:

т.е. перемножаются отдельно числители, отдельно знаменатели, первое произведение делают числителем, второе – знаменателем.

При умножении дроби на натуральное число, числитель дроби умножают на это число, а знаменатель оставляют без изменения.

Если множители являются смешанными числами, то сначала их нужно записать в виде неправильных дробей, затем воспользоваться правилом умножения дробей.

Деление обыкновенных дробей выполняют следующим образом:

т.е. делимое

умножают на дробь , обратную делителю .

Умножение обыкновенной дроби на целое число.

Чтобы умножить дробь на целое число, достаточно числитель дроби умножить на это число, оставив прежний знаменатель.

5.4.7. Примеры на сложение и вычитание обыкновенных дробей — математика-повторение

I. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тот же.

Примеры.

157

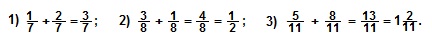
II. Если нужно сложить дроби с разными знаменателями, то сначала дроби приводят к наименьшему общему знаменателю, а затем складывают дроби с одинаковыми знаменателями.

Примеры.

158

III. Чтобы выполнить вычитание дробей с одинаковыми знаменателями, из числителя первой дроби вычитают числитель второй дроби, а знаменатель оставляют тот же.

Примеры.

159

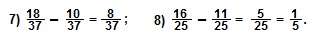
IV. Если нужно выполнить вычитание дробей с разными знаменателями, то их сначала приводят к общему знаменателю, а затем выполняют вычитание дробей с одинаковыми знаменателями.

Примеры.

160

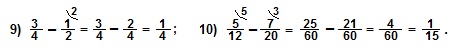
V. При выполнении действий сложения или вычитания смешанных чисел эти действия выполняют отдельно для целых частей и для дробных частей, а затем результат записывают в виде смешанного числа.

Примеры.

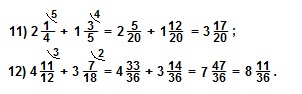161 Да, складывать нужно отдельно целые части и отдельно дробные части смешанного числа.

Нет, не нужно расписывать целые и дробные части смешанных чисел по отдельности.

Важно: не начинайте выполнять сложение, пока не приведете дробные части данных смешанных чисел к наименьшему общему знаменателю (НОЗ).

162

Помним, что единицу можно представить в виде обыкновенной дроби, числитель и знаменатель которой, являются любыми равными друг другу числами.

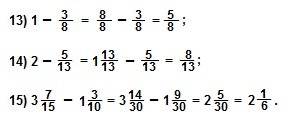
Важно: не начинайте выполнять вычитание, пока не приведете дробные части данных смешанных чисел к наименьшему общему знаменателю (НОЗ) и не убедитесь, что из числителя первой дроби можно вычесть числитель второй дроби. А если нельзя вычесть?

Тогда «занимаете» у целой части уменьшаемого одну целую единицу, представляете ее в виде неправильной дроби с таким же знаменателем (НОЗ), и добавляете эту неправильную дробь (раздробленную единицу) к дробной части уменьшаемого.

163

Содержание

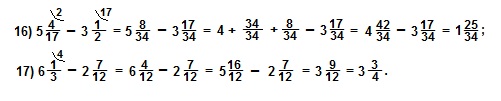
Умножение и деление дробей

2 августа 2011

В прошлый раз мы научились складывать и вычитать дроби (см. урок «Сложение и вычитание дробей»). Наиболее сложным моментом в тех действиях было приведение дробей к общему знаменателю.

Теперь настала пора разобраться с умножением и делением. Хорошая новость состоит в том, что эти операции выполняются даже проще, чем сложение и вычитание. Для начала рассмотрим простейший случай, когда есть две положительные дроби без выделенной целой части.

Чтобы умножить две дроби, надо отдельно умножить их числители и знаменатели. Первое число будет числителем новой дроби, а второе — знаменателем.

Чтобы разделить две дроби, надо первую дробь умножить на «перевернутую» вторую.

Обозначение:

Из определения следует, что деление дробей сводится к умножению. Чтобы «перевернуть» дробь, достаточно поменять местами числитель и знаменатель. Поэтому весь урок мы будем рассматривать в основном умножение.

В результате умножения может возникнуть (и зачастую действительно возникает) сократимая дробь — ее, разумеется, надо сократить. Если после всех сокращений дробь оказалась неправильной, в ней следует выделить целую часть. Но чего точно не будет при умножении, так это приведения к общему знаменателю: никаких методов «крест-накрест», наибольших множителей и наименьших общих кратных.

Задача. Найдите значение выражения:

По определению имеем:

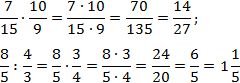
Умножение дробей с целой частью и отрицательных дробей

Если в дробях присутствует целая часть, их надо перевести в неправильные — и только затем умножать по схемам, изложенным выше.

Если в числителе дроби, в знаменателе или перед ней стоит минус, его можно вынести за пределы умножения или вообще убрать по следующим правилам:

Плюс на минус дает минус;
Минус на минус дает плюс.

До сих пор эти правила встречались только при сложении и вычитании отрицательных дробей, когда требовалось избавиться от целой части. Для произведения их можно обобщить, чтобы «сжигать» сразу несколько минусов:

Вычеркиваем минусы парами до тех пор, пока они полностью не исчезнут. В крайнем случае, один минус может выжить — тот, которому не нашлось пары;
Если минусов не осталось, операция выполнена — можно приступать к умножению. Если же последний минус не зачеркнут, поскольку ему не нашлось пары, выносим его за пределы умножения. Получится отрицательная дробь.

Задача. Найдите значение выражения:

Все дроби переводим в неправильные, а затем выносим минусы за пределы умножения. То, что осталось, умножаем по обычным правилам. Получаем:

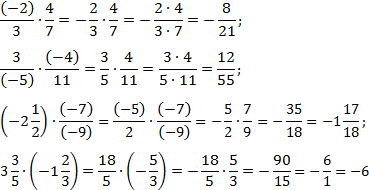
Умножение и деление отрицательных дробей - процесс

Еще раз напомню, что минус, который стоит перед дробью с выделенной целой частью, относится именно ко всей дроби, а не только к ее целой части (это касается двух последних примеров).

Также обратите внимание на отрицательные числа: при умножении они заключаются в скобки. Это сделано для того, чтобы отделить минусы от знаков умножения и сделать всю запись более аккуратной.

Сокращение дробей «на лету»

Умножение — весьма трудоемкая операция. Числа здесь получаются довольно большие, и чтобы упростить задачу, можно попробовать сократить дробь еще до умножения. Ведь по существу, числители и знаменатели дробей — это обычные множители, и, следовательно, их можно сокращать, используя основное свойство дроби. Взгляните на примеры:

Задача. Найдите значение выражения:

По определению имеем:

Умножение и деление дробей с одновременным сокращением

Во всех примерах красным цветом отмечены числа, которые подверглись сокращению, и то, что от них осталось.

Обратите внимание: в первом случае множители сократились полностью. На их месте остались единицы, которые, вообще говоря, можно не писать. Во втором примере полного сокращения добиться не удалось, но суммарный объем вычислений все равно уменьшился.

Однако ни в коем случае не используйте этот прием при сложении и вычитании дробей! Да, иногда там встречаются похожие числа, которые так и хочется сократить. Вот, посмотрите:

Так делать нельзя!

Ошибка возникает из-за того, что при сложении в числителе дроби появляется сумма, а не произведение чисел. Следовательно, применять основное свойство дроби нельзя, поскольку в этом свойстве речь идет именно об умножении чисел.

Других оснований для сокращения дробей просто не существует, поэтому правильное решение предыдущей задачи выглядит так:

Правильное решение:

Как видите, правильный ответ оказался не таким красивым. В общем, будьте внимательны.

Смотрите также:

Сложные выражения с дробями. Порядок действий
Тест к уроку «Сложение и вычитание дробей» (средний)
Тест к уроку «Площади многоугольников на координатной сетке» (средний)
Площади многоугольников на координатной сетке
Сводный тест по задачам B15 (2 вариант)
Как решать задачи про летающие камни?

Умножение и деление обыкновенных дробей. Онлайн калькулятор

Умножение дробей

Чтобы умножить одну обыкновенную дробь на другую, нужно умножить числитель первой дроби на числитель второй дроби (это произведение будет числителем результата), и знаменатель первой дроби на знаменатель второй дроби (это произведение будет знаменателем результата):

Правило умножения обыкновенных дробей в виде формулы:

Для упрощения вычислений, ещё до выполнения умножения дробей, можно сокращать любой множитель числителя с любым множителем знаменателя на общий делитель.

При сокращении числителей со знаменателями их обычно зачёркивают и рядом пишут число, которое получилось после сокращения:

В примере мы сократили 25 и 20 на общий делитель — 5, а 27 и 12 на общий делитель — 3.

Умножение дроби на натуральное число

Чтобы умножить натуральное число на обыкновенную дробь или наоборот — умножить дробь на натуральное число, можно числитель дроби умножить на это натуральное число, а знаменатель оставить без изменений:

Пример.

Деление дробей

При делении одной обыкновенной дроби на другую, нужно перевернуть вторую дробь и после этого умножить первую дробь на вторую, т. е. нужно числитель первой дроби умножить на знаменатель второй (это произведение будет числителем результата), а знаменатель первой дроби умножить на числитель второй (это произведение будет знаменателем результата):

Для проверки правильности выполненного деления, можно полученное частное умножить на делитель и посмотреть, получится ли у нас делимое, если делимое получено верно, значит деление было выполнено правильно:

Теперь осталось только сократить полученную дробь:

Правило деления обыкновенных дробей в виде формулы:

Иногда могут встретиться записи такого вида:

Так как дробная черта означает деление, то такие записи можно переписать в более удобном виде:

В записях, в которых дробная черта используется несколько раз, знак = ставится у дробной черты, означающей последнее по порядку действие деления:

Деление дроби на натуральное число

Чтобы обыкновенную дробь разделить на натуральное число или наоборот — натуральное число разделить на дробь, нужно просто представить натуральное число в виде дроби.

Примеры.

Калькулятор умножения и деления дробей

Данный калькулятор поможет вам выполнить умножение или деление обыкновенных дробей. Просто введите две дроби, выберите нужную операцию и нажмите кнопку Вычислить.

Сложение, вычитание, умножение и деление обыкновенных дробей и смешанных чисел. Математика, 5 класс: уроки, тесты, задания.

1.	Умножение дробей, правильная дробь Сложность: лёгкое
2.	Деление обыкновенных дробей (одинаковые знаменатели) Сложность: лёгкое
3.	Сумма дробей с равными знаменателями Сложность: лёгкое
4.	Разность дробей, равные знаменатели Сложность: лёгкое
5.	Число, обратное обыкновенной дроби Сложность: среднее
6.	Сумма целого числа и обыкновенной дроби Сложность: лёгкое
7.	Число, обратное смешанному Сложность: среднее
8.	Разность (смешанное число и единица) Сложность: лёгкое
9.	Число, обратное целому числу Сложность: среднее
10.	Вычитание из 1 правильной дроби Сложность: среднее
11.	Обыкновенная дробь в квадрате Сложность: среднее
12.	Вычитание из целого числа правильной дроби Сложность: среднее
13.	Обыкновенная дробь в кубе Сложность: среднее
14.	Вычитание дроби из смешанного числа Сложность: среднее
15.	Произведение смешанного числа и обыкновенной дроби Сложность: среднее
16.	Произведение двух смешанных чисел (разные знаменатели) Сложность: среднее
17.	Сумма смешанных чисел, одинаковые знаменатели Сложность: среднее
18.	Вычитание смешанных чисел Сложность: среднее
19.	Текстовая задача (два смешанных числа) Сложность: среднее
20.	Произведение десятичной дроби и обыкновенной Сложность: среднее
21.	Сумма смешанного числа и обыкновенной дроби (одинаковые знаменатели) Сложность: среднее
22.	Произведение двух отрицательных дробей Сложность: среднее
23.	Уравнение (неизвестная дробь) Сложность: среднее
24.	Деление целого числа на смешанное число Сложность: среднее
25.	Уравнение (неизвестный числитель дроби) Сложность: среднее
26.	Деление смешанного числа на обыкновенную дробь Сложность: среднее
27.	Сумма дробей, разные знаменатели Сложность: среднее
28.	Деление смешанного числа на обыкновенную дробь Сложность: среднее
29.	Разность дробей, знаменатели — взаимно простые числа Сложность: среднее
30.	Разность дробей, один знаменатель содержит второй как множитель Сложность: среднее
31.	Частное десятичной дроби и обыкновенной Сложность: среднее
32.	Вычитание дробей, знаменатели — большие разные числа Сложность: среднее
33.	Частное обыкновенных дробей с разными знаками Сложность: среднее
34.	Сумма смешанных чисел, разные знаменатели Сложность: среднее
35.	Частное двух отрицательных дробей Сложность: среднее
36.	Разность смешанного числа и дроби, разные знаменатели Сложность: среднее
37.	Текстовая задача Сложность: среднее
38.	Произведение трёх дробей Сложность: среднее
39.	Разность смешанных чисел, разные знаменатели Сложность: среднее
40.	Деление дроби на три другие дроби Сложность: среднее
41.	Уравнение Сложность: среднее
42.	Неизвестное слагаемое. Смешанные числа, разные знаменатели Сложность: среднее
43.	Неизвестное число Сложность: сложное
44.	Разность смешанных чисел (усложненный) Сложность: сложное
45.	Уравнение (произведение) Сложность: сложное
46.	Неизвестное вычитаемое. Смешанные числа, разные знаменатели Сложность: сложное
47.	Уравнение (сумма) Сложность: сложное
48.	Значение буквенного выражения Сложность: сложное

Основные правила математики с примерами. 5 класс

Содержание

Натуральные числа
Сравнение натуральных чисел
Свойства сложения
Формула пути
Корень уравнения
Правила решения уравнений
Отрезок, прямая, луч
Угол, биссектриса угла
Углы: развернутый, прямой, острый, тупой
Многоугольники. Равные фигуры
Треугольники: остроугольный, прямоугольный, тупоугольный
Треугольники: равнобедренный, равносторонний, разносторонний
Прямоугольник. Квадрат. Периметр
Умножение. Свойства умножения
Деление. Деление с остатком
Площадь. Площадь квадрата, прямоугольника
Объем. Объем прямоугольного параллелепипеда, куба
Дроби: правильная, неправильная, сравнение дробей
Сложение и вычитание дробей с одинаковыми знаменателями
Сложение и вычитание смешанных чисел
Преобразование неправильной дроби в смешанное число
Преобразование смешанного числа в неправильную дробь
Десятичные дроби: свойства, сравнение, округление
Десятичные дроби: сложение, вычитание
Десятичные дроби: умножение, деление
Среднее арифметическое
Процент

Натуральные числа

Числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 и т. д., которые используют при счете предметов, называют натуральными.

Сравнение натуральных чисел

Число меньше любого натурального числа.

$0 < 1,0 < 100$

Из двух натуральных чисел, которые имеют разное количество цифр большим является то, у которого количество цифр больше.

$\underbrace {2356}_4 > \underbrace {900}_3$

Из двух натуральных чисел с одинаковым количеством цифр большим является то, у которого больше первая (при чтении слева направо) из неодинаковых цифр

$35\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{6} 1 > 35\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{5} 9$

Свойства сложения

Переместительный закон:

Сочетательный закон:

Формула пути

S = Vt ,
где — пройденный путь, — скорость движения, — время, за которое пройден путь .

Корень уравнения

Корнем (решением) уравнения называют число, которое при подстановке его вместо буквы превращает уравнение в верное числовое равенство.

2 + 10 = 16

= 3 – корень, так как 2 · 3 + 10 = 16

Что значит “Решить уравнение”

Решить уравнение — это значит найти все его корни или убедиться, что их вообще нет.

Правила решения уравнений

Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.

$\underbrace {20}_{slagaemoe} + \underbrace x_{slagaemoe} = \underbrace {100}_{summa}$

$\begin{array}{*{20}c} {x = 100 - 20} \\ {x = 80} \\ \end{array}$

Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.

$\begin{array}{*{20}c} {\underbrace x_{ymenshaemoe} - \underbrace {10}_{vychitaemoe} = \underbrace {40}_{raznos$

Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.

$\begin{array}{*{20}c} {\underbrace {50}_{ymenshaemoe} - \underbrace x_{vychitaemoe} = \underbrace {40}_{raznost$

Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.

$\begin{array}{l} \underbrace x_{mnozitel$

Чтобы найти неизвестное делимое, надо делитель умножить на частное.

$\begin{array}{l} \underbrace x_{de\lim oe}:\underbrace 8_{delitel$

Чтобы найти неизвестный делитель, надо делимое разделить на частное.

$\begin{array}{l} \underbrace {42}_{de\lim oe}:\underbrace x_{delitel$

Отрезок, прямая, луч

Отрезок

Отрезок – часть прямой, ограниченная двумя точками(концами) и все точки между этими концами(внутренние точки отрезка)

Свойство длины отрезка

Если на отрезке отметить точку , то длина отрезка равна сумме длин отрезков и .

Равные отрезки

Два отрезка называют равными, если они совмещаются при наложении.

Свойство прямой

Через две точки проходит только одна прямая.

Измерить отрезок

Измерить отрезок означает подсчитать, сколько единичных отрезков в нем помещается

Ломаная

Ломаная — геометрическая фигура, состоящая из отрезков, последовательно соединенных друг с другом

Луч

Луч (полупрямая) — это геометрическая фигура, часть прямой, состоящая из точки(начала луча) и всех точек прямой, лежащих по одну сторону от начала луча.В названии луча присутствуют две буквы, например, . Причем первая буква всегда обозначает точку начала луча, поэтому менять местами буквы нельзя.

Угол, биссектриса угла

Угол

Фигуру, образованную двумя лучами, имеющими общее начало, называют углом.

Равные углы

Два угла называют равными, если они совмещаются при наложении.

Свойство величины угла

Если между сторонами угла ∠ ABC провести луч , то градусная мера ∠ ABC равна сумме градусных мер углов ∠ ABD и ∠ DBC , то есть ∠ ABC = ∠ ABD + ∠ DBC .

DBC

Биссектриса угла

Луч, который делит угол на два равных угла, называется биссектрисой угла.

DBC

Углы: развернутый, прямой, острый, тупой

Развернутый угол

Угол, стороны которого образуют прямую, называют развернутым. Градусная мера развернутого угла равна 180°.

Прямой угол

Угол, градусная мера которого равна 90°, называют прямым.

Острый угол

Угол, градусная мера которого меньше 90°, называют острым.

Тупой угол

Угол, градусная мера которого больше 90°, но меньше 180°, называют тупым.
DBC

Многоугольники. Равные фигуры

Равные многоугольники

Два многоугольники называют равными, если они совмещаются при наложении.

Равные фигуры

Две фигуры называют равными, если они совмещаются при наложении.

Треугольники: остроугольный, прямоугольный, тупоугольный

Остроугольный треугольник

Если все углы треугольника острые, то его называют остроугольным треугольником.

Прямоугольный треугольник

Если один из углов треугольника прямой, то его называют прямоугольным треугольником.

Тупоугольный треугольник

Если один из углов треугольника тупой, то его называют тупоугольным треугольником.
DBC

Треугольники: равнобедренный, равносторонний, разносторонний

Равнобедренный треугольник

Если две стороны треугольника равны, то его называют равнобедренным треугольником.

Равносторонний треугольник

Если три стороны треугольника равны, то его называют равносторонним треугольником.

Периметр равностороннего треугольника

Если сторона равностороннего треугольника равна , то его периметр вычисляют по формуле P=3a

Разносторонний треугольник

Если три стороны треугольника имеют разную длину, то его называют разносторонним треугольником.
P=3a

Прямоугольник. Квадрат. Периметр

Прямоугольник

Если в четырехугольнике все углы прямые, то его называют прямоугольником.

Свойство прямоугольника

Противоположные стороны прямоугольника равны.

Периметр прямоугольника

Если соседние стороны прямоугольника равны и , то его периметр вычисляют по формуле

Квадрат

Прямоугольник, у которого все стороны равны, называют квадратом.

Периметр квадрата

Если сторона квадрата равна , то его периметр вычисляют по формуле P=4a .
P=4a

Умножение. Свойства умножения

Умножение

$a \cdot b = \underbrace {a + a + \ldots + a}_b$

$5 \cdot 4 = \underbrace {5 + 5 + 5 + 5}_4$

Если один из двух множителей равен 1, то произведение равно второму множителю.

$1 \cdot 25 = 25\quad 25 \cdot 1 = 25$

Если один из множителей равен нулю, то произведение равно нулю.

$0 \cdot 25 = 0\quad 25 \cdot 0 = 0$

Если произведение равно нулю, то хотя бы один из множителей равен нулю.

Свойства умножения

Переместительный закон умножения: $a \cdot b = b \cdot a$

$6 \cdot 3 = 3 \cdot 6$

Сочетательный закон умножения: $(a \cdot b )c= a( b \cdot c)$

$(17 \cdot 5) \cdot 2 = 17 \cdot (5 \cdot 2)$

Распределительное свойство умножения относительно сложения:

2·(3 + 10) = 2 · 3 + 2 · 10

2 · 11 + 2 · 4 = 2·(11 + 4)

Распределительное свойство умножения относительно вычитания:

2·(15 – 7) = 2 · 15 – 2 · 7

3 · 10 – 3 · 4 = 3·(10 – 4)

Деление. Деление с остатком

Деление

Для натуральных чисел a, b, c равенство $a \div b = c$ является правильным, если является правильным равенство

$b \cdot c = a$

15 : 5 = 3 -правильное равенство, так как верно равенство 5 · 3 = 15

В равенстве $a \div b = c$ число называют делимым, число — делителем, число и запись $a \div b$ – частным от деления, отношением, долей.

На ноль делить нельзя.

Для любого натурального числа правильными являются равенства:

$0 \div a = 0$ ,

$a \div a = 1$

Деление с остатком

a=bq+r , где — делимое, — делитель, — неполное частное, — остаток, r < b .

$\underbrace {154}_{de\lim oe} = \underbrace {50}_{delitel$

Если остаток равен нулю, то говорят, что число делится нацело на число .

Площадь. Площадь квадрата, прямоугольника

Свойства площади фигуры

Равные фигуры имеют равные площади;

Площадь фигуры равна сумме площадей фигур, из которых она состоит.

Площадь прямоугольника

Площадь прямоугольника равна произведению длин его соседних сторон, выраженных в одних и тех же единицах.

Площадь квадрата

где — площадь квадрата, — длина его стороны.

Объем. Объем прямоугольного параллелепипеда, куба

Свойства объема фигуры

Равные фигуры имеют равные объемы;
Объем фигуры равен сумме объемов фигур, из которых она состоит.

Объем прямоугольного параллелепипеда

где — объем параллелепипеда, , и — его измерения, выраженные в одних и тех же единицах;

, где – площадь поверхности прямоугольного параллелепипеда.

где — площадь основания параллелепипеда, — его высота.

Объем куба

где — объем куба, — длина его ребра.

Дроби: правильная, неправильная, сравнение дробей

Правильная дробь

Дробь, числитель которой меньше знаменателя, называют правильной

$\frac{5} {7},\quad \frac{8} {9}$

Неправильная дробь

Дробь, числитель которой больше знаменателя или равен ему, называют неправильной.

$\frac{{11}} {7},\quad \frac{{27}} {9},\quad \frac{7} {7},\quad \frac{{13}} {{13}}$

Сравнение дробей

Из двух дробей с одинаковыми знаменателями больше та, числитель которой больше, и меньше та, числитель которой меньше.

$\frac{3} {4} > \frac{2} {4},\quad \frac{5} {8} < \frac{7} {8}$

Из двух дробей с одинаковыми числителями больше та, знаменатель которого меньше, и меньшая та, знаменатель которой больше.

$\frac{4} {5} > \frac{4} {7},\quad \frac{1} {8} < \frac{1} {5}$

Все правильные дроби меньше единицы, а неправильные — больше или равны единице.

$\frac{4} {5} < 1,\quad \frac{3} {2} > 1$

Любая неправильная дробь больше любой правильной дроби.

$\frac{7} {5} > \frac{4} {5},\quad \frac{7} {7} > \frac{6} {7}$

Сложение и вычитание дробей с одинаковыми знаменателями

Чтобы найти сумму двух дробей с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тот же.

$\frac{3} {7} + \frac{2} {7} = \frac{{3 + 2}} {7} = \frac{5} {7}$

Чтобы найти разность двух дробей с одинаковыми знаменателями, надо из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить тот же.

$\frac{4} {7} - \frac{1} {7} = \frac{{4 - 1}} {7} = \frac{3} {7}$

Сложение и вычитание смешанных чисел

Чтобы найти сумму двух смешанных чисел, надо отдельно сложить их целые и дробные части.

$2\frac{3} {5} + 1\frac{1} {5} = (2 + 1) + (\frac{3} {5} + \frac{1} {5}) = 3 + \frac{4} {5} = 3\frac{4} {5}$

Чтобы найти разность двух смешанных чисел, надо от целой и дробной части уменьшаемого вычесть соответственно целую и дробную части вычитаемого.

$4\frac{6} {7} - 1\frac{1} {7} = (4 - 1) + (\frac{6} {7} - \frac{1} {7}) = 3 + \frac{5} {7} = 3\frac{5} {7}$

Преобразование неправильной дроби в смешанное число

Чтобы неправильную дробь, числитель которой не делится нацело на знаменатель, преобразовать в смешанное число, нужно

числитель разделить на знаменатель;
полученное неполное частное записать как целую часть смешанного числа, а остаток — как числитель его дробной части.

Преобразование смешанного числа в неправильную дробь

Чтобы преобразовать смешанное число в неправильную дробь нужно

целую часть числа умножить на знаменатель дробной части;
к полученному произведению прибавить числитель дробной части;
эту сумму записать как числитель неправильной дроби;
в его знаменателе записать знаменатель дробной части смешанного числа.

Десятичные дроби: свойства, сравнение, округление

Свойства десятичной дроби

Если к десятичной дроби справа приписать любое количество нулей, то получим дробь, равную данной.

Значение дроби, которая заканчивается нулями, не изменится, если последние нули в его записи отбросить.

Сравнение десятичных дробей

Из двух десятичных дробей больше та, у которой целая часть больше.

Чтобы сравнить две десятичные дроби с равными целыми частями и разным количеством цифр после запятой, надо

с помощью приписывания нулей справа уравнять количество цифр в дробных частях,
после чего сравнить полученные дроби поразрядно.

Округление десятичных дробей

Для того чтобы десятичную дробь округлить до единиц, десятых, сотых и т. д., надо

все следующие за этим разрядом цифры отбросить.
если при этом первая из цифр, которые отбрасывают равна 0, 1, 2, или 4, то последнюю из цифр, которые оставляют, не меняют;
если же первая из цифр, которые отбрасывют, равна 5, 6, 7, 8 или 9, то последнюю из цифр, которые оставляют, увеличивают на единицу.

Десятичные дроби: сложение, вычитание

Сложение десятичных дробей

Чтобы найти сумму двух десятичных дробей, нужно:

уравнять количество цифр после запятых;
записать слагаемые друг под другом так, чтобы каждый разряд второго слагаемого оказался под соответствующим разрядом первого слагаемого;
сложить полученные числа так, как складывают натуральные числа;
поставить в полученной сумме запятую под запятыми.

Вычитание десятичных дробей

Чтобы найти разность двух десятичных дробей, нужно:

уравнять количество цифр после запятых;
записать вычитаемое под уменьшаемым так, чтобы каждый разряд вычитаемого оказался под соответствующим разрядом уменьшаемого;
выполнить вычитание так, как вычитают натуральные числа;
поставить в полученной разности запятую под запятыми.

Десятичные дроби: умножение, деление

Умножение десятичных дробей

Чтобы перемножить две десятичные дроби, надо:

перемножить их как натуральные числа, не обращая внимания на запятые;
в полученном произведении отделить запятой справа столько цифр, сколько их стоит после запятых в обоих множителях вместе.

Чтобы умножить десятичную дробь на 10, 100, 1000 и т. д., надо в этой дроби перенести запятую вправо на 1, 2, 3 и т. д. цифры.

Чтобы умножить десятичную дробь на 0,1; 0,01; 0,001 и т. д., надо в этой дроби перенести запятую влево соответственно на 1, 2, 3 и т. д. цифры.

Деление десятичных дробей

Чтобы разделить десятичную дробь на десятичную, надо:

перенести в делимом и в делителе запятую вправо на столько цифр, сколько их содержится после запятой в делителе;
выполнить деление на натуральное число.

Чтобы разделить десятичную дробь на 10, 100, 1000 и т. д., надо в этой дроби перенести запятую влево на 1, 2, 3 и т. д. цифры.

Среднее арифметическое

Средним арифметическим нескольких чисел называют результат деления сумму этих чисел на количество слагаемых.

Процент

Процентом называют сотую часть величины или числа 1%= $\frac{1}{{100}}$

Данная информация взята из УМК А.Г.Мерзляк, В.Б.Полонский, М.С. Якир

Деление дробей. Правила. Примеры. | tutomath

Следующее действие, которое можно выполнять с дробями это деление. Выполнять деление дробей достаточно просто главное знать несколько правил деления. Разберем правила деления и рассмотрим решение примеров на данную тему.

Деление дроби на дробь.

Чтобы делить дробь на дробь, нужно дробь, которая является делителем перевернуть, то есть получить обратную дробь делителю и потом выполнить умножение дробей.

$\bf \frac{a}{b} \div \frac{c}{d} = \frac{a}{b} \times \frac{d}{c}\\$

Пример:

Выполните деление обыкновенных дробей .

Деление дроби на число.

Чтобы разделить дробь на число, нужно знаменатель дроби умножить на число.

$\bf \frac{a}{b} \div n = \frac{a}{b} \div \frac{n}{1} = \frac{a}{b} \times \frac{1}{n}\\$

Рассмотрим пример:

Выполните деления дроби на натуральное число $\frac{4}{7} \div 3$.

Как мы уже знаем, что любое число можно представить в виде дроби $3 = \frac{3}{1} $.

$\frac{4}{7} \div 3 = \frac{4}{7} \div \frac{3}{1} = \frac{4}{7} \times \frac{1}{3} = \frac{4 \times 1}{7 \times 3} = \frac{4}{21}\\$

Деление числа на дробь.

Чтобы поделить число на дробь, нужно знаменатель делителя умножить на число, а числитель делителя записать в знаменатель. То есть дробь делитель перевернуть.

Рассмотрим пример:

Выполните деление числа на дробь.

Деление смешанных дробей.

Перед тем как приступить к делению смешанных дробей, их нужно перевести в неправильную дробь, а дальше выполнить деление по правилу деления дроби на дробь.

Пример:

Выполните деление смешанных дробей.

$2\frac{3}{4} \div 3\frac{1}{6} = \frac{11}{4} \div \color{red} {\frac{19}{6}} = \frac{11}{4} \times \color{red} {\frac{6}{19}} = \frac{11 \times 6}{4 \times 19} = \frac{11 \times \color{red} {2} \times 3}{2 \times \color{red} {2} \times 19} = \frac{33}{38}\\$

Деление числа на число.

Чтобы поделить простые числа, нужно представить их в виде дроби и выполнить деление по правилам деления дроби на дробь.

Пример:

$2 \div 5 = \frac{2}{1} \div \color{red} {\frac{5}{1}} = \frac{2}{1} \times \color{red} {\frac{1}{5}} = \frac{2 \times 1}{1 \times 5} = \frac{2}{5}\\$

Примечание к теме деление дробей:
На нуль делить нельзя.

Вопросы по теме:
Как делить дроби? Как разделить дробь на дробь?
Ответ: дроби делятся так, первую дробь делимое умножаем на дробь обратную дроби делителя.

Как делить дроби с разными знаменателями?
Ответ: не важно одинаковые или разные знаменатели у дробей, все дроби делятся по правилу деления дроби на дробь.

Пример №1:
Выполните деление и назовите делитель, дробь, обратную делителю: а) $\frac{5}{9} \div \frac{8}{13}$ б) $2\frac{4}{5} \div 1\frac{7}{8}$

Решение:
а) $\frac{5}{9} \div \frac{8}{13} = \frac{5}{9} \times \frac{13}{8} = \frac{65}{72}\\\\$

$ \frac{8}{13}$ – делитель, $ \frac{13}{8}$ – обратная дробь делителя.

б) $2\frac{4}{5} \div 1\frac{7}{8} = \frac{14}{5} \div \frac{15}{8} = \frac{14}{5} \times \frac{8}{15} = \frac{14 \times 8}{5 \times 15} = \frac{112}{75} = 1\frac{37}{75}\\\\$

$ \frac{15}{8}$ – делитель, $ \frac{8}{15}$ – обратная дробь делителя.

Пример №2:
Вычислите деление: а) $5 \div 1\frac{1}{4}$ б) $9\frac{2}{3} \div 8$

Решение:

а) $5 \div 1\frac{1}{4} = \frac{5}{1} \div \frac{5}{4} = \frac{5}{1} \times \frac{4}{5} = \frac{\color{red} {5} \times 4}{1 \times \color{red} {5}} = \frac{4}{1} = 4 \\\\$

б) $9\frac{2}{3} \div 8 = \frac{29}{3} \div \frac{8}{1} = \frac{29}{3} \times \frac{1}{8} = \frac{29 \times 1}{3 \times 8} = \frac{29}{24} = 1\frac{5}{24}\\\\$

90000 addition, subtraction, multiplication, and division of fractions and mixed numbers 90001 90002 You are here: 90003 Home → Worksheets → Fractions 1 90004 This worksheet generator produces a variety of worksheets for the four basic operations (addition, subtraction, multiplication, and division) with fractions and mixed numbers, including with negative fractions. You can make the worksheets in both html and PDF formats. You can choose like or unlike fractions, make missing number problems, restrict the problems to use proper fractions or to not to simplify the answers.Further, you can control the values of numerator, denominator, and the whole-number part to make the fractions or mixed numbers as easy or difficult as you like. 90005 90006 90007 Basic instructions for the worksheets 90008 90004 Each worksheet is randomly generated and thus unique. The 90010 answer key is automatically generated 90011 and is placed on the second page of the file. 90005 90004 You can generate the worksheets 90014 either in html or PDF format 90015 — both are easy to print.To get the PDF worksheet, simply push the button titled «90002 Create PDF 90003» or «90002 Make PDF worksheet 90003». To get the worksheet in html format, push the button «90002 View in browser 90003» or «90002 Make html worksheet 90003». This has the advantage that you can save the worksheet directly from your browser (choose File → Save) and then 90002 edit it 90003 in Word or other word processing program. 90005 90004 Sometimes the generated worksheet is not exactly what you want.Just try again! To get a different worksheet using the same options: 90005 90029 90030 PDF format: come back to this page and push the button again. 90031 90030 Html format: simply refresh the worksheet page in your browser window. 90031 90034 90006 90004 Tip: chose value 1 to be a fraction and value 2 to be a mixed number, and then tick the box of «Value 1 — Value 2 random switching» to make problems where either the first or the second number is a mixed number. Just experiment with the options to customize the worksheets as you like! 90005 90004 Here are some quick links for ready worksheets.Refresh the worksheet page to get another of the same kind. 90005 .90000 Division as repeated subtraction — a complete lesson for third grade 90001 90002 This is a complete lesson with teaching and exercises, showing how division can be seen as repeated subtraction. It is meant for third grade. 90003 90002 Students solve divisions by «subtracting» or crossing out equal-size groups from the total in the visual model, until there is nothing left. Examples show how divisions can be solved by repeatedly subtracting the same number (the divisor).Often, it is actually easier to add intead of subtract, and figure out how many times you will add the number (divisor) until you reach the dividend. 90003 90002 The lesson also shows how number-line jumps tie in with this concept: we jump backwards from the dividend, making jumps of same size (the size being the divisor), until we reach zero. The lesson also has several word problems to solve. 90003 90008 90009 90010 90011 90009 90010 90002 MULTIPLICATION has to do with 90015 90016 many groups of the same size 90017 90018.90003 Here is one group of four. Draw another group of four to the picture. 90020 And another group. And another. And one more group. 90021 90022 90023 90002 90003 90021 90027 90028 90002 You drew _____ groups of four. 5 × 4 = 4 + 4 + 4 + 4 + 4 = 20. 90003 90021 90027 90028 90034 90009 90010 90011 90009 90039 90015 Let’s reverse the process.Start out with 20 sticks. 90018 90002 Make one group of four. In your mind, «move it away» from the picture. Form another group of four. Again, «move it away», or subtract it from the picture. 90003 90002 Keep forming groups of four till you have none left. 90020 How many groups did you make? ______ 90003 90021 90048 90049 | | | | | | | | 90020 | | | | | | | | 90020 | | | | 90021 90027 90028 90055 20 — 4 — 4 — 4 — 4 — 4 = 0 90003 90002 This is repeated subtraction.You subtract 4 repeatedly till you reach zero. 90020 Each subtraction is a group of 4. 90020 90020 How many groups? _____ How many times did you subtract? _____ 90020 That is the answer to the division problem 20 ÷ 4. 90003 90021 90027 90028 90002 1. Make groups, but in your mind ‘move them away’ or subtract. Write a subtraction sentence. 90003 90068 90009 90070 90055 DIVISION can be solved by 90015 90016 repeated subtraction 90017 90018: 90003 90021 90027 90009 90080 90055 20 ÷ 4 = ?? 90003 90002 90003 90055 20 — 4 — 4 — 4 & min 90003 90021 90027 90028.90000 90001 Long Division and Repeated Subtraction 90002 90003 90004 90005 This is a complete lesson with examples and exercises about the repeated subtraction process, as it relates to division. I give several examples of comparing division to bagging fruits and using repeated subtraction in that context. Several exercises follow. Lastly the lesson shows a comparison of this process with the actual long division algorithm. The lesson is meant for fifth grade.90006 90007 90003 90009 You know how multiplication can be seen as 90010 repeated addition 90011. Division is the opposite of multiplication. So, it should be no surprise that division can be solved by 90012 90013 repeated (or continued) subtraction 90014 90015. Read through the examples carefully in order to understand that. 90016 90017 90003 90009 90013 Example 1 90014. Bag 771 apples, placing 3 apples in each bag.How many bags will you need? 90005 You might start by putting 3 apples into one bag, which leaves you with 768 apples. From then on, for each bag you use, subtract 3 apples. Keep counting the bags you use until you have no apples! 90006 90024 90003 90009 90027 90003 90009 771 90016 90031 — 3 90016 90031 — 3 90016 90031 — 3 90016 90031 — 3 90016 90031 — 3 90016 90031 — 3 90016 90009… 90016 90009 90010 keep subtracting! 90011 90016 90017 90003 90051 90031 1 bag 90016 90031 1 bag 90016 90031 1 bag 90016 90031 1 bag 90016 90031 1 bag 90016 90031 1 bag 90016 90009 … 90016 90009 90010 keep counting bags! 90011 90016 90017 90071 90016 90017 90071 90005 It just takes quite a long time to do it this way! Instead, you can take a 90013 shortcut: 90014 subtract 90012 90013 300 apples at a time 90014 90015 (which means 100 bags), as long as you can, then 30 apples at a time as long as you can (which means 10 bags), and lastly 3 apples at a time.90006 90083 90003 90009 90027 90003 90009 771 90016 90031 — 300 90016 90031 — 300 90016 90031 — 30 90016 90031 — 30 90016 90009 … 90016 90017 90003 90051 90031 100 bags 90016 90031 100 bags 90016 90031 10 bags 90016 90031 10 bags 90016 90009 … 90016 90017 90071 90016 90017 90071 90016 90017 90003 90009 90122 90003 90004 Let’s keep count of the bags as we subtract (Put into bags) the apples.Study carefully the two calculations on the right. 90005 In 90012 90013 method 1 90014 90015, we count the bags 100 bags at a time initially, and then 10 bags at a time. 90006 90005 Study method 1 now. 90006 90005 In 90012 90013 method 2 90014 90015, we start out by counting 200 bags and subtracting 600 apples all at once, instead of subtracting 300 apples two separate times. 90006 90005 Similarly, we then count 50 bags and subtract 150 apples all at once (150 is the largest possible multiple of 30 that we can subtract from 171).90006 90005 In total we need 200 + 50 + 7 = 90012 90013 257 bags 90014 90015 for all the apples. 90006 90005 We can write the division 90013 771 ÷ 3 = 257 90014. 90006 90016 90051 90153 90154 Method 1 — slower 90006 90016 90017 90071 90016 90017 90071 90016 90017 90071.90000 Worksheets for fraction addition 90001 90002 You are here: 90003 Home → Worksheets → Fraction addition 90004 90002 Create an unlimited supply of worksheets for adding fractions and mixed numbers (grades 4-7)! The worksheets can be made in html or PDF format — both are easy to print. You can also customize them using the generator below. 90003 90007 90004 Addition of fractions is typically taught starting in 4th grade, with like fractions (same denominator, such as 3/8 + 2/8).Children start out by using manipulatives so they can understand the concept, and then they can go on to abstract problems. 90007 90004 Next, in 5th grade, students tackle adding 90002 unlike 90003 fractions (fractions with different denominators, such as 3/4 + 2/5) and mixed numbers with unlike fractional parts. The procedure for this involves converting the fractions to be added to equivalent fractions with a common denominator. After the conversion, you have 90002 like fractions 90003 (fractions with the same denominator) which you can add easily.To understand how this is done, please see this video on adding unlike fractions on my other site (MathMammoth.com) 90007 90004 In 6th and 7th grades, students simply practice addition of fractions using larger denominators and more complex problems. 90007 90004 Jump to: 90007 90020 90021 Basic instructions for the worksheets 90022 90004 Each worksheet is randomly generated and thus unique. The 90024 answer key is automatically generated 90025 and is placed on the second page of the file.90007 90004 You can generate the worksheets 90028 either in html or PDF format 90029 — both are easy to print. To get the PDF worksheet, simply push the button titled «90002 Create PDF 90003» or «90002 Make PDF worksheet 90003». To get the worksheet in html format, push the button «90002 View in browser 90003» or «90002 Make html worksheet 90003». This has the advantage that you can save the worksheet directly from your browser (choose File → Save) and then 90002 edit it 90003 in Word or other word processing program.90007 90004 Sometimes the generated worksheet is not exactly what you want. Just try again! To get a different worksheet using the same options: 90007 90043 90044 PDF format: come back to this page and push the button again. 90045 90044 Html format: simply refresh the worksheet page in your browser window. 90045 90048 90020 90021 Fraction addition worksheets: grade 4 90022 90004 The fractions in grade 4 addition problems are limited to 90002 like 90003 fractions — fractions with a same denominator.90007 .