2. Подход «mr – mc» («предельная выручка – предельные издержки»).
Предельная выручка (MR – marginalrevenue) – это добавочный доход, приносимый выпуском (продажей) дополнительной, последней единицы продукции.
Она рассчитывается следующим образом:
Важным замечанием является то, что на рынке совершенной конкуренции предельная выручка фирмы всегда равна цене, так как каждая единица продукции реализуется по заданной цене:
MR=P
В соответствии с предельным подходом, фирма на каждом объеме выпуска Q должна сравнить предельные издержки MC и предельную выручку MR, и на основе этого соотношения найти оптимальный объем выпуска Q*.
Запишем возможные варианты этого соотношения схематично:
1.MR > MC → произ-во добавочной единицы прибыльно (МП – предельная прибыль > 0 →
2.MR < MC → произ-во добавочной единицы убыточно (МП< 0 → расширение производства невозможно
3. MR = MC → условие максимизации прибыли, когда отсутствуют стимулы к расширению произ-ва (МП = 0) → оптимальный объем выпуска Q* найден
Таким образом, для рынка совершенной конкуренции условием максимизации прибыли является соотношение MR = MC = P , так как предельная выручка признается равной цене.
Отметим, что не всегда можно подобрать такой объем выпуска, при котором будет наблюдаться именно равенство между MR и МС, так как это является идеальным вариантом для максимизации прибыли. В тех случаях, когда не представляется возможным достичь равенства, выбирают тот объем выпуска, при котором разница между MR и МС будет минимальной и обязательно положительной
, то есть:MR > MC и
MR – MC → min
Использование второго подхода позволяет не только определить оптимальный объем выпуска, но и определить величину максимально возможной прибыли:
Графически максимально возможная прибыль находится следующим образом (рис. 42):
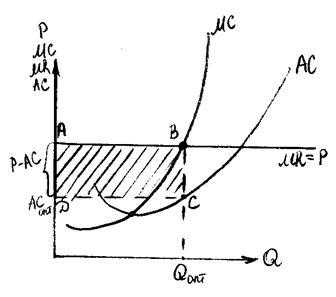
Рис. 42. Максимизация прибыли на рынке совершенной конкуренции
Оптимальный объем выпуска соответствует точки пересечения кривой MC и линии MR. Величина максимальной прибыли равна площади прямоугольника ABCD.
3. Минимизация убытков фирмой – совершенным конкурентом
В том случае, если цена становится ниже минимальных средних издержек (Р<min AC), то перед фирмой становится вопрос не максимизации прибыли, а минимизации убытков.
Минимальные убытки находятся как разница между общей выручкой TR и общими затратами TC:
При этом существует два варианта дальнейшего функционирования фирмы, выбор которых зависит от того, где убытки будут меньше:
1. Временное закрытие производства. При этом варианте объем выпуска равен нулю, а, следовательно, и общая выручка равна нулю. Что касается общих затрат ТС, то они в условиях закрытия производства будут равняться постоянным затратам FC, которые существуют даже при нулевом объеме выпуска. Таким образом, возможные убытки L будут равны сумме постоянных затрат FC.
Схематично отобразим нахождение убытков по первому варианту:
Q = 0TR = 0TC = FCL = TR – TC = 0 – FC = – FC
2. Продолжение убыточного производства. Фирма решает продолжать убыточное производство, получая выручку TR, которая не может покрыть общие затраты TC, состоящие из постоянных FC и переменных затрат VC.
Постоянные затраты существуют даже при нулевом объеме выпуска, поэтому фирме надо соизмерять общую выручку и переменные затраты. Если переменные затраты окажутся не столь велики, что даже останутся средства из выручки на покрытие постоянных затрат, то этот вариант будет предпочтительней, чем первый:
Q > 0TR > 0TC = FC + VC < 0L = TR – TC = TR – (FC + VC)TR > VC → этот вариант предпочтительней, чем первыйTR = ;То естьP > AVC
Таким образом, ориентиром для принятия решения закрывать производство или продолжать убыточное (первый или второй вариант) является соотношение цены и средних переменных затрат:
1. Если P >min AVC, то фирма принимает решение о продолжении убыточного производства (второй вариант) и выбирает тот объем выпуска, при котором MR = MC = P – условием минимизации убытков (такое же как и условие максимизации прибыли).
2 . Если P <min AVC , то фирма закрывает убыточное производство (первый вариант), а следовательно оптимальный объем выпуска равен нулю.
3 Если
studfiles.net
P=MR | Экономика для школьников
(действительно, если $MR(50)\neq MC(50)$, то можно чуть-чуть увеличить выпуск в случае $MR(50)>MC(50)$ или чуть-чуть уменьшить его в случае $MR(50)
Но по условию $P(50)=MR(50)$, и значит, $P(50)=c$. Поскольку у нас $MC=const$, то $AVC=const=MC=с$, и значит, $P(50)=AVC(50)$, то есть $\pi(50)=(P(50)-AVC(50))\cdot50-FC=0-FC=-FC$.
Теперь предъявим точку, в которой прибыль больше $(-FC)$. Тем самым мы придем к противоречию с тем, что $Q=50$ оптимальна.
Какую же точку предъявить?
Заметим, что в этом решении нам не понадобилась гладкость функции спроса. Более того, нам понадобилась дифференцируемость функции спроса лишь в точке $Q=50$ (чтобы функция выручки там тоже была дифференцируемой и там существовал $MR$).
Решение 2 (Григорий Хацевич)
Если MR в какой-то точке интервала (0,100) строго возрастает, то при постоянных MC эта точка не может быть оптимумом: даже если в ней MR=MC, то мы сможем увеличить прибыль – сдвинувшись чуть-чуть в любом направлении.
Осталось доказать, что такая точка существует.
Рассмотрим вспомогательную функцию спроса $P_2(Q)=P(Q)-P(50)$, определённую на промежутке (0;50]. Мы просто опустили старый спрос настолько, чтобы при Q=50 он пришёл в ноль. Заметим, что $MR_2(Q)=MR(Q)-P(50)$, т.е. он отличается от старого на константу (на ту же, что и спрос, но здесь нам это не важно).
Показать step 2
$P_2$ строго убывает, $P_2(50)=0$. Отсюда $TR_2(50)=0$ и $TR_2(Q)>0$ при любом $Q\in(0;50)$. Поэтому найдётся точка $Q_0\in(0;50)$, такая что $MR_2(Q_0)
iloveeconomics.ru
Доход и прибыль фирмы в краткосрочном периоде. Виды фирм
В рыночной экономике под доходом фирмы понимается денежная оценка результатов деятельности фирмы в виде денежной суммы, поступающей в ее непосредственное распоряжение. Она отражает экономическую результативность хозяйственной деятельности фирмы. Это значит, что условием получения денежного дохода является эффективное участие в экономической жизни общества.
Соответственно видам издержек подразделяются и доходы. Поэтому принято выделять общий, средний и предельный доход.
Общий доход (TR) — это сумма дохода, получаемого фирмой от продажи определенного количества благ: TR = P×Q, где TR — общий доход; P — цена; Q — проданное количество благ.
Средний доход (AR) — доход, приходящийся на единицу проданного блага. В условиях совершенной конкуренции средний доход равен рыночной цене: АR = TR/Q.
Предельный доход (MR) — это приращение дохода, вызванное продажей дополнительной единицы продукции: MR = ∆TR/∆Q.
Под прибылью фирмы понимают разницу между доходами и издержками: П = TR — TC, где П — прибыль, TR — совокупный доход, TC — совокупные издержки.
Напомним, сами издержки бывают внешними и внутренними. К внешним издержкам относятся платежи
внешним (по отношению к данной фирме) поставщикам. Вычитая из совокупной выручки (дохода) внешние
издержки, мы получаем
Вычитая из бухгалтерской прибыли внутренние издержки (некомпенсированные собственные издержки предпринимателя, не учтённые в себестоимости, в том числе «упущенная выгода», затраты на «стимулирование» чиновников в коррупционных экономиках, дополнительные премиальные работникам) мы получаем экономическую прибыль.
Таким образом, при определении объема реальной прибыли следует исходить из такой цены ресурса, которую получил бы его владелец при наилучшем его использовании.
Современная экономическая теория утверждает, что максимизация прибыли или минимизация издержек достигается при том объеме производства, когда предельный доход равен предельным издержкам (MR = МС). В условиях совершенной конкуренции максимизация прибыли достигается при объеме производства, соответствующем точке равенства предельных издержек и цены: MR = MC = Р. Это и есть условие равновесия фирмы в краткосрочном периоде.
В условиях краткосрочного равновесия можно выделить четыре типа фирм:
1. Фирма, у которой средние издержки равны цене (АТС = Р) называется допредельной фирмой с нормальной прибылью.
2. Фирма, которой удается покрывать лишь средние переменные издержки (AVC = P), называется предельной фирмой. Такой фирме удается быть «на плаву» лишь недолгое время. В случае повышения цен она сможет покрыть не только текущие (средние переменные), но и все издержки (средние общие), т.е. получать нормальную прибыль (как допредельная фирма).
3. Запредельная фирма. В случае снижения цен фирма перестает быть конкурентоспособной, т.к. не может покрывать даже текущие издержки (AVC > P) и вынуждена будет покинуть отрасль.
4. Фирма, у которой средние общие издержки меньше цены (АТС допредельной фирмой со сверхприбылью.
Другие статьи по данной теме:
www.ekonomika-st.ru
как называются в экономике TC,Q,P,R (формулы ,системы)
TC-общие затраты, Q-количество выпускаемой продукции, P-цена, R- не знаю что такое
R рентабельность
P — цена Q — количество D – спрос S — предложение QD – величина спроса QS – величина предложения Qдеф – дефицит (объем дефицита) Qпродаж – объём продаж QИЗБ – объём избытка (излишки) EDP– коэффициент эластичности спроса по цене ESP– коэффициент эластичности предложения по цене I – доход EDI— коэффициент эластичности спроса по доходу EDC— коэффициент перекрестной эластичности спроса TR – совокупный доход (выручка продавца) TC – общие затраты Pr – прибыль PD – цена спроса PS– цена предложения PE– равновесная цена II. Формулы: y= k*x+b – уравнение описывающее функцию спроса QD= k*P+b – функция спроса EDP= Δ QD (%)/ΔP (%) – коэффициент эластичности спроса по цене EDP= (Q2 –Q1): (Q2 + Q1)/ (P2 –P1): (P2 + P1) – формула средней точки, где P1 – цена товара до изменения, P2 – цена товара после изменения, Q1 – величина спроса до изменения цены, Q2 – величина спроса после изменения цены; EDI= (Q2 –Q1): (Q2 + Q1)/ (I2 –I1): (I2 + I1) – формула коэффициента эластичности спроса, где I1 – величина дохода до изменения, I2 – величина дохода после изменения, Q1 – величина спроса до изменения дохода, Q2 – величина спроса после изменения дохода; EDС = (Q2 –Q1): (Q2 + Q1)/ (P2 –P1): (P2 + P1) – формула средней точки, где P1 – цена второго товара до изменения, P2 – цена второго товара после изменения, Q1 – величина спроса первого товара до изменения цены, Q2 – величина спроса первого товара после изменения цены; TR = P*Q – формула расчета выручки продавца Pr= TR – TС – формула расчета прибыли; QD= k*P+b – функция предложения; ESP= (QS2 –QS1): (QS2 + QS1)/ (P2 –P1): (P2 + P1) – формула коэффициента предложения, где P1 – цена товара до изменения, P2 – цена товара после изменения, QS1 – величина предложения до изменения цены, QS2 – величина предложения после изменения цены; Qдеф = QD— QS– формула для определения объема дефицита; Qдеф = QS — QD– формула для определения объема излишек;
touch.otvet.mail.ru
Mrs что это такое в экономике: предельная норма замены
Но в какой мере может потребитель отказаться, например, от апельсинов, чтобы приобрести дополнительно еще одно яблоко? Это помогает определить т.н. предельная норма замещения.
Предельная норма замещения Y на Х (МRSху) – количество товара Y, от которого потребитель отказался бы, чтобы получить еще одну единицу товара X, при этом оставаясь на данной кривой безразличия. Кривизна изображенных ранее кривых безразличия означает, что количество Y, от которого потребитель хочет отказаться ради еще одной единицы X, уменьшается по мере увеличения количества X, замещающего Y в наборе.
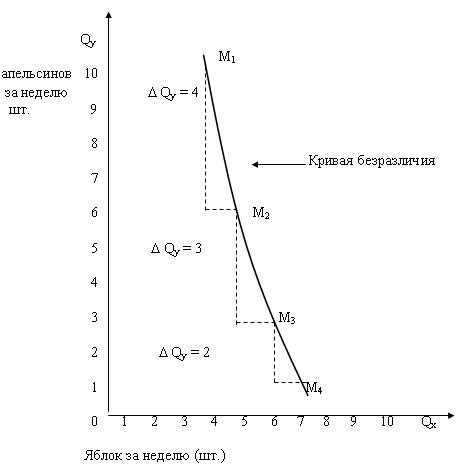
Чтобы увидеть это начнем двигаться вдоль кривой безразличия, изображенной на рис. 6.4. Qу – недельное потребление товара Y, от которого потребитель отказался бы, чтобы получить еще одну единицу товара X. Выигрыш в недельном потреблении единицы товара Х составляет Qх = 1.
Количество товара Y, которое будет обменено на единицу товара X, между любыми двумя точками на кривой может быть записано как Qу/Qх. Это наклон кривой безразличия, вдоль которой движется потребитель, отказываясь от единиц товара Y, для получения единиц товара X. Однако наклон кривых безразличия отрицателен.
Такое рассмотрение MRSху приводит к получению отрицательного числа. Предельная же норма замещения определяется как положительное количество товара Y, от которого потребитель желает отказаться ради дополнительной единицы X. Поэтому он есть произведение наклона кривых безразличия на -1.
Кривизна кривой безразличия, изображенная на рис. 6.4. подразумевает уменьшение предельной нормы замещения Y на X. Обратите внимание, как их наклон изменяется по мере того, как потребитель, следуя по данной кривой, замещает Y на X. По мере того, как Х замещает Y вдоль кривой, она становится менее крутой.
Рис. 6.4 – Уменьшение MRSху вдоль кривой безразличия
Таблица 6.2 – Предельная норма замещения Y на X
| Набор | Qу | Qх | MRSху |
М1 М2 М3 М4 | 10 6 3 1 | 4 5 6 7 | 4 ед. Y за 1 ед. Х 3 ед. Y за 1 ед. Х 2 ед. Y за 1 ед. Предельная норма замещенияХ |
Анализ кривых безразличия не требует, чтобы полезность была количественно измерима, достаточно только предположить, что потребители способны ранжировать альтернативы, то есть, что полезность порядково измерима (позиция ординалистов).
Если бы полезность была количественно измерима (позиция кардиналистов), была бы возможность вычислить, сколько полезности при добавлении в набор еще одной единицы товара или услуги. То есть предельную норму замещения вдоль кривой безразличия можно связать с предельными полезностями благ на каждой из осей.
Изъятие Qу единиц товара Y из набора наносит потребителю ущерб. Потеря полезности составляет Qу MUу, где МUу – предельная полезность Y для потребителя. При замене потерянного количества Y тем количеством X, которое необходимо для возвращения потребителя в состояние прежней удовлетворенности, приобретенная полезность составила бы
(где МUх – предельная полезность X). Если потребителю необходимо вернуться на ту же самую кривую безразличия, прирост полезности от добавления Х равен потери полезности от изъятия Y.
Таким образом:
Следовательно,
Предельная норма замещения Y на Х поэтому может рассматриваться как отношение предельной полезности Х к предельной полезности Y.
В нашем примере предельная полезность яблок (товар Х) уменьшается, когда его количество растет, и, соответственно она увеличивается у апельсинов (товар Y), когда их количество уменьшается. Поскольку МUх уменьшается, когда товар Х (яблоки) замещает товар Y (апельсины), в то время как МUу увеличивается, отношение МUх/МUу равное МRSху уменьшается.
Отсюда вытекает, что предельная норма замещения Y на Х тоже должна падать при замене Y на X, если предельные полезности Х и Y находятся в обратном отношении к количествам этих товаров, покупаемых за период.
Уменьшение предельной полезности товаров, при предположении количественной измеримости полезности, объяснило бы выпуклую форму кривых безразличия.
laservirta.ru
Микроэкономика
Задача №1
Предположите, что Вы потратили весь свой бюджет на приобретение двух товаров.
Используйте анализ кривых безразличия для доказательства невозможности низкого качества обоих товаров.
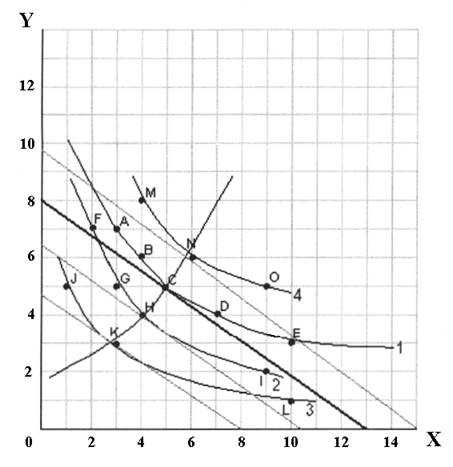
Пусть имеющийся в наличии бюджет составляет 200 у.е. «Истратим» его на приобретение двух товаров – Икс ( X) и Игрек ( Y) , по ценамP ( X ) = 15 у.е. , и P ( Y ) = 25 у.е. .
Для построения кривых безразличия на базе имеющихся данных составим несколько т.н. наборов безразличия — набор вариантов потребительского выбора, каждый из которых приносит один и тот же уровень удовлетворения. Наборы безразличия составляются на основании того, что сумма затрат на покупку некоторого количества обоих товаров было равно имеющемуся в наличии бюджету. Исходя из этого условия, составим варианты выбора покупателя в виде таблиц, каждая из которых представляет свой набор безразличия:
По составленным наборам отмечает соответствующие точки и проводим кривые безразличия. Эти кривые имеют отрицательный наклон, причем этот наклон уменьшается по мере продвижения вниз и вправо. Следовательно, что отношение предельной полезности Икса к предельной полезности Игрека убывает по мере того, как происходит продвижение.
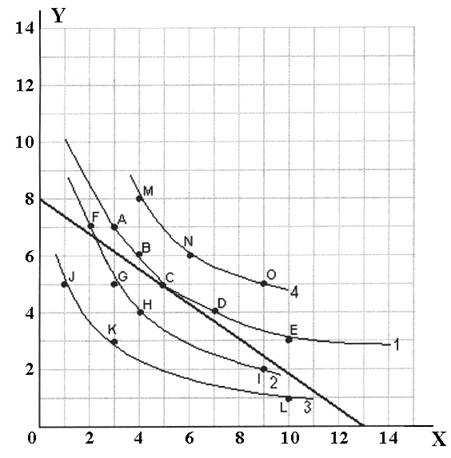
Возможные варианты выбора покупателя, обладающим фиксированным бюджетом при существующих ценах, определяются бюджетной линией или линией потребительских альтернатив. Эта линия показывает возможности потребления — т.е., имея в наличии 200 у.е., можно приобрести максимум 13 единиц Иксов по 15 у.е. или 8 Игреков по 25 у.е.
Равновесие потребителя.
Точка потребительского равновесия при имеющимся бюджетной линии и кривым безразличия — это точка С , которая отражает оптимальное и полное использование. Все точки, находящиеся на графике выше точки равновесия С — находятся за пределами финансовых возможностей покупателя. Остальные точки соответствуют наборам товаров в пределах финансовых возможностей покупателя, но расположены ниже точки равновесия, Т.е. являются менее желательными – имеет место неполное использование бюджета.
Изменение цены.
Если имеется фиксированный бюджет, но цены на товары изменяются – соответственно изменятся и точки равновесия, по которым будет возможно определить кривые спроса.
Построим бюджетные линии, соответствующие изменению цен на товары:
Икс — 10, 15, 20, 25, 30, 35 у.е. и Игрек — 15, 20, 25, 30, 40 у.е.
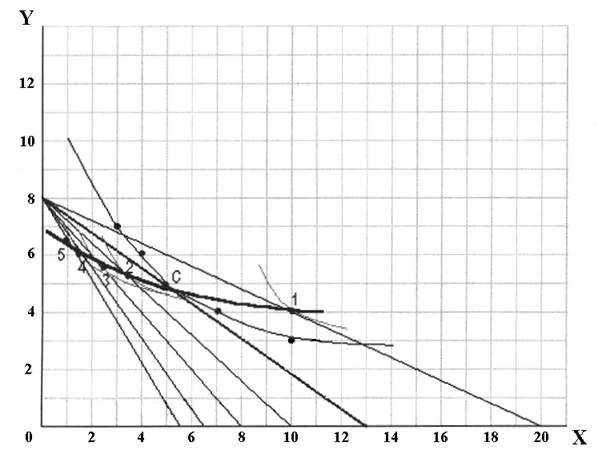
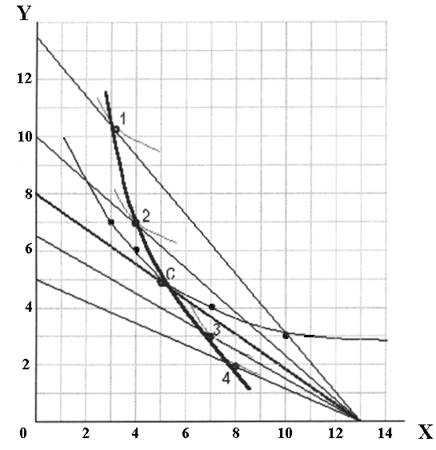
На каждой бюджетной линии есть точка, соответствующая точке потребительского равновесия при текущей цене. Это точки 1, 2, 3, 4, 5 для Икса и 1, 2, 3, 4 для Игрека .
Если эти точки соединить кривой – получаются кривые спроса.
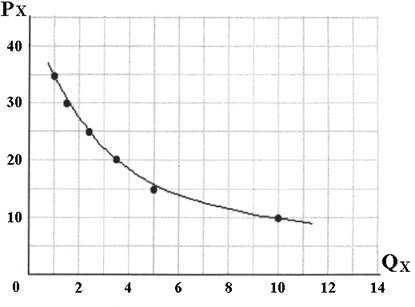
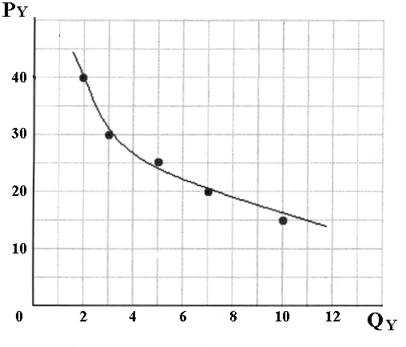
Кривые спроса обоих товаров имеют отрицательный наклон, характер которого свидетельствует, что эти кривые отражает достаточно эластичный спрос, причем при незначительном падении цен количество потребленного на рынке товара возрастает. Следовательно присутствует положительная эластичность спроса на эти товары, а значит эти товары не могут быть низкого качества.
Кривые Энгеля.
Этот метод рассматривает зависимость величины потребления от дохода. Если построить бюджетные линии для размеров бюджета покупателя 120, 160 и 240 у.е. и соединить полученные точки потребительского равновесия кривой — то получим, т.н. кривую Энгеля , описывающую соотношение «доход-потребление».
Так как эта кривая имеет положительный наклон относительно обоих товаров, следовательно, с увеличением дохода величина потребления товаров также увеличится, а это определяет их как качественные товары .
Задача №2
Как отличить качественный товар от некачественного? Начертите кривую Энгеля для товара, который потребитель будет рассматривать, как некачественный после того, как его доходы в неделю достигнут определённого уровня.
При решении предыдущей задачи был рассмотрен вариант,когда кривая Энгеля имеет положительный наклон, т.е. при увеличении дохода увеличивается и потребление – оба товара качественные.
Предположим, что товар Икс ( X ) – некачественный и доход покупателя увеличивается (C0 — C1 — C2). Это значит, что по отношению к товару Икс кривая «доход-потребление» имеет отрицательный наклон, потому что потребление этого товара будет уменьшаться при повышении дохода (C0 — C1 — C2) — X1<X0 и X2<X1.
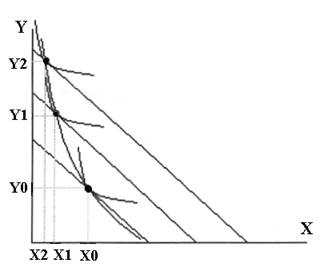
Для качественного товара Игрек ( Y ) : Y1>Y0 и Y2>Y1 потребление растет, следовательно, наклон кривой Энгеля остается положительным.
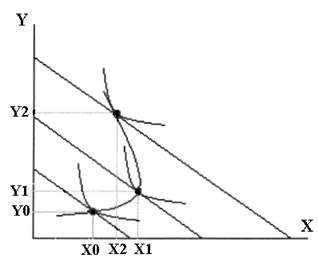
Если при достижении дохода потребителя определённого уровня спрос на менее качественный товар Икс падает, т.е. X1>X0, но X2<X1 — это значит что после пересечения бюджетной линии, соответствующей определенному уровню дохода кривая Энгеля меняет наклон с положительного на отрицательный.
В этом случае кривая Энгеля будет иметь такой вид:
Задача №3
Условия равновесия фирмы при совершенной конкуренции имеет такой вид:
МС = MR = АС = Р.
Как изменится это условие при несовершенной конкуренции («чистой» монополии)?
Вышеуказанное равенство действует в условиях совершенной конкуренции, т.е должны выполняться некоторые условия: большое число независимо действующих продавцов; более или менее однородная продукция; конкурентная фирма не может устанавливать цену, но может приспосабливаться к ней; свободное вступление и выход из отрасли.
Для совершенной конкуренции действует равенство предельного дохода и предельных издержек – фирма будет максимизировать прибыли или минимизировать убытки, производя в той точке, где предельный доход равен предельным издержкам (правило MR = MC ). Кривая спроса , или продаж, конкурентного продавца совершенно эластична при текущей рыночной цене. В результате цена продукта и предельный доход равны. При совершенной конкуренции цена и предельный доход взаимозаменяемы. Таким образом – чтобы максимизировать прибыль и минимизировать убытки, конкурентной фирме необходимо производить в точке, где цена равна предельным издержкам (P = MC ).
Абсолютная (чистая) монополия существует, когда одна фирма является единственным производителем продукта, у которых нет близких заменителей , т.е. фирма и отрасль – синонимы. Фирма осуществляет значительный контроль над ценой и существуют какие-либо барьеры для вступления в отрасль другой фирмы (экономические, юридические, и т.д.). Т.к. чистый монополист является отраслью, то его кривая спроса представляет собой кривую отраслевого спроса. Кривая отраслевого спроса не является совершенно эластичной и является нисходящей:
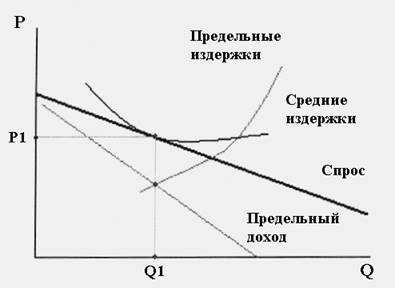
Нисходящая кривая спроса означает, что чистая монополия может увеличить свои продажи, только назначая более низкую цену на единицу своей продукции. Тот факт, что монополист должен понизить цену, чтобы повысить продажи, является причиной того, что предельный доход становится меньше, чем цена(средний доход) для каждого уровня выпуска, кроме первого. Т.е. P> MR .
Кривая предельного дохода всегда располагается ниже, чем кривая спроса. В случае простой монополии предельный доход, получаемый фирмой от продажи одной дополнительной единицы продукции, ниже, чем цена, по которой такая единица продаётся ( а не равна этой цене, как в случае совершенной конкуренции ). Разрыв между ценой и предельным доходом возникает потому, что фирма продаёт всю продукцию, произведённую в течение данного периода времени, по одинаковой цене. Это значит : если фирма хочет добиться увеличения объёма продаж, цена должна быть снижена на все единицы продукции, а не только на последнюю из них.
Монополист потеряет весь свой монопольный доход, если станет производить такое большое количество товара, что его цена предложения окажется равной цене спроса на этот товар. Количество товара, обеспечивающего максимум монопольного дохода, всегда значительно меньше. Равновесное количество товара, произведенного в условиях свободной конкуренции, оказывается всегда меньше, чем то, цена спроса которого равна монопольной цене предложения.
Стремящийся к прибыли монополист использует то же логическое обоснование, что и стремящаяся к прибыли фирма в конкурентной отрасли. Он будет производить каждую последующую единицу продукции до тех пор, пока её реализация обеспечивает больший прирост валового дохода, чем увеличение валовых издержек. Точнее говоря, фирма будет наращивать производство продукции до такого объёма, при котором предельный доход равен предельным издержкам. Другими словами, максимизация прибыли требует равенства предельного дохода и предельных издержек. Таким образом, максимизирующая свою прибыль фирма никогда не будет расширять свои объёмы продаж до величин, когда спрос по цене становится неэластичным. Таким образом МС= MR . (это точка пересечения кривых предельных издержек и предельного дохода на рисунке – Q 1 характеризует объём выпуска продукции).
mirznanii.com
Волшебная формула: когда MR = МС : Экономика для чайников : Юридическая библиотека
В типичном случае, когда рыночная цена достаточно высока для того, чтобы фирма хотела производить определенное количество продукта, для определения оптимального количества продукта, q, которое должна производить фирма, используется до смешного, простая формула. Фирма хочет производить тот уровень продукта, при котором предельный доход равен предельным издержкам (MR = МС), —
Производство, при котором MR = МС, позволяет получить следующие два результата.
Оно минимизирует убытки фирмы, если фирма терпит убытки из-за низкой продажной цены на свой продукт.
Оно максимизирует прибыль фирмы, если она может получать прибыль благодаря тому, что продажная цена достаточно высока.
Идея, заключенная в равенстве MR и МС, очень проста. К ней приводит анализ затрат и выгод. Если производство и продажа бутылки приносит больше дохода, чем затраты на ее производство, значит, ее нужно делать. Если же нет, значит, ее делать не нужно. Правда, это легко запомнить?
Давайте теперь снова вернемся к нашему примеру. Представьте, что корпорация LemonAid может продать каждую бутылку лимонада, которую она производит, за 2 долл. Экономистам нравится говорить, что предельный доход от каждой бутылки составляет 2 долл., поскольку каждая произведенная бутылка при продаже приносит дополнительные 2 долл.
Менеджеры фирмы должны решить, сколько бутылок лимонада должно быть произведено на их предприятии, основываясь на том, будет ли каждая данная бутылка стоить больше или меньше 2 долларов предельного дохода, который получит фирма в результате продажи лимонада.
Будьте очень внимательны на этом этапе. Вам нужно запомнить, что та стоимость, на которую обращают внимание менеджеры, — это предельная стоимость каждой отдельной бутылки, МС. Это потому, что если они решают производить именно эту бутылку, то нужно рассматривать стоимость производства этой бутылки отдельно от стоимости производства всех произведенных ранее бутылок для того, чтобы сравнить ее с доходом, который бутылка принесет, если ее произведут и продадут. Только МС отдельной бутылки имеет значение; все бутылки, произведенные ранее, остаются без внимания, а менеджеры нацелены на определение стоимости производства следующей.
Если МС этой бутылки меньше 2 долл., то ясно, что есть смысл ее производить; в этом случае менеджеры примут решение ее производить. С другой стороны, если МС будет превышать 2 долл., производство бутылки приведет к получению убытка; в таком случае менеджеры примут решение не производить ее.
Рассматривая МС каждой отдельной бутылки (первой, пятой, девяносто седьмой и т.д.) и сравнивая ее с предельным доходом, который может получить фирма от ее продажи, менеджеры могут точно определить, сколько бутылок нужно производить их предприятию. Необходимые сравнения могут быть проведены с помощью таблицы расходов, такой, как табл. 10.1, но еще проще будет это сделать с помощью графика.
На рис. 10.3 я начертил кривые предельных издержек (МС), средних переменных издержек (AVC) и средних совокупных издержек (АТС) корпорации LemonAid. Еще я провел горизонтальную линию, начинающуюся на отметке «2 долл.», — таков предельный доход от продажи каждой из бутылок, которую фирма может решить производить. Я обозначил линию формулой р = MR = 2 долл. для подтверждения того факта, что продажная цена бутылки составляет 2 долл., что совпадает с предельным доходом.
Взгляните на количество q*, которое соответствует точке пересечения горизонтальной линии р = MR = 2 долл. и кривой МС. Как вы видите, q* = 440 бутылок. Это уровень продукта, который выберет фирма для получения максимальной прибыли.
Для того чтобы понять, почему привязка к MR = МС максимизирует прибыль, давайте вернемся к табл. 10.1, приведенной ранее в этой главе, и рассмотрим каждую единицу продукции, q, для которой справедливо неравенство q < 440. Для всех этих единиц предельный доход будет больше предельной себестоимости (MR > МС), что значит: доходы от продажи каждой из этих бутылок превысят затраты на их производство. Например, давайте возьмем бутылку под номером 140. Ее предельная себестоимость составляет всего 0,89 долл., но ее можно продать за 2,00 долл. Понятно, что вам нужно произвести эту бутылку, поскольку от ее продажи вы получите больше денег, чем было затрачено на ее производство. Это утверждение справедливо для всех остальных бутылок, где q < 440; вам нужно производить их, потому что все они принесут вам прибыль.
С другой стороны, для всех единиц, превышающих уровень продукта q* (q > 440), справедливо обратное: предельный доход меньше предельной себестоимости (MR < МС).
Вы потеряете деньги, если вы произведете и продадите эти бутылки. Например, на уровне продукта в 470 бутылок, МС составит 2,67 долл., тогда как MR составляет всего 2,00 долл. Если вы произвели продукт на этом уровне, то на бутылке под номером 470 вы потеряете 67 центов. Ясно, что вам не захочется в этом участвовать.
Сравнивая предельный доход и предельные издержки на всех уровнях продукта, вы можете видеть, что менеджеры корпорации LemonAid хотят производить точно q* = 440 единиц — то количество единиц, при котором линии MR и МС пересекаются.
Как я упоминал во введении к этому разделу, производство, где MR = МС, не гарантирует вам прибыли, но оно хотя бы гарантирует, что вы производите бутылки, приносящие больше денег, чем было потрачено на их производство. Причина, по которой эта формула сама по себе не может гарантировать прибыль, заключена в том, что она не принимает в расчет фиксированные издержки, которые вам нужно платить безотносительно уровня продукта, который вы производите. Даже если вы производите бутылки, чей предельный доход по крайней мере равен предельной себестоимости, вы все еще можете не получить достаточно выручки для оплаты ващих фиксированных издержек.
bookzie.com
