Построение объемных фигур: Цифровое образование и обучение Мozaik

Содержание

Построение объемных фигур и сечений Geogebra 3d

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «МОРДОВСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ ИНСТИТУТ

ИМЕНИ М. Е. ЕВСЕВЬЕВА»

Физико-математический факультет

Кафедра информатики и вычислительной техники

РЕФЕРАТ

«Построение объемных фигур и сечений в GeoGebra 3D»

Выполнила:

студентка 5 курса группы МДИ-114

Сорочкина М.А.

Саранск 2018

Введение

GeoGebra – это бесплатная, кроссплатформенная динамическая математическая программа для всех уровней образования, включающая в себя геометрию, алгебру, таблицы, графы, статистику и арифметику, в одном удобном для использования пакете.

Кроме того, у программы богатые возможности работы с функциями (построение графиков, вычисление корней, экстремумов, интегралов и т. д.) за счёт команд встроенного языка (который, кстати, позволяет управлять и геометрическими построениями).

В отличии от других программ для динамического манипулирования геометрическими обьектами, идея GeoGebra заключается в интерактивном сочетании геометрического, алгебраического и числового представления. Вы можете создавать конструкции с точками, векторами, линиями, коническими сечениями, а также математическими функциями, а затем динамически изменять их.

Кроме того, GeoGebra позволяет напрямую вводить уравнения и манипулировать координатами. Таким образом, можно легко составлять графики функций, работать со слайдерами для подбора необходимых параметров, искать символические производные, и использовать мощные команды вроде корня и последовательности.

Интерфейс программы GeoGebra (ГеоГебра) напоминает классную доску, на которой можно рисовать графики, создавать геометрические фигуры и т.п. В окне программы будет наглядно отображены производимые изменения: если вы измените уравнение, кривая перестроится, изменится масштаб или ее положение в пространстве, уравнение, написанное рядом с кривой, автоматически будет скорректировано, согласно новым значениям.

Программу GeoGebra широко используют в мире миллионы пользователей для обучения алгебре и геометрии. Процесс обучения нагляден благодаря визуальной форме использования приложения.

Возможности программы по математике не ограничиваются только построением графиков, программу GeoGebra можно будет использовать для интерактивных чертежей при решении геометрических задач. Программа ГеоГебра обладает мощными и функциональными возможностями, которые позволяет наглядно и просто обучаться математике.

Приложение включает в себя геометрию, алгебру, есть возможность совершать арифметические операции, создавать таблицы, графики, возможна работа со статистикой, работа с функциями, поддерживается создание анимации и т.д. В программе GeoGebra можно будет создавать различные 2D и 3D фигуры, интерактивные ролики, которые затем можно будет размещать в интернете.

Все приложения, входящие в состав программы GeoGebra, доступны и синхронизируются между собой для работы в составе одного пакета.

GeoGebra была создана Маркусом Хохенвартером. Программа написана на языке Java, приложение поддерживает работу в различных операционных системах: Windows, Mac OS X, Linux, Android.

С сайта производителя можно будет скачать обычную версию программы GeoGebra для установки на компьютер. Также можно будет скачать переносную версию программы (GeoGebra Portable) для соответствующей операционной системы.

После запуска GeoGebra на компьютере, ознакомимся с интерфейсом программы.

Интерфейс GeoGebra

Интерфейс программы GeoGebra напоминает графический редактор. Программу можно использовать для черчения, но это не основное предназначение приложения.
Давайте рассмотрим основные элементы интерфейса программы GeoGebra:

Полоса меню. Из меню вы можете изменить настройки программы.
Панель инструментов. Здесь находятся инструменты для создания объектов. После щелчка по треугольнику в правом нижнем углу кнопки, будут открыты дополнительные инструменты. Операции, доступные в панели инструментов, можно производить с помощью строки ввода.
Панель объектов. В Панели объектов отображаются введенные переменные и функции. Вместо имен переменных здесь отображаются их значения. Для того, чтобы увидеть формулу в символьном виде, нужно будет кликнуть по ней правой кнопкой мыши.
Кнопки «Отменить» и «Повторить».
Строка ввода. Это основной инструмент при работе в программе GeoGebra. Здесь вводятся команды и формулы, задаются значения переменных. Справа от строки ввода расположена кнопка «Список команд». С помощью дополнительных команд можно будет вводить команды и отсутствующие на клавиатуре символы.
Рабочая область. Все построения в программе производятся в рабочей области. Вы можете изменить масштаб с помощью колесика мыши, перемещать по рабочей области ось координат.

Далее попытаемся выполнить некоторые элементарные действия в программе GeoGebra. » в программе GeoGebra обозначает возведение в степень.

Далее нажмите на кнопку «Enter». После этого в рабочей области будет построен график. Рисунок можно будет масштабировать с помощью колесика мыши. Для перемещения рабочей области нужно будет нажать на клавишу «Shift», одновременно удерживая нажатой левую кнопку мыши.

Вы можете перемещать сам график при помощи нажатой правой кнопки мыши, при этом, в Панели объектов будут отображены изменения в уравнении.

Создание треугольника в GeoGebra

Давайте попробуем начертить треугольник в программе GeoGebra. Для этого нужно будет перейти в «геометрический» режим для того, чтобы включить отображение сетки, и отключить отображение оси координат.

Кликните правой кнопкой мыши по оси координат, в контекстном меню выберите пункт «Сетка», а затем там кликните по пункту «Оси» для отключения оси координат. На панели инструментов нажмите на кнопку «Многоугольник».

После этого нарисуйте треугольник, последовательно установив три вершины. При необходимости, вы можете ввести точные координаты. Для этого вам нужно будет кликнуть по точке правой кнопкой мыши.

Далее вы можете создать биссектрису угла. Для этого нажмите на треугольную кнопку под кнопкой «Перпендикулярная прямая», а затем выберите из выпадающего списка инструмент «Биссектриса угла». После этого, кликните по двум отрезкам образующих угол, биссектриса будет создана.

Geogebra online

У программы GeoGebra имеется онлайн версия: Geogebra online (ГеоГебра онлайн). После перехода на сайт www.geogebra.org, вы можете открыть программу GeoGebra в своем браузере для выполнения необходимых действий. Таким образом, даже не устанавливая программу GeoGebra на свой компьютер, при наличии интернета, вы можете работать в этой математической программе, войдя на онлайн сервис со своего мобильного устройства.

Поскольку построение простейших геометрических фигур рассмотрено в предыдущей главе при описании инструментов, то в данной главе они рассматриваться не будут. Данная глава является практикумом по освоению среды GeoGebra (3DwithJOGL2) на примерах решения конкретных задач. Задачи подобраны таким образом, чтобы они в полной мере охватывали возможности геометрических построений с использованием среды GeoGebra (3DwithJOGL2).

Построение призмы

Задача:

Построить призму ABCDEA1B1C1D1E1.

Решение:

Выбираем функцию Призма и отмечаем 5 точек на координатной оси как показано на рисунке 15.

Рис 15

Нажимая по оси z на нужную нам высоту, получим призму ABCDEA1B1C1D1E1.(рис 16)

Рис 16

Построение пирамиды

Задача:

Построить пирамиду SABCDE.

Решение:

Выбираем функцию Пирамида и отмечаем 5 точек на координатной оси, как показано на рисунке 17.

Рис 17

Нажимая по оси z на нужную нам высоту и после переименования точки на оси zполучим пирамиду SABCDE.(рис 18)

Рис 18

Построение прямоугольного параллелепипеда

Задача:

Построить прямоугольный параллелепипед ABCDA1B1C1D1.

Решение:

При помощи строки ввода ставим 4 точки на плоскость XOY и одну точку на плоскость XYZ как показано на рисунке 19.

Рис 19

После выполнения вышеуказанных шагом выбираем опцию Призма соединяем точки A,B,C,D потом нажимаем на точку А и получаем прямоугольный параллелепипед ABCDA1B1C1D1.(рис 20)

Рис 20

Построение цилиндра

Задача:

Построить цилиндр с радиусом 2.

Решение:

Для построения цилиндра есть опция Цилиндр. Выбираем эту опцию и на оси z выбираем две точки, после чего выйдет окно с запросом на радиус как на рисунке 21.

Рис 21

Вводим значение радиуса и имеем цилиндр с данным радиусом.(рис 22)

Рис 22

Построение конуса

Задача:

Построить конус с радиусом 3.

Решение:

Для построения конуса есть опция Cone. Выбираем эту опцию и на оси

Z выбираем две точки после чего выйдет окно с запросом на радиус как на рисунке 23.

Рис 23

Вводим значение радиуса и имеем конус с данным радиусом. (рис 24)

Рис 24

Построение шара

Задача:

Построить шар с радиусом 3.

Решение:

Шар можно построить с помощью двух опций. Первая из них называется

Сфера по центру и точке. При этом нужно выбрать точку центра и другую точку, которая будет являться крайней точкой сферы. Вторая функция Сфера по центру и радиусу. В этом случае нужно выбрать точку центра и выскакивает окно с запросом ввести радиус как показано на рисунке 25.

Рис 25

После ввода значения радиуса строиться сфера (рис 26)

Рис 26

Построение сечения пирамиды

Задача:

На ребрах AB,BC и CD тетраэдра ABCD отмечены точки M,N и P (рис 27).

Построить сечение тетраэдра плоскостью MNP.

Рис 27

Решение:

Построим сначала прямую, по которой плоскость MNP пересекается с плоскостью грани ABC. Точка M является общей точкой этих плоскостей. Для построения еще одной общей точки продолжим отрезки NP и BC до их пересечения в точке E (рис.28), которая и будет второй общей точкой плоскостей MNP и ABC. Следовательно, эти плоскости пересекаются по прямой ME. Прямая ME пересекает ребро AC в некоторой точке Q. Четырехугольник MNPQ – искомое сечение.

Рис 28

Построение сечения прямоугольного параллелепипеда

Задача:

На ребрах параллелепипеда даны три точки A, B и C. Построить сечение параллелепипеда плоскостью ABC.

Решение:

Построение искомого сечения зависит от того, на каких ребрах параллелепипеда лежат точки A, B и C. Рассмотрим некоторые частные случаи. Если точки A,B и Cлежат на ребрах, выходящих из одной вершины (рис. 29), нужно провести отрезкиAB, BC и CA, и получится искомое сечение – треугольник ABC. Если точки A, B и Cрасположены так, как показано на рисунке 30, то сначала нужно провести отрезкиAB и BC, а затем через точку A провести прямую, параллельную AB. Пересечения этих прямых с ребрами нижней грани дают точки E и D. Остается провести отрезокED, и искомое сечение – пятиугольник ABCDE – построено. Более трудный случай, когда данные точки A,B и C расположены так, как показано на рисунке 31. В этом случае можно поступить так, сначала построим прямую, по которой секущая плоскость пересекается с плоскостью нижнего основания. Для этого проведем прямую AB и продолжим нижнее ребро, лежащее в той же грани, что и прямая AB, до пересечения с этой прямой в точке M. Далее через точку M проведем прямую, параллельную прямой BC. Это и есть прямая, по которой секущая плоскость пересекается с плоскостью нижнего основания. Эта прямая пересекается с ребрами нижнего основания в точках E и F. Затем через точку E проведем прямую, параллельную прямой AB, и получим точку D. Наконец, проводим отрезки AF и CD, и искомое сечение – шестиугольник ABCDEF – построено.

Рис 29 Рис 30

Рис 31

Заключение

Программа GeoGebra предназначена для обучения математике. С помощью этой программы можно работать в динамической математической среде, включающей в себя геометрию, алгебру и другие разделы, с широкими функциональными возможностями.

Использование программы GeoGebra на уроках позволяет:

–оптимизировать учебный процесс, более рационально используя время на различных этапах урока;

–осуществлять дифференцированный подход в обучении; — проводить индивидуальную работу, используя персональные компьютеры;

–снизить эмоциональное напряжение на уроке, внося в него элемент игры;

–расширять кругозор учащихся;

–способствует развитию познавательной активности учащихся.

Прогнозируемые эффекты от применения данной технологии:

–возможно повышение уровня самооценки;

–развитие навыка самоконтроля;

–побуждение к открытию и изучению нового в сфере информационных технологий, желанию поделиться с товарищами своими знаниями.

Список используемых источников

https://ru.wikipedia.org/wiki/GeoGebra
http://www.uchportal.ru/programma-trenazhyor-po-matematike-obyknovennye-drobi
http://my-soft-blog.net/397-geogebra.html
http://www.uchportal.ru/programma-trenazhyor-po-matematike-obyknovennye-drobi
http://www.uchportal.ru/kompyuternaya-programma-po-matematike-deliteli-naturalnogo-chisla
hhttp://soft.mydiv.net/win/download-GeoGebra.htmlttp://s427.spb.ru/attachments/article/480/matem_spo.pdf

«Построение объемных фигур и сечений в GeoGebra 3D»

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«МОРДОВСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ ИНСТИТУТ

ИМЕНИ М. Е. ЕВСЕВЬЕВА»

Физико-математический факультет

Кафедра информатики и вычислительной техники

РЕФЕРАТ

на тему:

«Построение объемных фигур и сечений в GeoGebra 3D»

Выполнила:

студентка 5 курса группы МДМ-213

Сурдина А. А.

Проверила:

кандидат физико-математических наук, доцент

Кормилицына Т. В.

Саранск 2018

Введение

GeoGebra – это бесплатная, кроссплатформенная динамическая математическая программа для всех уровней образования, включающая в себя геометрию, алгебру, таблицы, графы, статистику и арифметику, в одном удобном для использования пакете.

Кроме того, у программы богатые возможности работы с функциями (построение графиков, вычисление корней, экстремумов, интегралов и т.д.) за счёт команд встроенного языка (который, кстати, позволяет управлять и геометрическими построениями).

GeoGebra была создана Маркусом Хохенвартером. Программа написана на языке Java, приложение поддерживает работу в различных операционных системах: Windows, Mac OS X, Linux, Android.

После запуска GeoGebra на компьютере, ознакомимся с интерфейсом программы.

1. Интерфейс GeoGebra

При запуске окно программы имеет вид, приведенный на рисунке 1.

Интерфейс программы GeoGebra напоминает графический редактор. Программу можно использовать для черчения, но это не основное предназначение приложения.
Основные элементы интерфейса программы GeoGebra:

Полоса меню. Из меню можно изменить настройки программы.
Панель инструментов. Здесь находятся инструменты для создания объектов. После щелчка по треугольнику в правом нижнем углу кнопки, будут открыты дополнительные инструменты. Операции, доступные в панели инструментов, можно производить с помощью строки ввода.
Панель объектов. В Панели объектов отображаются введенные переменные и функции. Вместо имен переменных здесь отображаются их значения. Для того, чтобы увидеть формулу в символьном виде, нужно будет кликнуть по ней правой кнопкой мыши.
Кнопки «Отменить» и «Повторить».
Строка ввода. Это основной инструмент при работе в программе GeoGebra. Здесь вводятся команды и формулы, задаются значения переменных. Справа от строки ввода расположена кнопка «Список команд». С помощью дополнительных команд можно будет вводить команды и отсутствующие на клавиатуре символы.
Рабочая область. Все построения в программе производятся в рабочей области. Вы можете изменить масштаб с помощью колесика мыши, перемещать по рабочей области ось координат.

Рис 1 – Интерфейс программы GeoGebra

2. Использование инструментов для построений в Geogebra 3D

Для открытия полотна 3D нужно перейти в строке меню вкладку вид (Рисунок 2)

Легким нажатием мыши на вкладку Полотно 3D GeoGebra превращается в 3D конструктор (Рисунок 3а и 3б)

Самыми важными фигурами в геометрии являются пирамида и призма, поэтому данная подгруппа функций именно для этих фигур. Функции Пирамида и Призма позволяют строить данные фигуры через любые точки и в любой плоскости оси координат ( Рисунок 4).

Рис 4 – Функции Пирамиды и Призмы

С помощью функций Выдавить пирамиду или конус и Выдавить призму или цилиндр возможности построения увеличиваются в двойне. Последняя подгруппа функций которую хочу представить это функции Сфера по точке и центру, Сфера по центру и радиусу, Cone и Cylinder (Рисунок 5 ). Как видно по названиям эта подгруппа специализируется по строению сферических фигур.

Рис 5 – Функции Сферы

3. Построение объемных фигур

Построение призмы.

Задача. Построить призму ABCD..G.

Решение: 1) Нужно выбирать функцию Призма и отметить 4 точки на координатной оси как показано на рисунке.

2) Нажимая по оси z на нужную высоту получится призма ABCD. .G.

2. Построение пирамиды

Задача. Построить пирамиду SABCDE.

Решение: 1) Нужно выбрать функцию Пирамида и отметить 4 точки на координатной оси как показано на рисунке.

2) Нажать по оси z на нужную высоту и после переименования точки на осиz получим пирамиду SABCDE

3. Построение прямоугольного параллелепипеда

Задача. Построить прямоугольный параллелепипед ABCD..G.

Решение: При помощи строки ввода ставим 4 точки на плоскость XOYи одну точку на плоскость XYZ как показано на рисунке.

2) После выполнения вышеуказанных действий выбираем опцию Призма соединяем точки A,B,C,D потом нажимаем на точку и получаем прямоугольный параллелепипед ABCD..F

4. Построение цилиндра

Задача. Построить цилиндр с радиусом 3.

Решение: Для построения цилиндра есть опция Цилиндр. Выбираем эту опцию и на оси z выбираем две точки после чего выйдет окно с запросом на радиус как на рисунке 14.

Рис 14 – Окно с запросом на радиус

Вводим значение радиуса и имеем цилиндр с данным радиусом

5. Построение конуса

Задача. Построить конус с радиусом 3.

Решение: Для построения конуса есть опция Cone. Выбираем эту опцию и на оси z выбираем две точки после чего выйдет окно с запросом на радиус как на рисунке 16.

Рис 16 – Окно с запросом на радиус

Вводим значение радиуса и имеем конус с данным радиусом.

4. Построение плоских сечений

1. Построение сечения пирамиды

Задача 1. На ребрах AB, BC и CD тетраэдра ABCD отмечены точки M, N и P. Построить сечение тетраэдра плоскостью MNP.

Решение: Построим сначала прямую, по которой плоскость MNP пересекается с плоскостью грани ABC. Точка M является общей точкой этих плоскостей. Для построения еще одной общей точки продолжим отрезки NP и BC до их пересечения в точке E, которая и будет второй общей точкой плоскостей MNP и ABC. Следовательно, эти плоскости пересекаются по прямой ME.

Прямая ME пересекает ребро AC в некоторой точке Q. Четырехугольник MNPQ – искомое сечение.

Задача 2. Точка M лежит на боковой грани ADB тетраэдра DABC (рис.3). Построить сечение тетраэдра плоскостью, проходящей через точку M параллельно основанию ABC.

Решение: Так как секущая плоскость параллельна плоскости ABC, то она параллельна прямым AB, BC и CA. Следовательно, секущая плоскость пересекает боковые грани тетраэдра по прямым, параллельным сторонам треугольника ABC. Отсюда вытекает следующий способ построения искомого сечения. Проведём через точку M прямую, параллельную отрезку AB, и обозначим буквами P и Q точки пересечения этой прямой с боковыми ребрами DA и DB. Затем через точку P проведем прямую, параллельную отрезку AC, и обозначим буквой R точку пересечения этой прямой с ребром DC. Треугольник PQR–искомое сечение.

Построение сечения прямоугольного параллелепипеда

Задача 1. На ребрах параллелепипеда даны три точки A, B и C. Построить сечение параллелепипеда плоскостью ABC.

Решение: Построение искомого сечения зависит от того, на каких ребрах параллелепипеда лежат точки A, B и C. Рассмотрим некоторые частные случаи. Если точки A, B и C лежат на ребрах, выходящих из одной вершины, нужно провести отрезки AB, BC и CA, и получится искомое сечение–треугольник ABC. Если точки A, B и C расположены так, как показано на рисунке 6, то сначала нужно провести отрезки AB и BC, а затем через точку A провести прямую, параллельную AB. Пересечения этих прямых с ребрами нижней грани дают точки E и D. Остается провести отрезок ED, и искомое сечение–пятиугольник ABCDE–построено. Более трудный случай, когда данные точки A, B и C расположены так, как показано на рисунке 22. В этом случае можно поступить так, сначала построим прямую, по которой секущая плоскость пересекается с плоскостью нижнего основания. Для этого проведем прямую AB и продолжим нижнее ребро, лежащее в той же грани, что и прямая AB, до пересечения с этой прямой в точке M. Далее через точку M проведем прямую, параллельную прямой BC. Это и есть прямая, по которой секущая плоскость пересекается с плоскостью нижнего основания. Эта прямая пересекается с ребрами нижнего основания в точках E и F. Затем через точку E проведем прямую, параллельную прямой AB, и получим точку D. Наконец, проводим отрезки AF и CD, и искомое сечение –шестиугольник ABCDEF– построено.

Заключение

Программа GeoGebra предназначена для обучения математике. С помощью этой программы можно работать в динамической математической среде, включающей в себя геометрию, алгебру и другие разделы, с широкими функциональными возможностями.

Использование программы GeoGebra на уроках позволяет:

– оптимизировать учебный процесс, более рационально используя время на различных этапах урока;

– осуществлять дифференцированный подход в обучении; — проводить индивидуальную работу, используя персональные компьютеры;

– снизить эмоциональное напряжение на уроке, внося в него элемент игры;

– расширять кругозор учащихся;

– способствует развитию познавательной активности учащихся.

Прогнозируемые эффекты от применения данной технологии:

– возможно повышение уровня самооценки;

– развитие навыка самоконтроля;

– побуждение к открытию и изучению нового в сфере информационных технологий, желанию поделиться с товарищами своими знаниями.

Список используемых источников

Иванчук, Н.В. Использование компьютерной программы GeoGebra на уроках математики в 7-11 классах: Методическое пособие / Н. В. Иванчук, О. В. Эйкен. – Мурманск: МГПУ, 2013.– 36 с.
Погорелов, А.В. Геометрия: Учеб. Для 7–11 кл. общеобразоват. учреждений.–9-е изд.–М.:Просвещение, 2014.
GeoGebra [Электронный ресурс]. — Режим доступа: https://ru.wikipedia. org/wiki/GeoGebra
Внеклассные мероприятия по информатике [Электронный ресурс]. — Режим доступа: http://www.uchportal.ru/programma-trenazhyor-po-matematike-obyknovennye-drobi
Живая геометрия [Электронный ресурс]. — Режим доступа: http://my-soft-blog.net/397-geogebra.html
Использование GeoGebra на уроках математики [Электронный ресурс]. — Режим доступа: hhttp://soft.mydiv.net/win/download-GeoGebra.htmlttp://s427. spb.ru/attachments/article/480/matem_spo.pdf

Трехмерные фигуры (трехмерные фигуры)

Что такое трехмерные фигуры?

В геометрии трехмерная фигура может быть определена как твердая фигура, объект или форма, имеющая три измерения: длину, ширину и высоту. В отличие от двухмерных фигур, трехмерные фигуры имеют высоту, которая совпадает с толщиной или глубиной. Трехмерность также записывается как 3D, и, следовательно, эти фигуры также обычно называют 3D-формами. Все трехмерные фигуры занимают пространство, которое измеряется объемом.

Примеры трехмерных фигур

Куб, прямоугольная призма, сфера, конус и цилиндр — основные трехмерные фигуры, которые мы видим вокруг себя.

Реальные примеры трехмерных фигур

Трехмерные фигуры можно увидеть повсюду вокруг нас. Мы можем видеть кубик в кубике Рубика и кубике, прямоугольную призму в книге и коробке, сферу в глобусе и шаре, конус в морковке и рожке мороженого, цилиндр в ведерке и бочка вокруг нас.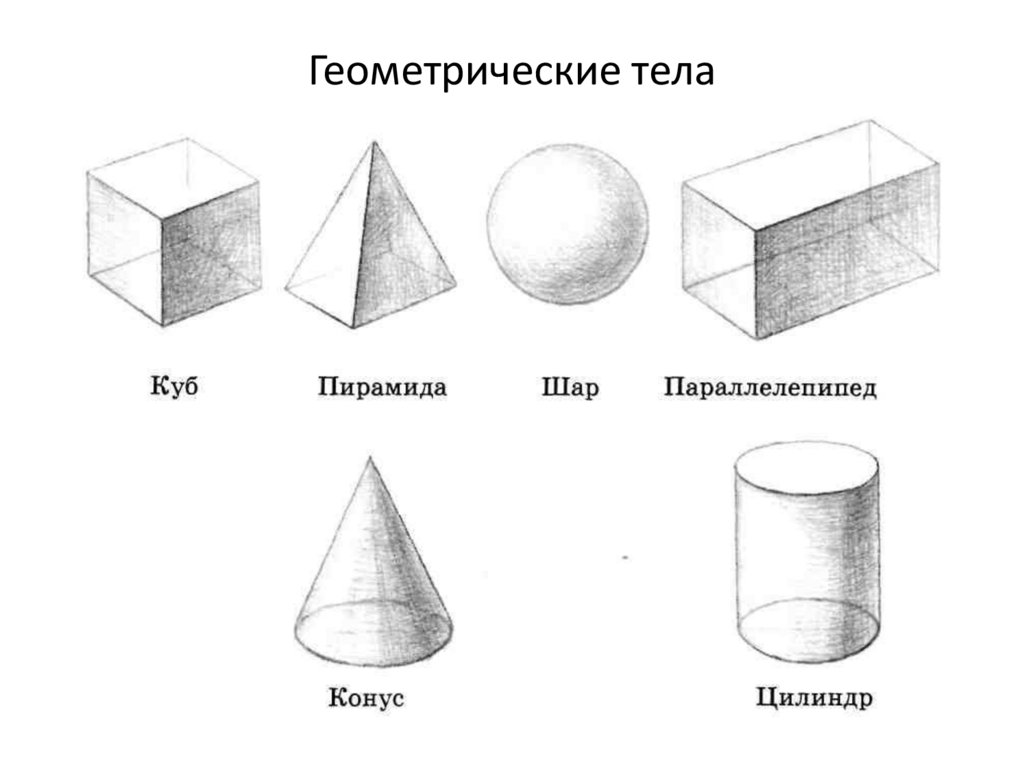

Атрибуты трехмерных фигур

У трехмерной фигуры есть три атрибута: грань, ребро и вершина. Давайте подробно разберемся с трехмерными формами и их свойствами.

Лицо: Каждая отдельная поверхность, плоская или изогнутая, трехмерной фигуры называется ее гранью.

Край: Линия, где встречаются две грани трехмерных фигур, называется его краем.

Вершина: каждый угол, где встречаются три грани трехмерных фигур, называется его вершиной. Вершины — это множественное число от вершины.

Список трехмерных фигур

Вот список названий трехмерных фигур с их изображениями и атрибутами.

Формула трехмерных фигур

Сеть трехмерных форм

Сеть — это узор, созданный при плоской поверхности трехмерной фигуры, показывающей каждую грань фигуры.

3D-фигуры могут иметь более одного шаблона цепей. Названия нескольких трехмерных фигур и их сетей показаны ниже:

Забавные факты :
Все трехмерные формы состоят из двухмерных форм.

Разница между 2D-формами и 3D-фигурами

Давайте различать 2D- и 3D-формы, разбираясь в двухмерных и трехмерных формах и их свойствах.

Решенные примеры

Пример 1: Что из следующего является трехмерной формой?

Конус Квадрат Сфера Кубовидный Цилиндр Параллелограмм

Решение:

Конус Сфера Кубовидно Цилиндр

Пример 2: Укажите, являются ли следующие верными или ложными .

Трехмерная форма имеет 3 измерения.
Трехмерные формы также называют плоскими формами.
Трехмерные фигуры занимают пространство.
Все трехмерные фигуры имеют плоские грани.

Решение:

Верно
Ложно. Трехмерные формы также называют объемными формами.
Верно
Ложно. Сфера представляет собой трехмерную форму без плоской грани.

Пример 3: Заполните таблицу атрибутами перечисленных трехмерных фигур.

Решение:

Пример 4: Сопоставьте объект с его формой.

Решение:

– (iii)
– (i)
– (iv)
– (ii)

4 единицы, длина 3 единицы и высота 5 единиц.

Решение:

Дан кубоид, имеющий три единицы длины, четыре единицы ширины и пять единиц высоты.

Площадь поверхности прямоугольного параллелепипеда $= 2 \times (\text{lw} + \text{wh} + \text{lh})$ квадратных единиц

$= 2 × (\text{lw} + \text{ wh} + \text{lh})$

$= 2[(3 \times 4) + (4 \times 5) + (3 \times 5)]$

$= 2(12 + 20 + 15) $

$= 2(47)$

$= 94$ квадратных единиц

Следовательно, площадь поверхности данного прямоугольного параллелепипеда равна 94 кв.ед.

Пример 6: Джейн любит пить молоко из цилиндрического стакана. Ее стакан имеет 15 единиц высоты и 3 единицы радиуса основания. Сколько молока она может налить в стакан?

Решение:

Учитывая, что высота стакана 15 единиц, а радиус основания 3 единицы.

Используя формулу объема цилиндра, мы можем найти объем стакана.

Объем стакана, $\text{V} = πr ² \text{h}$

$= π(3) ²(15)$

$= 135π$

$= 424,11 в ³ $

Следовательно, Джейн может налить в ее стакан примерно 424 кубических единицы молока.

Практические задачи

Какая фигура имеет две плоские грани и одну кривую?

Цилиндр

Сфера

Конус

Куб

Правильный ответ: Цилиндр
Цилиндр имеет две плоские поверхности, имеющие форму круга, и одну изогнутую поверхность.

Сколько квадратных фигур имеет сетка куба?

Правильный ответ: 6
Куб имеет 6 граней, которые являются квадратами. Итак, в сетке куба будет 6 квадратных фигур.

Что из следующего не имеет ребра?

Конус

Цилиндр

Куб

Сфера

Правильный ответ: Сфера
Сфера имеет одну сторону. Так что у него нет края.

Какая из данных фигур НЕ является трехмерной?

Трапеция

Призма

Пирамида

Куб

Правильный ответ: Трапеция
Трапеция представляет собой двумерную фигуру с четырьмя сторонами, одна пара противоположных сторон параллельна друг другу, а две другие стороны не равны параллельно.

Как называется пересечение двух граней объемной фигуры?

Вершина

Сторона

Грань

Край

Правильный ответ: Край
Ребра — это отрезки, соединяющие две грани. Грани куба пересекаются по линиям, называемым ребрами. Фигуры с несколькими ребрами называются сплошными фигурами. Пересечение нескольких плоскостей называется вершиной.

Объемные геометрические фигуры называются ________.

фигуры

тела

грани

многоугольники

Правильный ответ: тела
Трехмерные геометрические фигуры называются телами.

Что такое в математике сплошная заостренная фигура, соединенная с вершиной изогнутой поверхностью с плоским круглым основанием?

Конус

Сфера

Цилиндр

Пирамида

Правильный ответ: Конус
Конусы представляют собой трехмерные тела, состоящие из круглого основания, соединенного с одной точкой (называемой вершиной) изогнутыми сторонами. В качестве альтернативы вы можете думать о конусе как о круглой пирамиде.

Часто задаваемые вопросы

Какие существуют типы трехмерных фигур?

Куб, прямоугольный параллелепипед, цилиндр, сфера, конус, призма и пирамиды.

Каковы атрибуты трехмерных фигур?

Трехмерные фигуры имеют 3 измерения — длину, ширину и глубину. В результате этих размеров эти формы имеют атрибуты граней, ребер и вершин.

Что такое ребро?

Ребро — это линия, на которой встречаются две грани трехмерной формы.

Например, у куба 12 ребер.

Что такое вершины?

Вершины — это углы, в которых сходятся три грани. Например, прямоугольный параллелепипед имеет 8 вершин.

Какая польза от объема трехмерной формы?

Объем помогает найти пространство, занимаемое данной фигурой.

Кубическая сеть состоит из скольких квадратов?

Кубическая сеть состоит из шести квадратов.

Сети для построения 3D-форм: значение, типы, примеры

Автор Гурудат
Последнее изменение 19-07-2022

Сети для построения трехмерных фигур: Фигуры, имеющие только длину, называются одномерными фигурами. Линия – это одномерная фигура. Фигуры, имеющие длину и ширину, называются двумерными фигурами. Многоугольник, круг и т. д. являются двухмерными фигурами. Объекты и формы, имеющие длину, ширину и высоту, известны как трехмерные объекты и формы. Трехмерные формы известны как $3D$ формы.

В этой статье мы научимся рисовать сеть для некоторых трехмерных фигур. Сеть представляет собой трехмерное твердое тело, которое было сплющено. Это двухмерный контур скелета, который можно сложить и соединить вместе, чтобы получить трехмерную конструкцию. Сети используются для создания трехмерных фигур.

В нашей повседневной жизни мы видим вокруг себя несколько предметов, таких как книги, мячи, рожки для мороженого и т. д., которые имеют различную форму. Одна общая черта большинства этих объектов заключается в том, что все они имеют некоторую длину, ширину, высоту или глубину. То есть все они занимают пространство и имеют три измерения. Следовательно, они называются трехмерными формами.

Единственное различие между $2D$ и $3D$ формами заключается в том, что $2D$ формам не хватает толщины и глубины. В большинстве случаев $3D$ объекты создаются путем вращения $2D$ форм. $2D$ фигуры — это грани твердых фигур.

Изучение концепций 11-го экзамена CBSE

Куб, прямоугольный параллелепипед, конус, цилиндр, сфера, призма и т. д. представляют собой $3D$ формы. И тела изогнутой формы, и тела с прямыми сторонами, обращенными к многоугольнику, известные как многогранники, составляют $3D$ формы. Многогранники, которые построены на $2D$ структурах с прямыми сторонами, также известны как многогранники. Теперь давайте углубимся в особенности многогранников и криволинейных тел.

Различные твердые формы классифицируются на основе трех основных критериев. Три ключевые характеристики, отличающие $3D$ формы, перечислены ниже:

(i) Грани : Многоугольники, образующие многогранник, известны как грани.

(ii) Ребра: Отрезки прямых, общие для пересекающихся граней многогранника, называются его ребрами.

(iii) Вершины: Точки пересечения ребер многогранника называются его вершинами. В многограннике три или более ребра сходятся в одной точке, образуя вершину.

Многогранники

Слово «многогранники» является множественным числом от многогранника, который может быть определен как объемная форма, ограниченная многоугольниками. Как и многоугольник, у нас есть разные типы многогранников: правильные, неправильные, вогнутые и выпуклые многогранники.

Правильные многогранники с одинаковыми гранями также известны как платоновые тела. Двумя важными членами семейства многогранников являются призмы и пирамиды. Итак, дайте нам знать об этих двух многогранниках.

Призма

Призма представляет собой твердое тело, боковые грани которого представляют собой параллелограммы, концы (или основания) которых представляют собой конгруэнтные параллельные прямолинейные фигуры.

На приведенном выше рисунке изображена призма, концами которой являются прямолинейные фигуры $ABCDE$ и $A’B’C’D’E’$

Пирамида

Пирамида – это многогранник, основание которого многоугольник с любым числом сторон, остальные грани которого представляют собой треугольники с общей вершиной. Ниже приведен пример пятиугольной пирамиды.

Практика 11-го экзамена CBSE Вопросы

Криволинейные тела

Помимо многогранников, существуют изогнутые $3D$ формы, такие как сфера, конус и цилиндр. Конусы, например, имеют круглое основание, которое постепенно сужается от круглого основания к вершине. Поскольку все эти формы имеют изогнутые грани, их называют криволинейными телами.

Сети для построения трехмерных фигур

Чтобы лучше понять трехмерные объекты, мы пытаемся сформировать эти объекты из их сетей. Сеть для трехмерной формы есть не что иное, как контур скелета в $2$-измерении, который при складывании приводит к трехмерным формам. Чтобы понять это, давайте выполним следующее действие:

Возьмите картонную коробку. Обрежьте края, чтобы коробка лежала ровно. Теперь у вас есть сеть для этой коробки. Сеть представляет собой контур скелета в $2D$, как показано на первом рисунке, который при складывании, как показано на втором рисунке, дает $3D$ форму, как показано на третьем рисунке.

Правильно разделив края, вы смогли создать сеть. Можно ли повернуть процесс вспять?

Вот шаблон сетки для коробки на рисунке ниже. Скопируйте и увеличьте сетевую версию и попробуйте сделать коробку, подобающим образом складывая и склеивая. (Вы можете использовать подходящие единицы). Коробка солидная. Это $3D$ объект в форме прямоугольного параллелепипеда.

Таким образом, мы можем сказать, что сетка для трехмерной формы представляет собой двумерную форму, которую можно вырезать из листа бумаги или картона таким образом, чтобы, складывая ее, можно было сформировать трехмерную форму.

Попытка 11-го экзамена CBSE Пробные тесты

Сетка для куба

Куб — это трехмерный объект с шестью квадратными гранями одинакового размера и точных размеров. Куб имеет $6$ граней, $12$ ребер и $8$ вершин. Сетка для цельного куба показана ниже.

Мы можем нарисовать $11$ сетей для куба.

Сетка для прямоугольного параллелепипеда

Трехмерная твердая фигура с $6$ прямоугольными гранями, $8$ вершинами и $12$ ребрами называется прямоугольным параллелепипедом. Это одна из наиболее часто встречающихся форм вокруг нас.

Сетка для сплошного прямоугольного параллелепипеда показана ниже.

Мы можем нарисовать $54$ сети для прямоугольного параллелепипеда.

Сетка для цилиндра

Цилиндр представляет собой твердую трехмерную форму, состоящую из двух параллельных оснований, соединенных изогнутой поверхностью. Эти основания имеют форму круглого диска. Ось цилиндра — это линия, идущая от центра или соединяющая центры двух круглых оснований. Высота представляет собой расстояние между двумя основаниями цилиндра, которое называется перпендикулярным расстоянием.

Цилиндр имеет $3$ граней, $2$ ребер и $0$ вершин.

Сетка для сплошного цилиндра показана ниже.

Сетка для конуса

Трехмерная фигура с круглым основанием, сужающимся к острой точке, называемой вершиной, называется конусом.

Конус имеет одну вершину, одно изогнутое ребро, одну изогнутую грань и одну плоскую грань. Сетка для сплошного конуса показана ниже.

Шаблон сетки для треугольной призмы

Трехмерная фигура с двумя одинаковыми концами в форме треугольника, соединенных одинаковыми параллельными линиями, известна как треугольная призма. Это многогранник с тремя прямоугольными сторонами и двумя параллельными и конгруэнтными треугольными основаниями на каждой стороне.

Сетка для треугольной призмы показана ниже.

Сетка для квадратной пирамиды

Квадратная пирамида представляет собой трехмерную геометрическую форму с квадратным основанием и четырьмя треугольными гранями/сторонами, которые сходятся в одной точке. Эта пирамида является равносторонней квадратной пирамидой, если все треугольные грани имеют равные ребра.

Квадратная пирамида имеет $5$ граней, $5$ вершин и $8$ ребер.

Сетка для квадратной пирамиды показана ниже

Схема сетки для шестиугольной пирамиды

Шестиугольная пирамида представляет собой трехмерную пирамиду с шестиугольным основанием и сторонами или гранями в форме равнобедренных треугольников.

Ниже показана сетка для шестиугольной пирамиды.

Сетка для тетраэдра

Многогранник с $4$ гранями, $6$ ребрами и $4$ вершинами, а также треугольными гранями известен как тетраэдр.

Сетки для тетраэдра показаны ниже

Решенные примеры на сетках для построения трехмерных фигур

Вопрос 1. Определите сети, из которых можно сделать кубы.

Ответ : Куб имеет шесть квадратных граней. Таким образом, сети, используемые для изготовления кубов, следующие:
(ii), (iv) и (vi)

Q.2. Может ли следующее быть сеткой для игральной кости? Поясните свой ответ.

Ответ : Данную сетку кубика можно сложить, как показано ниже.

Здесь мы можем заметить, что при складывании данной сети противоположные грани штампа имеют $2$ и $5, 1$ и $4, 3$ и $6\ ). Если мы добавим их, мы получим \(7, 5, 9,$ соответственно. Но в игральной кости сумма чисел на противоположных гранях должна быть равна $7.$. Следовательно, данная сетка не может образовать игральную кость.

Q.3. Из следующих четырех сетей есть две правильных сети, образующих тетраэдр. Определите их.

Ответ : Из данных сетей тетраэдрами могут быть сети (i) и (iii).

Q.4. Вот неполная сетка для изготовления куба. Завершите его как минимум двумя разными способами. Помните, что у куба шесть граней. Сколько их здесь в сети? (Дайте две отдельные диаграммы.)

Ответ : В данной сети имеем $3$ граней. Мы можем завершить данную сеть для создания куба следующим образом.

Q.5. Напишите название многогранника, используя приведенную ниже сеть.

Ответ : Данная сеть состоит из двух треугольных граней и трех прямоугольных граней. Итак, данная сеть представляет собой треугольную призму.

Резюме

В этой статье мы изучили значение трехмерных фигур, определение многогранника и криволинейных тел. Трехмерные формы включают куб, прямоугольный параллелепипед, конус, цилиндр, сферу, призму и т. д. Кроме того, трехмерные формы составляют криволинейные тела и тела с прямыми сторонами, обращенными к многоугольнику, которые также называются многогранниками.

В этой статье мы узнали, что сеть для 3D-фигуры — это 2D-форма, вырезаемая на листе бумаги таким образом, чтобы можно было сформировать 3D-форму. Кроме того, мы узнали определение сетки трехмерного твердого тела и научились рисовать сеть для куба, прямоугольного параллелепипеда, цилиндра, конуса, треугольной призмы, квадратной пирамиды, шестиугольной пирамиды и тетраэдра. Также мы решили несколько примеров задач на основе сетей для построения трехмерных фигур.

Узнайте о различных геометрических фигурах

Часто задаваемые вопросы о сетях для построения трехмерных фигур

1. Что такое сети трехмерных фигур?
Ответ: Сеть для трехмерной формы представляет собой двухмерную форму, которую можно вырезать из листа бумаги или картона таким образом, чтобы, складывая ее, можно было сформировать трехмерную форму.

Q.2. Сколько сетей можно построить для куба?
Ответ: Мы можем нарисовать $11$ сетей для куба.

Q.3. Какую 3D-форму можно сделать из 2D-сети?
Ответ: Примерами $3D$ фигур являются куб, прямоугольный параллелепипед, конус, цилиндр, призма и т. д. Многогранники основаны на $2D$ формах с прямыми сторонами. Таким образом, мы можем сделать все многогранники и изогнутые тела в $3D$ форме, используя $2D$ сеть.

Q.4. Как сети полезны в реальной жизни?
Ответ: Чтобы найти площадь данного тела, мы можем использовать $2D$ сети.

Q.5. Может ли твердое тело иметь разные сети?

Ответ: Да, у твердого тела могут быть разные сети.

Построение объемных фигур и сечений Geogebra 3d

«Построение объемных фигур и сечений в GeoGebra 3D»

Трехмерные фигуры (трехмерные фигуры)

Что такое трехмерные фигуры?

Примеры трехмерных фигур

Реальные примеры трехмерных фигур

Атрибуты трехмерных фигур

Список трехмерных фигур

Формула трехмерных фигур

Сеть трехмерных форм

Разница между 2D-формами и 3D-фигурами

Решенные примеры

Практические задачи

Какая фигура имеет две плоские грани и одну кривую?

Сколько квадратных фигур имеет сетка куба?

Что из следующего не имеет ребра?

Какая из данных фигур НЕ является трехмерной?

Как называется пересечение двух граней объемной фигуры?

Объемные геометрические фигуры называются ________.

Что такое в математике сплошная заостренная фигура, соединенная с вершиной изогнутой поверхностью с плоским круглым основанием?

Часто задаваемые вопросы

Сети для построения 3D-форм: значение, типы, примеры

Многогранники

Призма

Пирамида

Криволинейные тела

Сети для построения трехмерных фигур

Сетка для куба

Сетка для прямоугольного параллелепипеда

Сетка для цилиндра

Сетка для конуса

Шаблон сетки для треугольной призмы

Сетка для квадратной пирамиды

Схема сетки для шестиугольной пирамиды

Сетка для тетраэдра

Решенные примеры на сетках для построения трехмерных фигур

Резюме

Часто задаваемые вопросы о сетях для построения трехмерных фигур

Добавить комментарий Отменить ответ