Вычисление определенных интегралов.
Страница 1 из 2
Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Формула Ньютона-Лейбница.
Если $F(x) -$ одна из первообразных непрерывной на $[a, b]$ функции $f(x),$ то справедлива следующая формула Ньютона-Лейбница: $$\int\limits_a^b f(x)\,dx=F(x)|_a^b=F(b)-F(a).$$
Примеры:
Используя формулу Ньютона-Лейбница, вычислить интегралы:
6.324. $\int\limits_{-1}^2x^3\,dx.$
Решение.
$$\int\limits_{-1}^2x^3\,dx=\left.\frac{x^4}{4}\right|_{-1}^2=\frac{(-1)^4}{4}-\frac{2^4}{4}=\frac{1}{4}-\frac{16}{4}=-\frac{15}{4}=-3,75.$$
Ответ: $-3,75.$
6.331. $\int\limits_{-\pi/4}^0\frac{dx}{\cos^2 x}.$
Решение.
$$\int\limits_{-\pi/4}^0\frac{dx}{\cos^2 x}=\left.tg x\right|_{-\pi/4}^0=tg 0-tg(-\pi/4)=0-(-1)=1.$$
Ответ: $1.$
6.335. $\int\limits_{1}^2\frac{dx}{2x-1}.$
Решение.
$$\int\limits_{1}^2\frac{dx}{2x-1}=\int\limits_1^2\frac{1}{2}d(\ln(2x-1))=\frac{1}{2}\left.\left(\ln(2x-1)\right)\right|_{1}^2=\ln3-\ln1=\ln 3.$$
Ответ: $\ln 3.$
6.347. $\int\limits_0^{\pi/2}\cos^3\alpha\,d\alpha.$
Решение.
$$\int\limits_{0}^{\pi/2}\cos^3\alpha\,d\alpha=\int\limits_0^{\pi/2}\cos^2xd\sin x=\int\limits_0^{\pi/2}(1-\sin^2 x)d\sin x=\left.\left(\sin x-\frac{\sin^3 x}{3}\right)\right|_{0}^{\pi/2}=$$ $$=\sin\frac{\pi}{2}-\frac{\sin^3{\pi/2}}{3}-\left(\sin 0-\frac{\sin^30}{3}\right)=1-\frac{1}{3}=\frac{2}{3}.$$
Ответ: $\frac{2}{3}.$
Свойства определенного интеграла:
1) Если $f(x)\geq 0$ на отрезке $[a, b],$ то $\int\limits_a^bf(x)dx\geq 0.$
2) Если $f(x)\leq g(x)$ на $[a, b]$ то $\int\limits_a^bf(x)\,dx\leq\int\limits_a^b g(x)\,dx.$
3) $|\int\limits_a^bf(x)\,dx|\leq\int\limits_a^b |f(x)|\,dx.$
4) Если $f(x)$ непрерывна на $[a, b], \,\, m -$ наименьшее, $M -$ наибольшее значения $f(x)$ на $[a, b],$ то $$m(b-a)\leq\int\limits_a^bf(x)\,dx\leq M(b-a)$$ (теорема об оценке определенного интеграла).
5) Если $f(x)$ непрерывна, а $g(x)$ интегрируема на $[a, b],\,\, g(x)\geq 0.$ $m$ и $M -$ наименьшее и наибольшее значения $f(x)$ на $[a, b],$ то $$m\int\limits_a^b g(x)\,dx\leq\int\limits_a^bf(x)g(x)dx\leq M\int\limits_a^bg(x)\,dx.$$ (обобщенная теорема об оценке определенного интеграла)
6) Если $f(x)$ непрерывна на $[a, b],$ то существует такая точка $c\in(a, b),$ что справедливо равенство $$\int\limits_a^bf(x)dx=f(c)(b-a).$$ (теорема о среднем значении)
Число $f(c)=\frac{1}{b-a}\int\limits_a^bf(x)\,dx$ называется средним значением функции $f(x)$ на отрезке $[a, b].$
7) Если $f(x)$ непрерывна а интегрируема на $[a, b]$ и $g(x)\geq 0,$ то существует такая точка $c\in(a, b),$ что справедливо равенство $$\int\limits_a^bf(x)g(x)dx=f(c)\int\limits_a^bg(x)dx$$ (обобщенная теорема о среднем).
8) Если $f^2(x)$ и $g^2(x)$ интегрируемы на $[a, b],$ то $$|\int\limits_a^bf(x)g(x)dx|=\sqrt{\int\limits_a^bf^2(x)dx\int\limits_a^bg^2(x)dx}$$ (неравенство Коши-Буняковского).
9) Интегрирование четных и нечетных функций в симметричных пределах. Если функция $f(x)$ четная, то $\int\limits_{-a}^af(x)dx=2\int\limits_0^af(x)dx.$ Если функция $f(x)$ нечетная, то $\int\limits_{-a}^af(x)dx=0.$
10) Если функция $f(x)$ непрерывна на отрезке $[a, b],$ то интеграл с переменным верхним пределом $$\Phi(x)=\int\limits_a^x f(t)dt$$ является первообразной для функции $f(x),$ т.е. $$\Phi'(x)=(\int\limits_a^x f(t)dt)’=f(x),\quad x\in[a, b].$$
11) Если функции $\phi(x)$ и $\psi(x)$ дифференцируемы в точке $x\in(a, b)$ и $f(t)$ непрерывна при $\phi(a)\leq t\leq \psi(b),$ то $$\left(\int\limits_{\phi(x)}^{\psi(x)} f(t)dt\right)_x’=f(\psi(x))\psi'(x)-f(\phi(x))\phi'(x).$$
Примеры.
6.364. а) Определить знак интеграла, не вычисляя его: $\int\limits_{-2}^1\sqrt[3]{x}\,dx.$
Решение.
Поскольку функция $\sqrt[3]x$ нечетная $(\sqrt[3]{-x}=-\sqrt[3]x),$ то, пользуясь 9-м свойством получаем $\int\limits_{-2}^2\sqrt[3]{x}\,dx=0.$ Далее воспользуемся равенством $$\int\limits_{-2}^1\sqrt[3]{x}\,dx=\int\limits_{-2}^2\sqrt[3]{x}\,dx-\int\limits_{1}^2\sqrt[3]{x}\,dx=-\int\limits_{1}^2\sqrt[3]{x}\,dx.$$
Ясно, что $\sqrt[3]x>0$ при $x\in[1, 2].$ Поэтому из первого свойства определенных интегралов следует, что $\int\limits_{1}^2\sqrt[3]{x}\,dx>0.$ Следовательно, $$\int\limits_{-2}^1\sqrt[3]{x}\,dx=-\int\limits_{1}^2\sqrt[3]{x}\,dx<0.$$
Ответ: $\int\limits_{-2}^1\sqrt[3]{x}\,dx<0.$
{jumi[*4]}
6.365. б) Не вычисляя интегралов, выяснить какой из интегралов больше $\int\limits_1^2\frac{dx}{x^2}$ или $\int\limits_1^2\frac{dx}{x^3}.$
Решение.
Воспользуемся вторым свойством определенных интегралов. На отрезке $[1, 2]$ выполняется неравенство $\frac{1}{x^2}\geq\frac{1}{x^3}.$ Проверим это: $$\frac{1}{x^2}\geq\frac{1}{x^3}\Rightarrow x^3\geq x^2\Rightarrow x\geq1.$$ Следовательно, $$\int\limits_1^2\frac{dx}{x^2}\geq\int\limits_1^2\frac{dx}{x^3}.$$ Строгое неравенство легко получить, представив заданные интегралы как сумму $$\int\limits_1^2\frac{dx}{x^2}=\int\limits_1^{3/2}\frac{dx}{x^2}+\int\limits_{3/2}^2\frac{dx}{x^2};$$ $$\int\limits_1^2\frac{dx}{x^3}=\int\limits_1^{3/2}\frac{dx}{x^3}+\int\limits_{3/2}^2\frac{dx}{x^3}.$$ На отрезке $[1, 3/2]$ выполняется неравенство $$\frac{1}{x^2}\geq\frac{1}{x^3}\Rightarrow\int\limits_1^{3/2}\frac{dx}{x^2}\geq\int\limits_{3/2}^2\frac{dx}{x^3};$$ На отрезке $[3/2, 2]$ выполняется неравенство $$\frac{1}{x^2}>\frac{1}{x^3}\Rightarrow\int\limits_1^{3/2}\frac{dx}{x^2}>\int\limits_{3/2}^2\frac{dx}{x^3}.$$ Таким образом, $$\int\limits_1^2\frac{dx}{x^2}=\int\limits_1^{3/2}\frac{dx}{x^2}+\int\limits_{3/2}^2\frac{dx}{x^2}>\int\limits_1^{3/2}\frac{dx}{x^3}+\int\limits_{3/2}^2\frac{dx}{x^3}=\int\limits_1^2\frac{dx}{x^3}.$$ Ответ: $\int\limits_1^2\frac{dx}{x^2}>\int\limits_1^2\frac{dx}{x^3}.$
6.366. в) Найти среднее значение функции на данном отрезке: $\cos x,\quad 0\leq x\leq\pi/2.$
Решение.
Воспользуемся 6-м свойством определенных интегралов. Средним значением функции $f(x)$ на отрезке $[a, b]$ называется число $f(c)=\frac{1}{b-a}\int\limits_a^bf(x)\,dx.$
Отсюда находим $$\cos c=\frac{1}{\pi/2-0}\int\limits_0^{\pi/2}\cos x\,dx=\frac{2}{\pi}\left.\sin x\right|_0^{\pi/2}=\frac{2}{\pi}(1-0)=\frac{2}{\pi}.$$
Ответ: $\frac{2}{\pi}.$
6.369. Оценить интеграл $\int\limits_0^{2\pi}\frac{dx}{\sqrt{5+2\sin x}}.$
Решение.
Оценим подынтегральную функцию:
$$-1\leq\sin x\leq 1\Rightarrow$$ $$3\leq 5+2\sin x\leq 7\Rightarrow$$ $$\sqrt 3\leq\sqrt{5+2\sin x}\leq 7\Rightarrow$$ $$\frac{1}{\sqrt 7}\leq\frac{1}{\sqrt{5+2\sin x}}\leq\frac{1}{\sqrt 3}.$$
Отсюда и из второго свойства определенных интегралов следует, что
$$\int\limits_0^{2\pi}\frac{1}{\sqrt 7}dx\leq\int\limits_0^{2\pi}\frac{1}{\sqrt{5+2\sin x}}dx\leq\int\limits_0^{2\pi}\frac{1}{\sqrt 3}dx.$$
Находим предельные интегралы: $$\int\limits_0^{2\pi}\frac{1}{\sqrt 7}dx=\frac{1}{\sqrt 7}(2\pi-0)=\frac{2\pi}{\sqrt 7};$$ $$\int\limits_0^{2\pi}\frac{1}{\sqrt 3}dx=\frac{1}{\sqrt 3}(2\pi-0)=\frac{2\pi}{\sqrt 3}.$$
Таким образом, $$\frac{2\pi}{\sqrt 7}\leq\int\limits_0^{2\pi}\frac{1}{\sqrt{5+2\sin x}}dx\leq\frac{2\pi}{\sqrt 3}.$$
Ответ: $\frac{2\pi}{\sqrt 7}\leq\int\limits_0^{2\pi}\frac{1}{\sqrt{5+2\sin x}}dx\leq\frac{2\pi}{\sqrt 3}.$
6.370. б) Оценить интеграл $\int\limits_0^1\sqrt{(1+x)(1+x^3)}\,dx,$ пользуясь неравенством Коши-Буняковского.
Решение.
Неравенство Коши-Буняковского дает $$|\int\limits_0^1\sqrt{(1+x)(1+x^3)}dx|\leq\sqrt{\int\limits_0^1(1+x)dx\int\limits_0^1(1+x^3)dx}.$$
Вычислим каждый интеграл, стоящей под корнем в правой части равенства:
$$\int\limits_0^1(1+x)dx=\left.\left(x+\frac{x^2}{2}\right)\right|_0^1=1+\frac{1}{2}-0=\frac{3}{2};$$ $$\int\limits_0^1(1+x^3)dx=\left.\left(x+\frac{x^4}{4}\right)\right|_0^1=1+\frac{1}{4}-0=\frac{5}{4};$$ Отсюда $$|\int\limits_0^1\sqrt{(1+x)(1+x^3)}dx|\leq\sqrt{\frac{3}{2}\cdot\frac{5}{4}}=\frac{\sqrt{30}}{4}.$$
Ответ: $|I|\leq\frac{\sqrt{30}}{4}.$
6.374. Найти производную следующей функции: $\Phi(x)=\int\limits_0^x\frac{\sin t}{t}\,dt.$
Решение.
Пользуемся свойством 10:
$$\Phi'(x)=f(x)=\frac{\sin x}{x}.$$
Ответ: $\frac{\sin x}{x}.$
6.376. Найти производную следующей функции: $\Phi(x)=\int\limits_x^0\frac{dt}{\sqrt{1+t^3}}.$
Решение.
$\Phi(x)=\int\limits_x^0\frac{dt}{\sqrt{1+t^3}}=-\int\limits_0^x\frac{dt}{\sqrt{1+t^3}}.$
Пользуемся свойством 10:
$$\Phi'(x)=f(x)=-\frac{1}{\sqrt{1+x^3}}.$$
Ответ: $-\frac{1}{\sqrt{1+x^3}}.$
mathportal.net
Как вычислить несобственный интеграл и выяснить сходимость
Несобственные интегралы первого рода: распространение понятия определённого интеграла на случаи интегралов с бесконечным верхним или нижними пределами интегрирования, или оба предела интегрирования бесконечны.
Несобственные интегралы второго рода: распространение понятия определённого интеграла на случаи интегралов от неограниченных функций, подынтегральная функция в конечном числе точек конечного отрезка интегрирования не существует, обращаясь в бесконечность.
Для сравнения. При введении понятия определённого интеграла предполагалось, что функция f(x) непрерывна на отрезке [a, b], а отрезок интегрирования является конечным, то есть ограничен числами, а не бесконечностью. Некоторые задачи приводят к необходимости отказаться от этих ограничений. Так появляются несобственные интегралы.
Геометрический смысл несобственного интеграла выясняется довольно просто. В случае, когда график функции y = f(x) находится выше оси Ox, определённый интеграл выражает площадь криволинейной трапеции, ограниченной кривой y = f(x), осью абсцисс и ординатами x = a, x = b. В свою очередь несобственный интеграл выражает площадь неограниченной (бесконечной) криволинейной трапеции, заключённой между линиями y = f(x) (на рисунке ниже — красного цвета), x = a и осью абсцисс.
Аналогичным образом определяются несобственные интегралы и для других бесконечных интервалов:
,.
Площадь бесконечной криволинейной трапеции может быть конечным числом и в этом случае несобственный интеграл называется сходящимся. Площадь может быть и бесконечностью и в этом случае несобственный интеграл называется расходящимся.
Использование предела интеграла вместо самого несобственного интеграла. Для того, чтобы вычислить несобственный интеграл, нужно использовать предел определённого интеграла. Если этот предел существует и конечен (не равен бесконечности), то несобственный интеграл называется сходящимся, а в противном случае — расходящимся. К чему стремится переменная под знаком предела, зависит от того, имеем мы дело с несобственным интегралом первого рода или второго рода. Узнаем об этом сейчас же.
Несобственные интегралы с бесконечным верхним пределом
Итак, запись несобственного интеграла как отличается от обычного определённого интеграла тем, что верхний предел интегрирования бесконечен.
Определение. Несобственным интегралом с бесконечным верхним пределом интегрирования от непрерывной функции f(x) на промежутке от a до ∞ называется предел интеграла этой функции с верхним пределом интегрирования b и нижним пределом интегрирования a при условии, что верхний предел интегрирования неограниченно растёт, т.е.
.
Если этот предел существует и равен некоторому числу, а не бесконечности, то несобственный интеграл называется сходящимся, а число, которому равен предел, принимается за его значение. В противном случае несобственный интеграл называется расходящимся и ему не приписывается никакого значения.
Пример 1. Вычислить несобственный интеграл
(если он сходится).Решение. На основании определения несобственного интеграла находим
Так как предел существует и равен 1, то и данный несобственный интеграл сходится и равен 1.
В следующем примере подынтегральная функция почти как в примере 1, только степень икса — не двойка, а буква альфа, а задача состоит в исследовании несобственного интеграла на сходимость. То есть предстоит ответить на вопрос: при каких значениях альфы данный несобственный интеграл сходится, а при каких расходится?
Пример 2. Исследовать на сходимость несобственный интеграл (нижний предел интегрирования больше нуля).
Решение. Предположим сначала, что , тогда
В полученном выражении перейдём к пределу при :
Нетрудно видеть, что предел в правой части существует и равен нулю, когда , то есть , и не существует, когда , то есть .
В первом случае, то есть при имеет место . Если , то и не существует.
Вывод нашего исследования следующий: данный несобственный интеграл сходится при и расходится при .
Применяя к изучаемому виду несобственного интеграла формулу Ньютона-Лейбница , можно вывести следующую очень похожую на неё формулу:
.
Это обобщённая формула Ньютона-Лейбница.
Пример 3. Вычислить несобственный интеграл (если он сходится).
Решение. С помощью метода замены переменной можно получить очень полезную формулу:
Доказывать эту формулу нет необходимости, но запомнить стоит — пригодится. Итак, применяя эту формулу для нахождения первообразной получим
Итак, несобственный интеграл сходится и равен 1.
Пример 4. Вычислить несобственный интеграл (если он сходится).
Решение. Находим
.
Но предел не существует, т. е. данный несобственный интеграл расходится.
Пример 5. Вычислить несобственный интеграл (если он сходится).
Решение. Подынтегральная функция непрерывна в каждой точке, поэтому определённый интеграл от неё на отрезке [0, b] существует при всяком b. Находим этот интеграл:
.
Находим предел этого интеграла:
.
По определению, значение данного несобственного интеграла:
Несобственные интегралы с бесконечным нижним пределом
Аналогично определяется несобственный интеграл от непрерывной функции с бесконечным нижним пределом интегрирования, обозначаемый символом , а именно
.
Если этот предел существует (и, значит, конечен, то есть, равен некоторому числу, а не бесконечности), то данный несобственный интеграл называется сходящимся.
Пример 6. Вычислить несобственный интеграл с бесконечным нижним пределом(если он сходится).
Решение. Находим предел данного интеграла:
Вывод: данный несобственный интеграл сходится, а его значение равно -1/2.
Несобственные интегралы с двумя бесконечными пределами
Несобственный интеграл с двумя бесконечными пределами интегрирования, обозначаемый символом , нужно предварительно представить в виде суммы двух несобственных интегралов, один из которых с конечным верхним пределом интегрирования, другой — с конечным нижним пределом интегрирования, т.е.
.
По определению,
,
причём этот несобственный интеграл считается сходящимся, если оба предела существуют, когда a и b независимо друг от друга неограниченно возрастают по абсолютной величине.
Пример 7. Вычислить несобственный интеграл с двумя бесконечными пределами (если он сходится).
Решение. На основании определения несобственного интеграла с двумя бесконечными пределами представляем данный интеграл как сумму двух несобственных интегралов:
.
Преобразуем подынтегральное выражение к форме , с помощью выделения полного квадрата:
(Эта формула, которой мы воспользовались, а также другие формулы, пригодные для интегрирования дробей, приведены в уроке Интегрирование некоторых рациональных дробей и иррациональностей).
Предел этого интеграла существует:
Второй интеграл, составляющий сумму, выражающую исходный интеграл:
Предел этого интеграла также существует:
.
Находим сумму двух интегралов, являющуюся и значением исходного несобственного интеграла с двумя бесконечными пределами:
.
Пусть функция f(x) задана на отрезке от a до b и неограниченна на нём. Предположим, что функция обращается в бесконечность в точке b, в то время как во всех остальных точках отрезка она непрерывна.
Определение. Несобственным интегралом функции f(x) на отрезке от a до b называется предел интеграла этой функции с верхним пределом интегрирования c, если при стремлении c к b функция неограниченно возрастает, а в точке x = b функция не определена, т.е.
.
Если этот предел существует, то несобственный интеграл второго рода называется сходящимся, в противном случае — расходящимся.
Используя формулу Ньютона-Лейбница, выводим:
.
Это также обобщённая формула Ньютона-Лейбница. Именно она применяется в решении задач на вычисление несобственных интегралов от неограниченных функций.
Решение. Подынтегральная функция при неограниченно возрастает, а в точке x = 0 функция не определена, то есть, не существует. Применяем обобщённую формулу Ньютона-Лейбница:
(так как при x = 0 первообразная непрерывна). Вывод: данный несобственный интеграл сходится и равен -3/2.
Пример 9. Вычислить несобственный интеграл (если он сходится).
Решение. Подынтегральная функция непрерывна в каждой точке полуотрезка [0, 1]. В точке x = 1 функция обращается в бесконечность. Если взять , то на [0, c] подынтегральная функция непрерывна и, следовательно, существует интеграл.
.
Найдём предел этого интеграла:
Результат предыдущих действий: несобственный интеграл сходится и его значение мы нашли.
Пример 10. Исследовать на сходимость несобственный интеграл (верхний предел интегрирования больше нижнего).
Решение. Подынтегральная функция обращается в бесконечность при x = b, в остальных точках она непрерывна. Предположим сначала, что , тогда для :
В полученном выражении перейдём к пределу при :
Нетрудно видеть, что предел в правой части существует и равен нулю, когда , то есть , и не существует, когда , то есть .
В первом случае, то есть при
.
Если , то
.
не существует.
Вывод нашего исследования следующий: данный несобственный интеграл сходится при и расходится при .
Начало темы «Интеграл»
Продолжение темы «Интеграл»
Поделиться с друзьями
function-x.ru
Приближенное вычисление определенного интеграла
Пусть требуется найти определенный интеграл , причем функция считается непрерывной на отрезке . Если от подынтегральной функции первообразная находится легко, то значение рассматриваемого интеграла находится по формуле Ньютона-Лейбница:
Но не в каждом случае отыскание первообразной для подынтегральной функции является достаточно простым, а также не для всякой непрерывной функции существует первообразная, выражающаяся через элементарные функции. В подобных случаях применяют приближенные формулы, которые позволяют вычислить определенный интеграл с любой степенью точности.
Наиболее часто используются три формулы приближенного вычисления определенного интеграла – формула прямоугольников, формула трапеций и формулу парабол или формула Симпсона, основанные на геометрическом смысле определенного интеграла: если функция непрерывна и положительна на отрезке , то определенный интеграл представляет собой площадь криволинейной трапеции, ограниченной линиями , , и (рис. 1).
1. Формула прямоугольников
Пусть на отрезке задана непрерывная функция . Вычислим численно определенный интеграл , который равен площади криволинейной трапеции.
Разобьем основание этой трапеции (отрезок ) на равных частей-отрезков длины
Величину будем называть шагом разбиения. В результате получим точки
Можно записать, что
В середине каждого такого элементарного отрезка отметим точку . Приняв ординату этой точки за высоту, построим прямоугольник с площадью (рис. 2).
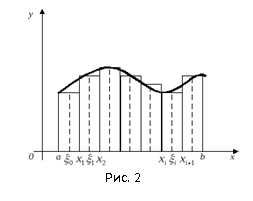
Тогда сумма площадей всех прямоугольников равна площади ступенчатой фигуры, которая представляет собой приближенное значение искомого определенного интеграла :
Полученная формула называется формулой прямоугольников.
Абсолютная погрешность последнего приближенного равенства удовлетворяет следующей оценке:
где – наибольшее значение на рассматриваемом отрезке .
2. Формула трапеций
Эту формулу получают аналогично формуле прямоугольников: на каждом частичном отрезке криволинейная трапеция заменяется обычной.
Пусть необходимо вычислить определенный интеграл . Разобьем отрезок интегрирования на равных частей длины . В результате получим точки (рис. 3). Пусть – соответствующие им ординаты функции. Тогда можно записать, что
Заменим кривую ломаной линией, звенья которой соединяют концы ординат и . Тогда площадь криволинейной трапеции приближенно равна сумме площадей обычных трапеций с основаниями , и высотой , то есть
Записанная формула называется формулой трапеций.
Абсолютная погрешность
где .
3. Формула парабол (Симпсона)
Если заменить график функции на каждом отрезке , которые получены после разбиения отрезка интегрирования на равных частей, не отрезками прямых, как в методах трапеций и прямоугольников, а дугами парабол, то получим более точную формулу приближенного вычисления определенного интеграла .
Как было сказано выше, разобьем отрезок на равных частей (отрезков) длиной точками
причем , . В точках разбиения находим значения подынтегральной функции
то есть (рис. 4).
Заменяем каждую пару соседних элементарных криволинейных трапеций с основаниями одной элементарной параболической трапецией с основанием . Тогда, например, на частичном отрезке парабола проходит через три точки , , и так далее.
Расчетная формула парабол (или Симпсона) для этого метода имеет вид:
Абсолютная погрешность вычисления по этой формуле оценивается соотношением
где .
ru.solverbook.com
