Баврин И.И. — Высшая математика (2004)

УЧЕБНИК ДЛЯ ВУЗОВ
И.И. БАВРИН
КУРС ВЫСШЕЙ
МАТЕМАТИКИ
2 е издание, переработанное и дополненное
Рекомендовано Министерством образования Российской Федерации в качестве учебника для студентов высших педагогических учебных заведений, обучающихся по направлению «Естествознание», специальности «Физика»
Москва
ГУМАНИТАРНЫЙ
ИЗДАТЕЛЬСКИЙ
ЦЕНТР
ВЛАДОС
УДК 51(075.8) ББК 21.1я73 Б13
Р е ц е н з е н т ы:
доктор физико математических наук, профессор кафедры математического анализа МГУ
им. М. В. Ломоносова В.И. Гаврилов; доктор педагогических наук, профессор,
заведующий кафедрой математического анализа МПУ
Г.Л. Луканкин
Баврин И. И.
Б13 Курс высшей математики: Учеб. для студ. высш. пед. учеб. заведений / 2 е изд., перераб. и доп. — М.: Гуманит. изд. центр ВЛАДОС, 2004. — 560 с.
ISBN 5 691 00117 5.
Агентство CIP РГБ.
Учебник соответствует примерной программе дисциплины «Ма тематика» для направления 540100 «Естествознание», специально сти «Физика» педагогических вузов.
Состоит из трех разделов. Первый раздел — аналитическая гео метрия и линейная алгебра, второй — математический анализ, тре тий — специальные главы высшей математики, в том числе теория поля, элементы теории функций комплексной переменной, интег рал Фурье, основные уравнения и задачи математической физики, теория вероятностей, элементы математической статистики, элемен ты вариационного и операционного исчислений. В приложении при ведены таблицы из теории вероятностей и математической статис тики, дополнительная таблица интегралов и основные соотношения и формулы из школьной математики. Приведено много разнообраз ных примеров и задач, иллюстрирующих понятия высшей матема тики и ее методы.
УДК 51(075.8) ББК 22.1я73
| © Баврин И. И., 2004 |
| © ООО «Гуманитарный издательский |
| центр ВЛАДОС», 2004 |
| © Серия «Учебник для вузов» |
| и серийное оформление. |
| ООО «Гуманитарный издательский |
| центр ВЛАДОС», 2004 |
| © Макет. ООО «Гуманитарный |
ISBN 5 691 00117 5 | издательский центр ВЛАДОС», 2004 |
Предисловие ко второму изданию
Первое издание учебника «Курс высшей математики» (М., 1992) переработано и до полнено в соответствии с новой примерной программой дисциплины «Математика» для направления 540100 «Естествознание» и программой по математике для специально сти 01.40.00 «Физика» педагогических выс ших учебных заведений.
Укажем наиболее существенные измене ния и дополнения книги.
Выделены глава «Линейная алгебра» и раздел «Специальные главы». В этот раз дел в качестве нового материала включены элементы теории функций комплексной переменной, математической статистики, операционного исчисления и некоторые численные методы.
И. И. Баврин
Ð à ç ä å ë I
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ И ЛИНЕЙНАЯ АЛГЕБРА
Глава 1. СИСТЕМА КООРДИНАТ НА ПЛОСКОСТИ
ÈОСНОВНЫЕ ПОНЯТИЯ
§1.1. Декартова прямоугольная и полярная системы
координат на плоскости
1. Декартовы прямоугольные координаты. Возьмем на плоскости две взаимно перпендикулярные прямые Ox и Oy с указанными на них положительными направлениями (рис. 1). Прямые Ox и Oy называются
координатными осями, точка их пересечения O — началом координат. Обычно полагают, что ось Ox горизонтальна, а ось Oy вертикальна относительно наблюдателя; положительное направление на Ox слева направо, на Oy — снизу вверх.
Выберем единицу масштаба (будем предполагать, что на обеих осях координат выбрана одна и та же единица масштаба). Координатные оси Ox, Oy с выбранной единицей масштаба называются декартовой прямоугольной (или кратко прямоугольной) системой координат на плоскости. (Декартова прямоугольная система координат носит имя французского математика, основателя аналитической геометрии Рене Декарта (1596–1650).)
Произвольной точке M плоскости поставим в соответствие два числа (рис. 1):
|
| абсциссу x, равную расстоянию |
|
| от точки М до оси Oy, взятому со |
|
| знаком «+», если М лежит правее |
|
| Oy, и со знаком «–»,если М лежит |
|
| левее Oy; |
|
| ординату у, равную расстоянию |
|
| от точки М до оси Ox, взятому со |
|
| знаком «+», если М лежит выше Ox, |
|
| |
|
| и со знаком «–»,если М лежит ни- |
|
| æå Ox. |
|
| Абсцисса х и ордината у называ- |
|
| |
Ðèñ. 1 | ются декартовыми прямоугольными | |

Ðèñ. 2
(или прямоугольными) координатами точки М. Запись М(х; у) читают: «Точка М с абсциссой, равной х, и ординатой,
равной у». Отметим, что каждой точ-
ке плоскости соответствует одна пара действительных чи-
сел x и y (ее координат). Верно
и обратное: каждой паре действительных чисел x и y соот-
ветствует одна точка плоскости. Это значит, что положение на плоскости произвольной точки
М полностью определяется ее координатами x и y.
Координатные оси Ox и Oy разбивают плоскость на I, II, III, IV к в а д р а н т ы (рис. 2). Знаки координат точек в различных квадрантах указаны в таблице:
| I | II | III | IV |
|
|
|
|
|
x | + | – | – | + |
|
|
|
|
|
y | + | + | – | – |
|
|
|
|
|
При этом если точка М(х; у) лежит на оси Oy, то х = 0; если М(х; у) лежит на оси Ox, то у = 0.
На рисунке 2 построены четыре точки М1(2; 1),Ì2(–4;3),Ì3(–4;–2)
èÌ4(0;–2).
2.Полярные координаты. Зафиксируем на плоскости точку О и
выходящую из нее полупрямую Op, а также выберем единицу масштаба (рис. 3). Точка О называется по-
люсом, полупрямая Оp — полярной осью. |
|
Произвольной точке М (отличной |
|
от О) плоскости поставим в соответствие |
|
два числа: |
|
полярный радиус r, равный расстоянию |
|
от точки М до полюса О; |
|
полярный угол ϕ, равный углу между |
|
полярной осью Op и полупрямой ОМ. | Ðèñ. 3 |

|
| Полярный угол ϕ измеряется в |
|
| |
|
| радианах, отсчет положительных |
|
| (отрицательных) значений ϕ ведет- |
|
| ся от Op против движения (по дви- |
|
| жению) часовой стрелки. При этом |
|
| обычно полагают, что –π< ϕ ≤ π. |
|
| Полюсу О соответствует поляр- |
|
| ный радиус r = 0, полярный угол для |
|
| |
Ðèñ. 4 | него не определен. | |
Запись М (r; ϕ) означает: точка М с полярными координатами r и ϕ. Найдем зависимость между прямоугольными и полярными коор-
динатами. Будем считать начало координат О прямоугольной системы хОу одновременно полюсом О, а луч Ox примем за полярную ось Op (рис. 4).
Из рисунка 4 видно, что для точки М (х; у) (М (r; ϕ)) справедливы соотношения
õ = r cos ϕ, ó = r sin ϕ | (1) | |||||
è |
|
|
|
|
| |
r = |
| , tgϕ = | y | . |
| |
x 2 + ó2 | (2) | |||||
| ||||||
|
|
| x |
| ||
Формулы (1) выражают прямоугольные координаты точки М через ее полярные координаты. Это можно доказать для любого расположения точки М на координатной плоскости. Формулы (2) выражают полярные координаты точки М через ее прямоугольные координаты и тоже верны при любом положении точки М.
Заметим, что tg ϕ = y дает два значения ϕ(–π< ϕ ≤ π). x
Поэтому для вычисления полярного угла ϕ точки М по ее прямоугольным координатам x и y предварительно выясняют, в каком квадранте лежит точка М.
П р и м е р 1. Даны прямоугольные координаты точки А: х = 1, у = 1. Найти ее полярные координаты. По формулам (2) находим: r = 12 + 12 =2, tgϕ = 1. Из двух значений
ϕ = π è ϕ = −3π выбираем ϕ =π, так как точка А лежит в первом квадранте. Итак, поляр- 4 4 4
ные координаты данной точки r = 2, ϕ =π. 4
П р и м е р 2. Полярные координаты точки А таковы: r = 2,ϕ = π. Тогда по формулам 2
(1) прямоугольные координаты этой точки будут x = 2 cos π = 0, y = 2 sinπ = 2. 2 2
§1.2. Простейшие задачи на плоскости
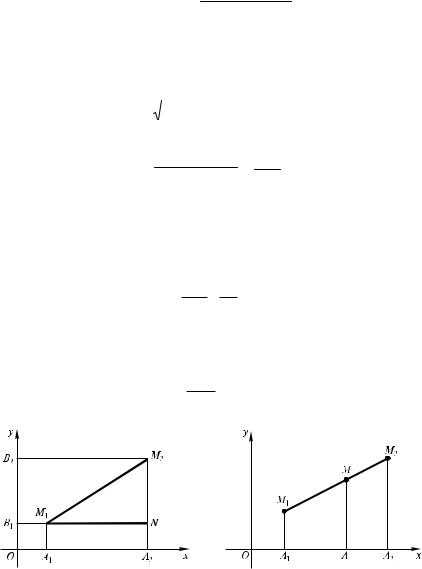
1.Расстояние между двумя точками. Найдем расстояние d между дву-
мя данными точками М1 (õ1; ó1) è Ì2 (õ2; ó2) (рис. 5). Из прямоугольного треугольника М1NM2 по теореме Пифагора имеем:
d = M1M2 =M1N2 + M2N2 .
Известно, что расстояние между точками А и В, расположенными на координатной прямой (оси), вычисляется по формуле d = АВ = |x – − õA|, ãäå õA è x — координаты точек А и В этой прямой. Но М1N = À1À2 = = |x2 – õ1|, N Ì2 = Â1Â2 = |ó2 – ó1|. Поэтому
|
|
|
|
d = (x 2 − x1 )2 + ( y2 − y1 )2 . | (1) | ||
П р и м е р. Найти расстояние между точками À(–1;–2)èÂ(–4;2). По формуле (1) имеем:
AB = (−4 + 1)2 + (2 + 2)2 =9 + 16 = 5.
2. Деление отрезка в данном отношении. Пусть даны точки М1(õ1; ó1) è Ì2(õ2; ó2). Требуется найти точку М(х; у), лежащую на отрезке М1 Ì2 и делящую его в данном отношении:
ÌÌ2
Опустив из точек М1, Ì è Ì2 перпендикуляры на ось Ox (рис. 6), получим:
Ì1 Ì= À1 À. ÌÌ2 ÀÀ2
При выбранном расположении точек имеем:
À1À = õ − õ1, ÀÀ2 = õ2 − õ.
Поэтому заданное отношение (2) принимает вид:
x− x1 = λ,
x2 − x
откуда |
|
|
|
|
|
õ = |
| õ1 + λõ2 | . | (3) | |
|
|
| |||
|
| 1 + λ |
| ||
Аналогично |
|
|
|
|
|
ó= | ó1 +λ ó2 | . | (4) | ||
|
| 1 + λ |
| ||
В частности, если λ = 1, т. е. при делении отрезка М1 Ì2 пополам, получаем:
õ = õ1 + õ2 , ó=ó1 + ó2 .
22
Ïр и м е ч а н и е. Формулы (3) и (4) верны при любом расположении точек М1 è Ì2.
Ïр и м е р. Вычислить координаты точки М (х; у), делящей отрезок М1Ì2, ãäå Ì1(1; 1)
èÌ2(4; 7), в отношенииÌ1 Ì = 2.Согласно формулам (3) и (4) имеем:
ÌÌ2
õ = 1 + 2 4 = 3, ó=1 + 2 7 = 5.
33
§1.3. Геометрическое истолкование уравнения
ñдвумя переменными
Прямоугольная и полярная системы координат позволяют задавать различные линии на плоскости их уравнениями.
О п р е д е л е н и е. Уравнением линии на плоскости в прямоугольной системе координат хОу называется уравнение f (х, у) = 0, которому удовлетворяют координаты каждой точки данной линии и не удовлетворяют координаты любой точки плоскости, не лежащей на этой линии.
Переменные х и у уравнения линии называются текущими координатами.
Покажем, например, что уравнение х – у = 0, èëè
является уравнением биссектрисы I и III координатных углов.
По свойству биссектрисы угла для произвольной точки М (х; у) (лежащей на биссектрисе) имеем N2M= N1M èëè ÎN1 = ÎN2 (рис. 7), и поэтому х= у, т. е. координаты всех точек биссектрисы удовлетворяют уравнению (1). Очевидно также, что у любой точки, не лежащей на данной биссектрисе, координаты не равны между собой и, значит, не удовлетворяют уравнению (1).
Обратно, если координаты x и y какой-нибудьточки М (х; у) удовлетворяют уравнению (1), то эта точка, очевидно, лежит на биссектрисе I и III координатных углов.

Однако геометрическим образом данного заранее уравнения не всегда будет линия. Может случиться, что уравнению соответствует лишь несколько точек (уравнению х2 + ó2 = 0, например, на плоскости соответствует только одна точка (0; 0)). Встречаются и такие случаи, когда заданному уравнению не соответствует на плоскости ни одна точка (как, например, уравнению х2 + ó2 + 1= 0).
В связи с изложенным заметим, что всякой линии на плоскости соответствует некоторое уравнение между текущими координатами (х, у) точки этой линии. Наоборот, всякому уравнению между х и у, где х и у — координаты точки на плоскости, соответствует, вообще говоря, некоторая линия, свойства которой вполне определяются данным уравнением.
Отсюда, естественно, возникают две основные задачи аналитиче- ской геометрии на плоскости.
1)Дана линия, рассматриваемая как множество точек. Составить уравнение этой линии.
2)Дано уравнение некоторой линии. Изучить по этому уравнению
ååгеометрические свойства (форму и расположение).
§1.4. Прямая линия
1.Уравнение прямой с угловым коэффициентом. Пусть прямая l не параллельна оси Оу (рис. 8). Обозначим точку пересечения l с осью Оу буквой В(0; b), а угол между положительным направлением оси Ox и l
обозначим ϕ. Угол ϕ, отсчитываемый от оси Ox против часовой стрелки (0 ≤ ϕ < π), называется углом наклона прямой l к оси Ox.
Выведем уравнение прямой l.
Пусть М(х; у) — произвольная точка прямой l с текущими координатами х и у. Из прямоугольного треугольника ВМN (рис. 8) имеем:
tg ϕ = | y − b | . | (1) |
| |||
| x |
| |
studfiles.net
Баврин И.И. Высшая математика [EXE]
Учебник для студентов естественнонаучных специальностей педагогических вузов. — М.: Академия, 2010. — 616 с.Профессионально ориентированный учебник содержит изложение основ аналитической геометрии и математического анализа, элементов теории вероятностей и математической статистики, сопровождаемое рассмотрением математических моделей из естественно–научных дисциплин (физики, химии, биологии, географии), а также упражнения ко всем излагаемым вопросам. Все основные понятия иллюстрируются примерами из этих дисциплин.Для студентов естественно–научных специальностей высших педагогических учебных заведений. Может быть использован студентами других вузов и учреждений среднего профессионального образования.Основы аналитической геометрии и математического анализа.
Введение.
Аналитическая геометрия.
Аналитическая геометрия на плоскости.
Метод координат на плоскости.
Прямая линия.
Основные задачи на прямую.
Кривые второго порядка.
Векторная и линейная алгебра.
Понятие вектора и линейные операции над векторами.
Нелинейные операции над векторами.
Матрицы и действия над ними.
Определители.
Выражение векторного и смешанного произведении векторов через координаты сомножителей.
Системы линейных уравнений.
Аналитическая геометрия в пространстве.
Плоскость.
Прямая в пространстве.
Основные задачи на плоскость и прямую в пространстве.
Изучение поверхностей второго порядка по их каноническим уравнениям.
Математический анализ.
Функции, пределы, непрерывность.
Определение и способы задания функции.
Обзор элементарных функций и их графиков.
Предел функции.
Бесконечно малые и бесконечно большие величины.
Основные теоремы о пределах и их применение.
Непрерывность функции.
Комплексные числа.
Дифференциальное исчисление.
Понятие производной, ее механическим и геометрический смысл.
Правила дифференцирования п производные элементарных функций.
Дифференциал функции.
Производные и дифференциалы высших порядков.
Параметрическое задание функции и ее дифференцирование.
Свойства дифференцируемых функций.
Возрастание и убывание функции. Максимумы и минимумы. Асимптоты.
Построенне графиков функций.
Формула Тейлора.
Интегральное исчисление.
Первообразная функция и неопределенный интеграл.
Основные методы интегрирования.
Интегрирование дробно–рациональных функций.
Интегрирование тригонометрических выражений.
Интегрирование простейших иррациональностей.
Понятие определенного интеграла.
Основные свойства определенного интеграла.
Приближенное вычисление определенного интеграла.
Виды несобственных интегралов, их сходимость.
Геометрические приложения определенного интеграла.
Приложения определенного интеграла в естествознании.
Вектор–функция скалярного аргумента.
Дифференциальное и интегральное исчисления функции нескольких переменных.
Функции нескольких переменных. Предел м непрерывность функции.
Частные производные. Полный дифференциал.
Частные производные и дифференциалы высших порядков.
Экстремум функций двух переменных.
Скалярные поля.
Двойные интегралы.
Тройные интегралы.
Криволинейные интегралы.
Поверхностные интегралы.
Элементы теории поля.
Ряды.
Числовые ряды.
Функциональные ряды.
Степенные ряды в действительной области.
Степенные ряды в комплексной области.
Тригонометрические ряды.
Интеграл Фурье. Дельта–функция.
Дифференциальные уравнения.
Задачи, приводящие к дифференциальным уравнениям.
Дифференциальные уравнения первого порядка, их частные случаи. Приложения в естествознании.
Уравнения высших порядков.
Линейные уравнения второго порядка.
Дифференциальные уравнения в естествознании.
Уравнения и задачи математической физики.
Элементы корни вероятностен и математической статистики.
Событие и вероятность.
Основные понятия. Определение вероятности.
Свойства вероятности.
Приложения в биологии.
Дискретные и непрерывные случайные величины.
Случайные величины.
Математнческое ожидание дискретной случайной величины.
Дисперсия дискретной случайной величины.
Непрерывные случайные величины.
Некоторые законы распределения случайных величин.
Закон больших чисел.
Элементы математической статистики.
Генеральная совокупность и выборка.
Оценки параметров генеральной совокупности по ее выборке.
Доверительные интервалы для параметров нормального распределения.
Проверка статистических гипотез.
Линейная корреляция.
Приложения.
www.twirpx.com
| Курс высшей математики. Баврин И.И. | |||
Курс высшей математики. Баврин И.И. ОГЛАВЛЕНИЕ
|
www.1variant.ru
Высшая математика. Баврин И.И., Матросов В.Л.
М.: 2004.— 400 с.
В учебнике излагаются аналитическая геометрия, математический анализ и теория вероятностей. Теоретический материал сопровождается большим числом разобранных примеров и задач, а также упражнениями для самостоятельной работы.
Книга адресована студентам высших учебных заведений, а также преподавателям средних учебных заведений, стремящихся повысить свое педагогическое мастерство.
Формат: pdf / zip
Размер: 4,1 Мб
Скачать: Учебный центр — английский язык
Готовые домашние задания (гдз)
ОГЛАВЛЕНИЕ
Предисловие 3
РАЗДЕЛ I. Аналитическая геометрия.
Глава 1. Система координат на плоскости и основные понятия 4
Глава 2. Векторная алгебра 21
Глава 3. Матрицы и определители 45
Глава 4. Плоскость и прямая в пространстве 63
Глава 5. Кривые второго порядка в канонической форме 72
Глава 6. Поверхности второго порядка в канонической форме 80
РАЗДЕЛ II. Математический анализ.
Глава 7. Введение в анализ 87
Глава 8. Дифференциальное исчисление функций одной переменной 129
Глава 9. Интегральное исчисление функций одной переменной 162
Глава 10. Ряды 218
Глава 11. Дифференциальное исчисление функций нескольких переменных 254
Глава 12. Интегральное исчисление функций нескольких переменных 278
Глава 13. Дифференциальные уравнения 318
Глава 14. Векторный анализ 345
РАЗДЕЛ III. Теория вероятностей.
Глава 15. Событие и вероятность 362
Глава 16. Случайные величины 372
Литература 398
Как скачивать и открывать электронные …
Отдохни — посмотри картинки,приколы и смешные статусы
Разные афоризмы
Бывают такие удивительные лица, мимо которых невозможно пройти — надо обязательно остановиться и дать в морду.
Цитаты и Статусы со смыслом
Спасибо тем, кто меня ненавидит. Вы делаете меня сильнее!
Приколы из школьных сочинений
Наш щенок часто прячет мой дневник. Подальше от дедушки!
Фото приколы

Смотрим еще приколы и все для учебы (на новой странице)
advice-me.ru
Курс высшей математики. Баврин И.И.
2-е изд., перераб. и доп. — М.: 2004.— 560 с.
Учебник соответствует примерной программе дисциплины «Математика» для направления 540100 «Естествознание», специальности «Физика» педагогических вузов. Состоит из трех разделов. Первый раздел — аналитическая геометрия и линейная алгебра, второй — математический анализ, третий — специальные главы высшей математики, в том числе теория поля, элементы теории функций комплексной переменной, интеграл Фурье, основные уравнения и задачи математической физики, теория вероятностей, элементы математической статистики, элементы вариационного и операционного исчислений. В приложении приведены таблицы из теории вероятностей и математической статистики, дополнительная таблица интегралов и основные соотношения и формулы из школьной математики. Приведено много разнообразных примеров и задач, иллюстрирующих понятия высшей математики и ее методы.
Формат: pdf / zip
Размер: 3,2 Мб
Скачать: Учебный центр — английский язык
Готовые домашние задания (гдз)
ОГЛАВЛЕНИЕ
Предисловие ко второму изданию 3
Раздел I. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ И ЛИНЕЙНАЯ АЛГЕБРА 4
Глава 1. СИСТЕМА КООРДИНАТ НА ПЛОСКОСТИ И ОСНОВНЫЕ ПОНЯТИЯ . . . . 4
§ 1.1. Декартова прямоугольная и полярная системы координат на плоскости . . . . 4
§ 1.2. Простейшие задачи на плоскости 7
§ 1.3. Геометрическое истолкование уравнения с двумя переменными 8
§ 1.4. Прямая линия 9
§ 1.5. Основные задачи на прямую 18
§ 1.6. Уравнение линии 19
Глава 2. ВЕКТОРНАЯ АЛГЕБРА 23
§ 2.1. Понятие вектора и линейные операции над векторами …
Отдохни — посмотри картинки,приколы и смешные статусы
Разные афоризмы
Мойте руки перед и зад
Цитаты и Статусы со смыслом
Ищу зарплатодателя. Работодателей просьба не беспокоить!
Приколы из школьных сочинений
Дед Мороз раздавал подарки: мандарины, куклы и другие фрукты.
Фото приколы

Смотрим еще приколы и все для учебы (на новой странице)
advice-me.ru
