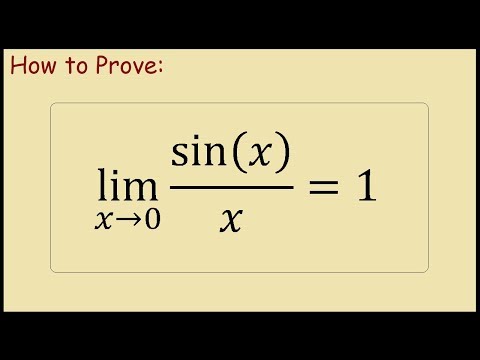Lim sin x 1: Mathway | Популярные задачи

2Исчисление

— Сомнение в доказательстве того, что $\lim_{x\rightarrow0}{\frac{\sin{x}}{x}}=1$

спросил 4 года 9 месяцев назад

Изменено 4 года, 9 месяцев назад

Просмотрено 291 раз

$\begingroup$

Полное доказательство можно найти здесь. По сути, мы сравниваем три площади, зависящие от $x$, в круге радиусом $1$, показанном ниже. 92>0$ и $\frac{1}{2}(\cos{x})(\sin{x})<0$). Как мы можем обойти это?

Заранее спасибо.

• исчисление
• пределы
• тригонометрия

$\endgroup$

1

$\begingroup$

1) Когда мы говорим о $x\to0$, мы имеем в виду те $x$, которые близки к $0$, но не равны $0$.

Значение функции при $x=0$ просто не имеет значения. Так что $<$ правильно. 92<\frac{1}{2}(\cos{x})(\sin{x})<\frac{x}{2}$$

Отсюда следует, что

$$\cos x<\frac {\sin x}{x}<\frac{1}{\cos x}$$

Для $\frac{-\pi}{2}y>0$ и, следовательно,

$$\cos y<\frac{\sin y}{y}<\frac{1}{\cos y}$$

Обратите внимание, что $\sin x=\sin(-y)=-\sin y$ и $\cos x=\cos(-y)=\cos y$.

Таким образом, у нас все еще есть

$$\cos x<\frac{\sin x}{x}<\frac{1}{\cos x}$$

$\endgroup$

$\begingroup$

1. Да, если вы допускаете вырожденные фигуры, такие как треугольники без площади, то вместо строгого неравенства у вас будет слабое неравенство. На самом деле обычная версия теоремы о сжатии требует, чтобы было слабым неравенством. Хотя, поскольку эта предельная точка находится за пределами этого строгого неравенства, вполне нормально, что в вашем тексте используется strict.

2. при $x=\pi/2$ формула больше не верна, так как площадь треугольника равна нулю, а круговые сектора — нет. Просто посмотрите на свою фигуру. 92>\frac{1}{2}(\cos{x})(\frac {sin{x}}{x})>\frac{1}{2}$$ Обратите внимание, что если $x$ приближается к $0$ мы по-прежнему получаем желаемый результат $$\lim_{x\to 0} \frac {\sin x}{x}=1$$.

   $\endgroup$

   $\begingroup$

   @sirous, Вы не можете использовать правило Лопиталя для оценки этого предела. Это приводит к Circular Reasoning , потому что как вы узнали, что (sinx)’ = cosx? Для оценки требуется знание желаемого предела. Следовательно, использование правила Лопиталя приводит к математической ошибке. Лучшие ответы были указаны выше. 9{+}$ и, таким образом, мы можем взять $x>

   0$. Кроме того, предел зависит от поведения функции в сколь угодно малой окрестности $0$, и, таким образом, можно взять интервал $(0,\pi/2)$ в качестве диапазона значений $x$, чтобы иметь дело с этой предельной оценкой.

   $\endgroup$

   $\begingroup$

   $$\lim_{x\to0}\frac{\sin(x)}{x}=\lim_{x\to0}\left(\frac {(\sin(x))’}{x’} \right)=\left(\frac{\cos(x)}{1}\right)\large|_{x=0}=1$$

   $\endgroup$

   Зарегистрируйтесь или войдите в систему

   Зарегистрируйтесь с помощью Google

   Зарегистрироваться через Facebook

   Зарегистрируйтесь, используя электронную почту и пароль

   Опубликовать как гость

   Электронная почта

   Требуется, но никогда не отображается

   Опубликовать как гость

   Электронная почта

   Требуется, но не отображается

   Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

   .

   No related posts.