Хорда в окружности – Секущие и хорды в окружности. Подробная теория с примерами.

Содержание

Свойства касательной, секущей и хорды окружности

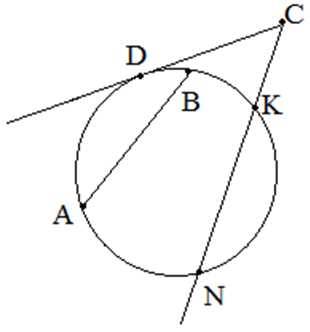
Отрезок, соединяющий две точки окружности, называется хордой (на рисунке это отрезок ). Хорда, проходящая через центр окружности, называется диаметром окружности.

Хорда окружности обладает следующими свойствами

Хорды, находящиеся на одинаковом расстоянии от центра окружности, равны.
Если хорды стягивают равные центральные углы, то они равны.
Если диаметр перпендикулярен хорде, то он проходит через ее середину.
Если вписанные углы опираются на одну хорду, то они равны.
Две дуги равны, если они заключены между двумя равными хордами.
Если пара вписанных углов опирается на одну и ту же хорду, а их вершины лежат по разные стороны хорды, то их сумма составляет 180°.
Для любых двух хорд и , пересекающихся в точке О, выполняется равенство: .

Прямая, имеющая с окружностью одну общую точку, называется касательной (на рисунке отрезок ).

Прямая, имеющая с окружностью две общие точки, называется секущей (отрезок ).

Свойства касательной и секущей

Касательная перпендикулярна радиусу, проведенному в точку касания.
Отрезки касательных, проведенных из одной точки, равны.
Если из точки, лежащей вне окружности, проведены касательная и секущая, то квадрат длины касательной равен произведению секущей на ее внешнюю часть:

Примеры решения задач

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

Ответы@Mail.Ru: Что такое Хорда Окружности???

Отрезок, соединяющий две точки окружности, называется ее хордой. Хорда, проходящая через центр окружности, называется диаметром. Диаметр (радиус) , перпендикулярный к хорде, делит эту хорду и обе стягиваемые ею дуги пополам. Верна и обратная теорема: если диаметр (радиус) делит пополам хорду, то он перпендикулярен этой хорде. Дуги, заключенные между параллельными хордами, равны. В окружности равные хорды равноудалены от центра окружности. Если две хорды окружности, AB и CD пересекаются в точке M, то произведение отрезков одной хорды равно произведению отрезков другой хорды: AM•MB = CM•MD.

Хорда — это линия между диаметром и радиусом окружности

отрезок прямой линии, соединяющей две точки данной кривой (например, окружности, эллипса, параболы) <img src=»//otvet.imgsmail.ru/download/af81887a486e6ca76ce19db9730f4e4d_i-4.jpg» > 1 — секущая, 2 — хорда AB (отмечена красным цветом) , 3 — сегмент (отмечен зеленым цветом) , 4 — дуга

Это отрезок соединяющий две точки, принадлежащие данной окружности. И диаметр тоже хорда

хорда-отрезок, соединяющий две точки данной кривой

touch.otvet.mail.ru

Хорда, секущая окружности. Касательная к окружности

Категория: Справочные материалы

Елена Репина 2013-07-27 2017-11-20

Определения

Хорда – отрезок, соединяющий две точки окружности.

В частности, хорда, проходящая через центр окружности, называется диаметром.

Секущей к окружности называется прямая, которая пересекает окружность в двух различных точках.

Касательная к окружности — прямая, имеющая с окружностью единственную общую точку.

Свойства

Радиус, проведенный в точку касания, перпендикулярен касательной

Отрезки касательных, проведенных к окружности из одной точки, равны.

Отрезки пересекающихся хорд связаны соотношением:

Произведения отрезков секущих, проведенных из одной точки, равны:

Квадрат отрезка касательной равен произведению отрезков секущей, проведенной из той же точки:

Автор: egeMax | Нет комментариев

egemaximum.ru

хорда окружности — это… Что такое хорда окружности?

хорда окружности: мат. chord of circle

хорда лопасти
хорда элерона

Смотреть что такое «хорда окружности» в других словарях:

Хорда окружности — Окружность и её центр Окружность геометрическое место точек плоскости, равноудаленных от заданной точки, называемой её центром. В Викисловаре есть статья «окружность» Вписанная окружность Описанная окружность Окружность Аполлония Единичная… … Википедия
Хорда — В Викисловаре есть статья «хорда» Хорда: Хорда окружности в планиметрии отрезок прямой линии, соединяющей две точки данной кривой (круг … Википедия
ХОРДА — (греч. chorde). В геометрии: прямая линия, соединяющая концы дуги. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ХОРДА 1) в геометрии прямая линия, соединяющая две какие нибудь точки окружности, но не проходящая… … Словарь иностранных слов русского языка
ХОРДА — ХОРДА, хорды, жен. (греч. chorde струна). 1. Прямая, соединяющая две точки какой н кривой линии, напр. концы дуги окружности (мат.). 2. Осевой скелет, упругий эластичный тяж, спинная струна (лат. chorda dorsalis у некоторых животных (напр. рыб, т … Толковый словарь Ушакова
ХОРДА 1 — ХОРДА 1, ы, ж. В математике: прямая, соединяющая две точки кривой, напр. дуги, окружности. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
хорда — ХОРДА, ы, жен. В математике: прямая, соединяющая две точки кривой, напр. дуги, окружности. II. ХОРДА, ы, жен. (спец.). Спинная струна первичная скелетная ось у высших животных и человека. | прил. хордовый, ая, ое. Тип хордовых (сущ.; тип высших… … Толковый словарь Ожегова
Хорда (геометрия) — У этого термина существуют и другие значения, см. Хорда. 1 секущая, 2 хорда … Википедия
ХОРДА — (от греч. chorde струна) отрезок прямой, соединяющий 2 точки к. л. кривой линии, например окружности … Большой энциклопедический политехнический словарь
Фокальная хорда — Кривая второго порядка геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида a11x2 + a22y2 + 2a12xy + 2a13x + 2a23y + a33 = 0, в котором по крайней мере один из коэффициентов отличен от нуля.… … Википедия
Парадокс Бертрана (вероятность) — Для термина «Парадокс Бертрана» см. другие значения. Парадокс Бертрана проблема классического определения теории вероятностей. Жозеф Бертран описал парадокс в своей работе Calcul des probabilités (1888) в качестве примера того, что вероятность не … Википедия
ГОСТ 16531-83: Передачи зубчатые цилиндрические. Термины, определения и обозначения — Терминология ГОСТ 16531 83: Передачи зубчатые цилиндрические. Термины, определения и обозначения оригинал документа: 5.3.1. Воспринимаемое смещение Разность межосевого расстояния цилиндрической зубчатой передачи со смещением и ее делительного… … Словарь-справочник терминов нормативно-технической документации

dic.academic.ru

Ответы@Mail.Ru: что такое хорда??

струна, протянутая вдоль геометрической фигуры

1 Прямая, соединяющая 2 точки окружности 2 Твёрдое основание позвоночных — скелет.

Прямая линия, соединяющая 2 точки окружности …Если о геометрии разговор…

В геометрии — прямая, соединяющая две точки кривой, например дуги, окружности. В биологии — первичная скелетная ось у высших животных и человека.

Это прямая находящаяся на окружножности и не проходящая через её центр.

1 Прямая, соединяющая 2 точки окружности 2 Твёрдое основание позвоночных — скелет

Хорда — это отрезок, соединяющий две точки окружности.

отрезок соединяющий 2 точки

это отрезок соединяюший две точки

Балбесы! отрезок соединяющий 2 точки на окружности. В принципе даже прямая, проходящая через центр окружности, тоже будет являться хордой.

хорда в плениметрии отрезок, соединяющий 2 точки данной окружности. хорда находится на секущей прямой- прямой линии.

ето прямая соединяющая две или более точки

touch.otvet.mail.ru

Хорда окружности — Википедия

Материал из Википедии — свободной энциклопедии

У этого термина существуют и другие значения, см. Хорда. 1 — секущая, 2 — хорда AB (отмечена красным цветом), 3 — сегмент (отмечен зелёным цветом), 4 — дуга

Хо́рда (от греч. χορδή — струна) в планиметрии — отрезок, соединяющий две точки данной кривой (например, окружности, эллипса, параболы, гиперболы).

Хорда находится на секущей прямой — прямой линии, пересекающей кривую в двух или более точках. Плоская фигура, заключённая между кривой и её хордой называется сегментом, а часть кривой, находящаяся между двумя крайними точками хорды называется дугой. В случае с замкнутыми кривыми (например, окружностью, эллипсом) хорда образует пару дуг с одними и теми же крайними точками по разные стороны хорды. Хорда, проходящая через центр окружности, является её диаметром. Диаметр — самая длинная хорда в окружности.

Свойства хорд окружности[ | ]

Хорда и расстояние до центра окружности[ | ]

Если расстояния от центра окружности до хорд равны, то эти хорды равны.
Если хорды равны, то расстояния от центра окружности до этих хорд равны.

encyclopaedia.bid

❶ Что такое хорда 🚩 что такое хода 🚩 Естественные науки

Чтобы получить геометрическую хорду, начертите окружность. Обозначьте на ней две точки и проведите через них секущую. Отрезок, находящийся между точками пересечения этой линии и окружности, и будет хордой.

Рассмотрите свойства хорды. Разделите ее пополам и проведите из этой точки перпендикуляр. Он пройдет и через центр окружности. Если же поступить наоборот и провести из центра радиус, перпендикулярный к хорде, то он разделит ее на 2 равные части.

Проведите вторую хорду, равную по длине уже имеющейся и параллельную ей. Соедините точки пересечения обеих хорд с ее центром. Вы получите 2 треугольника, которые равны между собой по трем сторонам (отрезки от центра до линий пересечения хорд с окружностью представляют собой радиусы, а сами хорды равны между собой по условиям задания). Соответственно, высоты, проведенные к равным сторонам, тоже равны между собой. То есть эти хорды удалены от центра окружности на равные расстояния. Из равенства треугольников следует и другое свойство равных и параллельных хорд — дуги, заключенные между ними, равны между собой.

Особые свойства есть и у не параллельных хорд, пересекающих одну и ту же окружность. Если они пересекаются, то делятся на отрезки, и их соотношение можно вычислить. Произведение отрезков, на которые делится в точке пересечения одна из хорд, равно произведению отрезков другой.

На первый взгляд может показаться, что математический и зоологический термины между собой не связаны. Но это не совсем так. Это слово в переводе с греческого означает «струна». В геометрии это — струна, стягивающая сегмент, а в зоологии — спинная струна, то есть несегментиованная скелетная ось. Организмы, имеющие такую ось, называются хордовыми.

Хордовые — тип вторичнополостных животных, он включает несколько подтипов. У всех животных этого типа есть спинномозговая трубка и жаберные щели. У большинства организмов, относящихся к хордовым, сама спинная струна присутствует только в начале развития. Потом вместо нее появляется позвоночник. Однако есть и низшие хордовые, у которых такая скелетная ось сохраняется на всю жизнь. К таким животным относятся, например, ланцетники, ойкоплевра.

В биологии и медицине встречаются и другие хорды. Хордой принято называть любую нитевидную структуру. Бывают сухожильные хорды, нервные волокна. хорда эмбриона. Последняя как раз и является примером спинной струны, которая у человека исчезает по мере развития зародыша.

Этот термин достаточно широко применяется в технике. Как и в геометрии, он обозначает прямую, соединяющую две точки кривой. Например, в авиации есть термин «хорда крыла» Средняя аэродинамическая хорда является одним из важнейших параметров летательного аппарата.