Знайти похідну – Онлайн калькулятор. Розв’язання похідних онлайн

Онлайн калькулятор. Розв’язання похідних онлайн

Оператор	Опис
Найпростіші математичні операції
+ — * / ()	Додавання, віднімання, множення, ділення та групуючі символи: + — * / () . Знак множення * — необов’язковий: вираз 2sin(3x) еквівалентний 2*sin(3*x). Дужки використовуються для групування виразів.
0.5	Десяткові дроби записуються через точку: 0.5 — вірний запис; 0,5 — невірний запис.
Елементарні функції
xn	Піднесення до степеню: x^n, наприклад, щоб ввести x2 використовується x^2
√x	Квадратний корінь: \sqrt(x) або x^(1/2)
3√x	Кубічний корінь: x^(1/3)
n√x	Корінь n-того степеню з x: x^(1/n)
ln(x)	Натуральний логарифм (логарифм з основою e): log(x)
logax	Логарифм от x з основою a: log(x)/log(a)
lg(x)	Десятковий логарифм (логарифм з основою 10): log(x)/log(10)
ex	Експоненційна функція: exp(x)
Тригонометричні функції
sin(x)	Синус від x: sin(x)
cos(x)	Косинус від x: cos(x)
tg(x)	Тангенс x: tan(x)
ctg(x)	Котангенс x: 1/tan(x)
arcsin(x)	Арксинус x: arcsin(x)
arccos(x)	Арккосинус x: arccos(x)
arctan(x)	Арктангенс x: arctan(x)
arcctg(x)	Арккотангенс x: \pi/2 — arctan(x)
Деякі константи
e	Число Ейлера e: \e
π	Число π: \pi

ua.onlinemschool.com

Похідна функції, як знайти похідну функції

Означення: Похідною функції в точці називається границя відношення приросту функції в точці до приросту аргументу, коли приріст аргументу прямує до нуля (можна позначити або )

Операція знаходження похідної називається диференціюванням

Поняття приросту аргументу і функції

Приріст аргументу

 

 

Приріст функції

Похідні елементарних функцій

Похідні елементарних функцій знаходяться за допомогою таблиці:

Всі похідні елементарних функцій можна знайти тут!

Складена функція. Як знайти складену функцію

Похідна суми (різниці) двох функцій, кожна з яких має похідну, дорівнює сумі (різниці) похідних цих функцій:

Похідна добутку двох функцій, кожна з яких має похідну, дорівнює сумі добутків кожної функції на похідну другої функції:

Похідну частки частки двох функцій f(x) і g(x), кожна з яких має похідну і g(x)≠0, знаходять за формулою

Сталий множник можна виносити за знак похідної:

Наведені формули називають правилами диференціювання.

Геометричний зміст похідної

Дотичною до кривої в даній точці називається граничне положення січної , коли точка наближається вздовж кривої до точки

 

 

— кутовий коефіцієнт дотичної

 

Рівняння дотичної до графіка функції в точці з абцисою

 

 

Значення похідної в точці дорівнює кутовому коефіцієнту дотичної до графіка функції в точці з абцисою і дорівнює тангенсу кута нахилу цієї дотичної до осі

Фізичний зміст похідної

Похідна характеризує швидкість зміни функції при зміні аргументу

— залежність пройденого шляху від часу

— швидкість прямолінійного руху

— прискорення прямолінійного руху

cubens.com

Знайти похідні за формулами диференціювання

Для практичного ознайомлення з таблицею основних формул диференціювання розглянемо популярні варіанти завдань на похідні.

Приклад 1. Обчислити похідні функцій

1)

Розв’язок. За формулами диференціювання (1), (3), (9) знаходимо похідну полінома


Похідна від сталої рівна нулю. Це правило найлегше, тому запам’ятайте його в числі перших.

 

2)

Розв’язок. Вводимо дробові та від’ємні степені, та перетворюємо задану функцію до вигляду

Використовуючи формули (3), (4), (9), знаходимо похідні


Вкінці записуємо результат через корені.

 

3)

Розв’язок. Похідну дробової функції знаходимо за правилом похыдної частки

Обчислення не складні — в результататі диференціювання отримаємо різницю простих дробів 1 та 2 типу.

 

4)

Розв’язок. Похідну кореневої залежності шукаємо за правилом складної функції


При роботі з дробовими показниками будьте уважні!

 

5)

Розв’язок. Похідну від добутку кореня на поліном знаходимо за правилом добутку функцій та формулою похідної від складної функції. В результаті отримаємо наступні перетворення



Записів багатенько, проте на практиці буде не легше, тож вивчайте правили диференціювання.

 

6)

Розв’язок. За формулою похідної від складної функції отримаємо


Останній вираз можете спростити, підсумувавши показники змінної.

 

7)

Розв’язок. Багато студентів, які ще добре не знають правил, спочатку підносять до квадрату вираз в дужках, а потім проводять диференціювання. Це неправильно, довго і важко. Скориставшись правилом диференціювання складної функції, отримаємо похідну від квадрату домножену на похідну кубічної функції



Якщо Ви будете підносити до квадрату, а потім диференціювати то отримаєте многочлен, який ще треба буде зводити до компактного вигляду. Результат буде правильний, але навіщо йти складним шляхом, якщо за нас вже давно придумали правила диференціювання, які спрощують обчислення. Вивчайте їх та користуйтеся на практиці.

yukhym.com

Як знайти похідну?

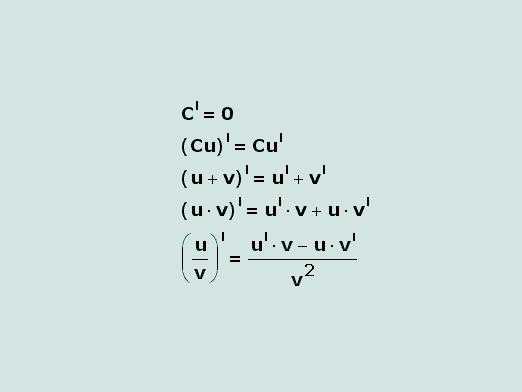
Завдання знаходження похідної від заданої функціїє однією з основних в курсі математики старшої школи і в вищих навчальних закладах. Неможливо повноцінно дослідити функцію, побудувати її графік без взяття її похідної. Похідну функції легко можна знайти, знаючи основні правила диференціювання, а також таблицю похідних основних функцій. Давайте розберемося, як знайти похідну функції.

Похідної функції називають границя відношення приросту функції до приросту аргументу, коли приріст аргументу прямує до нуля.

Зрозуміти це визначення досить складно, так якпоняття межі в повній мірі не вивчається в школі. Але для того, щоб знаходити похідні різних функцій, розуміти визначення не обов’язково, залишимо його фахівцям математикам і перейдемо відразу до знаходження похідної.

Процес знаходження похідної називається диференціюванням. При диференціюванні функції ми будемо отримувати нову функцію.

Для їх позначення будемо використовувати латинські букви f, g і ін.

Існує багато всіляких позначень похідних. Ми будемо використовувати штрих. Наприклад запис g «означає, що ми будемо знаходити похідну функції g.

Таблиця похідних

Для того щоб дати відповідь на питання як знайтипохідну, необхідно привести таблицю похідних основних функцій. Для обчислення похідних елементарних функцій не обов’язково робити складні обчислення. Досить просто подивитися її значення в таблиці похідних.

1. З «= 0
2. (Sin x) «= cos x
3. (Cos x) «= -sin x
4. (xⁿ) «= N x^n-1
5. (e^x) «= E^x
6. (Ln x) «= 1 / x
7. (a^x) «= A^xln a
8. (log_ax) «= 1 / x ln a
9. (Tg x) «= 1 / cos²x
10. (Ctg x) «= — 1 / sin²x
11. (Arcsin x) «= 1 / √ (1-x²)
12. (Arccos x) «= — 1 / √ (1-x²)
13. (Arctg x) «= 1 / (1 + x²)
14. (Arcctg x) «= — 1 / (1 + x²)

Приклад 1. Знайдіть похідну функції y = 500.

Ми бачимо, що це константа. По таблиці похідних відомо, що похідна константи, дорівнює нулю (формула 1).

(500) «= 0

Приклад 2. Знайдіть похідну функції y = x¹⁰⁰.

Це статечна функція в показнику якої 100 і щоб знайти її похідну потрібно помножити функцію на показник і знизити на 1 (формула 3).

(x¹⁰⁰

) «= 100 x⁹⁹

Приклад 3. Знайдіть похідну функції y = 5^x

Це показова функція, обчислимо її похідну за формулою 4.

(5^x) «= 5^xln5

Приклад 4. Знайдіть похідну функції y = log₄x

Похідну логарифма знайдемо за формулою 7.

(log₄x) «= 1 / x ln 4

Правила диференціювання

Давайте тепер розберемося, як знаходитипохідну функції, якщо її немає в таблиці. Більшість досліджуваних функцій, не є елементарними, а являють собою комбінації елементарних функцій за допомогою найпростіших операцій (додавання, віднімання, множення, ділення, а також множення на число). Для знаходження їх похідних необхідно знати правила диференціювання. Далі буквами f і g позначені ф

uk.kagouletheband.com

Знаходження похідних вищих порядків

Під похідною вищих порядків розуміють диференціювання функції більше ніж один раз. Якщо похідну y'(x) повторно диференціювати, то одержимо похідну другого порядку, або другу похідну функції y=f(x), і вона позначається

Похідна третього порядку матиме запис

Аналагічно отримують формули для знаходження похідних вищих порядків. При знаходженні похідної (n+1) порядку необхідно знати похідну n-го порядку. Вийняток становлять функції, для яких можна помітити закономірність зміни похідних. Це степеневі, деякі тригонометричні та експоненціальні функції:

В інших випадках, для знаходження похідних вищих порядків від заданої функції потрібно послідовно знаходити всі її похідні нижчих порядків. Для практичного вивчення матеріалу розглянемо приклади.

Приклад 1. Обчислити похідні другого порядку

1)

Розв’язок. За правилами диференціювання параметричних функцій маємо

Застосуємо до заданої функції. Знайдемо похідну y’


Диференціюємо функцію повторно. За правилом диференціювання отримаємо

За формулою обчисюємо y»

Вивчайте формулу другої похідної, вона не така очевидна для параметричної функції, але іншої немає.

 

2)

Розв’язок. Визначаємо першу похідну для кореневої функції

Обчислюємо другу похідну за правилом похідної частки

Ящо пи обчисленні Ви отримаи вираз другої похідної через першу, то потрібно замість першої підставити її значення. Добре перегляньте як тут спростиася підстанова першої похідної.

 

3)

Розв’язок. Обчислимо першу похідну поліному

а потім другу

При знаходженні похідної другого і вищих порядків для даного прикладу і йому подібних можна користуватися наступним правилами:
(1) якщо степінь функції менший порядку похідної k, то даний доданок вкладу не дає

(2) всі старші степені дають вклад

За такою схемою другу похідну можна було знайти за один прохід


Для практики другий спосіб ефективніший, особливо якщо потрібно знайти похідні набагато вищих порядків ніж другий.

 

4)y=e^3x

Розв’язок. Похідна функції першого порядку матиме вигляд

Повторне диференціювання експоненти множником винесе степінь

По аналогії можна вивести формулу похідної експоненціальної функції k-го порядку

Розв’язуючи приклади для синус і косинус функцій можна замітити подібність при обчисленні старших похідних і вивести наступні залежності








Користуйтеся формулами і нехай не виникає проблем з похідними вищих порядків.

yukhym.com

Часткові похідні першого та другого порядку

Завдання на часткові похідні розв’язують студенти на1, 2 курсі навчання. Такі приклади задають і заочникам і студентам стаціонарної форми. Початкові прилади досить прості, однак на контрольній та тестах попадають складні приклади на обчислення часткових похідних. Все залежить від складності функції – поліноми та прості тригонометричні функції піддаються диференціюванню без значних труднощів, а от дробово-раціональні функції, комбінації раціональних та показникових вимагають більшої уваги та часу для знаходження похідних. Схема обчислень похідної від функції 2 змінних достатньо проста – змінну по якій не диференціюють вважають константою при обчисленні і першої, і другої похідної. На практиці це виглядає наступним чином.

Приклад 1. Знайти часткові похідні й повний диференціал першого порядку функції
в точці N(1;2) при заданому аргументі : delta[x]=0,03; delta[y]=-0,02

Розв’язання: Знайдемо часткові похідні першого порядку від заданої функції двох змінних:

В точці N(1;2) обчислюємо часткові похідні рівні


Повний диференціал знайдемо за формою

Із обчислень бачимо, що знайти повний диференціал функції під силу кожному.

 

Приклад 2. Знайти часткові похідні другого порядку функції
Розв’язання: Обчислюємо часткові похідні першого порядку від заданої функції двох змінних:


Далі повторним диференціюванням по кожній із двох змінних знаходимо часткові похідні другого порядку.
Друга похідна по «ікс» прийме значення


Друга похідна по «ігрику»


Друга похідна по «ікс ігрик»


При обчисленні похідних використовували правило похідної частки функцій.

Приклад 3. Обчислити часткові похідні другого порядку функції
Розв’язання: Знаходимо часткові похідні першого порядку від квадрату синус функції від двох змінних:

Тут спростили вираз за формулою подвійного кута.

Повторним застосуванням похідної знаходимо часткові похідні другого порядку



Це і є відповіддю до задачі.

Приклад 4. Дослідити на екстремум функцію двох змінних
Розв’язання: Знайдемо критичні точки функції. Для цього обчислюємо часткові похідні першого порядку


та прирівнюємо їх до нуля. В результаті отримаємо систему двох рівнянь, яку і розв’язуємо



Критична точка із системи рівнянь рівна (0;-2).
Щоб встановити, чи функція в критичній точці набуває максимуму чи мінімуму слід знайти похідні другого порядку в критичній точці



і визначити характер критичної точки зі знаку

Оскільки A>0 та параметр A*C-B*B>0 більший нуля, то функція має мінімум в знайденій точці. Знайдемо значення функції в точці мінімуму

Графік функції двох змінних в околі точки мінімуму має вигляд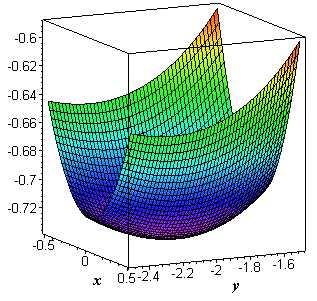
Такого роду приклади на часткові похідні зустрічаються на першому другому курсі навчання математичних дисциплін. Якщо Вам не під силу знайти часткові похідні функції першого та другого порядку, в навчанні зустрічаються складні функції, або навчаєтеся заочно тоді звертайтеся до нас. Через форму зворотнього зв’язку Ви завжди можете замовити у нас тести чи контрольну. Пам’ятайте, що наш сервіс працює для того, щоб полегшити Вам навчання!

yukhym.com

Знаходження похідних від неявно заданих функцій

Часто на практиці зустрічаються функції, в яких незалежна змінна x і функція y зв’язані між собою формулою
f(x,y)=0
з якої не можна відокремити саму функцію. В цьому випадку функція y(x) називається неявною функцією від аргумента x.

Однак саму похідну від функції по змінній x можна обчислити. Для цього диференціюють функцію f(x,y) по x, при цьому враховують, що сама функція залежна від змінної y=y(x). З одержаного рівняння згруповують доданки, що містяться при похідній y’ і виражають її.
Як це виглядає на пракиці проілюстровано на прикладах із Дубовика В.П., Юрика І.І. «Вища математика. Збірник задач».

Приклад 1. Знайти похідні неявно від заданих функцій y(x) .

1) (5.219) 3^x+3^y=3^x-y

Розв’язок:Продиференціюємо праву і ліву частини

Отриманий вираз поділимо на спільний множник ln(3) та згрупуємо доданки, що містять похідну y'(x) і перенесемо їх в одну сторону за знак рівності. В результаті отримаємо

Поділивши на множник при похідній y'(x) отримаємо її значення

Для спрощення винесемо із чисельника та знаменника спільні множники 3^x та 3^y відповідно. В результаті отримаємо:

Як бачите, нічого складного ми не робили, проте швидко відшукали похідну неявно заданої функції. Розглянемо наступне завдання.

 

2) (5.223)

Розв’язок:Проведемо диференціювання виразу. Перший доданок дасть 2, похідну від арккосинуса знаходимо за правилом складеної фунції

Виділяємо доданки, що містять похідну y'(x)

Поділимо на множник при похідній та відшукаємо її значення

Завдання повністю розв’язане.

 

3) (5.227)

Розв’язок:Обчислимо похідну правої і лівої частини, від косинуса знаходимо, як від складеної функції

Похідну від частки функцій рівна

Перших два множники рівні синусу подвійного кута. Тому похідні можемо згрупувати у вигляді

Домножимо праву та ліву частини на множник , щоб позбутися знаменників та згрупуємо доданки при похідній y'(x)


З останньої залежності знаходимо значення потрібної похідної

В такого роду прикладах головне не помилитися при відшуканні похідних. Фугкції тут взято доволі складні, заодно вивчете інші правила диференціювання.

 

4) (5.236)

Розв’язок:Диференціюємо неявно задану функцію по змінній

Перегрупуємо доданки, що містять y’

Зводимо вирази до спільного знаменника

та підставляємо їх на свої місця


Звідси виражаємо похідну функції

На цьому завдання розв’язано.
При обчисленні похідної неявно заданої функції типовими помилками на практиці є неправильне взяття похідної та плутанина зі знаками при групуванні подібних доданків. Будьте уважні в таких ситуаціях та не допускайте помилок. На скадних умовах Ви побачили як брати похідну від неявно заданої функцій, тому, якщо попрацюєте самостійно, то з даної теми отримаєте хороші результати на тастах, контрольних.

yukhym.com