Рубрика: Разное

Почему важно правильно выбрать позу для кормления грудью

Правильно подобранная поза для кормления грудью имеет огромное значение как для матери, так и для ребенка. От того, насколько комфортно чувствует себя мама во время кормления, во многом зависит длительность и успешность грудного вскармливания.

Вот несколько причин, почему так важно уделить внимание выбору позы:

• Комфорт матери. При удобной позе мама не испытывает боли и напряжения в спине, шее и руках. Это позволяет ей расслабиться и наслаждаться процессом кормления.
• Правильный захват груди. От позы зависит, насколько хорошо малыш сможет захватить грудь и эффективно сосать молоко.
• Достаточное опорожнение груди. Разные позы позволяют равномерно опорожнять все отделы молочной железы.
• Профилактика застоев. Чередование поз помогает предотвратить застои молока.
• Стимуляция лактации. При смене положений лучше стимулируется выработка молока.

Таким образом, правильная поза — это залог комфортного и эффективного кормления для мамы и малыша.

Основные позы для кормления грудью сидя

Кормление в положении сидя — самый распространенный вариант. Рассмотрим основные позы:

Поза «Колыбелька»

Это классическая и самая популярная поза. Как правильно расположиться:

• Сядьте удобно, расслабив спину и плечи.
• Положите ребенка на руку, соответствующую груди, которой будете кормить.
• Головка малыша должна лежать на сгибе локтя.
• Тело ребенка прижато к вашему животу.
• Свободной рукой направляйте грудь в рот малышу.

Эта поза отлично подходит для новорожденных и маленьких детей. Она позволяет хорошо контролировать процесс кормления.

Поза «Из-под руки»

Эта поза особенно полезна при застоях в наружных отделах груди. Как ее выполнить:

• Посадите ребенка сбоку от себя на подушку.
• Поддерживайте его спину и шею рукой, как бы держа мяч.
• Ножки малыша должны быть заведены за вашу спину.
• Направляйте грудь в рот ребенка свободной рукой.

Такое положение помогает лучше опорожнять боковые отделы молочной железы.

Поза «Перекрестная колыбель»

Эта вариация позы «колыбелька» особенно удобна для недоношенных детей:

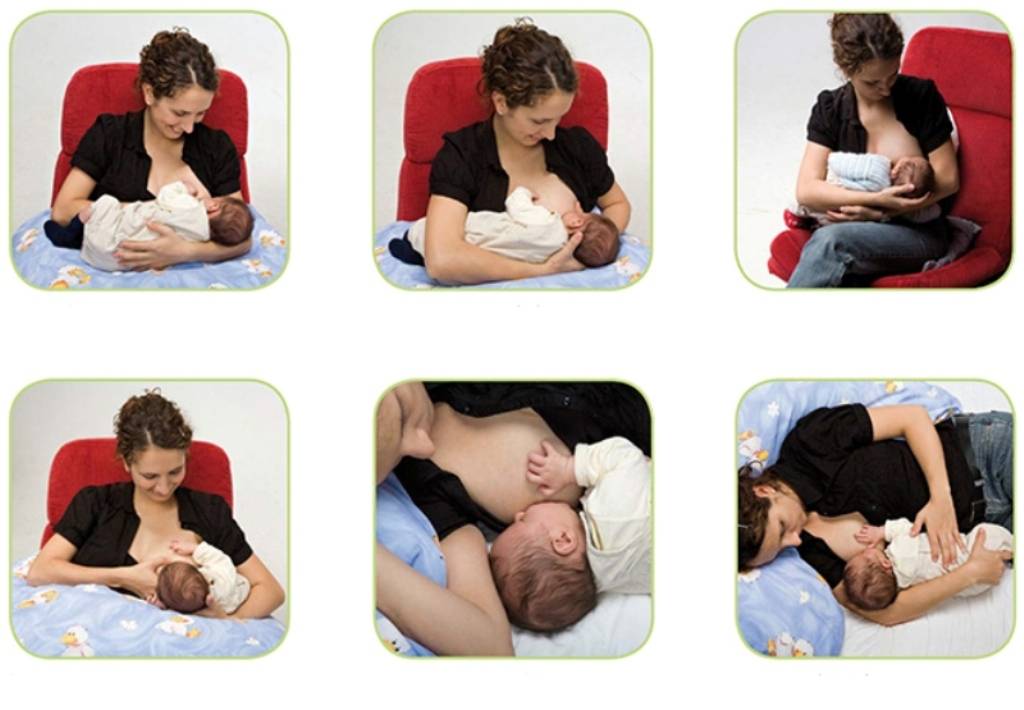
• Держите малыша на руке, противоположной кормящей груди.
• Поддерживайте головку и шею ребенка ладонью.
• Свободной рукой направляйте грудь.

Такое положение обеспечивает хороший контроль над головой малыша.

Позы для кормления лежа

Кормление лежа особенно актуально в ночное время и в первые недели после родов. Рассмотрим основные варианты:

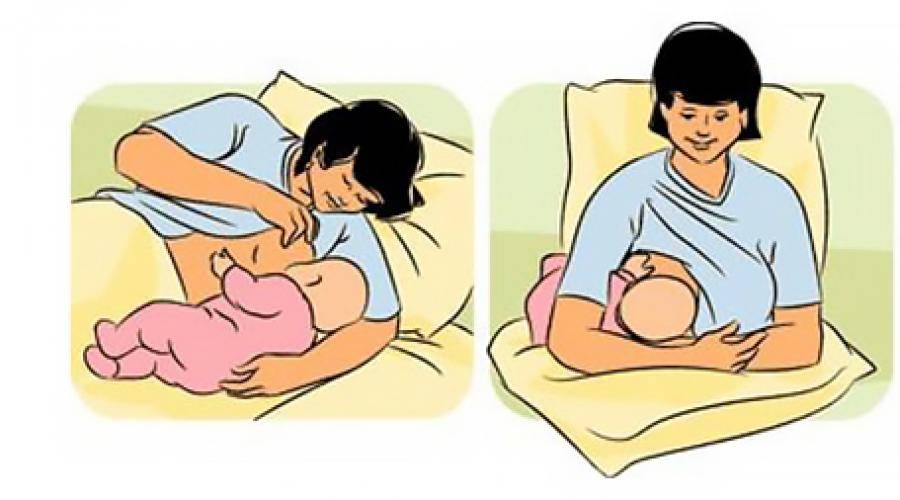
Поза «Лежа на боку»

Как правильно расположиться:

• Лягте на бок, подложив подушку под голову и шею.
• Положите ребенка рядом, животиком к себе.
• Нижней рукой поддерживайте спинку малыша.
• Верхней рукой направляйте грудь.

Эта поза позволяет отдохнуть во время кормления и подходит для ночных кормлений.

Поза «Лежа на спине»

Помогает при слишком сильном потоке молока:

• Лягте на спину.
• Положите ребенка на себя, животиком вниз.
• Поддерживайте малыша руками.

В таком положении поток молока замедляется, что помогает при проблемах с сильным рефлексом выделения молока.

Особые позы для решения проблем с лактацией

Иногда возникают ситуации, требующие специальных поз для кормления. Рассмотрим некоторые из них:

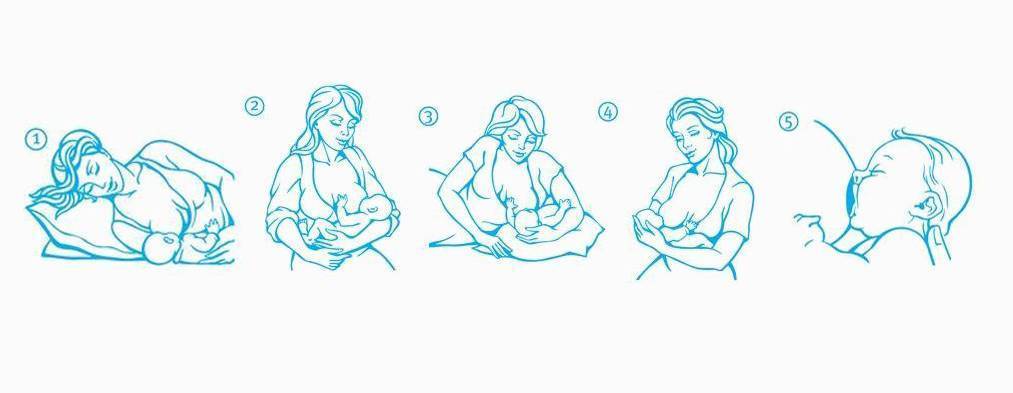
Поза «На четвереньках»

Помогает при застоях молока и затрудненном оттоке:

• Встаньте на четвереньки над лежащим ребенком.
• Наклонитесь, чтобы малыш мог захватить грудь.
• Грудь свободно свисает, что улучшает отток молока.

Эта поза эффективна, но не очень удобна для длительного кормления.

Направленное кормление при застоях

При локальных застоях молока важно правильно расположить ребенка:

• Подбородок малыша должен быть направлен на зону застоя.
• Выбирайте позу, при которой проблемный участок будет внизу.

Такой подход помогает эффективно разрешить застой в конкретном отделе молочной железы.

Как выбрать подходящую позу для кормления

Выбор оптимальной позы для кормления грудью — индивидуальный процесс. На что стоит обратить внимание при выборе:

• Комфорт матери. Поза не должна вызывать боль или напряжение.
• Удобство ребенка. Малышу должно быть легко захватывать и удерживать грудь.
• Эффективность кормления. Ребенок должен хорошо высасывать молоко.
• Состояние здоровья матери. Учитывайте наличие швов, травм и других особенностей.
• Возраст и размер ребенка. Для новорожденных и подросших детей подходят разные позы.

Не бойтесь экспериментировать и пробовать разные варианты. Со временем вы найдете наиболее удобные для вас позиции.

Правила правильного прикладывания к груди

Независимо от выбранной позы, важно соблюдать основные правила прикладывания ребенка к груди:

• Ребенок должен захватывать не только сосок, но и часть ареолы.
• Нижняя губа малыша должна быть вывернута наружу.
• Подбородок ребенка прижат к груди, нос свободен.
• При правильном захвате сосание не вызывает боли у матери.
• Щеки ребенка не должны втягиваться при сосании.

Соблюдение этих правил обеспечивает эффективное кормление и предотвращает проблемы с сосками у матери.

Распространенные ошибки при выборе позы для кормления

При выборе позы для кормления грудью часто допускаются следующие ошибки:

• Наклон над ребенком вместо приближения его к груди. Это вызывает напряжение в спине и шее матери.
• Поддержка груди пальцами близко к соску, что мешает ребенку правильно захватить ареолу.
• Неправильное расположение головы ребенка — слишком высоко или низко относительно груди.
• Использование только одной позы, что может привести к неравномерному опорожнению груди.
• Игнорирование дискомфорта — продолжение кормления в неудобной позе.

Избегание этих ошибок поможет сделать процесс кормления более комфортным и эффективным.

Дополнительные приспособления для удобного кормления

Для повышения комфорта во время кормления грудью можно использовать специальные приспособления:

• Подушка для кормления. Помогает поддерживать ребенка на нужной высоте, снимая нагрузку с рук матери.
• Кресло для кормления. Обеспечивает правильную поддержку спины.
• Подставка для ног. Помогает принять более удобное положение при кормлении сидя.
• Слинг. Позволяет кормить ребенка «на ходу», оставляя руки свободными.
• Накладки на соски. Могут помочь при проблемах с захватом груди или болезненности сосков.

Эти приспособления не являются обязательными, но могут значительно облегчить процесс кормления, особенно в первые месяцы.

Нормальный стул новорожденного: как выглядит и когда стоит беспокоиться

Стул здорового новорожденного имеет следующие характеристики:

• Цвет — светло-золотистый или желтый
• Консистенция — кашицеобразная, умеренно жидкая
• Запах — слабый кисловатый
• Частота — от 1-2 до 7-8 раз в сутки

Небольшое количество прозрачной слизи в стуле грудничка считается нормой и не должно вызывать беспокойства. Однако постоянное наличие большого количества слизи требует внимания.

Когда слизь в стуле является поводом для обращения к врачу:

• Слизь присутствует в большом количестве при каждом акте дефекации
• Слизь имеет белый, зеленый или кровянистый оттенок
• Помимо слизи в стуле есть прожилки крови
• Стул имеет резкий неприятный запах
• Консистенция стула неоднородная, с комочками
• У ребенка наблюдается диарея, колики, снижение аппетита

Основные причины появления слизи в кале грудничка

Существует ряд факторов, которые могут спровоцировать выделение слизи в стуле новорожденного:

1. Особенности питания кормящей матери

Употребление аллергенных продуктов, острой, жирной или жареной пищи может отразиться на качестве грудного молока и вызвать раздражение кишечника младенца. Это приводит к усиленной выработке слизи для защиты слизистой оболочки.

2. Лактазная недостаточность

При недостатке фермента лактазы молочный сахар не расщепляется полностью, что вызывает брожение в кишечнике и повышенное газообразование. В результате в стуле появляется слизь.

3. Неправильное введение прикорма

Слишком раннее или неправильное введение прикорма может привести к нарушению пищеварения и появлению слизи в кале. Особенно это касается введения в рацион новых фруктов и овощей.

4. Прием лекарственных препаратов

Некоторые лекарства, например, антибиотики или препараты от колик, могут вызвать изменения в работе кишечника и появление слизи в стуле.

5. Недостаточная зрелость пищеварительной системы

У новорожденных пищеварительная система еще не полностью сформирована, что может приводить к временным нарушениям и выделению слизи.

Диагностика причин появления слизи в стуле грудничка

Для определения точной причины появления слизи в кале новорожденного проводится комплексное обследование:

1. Общий анализ кала
2. Бактериологический посев кала
3. Анализ кала на дисбактериоз
4. Копрограмма
5. Анализ крови на аллергены
6. УЗИ органов брюшной полости

На основании результатов обследования врач ставит диагноз и назначает соответствующее лечение.

Лечение и профилактика появления слизи в стуле грудничка

Тактика лечения зависит от выявленной причины. Основные методы включают:

• Коррекция питания кормящей матери
• Подбор специальной смеси при искусственном вскармливании
• Временная отмена прикорма
• Прием пробиотиков для нормализации микрофлоры кишечника
• Ферментные препараты при лактазной недостаточности
• Лечение основного заболевания, вызвавшего появление слизи

Для профилактики рекомендуется:

• Соблюдение диеты кормящей матерью
• Правильное введение прикорма
• Регулярное наблюдение у педиатра
• Поддержание гигиены

Когда необходимо срочно обратиться к врачу

Немедленная консультация педиатра требуется в следующих случаях:

• В стуле присутствует кровь или гной
• Слизь имеет белый или зеленый цвет
• У ребенка высокая температура
• Наблюдается обезвоживание (сухость во рту, редкое мочеиспускание)
• Ребенок отказывается от еды
• Наблюдается сильная диарея или рвота

Эти симптомы могут указывать на серьезные заболевания, требующие срочного медицинского вмешательства.

Особенности стула у детей на грудном и искусственном вскармливании

Характер стула может различаться в зависимости от типа вскармливания ребенка:

Грудное вскармливание:

• Стул чаще жидкий, желтого цвета
• Частота стула до 6-8 раз в сутки
• Допустимо небольшое количество слизи

Искусственное вскармливание:

• Стул более плотный, светло-коричневого цвета
• Частота стула 1-2 раза в сутки
• Слизь в норме отсутствует

При переводе ребенка с грудного на искусственное вскармливание возможно временное появление слизи в стуле, что является нормальной реакцией организма на смену питания.

Влияние прикорма на характер стула грудничка

Введение прикорма — важный этап в развитии ребенка, который может отразиться на характере стула:

• При введении овощного пюре стул может стать более густым и темным
• Фруктовое пюре может вызвать разжижение стула
• Каши способствуют формированию более плотного стула
• Возможно временное появление небольшого количества слизи

Важно вводить прикорм постепенно, начиная с небольших порций, чтобы минимизировать риск нарушений пищеварения и появления слизи в стуле.

Роль микрофлоры кишечника в формировании стула новорожденного

Микрофлора кишечника играет ключевую роль в процессах пищеварения и формировании нормального стула:

• Защищает от патогенных микроорганизмов
• Участвует в синтезе витаминов
• Способствует усвоению питательных веществ
• Регулирует моторику кишечника

Нарушение баланса микрофлоры (дисбактериоз) может привести к появлению слизи в стуле, диарее или запорам. Для поддержания здоровой микрофлоры важно:

• Правильное питание кормящей матери
• Грудное вскармливание
• Своевременное и правильное введение прикорма
• Прием пробиотиков по рекомендации врача

Психологические аспекты: как справиться с тревогой родителей

Появление слизи в стуле новорожденного часто вызывает сильное беспокойство у родителей. Важно помнить:

• Небольшое количество слизи может быть нормой
• Не стоит паниковать и самостоятельно назначать лечение
• При сомнениях лучше проконсультироваться с педиатром
• Ведение дневника стула поможет отслеживать изменения
• Доверяйте своей интуиции, но не игнорируйте мнение специалистов

Помните, что большинство случаев появления слизи в стуле не представляют серьезной угрозы здоровью ребенка и легко корректируются при правильном подходе.

Нормы веса новорожденной девочки

Вес ребенка при рождении — один из ключевых показателей его физического развития. Для новорожденных девочек нормальным считается вес в диапазоне от 2,8 до 4 кг. При этом средний вес новорожденной девочки в России составляет около 3350 г.

Важно понимать, что небольшие отклонения от этих значений не всегда являются поводом для беспокойства. Каждый ребенок индивидуален, и на его вес при рождении влияет множество факторов.

Факторы, влияющие на вес новорожденной

На массу тела девочки при рождении оказывают влияние следующие факторы:

• Наследственность
• Питание матери во время беременности
• Здоровье матери
• Течение беременности
• Срок гестации
• Количество плодов при беременности

Врачи всегда учитывают эти факторы при оценке веса новорожденной девочки.

Последствия отклонений от нормы веса при рождении

Как низкий, так и избыточный вес при рождении могут оказывать влияние на дальнейшее развитие ребенка:

Низкий вес при рождении:

• Повышенный риск развития диабета 2 типа во взрослом возрасте
• Склонность к центральному ожирению в подростковом и взрослом возрасте
• Возможные проблемы с иммунитетом

Избыточный вес при рождении:

• Риск ожирения в дальнейшей жизни
• Возможные проблемы с обменом веществ
• Повышенная нагрузка на опорно-двигательный аппарат

Однако важно помнить, что при правильном уходе и питании многие потенциальные проблемы можно предотвратить.

Динамика веса в первые дни жизни

В первые дни после рождения у девочек, как и у мальчиков, наблюдается физиологическое снижение веса. Это нормальное явление, связанное с адаптацией организма к внеутробной жизни.

• Максимальная потеря веса обычно приходится на 4-5 сутки жизни
• У доношенных детей допустимо снижение веса до 7-8% от массы при рождении
• У недоношенных детей потеря веса может достигать 12-14%

После этого начинается постепенный набор веса. К 10-14 дню жизни большинство детей восстанавливают свой первоначальный вес.

Особенности набора веса у девочек в первый год жизни

В течение первого года жизни вес ребенка активно увеличивается. Для девочек характерна следующая динамика:

• К 5 месяцам вес обычно удваивается по сравнению с весом при рождении
• К году вес утраивается
• Средний набор веса в первые 6 месяцев составляет 600-800 г в месяц
• Во втором полугодии темпы набора веса снижаются до 400-500 г в месяц

Однако эти цифры являются усредненными, и индивидуальные показатели могут отличаться.

Влияние веса при рождении на распределение жира в подростковом возрасте

Исследования показывают интересную связь между весом девочки при рождении и распределением жира в ее организме в подростковом возрасте:

• Девочки, родившиеся с низким весом, но имеющие избыточный вес в подростковом возрасте, склонны к центральному типу ожирения
• У девочек с индексом массы тела выше среднего наблюдается увеличение соотношения подлопаточной и трицепсовой кожных складок на 9% на каждый килограмм снижения массы тела при рождении
• Эта тенденция еще более выражена у девочек с избыточным весом (ИМТ более 25)

Эти данные подчеркивают важность поддержания здорового веса в подростковом возрасте, особенно для девочек, родившихся с низкой массой тела.

Рекомендации для родителей

Чтобы обеспечить здоровое развитие девочки, родителям следует:

• Регулярно посещать педиатра и следить за динамикой веса ребенка
• Обеспечить полноценное грудное вскармливание (при возможности)
• Вводить прикорм своевременно, следуя рекомендациям врача
• Поощрять физическую активность ребенка
• Формировать правильные пищевые привычки с раннего возраста

При любых беспокойствах относительно веса ребенка следует обращаться к педиатру.

Заключение

Вес при рождении — важный, но не единственный показатель здоровья новорожденной девочки. Гораздо важнее динамика развития ребенка в первые месяцы и годы жизни. Правильное питание, регулярное наблюдение у врача и здоровый образ жизни помогут обеспечить гармоничное развитие ребенка, независимо от его веса при рождении.

Причины появления сыпи у новорожденных

Сыпь на коже новорожденного ребенка — довольно частое явление, которое может иметь различные причины:

• Гормональные изменения после рождения
• Аллергические реакции
• Инфекционные заболевания
• Перегрев или переохлаждение
• Недостаточная гигиена
• Контакт с раздражающими веществами

Важно правильно определить причину появления сыпи, чтобы назначить адекватное лечение. В некоторых случаях сыпь может пройти самостоятельно, но иногда требуется медицинская помощь.

Основные виды сыпи у новорожденных

У младенцев могут встречаться различные виды сыпи, отличающиеся по внешнему виду и локализации:

Потница

Потница проявляется мелкими красными прыщиками на коже, чаще всего в местах повышенного потоотделения — на шее, в складках кожи. Возникает из-за закупорки потовых желез при перегреве.

Неонатальные угри

Неонатальные угри выглядят как мелкие белые или красные прыщики на лице ребенка. Появляются из-за гормонального всплеска после рождения. Обычно проходят самостоятельно через 1-2 месяца.

Милиумы

Милиумы — это мелкие белые пузырьки на носу и щеках новорожденного. Они возникают из-за закупорки сальных желез и обычно исчезают в течение нескольких недель.

Токсическая эритема

Токсическая эритема проявляется красными пятнами и папулами на теле ребенка. Возникает как реакция на попадание чужеродных белков в организм новорожденного. Обычно проходит самостоятельно через 5-7 дней.

Методы лечения сыпи у новорожденных

Лечение сыпи у младенцев зависит от ее причины и вида. Однако существуют общие рекомендации:

• Соблюдение правил гигиены — регулярное купание, смена подгузников
• Использование мягких гипоаллергенных средств по уходу за кожей
• Контроль температуры в помещении, предотвращение перегрева
• Воздушные ванны
• Применение специальных кремов и мазей по назначению врача

При необходимости педиатр может назначить антигистаминные или противовоспалительные препараты. Самолечение недопустимо, так как некоторые средства могут навредить нежной коже младенца.

Когда необходимо обратиться к врачу

В большинстве случаев сыпь у новорожденных проходит самостоятельно и не требует специального лечения. Однако есть ситуации, когда необходима консультация педиатра:

• Сыпь сопровождается повышением температуры
• Высыпания имеют гнойный характер
• Ребенок отказывается от еды, становится вялым
• Сыпь не проходит в течение недели
• Появляются новые высыпания на фоне лечения

Врач проведет осмотр, при необходимости назначит дополнительные исследования и подберет оптимальную схему лечения.

Профилактика появления сыпи у новорожденных

Чтобы снизить риск возникновения сыпи у младенца, следует придерживаться следующих рекомендаций:

• Регулярно проводить гигиенические процедуры
• Использовать только качественные средства по уходу за кожей
• Одевать ребенка по погоде, не допуская перегрева
• Выбирать одежду из натуральных «дышащих» тканей
• Проветривать помещение и поддерживать оптимальную влажность
• Своевременно менять подгузники

Соблюдение этих простых правил поможет сохранить кожу малыша здоровой и предотвратить появление раздражений.

Особенности ухода за кожей новорожденного с сыпью

При наличии сыпи у младенца требуется особенно тщательный уход за кожей:

• Купать ребенка нужно ежедневно в теплой воде с добавлением отвара ромашки
• После купания кожу следует промокнуть мягким полотенцем, не растирая
• Складки кожи необходимо обрабатывать детским маслом или специальным кремом
• Одежда должна быть свободной, из натуральных тканей
• Подгузники нужно менять каждые 3-4 часа, обрабатывая кожу под ними

Важно помнить, что любые средства для ухода за кожей ребенка с сыпью должны быть согласованы с педиатром.

Народные средства лечения сыпи у новорожденных

Некоторые народные методы могут помочь облегчить состояние кожи при сыпи у младенца:

• Ванночки с отваром ромашки или череды
• Примочки из настоя календулы
• Обработка кожи кисломолочными продуктами (кефиром, простоквашей)
• Компрессы из картофельного крахмала

Однако перед применением любых народных средств обязательно проконсультируйтесь с врачом. Некоторые компоненты могут вызвать аллергическую реакцию у ребенка.

Влияние питания матери на появление сыпи у грудного ребенка

Питание кормящей матери может оказывать влияние на состояние кожи грудного ребенка. Некоторые продукты способны вызывать аллергические реакции, проявляющиеся в виде сыпи:

• Цитрусовые
• Шоколад
• Орехи
• Мед
• Коровье молоко
• Яйца

При появлении сыпи у ребенка на грудном вскармливании стоит пересмотреть рацион матери, исключив потенциально аллергенные продукты. Однако делать это нужно постепенно, наблюдая за реакцией малыша.

Возможные осложнения при неправильном лечении сыпи у новорожденных

Несвоевременное или неправильное лечение сыпи у младенцев может привести к серьезным осложнениям:

• Присоединение вторичной инфекции
• Распространение сыпи на большие участки тела
• Формирование хронических кожных заболеваний
• Нарушение сна и питания ребенка

Чтобы избежать этих проблем, важно своевременно обращаться к врачу и строго следовать его рекомендациям по лечению и уходу за кожей малыша.

Процесс заживления пупочной ранки у новорожденного

Пупочная ранка у новорожденного образуется после отпадения остатка пуповины, что обычно происходит на 5-15 день после рождения. При нормальном течении процесса заживление пупочной ранки занимает 2-4 недели.

Основные этапы заживления пупочной ранки:

• Отпадение остатка пуповины вместе с зажимом
• Образование небольшой ранки на месте пуповины
• Постепенное уменьшение размера ранки и образование корочки
• Полное заживление и формирование пупка

При правильном уходе пупочная ранка заживает без осложнений. Однако в некоторых случаях могут возникнуть проблемы, требующие внимания родителей и врача.

Симптомы проблем с заживлением пупочной ранки

На какие симптомы стоит обратить внимание родителям при уходе за пупком новорожденного?

• Покраснение и отек кожи вокруг пупка
• Гнойные или кровянистые выделения из ранки
• Неприятный запах из области пупка
• Мокнутие ранки более 2 недель
• Образование грануляций (разрастаний ткани) в пупке
• Повышение температуры тела у ребенка

При появлении любого из этих симптомов необходимо показать ребенка педиатру. Своевременное обращение к врачу поможет избежать развития серьезных осложнений.

Причины воспаления пупочной ранки у новорожденного

Почему у некоторых младенцев возникают проблемы с заживлением пупка? Основные причины воспаления пупочной ранки включают:

• Несоблюдение правил гигиены при уходе за пупком
• Попадание инфекции в ранку
• Травмирование пупочной области одеждой или подгузником
• Индивидуальные особенности заживления у ребенка
• Наличие пупочной грыжи
• Снижение иммунитета у недоношенных детей

Правильный уход и соблюдение гигиены помогают предотвратить большинство проблем с заживлением пупочной ранки у новорожденного.

Методы лечения воспаления пупка у младенца

При обнаружении признаков воспаления пупочной ранки педиатр может назначить следующее лечение:

• Обработка ранки антисептическими растворами (перекись водорода, хлоргексидин)
• Применение местных антибактериальных препаратов (мази, порошки)
• В тяжелых случаях — системная антибиотикотерапия
• Физиотерапевтические процедуры (УФО-облучение)
• При грануляциях — прижигание нитратом серебра

Лечение назначается индивидуально в зависимости от состояния ребенка и тяжести воспаления. Самолечение недопустимо, так как может привести к осложнениям.

Правила ухода за пупком новорожденного

Для профилактики проблем с заживлением пупочной ранки важно соблюдать следующие правила ухода:

1. Обрабатывать пупок 2-3 раза в день антисептическими растворами
2. Держать область пупка сухой и чистой
3. Не использовать тугое пеленание
4. Подбирать подгузники с вырезом для пупка
5. Не допускать попадания мочи и кала на ранку
6. Проветривать пупок, устраивая воздушные ванны
7. Купать ребенка только после полного заживления ранки

При правильном уходе процесс заживления пупочной ранки проходит быстро и без осложнений.

Когда необходимо срочно обратиться к врачу?

В каких ситуациях родителям новорожденного нужно незамедлительно показать ребенка педиатру?

• Обильные гнойные или кровянистые выделения из пупка
• Сильное покраснение и отек кожи вокруг пупка
• Повышение температуры тела выше 38°C
• Отказ ребенка от еды, вялость, беспокойство
• Неприятный запах из области пупка
• Отсутствие признаков заживления более 3 недель

Своевременное обращение к врачу позволит предотвратить развитие серьезных осложнений и ускорить процесс выздоровления малыша.

Возможные осложнения при неправильном уходе за пупком

К чему может привести несвоевременное лечение воспаления пупочной ранки у новорожденного?

• Омфалит — гнойное воспаление пупочной ранки и окружающих тканей
• Фунгус пупка — избыточное разрастание грануляционной ткани
• Пупочный свищ — незаращение пупочного протока
• Флегмона передней брюшной стенки
• Сепсис — генерализованная инфекция

Большинства осложнений можно избежать при правильном уходе за пупком и своевременном обращении к врачу при появлении тревожных симптомов.

Особенности ухода за пупком у недоношенных детей

Уход за пупочной ранкой у недоношенных новорожденных имеет свои особенности:

• Более длительный процесс заживления (до 4-6 недель)
• Повышенный риск инфицирования из-за незрелости иммунной системы
• Необходимость более частой обработки пупка (до 4-5 раз в день)
• Использование стерильных материалов при уходе
• Более строгий контроль состояния пупочной ранки

Родителям недоношенных детей следует тщательно соблюдать все рекомендации врача по уходу за пупком, чтобы избежать возможных осложнений.

Что такое свечи от запора и как они работают

Свечи от запора (суппозитории) — это лекарственная форма, которая вводится в прямую кишку ребенка для облегчения опорожнения кишечника. Основные виды свечей от запора для детей:

• Глицериновые свечи
• Бисакодиловые свечи
• Свечи с натрия гидрокарбонатом

Принцип действия свечей заключается в следующем:

1. Они оказывают местное раздражающее действие на слизистую прямой кишки
2. Усиливают перистальтику кишечника
3. Размягчают каловые массы
4. Облегчают процесс дефекации

Эффект от применения свечей обычно наступает через 15-30 минут. Они помогают быстро справиться с острым запором у ребенка.

В каких случаях назначают свечи от запора детям

Основные показания к применению свечей от запора у детей:

• Острый запор (отсутствие стула более 3-4 дней)
• Затрудненная и болезненная дефекация
• Необходимость подготовки к диагностическим процедурам
• Запор на фоне приема некоторых лекарств
• Запор при смене питания или режима дня

Важно понимать, что свечи не лечат причину запора, а лишь облегчают симптомы. Поэтому их не рекомендуется применять длительно без консультации с врачом.

Как правильно использовать свечи от запора у детей

Правила применения свечей от запора у детей:

1. Тщательно вымойте руки перед процедурой
2. Уложите ребенка на бок или на спину с согнутыми ногами
3. Аккуратно введите свечу в анальное отверстие острым концом вперед
4. Удерживайте ягодицы ребенка сжатыми 1-2 минуты
5. Оставьте свечу на 15-20 минут для полного растворения

Не рекомендуется применять свечи чаще 1 раза в сутки и дольше 5-7 дней подряд. При отсутствии эффекта обратитесь к врачу.

Эффективность и безопасность свечей от запора для детей

Свечи от запора считаются достаточно эффективным и безопасным средством при правильном применении. Их преимущества:

• Быстрое наступление эффекта (15-30 минут)
• Минимальное системное действие на организм
• Возможность применения с первых дней жизни (по назначению врача)
• Удобство использования

Однако у свечей есть и недостатки:

• Возможность раздражения слизистой прямой кишки
• Риск привыкания при длительном применении
• Неэффективность при хронических запорах

Поэтому важно применять свечи строго по назначению врача и не злоупотреблять ими.

Противопоказания и побочные эффекты свечей от запора у детей

Основные противопоказания к применению свечей от запора у детей:

• Кишечная непроходимость
• Острые воспалительные заболевания кишечника
• Кровотечения из прямой кишки
• Трещины заднего прохода
• Аллергия на компоненты свечей

Возможные побочные эффекты при использовании свечей:

• Раздражение и зуд в области ануса
• Болезненные ощущения при введении
• Спазмы кишечника
• Диарея при передозировке

При появлении любых нежелательных реакций следует прекратить применение свечей и обратиться к врачу.

Как выбрать подходящие свечи от запора для ребенка

При выборе свечей от запора для ребенка следует учитывать:

1. Возраст ребенка (есть свечи для новорожденных и детей постарше)
2. Причину и длительность запора
3. Наличие хронических заболеваний
4. Индивидуальную переносимость компонентов
5. Рекомендации педиатра

Не стоит выбирать свечи самостоятельно — проконсультируйтесь с врачом. Он подберет оптимальный вариант с учетом особенностей ребенка.

Альтернативные способы борьбы с запорами у детей

Помимо свечей существуют и другие методы лечения запоров у детей:

• Коррекция питания (увеличение количества клетчатки, жидкости)
• Массаж живота
• Гимнастика для кишечника
• Применение пробиотиков
• Прием осмотических слабительных (например, лактулозы)

В большинстве случаев комплексный подход позволяет справиться с запорами без применения свечей. Однако в острых ситуациях свечи могут быть полезны как экстренная помощь.

Когда необходимо обратиться к врачу при запорах у ребенка

Обязательно покажите ребенка педиатру, если наблюдаются следующие симптомы:

• Запор длится более 5-7 дней
• Сильные боли в животе
• Кровь в стуле
• Повышение температуры
• Отсутствие аппетита, тошнота, рвота
• Потеря веса

Эти признаки могут указывать на серьезные заболевания, требующие тщательной диагностики и лечения. Не занимайтесь самолечением — доверьтесь специалисту.

Особенности выбора мази от аллергии для детей до 1 года

При выборе мази от аллергии для малышей до года следует учитывать несколько важных факторов:

• Безопасность и мягкость действия препарата
• Отсутствие агрессивных компонентов в составе
• Гипоаллергенность
• Разрешенный возраст применения с рождения
• Быстрое устранение зуда и раздражения
• Восстановление защитных функций кожи

Лучше отдавать предпочтение негормональным средствам природного происхождения. Гормональные мази назначаются врачом только в крайних случаях при тяжелых формах аллергии.

Топ негормональных мазей от аллергии для детей до года

Рассмотрим наиболее эффективные и безопасные негормональные средства для лечения аллергии у младенцев:

1. Бепантен

Мазь на основе декспантенола оказывает противовоспалительное и регенерирующее действие. Ускоряет заживление, устраняет зуд и раздражение. Разрешена с рождения.

2. Д-Пантенол

Аналог Бепантена с аналогичным составом и действием. Эффективно увлажняет и восстанавливает кожу. Гипоаллергенна, подходит для новорожденных.

3. Деситин

Цинковая мазь с противовоспалительным эффектом. Подсушивает мокнущие участки, заживляет микротрещины. Безопасна с первых дней жизни.

4. Судокрем

Комбинированное средство с цинком, ланолином и бензилбензоатом. Снимает воспаление, зуд, покраснение. Создает защитный барьер на коже. Можно использовать с рождения.

Гормональные мази от аллергии: особенности применения у детей до года

Гормональные препараты обладают мощным противоаллергическим действием, но имеют ряд ограничений для маленьких детей:

• Назначаются только врачом в крайних случаях
• Применяются коротким курсом 3-5 дней
• Наносятся очень тонким слоем
• Нельзя использовать на большие участки кожи
• Противопоказаны при инфекционных поражениях

К разрешенным гормональным мазям для детей до года относятся:

1. Адвантан

Мазь с метилпреднизолона ацепонатом. Оказывает противовоспалительное, противоаллергическое, противозудное действие. Разрешена с 4 месяцев.

2. Элоком

Содержит мометазона фуроат. Быстро устраняет симптомы аллергии. Разрешен к применению с 2 лет, но в исключительных случаях врач может назначить и младенцам.

Правила нанесения мазей от аллергии детям до года

При использовании любых средств для лечения аллергии у малышей важно соблюдать следующие правила:

1. Тщательно очистить и подсушить кожу перед нанесением
2. Наносить тонким слоем, не втирая
3. Избегать попадания на слизистые
4. Не наносить на большие участки тела
5. Не использовать под подгузник
6. Соблюдать кратность применения по инструкции
7. Не превышать рекомендованный курс лечения

Как выбрать эффективную мазь от аллергии для ребенка до года

При выборе средства для лечения аллергии у малышей следует учитывать несколько важных критериев:

• Возраст ребенка и разрешенный производителем возраст применения
• Форма и локализация аллергических высыпаний
• Наличие дополнительных симптомов (зуд, покраснение, отек)
• Индивидуальная переносимость компонентов
• Рекомендации педиатра

Важно помнить, что самолечение аллергии у детей до года недопустимо. Перед применением любых средств необходимо проконсультироваться с врачом.

Народные средства от аллергии для детей до 1 года

В дополнение к аптечным препаратам можно использовать некоторые народные методы для облегчения симптомов аллергии у малышей:

• Ванночки с отваром ромашки или череды
• Примочки из настоя календулы
• Протирания кожи отваром коры дуба
• Компрессы из картофельного сока
• Смазывание облепиховым маслом

Однако перед применением любых народных средств также следует проконсультироваться с педиатром, чтобы исключить возможные противопоказания и побочные эффекты.

Профилактика аллергических реакций у детей до года

Чтобы снизить риск развития аллергии у малышей, рекомендуется соблюдать следующие меры профилактики:

1. Грудное вскармливание минимум до 6 месяцев
2. Правильное введение прикорма с учетом индивидуальных особенностей
3. Гипоаллергенная диета кормящей мамы
4. Регулярное проветривание и влажная уборка в доме
5. Использование гипоаллергенных средств гигиены и бытовой химии
6. Ограничение контакта с потенциальными аллергенами (пыль, шерсть животных и т.д.)

При соблюдении этих рекомендаций можно значительно снизить вероятность возникновения аллергических реакций у ребенка в первый год жизни.

Антигистаминные сиропы для детей: особенности и преимущества

Аллергические реакции у детей — распространенная проблема, с которой сталкиваются многие родители. Одним из эффективных способов борьбы с симптомами аллергии являются антигистаминные сиропы. Рассмотрим основные особенности и преимущества использования сиропов от аллергии у детей:

• Удобная форма приема для детей разного возраста
• Быстрое всасывание и наступление эффекта
• Возможность точного дозирования
• Приятный вкус, маскирующий горечь действующего вещества
• Минимальный риск побочных эффектов при правильном применении

Сиропы от аллергии для детей обычно содержат антигистаминные компоненты нового поколения, которые действуют избирательно и не вызывают выраженной сонливости. Это позволяет применять их длительными курсами при хронических аллергических заболеваниях.

Популярные детские сиропы от аллергии: обзор эффективных препаратов

На фармацевтическом рынке представлен широкий выбор антигистаминных сиропов для детей. Рассмотрим наиболее популярные и эффективные препараты:

Зиртек

Действующее вещество — цетиризин. Применяется с 6 месяцев. Оказывает длительное противоаллергическое действие в течение 24 часов. Хорошо переносится, не вызывает выраженной седации.

Эриус

Содержит дезлоратадин. Разрешен к применению с 6 месяцев. Обладает противовоспалительным эффектом. Действует быстро, эффект сохраняется до суток.

Кларитин

Активный компонент — лоратадин. Назначается детям с 2 лет. Устраняет симптомы аллергии в течение 24 часов. Не проникает через гематоэнцефалический барьер, не вызывает сонливости.

При выборе конкретного препарата следует учитывать возраст ребенка, форму и тяжесть аллергического заболевания, наличие сопутствующих патологий. Окончательное решение о назначении того или иного сиропа должен принимать врач.

Правила безопасного применения антигистаминных сиропов у детей

Чтобы лечение было эффективным и безопасным, необходимо соблюдать следующие правила:

• Строго следовать инструкции и назначенной врачом дозировке
• Не превышать максимальную суточную дозу препарата
• Соблюдать кратность приема и длительность курса лечения
• Не комбинировать разные антигистаминные средства без назначения врача
• Прекратить прием при появлении побочных эффектов и обратиться к педиатру

Перед применением сиропа обязательно встряхните флакон. Используйте прилагаемый мерный стаканчик или шприц для точного дозирования. Не давайте препарат детям младше разрешенного возраста.

Возможные побочные эффекты антигистаминных сиропов у детей

Современные препараты обычно хорошо переносятся, но в некоторых случаях могут возникать побочные реакции:

• Сонливость, вялость, снижение концентрации внимания
• Сухость во рту, жажда
• Нарушения аппетита, тошнота, диарея
• Головная боль, головокружение
• Раздражительность, беспокойство

При появлении любых необычных симптомов нужно прекратить прием препарата и проконсультироваться с врачом. В большинстве случаев побочные эффекты проходят самостоятельно после отмены лекарства.

Натуральные альтернативы синтетическим антигистаминным сиропам

Некоторые родители предпочитают использовать натуральные средства для облегчения симптомов аллергии у детей. К ним относятся:

• Сиропы на основе трав (ромашка, мята, фенхель)
• Гомеопатические препараты
• Витамин С и биофлавоноиды
• Пробиотики для укрепления иммунитета

Однако эффективность таких средств научно не доказана. При тяжелых аллергических реакциях они не могут заменить традиционные антигистаминные препараты. Применять любые альтернативные методы лечения следует только после консультации с врачом.

Когда необходимо обратиться к аллергологу

В некоторых случаях самостоятельное применение антигистаминных сиропов недостаточно эффективно. Обратиться к детскому аллергологу необходимо, если:

• Симптомы аллергии сохраняются длительное время, несмотря на лечение
• Аллергические реакции возникают часто и имеют тяжелое течение
• Есть подозрение на пищевую аллергию или непереносимость
• Требуется подбор индивидуальной схемы лечения
• Необходимо провести аллергологическое обследование для выявления причины

Специалист проведет необходимую диагностику, определит тип аллергии и назначит комплексное лечение с учетом особенностей ребенка. Это поможет эффективно контролировать симптомы и улучшить качество жизни маленького пациента.

Профилактика аллергических реакций у детей

Наряду с применением лекарственных средств важно проводить профилактические мероприятия:

• Исключить контакт с аллергенами (пыльца, шерсть животных и др.)
• Соблюдать гипоаллергенную диету
• Проводить регулярную влажную уборку в доме
• Использовать очистители воздуха с HEPA-фильтрами
• Укреплять иммунитет ребенка

Комплексный подход, включающий правильно подобранное лечение и профилактические меры, позволит значительно облегчить течение аллергических заболеваний у детей и улучшить качество их жизни.

Как определить размер головы новорожденного

Выбор правильного размера чепчика для новорожденного — важная задача для будущих родителей. Размер головы малыша может значительно варьироваться, поэтому важно знать, как правильно его измерить.

Средний обхват головы новорожденного составляет:

• У мальчиков — 35 см
• У девочек — 34 см

Однако это усредненные показатели. Фактический размер может быть как меньше, так и больше.

По данным Всемирной организации здравоохранения, обхват головы новорожденных до 1 месяца может находиться в следующих диапазонах:

• Очень низкий показатель — 30,5 см
• Низкий — 31,7 см
• Ниже среднего — 33 см
• Средний — 34,5 см
• Выше среднего — 35,5 см
• Высокий — 36,5 см
• Очень высокий — 38 см

Как правильно измерить голову новорожденного

Чтобы точно определить размер чепчика, необходимо правильно измерить обхват головы малыша:

1. Используйте мягкую сантиметровую ленту
2. Оберните ленту вокруг головы по самым выступающим точкам — лоб, уши, затылок
3. Измерение проводите на уровне примерно 1-1,5 см выше бровей
4. Лента должна плотно прилегать, но не сдавливать кожу
5. Запишите полученный результат в сантиметрах

Важно измерять голову ребенка регулярно, так как в первые месяцы жизни она активно растет:

• С рождения до 3 месяцев — на 2 см в месяц
• С 4 до 6 месяцев — на 1 см в месяц
• После 6 месяцев — на 0,5 см в месяц

Таблица размеров чепчиков для новорожденных

После измерения обхвата головы, воспользуйтесь следующей таблицей для выбора подходящего размера чепчика:

Учтите, что это ориентировочные данные. Размеры могут немного отличаться у разных производителей.

Факторы, влияющие на выбор размера чепчика

При выборе чепчика для новорожденного следует учитывать ряд факторов:

• Возраст ребенка
• Индивидуальные особенности развития
• Сезон (зимние чепчики могут быть чуть больше)
• Материал (трикотажные чепчики более эластичные)
• Производитель (размеры могут немного отличаться)

Не стоит брать чепчик «на вырост» — он должен хорошо сидеть и не спадать с головы малыша.

Особенности выбора чепчика для роддома

Чепчик — один из важных предметов в списке вещей для роддома. При его выборе обратите внимание на следующие моменты:

• Размер — возьмите 2-3 чепчика разных размеров (34-36 см и 36-38 см)
• Материал — натуральный хлопок или смесовые ткани с преобладанием хлопка
• Швы — должны быть мягкими, не натирать нежную кожу
• Резинки — лучше выбрать модель без тугих резинок
• Завязки — удобны для регулировки размера
• Сезон — летом подойдут тонкие чепчики, зимой — более теплые

Лучше взять несколько чепчиков, чтобы была возможность подобрать наиболее подходящий.

Как проверить правильность выбора чепчика

После покупки чепчика важно проверить, насколько хорошо он сидит на голове малыша:

1. Чепчик должен плотно прилегать, но не сдавливать голову
2. Между краем чепчика и бровями должно оставаться 1-1,5 см
3. Ушки должны быть полностью закрыты
4. Чепчик не должен съезжать на глаза или спадать на затылок
5. Под края чепчика должен проходить палец

Если чепчик соответствует этим критериям, значит, размер выбран правильно.

Распространенные ошибки при выборе размера чепчика

При покупке чепчика для новорожденного родители часто допускают следующие ошибки:

• Покупка чепчика «на вырост» — он будет спадать и доставлять дискомфорт
• Выбор слишком маленького размера — может пережимать голову
• Ориентация только на возраст без учета индивидуальных особенностей
• Покупка чепчика без примерки или измерения
• Выбор модели с грубыми швами или тугими резинками

Чтобы избежать этих ошибок, внимательно измеряйте голову малыша и ориентируйтесь на рекомендации по выбору размера.

Как ухаживать за чепчиком новорожденного

Правильный уход за чепчиком поможет сохранить его форму и размер:

• Стирайте чепчик перед первым использованием
• Используйте мягкие детские моющие средства
• Стирайте при температуре не выше 40°C
• Не используйте отбеливатели и кондиционеры
• Сушите в расправленном виде вдали от источников тепла
• Гладьте при низкой температуре с изнаночной стороны

Соблюдение этих правил поможет сохранить чепчик в хорошем состоянии на долгое время.

Распространенные мифы о прививках и их опровержение

Вокруг темы вакцинации существует множество противоречивой информации. Рассмотрим наиболее распространенные мифы о прививках и факты, которые их опровергают:

Миф 1: Прививки вызывают аутизм

Это один из самых стойких мифов, возникший после публикации в 1998 году исследования британского врача Эндрю Уэйкфилда. Он заявил о связи между вакциной против кори, краснухи и паротита (MMR) и развитием аутизма у детей. Однако дальнейшие исследования полностью опровергли эту теорию:

• Многочисленные крупномасштабные исследования не выявили никакой связи между вакциной MMR и аутизмом
• Работа Уэйкфилда была признана ошибочной и отозвана журналом The Lancet
• Сам Уэйкфилд был лишен медицинской лицензии за неэтичное поведение и фальсификацию данных

Таким образом, научных доказательств связи между прививками и аутизмом не существует.

Миф 2: Лучше получить естественный иммунитет, переболев болезнью

Сторонники этой идеи утверждают, что естественный иммунитет после перенесенного заболевания сильнее и надежнее, чем иммунитет от вакцины. Однако это не всегда так:

• Многие инфекционные заболевания могут привести к серьезным осложнениям и даже смерти
• Вакцины позволяют получить иммунитет без риска тяжелого течения болезни
• В некоторых случаях иммунитет от вакцины даже сильнее, чем после перенесенной инфекции
• Вакцинация помогает защитить не только привитого человека, но и окружающих (коллективный иммунитет)

Специалисты считают, что риски от самой болезни намного превышают возможные побочные эффекты вакцин.

Миф 3: Вакцины содержат опасные токсины

Действительно, в составе некоторых вакцин присутствуют вещества, которые в больших дозах могут быть токсичными. Однако:

• Количество этих веществ в вакцинах крайне мало и не представляет опасности
• Многие «токсины» естественным образом присутствуют в организме человека
• Некоторые вещества (например, алюминий) помогают усилить иммунный ответ
• Состав вакцин постоянно совершенствуется для повышения безопасности

Современные вакцины проходят строжайший контроль качества и безопасности перед применением.

Почему некоторые родители отказываются от вакцинации детей

Несмотря на доказанную эффективность и безопасность вакцин, некоторые родители все же отказываются прививать своих детей. Основные причины такого решения:

• Недоверие к фармацевтическим компаниям и системе здравоохранения
• Страх перед возможными побочными эффектами
• Вера в теории заговора о вакцинации
• Религиозные или философские убеждения
• Недостаток достоверной информации о вакцинах

Важно понимать, что отказ от прививок может иметь серьезные последствия не только для конкретного ребенка, но и для общества в целом.

Научные факты об эффективности вакцинации

Многочисленные научные исследования подтверждают высокую эффективность вакцин в борьбе с инфекционными заболеваниями:

• Благодаря вакцинации полностью ликвидирована натуральная оспа
• Заболеваемость полиомиелитом снизилась на 99% с момента начала массовой вакцинации
• Вакцина против кори предотвратила около 23,2 миллиона смертей в период с 2000 по 2018 год
• Прививки от гриппа ежегодно спасают тысячи жизней, особенно среди пожилых людей

Эти данные убедительно доказывают, что вакцинация — один из самых эффективных способов защиты от опасных инфекций.

Возможные побочные эффекты вакцин: что нужно знать

Как и любое медицинское вмешательство, вакцинация может вызывать побочные эффекты. Однако в большинстве случаев они незначительны и быстро проходят:

• Покраснение и болезненность в месте укола
• Небольшое повышение температуры
• Легкое недомогание

Серьезные побочные эффекты от вакцин крайне редки. Вероятность их возникновения намного ниже, чем риск осложнений от самих инфекционных заболеваний.

Как принять взвешенное решение о вакцинации ребенка

Решение о вакцинации должно быть осознанным и основанным на достоверной информации. Вот несколько рекомендаций для родителей:

• Обсудите вопросы вакцинации с квалифицированным педиатром
• Изучите научно обоснованную информацию из надежных источников
• Ознакомьтесь с национальным календарем профилактических прививок
• Оцените риски и преимущества вакцинации для вашего ребенка
• Не принимайте решение на основе слухов или непроверенной информации из интернета

Помните, что вакцинация — это не только защита вашего ребенка, но и вклад в общественное здоровье.

Вакцинация и коллективный иммунитет: почему это важно

Коллективный иммунитет — это ситуация, когда достаточно большая часть населения имеет иммунитет к определенному заболеванию, что затрудняет его распространение. Это особенно важно для защиты тех, кто не может быть привит по медицинским показаниям:

• Младенцы, еще не получившие все необходимые прививки
• Люди с ослабленной иммунной системой
• Пациенты, проходящие химиотерапию
• Пожилые люди

Отказываясь от вакцинации, человек не только подвергает риску себя, но и ослабляет коллективный иммунитет, что может привести к вспышкам заболеваний.

Современные тенденции в разработке вакцин

Наука о вакцинах постоянно развивается. Вот некоторые перспективные направления:

• Разработка универсальной вакцины против гриппа
• Создание вакцин против ВИЧ и малярии
• Использование новых технологий (например, мРНК-вакцины)
• Разработка вакцин против некоторых видов рака
• Усовершенствование способов доставки вакцин (например, назальные спреи)

Эти инновации могут сделать вакцинацию еще более эффективной и безопасной в будущем.