как найти значение, расчёт примеров для 7 класса, площадь фигуры
Математика
12.11.21
12 мин.
Форма объекта и его линейные размеры определяют один из важных с геометрической точки зрения параметров — объём. Формула для прямоугольника, позволяющая его вычислить, довольно проста и основана на знании стороны и высоты. Но при решении не всегда известны значения рёбер фигуры, поэтому приходится использовать свойства параллелограмма, а именно — способы нахождения площади.
Оглавление:
- Общие сведения
- Вычисление объёма
- Решение задач
- Использование калькулятора
Общие сведения
По своей сути объём является количественной характеристикой пространства, которое занимает тело или вещество. Простыми словами, этот параметр показывает вместимость. В качестве единицы измерения, согласно СИ, принят кубический метр. За обозначение же объёма взята латинская буква V.
За обозначение же объёма взята латинская буква V.
У тел, имеющих простую форму, характеристики находятся путём перемножения площади на высоту. Например, для куба он равен a3, прямоугольной призмы — h * b * a, пирамиды — (S * b * h) / 3. В эллипсоидных фигурах при расчётах используется радиус. Так, для конуса объём равен (p * R2 * h) / 3, сферы — (4 * p * R3) / 3, тора — 2 * p2 * R1 * R22.
Объём плоских фигур, таких как треугольник, круг, квадрат, прямоугольник, равен нулю. Но если их стороны или окружности имеют связанные с ними попарно параллельные линии, то они уже являются объёмными фигурами. Например, прямоугольник в пространстве называют параллелепипедом. Таким образом, чтобы найти объём прямоугольника, необходимо, чтобы он представлял собой прямоугольный параллелепипед, иначе действие будет бессмысленным.
Определить объём — значит, знать две основные величины фигуры:
- площадь — двумерная характеристика, определяющая размер фигуры;
- высоту — это длина перпендикуляра, опущенного из вершины на основание в трёхмерном пространстве.

Так как площадь измеряется в метрах квадратных, а высота просто в метрах, то перемножение площади и высоты как раз и даст единицу измерения объёма — метр кубический.
Чтобы узнать площадь прямоугольника, используют его свойства. Изучают их обычно в седьмом классе средней школы. К основным из них относят правило равенства противоположных сторон и углов, деление диагонали пополам в точке пересечения и их равенство.
Именно одинаковые диагонали являются отличительным свойством прямоугольника от параллелограмма. Фактически же диагональ делит фигуру на два прямоугольных треугольника. Это свойство довольно часто используют при проведении расчётов площади или объёма.
Вычисление объёма
Существует теорема сообщающая, что объём параллелепипеда, то есть тела основанием которой является параллелограмм, можно рассчитать, умножив площадь основания на высоту фигуры. Записывается это формула как V = h * S, при этом S является произведением сторон прямоугольника.
Записывается это формула как V = h * S, при этом S является произведением сторон прямоугольника.
Исходя из этого вычислить объём прямоугольника (параллелепипеда) можно по формуле: V = a * b * h, где: a, b — рёбра фигуры; h — высота тела.
Другими словами, параметр находится как произведение трёх измерений фигуры. Для доказательства нужно рассмотреть два возможных случая.
- Пусть имеется фигура, которая состоит из трёх измерений: a, b, c. Первые два являются основанием, к которому пристроена третье. Основание можно представить, как совокупность прямоугольников с площадью S = a * b, состоящую их квадратных единиц. На каждом из квадратов размещается кубическая единица. В итоге получается слой, состоящий из S единиц в кубе. Учитывая, что высота слоя это одна линейная единица, а высота всей фигуры состоит из энного количества таких единиц, то внутри тела можно поместить энное число слоёв. А значит, объём тела равен произведению этих кубических единиц, то есть V = a * b * c.

- Имеется прямоугольный параллелепипед. В его основании лежит прямоугольник с вершинами A, A1, B, B1. Соответственно плоскости ABCD и A1B1C1D1 будут боковыми гранями. В середине фигуры можно построить перпендикулярную плоскость MNPQ являющуюся сечением. Она будет равновеликим прямому параллелепипеду с основанием MNPQ и высотой (боковым ребром) BC. По признаку перпендикулярности, плоскости с двугранными углами являются прямыми. Отсюда можно утверждать, что MNPQ — прямоугольное тело, а значит и параллелепипед прямоугольный. Значит, его объём можно найти как произведение MN * MQ * BC. Исходя из того, что MQ перпендикулярно BC, площадь основания можно рассчитать как MQ * BC. А так как MN высота, то объём параллелепипеда можно вычислить, умножив площадь его основания на высоту.
Действительно, можно понять и без доказательств, что формула объёма верна. Если представить замкнутую фигуру с любым основанием, образованную в пространстве прямыми линиями, то в её середину можно будет поместить столько оснований, сколько позволит высота тела.
Используя законы умножения, чтобы узнать, сколько же поместится в середине фигуры таких площадей, нужно основание умножить на высоту. То есть и получается доказываемая формула: V = S * h.
Решение задач
На самом деле вычисление объёма не только выполняют на уроках математики. Это знание востребовано в довольно многих специальностях и науках. Например, при строительстве, в архитектуре, инженерии, физике, химии. Поэтому знание нахождения параметра может пригодиться не только в школе. Теорию обязательно необходимо закреплять на практике. Вот некоторые задачи, которые помогут усвоить рассматриваемый материал:
- Пусть есть параллелепипед с прямыми сторонами. Его рёбра у основания равняются 19 и 20 сантиметрам. Размер же боковой грани составляет 10 сантиметров. Вычислить объём фигуры. Эта задача на одну формулу, все данные для подстановки в неё известны.
 Так, V = a * b * c = 19 * 20 * 10 = 3 800 см3 = 0,0038 м³.
Так, V = a * b * c = 19 * 20 * 10 = 3 800 см3 = 0,0038 м³. - Пусть имеется параллелепипед с основанием 1 см на 1,2 см и высотой 0,8 см. Из него был удалено другое прямоугольное тело с размерами 0,3 x 0,55 x 0,5. Найти объём получившейся фигуры. Так как искомый параметр новой фигуры равен разнице изначального и удалённого объёмов, то зная формулу найти ответ не составит труда: V = 0,8 * 1 * 1,2 — 0,3 * 0,5 * 0,55 = 0,877 см3.
- Дан прямоугольный параллелепипед с вершинами ABCD и A1B1C1D1. Сравнить объём образованного в середине пирамиды AA1BD тела со значением фигуры. Для удобства решения стороны AB, AD, AA соответственно можно обозначить как x, y, z. Тогда объём прямоугольного тела будет равен Vп = Sп * AA1 = x * y * z. Если начертить условие на рисунке, то можно отметить, что площадь пирамиды вполовину меньше площади основания прямоугольника. То есть, Sabd = 0,5 * Sabd. Тогда V = Sabd * AA1 / 3 = x * y * z / 3 * 2 = x * y* z / 6. Значит, объём вписанной пирамиды меньше в шесть раз чем у фигуры.

- В гальванической ванне помещается три тысячи литров раствора. Высота наполнения ёмкости при этом достигает 75 сантиметров. В ванную поместили заготовку, после чего уровень поднялся на два сантиметра. Найти объём заготовки в метрах кубических. Итак, в одном кубическом метре содержится тысяча литров. Поэтому изначально в ёмкости было 3 м³ раствора. Значит, изначально в ванне раствор занимал: 3 = S * 75. Отсюда s = 3/75 = 1/25 см2. Объём детали составляет: V = S * 2 = (1/25) * 2 = 2 / 25 = 0,08 м³.
Использование калькулятора
Конечно же, на обычном калькуляторе объём прямоугольника не подсчитаешь. Разве что известны три его грани и формула нахождения параметра. Тогда нужно будет просто перемножить три числа. В других же случаях, когда нужно решить сложную задачу, связанную с громоздкими вычислениями, можно использовать математические сайты, имеющие название онлайн-калькуляторы.
Это интернет-сервисы, предлагающие своим пользователям бесплатно воспользоваться услугами по вычислению объёма геометрических фигур и выполнить другие математические операции. Для того чтобы воспользоваться сайтами-решателями, нужно иметь любой гаджет с возможностью подключения его к интернету и установленным на него веб-обозревателем.
После загрузки онлайн-калькулятора все действия пользователя сводятся к заполнению специальной формы в которую вносится условие задания. Конечно же, такое решение не может называться самостоятельным, но для проверки полученного результата или выявления ошибок в расчёте подходит идеально. Кроме, непосредственно автоматического вычисления объёма большинство сайтов содержат на своих страницах теоретический материал, а также примеры решений типовых заданий. Так что при обучении учащихся их использование на первых порах вполне оправданно.
Расчет массы и объема тела по его плотности – конспект урока – Корпорация Российский учебник (издательство Дрофа – Вентана)
Внимание! Администрация сайта rosuchebnik.ru не несет ответственности за содержание методических разработок, а также за соответствие разработки ФГОС.
Методическая разработка урока физики для 7 класса по теме «Расчет массы и объема тела по его плотности.
Класс: 7
Цели урока: повторить тему «Плотность тела», научиться определять объем тела и его массу по известной плотности, научиться решать задачи с применением этих формул.
Задачи урока: применять полученные знания в новой ситуации; развивать интерес к предмету путём выполнения разных заданий: практических и теоретических.
Дидактические материалы и оборудование к уроку: презентация, плакаты «Международная система единиц», «Приставки для образования кратных и дольных единиц», индивидуальные карточки с проверочными заданиями; весы с разновесами, мензурка, линейка, мыло, картофелина, камень.
I. Организационный момент
II. Актуализация знаний
1. Фронтальный опрос по теоретическому материалу
2. Заполнить таблицу (устно)
v |
t |
ρ |
V |
||
кг |
м |
3. Назовите число, составленное вами из номеров верных формул.
- v = S/t;
- v = St;
- S = vt;
- ρ = mv;
- ρ = m/V;
- m = ρ/V.

3. Выразите в СИ.
4,8 т; 502 г; 175 г; 35 см; 2341 мм; 584 л; 3846 см3; 0,00567 г/см3
III Проверка д/з
Проверочная работа по теме «Масса. Плотность»
Вариант 1
1) При нагревании тело расширяется. При этом плотность вещества, из которого оно сделано, …
а) не меняется б) увеличивается в) уменьшается г) увеличивается, потом уменьшается
2) Из некоторого вещества изготовили тело массой 42 г в форме параллелепипеда. Параллелепипед имеет следующие размеры: высота 1 см, ширина 2 см, длина 3 см. Определите его плотность.
3) После того как на одну чашу весов поместили тело, а на другую – набор гирь (20 г, 500 мг, 200 мг, 100 мг, 10 мг, 20 мг, 20 мг и 50 мг), весы пришли в равновесие. Чему равна масса тела?
Вариант 2
1) При охлаждении тело сжимается. При этом плотность вещества, из которого оно сделано, …
а) не меняется б) увеличивается в) уменьшается г) увеличивается, потом уменьшается
2) Канистра имеет размеры: высота 3 дм, ширина 1 дм, длина 5 дм. Масса пустой канистры 1 кг, заполненной – 13 кг. Чему равна плотность жидкости.
Масса пустой канистры 1 кг, заполненной – 13 кг. Чему равна плотность жидкости.
3) После того как на одну чашу весов поместили тело, а на другую – набор гирь (50 г, 500 мг, 200 мг, 100 мг, 10 мг, 10 мг, 20 мг и 50 мг), весы пришли в равновесие. Чему равна масса тела?
IV. Решение практических задач
1) Перед вами лежит кусочек камня. Какие измерения и расчеты необходимо выполнить для определения его плотности? С помощью какого прибора удобно измерить объем тела неправильной формы? Оформите задачу с решением.
2) Теперь вы видите кусок мыла. Какие измерения и расчеты необходимо выполнить для определения плотности этого тела? С помощью какого прибора удобно измерить объем мыла? Оформите задачу с решением.
Постановка проблемы
3) Недавно в одной из телепередач был показан сюжет о крестьянском хозяйстве, в котором вырастили замечательную картошку. Из всех городов приезжают закупать картофель, но только картофелины берут определенного объема. Примерно вот такую картофелину я вам принесла на урок. Давайте, определим ее объем. Вот только в мензурку, да и в отливной стакан она не войдет. Ваши предложения?
Примерно вот такую картофелину я вам принесла на урок. Давайте, определим ее объем. Вот только в мензурку, да и в отливной стакан она не войдет. Ваши предложения?
Это и есть тема нашего урока: Расчет массы и объема тела по его плотности.
Оформите эту задачу в тетрадях: Как найти объем тела, если известна масса тела и его плотность?
Рассмотрим примеры решения задач.
1) Перед вами в мензурке находятся вода, молоко и подсолнечное масло. Необходимо рассчитать массы этих жидкостей, зная их плотности.
2) Рядом с мензурками находятся пластмассовый и стальной шарики, электронные весы. По таблице из учебника выясните плотности этих веществ. Рассчитайте объемы шариков.
V. Самостоятельное решение расчетных задач
- Масса чугунного шара 800 г, его объем 125 см3. Сплошной этот шар или полый?
- Чему равна масса железного листа длиной 1 м, шириной 80 см, толщиной 1 мм?
- Дубовый брусок имеет массу 800 г.
 Определите его объем, если плотность дуба 800 кг/м3.
Определите его объем, если плотность дуба 800 кг/м3.
VI. Рефлексия (подведение итогов урока, оценки)
Что ж, наше занятие подходит к завершению. Я надеюсь, что полученные вами знания вы сможете использовать не только на уроках по различным предметам, но и будете применять их в повседневной жизни. А теперь рубрика обратной связи. На экране вы видите высказывания. Выберите любое и закончите его (устно).
Предлагаются варианты ответов: Сегодня я узнал… Было интересно… Было трудно… Я понял, что… Я научился… Меня удивило…
VII. Д/з
1) § 23 – учить
2) Придумать 3 интересные задачи на расчет плотности, массы или объема тел, применяемых в быту (оформить на А4 с решением и иллюстрациями, принести эти тела в класс для решения некоторых задач)
Калькулятор объема жидкости — Академия калькуляторов
Конвертер единиц измерения
Введите плотность жидкости и массу жидкости в калькулятор, чтобы определить объем жидкости. Этот калькулятор также может определить либо плотность, либо массу жидкости, если известны другие переменные.
Этот калькулятор также может определить либо плотность, либо массу жидкости, если известны другие переменные.
- Все калькуляторы объема
- Калькулятор объемного отношения
- Калькулятор объемного расхода
- Калькулятор молярного объема
- Калькулятор времени удерживания
- Калькулятор объема колонки
- Калькулятор емкости на входе
Формула объема жидкости
Ниже приведена формула объема жидкости:
LV = M/d
- Где LV — масса объема жидкости
7 M 9 жидкость
- d плотность жидкости
Чтобы рассчитать объем жидкости, разделите массу жидкости на плотность жидкости.
Определение объема жидкости
Объем жидкости просто определяется как общий объем любой жидкости или комбинации жидкостей.
Вы можете измерить объем жидкости?
Один из способов измерения объема жидкости состоит в том, чтобы налить жидкость в ограниченный контейнер, измерить высоту, на которой она заполняет контейнер, а затем определить объем жидкости путем вычисления содержащегося объема и умножения на отношение высоты жидкости к общей высоте .
Изменяют ли жидкости объем?
В большинстве случаев такие жидкости, как вода, считаются несжимаемыми, а это означает, что их объем не изменяется при изменении давления или температуры. Есть некоторые исключения из этого правила, но в целом оно верно.
Имеет ли жидкость объем?
Да, жидкости абсолютно имеют объем, но если жидкость не определена в контейнере, было бы невозможно измерить объем указанной жидкости обычными методами. Один из способов определить объем — использовать приведенную выше формулу.
Объем жидкости равен емкости?
Объем жидкости может совпадать с емкостью только в том случае, если емкость определена таким образом, что объем жидкости на 100 % контейнера указан как емкость.
Почему объемы жидкости следует считывать на уровне глаз?
Жидкости, такие как вода, обладают свойством, называемым адгезией. Это притяжение воды к другим поверхностям. Глядя на емкость, наполненную водой, важно читать измерения на уровне глаз, потому что вода будет прилипать к стенкам и может казаться немного выше, чем она есть на самом деле, если вы смотрите на нее под углом.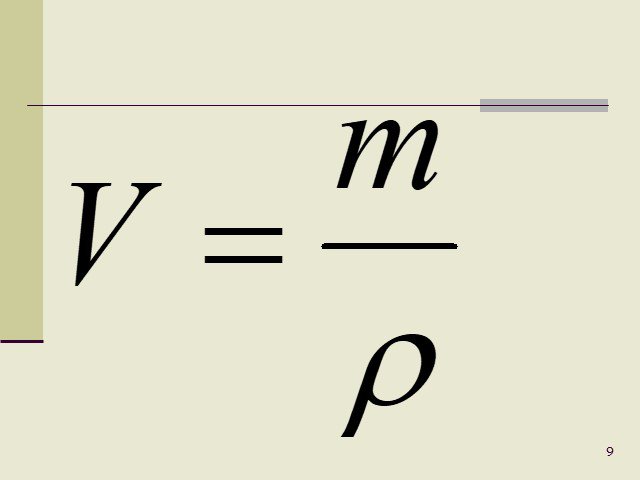
Какой прибор измеряет объем жидкости?
Наиболее распространенным инструментом, используемым для измерения объема жидкости, являются градуированные цилиндры. Это контейнеры с измерениями объема жидкости, когда жидкость наливается в химический стакан. 93.
вопросов и ответов — Сколько атомов в голове человека?
Предыдущий вопрос
(Есть ли способ узнать, сколько атомов содержится в объекте?)
Вопросы и ответы
Основной индекс
Следующий вопрос
(Сколько атомов в теле человека?)
Предыдущий вопрос
(Есть ли способ узнать, сколько атомов содержится в объекте?)
Вопросы и ответы Основной индекс
Следующий вопрос
(Сколько атомов в теле человека?)
Вопросы и ответы Основной индекс
Сколько атомов в голове человека?
Мы можем подсчитать количество атомов в вашей голове, если мы знаем плотность и константу, называемую числом Авогадро. Это всего лишь оценка, но она будет хорошей. Уравнение довольно простое. Количество атомов ЛЮБОГО вещества в объеме:
Это всего лишь оценка, но она будет хорошей. Уравнение довольно простое. Количество атомов ЛЮБОГО вещества в объеме:
# атомов = N * (плотность) * объем / (молекулярная масса).
N — константа, называемая числом Авогадро, равная 6,022*10 23 атомов/моль. Это также могут быть молекулы на моль. В приведенной выше формуле плотность, умноженная на объем, — это просто масса. Если вы знаете, насколько что-то тяжелое или каковы его объем и плотность, вы можете легко это сделать.
Давайте начнем с простой задачи. В литре воды 1000 кубических сантиметров. Вода легкая, потому что каждый кубический сантиметр имеет 1 грамм массы. Вода состоит из 2 атомов водорода и одного атома кислорода. Водород имеет атомный вес 1, а кислород имеет атомный вес 16. Молекулярный вес воды 18. В литре воды 1000 граммов. Количество молей равно 1000/18 = 55,556 молей. Таким образом, число молекул равно 6,022*10 23 * 55,556 = 3,346*10 25 молекул. Количество атомов в 3 раза больше, потому что каждая молекула состоит из трех атомов, поэтому в литре воды 1,0038*10 26 атомов.
Теперь мы знаем достаточно, чтобы ответить на ваш вопрос. Типичная человеческая голова весит около 10-12 фунтов. Мы большей частью состоим из воды. Когда вы идете плавать, вы, наверное, замечали, что почти все плавают только частью головы над водой. Это наблюдение приведет вас к выводу, что наша плотность очень близка к плотности воды. Вооружившись всем этим, мы можем оценить количество атомов в вашей голове. Фунт равен 454 граммам, поэтому человеческая голова весом 10 фунтов весит 4540 граммов. Если я предположу, что в среднем мы в основном состоим из воды, потому что наша средняя плотность примерно равна плотности воды, то я могу использовать приведенную выше информацию о воде, чтобы получить ответ.
Моль на голову = (4540 г) / (18 г/моль) = 252,22 моль
Молекул на моль = 6,022*10 23 * 252,22 моль = 1,519*10 26 молекул
атомов на голову = 3 *с на голову = 4,56*10 26
Это 456 триллионов триллионов атомов!
Завершу историческую справку.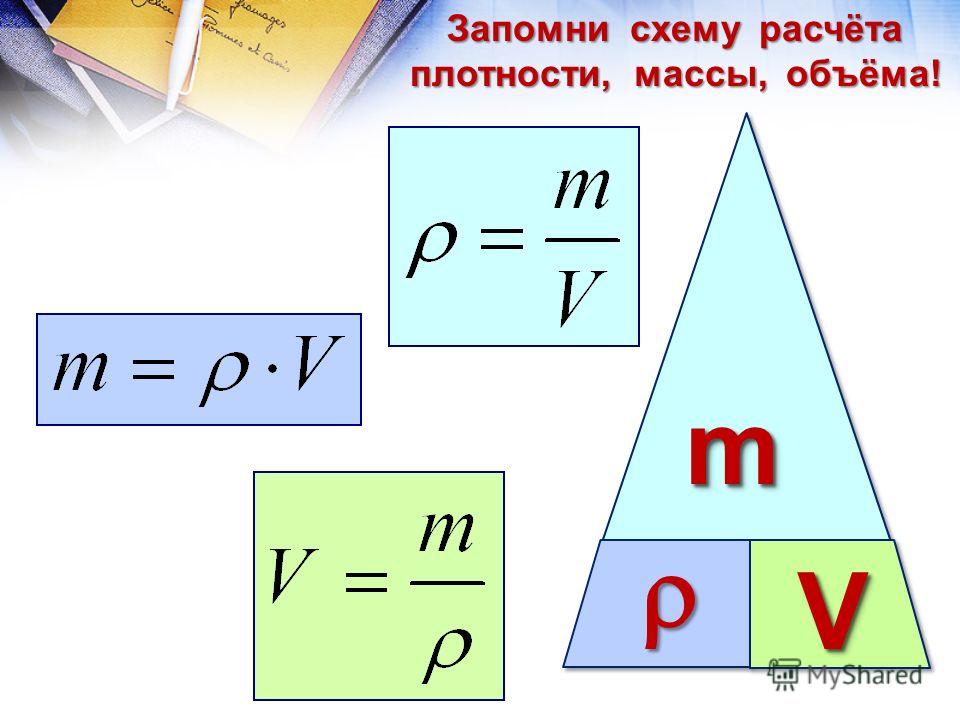



 Используя законы умножения, чтобы узнать, сколько же поместится в середине фигуры таких площадей, нужно основание умножить на высоту. То есть и получается доказываемая формула: V = S * h.
Используя законы умножения, чтобы узнать, сколько же поместится в середине фигуры таких площадей, нужно основание умножить на высоту. То есть и получается доказываемая формула: V = S * h. Так, V = a * b * c = 19 * 20 * 10 = 3 800 см
Так, V = a * b * c = 19 * 20 * 10 = 3 800 см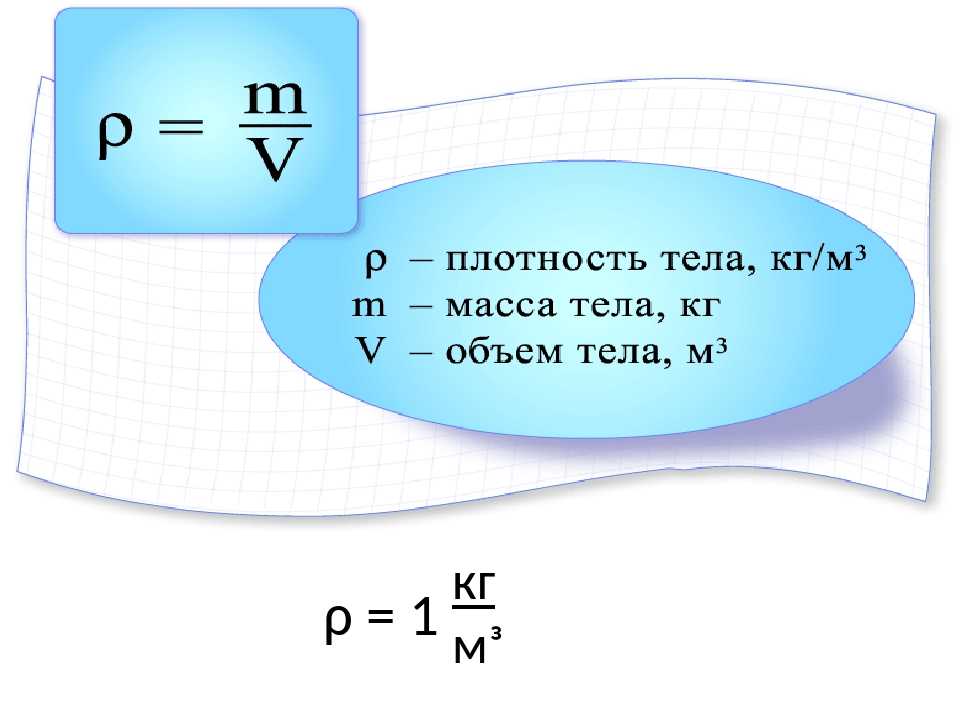

 Определите его объем, если плотность дуба 800 кг/м3.
Определите его объем, если плотность дуба 800 кг/м3.