Отношения в математике как решать – Отношение двух чисел — урок. Математика, 6 класс.

Тема 5. Отношения на множестве

Содержание

1. Понятие отношения между элементами одного множества.

2. Способы задания отношений.

3. Свойства бинарных отношений.

4. Отношение эквивалентности. Отношение порядка.

Основная литература 7, 10, 11, 16, 23, 33, 34;

Дополнительная литература 1, 10, 14, 74

1. Понятие отношения между элементами одного множества

В математике изучают не только сами объекты (числа, фигуры, величины), но и связи, отношения между ними.

Отношения многообразны. Между понятиями – это отношения рода и вида, части и целого; между предложениями – отношения следования и равносильности; между числами – «больше», «меньше», «равно», «больше на…», «следует» и др.

Изучение отношений между объектами важно для познания как самих объектов, так и для познания реального мира в целом. В нашем курсе мы будем рассматривать в основном бинарные отношения, т.е отношения между двумя элементами, но чтобы увидеть общность методических подходов к изучению в начальном курсе математики конкретных отношений, понять важнейшие математические идеи, связанные с отношениями, учителю полезно знать, какова математическая сущность любого отношения, какими свойствами они могут обладать, какие основные виды отношений изучает математика.

Чтобы определить общее понятие отношения на множестве, рассмотрим сначала конкретный пример. Пусть на множестве Х = 2, 4, 6, 8 задано отношение «меньше». Это означает, что для любых двух чисел из множества Х можно сказать, какое из них меньше: 2 4, 2  6, 2  8, 4  6, 4  8, 6  8. Но все эти пары есть элементы декартова произведения ХХ, поэтому об отношении «меньше», заданном на множестве Х, можно сказать, что оно является подмножеством множества ХХ.

Определение. Отношением между элементами множества Х или отношением на множестве Х называется всякое подмножество декартова произведения ХХ.

Так как в дальнейшем мы будем рассматривать только бинарные отношения, то определимся, на множестве Х мы их будем определять следующим образом:

Определение. Бинарным отношением на множестве Х называется всякое подмножество декартова произведения ХХ.

Условимся отношения обозначать буквами R, S, T, P и др.

Если R – отношения на множестве Х, то, согласно определению, R ХХ. С другой стороны, если задано некоторое подмножество множества ХХ , то оно определяет на множестве Х некоторое отношение R.

Замечание. Утверждение о том, что элементы х и у находятся в отношении R, можно записать так: (х,у)

 R или х R у. Последняя запись читается : “Элемент х находится в отношении R с элементом у”.

2. Способы задания отношений

По определению отношения R между элементами множества Х есть всякое подмножество декартова произведения Х  Х, т.е. множество, элементами которого являются упорядоченные пары. Поэтому способы задания отношений, по существу, такие же, как и способы задания множеств.

Отношение R на множестве Х можно задать, перечислив все пары элементов, взятых из множества Х и связанных этим отношением.

Формы записи при этом могут быть различными. Например, некоторое отношение R на множестве Х = 4, 5, 6, 7, 9можно задать, записав множество пар: (5,4),(6,4),(6,5),(7,4),(7,5),(7,6),(9, 4),(9,5),(9,6),(9,7).То же отношение можно задать при помощи графа.

Отношения на конечном множестве Х можно представлять наглядно, при помощи особых чертежей, состоящих из точек, соединенных стрелками. Такие чертежи называют

графами.

Построим граф отношения «меньше», заданного на множестве Х = 2, 4, 6, 8. Для этого элементы множества Х изобразим точками (их называют вершинами графа), а отношение «меньше» – стрелкой.

2• •4

8   6

Пример

На том же множестве Х можно рассмотреть другое отношение – «кратно». Граф этого отношения будет в каждой вершине иметь петлю (стрелку, начало и конец которой совпадают), так как каждое число кратно самому себе.

2   4

8   6

Чаще отношение R на множестве Х задают, указав характеристическое свойство всех пар элементов, находящихся в отношении R. Это свойство задается при помощи предложения с двумя переменными.

Пример. Пусть заданы рассмотренные выше отношения «меньше» и «кратно», причем использована краткая форма предложений«число х меньше числа у» и «число х кратно числу у». Некоторые такие предложения можно записать используя символы. Например, отношения «меньше» и «кратно» можно было записать в таком виде: «х  у», «ху». Отношение «х больше у на 3» можно записать в виде равенства х = у + 3 (или х – у = 3). Отношение между прямыми плоскости задают, используя символы: х // у, х у.

Для отношения R, заданного на множестве Х, всегда можно задать отношение R ^-1 , ему обратное. Например, если R – отношение “х меньше у”, то обратным ему будет отношение “ у меньше х”.

Понятием отношения, обратного данному, часто пользуются при начальном обучении математике. Например, чтобы предупредить ошибку в выборе действия, с помощью которого решается задача: «У Пети 7 карандашей, что на 2 меньше, чем у Бори. Сколько карандашей у Бори?» – ее переформулируют: «У Пети 7 карандашей, а у Бори на 2 больше. Сколько карандашей у Бори?». Видим, что переформулировка свелась к замене отношения «меньше на 2» обратным ему отношением «больше на 2».

studfiles.net

Что такое «отношение» в математике?

Отношение — математическая структура, которая формально определяет свойства различных объектов и их взаимосвязи. Отношения обычно классифицируются по количеству связываемых объектов (арность) и собственным свойствам (симметричность, транзитивность и пр.) . В математике примерами отношений являются равенство (=), коллинеарность, делимость и т. д. Отношение может также означать результат операции деления, например * двойное отношение, * отношение направленных отрезков.

Отношение — математическая структура, которая формально определяет свойства различных объектов и их взаимосвязи. Отношения обычно классифицируются по количеству связываемых объектов (арность) и собственным свойствам (симметричность, транзитивность и пр.) . В математике примерами отношений являются равенство (=), коллинеарность, делимость и т. д. Отношение может также означать результат операции деления, например двойное отношение, отношение направленных отрезков.

Отношение — математическая структура, которая формально определяет свойства различных объектов и их взаимосвязи.

Отношение показывает во сколько раз одно число больше или меньше другого

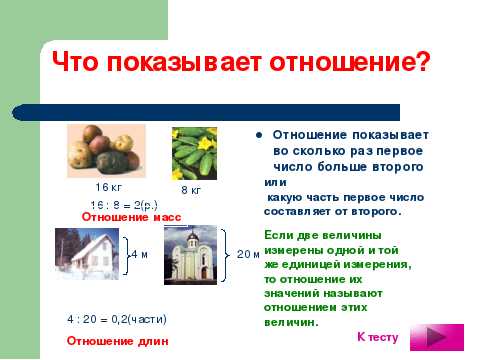
Частное двух чисел называются отношением этих чисел. Отношения показывает, во сколько раз первое число больше второго, или какую часть первое число составляет от второго.

touch.otvet.mail.ru

Урок математики на тему: «Отношения»

Урок. Отношения.

Предмет: математика

Класс: 6

Цели:

Тип: изучения и первичного закрепления

Вид: урок-беседа

Методы: объяснительно-иллюстративный, проблемного изложения.

Формы: фронтальная, индивидуальная, парная

Материалы и оборудование: учебник математики за 6 класс, рабочая тетрадь, презентация, компьютер, интерактивная доска, проектор.

Ход урока

1. Организационный момент.

Девиз нашего урока «Математика – это гимнастика ума».

1. Актуализация опорных знаний.

1. Найдите 20% от чисел: 40, 200, 18, 1000, 3, 120.(Ответы: 8, 40, 3,6; 0,6; 200; 24)

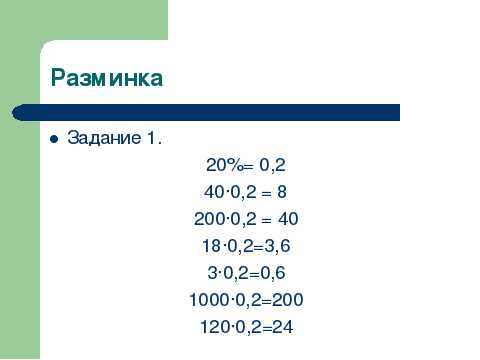
1. Найдите значение выражений:

5	25/9	0	15	25/3	10	1	25/81	5/9	1/9	5/81	Не им смысла

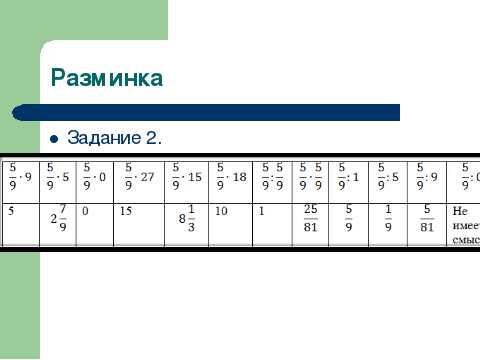
1. Периметр прямоугольника равен 48 см, длина на 4 см больше ширины. Найдите стороны прямоугольника.(Ответ: 10 см и 14 см)

Решение.

Дано: P=____ см ab на ____ см	Решение: Пусть ширина x, тогда длина _____. P=2∙(a +__)=2∙(__+_____) 2∙(x+4+x)=__ __x+8=__ __x= __ — 4 __x=__ x=____ — ширина, длина x + 4 = __ + __=
Найти: a, b — ?	Ответ: ширина прямоугольника __ см, длина __ см.

Ребята, подведем итог. Какие правила мы с вами повторили? (Нахождение дроби от числа, умножение и деление обыкновенных дробей, формула периметра прямоугольника.)

1. Сообщение темы урока.

Сегодня на уроке мы познакомимся с понятием «отношение двух чисел» и узнаем, что оно показывает.

«Отношение — взаимная связь разных величин, предметов, действий.» Ожегов С.И.

1. Изучение нового материала.

Алгоритм работы в парах:

1. Прочитайте задачу 1 п. 20 с. 117 (один читает другой слушает).

2. Разберите решение этой задачи.

3. Запишите решение в тетрадь. Если есть вопросы, обсудите их с партнером по парте или проконсультируйтесь у учителя.

4. Прочитайте 1 предложение, выделенное жирным шрифтом. Что это такое? (Определение)

5. Запишите в тетрадь определение.

6. Расскажите друг другу определения, проверяя по учебнику.

Фронтальная работа.

Проверка выполненных ответов (проговаривание ответов).

Если остается один ученик без пары, то он работает на обратной стороне доски.

Отношение – содержание, пропорция, вывод сравнения двух чисел, вычитанием (отношение арифметическое), делением (отношение геометрическое). (Толковый словарь Даля)

Вернемся к рассмотренной вами задаче. Прочитайте ответ. Сколько вариантов ответа?(Два: один в виде обыкновенной дроби, другой – в виде десятичной, которая переведена в проценты.)

Отношение может быть выражено в процентах, тогда его называют процентным отношением. Что оно показывает? (Сколько процентов одно число составляет от другого.)

Как найти процентное отношение?(Надо найти отношение и потом выразить его в процентах.)

1. Закрепление изученного материала.

Задача 2. Укажи, отношение каких величин составлено:

16кг:8кг — отношение масс

4м:20м – отношение длин

180мин.:30мин. – отношение времени

64м²:0,4м² – отношение площадей

1,6м³:3,2м³ – отношение объемов

Задача 3. Найди ошибку.

Незнайка решил найти отношение массы мышки к массе слона. Мышка весит 50 грамм, а слон – 5 тонн. «Составим отношение 50: 5, — сказал Незнайка. — Мышка в 10 раз тяжелее слона».

Решение:

5 т = 5000 кг = 5000000 г

5000000 : 50 = 100000

Ответ: мышка в 100000 раз легче слона.

Задача 4. В сосуд налили 240 г воды и положили 10 г соли. Найдите процентное содержание соли в растворе?

Решение:

10:250 = 0,04 = 4%

Ответ: процентное содержание соли 4%.

Луна́ — единственный естественный спутник Земли. Второй по яркости объект на земном небосводе после Солнца и пятый по величине естественный спутник планет Солнечной системы. Также является первым и единственным небесным телом, помимо Земли, на котором побывал человек.

Задача 5. Расстояние на карте от Земли до Луны 38,4 см. Найти расстояние между ними, если масштаб карты 1:1 000 000 000.

Решение:

Обозначим длину (в см) до Луны буквой ___.

38,4 : x = 1 : 1 000 000 000

х = (38,4 · 1 000 000 000) : 1 = 38400000000 см = 384 000 км

Ответ: расстояние до Луны 384000 км.

А почему эта задача решается таким способом мы с вами узнаем на следующем уроке!

Тест.

	1	2	3	4	5
Вариант ___

VI. Итог урока.

Что называют отношением двух чисел?

Что показывает отношение двух чисел?

Что такое процентное отношение двух чисел?

Оцените свою работу и работу своего товарища, отметку обоснуйте.

1. Домашнее задание.

С. 117 п.20, с. 122 №751, №754

videouroki.net