Формула сокращение: Формулы сокращенного умножения 💣

alexxlab / / Разное

Содержание

Формулы сокращенного умножения 💣

Формулы сокращенного умножения

Вместо букв a, b могут быть любые числа, переменные или даже целые выражения. Для быстрого решения задач лучше выучить основные 7 формул сокращенного умножения (ФСУ) наизусть. Да, алгебра такая, нужно быть готовым много запоминать.

Ниже удобная табличка, которую можно распечатать и использовать, как закладку для быстрого запоминания формул.

Как читать формулы сокращенного умножения

Учимся проговаривать формулы сокращенного выражения:

 
  1. Разность квадратов двух выражений равна произведению их разности и их суммы.

  2. Квадрат суммы двух выражений равен квадрату первого плюс удвоенное произведение первого на второе плюс квадрат второго.

  3. Квадрат разности двух выражений равен квадрату первого минус удвоенное произведение первого на второе плюс квадрат второго.

  4. Сумма кубов двух выражений равна произведению суммы первого и второго на неполный квадрат их разности.

  5. Разность кубов двух выражений равна произведению разности первого и второго на неполный квадрат их суммы.

  6. Куб суммы двух выражений равен кубу первого плюс утроенное произведение квадрата первого на второе плюс утроенное произведение первого на квадрат второго плюс куб второго.

  7. Куб разности двух выражений равен кубу первого минус утроенное произведение квадрата первого на второе плюс утроенное произведение первого на квадрат второго минус куб второго.

Доказательство формул сокращенного умножения

Напомним, что разность квадратов двух чисел a и b равна произведению их разности и их суммы: a2 — b2 = (a — b) * (a + b).

Иначе говоря, произведение суммы a и b на их разность равна разности их квадратов: (a — b) * (a + b) = a2 — b2.

Важно знать, что разность квадратов не равна квадрату разности: a

2 — b2 ≠ (a — b)2.

Докажем, что a2 — b2 = (a — b) * (a + b).

Поехали:

  1. Используя искусственный метод, прибавим и отнимем одно и тоже a * b.

    + a * b — a * b = 0

    a2 — b2 = a2 — b2 + ab — ab

  1. Сгруппируем иначе: a2 — b2 + a * b — a * b = a2 — a * b + a * b — b2

  2. Продолжим группировать: a2 — a * b — b2 +a * b = (a2 — a * b) + (a * b — b2)

  3. Вынесем общие множители за скобки:

    (a2 — a * b) + (a * b — b2) = a *(a — b) + b *(a — b)

  1. Вынесем за скобки (a — b). a * (a — b) + b * (a — b) = (a — b) * (a + b)

  2. Результат доказательства: a2 — b2 = (a — b) * (a + b)

  3. Для того, чтобы доказать в обратную сторону: (a — b) * (a + b) = a2 — b2, нужно раскрыть скобки: (a — b) * (a + b) = a * a + a * b — b * a — b * b = a2 — b2.

Остальные ФСУ можно доказать аналогичным методом.

 

Дополнительные формулы сокращенного умножения

К таблице основных ФСУ следует добавить еще несколько важных тождеств, которые пригодятся для решения задач.

Бином Ньютона

Формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных. Записывается вот так:

Пример вычисления биномиальных коэффициентов, которые стоят в строке под номером n в треугольнике Паскаля:

ФСУ для квадрата и куба суммы и разности — являются частными случаями формулы бинома Ньютона при n = 2 и n = 3.

Формула возведения в квадрат суммы трех, четырех и более слагаемых

Пригодится, если слагаемых в сумме, которую нужно возвести в степень, больше, чем два. 

(a1+a2+…+an)2 = a12 + a22 + … + an-12 + an2 + 2 * a1 * a2 + 2 * a1 * a3 + 2 * a1 * a4 + … +

+ 2 * a1 * an-1 + 2 * a1 * an + 2 * a2 * a3 + 2 * a2 * a4 + … + 2 * a2 * an-1 + 2 * a2 * an +…+

+ 2 * an-1 * an

Читается так: квадрат суммы n слагаемых равен сумме квадратов всех этих слагаемых и удвоенных произведений всех возможных пар этих слагаемых.

Формула разности n-ых степеней двух слагаемых

an − bn = (a − b) * (an-1 + an-2

* b + an-3 * b2 + … + a * bn-2 + bn-1).

Для четных показателей можно записать так:

a2*m − b2*m = (a2 − b2) *(a2*m−2 + a2*m−4 * b2 + a2*m−6 * b4 + … + b2*m−2).

Для нечетных показателей:

a2*m+1 − b2*·m+1 = (a − b) * (a2*m + a2*m−1 * b + a2*m−2 * b2 + … + b2*m).

Частными случаями являются формулы разности квадратов и кубов при n = 2 и n = 3. Для разности кубов b можно также заменить на −b.

Решение задач

Давайте потренируемся и рассмотрим примеры с дробями.

Задание 1

Что сделать: вычислить квадрат произведения (55 + 10)2.

Как решаем:

воспользуемся формулой квадрата суммы: (55 + 10)2 = 552 + 2 * 55 * 10 + 102 = 3025 + 1100 + 100 = 4225.

Задание 2

Что сделать: упростить выражение 64 * с3 – 8.

Как решаем: применим разность кубов: 64 * с3 – 8 = (4 * с)3 – 23 = (4 * с – 2)((4 * с)2 + 4 * с * 2 + 22) = (4 * с – 2)(16 * с2 + 8 * с + 4).

Задание 3

Что сделать: раскрыть скобки (7 * y — x) * (7 * y + x).

Как решаем:

  1. Произведем умножение: (7 * y — x) * (7 * y + x) = 7 * y * 7 * y + 7 * y * x — x * 7 * y — x * x = 49 * y2 + 7 * y * x — 7 * y * x — x2 = 49 * y2 — x2.
  2. Используем формулу сокращенного умножения: (7 * y — x) * (7 * y + x) = (7 * y)2 — x2 = 49 * y2 — x2.

Многочленов бояться не стоит, просто совершайте последовательно каждое действие. С формулами решать задачки быстрее и удобнее — сохраняйте шпаргалку, запоминайте и радуйте своих учителей 🙂

Запишите вашего ребенка на увлекательные уроки математики в детскую школу Skysmart. Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем. 

Формулы сокращенного умножения

Продолжаем изучать многочлены. В данном уроке мы научимся перемножать многочлены с помощью формул сокращённого умножения.

Предварительные навыки

Квадрат суммы двух выражений

Существует ряд случаев, когда умножение многочлена на многочлен можно значительно упростить.

Таковым к примеру является случай (2x + 3y)2.

Выражение (2x + 3y)2 это перемножение двух многочленов, каждый из которых равен (2x + 3y)

(2x + 3y)2 = (2x + 3y)(2x + 3y)

Получили умножение многочлена на многочлен. Выполним его:

(2x + 3y)2 = (2x + 3y)(2x + 3y) = 4x2 + 6xy + 6xy + 9y2 = 4x2 + 12xy + 9y2

То есть выражение (2x + 3y)2 равно 4x2 + 12xy + 9y2

(2x + 3y)2 = 4x2 + 12xy + 9y

2

Решим аналогичный пример, который попроще:

(a + b)2

Выражение (a + b)2 это перемножение двух многочленов, каждый из которых равен (a + b)

(a + b)2 = (a + b)(a + b)

Выполним это умножение:

(a + b)2 = (a + b)(a + b) = a2 + ab + ab + b2 = a2 + 2ab + b2

То есть выражение (a + b)2 равно a2 + 2ab + b2

(a + b)2 = a2 + 2ab + b2

Оказывается, что случай (a + b)2 можно распространить для любых a и b.

Первый пример, который мы решили, а именно (2x + 3y)2 можно решить с помощью тождества (a + b)2 = a2 + 2ab + b2. Для этого нужно подставить вместо переменных a и b соответствующие члены из выражение (2x + 3y)2. В данном случае переменной a соответствует член 2x, а переменной b соответствует член 3y

a = 2x

b = 3y

И далее можно воспользоваться тождеством (a + b)2 = a2 + 2ab + b2, но вместо переменных a и b нужно подставлять выражения 2x и 3y соответственно:

(2x + 3y)2 = (2x)2 + 2 × 2x × 3y + (3y)2 = 4x2 + 12xy + 9y

2

Как и в прошлый раз получили многочлен 4x2 + 12xy + 9y2. Решение обычно записывают покороче, выполняя в уме все элементарные преобразования:

(2x + 3y)2 = 4x2 + 12xy + 9y2

Тождество (a + b)2 = a2 + 2ab + b2 называют формулой квадрата суммы двух выражений. Эту формулу можно прочитать так:

Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

Рассмотрим выражение (2 + 3)2. Его можно вычислить двумя способами: выполнить сложение в скобках и возвести полученный результат в квадрат, либо воспользоваться формулой квадрата суммы двух выражений.

Первый способ:

(2 + 3)2 = 52 = 25

Второй способ:

(2 + 3)2 = 22 + 2 × 2 × 3 + 32 = 4 + 12 + 9 = 25

Пример 2. Преобразовать выражение (5a + 3)2 в многочлен.

Воспользуемся формулой квадрата суммы двух выражений:

(a + b)2 = a2 + 2ab + b2

(5a + 3)2 = (5a)2 + 2 × 5a × 3 + 32 = 25a2 + 30a + 9

Значит, (5a + 3)2 = 25a2 + 30a + 9.

Попробуем решить данный пример, не пользуясь формулой квадрата суммы. У нас должен получиться тот же результат:

(5a + 3)2 = (5a + 3)(5a + 3) = 25a2 + 15a + 15a + 9 = 25a2 + 30a + 9

Формула квадрата суммы двух выражений имеет геометрический смысл. Мы помним, что для вычисления площади квадрата нужно возвести во вторую степень его сторону.

Например, площадь квадрата со стороной a будет равна a2. Если увеличить сторону квадрата на b, то площадь будет равна (a + b)2

Рассмотрим следующий рисунок:

Представим, что сторону квадрата, изображённого на данном рисунке увеличили на b. У квадрата все стороны равны. Если его сторону увеличить на b, то остальные стороны тоже увеличатся на b

Получился новый квадрат, который больше предыдущего. Чтобы хорошо увидеть его, достроим отсутствующие стороны:

Чтобы вычислить площадь этого квадрата, можно по отдельности вычислить квадраты и прямоугольники, входящие в него, затем сложить полученные результаты.

Сначала можно вычислить квадрат со стороной a — его площадь будет равна a2. Затем можно вычислить прямоугольники со сторонами a и b — они будут равны ab. Затем можно вычислить квадрат со стороной b

В результате получается следующая сумма площадей:

a2 + ab + ab + b2

Сумму площадей одинаковых прямоугольников можно заменить на умножение 2ab, которое буквально будет означать «повторить два раза площадь прямоугольника ab». Алгебраически это получается путём приведения подобных слагаемых ab и ab. В результате получается выражение a2 + 2ab + b2, которое является правой частью формулы квадрата суммы двух выражений:

(a + b)2 = a2 + 2ab + b2

Квадрат разности двух выражений

Формула квадрата разности двух выражений выглядит следующим образом:

(a − b)2 = a2 − 2ab + b2

Эту формулу можно прочитать так:

Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

Формула квадрата разности двух выражений выводится таким же образом, как и формула квадрата суммы двух выражений. Выражение (a − b)2 представляет собой произведение двух многочленов, каждый из которых равен (a − b)

(a − b)2 = (a − b)(a − b)

Если выполнить это умножение, то получится многочлен a2 − 2ab + b2

(a − b)2 = (a − b)(a − b) = a2 − ab − ab + b2 = a2 − 2ab + b2

Пример 1. Преобразовать выражение (7x − 5)2 в многочлен.

Воспользуемся формулой квадрата разности двух выражений:

(a − b)2 = a2 − 2ab + b2

(7x − 5)2 = (7x)2 − 2 × 7x × 5 + 52 = 49x2 − 70x + 25

Значит, (7x − 5)2 = 49x2 − 70x + 25.

Попробуем решить данный пример, не пользуясь формулой квадрата разности. У нас должен получиться тот же результат:

(7x − 5)2 = (7x − 5)(7x − 5) = 49x2 − 35x − 35x + 25 = 49x2 − 70x + 25.

Формула квадрата разности двух выражений тоже имеет геометрический смысл. Если площадь квадрата со стороной a равна a2, то площадь квадрата, сторона которого уменьшена на b, будет равна (a − b)2

Рассмотрим следующий рисунок:

Представим, что сторону квадрата, изображённого на данном рисунке уменьшили на b. У квадрата все стороны равны. Если одну сторону уменьшить на b, то остальные стороны тоже уменьшатся на b

Получился новый квадрат, который меньше предыдущего. На рисунке он выделен жёлтым. Сторона его равна a − b, поскольку старая сторона a уменьшилась на b. Чтобы вычислить площадь этого квадрата, можно из первоначальной площади квадрата a2 вычесть площади прямоугольников, которые получились в процессе уменьшения сторон старого квадрата. Покажем эти прямоугольники:

Тогда можно написать следующее выражение: старая площадь a2 минус площадь ab минус площадь (a − b)b

a2 − ab − (a − b)b

Раскроем скобки в выражении (a − b)b

a2 − ab − ab + b2

Приведем подобные слагаемые:

a2 − 2ab + b2

В результате получается выражение a2 − 2ab + b2, которое является правой частью формулы квадрата разности двух выражений:

(a − b)2 = a2 − 2ab + b2

Формулы квадрата суммы и квадрата разности в общем называют формулами сокращённого умножения. Эти формулы позволяют значительно упростить и ускорить процесс перемножения многочленов.

Ранее мы говорили, что рассматривая член многочлена по отдельности, его нужно рассматривать вместе со знаком, который перед ним располагается.

Но применяя формулы сокращённого умножения, знак исходного многочлена не следует рассматривать в качестве знака самого этого члена.

Например, если дано выражение (5x − 2y)2, и мы хотим воспользоваться формулой (a − b)2 = a2 − 2ab + b2, то вместо b нужно подставлять 2y, а не −2y. Это особенность работы с формулами, которую не следует забывать.

(5x − 2y)2
a = 5x
b = 2y
(5x − 2y)2 = (5x)2 − 2 × 5x × 2y + (2y)2 = 25x2 − 20xy + 4y2

Если подставлять −2y, то это будет означать, что разность в скобках исходного выражения была заменена на сумму:

(5x − 2y)2 = (5x + (−2y))2

и в таком случае нужно применять не формулу квадрата разности, а формулу квадрата суммы:

(5x + (−2y)2
a = 5x
b = −2y
(5x + (−2y))2 = (5x)2 + 2 × 5x × (−2y) + (−2y)2 = 25x2 − 20xy + 4y2

Исключением могут быть выражения вида (x − (−y))2. В данном случае, применяя формулу (a − b)2 = a2 − 2ab + b2 вместо b следует подставить (−y)

(x − (−y))2 = x2 − 2 × x × (−y) + (−y)2 = x2 + 2xy + y2

Но возводя в квадрат выражения вида x − (−y), удобнее будет заменять вычитание на сложение x + y. Тогда первоначальное выражение примет вид (x + y)2 и можно будет воспользоваться формулой квадрата суммы, а не разности:

(x + y)2 = x2 + 2xy + y2

Куб суммы и куб разности

Формулы куба суммы двух выражений и куба разности двух выражений выглядят следующим образом:

(a + b)3 = a3 + 3a2b + 3ab2 + b3

(a − b)3 = a3 − 3a2b + 3ab2 − b3

Формулу куба суммы двух выражений можно прочитать так:

Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.  

А формулу куба разности двух выражений можно прочитать так:

Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения. 

При решении задач желательно знать эти формулы наизусть. Если не запомнили — не беда! Их можно выводить самостоятельно. Мы это уже умеем.

Выведем формулу куба суммы самостоятельно:

(a + b)3

Выражение (a + b)3 представляет собой произведение из трёх многочленов, каждый из которых равен (a + b)

(a + b)3 = (a + b)(a + b)(a + b)

Но выражение (a + b)3 также может быть записано как (a + b)(a + b)2

(a + b)3 = (a + b)(a + b)2

При этом сомножитель (a + b)2 является квадратом суммы двух выражений. Этот квадрат суммы равен выражению a2 + 2ab + b2.

Тогда (a + b)3 можно записать как (a + b)(a2 + 2ab + b2).

(a + b)3 = (a + b)(a2 + 2ab + b2)

А это есть умножение многочлена на многочлен. Выполним его:

(a + b)3 = (a + b)(a2 + 2ab + b2) = a3 + 2a2b + ab2 + a2b + 2ab2 + b3 = a3 + 3a2b + 3ab2 + b3

Аналогично можно вывести формулу куба разности двух выражений:

(a − b)3 = (a − b)(a2 − 2ab + b2) = a3 − 2a2b + ab2 − a2b + 2ab2 − b3 = a3 − 3a2b + 3ab2 − b3

Пример 1. Преобразуйте выражение (x + 1)3 в многочлен.

Воспользуемся формулой куба суммы двух выражений:

(a + b)3 = a3 + 3a2b + 3ab2 + b3

(x + 1)3 = x3 + 3 × x2 × 1 + 3 × x × 12 + 13 = x3 + 3x2 + 3x + 1

Попробуем решить данный пример, не используя формулу куба суммы двух выражений. У нас получится тот же результат, но решение станет длиннее:

(x + 1)3 = (x + 1)(x + 1)(x + 1) = (x + 1)(x2 + 2x + 1) = x3 + 2x2 + x + x2 + 2x + 1 = x3 + 3x2 + 3x + 1

Пример 2. Преобразовать выражение (6a2 + 3b3)3 в многочлен.

Воспользуемся формулой куба суммы двух выражений:

(a + b)3 = a3 + 3a2b + 3ab2 + b3

(6a2 + 3b3)3= (6a2)3 + 3 × (6a2)2 × 3b3 + 3 × 6a2 × (3b3)2 + (3b3)3 = 216a6 + 3 × 36a4 × 3b3 + 3 × 6a2 × 9b6 + 27b9

Пример 3. Преобразовать выражение (n2 − 3)3 в многочлен.

Воспользуемся формулой куба разности двух выражений:

(a − b) = a3 − 3a2b + 3ab2 − b3

(n2 − 3)3 = (n2)3 − 3 × (n2)2 × 3 + 3 × n2 × 32 − 33 = n6 − 9n4  + 27n2 − 27

Пример 4. Преобразовать выражение (2x2 − x3)3 в многочлен.

Воспользуемся формулой куба разности двух выражений:

(a − b) = a3 − 3a2b + 3ab2 − b3

(2x2 − x3)3 = (2x2)3 − 3 × (2x2)2 × x3 + 3 × 2x2 × (x3)2 − (x3)3 =
8x6 − 3 × 4x4 × x3 + 3 × 2x2 × x6 − x9 =
8x6 − 12x7 + 6x8 − x9

Умножение разности двух выражений на их сумму

Встречаются задачи, в которых требуется умножить разность двух выражений на их сумму. Например:

(a − b)(a + b)

В этом выражении разность двух выражений a и b умножена на сумму этих же двух выражений. Выполним данное умножение:

(a − b)(a + b) = a2 + ab − ab − b2 = a2 − b2

То есть выражение (a − b)(a + b) равно a2 − b2

(a − b)(a + b) = a2 − b2

Видим, что при умножении разности двух выражений на их сумму, получается разность квадратов этих выражений.

Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.

Случай (a − b)(a + b) можно распространить для любых a и b. Проще говоря, если при решении задачи потребуется умножить разность двух выражений на их сумму, то это умножение можно заменить на разность квадратов этих выражений.

Пример 1. Выполнить умножение (2x − 5)(2x + 5)

В этом примере разность выражений 2x и 5 умножена на сумму этих же выражений. Тогда согласно формуле (a − b)(a + b) = a2 − b2 имеем:

(2x − 5)(2x + 5) = (2x)2 − 52

Вычислим правую часть, получим 4x2 − 25

(2x − 5)(2x + 5) = (2x)2 − 52 = 4x2 − 25

Попробуем решить данный пример, не пользуясь формулой (a − b)(a + b) = a2 − b2. У нас получится тот же результат 4x2 − 25

(2x − 5)(2x + 5) = 4x2 − 10x + 10x − 25 = 4x2 − 25

Пример 2. Выполнить умножение (4x − 5y)(4x + 5y)

Воспользуемся формулой умножения разности двух выражений на их сумму:

(a − b)(a + b) = a2 − b2

(4x − 5y)(4x + 5y) = (4x)2 − (5y)2 = 16x2 − 25y2

Пример 3. Выполнить умножение (2a + 3b)(2a − 3b)

Воспользуемся формулой умножения разности двух выражений на их сумму:

(a − b)(a + b) = a2 − b2

(2a + 3b)(2a − 3b) = (2a)2 − (3b)2 = 4a2 − 9b2

В данном примере сумма членов 2a и 3b располагалась раньше, чем разность этих членов. А в формуле (a − b)(a + b) = a2 − b2 разность располагается раньше.

Нет никакой разницы как располагаются сомножители (a − b) в (a + b) в формуле. Они могут быть быть записаны как (a − b)(a + b), так и (a + b)(a − b). Результат по прежнему будет равен a2 − b2, поскольку от перестановки сомножителей произведение не меняется.

Так и в данном примере сомножители (2a + 3b) и (2a − 3b) можно записать как (2a + 3b)(2a − 3b), так и (2a − 3b)(2a + 3b). Результат всё так же будет равен 4a2 − 9b2.

Пример 3. Выполнить умножение (7 + 3x)(3x − 7)

Воспользуемся формулой умножения разности двух выражений на их сумму:

(a − b)(a + b) = a2 − b2

(7 + 3x)(3x − 7) = (3x)2 − 72 = 9x2 − 49

Пример 4. Выполнить умножение (x2 − y3)(x2 + y3)

(a − b)(a + b) = a2 − b2

(x2 − y3)(x2 + y3) = (x2)2 − (y3)2 = x4 − y6

Пример 5. Выполнить умножение (−5x − 3y)(5x − 3y)

В выражении (−5x − 3y) вынесем за скобки −1, тогда исходное выражение примет следующий вид:

(−5x − 3y)(5x − 3y) = −1(5x + 3y)(5x − 3y)

Произведение (5x + 3y)(5x − 3y) заменим на разность квадратов:

(−5x − 3y)(5x − 3y) = −1(5x + 3y)(5x − 3y) = −1((5x)2 − (3y)2)

Разность квадратов была заключена в скобки. Если этого не сделать, то получится, что −1 умножается только на (5x)2. А это приведет к ошибке и изменению значения исходного выражения.

Далее вычисляем выражение в скобках:

(−5x − 3y)(5x − 3y) = −1(5x + 3y)(5x − 3y) = −1((5x)2 − (3y)2) = −1(25x2 − 9y2)

Теперь умножим −1 на выражение в скобках и получим окончательный результат:

(−5x − 3y)(5x − 3y) = −1(5x + 3y)(5x − 3y) = −1((5x)2 − (3y)2) =
−1(25x2 − 9y2) = −25x2 + 9y2

Умножение разности двух выражений на неполный квадрат их суммы

Встречаются задачи, в которых требуется умножить разность двух выражений на неполный квадрат их суммы. Выглядит это произведение следующим образом:

(a − b)(a2 + ab + b2)

Первый многочлен (a − b) является разностью двух выражений, а второй многочлен (a2 + ab + b2) является неполным квадратом суммы этих двух выражений.

Неполный квадрат суммы это многочлен вида a2 + ab + b2. Он похож на обычный квадрат суммы a2 + 2ab + b2 за исключением того, что в нём произведение первого и второго выражений не удваивается.

Например, выражение 4x2 + 6xy + 9y2 является неполным квадратом суммы выражений 2x и 3y.

Действительно, первый член выражения 4x2 + 6xy + 9y2, а именно 4x2 является квадратом выражения 2x, поскольку (2x)2 = 4x2. Третий член выражения 4x2 + 6xy + 9y2, а именно 9y2 является квадратом выражения 3y, поскольку (3y)2 = 9y2. Член находящийся в середине 6xy, является произведением выражений 2x и 3y.

Итак, умножим разность (a − b) на неполный квадрат суммы a2 + ab + b2

(a − b)(a2 + ab + b2) = a(a2 + ab + b2) − b(a2 + ab + b2) =
a3 + a2b + ab2 − a2b − ab2 − b3 = a3 − b3

То есть выражение (a − b)(a2 + ab + b2) равно a3 − b3

(a − b)(a2 + ab + b2) = a3 − b3

Это тождество называют формулой умножения разности двух выражений на неполный квадрат их суммы. Эту формулу можно прочитать так:

Произведение разности двух выражений и неполного квадрата их суммы равно разности кубов этих выражений.

Пример 1. Выполнить умножение (2x − 3y)(4x2 + 6xy + 9y2)

Первый многочлен (2x − 3y) это разность двух выражений 2x и 3y. Второй многочлен 4x2 + 6xy + 9y2 это неполный квадрат суммы двух выражений 2x и 3y. Это позволяет не приводя длинных вычислений, воспользоваться формулой (a − b)(a2 + ab + b2) = a3 − b3. В нашем случае умножение (2x − 3y)(4x2 + 6xy + 9y2) можно заменить на разность кубов 2x и 3y

(2x − 3y)(4x2 + 6xy + 9y2) = (2x)3 − (3y)3 = 8x3 − 27y3

Попробуем решить этот же пример, не пользуясь формулой (a − b)(a2 + ab + b2) = a3 − b3. У нас получится тот же результат, но решение станет длиннее:

(2x − 3y)(4x2 + 6xy + 9y2) = 2x(4x2 + 6xy + 9y2) − 3y(4x2 + 6xy + 9y2) =
8x3 + 12x2y + 18xy2 − 12x2y − 18xy2 − 27y3 = 8x3 − 27y3

Пример 2. Выполнить умножение (3 − x)(9 + 3x + x2)

Первый многочлен (3 − x) является разностью двух выражений, а второй многочлен является неполным квадратом суммы этих двух выражений. Это позволяет воспользоваться формулой (a − b)(a2 + ab + b2) = a3 − b3

(3 − x)(9 + 3x + x2) = 33 − x3 = 27 − x3

Умножение суммы двух выражений на неполный квадрат их разности

Встречаются задачи, в которых требуется умножить сумму двух выражений на неполный квадрат их разности. Выглядит это произведение следующим образом:

(a + b)(a2 − ab + b2)

Первый многочлен (a + b) является суммой двух выражений, а второй многочлен (a2 − ab + b2) является неполным квадратом разности этих двух выражений.

Неполный квадрат разности это многочлен вида a2 − ab + b2. Он похож на обычный квадрат разности a2 − 2ab + b2 за исключением того, что в нём произведение первого и второго выражений не удваивается.

Например, выражение 4x2 − 6xy + 9y2 является неполным квадратом разности выражений 2x и 3y. 

(2x)2 − 2x × 3y + (3y)2 = 4x2 − 6xy + 9y2

Вернёмся к изначальному примеру. Умножим сумму a + b на неполный квадрат разности a2 − ab + b2

(a + b)(a2 − ab + b2) = a(a2 − ab + b2) + b(a2 − ab + b2) =
a3 − a2b + ab2 + a2b − ab2 + b3 = a3 + b3

То есть выражение (a + b)(a2 − ab + b2) равно a3 + b3

(a + b)(a2 − ab + b2) = a3 + b3

Это тождество называют формулой умножения суммы двух выражений на неполный квадрат их разности. Эту формулу можно прочитать так:

Произведение суммы двух выражений и неполного квадрата их разности равно сумме кубов этих выражений.

Пример 1. Выполнить умножение (2x + 3y)(4x2 − 6xy + 9y2)

Первый многочлен (2x + 3y) это сумма двух выражений 2x и 3y, а второй многочлен 4x2 − 6xy + 9y2 это неполный квадрат разности этих выражений. Это позволяет не приводя длинных вычислений, воспользоваться формулой (a + b)(a2 − ab + b2) = a3 + b3. В нашем случае умножение (2x + 3y)(4x2 − 6xy + 9y2) можно заменить на сумму кубов 2x и 3y

(2x + 3y)(4x2 − 6xy + 9y2) = (2x)3 + (3y)3 = 8x3 + 27y3

Попробуем решить этот же пример, не пользуясь формулой (a + b)(a2 − ab + b2) = a3 + b3. У нас получится тот же результат, но решение станет длиннее:

(2x + 3y)(4x2 − 6xy + 9y2) = 2x(4x2 − 6xy + 9y2) + 3y(4x2 − 6xy + 9y2) =
8x3 − 12x2y + 18xy2 + 12x2y − 18xy2 + 27y3 = 8x3 + 27y3

Пример 2. Выполнить умножение (2x + y)(4x2 − 2xy + y2)

Первый многочлен (2x + y) является суммой двух выражений, а второй многочлен (4x2 − 2xy + y2) является неполным квадратом разности этих выражений. Это позволяет воспользоваться формулой (a + b)(a2 − ab + b2) = a3 + b3

(2x + y)(4x2 − 2xy + y2) = (2x)3 + y3 = 8x3 + y3

Попробуем решить этот же пример, не пользуясь формулой (a + b)(a2 − ab + b2) = a3 + b3. У нас получится тот же результат, но решение станет длиннее:

(2x + y)(4x2 − 2xy + y2) = 2x(4x2 − 2xy + y2) + y(4x2 − 2xy + y2) = 
8x3 − 4x2y + 2xy2 + 4x2y − 2xy2 + y3 = 8x3 + y3

Задания для самостоятельного решения

Задание 1. Преобразуйте выражение (m + n)2 в многочлен.

Решение:

(m + n)2 = m2 + 2mn + n2

Задание 2. Преобразуйте выражение (x + 8)2 в многочлен.

Решение:

(x + 8)2 = x2 + 2 × x × 8 + 82 = x2 + 16x + 64

Задание 3. Преобразуйте выражение (2x2 + 3x3)2 в многочлен.

Решение:

(2x2 + 3x3)2 = (2x2)2 + 2 × 2x2 × 3x3 + (3x3)2 = 4x4 + 12x5 + 9x6

Задание 4. Преобразуйте выражение (5a + 5)2 в многочлен.

Решение:

(5a + 5)2 = (5a)2 + 2 × 5a × 5 + 52 = 25a2 + 50a + 25

Задание 5. Преобразуйте выражение (9 − x)2 в многочлен.

Решение:

(9 − x)2 = 92 − 2 × 9 × x + x2 = 81 − 18x + x2

Задание 6. Преобразуйте выражение (x − 25)2 в многочлен.

Решение:

(x − 25)2 = x2 − 2 × x × 25 + 252 = x2 − 50x + 625

Задание 7. Преобразуйте выражение (3x2 − y3)2 в многочлен.

Решение:

(3x2 − y3)2 = (3x2)2 − 2 × 3x2 × y3 + ( y3)2 = 9x4 − 6x2y3 + y6

Задание 8. Выполните умножение (x − y)(x + y)

Решение:

(x − y)(x + y) = x2 − y2

Задание 9. Выполните умножение (2x − y)(2x + y)

Решение:

(2x − y)(2x + y) = (2x)2 − y2 = 4x2 − y2

Задание 10. Выполните умножение (7 + 3y)(3y − 7)

Решение:

(7 + 3y)(3y − 7) = (3y)2 − 72 = 9y2 − 49

Задание 11. Выполните умножение (x2 − 5)(x2 + 5)

Решение:

(x2 − 5)(x2 + 5) = (x2)2 − 52 = x4 − 25

Задание 12. Выполните умножение (a3 − b2)(a3 + b2)

Решение:

(a3 − b2)(a3 + b2) = (a3)2 − (b2)2 = a6 − b4

Задание 13. Выполните умножение (5a2 + 2b3)(5a2 − 2b3)

Решение:

(5a2 + 2b3)(5a2 − 2b3) = (5a2)2 − (2b3)2 = 25a4 − 4b6

Задание 14. Выполните умножение (9x − y2)(y2 + 9x)

Решение:

(9x − y2)(y2 + 9x) = (9x)2 − (y2)2 = 81x2 − y4

Задание 15. Выполните умножение (2 − x)(4 + 2x + x2)

Решение:

(2 − x)(4 + 2x + x2) = 23 − x3 = 8 − x3

Задание 16. Выполните умножение (3 − 2)(9 + 6 + 4)

Решение:

(3 − 2)(9 + 6 + 4) = 33 − 23 = 27 − 8 = 19

Задание 17. Выполните умножение (4x + 1)(16x2 − 4x + 1)

Решение:

(4x + 1)(16x2 − 4x + 1) = (4x)3 + 13 = 64x3 + 1

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Навигация по записям

Формулы сокращенного умножения

Формулы сокращенного умножения

      Формулы сокращенного умножения применяются в математике, а точнее в алгебре, для быстрого получения результата некоторых алгебраических выражений. Получаются формулы сокращенного умножения из алгебраических правил умножения многочленов. Применение формул сокращенного умножения позволяет более быстро решать математические задачи, производить сокращение громоздких алгебраических выражений. Правила алгебры разрешают произвольно выполнять преобразования выражений по формулам сокращенного умножения: можно левую часть равенства представить в виде правой части или правую часть равенства преобразовать в виде левой части равенства. Формулы сокращенного умножения рекомендуется знать наизусть, поскольку они часто применяются при решении задач и уравнений по алгебре, математике. Наиболее часто встречаются первые три формулы сокращенного умножения.

      Рекомендуется сохранить приведенный рисунок на свой компьютер в качестве шпаргалки по математике, алгебре. Представленные на рисунке формулы не являются полным перечнем формул сокращенного умножения. В алгебре существуют и другие формулы сокращенного умножения и деления. Все эти формулы имеют свои собственные названия. Рассмотрим более подробно названия приведенных формул сокращенного умножения.

      Первым [1] на картинке представлен квадрат суммы. Квадрат суммы равняется квадрату первого члена двучлена плюс удвоенное произведение первого члена на второй член двучлена плюс квадрат второго члена двучлена:

(a + b)² = a² + 2ab + b²

      Вторая [2] формула сокращенного умножения называется квадрат разности. Квадрат разности равняется квадрату первого члена двучлена минус удвоенное произведение первого члена на второй член двучлена плюс квадрат второго члена двучлена. Эта формула очень похожа на формулу квадрата суммы и отличается только знаком перед удвоенным произведением:

(a — b)² = a² — 2ab + b²

      В общем виде квадрат суммы и квадрат разности можно записать так:

(a ± b)² = a² ± 2ab + b²

      Формула номер три [3] называется разность квадратов. Разность квадратов равняется сумме двух первых членов двучлена умноженной на разность первого и второго членов двучлена:

a² — b² = (a + b)·(a – b)

      Четвертая [4] формула называется куб суммы. Куб суммы равняется сумме кубов первого и второго членов двучлена, утроенных произведений квадрата первого члена двучлена на второй и квадрата второго члена двучлена на первый:

(a + b)³ = a³ + 3a²b + 3b²a + b³

      Пятая [5] формула похожа на куб суммы и называется куб разности. Куб разности равен кубу первого члена двучлена минус утроенное произведение квадрата первого члена двучлена на второй плюс утроенное произведение первого члена двучлена на квадрат второго минус куб второго члена двучлена:

(a — b)³ = a³ — 3a²b + 3b²a — b³

      Одной формулой куб суммы и куб разности можно записать, используя знаки плюс-минус:

(a ± b)³ = a³ ± 3a²b + 3b²a ± b³

      Шестая [6] формула называется сумма кубов. Сумма кубов равняется сумме первого и второго членов двучлена умноженной на квадрат первого члена двучлена минус произведение первого и второго членов двучлена плюс квадрат второго члена двучлена:

a³ + b³ = (a + b)·( a² — 2ab + b²)

      Седьмая [7] формула похожа на предыдущую и называется разность кубов. Разность кубов равняется разности первого и второго членов двучлена умноженной на квадрат первого члена двучлена плюс произведение первого и второго членов двучлена плюс квадрат второго члена двучлена:

a³ — b³ = (a — b)·( a² + 2ab + b²)

      Одной формулой куб суммы и куб разности можно записать, используя знаки плюс-минус и минус-плюс.

Если вам понравилась публикация и вы хотите знать больше, помогите мне в работе над другими материалами.

      9 августа 2010 года — 22 сентября 2019 года.

© 2006 — 2021 Николай Хижняк.
Все права защищены.

Сокращение простой формулы IF в Xcel



Каков простой способ развернуть следующую формулу, чтобы она применялась к строкам 2-20 моей электронной таблицы:

=SUM(IF(B2=1,M2),IF(B3=1,M3),IF(B4=1,M4))
excel excel-formula
Поделиться Источник NancyQ     31 января 2018 в 23:51

3 ответа

  • Сокращение данных через IMPORTRANGE

    Я пытаюсь сделать некоторое сокращение данных в моем Google Sheets, используя следующую формулу IMPORTRANGE: =query(importrange(https://docs.google.com/a/ap.averydennison.com/spreadsheets/d/1xz1lXY-w5Ii_aWqVAhHgRCmeoes9ltSUtibE4kzhMHA/edit#gid=2051232966,SF_Flex_Rel!a:l), select * where Col1 =…

  • Объедините две вложенные формулы IF

    У меня есть следующие две формулы excel, которые я пытаюсь объединить в одно утверждение. =IF(U1=,,IF(AND(T1=SHIFT,U1>=210,I1=BURNABY),SHOT20,SHOT10)) =IF(U1=,,IF(AND(T1=SHIFTP,U1<480),SHOT10,SHOT15)) Когда я попробовал, я получил ошибку, что я делаю слишком много аргументов.


1

= SUMPRODUCT( ( B2:B20 = 1 ) * M2:M20 )

или

= SUMIF(B2:B20, 1, M2:M20)

Поделиться Slai     01 февраля 2018 в 00:24


0

=INDEX($M$2:$M$20,MATCH(1,$B$2:$B$20,0))

Поделиться Variatus     01 февраля 2018 в 00:13


0

Эта формула сложит строки в столбце M, если та же строка столбца B = 1.

SUMIF(B2:B20,1,M2:M20)

Поделиться Karl Kristjansson     01 февраля 2018 в 00:31

  • Выпуск Формулы Crystal report в if statement

    Я создал отчет crystal и добавил поле Формулы (stock). Это формула, которую я добавил в это поле (базовый синтаксис): if not IsNull ({LigneBonLivraison.Quantite}) Then {@stock} = {Article.StockActuel} — {LigneBonLivraison.Quantite} else {@stock} = {Article.StockActuel} Но я получаю эту ошибку A…

  • Вложенные формулы IF

    У меня есть электронная таблица Excel 2013, в которой я пытаюсь вложить 2 формулы в одну ячейку. У меня есть 1-я формула: это = IF (B2+15>N2, X, Y), где B2 & N2-даты. Мне нужно добавить еще одну формулу, где N2 пуст, что-то вроде =IF(B2 Не могли бы вы порекомендовать какое-нибудь решение?

Похожие вопросы:


Получение имени формулы Crystal Reports внутри формулы

Можно ли использовать имя формулы Crystal Reports внутри самой формулы (в Кристалле 8.5)? Например, предположим, что у меня есть такие формулы, как: @MOISTURE @PROTEIN @ACIDITY @PROPERTYX @PROPERTYY…


Excel Условное Форматирование-‘IF’ Синтаксис Формулы

Я хотел бы использовать эту формулу в качестве условной формулы форматирования: =IF(COUNTIFS(AccountsMonthsOrdered[Account],’Account Summary 2013′!$A$1,AccountsMonthsOrdered[Month],’Account Summary. ..


Преобразование формулы excel IF в Формулу Powerpivot DAX

Я изо всех сил пытаюсь найти решение для преобразования формулы из excel в powerpivot. Это относительно просто в excel. Я хочу вернуть значение, которое говорит >8000 или <8000 в зависимости от…


Сокращение данных через IMPORTRANGE

Я пытаюсь сделать некоторое сокращение данных в моем Google Sheets, используя следующую формулу IMPORTRANGE:…


Объедините две вложенные формулы IF

У меня есть следующие две формулы excel, которые я пытаюсь объединить в одно утверждение. =IF(U1=,,IF(AND(T1=SHIFT,U1>=210,I1=BURNABY),SHOT20,SHOT10))…


Выпуск Формулы Crystal report в if statement

Я создал отчет crystal и добавил поле Формулы (stock). Это формула, которую я добавил в это поле (базовый синтаксис): if not IsNull ({LigneBonLivraison.Quantite}) Then {@stock} =…


Вложенные формулы IF

У меня есть электронная таблица Excel 2013, в которой я пытаюсь вложить 2 формулы в одну ячейку. У меня есть 1-я формула: это = IF (B2+15>N2, X, Y), где B2 & N2-даты. Мне нужно добавить еще одну…


Комбинируйте формулы VLOOKUP и IF

У меня есть следующие две формулы. Я хочу иметь одну формулу для одного столбца вместо использования двух. =VLOOKUP(A2,eodcpos!B:I,8,FALSE =IF(U2=Long,B,S) Я использую первый, чтобы внести значение…


Основы формулы массива вместо вложенного if-else

Я прочесал сайт в поисках формул массива, но меня беспокоит какая-то основная проблема формулы массива, которую я не могу понять. в следующей таблице перечислены цены и различные отсечки для оптовых…


IF statement формулы

Нужна помощь в создании формулы для расчета количества дней хранения. Прилагаемое изображение электронной таблицы, которую я использую, показывает массив дат. Мне нужна формула в столбце E Live Days…

ЛЕВСИМВ, ЛЕВБ (функции ЛЕВСИМВ, ЛЕВБ)

В этой статье описаны синтаксис формулы и использование функций ЛЕВ ЛЕВБ и ЛЕВБ в Microsoft Excel.

Описание

Функция ЛЕВСИМВ возвращает первый символ или несколько первых символов текстовой строки на основе заданного числа символов.

Функция ЛЕВБ возвращает первый символ или несколько первых символов текстовой строки на основе заданного числа байтов.

Важно: 

  • Эти функции могут быть доступны не на всех языках.

  • Функция ЛЕВБ отсчитывает по два байта на каждый символ, только если языком по умолчанию является язык с поддержкой двухбайтовой кодировки. В противном случае функция ЛЕВБ работает так же, как функция ЛЕВСИМВ, и отсчитывает по одному байту на каждый символ.

К языкам, поддерживающим БДЦС, относятся японский, китайский (упрощенное письмо), китайский (традиционное письмо) и корейский.

Синтаксис

ЛЕВСИМВ(текст;[число_знаков])

ЛЕВБ(текст;[число_байтов])

Аргументы этих функций описаны ниже.

  • Текст    Обязательный. Текстовая строка, содержащая символы, которые требуется извлечь.

  • Число_знаков    Необязательный. Количество символов, извлекаемых функцией ЛЕВСИМВ.

    • «Число_знаков» должно быть больше нуля или равно ему.

    • Если «число_знаков» превышает длину текста, функция ЛЕВСИМВ возвращает весь текст.

    • Если значение «число_знаков» опущено, оно считается равным 1.

  • Num_bytes     Необязательный. Количество символов, извлекаемых функцией ЛЕВБ.

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Данные

Цена продажи

Швеция

Формула

Описание

Результат

=ЛЕВСИМВ(A2;4)

Первые четыре символа первой строки

Продажа

=ЛЕВСИМВ(A3)

Первый символ второй строки

Ш

Формулы сокращенного умножения

Формулы сокращенного умножения
НомерНазвание формулыКороткая записьРаскрытие скобок/разложение на множители
(1) Разность квадратовa2-b2(a-b)(a+b)
(2) Квадрат суммы/разности(a±b)2a2±2ab+b2
(3) Квадрат суммы для n переменных(a1+a2+. ..+an)2a12+a22+…+an2+2∑i,jaiaj
(4) Сумма/разность кубовa3±b3(a±b)(a2∓ab+b2)
(5) Куб суммы/разности(a±b)3a3±3a2b+3ab2±b3
(6) Куб суммы для n переменных(a1+a2+…+an)3a13+a23+…+an3+3∑i,jai2aj+6∑i,j,kaiajak
(7) Разность четвертых степенейa4-b4(a-b)(a+b)(a2+b2)
(8) Четвертая степень суммы/разности(a±b)4a4±4a3b+6a2b2±4ab3+b4
(9) Сумма/разность nх степенейan-bn(a±b)(an-1+an-2b+an-3b2+. ..+bn-3a2+bn-2a+bn-1)
(10) Сумма (2n+1)х степенейa2n+1+b2n+1(a+b)(a2n-a2n-1b+a2n-2b2+…+b2n-2a2-b2n-1a+b2n)
(11) Nая степень суммы/разности(a±b)nan±(n1)an-1b+(n2)an-2b2±..+(nn-2)a2bn-2±(nn-1)abn-1+bn

— версия для печати
Определение
Nая степень числа — результат умножения числа на себя n раз. Также квадратом числа называется результат возведения числа в степень n (в nую степень).
Пример:
(4a—3b)3 = 64a3 — 144a2b + 108ab2 — 27b3
Пояснение
Под (nk) подразумевается биномиальный коэффициент, равный
Если у вас есть мысли по поводу данной страницы или предложение по созданию математической (см. раздел «Математика») вспомогательной памятки, мы обязательно рассмотрим ваше предложение. Просто воспользуйтесь обратной связью.

© Школяр. Математика (при поддержке «Ветвистого древа») 2009—2016

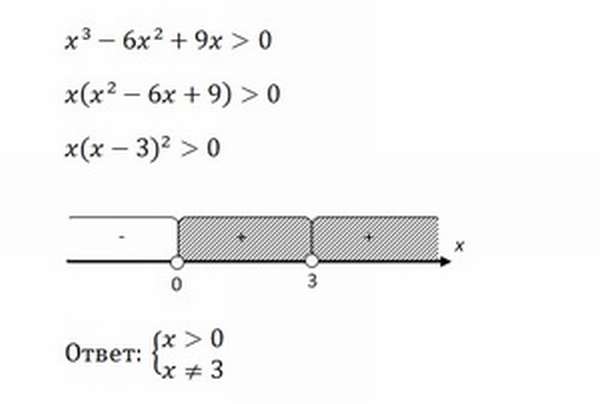
Формулы сокращенного умножения. Разность квадратов, квадрат суммы, разность кубов, бином Ньютона.


Откровенно говоря, эти формулы должен помнить любой ученик седьмого класса. Изучать алгебру даже на школьном уровне и не знать формулу разности квадратов или квадрата суммы просто невозможно. Они постоянно встречаются при упрощении алгебраических выражений, при сокращении дробей и даже могут помочь в арифметических вычислениях. Ну, например, вам нужно вычислить в уме: 3,162 — 2 • 3,16 • 1,16 + 1,162. Если вы начнете считать это «в лоб», получится долго и скучно, а если воспользуетесь формулой квадрата разности, ответ получите за 2 секунды!

Итак, семь формул «школьной» алгебры, которые должны знать все:


Название Формула
Квадрат суммы (A + B)2 = A2 + 2AB + B2
Квадрат разности (A — B)2 = A2 — 2AB + B2
Разность квадратов (A — B)(A + B) = A2 — B2
Куб суммы (A + B)3 = A3 + 3A2B + 3AB2+ B3
Куб разности (A — B)3 = A3 — 3A2B + 3AB2 — B3
Сумма кубов A3 + B3 = (A + B)(A2 — AB + B2)
Разность кубов A3 — B3 = (A — B)(A2 + AB + B2)

Версия для печати в формате png

Обратите внимание: никакой формулы суммы квадратов не существует! Не позволяйте своей фантазии заходить слишком далеко.

Как проще всего запомнить все эти формулы? Ну, скажем, увидеть определенные аналогии. Например, формула квадрата суммы похожа на формулу квадрата разности (отличие лишь в одном знаке), а формула куба суммы — на формулу куба разности. Далее, в составе формул разности кубов и суммы кубов мы видим нечто похожее на квадрат суммы и квадрат разности (только коэффициента 2 не хватает).

Но лучше всего эти формулы (как и любые другие!) запоминаются на практике. Решайте больше примеров на упрощение алгебраических выражений, и все ф-лы запомнятся сами собой.

Любознательным школьникам будет, вероятно, интересно обобщить приведенные факты. Вот, скажем, существуют формулы квадрата и куба суммы. А что, если рассмотреть выражения типа (A + B)4, (A + B)5 и даже (A + B)n, где n — произвольное натуральное число? Можно ли увидеть здесь какую — либо закономерность?

Да, подобная закономерность существует. Выражение вида (A + B)n называется биномом Ньютона. Я рекомендую пытливым школьникам самим вывести формулы для (A + B)4 и (A + B)5, а далее попытаться увидеть общий закон: сравнить, например, степень соответствующего бинома и степень каждого из слагаемых, которые получаются при раскрытии скобок; сравнить степень бинома с количеством слагаемых; попытаться найти закономерности в коэффициентах. Мы не будем сейчас углубляться в эту тему (для этого нужен отдельный разговор!), а лишь запишем готовый результат:

(A + B)n = An + Cn1An-1B + Cn2An-2B2 + … + CnkAn-kBk + … + Bn.

Здесь Cnk = n!/(k! • (n-k)!).

Напоминаю, что n! — это 1 • 2 • … • n — произведение всех натуральных чисел от 1 до n. Называется это выражение факториалом числа n. Например, 4! = 1 • 2 • 3 • 4 = 24. Факториал нуля считается равным единице!

А что можно сказать по поводу разности квадратов, разности кубов и т. п.? Существует ли здесь какая-либо закономерность? Можно ли привести общую формулу для An — Bn?

Да, можно. Вот эта формула:

An — Bn = (A — В)(An-1 + An-2B + An-3B2 + … + Bn-1).

Более того, для нечетных степеней n существует аналогичная ф-ла и для суммы:

An + Bn = (A + В)(An-1 — An-2B + An-3B2 — … + Bn-1).

Мы не будем сейчас выводить эти формулы (кстати, это не очень сложно), но знать об их существовании, безусловно, полезно.


Двуугловые, полуугловые и редукционные формулы · Алгебра и тригонометрия

Формулы двойного угла, полуугла и редукции · Алгебра и тригонометрия

В этом разделе вы:

  • Используйте формулы двойного угла, чтобы найти точные значения.
  • Используйте формулы двойного угла для проверки идентичности.
  • Используйте формулы сокращения, чтобы упростить выражение.
  • Используйте формулы половинного угла, чтобы найти точные значения.

Велосипедные пандусы, изготовленные для соревнований (см. [Ссылка]), должны различаться по высоте в зависимости от уровня навыков участников.Для опытных участников угол между рампой и землей должен составлять θ

.

такой, что tan θ = 53.

Для новичков угол делится пополам. Какая крутизна ската для новичков? В этом разделе мы исследуем три дополнительные категории идентичностей, которые мы можем использовать, чтобы ответить на такие вопросы, как этот.

Использование формул двойного угла для поиска точных значений

В предыдущем разделе мы использовали формулы сложения и вычитания для тригонометрических функций.Теперь мы еще раз посмотрим на те же формулы. Формулы двойного угла являются частным случаем формул суммы, где α = β.

Вывод формулы двойного угла для синуса начинается с формулы суммы,

sin (α + β) = sin α cos β + cos α sin β

Если положить α = β = θ,

, тогда у нас

sin (θ + θ) = sin θ cos θ + cos θ sin θsin (2θ) = 2sin θ cos θ

Получение двойного угла для косинуса дает нам три варианта. Во-первых, исходя из формулы суммы, cos (α + β) = cos α cos β − sin α sin β,

и положив α = β = θ,

у нас

cos (θ + θ) = cos θ cos θ − sin θ sin θcos (2θ) = cos2θ − sin2θ

Используя свойства Пифагора, мы можем расширить эту формулу двойного угла для косинуса и получить еще два варианта.Первый вариант:

cos (2θ) = cos2θ − sin2θ = (1 − sin2θ) −sin2θ = 1−2sin2θ

Вторая вариация:

cos (2θ) = cos2θ − sin2θ = cos2θ− (1 − cos2θ) = 2 cos2θ − 1

Аналогично, чтобы вывести формулу двойного угла для касательной, заменив α = β = θ

в формуле суммы дает

tan (α + β) = tan α + tan β1 − tan α tan βtan (θ + θ) = tan θ + tan θ1 − tan θ tan θtan (2θ) = 2tan θ1 − tan2θ

Формулы двойного угла

Формулы двойного угла резюмируются следующим образом:

sin (2θ) = 2 sin θ cos θ

cos (2θ) = cos2θ − sin2θ = 1-2 sin2θ = 2 cos2θ − 1

tan (2θ) = 2 tan θ1 − tan2θ

Зная тангенс угла и квадрант, в котором он расположен, используйте формулы двойного угла, чтобы найти точное значение.

  1. Нарисуйте треугольник, чтобы отразить данную информацию.
  2. Определите правильную формулу двойного угла.
  3. Подставить значения в формулу, основанную на треугольнике.
  4. Упростить.

Использование формулы двойного угла для нахождения точного значения касательной

Учитывая, что tan θ = −34

и θ

находится в квадранте II, найдите следующее:

  1. грех (2θ)
  2. cos (2θ)
  3. загар (2θ)

Если мы нарисуем треугольник, чтобы отразить данную информацию, мы сможем найти значения, необходимые для решения проблем на изображении.Нам дано значение tan θ = −34,

такой, что θ

находится в квадранте II. Тангенс угла равен противоположной стороне по соседней стороне, и поскольку θ

находится во втором квадранте, соседняя сторона находится на оси x и является отрицательной. Используйте теорему Пифагора , чтобы найти длину гипотенузы:

(−4) 2+ (3) 2 = c216 + 9 = c225 = c2c = 5

Теперь мы можем нарисовать треугольник, подобный показанному в [ссылка].

  1. Начнем с написания формулы двойного угла для синуса.

    sin (2θ) = 2 sin θ cos θ

    Мы видим, что нам нужно найти sin θ

    и cos θ.

    На основании [ссылка] мы видим, что гипотенуза равна 5, поэтому sin θ = 35,

    и cos θ = −45.

    Подставьте эти значения в уравнение и упростите.

    Таким образом,

    sin (2θ) = 2 (35) (- 45) = — 2425

  2. Напишите формулу двойного угла для косинуса.

    cos (2θ) = cos2θ − sin2θ

    Снова подставьте значения синуса и косинуса в уравнение и упростите.

    cos (2θ) = (- 45) 2− (35) 2 = 1625−925 = 725

  3. Напишите формулу двойного угла для касательной.

    tan (2θ) = 2 tan θ1 − tan2θ

    В этой формуле нам нужен тангенс, который мы получили как tan θ = −34.

    Подставьте это значение в уравнение и упростите.

    загар (2θ) = 2 (−34) 1 — (- 34) 2 = −321−916 = −32 (167) = — 247

Учитывая sin α = 58,

с θ

в квадранте I, найти cos (2α).

cos (2α) = 732

Использование формулы двойного угла для косинуса без точных значений

Используйте формулу двойного угла для косинуса, чтобы записать cos (6x)

в пересчете на cos (3x).

cos (6x) = cos (2 (3x)) = 2cos2 (3x) −1

Анализ

Этот пример показывает, что мы можем использовать формулу двойного угла, не имея точных значений.Он подчеркивает, что образец — это то, что нам нужно запомнить, и что идентичности верны для всех значений в области определения тригонометрической функции.

Использование формул двойного угла для проверки личности

Установление тождеств с использованием формул двойного угла выполняется с использованием тех же шагов, которые мы использовали для вывода формул суммы и разности. Выберите более сложную часть уравнения и переписывайте ее, пока она не совпадет с другой стороной.

Использование формул двойного угла для проверки личности

Проверьте следующую идентичность, используя формулы двойного угла:

1 + грех (2θ) = (грех θ + соз θ) 2

Мы будем работать с правой частью знака равенства и перепишем выражение, пока оно не совпадет с левой частью.

(sin θ + cos θ) 2 = sin2θ + 2 sin θ cos θ + cos2θ = (sin2θ + cos2θ) +2 sin θ cos θ = 1 + 2 sin θ cos θ = 1 + sin (2θ)

Анализ

Этот процесс несложен, если мы вспомним формулу полного квадрата из алгебры:

(a ± b) 2 = a2 ± 2ab + b2

, где a = sin θ

и b = cos θ.

Часть успеха в математике — это способность распознавать закономерности. Хотя термины или символы могут меняться, алгебра остается непротиворечивой.

Проверить идентичность: cos4θ − sin4θ = cos (2θ).

cos4θ − sin4θ = (cos2θ + sin2θ) (cos2θ − sin2θ) = cos (2θ)

Проверка идентичности двойного угла на касательную

Подтвердите личность:

tan (2θ) = 2cot θ − tan θ

В этом случае мы будем работать с левой частью уравнения и упрощать или переписывать, пока она не станет правой частью уравнения.

tan (2θ) = 2 tan θ1 − tan2θ Формула двойного угла = 2 tan θ (1tan θ) (1 − tan2θ) (1tan θ) Умножьте на член, который дает желаемый числитель.= 21tan θ − tan2θtan θ = 2cot θ − tan θ Используйте обратное тождество для 1tan θ.

Анализ

Вот случай, когда более сложная часть исходного уравнения появилась справа, но мы решили работать с левой стороной. Однако, если бы мы выбрали левую сторону для переписывания, мы бы работали в обратном направлении, чтобы прийти к эквивалентности. Например, предположим, что мы хотим показать

2tan θ1 − tan2θ = 2cot θ − tan θ

Давайте поработаем над правой стороной.

2cot θ − tan θ = 21tan θ − tan θ (tan θtan θ) = 2 tan θ1tan θ (tan θ) −tan θ (tan θ) = 2 tan θ1 − tan2θ

При использовании тождеств для упрощения тригонометрического выражения или решения тригонометрического уравнения обычно существует несколько путей к желаемому результату. Не существует установленного правила относительно того, какой стороной следует манипулировать. Однако начать следует с изложенных ранее рекомендаций.

Проверьте тождество: cos (2θ) cos θ = cos3θ − cos θ sin2θ.

cos (2θ) cos θ = (cos2θ − sin2θ) cos θ = cos3θ − cos θsin2θ

Использование формул сокращения для упрощения выражения

Формулы двойного угла могут использоваться для вывода формул редукции , которые представляют собой формулы, которые мы можем использовать для уменьшения степени данного выражения, включающего четные степени синуса или косинуса. Они позволяют нам переписать четные степени синуса или косинуса в терминах первой степени косинуса. Эти формулы особенно важны на курсах математики более высокого уровня, в частности, в математическом анализе. Также называемые формулами уменьшения мощности, включены три тождества, которые легко выводятся из формул двойного угла.

Мы можем использовать две из трех формул двойного угла для косинуса, чтобы получить формулы приведения для синуса и косинуса. Начнем с cos (2θ) = 1-2 sin2θ.

Решить относительно sin2θ:

cos (2θ) = 1−2 sin2θ2 sin2θ = 1 − cos (2θ) sin2θ = 1 − cos (2θ) 2

Далее используем формулу cos (2θ) = 2 cos2θ − 1.

Решить относительно cos2θ:

cos (2θ) = 2 cos2θ − 11 + cos (2θ) = 2 cos2θ1 + cos (2θ) 2 = cos2θ

Последняя формула приведения получается записью тангенса через синус и косинус:

tan2θ = sin2θcos2θ = 1 − cos (2θ) 21 + cos (2θ) 2 Подставим формулы редукции. = (1 − cos (2θ) 2) (21 + cos (2θ)) = 1 − cos (2θ) 1 + cos ( 2θ)

Формулы приведения

Формулы сокращения резюмируются следующим образом:

sin2θ = 1 − cos (2θ) 2

cos2θ = 1 + cos (2θ) 2

tan2θ = 1 − cos (2θ) 1 + cos (2θ)

Написание эквивалентного выражения, не содержащего степени больше 1

Напишите эквивалентное выражение для cos4x

, в котором не используются степени синуса или косинуса больше 1.

Мы применим формулу приведения косинуса дважды.

cos4x = (cos2x) 2 = (1 + cos (2x) 2) 2 Формула сокращения для cos2x. = 14 (1 + 2cos (2x) + cos2 (2x)) = 14 + 12 cos (2x) +14 (1+ cos2 (2x) 2) Заменить формулу сокращения для cos2x. = 14 + 12 cos (2x) + 18 + 18 cos (4x) = 38 + 12 cos (2x) +18 cos (4x)

Анализ

Решение находится путем двойного использования формулы редукции, как уже отмечалось, и формулы полного квадрата из алгебры.

Использование формул уменьшения мощности для доказательства личности

Используйте формулы уменьшения мощности, чтобы доказать

sin3 (2x) = [12 sin (2x)] [1 − cos (4x)]

Мы будем работать над упрощением левой части уравнения:

sin3 (2x) = [sin (2x)] [sin2 (2x)] = sin (2x) [1 − cos (4x) 2] Подставьте формулу уменьшения мощности.= sin (2x) (12) [1 − cos (4x)] = 12 [sin (2x)] [1 − cos (4x)]

Анализ

Обратите внимание, что в этом примере мы заменили

1 − cos (4x) 2

для sin2 (2x).

В формуле указано

sin2θ = 1 − cos (2θ) 2

Положим θ = 2x,

, поэтому 2θ = 4x.

Используйте формулы уменьшения мощности, чтобы доказать, что 10 cos4x = 154 + 5 cos (2x) +54 cos (4x).

10cos4x = 10 (cos2x) 2 = 10 [1 + cos (2x) 2] 2 Заменить формулу сокращения для cos2x.= 104 [1 + 2cos (2x) + cos2 (2x)] = 104 + 102cos (2x) +104 (1 + cos2 (2x) 2) Подставляем формулу сокращения для cos2x. = 104 + 102cos (2x) + 108 + 108cos (4x) = 308 + 5cos (2x) + 108cos (4x) = 154 + 5cos (2x) + 54cos (4x)

Использование формул полуугла для нахождения точных значений

Следующий набор тождеств — это набор формул для половинного угла , которые могут быть выведены из формул приведения и мы можем использовать, когда у нас есть угол, который составляет половину размера специального угла. Если заменить θ

с α2,

формула половинного угла для синуса находится путем упрощения уравнения и решения для sin (α2).

Обратите внимание, что формулам половинного угла предшествует ±

.

знак. Это не означает, что допустимы как положительные, так и отрицательные выражения. Скорее, это зависит от квадранта, в котором α2

завершается.

Формула половинного угла для синуса выводится следующим образом:

sin2θ = 1 − cos (2θ) 2sin2 (α2) = 1− (cos2⋅α2) 2 = 1 − cos α2sin (α2) = ± 1 − cos α2

Чтобы вывести формулу половинного угла для косинуса, мы имеем

cos2θ = 1 + cos (2θ) 2cos2 (α2) = 1 + cos (2⋅α2) 2 = 1 + cos α2cos (α2) = ± 1 + cos α2

Для касательной идентичности имеем

tan2θ = 1 − cos (2θ) 1 + cos (2θ) tan2 (α2) = 1 − cos (2⋅α2) 1 + cos (2⋅α2) = 1 − cos α1 + cos αtan (α2) = ± 1− cos α1 + cos α

Формулы полуугла

Формулы полуугла следующие:

sin (α2) = ± 1 − cos α2

cos (α2) = ± 1 + cos α2

tan (α2) = ± 1 − cos α1 + cos α = sin α1 + cos α = 1 − cos α sin α

Использование формулы полуугла для нахождения точного значения синусоидальной функции

Найти грех (15 °)

по формуле половинного угла.

Поскольку 15 ° = 30 ° 2,

мы используем формулу половинного угла для синуса:

sin 30 ° 2 = 1 − cos30 ° 2 = 1−322 = 2−322 = 2−34 = 2−32

Помните, что мы можем проверить ответ с помощью графического калькулятора.

Анализ

Обратите внимание, что мы использовали только положительный корень, потому что sin (15 °)

положительный.

Зная тангенс угла и квадрант, в котором находится угол, найдите точные значения тригонометрических функций половины угла.

  1. Нарисуйте треугольник для представления данной информации.
  2. Определите правильную формулу полуугла.
  3. Подставить значения в формулу, основанную на треугольнике.
  4. Упростить.

Нахождение точных значений с использованием идентичностей половинных углов

Учитывая, что tan α = 815

и α

находится в квадранте III, найдите точное значение следующего:

  1. грех (α2)
  2. cos (α2)
  3. загар (α2)

Используя данную информацию, мы можем нарисовать треугольник, показанный в [ссылка]. Используя теорему Пифагора, мы находим, что гипотенуза равна 17. Следовательно, мы можем вычислить sin α = −817

и cos α = −1517.

  1. Прежде чем мы начнем, мы должны помнить, что если α

    находится в квадранте III, затем

    180 ° <α <270 °,

    так

    180 ° 2 <α2 <270 ° 2.

    Это означает, что сторона терминала

    α2

    находится во втором квадранте, поскольку

    90 ° <α2 <135 °.

    Найти sin α2,

    мы начинаем с написания формулы половинного угла для синуса.Затем мы подставляем значение косинуса, найденного в треугольнике, в [ссылка] и упрощаем.

    sin α2 = ± 1 − cos α2 = ± 1 — (- 1517) 2 = ± 32172 = ± 3217⋅12 = ± 1617 = ± 417 = 41717

    Выберем положительное значение sin α2

    , потому что угол заканчивается в квадранте II, а синус положительный в квадранте II.

  2. Найти cos α2,

    мы запишем формулу половинного угла для косинуса, подставим значение косинуса, которое мы нашли из треугольника в [ссылка], и упростим.

    cos α2 = ± 1 + cos α2 = ± 1 + (- 1517) 2 = ± 2172 = ± 217⋅12 = ± 117 = −1717

    Выберем отрицательное значение cos α2

    , потому что угол находится в квадранте II, потому что косинус отрицателен в квадранте II.

  3. Найти tan α2,

    запишем формулу полуугла для тангенса. Опять же, мы подставляем значение косинуса, найденного в треугольнике, в [ссылка] и упрощаем.

    tan α2 = ± 1 − cos α1 + cos α = ± 1 — (- 1517) 1 + (- 1517) = ± 3217217 = ± 322 = −16 = −4

    Выберем отрицательное значение tan α2

    , потому что α2

    лежит во втором квадранте, а касательная во втором квадранте отрицательна.

Учитывая, что sin α = −45

и α

находится в квадранте IV, найдите точное значение cos (α2).

−25

Нахождение измерения полуугла

Теперь вернемся к задаче, поставленной в начале раздела. Велосипедная рампа предназначена для соревнований высокого уровня с углом θ

.

образован пандусом и землей.Другой пандус будет построен наполовину крутым для соревнований новичков. Если tan θ = 53

для соревнований более высокого уровня, что такое измерение угла для соревнований новичков?

Поскольку угол для соревнований новичков измеряет половину крутизны угла для соревнований высокого уровня, и tan θ = 53

для высокой конкуренции, мы можем найти cos θ

из прямоугольного треугольника и теоремы Пифагора, так что мы можем использовать тождества половинных углов.См. [Ссылка].

32 + 52 = 34c = 34

Мы видим, что cos θ = 334 = 33434.

Мы можем использовать формулу половинного угла для тангенса: tan θ2 = 1 − cos θ1 + cos θ.

Так как tan θ

находится в первом квадранте, как и tan θ2.

тангенс угла θ2 = 1−334341 + 33434 = 34−3343434 + 33434 = 34−33434 + 334≈0,57

Мы можем использовать арктангенс, чтобы найти угол: tan − 1 (0,57) ≈29,7 °.

Таким образом, угол пандуса для соревнований новичков ≈29.7 °.

Ключевые уравнения

Формулы двойного угла sin (2θ) = 2sin θ cos θcos (2θ) = cos2θ − sin2θ = 1−2sin2θ = 2cos2θ − 1tan (2θ) = 2tan θ1 − tan2θ
Формулы приведения sin2θ = 1 − cos (2θ) 2cos2θ = 1 + cos (2θ) 2tan2θ = 1 − cos (2θ) 1 + cos (2θ)
Формулы полууглов sin α2 = ± 1 − cos α2cos α2 = ± 1 + cos α2tan α2 = ± 1 − cos α1 + cos α = sin α1 + cos α = 1 − cos αsin α

Ключевые понятия

  • Двойные угловые тождества выводятся из формул суммы основных тригонометрических функций: синуса, косинуса и тангенса.См. [Ссылка], [ссылка], [ссылка] и [ссылка].
  • Формулы приведения особенно полезны в исчислении, поскольку они позволяют уменьшить степень тригонометрического члена. См. [Ссылка] и [ссылка].
  • Формулы полууглов позволяют нам найти значение тригонометрических функций, включающих полууглы, независимо от того, известен ли исходный угол или нет. См. [Ссылка], [ссылка] и [ссылка].

Упражнения по разделам

Устный

Объясните, как определить тождества редукции из тождества двойного угла cos (2x) = cos2x − sin2x.

Используйте тождества Пифагора и выделите квадратный член.

Объясните, как определить формулу двойного угла для tan (2x)

с использованием формулы двойного угла для cos (2x)

и грех (2х).

Мы можем определить формулу половинного угла для tan (x2) = 1 − cos x1 + cos x

путем деления формулы для sin (x2)

по cos (x2).

Объясните, как определить две формулы для tan (x2)

, которые не содержат квадратных корней.

1 − cos xsin x, sin x1 + cos x,

умножение верха и низа на 1 − cos x

и 1 + cos x,

соответственно.

Для формулы половинного угла, приведенной в предыдущем упражнении для tan (x2),

объясняет, почему деление на 0 не имеет значения. (Подсказка: изучите значения cos x

необходимо, чтобы знаменатель был равен 0.)

Алгебраические

Для следующих упражнений найдите точные значения a) sin (2x),

б) cos (2x),

и c) загар (2x)

без решения относительно x.

Если sin x = 18,

и x

находится в квадранте I.

а) 3732

б) 3132

в) 3731

Если cos x = 23,

и x

находится в квадранте I.

Если cos x = −12,

и x

находится в квадранте III.

а) 32

б) −12

в) −3

Если tan x = −8,

и x

находится в квадранте IV.

Для следующих упражнений найдите значения шести тригонометрических функций, если указанные условия выполнены.

cos (2θ) = 35

и 90 ° ≤θ≤180 °

cos θ = −255, sin θ = 55, tan θ = −12, csc θ = 5, sec θ = −52, cot θ = −2

cos (2θ) = 12

и 180 ° ≤θ≤270 °

Упростите следующие упражнения до одного тригонометрического выражения.

2 sin (π4) 2 cos (π4)

2 грех (π2)

Для следующих упражнений найдите точное значение, используя формулы половинного угла.

Для следующих упражнений найдите точные значения a) sin (x2),

б) cos (x2),

и c) загар (x2)

без решения относительно x,

при 0 ° ≤x≤360 °.

Если tan x = −43,

и x

находится в квадранте IV.

Если sin x = −1213,

и x

находится в квадранте III.

а) 31313

б) −21313

в) −32

Если csc x = 7,

и x

находится в квадранте II.

Если sec x = −4,

и x

находится в квадранте II.

а) 104

б) 64

в) 153

Для следующих упражнений используйте [ссылка], чтобы найти требуемые половинные и двойные углы.

Найдите sin (2θ), cos (2θ),

и загар (2θ).

Найти sin (2α), cos (2α),

и загар (2α).

120169, –119169, –120119

Найдите sin (θ2), cos (θ2),

и tan (θ2).

Найдите sin (α2), cos (α2),

и tan (α2).

21313,31313,23

Для следующих упражнений упростите каждое выражение. Не оценивайте.

2cos2 (37 °) −1

cos (74 °)

cos2 (9x) −sin2 (9x)

cos (18x)

6 sin (5x) cos (5x)

3син (10х)

Подтвердите свою личность в следующих упражнениях.

(sin t − cos t) 2 = 1 − sin (2t)

sin (2x) = — 2 sin (−x) cos (−x)

−2 sin (−x) cos (−x) = — 2 (−sin (x) cos (x)) = sin (2x)

детская кроватка x − tan x = 2 детская кроватка (2x)

sin (2θ) 1 + cos (2θ) tan2θ = tan3 θ

sin (2θ) 1 + cos (2θ) tan2θ = 2sin (θ) cos (θ) 1 + cos2θ − sin2θtan2θ = 2sin (θ) cos (θ) 2cos2θtan2θ = sin (θ) cos θtan2θ = cot (θ) tan2θ = tan3 θ

Для следующих упражнений перепишите выражение с показателем степени не выше 1.

sin4 (3x)

3 + cos (12x) −4cos (6x) 8

cos4x sin2x

2 + cos (2x) −2cos (4x) −cos (6x) 32

Технологии

Для следующих упражнений сократите уравнения до степени единицы, а затем проверьте ответ графически.

загар4x

3 + cos (4x) −4cos (2x) 3 + cos (4x) + 4cos (2x)

sin2x cos2x

1 − cos (4x) 8

tan4x cos2x

3 + cos (4x) −4 cos (2x) 4 (cos (2x) +1)

cos2 (2x) грех x

(1 + соз (4x)) грех x2

Для следующих упражнений найдите алгебраически эквивалентную функцию, только в единицах sin x

и / или cos x,

, а затем проверьте ответ, построив графики обеих функций.

грех (4x)

4sin xcos x (cos2x − sin2x)

Расширения

Для следующих упражнений подтвердите личность.

грех (2x) = 2 загар x1 + загар 2x

2tan x1 + tan2x = 2sin xcos x1 + sin2xcos2x = 2sin xcos xcos2x + sin2xcos2x = 2sin xcos x.cos2x1 = 2sin xcos x = sin (2x)

cos (2α) = 1 − tan2α1 + tan2α

загар (2x) = 2 sin x cos x2cos2x − 1

2sin xcos x2cos2x − 1 = sin (2x) cos (2x) = tan (2x)

(sin2x − 1) 2 = cos (2x) + sin4x

грех (3x) = 3 грех х cos2x − sin3x

sin (x + 2x) = sin xcos (2x) + sin (2x) cos x = sin x (cos2x − sin2x) + 2sin xcos xcos x = sin xcos2x − sin3x + 2sin xcos2x = 3sin xcos2x − sin3x

cos (3x) = cos3x − 3sin2x cos x

1 + cos (2t) sin (2t) −cos t = 2 cos t2 sin t − 1

1 + cos (2t) sin (2t) −cost = 1 + 2cos2t − 12sintcost − cost = 2cos2tcost (2sint − 1) = 2cost2sint − 1

sin (16x) = 16 sin x cos x cos (2x) cos (4x) cos (8x)

cos (16x) = (cos2 (4x) −sin2 (4x) −sin (8x)) (cos2 (4x) −sin2 (4x) + sin (8x))

(cos2 (4x) −sin2 (4x) −sin (8x)) (cos2 (4x) −sin2 (4x) + sin (8x)) == (cos (8x) −sin (8x)) (cos (8x) + sin (8x)) = cos2 (8x) −sin2 (8x) = cos (16x)

Глоссарий

формулы двойного угла
тождеств, полученных из формул суммы для синуса, косинуса и тангенса, в которых углы равны
формулы половинного угла
тождеств, полученных из формул приведения и используемых для определения значений половинного угла тригонометрических функций
формулы восстановления
тождеств, полученных из формул двойного угла и используемых для уменьшения мощности тригонометрической функции

Эта работа находится под лицензией Creative Commons Attribution 4.2 + 9} \, dx \ end {уравнение}

Как бы вы их интегрировали? В первом используется функция арктангенса, во втором — логарифмы, а в третьем — деление. Можете ли вы проинтегрировать эти три интеграла?

Формула интеграции по частям

Пусть $ f $ и $ g $ — дифференцируемые функции. Напомним, из правила произведения следует, что $ fg $ — дифференцируемая функция и \ begin {Equation} [f (x) g (x)] ‘= f’ (x) g (x) + f (x) g ‘(x ). \ end {уравнение} Если мы проинтегрируем обе части, мы получим \ begin {уравнение} \ int [f (x) g (x)] ‘dx = \ int f’ (x) g (x) \, dx + \ int f (х) д ‘(х) \, dx.\ end {Equation} Может случиться так, что один из интегралов в правой части проще интегрировать, чем другой.

Теорема . ( Интегрирование по частям ) Пусть $ u = f (x) $ и $ v = g (x) $ — дифференцируемые функции. Дифференциалы равны $ du = f ‘(x) \, dx $ и $ dv = g’ (x) \, dx $ и формула \ begin {Equation} \ int u \, dv = uv — \ int v \, du \ end {уравнение} называется интегрированием по частям .

Пример .x + C \ end {align *}, где $ C $ — произвольная константа.

Пример . Найдите $ \ displaystyle \ int x \ sin x \, dx. $

Решение . Пусть $ u = x $ и $ dv = \ sin x \, dx $. Тогда $ du = dx $ и $ v = — \ cos x $, у нас есть \ begin {align *} \ int x \ sin x \, dx & = — x \ cos x \ — \ int (- \ cos x) \, dx \\ & = -x \ cos x + \ sin x + C \ end {align *}, где $ C $ — произвольная константа.

Теорема . Пусть $ f (x) $ и $ g (x) $ — дифференцируемые функции.{n-1} \ sin x \, dx $

Формула снижения мощности

Назначение формул уменьшения мощности — написать эквивалентное выражение без показателя степени. Они используются для упрощения вычислений и выводятся с использованием формул двойного угла и половинного угла и тождества Пифагора.

Квадраты

Кубики


Четвертые

Пятые


Пример: Найдите

Шаг 1: запишите sin 4 x в виде квадрата

sin 4 x = (sin 2 x) 2


Шаг 2: используйте правило уменьшения мощности в квадрате для синуса


Шаг 3: замените на


Шаг 4. Упростите


Хотя можно было бы использовать формулу для четвертой степени, гораздо проще записать четвертую степень в квадрате степени, так что формулу двойного угла или половинного угла также не нужно использовать.Формулы уменьшения мощности становятся очень удобными в расчетах, поскольку позволяют избавиться от показателей в тригонометрических функциях, чтобы найти меру угла. Формула восстановления

— объяснение, часто используемые формулы восстановления и решенные примеры

Формула сокращения считается важным методом интегрирования. Интеграция по формулам редукции позволяет решать сложные задачи интеграции. Его можно использовать для тригонометрических функций, степени элементарных функций, произведения двух или более сложных функций и т. Д.Эти функции нелегко интегрировать. Следовательно, чтобы упростить процесс интегрирования, мы можем использовать некоторые формулы редукции для определения решения интегральных задач. Эти формулы редукции помогают нам минимизировать степень интегралов и формулировать интегралы за конечное число шагов.

Некоторые из обычно используемых формул приведения интегралов, включая общие функции, обсуждаются ниже.

Формулы редукции для тригонометрических функций

Здесь мы обсудим некоторые важные формулы редукции для тригонометрических функций.

  • ∫ Sinn (y) dy = -sinn-1 (y) cos (y) / n + n-1 / n Sinn-2 (y) dy

  • ∫ yn Sinn (y) dy = — yncos (y) + n ∫ yn-1 cos (y) dy

  • ∫ yn Cos (y) dy = ynSin (y) — n ∫ yn-1 sin (y) dy

  • ∫ tann (y ) dy = — tann-1 (y) / n-1 — ∫ tann-2 (y) dy

  • ∫ Sinn (y) dy Cosm (y) dy = sinn + 1 (y) cosm-1 (y ) / n + m + m-1 / n + m ∫ Sinn (y) Cosm-2 (y) dy

Формула редукции для экспоненциальной функции

  • ∫ yn emy dy = 1 / mynemy –n / m yn-1 emydy

  • ∫ emy / yn dy = emy (n-1) yn-1 + m / n-1 ∫ emx / xn-1 y

  • ∫ dy / sinhny = -1 / n sinhn -1 y ch y — (n-1 / n) ∫ sh n-2 y dy

  • ∫ Sinhn y dy = -1 / n Sin hn-1 cosh y — n-1 / n ∫ Sinhn-2 y dy

Формула приведения для алгебраических функций

  • ∫ yn / ayn + b dy = y / ab / a ∫ dy / ayn + b

  • ∫ dy (ay2 + by + C) n = — 2ay- b / (n-1) (b2 — 4ac) (ay2 + by + C) n-1 -2 (2n-3) a / (n-1) (b2 — 4ac) ∫ dy / (ay2 + by + C) n-1, n ≠ 1

  • ∫ dy / (y2- a2) n = x / 2 (n-1) a2 (y2 — a2) n-1 — 2n-3 / 2 (n-1) a2 ∫ dy (y2 — a2) n-1, n ≠ 1

  • ∫ dy / (y2 + a2) n = x / 2 (n-1) a2 (y2 — a2) n-1 + 2n-3/2 (n-1) a2 ∫ dy (y2 — a2) n-1, n ≠ 1

Формулы приведения для тригонометрических функций

Формула приведения для обратной тригонометрической функции

  • ∫ yn arcsin y dy = yn + 1 / n + 1 arcsin y -1 / n + 1 ∫ yn-1 / \ [\ sqrt {1-y ^ 2dy} \]

  • ∫ yn arc cos y dy = yn + 1 / n + 1 arc cos y -1 / n + 1 ∫ yn-1 / \ [\ sqrt {1-y ^ 2dy} \]

  • ∫ yn arctan y dy = yn + 1 / n + 1 arctan y -1 / n + 1 ∫ yn-1 / \ [\ sqrt {1-y ^ 2dy} \]

Время викторины

  1. Найдите \ [\ int_ {0} ^ {π / 2 } \] sin⁶ (x) dx

  1. 0

  2. π / 8

  3. π / 4

  4. 15π / 96

2.{π / 2} \] sin10 (x) cos (x) dx

  1. 1

  2. 0

  3. 13π / 1098

  4. 21π / 2048

Пример формулы восстановления с решениями

1. По формуле приведения

In = ∫ sin y dy = 1 / n cos y sinn-1 y + n-1 / n In-2

Вычислить

∫ Sin4 y dy;

Решение:

Использование формулы сокращения с n = 4 дает

∫ Sin4 y dy = -1/4 cos y sin3 y + ¾ I2

Нам нужно вычислить I2 = sin2 y dy, где соответствует n = 2

Используя уравнения интегралов, получаем:

∫ Sin2 y dy = y / 2-1 / 2 sin y cos y + K

Без объединения всего вместе получаем

∫ Sin4 y dy

= -¼ Cos y Sin3 y + ¾ [y / 2 — 1 / sin y cos y + K]

= -1/4 -¼ Cos y Sin3 y + 3 / 8y — cos y sin y + K ‘

= 3/8 y — 1/4 sin (2y) + 1/32 sin 4 (y) + K ‘

Примечание. Мы использовали значения K и K’, поскольку значения констант на самом деле различаются.

2. Вычислить интеграл

y⁷ (8 + 3y⁴) ⁸ dy

Решение:

u = 8 + 3y⁴ ￫ du = 12y³dy ￫ y³dy = 1/12 du

Перепишем целое число

Вычислите интеграл

∫ y7 (8 + 3y4) ⁸ dy = ∫ y4y3 (8 + 3y4) 8 dy = ∫ y4 (8 + 3y4) y3dy

Теперь предположим, что мы можем преобразовать все y в подынтегральное выражение, исключая y4, что находится впереди. Из подстановки мы можем считать, что мы можем решить это для y4, чтобы получить,

y4 = 1/3 (u-8)

Теперь мы сделаем замену и вычислим интеграл

y7 (8 + 3y4) = 1 / 12 1/3 (u-8) u8 du = 1/36 u9 — 8u8 du = 1/36 (1/10 u10 -8 / 9u9 + C

= 1/36 (1/10 (8 + 3Y4) 10 — 8/9 (8 + 3y4) 9) + С

Ваше секретное оружие в оценке литературы — tl; dr Pharmacy

Посмотрите на него.Так бдительно. Готов в любой момент познакомить вас с деловым концом своего кулака. Думайте об этом маленьком парне всякий раз, когда читаете новое исследование или журнальную статью. Пусть он будет вашей совестью и путеводной звездой.

Абсолютный риск против относительного риска

Пришло время пополнить запас слов. Абсолютный риск — это общий риск возникновения данной «вещи» после суммирования всех факторов риска и смешивающих переменных. Например, вы можете суммировать свой пожизненный риск наличия атеросклеротического события на основе заболеваемости и распространенности вашей демографической группы.

Относительный риск другой. Это риск данной «вещи» по сравнению (т. Е. Относительно) с чем-то еще . Например, ваш риск развития ТГВ у курильщика по сравнению с тем, если вы не курили.

Когда мы говорим о Relative Risk Reduction (RRR) и Absolute Risk Reduction (ARR) , мы говорим о вмешательстве. Мы снижаем на абсолютный и относительный риск, проводя некоторое лечение. Абсолютное снижение риска — это полное снижение риска в результате выбора данного лечения. Это число часто сильно отличается от относительного снижения риска .

С RRR снижение риска по сравнению с некоторой другой группой. Вы можете сравнить эффективность Entresto в снижении смертности от сердечной недостаточности с существующим лечением, таким как эналаприл. Или вы можете сравнить Paxil CR с отсутствием вмешательства (плацебо) для уменьшения симптомов депрессии.

Отлично. Итак, что все это значит для вас как врача?

Вы можете весело провести время с относительным риском…

Например, скажем, я боюсь летать (не из-за COVID, я просто боюсь умереть в авиакатастрофе).Чтобы уменьшить этот страх, я мог больше не летать на самолетах. Это снизит мой относительный риск смерти в авиакатастрофе почти до нуля. Мы бы сравнили относительный риск следующего:

Если бы я решил НЕ летать на самолетах, может быть, мой относительный риск смерти в авиакатастрофе будет где-то около 99,999% (потому что горящий самолет может врезаться в меня, пока я » м занимаюсь дворовой работой что ли). Это ОГРОМНОЕ сокращение и очень привлекательная цифра. Разве вы не хотите снизить риск смерти в авиакатастрофе на 99?99%?

Но вы должны спросить себя… каков базовый риск смерти в авиакатастрофе (даже если вы ДЕЙСТВИТЕЛЬНО летаете на самолетах)? У нас есть доступ к этим данным, и ваш абсолютный риск составляет 0,000009%. Снижение на 99,999% с 1 из 11 миллионов не так уж и важно, не так ли? Можете ли вы представить себе рекламу этого, когда вы просматриваете ленту IG?

«Человек использует этот 1 ПРОСТОЙ УДЕЛКУ, чтобы снизить риск смерти в авиакатастрофе на 0,000009%»

Не очень интересно.Намного менее сексуально, чем 99,99%.

Давайте продолжим с лекарством от сердечной недостаточности Entresto. У вас есть исследование, которое показывает снижение относительного риска сердечно-сосудистой смерти на 19,4% у пациентов с сердечной недостаточностью, принимающих Entresto, по сравнению с эналаприлом. Если вы практиковали несколько лет назад, когда он впервые появился, вы, вероятно, видели новости, в которых смело утверждалось, что Entresto снижает риск смерти на 20% (из-за округления). Если бы вы взглянули на эти исследования и подсчитали абсолютное снижение риска, вы бы обнаружили, что их было 3.2%.

Снижение смертности на 3,2% от такого распространенного заболевания, как сердечная недостаточность, не вызывает чихания (это исследование было фактически остановлено досрочно из-за положительного эффекта, наблюдаемого в группе Entresto). Но вам, вероятно, не нужно, чтобы я говорил вам, что 3,2% намного меньше 20%.

И это то, к чему мы здесь идем с абсолютным риском. Это помогает предоставить вам перспективу к уравнению.

Как рассчитать абсолютное снижение риска

Относительное снижение риска — неплохой парень.Его просто неправильно поняли. В конце концов, RRR и ARR — это просто разные способы измерения размера вмешательства. Это способ помочь вам определить клиническую ценность лекарства. Оба они могут помочь вам решить, будет ли новое лечение X полезным для вашего пациента.

Но есть причина, по которой я пишу эту статью. Как я уже сказал выше, вам обычно нужно рассчитать абсолютное снижение риска, потому что оно вам не сообщается. Относительный риск более привлекателен, и не всегда приводит к феноменальной клинической пользе.Кроме того, в мире медицины «сексуальность» означает «чрезвычайно дорогое удовольствие». Абсолютное снижение риска абсолютно необходимо, если вы хотите провести какой-либо анализ затрат и выгод.

Итак, какова формула абсолютного снижения риска?

Вернемся к нашему исследованию Entresto. И давайте сосредоточимся на уровне смертности от сердечно-сосудистых заболеваний. Вы увидите, что в контрольной группе (эналаприл) 16,5% пациентов умерли от сердечно-сосудистых причин. В экспериментальной группе (Entresto) 13.3% умерли от сердечно-сосудистых причин.

Абсолютное снижение риска — это частота контрольных событий (CER) минус частота экспериментальных событий (EER).

CER — EER = ARR

0,165 — 0,133 = 0,032

Или, как мы упоминали выше, 3,2%. Если вы делаете это с исследованием (или контрольным вопросом), которое не дает вам процентов, вам придется вручную вычислить их на основе исследования. Таким образом, если у 800 пациентов в контрольной группе из 1000 человек произошло событие, ваш CER составляет 80% (или 0.80).

Формула снижения относительного риска там также довольно проста :

(CER — EER) / CER = RRR

(0,165 — 0,133) / 0,165 = 0,1939

Или (также как мы упоминали выше), 19,4%.

Вы заметите, что мы переводим проценты в их десятичную форму для выполнения этих вычислений. Это лучший метод, который предотвратит появление ошибок с десятичной запятой. Также необходимо работать в десятичной форме, чтобы вычислить число , необходимое для обработки (NNT ).

Ни одно обсуждение абсолютного снижения риска не будет полным без упоминания количества, необходимого для лечения. NNT — это просто еще один способ выражения ARR. Число, необходимое для лечения, — это количество пациентов, которых вы должны лечить, чтобы предотвратить одно «событие». Событием в этом случае будет смерть от сердечно-сосудистой системы от сердечной недостаточности.

NNT — это величина, обратная ARR.

1 / ARR = NNT

Используя наши числа Entresto …

1 / 0,032 = 31.25

В этом случае NNT будет 32. Почему 32? Потому что число, необходимое для лечения, всегда целое число (целое число). Нельзя лечить 0,25 человека. Поэтому, когда ваше число, которое нужно обработать, заканчивается десятичной точкой, округлите до следующего целого числа.

Чтобы применить это «в реальном выражении», вам нужно дать Entresto 32 пациентам, прежде чем вы предотвратите одну сердечно-сосудистую смерть.

Как использовать абсолютное снижение риска для принятия клинических решений

Вы должны использовать ARR, NNT и даже RRR, чтобы определить, стоит ли вмешательство того, что вам нужно для вашего пациента.Как вы видели здесь, вы можете очень легко рассчитать ARR и NNT. Вы будете использовать эту информацию в дополнение к критериям, которые вы уже используете при оценке. Когда вы взвешиваете варианты лечения для пациентов, рассчитывайте ARR для нескольких различных вариантов. Посмотрите, сколько будет стоить препарат пациенту. Посмотрите на график дозирования и определите, не будет ли проблем с его соблюдением. Посмотрите на лекарственные взаимодействия и любые другие важные моменты для каждого отдельного препарата в классе.

Затем вы можете передать эту информацию пациенту и медицинской бригаде и сделать совместный выбор , который лучше всего подходит для пациента .Когда все вовлечены (особенно пациент), все выигрывают.

И снова вам понадобится вся эта информация для экзаменов NAPLEX и BPS. Так что, если быть отличным клиницистом для вас недостаточно, позвольте необходимости повлиять на ваше решение, чтобы вам было как можно комфортнее.

В заключение. Когда сомневаешься. Только подумайте, что бы сделал Пират ARR (и его осуждающий взгляд).

Учебная лаборатория PChem | Теория групп

Учебная лаборатория PChem | Теория групп

ВЕБ-РУКОВОДСТВО — Теория групп

The Reduction Forumla

Каждая часть важна и будет иметь значение для ввода:


ВАЖНЫЕ ЗАМЕЧАНИЯ:

Формула редукции ВСЕГДА дает либо 0, либо положительное целое число.Если это не тот случай, когда вы выполняете расчет, вы где-то ошиблись. Часто это арифметическая ошибка или неправильно рассчитанное значение рэнд.

Пример формулы сокращения в действии: Для C 2v строка таблицы символов A 1

C 2v E C 2 (z) v (xz) v (yz) Функции линейного поворота

функции поворота


 Cubic
функции
A 1 +1 +1 +1 +1 z x 2 , y 2 , z 4 2 95011453 3 , x 2 z, y 2 z
A 2 +1 +1-1-1 R z 50 x xyz
B 1 +1 -1 +1-1 x, R y xz xz 2 , x 3 2
B 2 +1-1-1 +1 y, R x yz yz 2 , y 3 , x 2 y
Количество элементов симметрии, h = 4
Где h = 4 и R Значения (для количества неизмененных связей при выполнении элемента симметрии) равны 2, 0, 2, 0.

Применить к строке A 1 :
Цифры в круглых скобках означают ( N x R x I )
1/4 [(1 x 2 x 1) + (1 x 0 x 1) + (1 x 2 x 1) + (1 x 0 x 1)] = 1/4 x (4) = 1

Формулы двойного угла, полуугла и редукции — алгебра и тригонометрия

Цели обучения

В этом разделе вы:

  • Используйте формулы двойного угла, чтобы найти точные значения.
  • Используйте формулы двойного угла для проверки идентичности.
  • Используйте формулы сокращения, чтобы упростить выражение.
  • Используйте формулы половинного угла, чтобы найти точные значения.
Рис. 1. Велосипедные пандусы для опытных гонщиков имеют более крутой уклон, чем те, что предназначены для новичков.

Велосипедные пандусы, изготовленные для соревнований (см. (Рисунок)), должны различаться по высоте в зависимости от уровня навыков участников. Для опытных спортсменов угол между рампой и землей должен быть таким, чтобы для новичков угол делился пополам.Какая крутизна ската для новичков? В этом разделе мы исследуем три дополнительные категории идентичностей, которые мы можем использовать, чтобы ответить на такие вопросы, как этот.

Использование формул двойного угла для поиска точных значений

В предыдущем разделе мы использовали формулы сложения и вычитания для тригонометрических функций. Теперь мы еще раз посмотрим на те же формулы. Формулы двойного угла являются частным случаем формул суммы, где получение формулы двойного угла для синуса начинается с формулы суммы,

Если дать, то у нас будет

Получение двойного угла для косинуса дает нам три варианта.Во-первых, исходя из формулы суммы и имея

Используя свойства Пифагора, мы можем расширить эту формулу двойного угла для косинуса и получить еще два варианта. Первый вариант:

Вторая вариация:

Аналогичным образом, чтобы вывести формулу двойного угла для касательной, замена в формуле суммы дает

Формулы двойного угла

Формулы двойного угла резюмируются следующим образом:

Как к

Зная тангенс угла и квадрант, в котором он расположен, используйте формулы двойного угла, чтобы найти точное значение.

  1. Нарисуйте треугольник, чтобы отразить данную информацию.
  2. Определите правильную формулу двойного угла.
  3. Подставить значения в формулу, основанную на треугольнике.
  4. Упростить.
[show-answer q = ”fs-id1418852 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1418852 ″]

Если мы нарисуем треугольник, чтобы отразить данную информацию, мы сможем найти значения, необходимые для решения проблем на изображении. Нам дано такое, что находится во втором квадранте.Тангенс угла равен противоположной стороне по соседней стороне, и, поскольку он находится во втором квадранте, соседняя сторона находится на оси x и является отрицательной. Используйте теорему Пифагора, чтобы найти длину гипотенузы:

Теперь мы можем нарисовать треугольник, подобный показанному на (Рисунок).

Рисунок 2.
  1. Начнем с написания формулы двойного угла для синуса.

    Мы видим, что нам нужно найти, и на основе (рисунок) мы видим, что гипотенуза равна 5, поэтому подставляем эти значения в уравнение и упрощаем.

    Таким образом,

  2. Напишите формулу двойного угла для косинуса.

    Снова подставьте значения синуса и косинуса в уравнение и упростите.

  3. Напишите формулу двойного угла для касательной.

    В этой формуле нам нужен тангенс, который мы получили в виде Подставляем это значение в уравнение и упрощаем.

    [/ скрытый-ответ]

Попробуй

В квадранте I найти

[show-answer q = ”fs-id1338288 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1338288 ″]

[/ hidden-answer]

Использование формулы двойного угла для косинуса без точных значений

Используйте формулу двойного угла для косинуса, чтобы записать в единицах

[show-answer q = ”1928247 ″] Показать решение [/ show-answer] [hidden-answer a =” 1928247 ″]

[/ скрытый-ответ]
Анализ

Этот пример показывает, что мы можем использовать формулу двойного угла, не имея точных значений.Он подчеркивает, что образец — это то, что нам нужно запомнить, и что идентичности верны для всех значений в области определения тригонометрической функции.

Использование формул двойного угла для проверки личности

Установление тождеств с использованием формул двойного угла выполняется с использованием тех же шагов, которые мы использовали для вывода формул суммы и разности. Выберите более сложную часть уравнения и переписывайте ее, пока она не совпадет с другой стороной.

Попробуй

Подтвердите личность:

[show-answer q = ”fs-id1313281 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1313281 ″]

[/ hidden-answer]

Проверка идентичности двойного угла по касательной

Подтвердите личность:

[show-answer q = ”fs-id1333908 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1333908 ″]

В этом случае мы будем работать с левой частью уравнения и упрощать или переписывать, пока она не станет правой частью уравнения.

[/ скрытый-ответ]
Анализ

Вот случай, когда более сложная часть исходного уравнения появилась справа, но мы решили работать с левой стороной. Однако, если бы мы выбрали левую сторону для переписывания, мы бы работали в обратном направлении, чтобы прийти к эквивалентности. Например, предположим, что мы хотим показать

Давайте поработаем над правой стороной.

При использовании тождеств для упрощения тригонометрического выражения или решения тригонометрического уравнения обычно существует несколько путей к желаемому результату.Не существует установленного правила относительно того, какой стороной следует манипулировать. Однако начать следует с изложенных ранее рекомендаций.

Попробуй

Подтвердите личность:

[show-answer q = ”fs-id2243554 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id2243554 ″]

[/ hidden-answer]

Использование формул полуугла для нахождения точных значений

Следующий набор тождеств — это набор формул половинного угла, который можно вывести из формул редукции и использовать, когда у нас есть угол, который составляет половину размера особого угла.Если мы заменим формулу половинного угла, синус будет найден путем упрощения уравнения и решения для Обратите внимание, что формулам половинного угла предшествует asign. Это не означает, что допустимы как положительные, так и отрицательные выражения. Скорее, это зависит от квадранта, в котором заканчивается.

Формула половинного угла для синуса выводится следующим образом:

Чтобы вывести формулу половинного угла для косинуса, мы имеем

Для касательной идентичности имеем

Формулы полуугловых

Формулы полуугла следующие:

Использование формулы полуугла для нахождения точного значения синусоидальной функции

Найти с помощью формулы половинного угла.

[show-answer q = ”fs-id2281042 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id2281042 ″]

Так как мы используем формулу половинного угла для синуса:

Помните, что мы можем проверить ответ с помощью графического калькулятора.

[/ hidden-answer]

Анализ

Обратите внимание, что мы использовали только положительный корень, потому что он положительный.

Как к

Зная тангенс угла и квадрант, в котором находится угол, найдите точные значения тригонометрических функций половины угла.

  1. Нарисуйте треугольник для представления данной информации.
  2. Определите правильную формулу полуугла.
  3. Подставить значения в формулу, основанную на треугольнике.
  4. Упростить.
[show-answer q = ”fs-id1631214 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1631214 ″]

Используя данную информацию, мы можем нарисовать треугольник, показанный на (Рисунок). Используя теорему Пифагора, мы находим, что гипотенуза равна 17. Следовательно, мы можем вычислить и

. Рисунок 3.
  1. Прежде чем мы начнем, мы должны помнить, что if находится в квадранте III, следовательно, это означает, что конечная сторона находится в квадранте II, так как

    Чтобы найти, мы начнем с написания формулы половинного угла для синуса. Затем мы подставляем значение косинуса, которое мы нашли из треугольника на (Рисунок), и упрощаем.

    Мы выбираем положительное значение, потому что угол заканчивается в квадранте II, а синус положительный в квадранте II.

  2. Чтобы найти, мы напишем формулу половинного угла для косинуса, подставим значение косинуса, которое мы нашли из треугольника на (Рисунок), и упростим.

    Мы выбираем отрицательное значение, потому что угол находится в квадранте II, потому что косинус отрицательный в квадранте II.

  3. Чтобы найти, запишем формулу половинного угла для тангенса. Опять же, мы подставляем значение косинуса, которое мы нашли из треугольника на (Рисунок), и упрощаем.

    Мы выбираем отрицательное значение причин в квадранте II, а тангенс отрицательное во втором квадранте. [/ Hidden-answer]

Попробуй

Учитывая, что находится в квадранте IV, найдите точное значение

. [show-answer q = ”fs-id1762529 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1762529 ″]

[/ hidden-answer]

Ключевые понятия

  • Двойные угловые тождества выводятся из формул суммы основных тригонометрических функций: синуса, косинуса и тангенса.См. (Рисунок), (Рисунок), (Рисунок) и (Рисунок).
  • Формулы приведения особенно полезны в исчислении, поскольку они позволяют уменьшить степень тригонометрического члена. См. (Рисунок) и (Рисунок).
  • Формулы полууглов позволяют нам найти значение тригонометрических функций, включающих полууглы, независимо от того, известен ли исходный угол или нет. См. (Рисунок), (Рисунок) и (Рисунок).

Упражнения по разделам

Алгебраические

Для следующих упражнений найдите точные значения а) б) и в), не решая для

.

Ифандис в квадранте I.

Ифандис в квадранте IV.

Для следующих упражнений найдите значения шести тригонометрических функций, если указанные условия выполнены.

и

[show-answer q = ”fs-id2056415 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id2056415 ″]

[/ hidden-answer]

и

Упростите следующие упражнения до одного тригонометрического выражения.

[show-answer q = ”fs-id1575788 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1575788 ″]

[/ hidden-answer]

Для следующих упражнений найдите точное значение, используя формулы половинного угла.

[show-answer q = ”fs-id1267577 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1267577 ″]

[/ hidden-answer]

[show-answer q = ”fs-id2786199 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id2786199 ″]

[/ hidden-answer]

[show-answer q = ”fs-id1541638 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1541638 ″]

[/ hidden-answer]

[show-answer q = ”fs-id2564655 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id2564655 ″]

[/ hidden-answer]

Для следующих упражнений найдите точные значения a) b) и c), не решая, когда

Ифандис в квадранте IV.

Ифандис в квадранте II.

Для следующих упражнений используйте (Рисунок), чтобы найти требуемые половинные и двойные углы.

Рисунок 5.

Findand

Findand

[show-answer q = ”fs-id1475703 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1475703 ″]

[/ hidden-answer]

Findand

Findand

[show-answer q = ”fs-id1740867 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1740867 ″]

[/ hidden-answer]

Для следующих упражнений упростите каждое выражение.Не оценивайте.

[show-answer q = ”fs-id1615373 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1615373 ″]

[/ hidden-answer]

[show-answer q = ”fs-id1615567 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1615567 ″]

[/ hidden-answer]

[show-answer q = ”fs-id2

2 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id2

2 ″]

[/ hidden-answer]

Подтвердите свою личность в следующих упражнениях.

[show-answer q = ”fs-id2038543 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id2038543 ″]

[/ hidden-answer]

[show-answer q = ”fs-id2259858 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id2259858 ″]

[/ hidden-answer]

Для следующих упражнений перепишите выражение с показателем не выше 1.

[show-answer q = ”fs-id2296538 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id2296538 ″]

[/ hidden-answer]

[show-answer q = ”fs-id2430151 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id2430151 ″]

[/ hidden-answer]

[show-answer q = ”fs-id505042 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id505042 ″]

[/ hidden-answer]

Технологии

Для следующих упражнений сократите уравнения до степени единицы, а затем проверьте ответ графически.

[show-answer q = ”fs-id1154392 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1154392 ″]

[/ hidden-answer]

[show-answer q = ”fs-id2896955 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id2896955 ″]

[/ hidden-answer]

[show-answer q = ”fs-id1899789 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1899789 ″]

[/ hidden-answer]

[show-answer q = ”fs-id2186001 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id2186001 ″]

[/ hidden-answer]

Для следующих упражнений алгебраически найдите эквивалентную функцию, только в терминах и / или, а затем проверьте ответ, построив графики обеих функций.

[show-answer q = ”fs-id1643964 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1643964 ″]

[/ hidden-answer]

Расширения

Для следующих упражнений подтвердите личность.

[show-answer q = ”fs-id2749007 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id2749007 ″]

[/ hidden-answer]

[show-answer q = ”fs-id17

″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id17

″]

[/ hidden-answer]

[show-answer q = ”fs-id2569931 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id2569931 ″]

[/ hidden-answer]

[show-answer q = ”fs-id1506519 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1506519 ″]

[/ hidden-answer]

[show-answer q = ”fs-id2141257 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id2141257 ″]

[/ hidden-answer]

Глоссарий

формулы двойного угла
тождеств, полученных из формул суммы для синуса, косинуса и тангенса, в которых углы равны
формулы половинного угла
тождеств, полученных из формул приведения и используемых для определения значений половинного угла тригонометрических функций
формулы восстановления
тождеств, полученных из формул двойного угла и используемых для уменьшения мощности тригонометрической функции
.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *

Формула сокращение: Формулы сокращенного умножения

alexxlab / / Разное

Дроби. Формулы сокращенного умножения

Факт 1.
\(\bullet\) Множество натуральных чисел \(\mathbb{N}\) – это числа \(1, \ 2, \ 3, \ 4 \ \) и т.д.
\(\bullet\) Множество целых чисел \(\mathbb{Z}\) состоит из натуральных чисел, противоположных им (\(-1, \ -2, \ -3 \) и т.д.) и нуля \(0\).
\(\bullet\) Рациональные числа \(\mathbb{Q}\) – числа вида \(\dfrac ab\), где \(a\in \mathbb{Z}\), \(b\in \mathbb{N}\).   Таким образом, существует включение: \(\mathbb{N}\) содержится в \(\mathbb{Z}\), а \(\mathbb{Z}\) содержится в \(\mathbb{Q}\).  

Факт 2.
\(\bullet\) Правила сложения дробей: \[\begin{aligned} &\dfrac ab+\dfrac cb=\dfrac{a+c}b\\[2ex] &\dfrac ab+\dfrac cd=\dfrac{ad+bc}{bd}\end{aligned}\] Пример: \(\dfrac {31}6+\dfrac {67}6=\dfrac{31+67}6=\dfrac{98}6\)   \(\bullet\) Правила умножения дробей: \[\dfrac ab\cdot \dfrac cd=\dfrac{ac}{bd}\] Пример: \(\dfrac 47\cdot \dfrac{14}5=\dfrac{4\cdot 14}{7\cdot 5}\)   \(\bullet\) Правила деления дробей: \[\dfrac ab: \dfrac cd=\dfrac ab\cdot \dfrac dc\] Пример: \(\dfrac 45 :\dfrac 67=\dfrac 45\cdot \dfrac 76\)  

Факт 2.
\(\bullet\) Сокращение дробей – деление числителя и знаменателя на одно и то же число, отличное от нуля.
Пример:   \(\begin{aligned} &\dfrac{98}6=\dfrac{49\cdot 2\llap{/}}{3\cdot 2\llap{/}}=\dfrac{49}3\\[2ex] &\dfrac{4\cdot 14}{7\cdot 5}=\dfrac{4\cdot 2\cdot 7\llap{/}}{7\llap{/}\cdot 5}=\dfrac 85\\[2ex] &\dfrac{4\cdot 7}{5\cdot 6}=\dfrac {2\llap{/}\cdot 2\cdot 7}{5\cdot 3\cdot 2\llap{/}}=\dfrac{14}{15}\end{aligned}\)   \(\bullet\) Если \(\dfrac ab\) – несократимая дробь, то ее можно представить в виде конечной десятичной дроби тогда и только тогда, когда знаменатель \(b\) делится только на числа \(2\) и \(5\).
Пример: дробь \(\dfrac2{65}\) нельзя представить в виде конечной десятичной дроби, так как \(65=5\cdot 13\), то есть \(\dfrac2{65}=0,0307…\)
дробь \(\dfrac3{160}\) можно представить в виде конечной десятичной дроби, так как \(160=2^5\cdot 5\), то есть \(\dfrac3{160}=0,01875\).  

Факт 3.
\(\bullet\) Формулы сокращенного умножения:
\(\blacktriangleright\) Квадрат суммы и квадрат разности: \[(a+b)^2=a^2+2ab+b^2\] \[(a-b)^2=a^2-2ab+b^2\]

\(\blacktriangleright\) Куб суммы и куб разности: \[(a+b)^3=a^3+3a^2b+3ab^2+b^3\quad {\small{\text{или}}}\quad (a+b)^3=a^3+b^3+3ab(a+b)\] \[(a-b)^3=a^3-3a^2b+3ab^2-b^3\quad {\small{\text{или}}}\quad (a-b)^3=a^3-b^3-3ab(a-b)\]

Заметим, что применение данных формул справа налево часто помогает упростить вычисления:
\(13^3+3\cdot 13^2\cdot 7+3\cdot 13\cdot 49+7^3=(13+7)^3=20^3=8000\)

 

\(\blacktriangleright\) Разность квадратов: \[a^2-b^2=(a-b)(a+b)\]

\(\blacktriangleright\) Сумма кубов и разность кубов: \[a^3+b^3=(a+b)(a^2-ab+b^2)\] \[a^3-b^3=(a-b)(a^2+ab+b^2)\]

Заметим, что не существует формулы суммы квадратов \(a^2+b^2\).
Заметим, что применение данных формул слева направо часто помогает упростить вычисления:

 

\(\dfrac{7^6-2^6}{7^4+14^2+16}= \dfrac{(7^2-2^2)(7^4+7^2\cdot2^2+2^4)} {7^4+(7\cdot2)^2+2^4}=7^2-2^2=45\)  

Факт 4.
\(\bullet\) Квадрат суммы нескольких слагаемых равен сумме квадратов этих слагаемых и удвоенных попарных произведений: \[\begin{aligned} &(a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc\\[2ex] &(a+b+c+d)^2=a^2+b^2+c^2+d^2+2ab+2ac+2ad+2bc+2bd+2cd\\[2ex] &{\small{\text{и т.д.}}}\end{aligned}\]

Формулы сокращённого умножения. Неполный квадрат суммы и разности

При выполнении преобразований разных выражений часто встречаются некоторые частные случаи умножения. Равенства, выражающие эти случаи, называются формулами сокращённого умножения.

Формулы сокращённого умножения — это выражения, в которых пропущены промежуточные вычисления, поэтому их и называют сокращёнными.

a2 + b2 = (a + b)2 — 2ab  —  сумма квадратов;

a2 — b2 = (a + b)(a — b)  —  разность квадратов;

(a + b)2 = a2 + 2ab + b2  —  квадрат суммы;

(a — b)2 = a2 — 2ab + b2  —  квадрат разности;

a3 + b3 = (a + b)(a2 — ab + b2)  —  сумма кубов;

a3 — b3 = (a — b)(a2 + ab + b2)  —  разность кубов;

(a + b)3 = a3 + 3a2b + 3ab2 + b3  —  куб суммы;

(a — b)3 = a3 — 3a2b + 3ab2 — b3  —  куб разности.

Обратите внимание, что  a  и  b  в формулах сокращённого умножения могут быть как числами, так и выражениями.

Разложение формул сокращенного умножения

Рассмотрим каждую формулу подробнее и приведём доказательство верности формул сокращённого умножения.

Сумма квадратов двух чисел равна разности квадрата суммы этих чисел и их удвоенного произведения:

a2 + b2 = (a + b)2 — 2ab.

Доказательство: выполним преобразование правой части формулы, приведём подобные члены и получим левую часть формулы:

(a + b)2 — 2ab = (a + b)(a + b) — 2ab = a2 + ab + ab + b2 — 2ab = a2 + b2.

Разность квадратов двух чисел равна произведению суммы этих чисел на их разность:

a2 — b2 = (a + b)(a — b).

Доказательство: выполним умножение многочленов из правой части формулы, приведём подобные члены и получим левую часть формулы:

(a + b)(a — b) = a2 — ab + ab — b2 = a2 — b2.

Квадрат суммы двух чисел равен сумме квадрата первого числа, удвоенного произведения первого числа на второе и квадрата второго числа:

(a + b)2 = a2 + 2ab + b2.

Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:

(a + b)2 = (a + b)(a + b) = a2 + ab + ab + b2 = a2 + 2ab + b2.

Квадрат разности двух чисел равен квадрату первого числа, минус удвоенное произведение первого числа на второе, плюс квадрат второго числа:

(

a — b)2 = a2 — 2ab + b2.

Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:

(a — b)2 = (a — b)(a — b) = a2 — ab — ab + b2 = a2 — 2ab + b2.

Сумма кубов двух чисел равна произведению суммы первого и второго числа на неполных квадрат разности этих чисел:

a3 + b3 = (a + b)(a2 — ab + b2).

Доказательство: выполним умножение многочленов из правой части формулы, приведём подобные члены и получим левую часть формулы:

(a + b)(a2 — ab + b2) = a3 — a2b + ab

2 + a2b — ab2 + b3 = a3 + b3.

Разность кубов двух чисел равна произведению разности первого и второго числа на неполный квадрат суммы этих чисел:

a3 — b3 = (a — b)(a2 + ab + b2).

Доказательство: выполним умножение многочленов из правой части формулы, приведём подобные члены и получим левую часть формулы:

(a — b)(a2 + ab + b2) = a3 + a2b + ab2 — a2b — ab2 — b3 = a3 — b3.

Куб суммы двух чисел равен сумме четырёх слагаемых: куб первого числа, утроенное произведение квадрата первого числа на второе число, утроенное произведение первого числа на квадрат второго и куб второго числа:

(a + b)3 = a3 + 3a2b + 3ab2 + b3.

Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:

(a + b)3 = (a + b)(a + b)2 = (a + b)(a2 + 2ab + b2) = a3 + 2a2b + ab2 + a2b + 2ab2 + b3 = a3 + 3a2b + 3ab2 + b3.

Куб разности двух чисел равен кубу первого числа, минус утроенное произведение квадрата первого числа на второе число, плюс утроенное произведение первого числа на квадрат второго, минус куб второго числа:

(a — b)3 = a3 — 3a2b + 3ab2 — b3.

Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:

(a — b)3 = (a — b)(a — b)2 = (a — b)(a2 — 2ab + b2) = a3 — 2a2b + ab2 — a2b + 2ab2 — b3 = a3 — 3a2b + 3ab2 — b3.


Неполный квадрат суммы

Выражение:

a2 + 2ab + b2

это квадрат суммы, которое также называется полным квадратом суммы, относительно выражения:

a2 + ab + b2,

которое называется неполным квадратом суммы. Неполный квадрат суммы — это сумма квадратов двух чисел и их произведения. Неполный квадрат суммы отличается от полного только произведением чисел, которое не удваивается.

Неполный квадрат разности

Выражение:

a2 — 2ab + b2

это квадрат разности, который также называется полным квадратом разности относительно выражения:

a2 — ab + b2,

которое называется неполным квадратом разности. Неполный квадрат разности двух чисел равен квадрату первого числа, минус произведение первого числа на второе, плюс квадрат второго числа. Неполный квадрат разности отличается от полного только произведением чисел, которое не удваивается.

Формулы сокращенного умножения. Разложение на множители. 🐲 СПАДИЛО.РУ

Очень часто нам встречаются выражения, которые требуют различных преобразований. Для того, чтобы это  короче выполнять в некоторых случаях, существуют специальные формулы сокращенного умножения.

Квадрат суммы и квадрат разности

Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений плюс квадрат второго выражения:

(a+b)2=a2+2ab+b2

Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений плюс квадрат второго выражения:

(a–b)2=a2–2ab+b2

Если сравнить два этих правила и формулы, то видно, что при возведении в квадрат есть отличие в знаках только перед удвоенным произведением. Рассмотрим применение данных формул на примерах.

Пример №1. Преобразуем выражение в многочлен: (с+8)2. По правилу выполняем последовательно: квадрат первого выражения это с2; удвоенное произведение первого и второго выражения – это 2с8; квадрат второго выражения – это 82. Выполним запись: (с+8)2=с2+2с8+82. Теперь выполним умножение и возведение в степень чисел: (с+8)2=с2+2с8+82=с2+16с+64. Получим многочлен. Промежуточные действия, выделенные жирным шрифтом, можно не записывать, а выполнять их устно.

Пример №2. Представим в виде многочлена выражение (2х–11)2. Выполним возведение в квадрат по правилу квадрата разности двух выражений: (2х–11)2=(2х)2–2•2х•11+112=4х2–44х+121.

Пример №3. Представим в виде многочлена квадрат двучлена (–9х+4у)2

. В данном выражении на первом месте стоит отрицательное число, на втором положительное, что не привычно для нас по работе с формулой. Но мы знаем, что можно просто поменять слагаемые местами, тогда получится разность двух выражений, которую возводим в квадрат по соответствующей формуле:  (–9х+4у)2=(4у–9х)2=16у2–72ху+81х2.

Пример №4. Представим в виде многочлена выражение (–6с–10)2. Данное выражение содержит два слагаемых с минусом. Надо просто запомнить, что оно будет равносильно выражению (6с+10)2, потому что квадраты противоположных чисел равны (а2=(–а)2) . Возведем данное выражение в квадрат по формуле квадрата суммы двух выражений: (–6с–10)2=(6с+10)2=36с2+120с+100.

Куб суммы и разности

Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения и второго плюс утроенное произведение первого выражения и квадрата второго плюс куб второго выражения:

(a+b)3=a3+3a2b+3ab2+b3

Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения и второго плюс утроенное произведение первого выражения и квадрата второго минус куб второго выражения:

(a–b)3=a3–3a2b+3ab2–b3

Используя данные формулы, можно возводить в куб сумму и разность двух выражений. В данном случае не нужно выполнять промежуточные действия устно, чтобы избежать ошибок.

Пример №5. Возведем в куб сумму с+5а. Всё выполним и распишем строго по формуле:

(с+5а)3=с3+3с2 •5а+3с(5а)2+(5а)3=с3+15ас2+75а2с+125а3.

Пример №6. Возведем в куб разность:

(х–10)3=х3–3х210+3х102–103=х3–30х2+300х–1000.

Разность квадратов

Произведение разности двух выражений и их суммы равно разности квадратов этих выражений:

a2–b2=(a–b)(a+b)

Пример №7. Выполним умножение: (4–с)(4+с)=42–с2=16–с2 в данном выражении выполнили всё в соответствии с формулой: возвели в квадрат 4 и число с. Промежуточные записи (выделены жирным шрифтом) можно не делать, а выполнять их устно.

Пример №8.  Упростим выражение: (5с+а)(5с–а)=25с2–а2 в данном выражении мы видим, что первый множитель сумма, а второй – разность. Для выполнения задания по данной формуле это не имеет значения, так как мы знаем, что от перестановки множителей произведение не изменяется.

Применение формул сокращенного умножения для разложения многочленов на множители

Рассмотрим тождество, которое называют разностью квадратов двух выражений:

a2–b2=(a–b)(a+b)

Разность квадратов двух выражений равна произведению разности этих выражений и их суммы. Эту формулу применяют для разложения на множители многочлена, содержащего разность квадратов. Рассмотрим на примерах.

Пример №9. Разложить на множители многочлен 100–с2. Из условия видно, что число 100 – это квадрат числа 10,  следовательно, 100–с2=102–с2, значит можно разложить на множители по формуле: 100–с2=102–с2=(10–с)(10+с). Выделенное жирным шрифтом выражение можно не записывать, а выполнять устно.

Пример №10. Разложить на множители: х2у2–81=(ху–9)(ху+9). В данном выражении выполнено всё в соответствии с формулой, промежуточные записи не использованы.

Пример №11. Представим в виде произведения: х4–36=(х2–6)(х2+6). В данном выражении мы видим, что степень переменной может быть не только вторая, но и любая четная, чтобы ее можно было представить в виде квадрата переменной.

Пример №12. Представим в виде произведения х10с6–25=(х5с3–5)(х5с3+5). Здесь показаны разные четные степени переменных.

 Для разложения на множители суммы и разности кубов существуют определенные правила и формулы.

Сумма и разность кубов

Сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности:

a3+b3=(a+b)(a2–ab+b2)

Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы:

a3–b3=(a–b)(a2+ab+b2)

Пример №13. Разложим на множители многочлен 8+с3. В данном случае мы видим число 8, которое нужно представить в виде куба числа, это будет 23. Значит, 8+с3=23+с3. Далее распишем по формуле суммы кубов: 8+с3=23+с3=(2+с)(4–2с+с2).

Пример №14. Запишем в виде произведения разность х3–а12. В этом выражении есть степень, отличная от третьей, поэтому представим а12 в виде куба числа (а4)3. Получим: х3–а12=х3–(а4)3. Разложим на множители по формуле разности кубов: х3–а12=х3–(а4)3=(х–а4)(х2+ха4+а8).

Разложение многочлена формулой квадрата суммы и разности

Формулы квадрата суммы и квадрата разности также используют для разложения многочлена на множители. Для этого формулы записываются в обратном порядке, то есть меняются левая и правая части местами:

a2+2ab+b2=(a+b)2

a2–2ab+b2=(a–b)2

Пример №15. Преобразовать трехчлен 4х2+12х+9 в квадрат двучлена. Для этого определим, где здесь числа, которые можно представить в виде квадрата, это будут 4х2 и 9, так как 4х2=(2х)2, а 9=32. Соответственно проверим, является ли 12х удвоенным произведением чисел 2х и 3: 22х3=12х. Выполняем запись: 4х2+12х+9=(2х)2+2•2х•3+32=(2х+3)2. Обычно промежуточное действие (выделено жирным) не записывается, квадраты чисел определяются устно.

Пример №16. Разложить на множители многочлен –16с+с2+ Определяем, где здесь квадраты чисел – это с2 и 64=82. Слагаемое –16с не может быть квадратом числа, так как оно отрицательное и степень числа с первая, поэтому –16с это удвоенное произведение чисел с и 8. Выполняем разложение на множители: –16с+с2+64=(с–8)2. Обратим внимание на тот момент, что числа с и 8 можно записывать наоборот в ответе, так как квадраты противоположных чисел равны, то есть –16с+с2+64=(8–с)2

P.S. Все формулы на одной картинке:

Формулы сокращённого умножения | Александр Будников

        Формулы сокращённого умножения необходимы во всех разделах математики. От элементарной до высшей. Они применяются практически везде – в упрощении выражений, решении уравнений и неравенств, сокращении дробей, вычислении пределов, решении интегралов – список можно продолжать ещё долго…

        Следовательно, нужно основательно разобраться с этими формулами. Понять, откуда они берутся, зачем они нужны, как их применять на практике и, самое главное, как их запомнить. А запомнить всё-таки придётся, да…

        Поехали?

 

Квадрат суммы, квадрат разности, разность квадратов, куб суммы, куб разности, сумма кубов, разность кубов – что за звери?

 

        Итак, вот они, формулы сокращённого умножения:

        Эти семь формул – полный джентльменский набор. Последние две формулы (сумма и разность кубов) записаны не так как в большинстве учебников, а наоборот – справа налево. Это не просто так.) Любая формула в математике работает в обоих направлениях – как туда, так и обратно. Именно такая запись наиболее наглядно показывает, откуда берутся формулы сокращённого умножения.

        Они берутся из… умножения. Вот ведь удивил, да?) Что ж, смотрите сами. Берём, например, самую первую формулу по списку:

        (a+b)2 = (a+b)(a+b) = a2+ab+ba+b2 = a2+2ab+b2

        Вот и все дела. Самое обычное перемножение скобок и приведение подобных. Именно так и получаются все формулы сокращённого умножения. Сокращённое умножение – потому, что в самих формулах нет раскрытия скобок и приведения подобных. Эти промежуточные действия сокращены. Сразу дан готовый результат. Пользуйтесь на здоровье!

        Эти формулы надо знать наизусть. Без знания первых трёх формул, с квадратами, даже не мечтайте о тройке! Без всех остальных (с кубами) – о четвёрке и выше. Нет-нет, бросаться зубрить весь этот список прямо сейчас мы не будем.) Об этом позже. Пока просто знакомимся.)

 

Зачем нужны формулы сокращённого умножения?

        Полезная вещь первая – самая очевидная. Это быстрое (т.е. сокращённое) умножение многих алгебраических выражений без промежуточных выкладок. Меньше выкладок – меньше и ошибок. Но это не самая главная полезная вещь! А вот вторая.

        Дело в том, что вся математика строится на преобразованиях выражений. Вся! От школьной до высшей. Сообразил, что, где и как преобразовать и упростить – решил пример. Не сообразил – увы, не решил. Есть, допустим, выражение (a—b)(a+b). Как его можно преобразовать? Да просто тупо перемножить скобки и привести подобные. Не вопрос.) А вот что делать с a2–b2? Чему это равняется? Попробуй, догадайся! Только знания и спасают, да…

        Сравним два равенства:

        (a—b)(a+b) = a2–b2

        и

        a2–b2 = (a—b)(a+b)

        Для математики эти два равенства абсолютно одинаковы. А вот для нас с вами – не совсем. Возьмём первую запись, слева направо:

        (a—b)(a+b) = a2–b2

        Это самое обычное умножение скобок, не более того. Никаких принципиально новых возможностей. А теперь возьмём второй вариант того же равенства, справа налево:

        a2–b2 = (a—b)(a+b)

        А вот такая запись резко повышает уровень вашей математической культуры! Почему? Потому, что такая запись формулы, справа налево, – это разложение на множители! А разложение на множители – процедура поважнее простого умножения, да…) Сомневаетесь? Не надо. В соответствующей теме подробно расскажу.)

        И такое разложение на множители имеет место быть во всех формулах сокращённого умножения! Почему? Давайте внимательно посмотрим на наш список. В левой части каждой формулы мы увидим перемножение скобок:

        (a+b)2 = (a+b)(a+b) =…

        (a-b)2 = (a-b)(a-b) = …

        (a-b)(a+b) = …

        (a+b)3 = (a+b)(a+b)(a+b) =…

        и т.д.

        Стало быть, левая часть каждой формулы разложена на множители, а вот правая часть – нет. Список, что приведён выше, – это, действительно, всего лишь сокращённое умножение. Но! Стоит только поменять местами левую и правую части каждой из формул, как тот же самый список становится формулами разложения на множители!

        Для полного понимания перепишу этот список ещё разок, но справа налево. Вот так:

        Такая обратная запись формул сокращённого умножения идеально подходит для разложения на множители многочленов, для сокращения алгебраических дробей и для решения самых разнообразных примеров. Но есть существенная проблема. Как их запомнить?

 

Запоминаем формулы сокращённого умножения! Секретные приёмы…

        Начинаем с самого простого – запоминаем названия формул. Это совсем легко. Смотрим в таблицу и видим выражение (a+b)2. Или квадрат скобок. А в скобках что? Правильно, сумма! Стало быть, выражение (a+b)2 называется квадрат суммы. Аналогично, (a—b)2 называется квадрат разности. Элементарно, Ватсон!

        С выражениями (a+b)3 и (a—b)3 всё то же самое – куб суммы и куб разности соответственно.

        А как назвать a2–b2?  «Одно выражение в квадрате минус другое выражение в квадрате?» Точно, но слишком уж длинно. Зато разность квадратов – и точно, и кратко!

        Надеюсь, что названия сумма кубов и разность кубов у вас уже не вызовут недоумения?

 

        А вот теперь начинается самое сложное – запоминание самих формул, со всеми этими выражениями. К сожалению, здесь тот самый случай, когда без механической памяти не обойтись. Это огорчает.

        Однако здесь у нас с вами тайные знания! Эти знания помогут вам побыстрее сориентироваться во всех этих скобках, плюсах/минусах, квадратах/кубах, сведя механическую зубрёжку к минимуму. Читаем дальше и вникаем.

 

        Итак, начинаем с квадрата суммы:

        Просто медитировать, сверля формулу взглядом, будет недостаточно. Для лучшего запоминания настоятельно рекомендую выучить (да-да, именно выучить!) словесную формулировку:

        Квадрат суммы двух выражений равен квадрату первого выражения ПЛЮС удвоенное произведение первого выражения на второе ПЛЮС квадрат второго выражения.

 

        Эта мантра реально облегчает жизнь во многих разделах школьной математики! Да и в институте, при работе со всякими там пределами да интегралами, тоже. Ещё не раз вспомните эту формулировку добрым словом!)

        Если вы запомнили квадрат суммы, то дальше будет проще. Можно включать логику и здравый смысл. Переходим к квадрату разности:

        Сравните с квадратом суммы! Нашли отличие? Да! Перед удвоенным произведением появился минус. Ведь должен же он где-то появиться?! Перед a2 и b2 он появиться никак не может, ибо любое число в квадрате есть число положительное. Остаётся только серединка.) Для понимания рекомендую просто перемножить скобки сами на себя да привести подобные. И тогда у вас пропадут все вопросы.

        В словесной расшифровке:

        Квадрат разности двух выражений равен квадрату первого выражения МИНУС удвоенное произведение первого выражения на второе ПЛЮС квадрат второго выражения.

 

        Разность квадратов:

        Эта формула обычно и так легко запоминается. Единственное, можно случайно влепить в скобки два плюса или два минуса. Но тогда это уже будут квадрат суммы и квадрат разности. А это – совсем другие формулы…

        Итак:

        Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.

 

        Переходим к следующей группе формул – к сумме и разности кубов:

        Приём для запоминания здесь следующий. В первых скобках (маленьких) знак совпадает со знаком в исходном выражении: плюс-плюс, минус-минус. А вот во вторых (больших) скобках – меняется на противоположный. Причём меняется не перед квадратами, а снова посерединке! Квадраты a2 и b2 – положительные!

        Кстати, посмотрите внимательнее на большие скобки в каждой из формул и сравните с формулами квадрата суммы и квадрата разности!

        Нашли отличия? Да! В кубах не хватает двойки посерёдке. Именно по этой причине выражения в больших скобках

        a2+ab+b2

        и

        a2—ab+b2

        часто называют неполным квадратом суммы/разности.

        А теперь можно и шаблонные словесные формулировки из учебников привести:

        Сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.

        Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы.

        Вот так. Слово «неполный» хорошо помогает не запутаться. Допустим, в тревожной боевой обстановке на контрольной или экзамене нахлынули сомнения – писать двойку в сумме/разности кубов или нет?  Вот тут самое время вспомнить, что в кубах стоят неполные квадраты. А для полных квадратов есть свои формулы. Которые к кубам не имеют никакого отношения.

        Остаётся последняя парочка – куб суммы и куб разности:

        Эти две формулы встречаются в заданиях пореже предыдущих пяти, но знать их тоже не помешает, да. Претендуете на пятёрку? Тогда читаем дальше!

        Итак, как запомнить куб суммы? Во-первых, все знаки в формуле – плюсы! Оно и естественно. Ведь мы же перемножаем только положительные выражения, так с какого перепугу минусам-то взяться? Первое и последнее слагаемые – чистые кубы первого и второго выражений. А вот по центру – утроенные произведения.

        Обратите внимание, как в формуле идут переменные a и b! Переменная a идёт по убыванию степени – сначала a3, потом a2, потом просто a (т.е. a1), а в последнем слагаемом буква a и вовсе исчезает, превращаясь в единичку или a0. Для полной ясности ситуации последнее слагаемое b3 я перепишу вот так:

        b3 = 1∙b3 = a0∙b3

        А вот переменная b – наоборот, идёт по возрастанию степени. От нуля и до тройки включительно: в первом слагаемом переменной b нет (т.е. она сидит в виде единички, или b0), во втором b1, в третьем b2, в четвёртом b3.

        Но и это ещё не всё! Смотрите-ка, какая интересная штука: сумма степеней a и b в каждом из слагаемых всегда равна трём! Например:

        a3 = a3·b0          (3+0=3)

        3a2b = 3a2b1     (2+1=3)

        и так далее…

        Такой порядок хорошо помогает не запутаться.)

        Если вы уловили принцип запоминания куба суммы, то куб разности запомнится без проблем. Всё то же самое, только минусы надо правильно расставить. А это очень легко сообразить! Какая переменная у нас с минусом? Правильно, переменная b! Следовательно, в слагаемых, где b стоит в первой степени и в кубе – будет минус. Ибо любой минус в нечётной степени всегда даёт минус. А вот минус в квадрате (b2) даст плюс. И все дела.)

        Разумеется, изложенные выше советы – это не жёсткие правила математики. Это просто практические приёмы, помогающие более быстрому и комфортному запоминанию. Чисто для себя. Куда уж лучше, чем механическая зубрёжка, правда?)

        Но, как ни крути, самый надёжный способ запомнить эти формулы – решать побольше примеров. Тогда весь этот перечень запомнится очень быстро. Сам собой, можно сказать.

        Ну что, потренируемся?)

 

Примеры на формулы сокращённого умножения.

        Начнём с самого простого – с прямого применения формул. Для разминки.)

        Преобразовать в многочлен:

        (5x+4y)2

        Сразу видим квадрат скобок. А в скобках – сумму. Значит, работаем по самой первой формуле, вот этой:

        Вспоминаем словесную формулировку: «Квадрат первого выражения…». За первое выражение у нас идёт 5x. Квадрат будет 25х2. Вот и пишем:

        (5x+4y)2 = 25х2….

        Идём дальше: «Плюс удвоенное произведение первого выражения на второе…». Удвоенное – это умножение на двойку. Первое выражение – это 5x, второе – это 4y. Продолжаем:

        (5x+4y)2 = 25х2+2∙5x∙4y….

        «Плюс квадрат второго выражения.» В роли второго выражения у нас 4y. Квадрат – это 16y2. Получим:

        (5x+4y)2 = 25х2+2∙5x∙4y+16y2

        Практически всё. Осталось «причесать» удвоенное произведение (перемножить 2∙5∙4) и получим окончательный ответ:

        (5x+4y)2 = 25х2+40xy+16y2

        Это было разминочное задание. А теперь примерчик посерьёзнее.

 

        Разложить на множители:

        4x2–20x+25

 

        Что, внушает? Опять смотрим на наш список. Но не на тот, что в начале урока (для умножения), а на второй, для разложения на множители. Вот на этот:

        Тут, разумеется, нашего выражения нет. Ну и что? Здесь важно понимать, что под буквами a и b может скрываться всё что угодно – и числа, и другие буквы, и более сложные выражения. Поэтому смотрим на список и ищем похожую формулу. И зацепкой будут степени переменной.

        В нашем выражении есть x2 и просто x. Ясное дело, отбрасываем все формулы с кубами – у нас их явно нет. Далее выкидываем из рассмотрения формулу разности квадратов: там нет переменных в первой степени, только квадраты. А у нас – есть.

        Остаются первые две формулы – квадрат суммы или квадрат разности. Уже проще, не так ли? Осталось сообразить, что в формуле квадрата суммы – только плюсы. А в нашем выражении в серединке стоит минус. Стало быть, похожая формула – это квадрат разности.

        Но не факт, что квадрат разности сработает, совсем не факт… Наша задача – убедиться, что предложенное выражение 4x2–20x+25 точно соответствует квадрату разности. Только тогда у нас появится возможность записать и правую часть равенства (т.е. разложение на множители).

        Для удобства я перепишу формулу и исходное выражение прямо одно под другим:

        a2—2ab+b2 = (a—b)2

        4x2–20x+25 = ….

        Надо выяснить, что скрывается под буквами a и b в нашем выражении. Начинаем по порядочку – с самого первого слагаемого. Допустим, a2 – это 4x2. Тогда чему равно само а? Какое выражение в квадрате даёт 4x2? Очевидно, что 2х. Тогда a=2x. Есть! Первое выражение нашли.

        А что может скрываться под b2. Ну, точно не 20х! Во-первых, икс уже в букве a сидит, а во-вторых, b2 должно быть с плюсом. А 20х у нас с минусом. Значит, под b2 скрывается число 25! Стало быть, b – это пятёрка!

        Итого: a=2x,  b=5

        Всё? Можно записывать разложение? Пока нет.

        Нужна последняя, контрольная проверка по выражению 20х. Надо убедиться, что наши 20х точно соответствуют удвоенному произведению 2ab.

        Итак, затаив дыхание составляем удвоенное произведение первого и второго выражений:

        2ab = 2∙2x∙5 = 20x

        Ура! Совпало! Значит, наше выражение – это действительно квадрат разности 2х и 5. Вот теперь можно со спокойной душой записывать ответ:

        4x2–20x+25 = (2х-5)2

        Идея ясна? Сначала ищем в списке похожую формулу, а затем сверяем с ней выражение, предложенное в задании, на полное соответствие. Если повезло и всё совпало, то записываем ответ. Если не повезло, то, значит, раскладывать надо как-то иначе.

 

        Это были самые простые примеры, для младшеньких. А теперь переместимся в старшие классы, с их синусами да логарифмами. Да-да, старшеньким формулы сокращённого умножения тоже бывают нужны!

        Например, такое задание:

        Упростить:

        cos4x – 2cos2x∙sin2x + sin4x

        Вся мощь тригонометрии слабо помогает в этом примере. Только алгебра седьмого класса и спасает, да…

        Конечно, это выражение сильно смахивает на квадрат разности. Вот и пробуем применить эту формулу к нашему выражению! Что будет скрываться под буквами a и b? Конечно же, cos2x и sin2x. Удвоенное произведение, ясен перец, будет 2cos2x∙sin2x, как, собственно, в нашем выражении и записано. Смело сворачиваем нашего монстра в квадрат разности по формуле:

        cos4x – 2cos2x∙sin2x + sin4x = (cos2x — sin2x)2

        А вот теперь и тригонометрия в игру вступает! Что у нас в скобочках? У нас в скобочках косинус двойного угла!

        cos2x — sin2x = cos2x

        Вот вам и ответ:

        cos4x – 2cos2x∙sin2x + sin4x = cos22x

 

        Или такое задание:

        Вычислить:

        

        Пример не подарок, прямо скажем… Логарифмические формулы явно не катят, да и сами логарифмы ровно не считаются… Проверим на алгебру? Числитель явно намекает на применение формулы разности квадратов.

        Вот этой: a2–b2 = (a-b)(a+b)

        В роли a и b у нас логарифмы. Ну и что? Это формулу никак не портит, ибо законы алгебры работают во всей математике. Смело заменяем числитель дроби на произведение скобок и пишем:

        

        А вот теперь и логарифмические формулы заработали! В первых скобках (разность) получается lg4, который и сокращается благополучно со знаменателем. А во вторых скобках (сумма) будет lg100. Что по свойствам логарифмов есть 2.

        Конечно, подобные примеры в этом уроке легко решаются. Но на практике, когда ученик глубоко погружён в синусы/косинусы да логарифмы, разложение на множители просто не приходит в голову…

        Посему практический совет:

        Проверяем замороченные примеры на алгебру седьмого класса! В частности, на формулы сокращённого умножения.

 

        И напоследок…

        О типичном ляпе, который сразу же показывает блистательное отсутствие хоть какого-то понимания. Ляп настолько часто встречается, что хочется заявить громко:

        

        И запомните это крепко-накрепко!

        Формулы – штука жёсткая! Раз требуют удвоенного произведения 2ab, помимо чистых квадратов, значит спорить бессмысленно. Напишете такое на контрольной – будьте готовы получить заслуженную двойку! Такого не прощают. Вот так.

        Наглядный пример на добрую память с квадратом суммы. Всё-таки картинки иногда проливают свет на очень многие волнующие вопросы. Нарисуем в тетрадке квадрат со стороной a+b. Можно по клеточкам. Допустим, для конкретики, a – это 4 клетки, a b – это 2 клетки.

        Вот так:

        Очевидно, площадь всего квадрата будет равна квадрату его стороны, т.е. как раз (a+b)2. В числах, безо всяких формул, это будет (4+2)2 = 62 = 36.

        А теперь, глядя на картинку, соображаем: из чего складывается эта площадь? Правильно! Из большого (зелёного) квадрата площадью a2, маленького (жёлтого) квадратика площадью b2 и двух прямоугольников по ab площадью каждый.

        Вот и получается: (a+b)2 = a2+ab+ab+b2 = a2+2ab+b2

        Или, в числах, для a=4 и b=2:

        (a+b)2 = a2+2ab+b2= 42+2∙4∙2+22 = 16+16+4 = 36

        Вот и все дела.)

 

        Упражнение для интересующихся: аналогичным образом доказать геометрически (т.е. через квадраты и прямоугольники) две другие формулы сокращённого умножения с квадратами – квадрат разности и разность квадратов. Попробуйте! Интересно.)

 

        Ну что, порешаем?)

        1. Преобразовать в многочлен стандартного вида:

        (5a+1)2=

        (3y-4)2=

        (a-y3)2=

        (a2+b2)2=

        (3b-1)(3b+1)=

        (x+7)(7-x)=

        (3x+2)3=

 

        Ответы (в беспорядке):

        9b2 – 1

        9y2-24y+16

        27x3+18x2+36x+8

        a4+2a2b2+b4

        25a2+10a+1

        49-x2

        a2-2ay3+y6

 

        Ну как, размялись? Получилось? Тогда продолжаем:

        Разложить на множители:

        16x2+8x+1 =

        36x2y4-60xy2+25=

        y2-100=

        81a2-64x2y6=

        27m3+8=

        64x3-y6=

 

        Ответы (в беспорядке):

        (y-10)(y+10)

        (4x-y2)(16x2+4xy2+y4)

        (4x+1)2

        (9a-8xy3)(9a+8xy3)

        (6xy2-5)2

        (3m+2)(9m2-6m+4)

 

        И это получилось? Блеск! Значит, формулы сокращённого умножения на самом минимально необходимом уровне вы освоили. Можно браться за задания посерьёзнее.

        Что-то не срослось? Бывает… Возможно, проблема не в самих формулах, а в банальной арифметике – знаках, действиях со степенями. Повторите степени! Без отточенного навыка работы со степенями дальше идти нельзя. К сожалению…

        А вообще, рецепт здесь простой – решать побольше заданий! Да-да! Задания этого урока – капля в море. Помогут, но не сильно. Маловато их… Берите любой учебник 7-го класса и решайте, решайте! До автоматизма. А сайт – ваш надёжный помощник! Тогда формулы сами собой и запомнятся. А труды окупятся. Проверено!)

 

Семь формул сокращённого (краткого) умножения: упрощение выражений, примеры задач с решением

Одной из первых тем, изучаемых в курсе алгебры, являются формулы сокращённого умножения. В 7 классе они применяются в самых простых ситуациях, где требуется распознать в выражении одну из формул и выполнить разложение многочлена на множители или, наоборот, быстро возвести сумму или разность в квадрат или куб. В дальнейшем ФСУ используют для быстрого решения неравенств и уравнений и даже для вычисления некоторых числовых выражений без калькулятора.

Как выглядит список формул

Как применять формулы сокращённого умноженияСуществует 7 основных формул, позволяющих быстро осуществить перемножение многочленов в скобках.

Иногда в этот список также включается разложение для четвёртой степени, которое следует из представленных тождеств и имеет вид:

a⁴ b⁴ = (a — b)(a + b)(a² + b²).

Все равенства имеют пару (сумма — разность), кроме разности квадратов. Для суммы квадратов формула не приводится.

Остальные равенства легко запоминаются:

  1. Решение формулами сокращённого умноженияРазница между квадратом суммы и разности заключается в знаке перед удвоенным произведением величин.
  2. В случае с суммой и разностью кубов в (a ± b) знак совпадает со знаком (a3±b3). Второй сомножитель — так называемый неполный квадрат, поскольку он напоминает квадратный трёхчлен, возникающий после раскрытия скобок в квадрате суммы или разности. Здесь в ситуации с суммой появляется знак минуса перед ab, в противном случае знак заменяется на +.
  3. В кубе суммы все знаки положительные, в случае с разностью появляются минусы перед 3a²b и b³.

Следует помнить, что ФСУ работают в любом случае и для любых величин a и b: это могут быть как произвольные числа, так и целые выражения.

В ситуации, если вдруг не получается вспомнить, какой знак стоит в формуле перед тем или иным слагаемым, можно раскрыть скобки и получить тот же результат, что и после использования формулы. Например, если проблема возникла при применении ФСУ куба разности, нужно записать исходное выражение и поочерёдно выполнить умножение:

(a — b)³ = (a — b)(a — b)(a — b) = (a² ab — ab + b²)(a — b) = a³ a²b — a²b + ab² a²b + ab² + ab² b³ = a³ 3a²b + 3ab² b³.

В результате после приведения всех подобных членов был получен такой же многочлен, как и в таблице. Такие же манипуляции можно проводить и со всеми остальными ФСУ.

Как легко решать задачи формулами сокращённого умножения

Применение ФСУ для решения уравнений

К примеру, нужно решить уравнение, содержащее многочлен 3 степени:

x³ + 3x² + 3x + 1 = 0.

В школьной программе не рассматриваются универсальные приёмы для решения кубических уравнений, и подобные задания чаще всего решаются более простыми методами (например, разложением на множители). Если заметить, что левая часть тождества напоминает куб суммы, то уравнение можно записать в более простом виде:

(x + 1)³ = 0.

Корень такого уравнения вычисляется устно: x = -1.

Аналогичным способом решаются неравенства. Для примера можно решить неравенство x³ 6x² + 9x &gt, 0.

Применение формул сокращённого умножения

В первую очередь необходимо разложить выражение на множители. Вначале нужно вынести за скобку x. После этого следует обратить внимание, что выражение в скобках можно преобразовать в квадрат разности.

Затем необходимо найти точки, в которых выражение принимает нулевые значения, и отметить их на числовой прямой. В конкретном случае это будут 0 и 3. Затем методом интервалов определить, в каких промежутках x будет соответствовать условию неравенства.

ФСУ могут оказаться полезными при выполнении некоторых расчётов без помощи калькулятора:

703² 203² = (703 + 203)(703 — 203) = 906 ∙ 500 = 453000.

Кроме того, раскладывая выражения на множители, можно легко выполнять сокращение дробей и упрощение различных алгебраических выражений.

Примеры задач для 7−8 класса

В заключение разберём и решим два задания на применение формул сокращённого умножения по алгебре.

Задача 1. Упростить выражение:

(m + 3)² + (3m + 1)(3m — 1) — 2m (5m + 3).

Решение. В условии задания требуется упростить выражение, т. е. раскрыть скобки, выполнить действия умножения и возведения в степень, а также привести все подобные слагаемые. Условно разделим выражение на три части (по числу слагаемых) и поочерёдно раскроем скобки, применяя ФСУ там, где это возможно.

  • (m + 3)² = m² + 6m + 9 (квадрат суммы),
  • (3m + 1)(3m — 1) = 9m² 1 (разность квадратов),
  • В последнем слагаемом необходимо выполнить перемножение: 2m (5m + 3) = 10m² + 6m.

Как запомнить формулы сокращённого умножения

Подставим полученные результаты в исходное выражение:

(m² + 6m + 9) + (9m² 1) — (10m² + 6m).

С учётом знаков раскроем скобки и приведём подобные слагаемые:

m² + 6m + 9 + 9m² 1 — 10m² 6m = 8.

Задача 2. Решить уравнение, содержащее неизвестное k в 5 степени:

k⁵ + 4k⁴ + 4k³ 4k² 4k = k³.

Решение. В этом случае необходимо воспользоваться ФСУ и методом группировки. Нужно перенести последнее и предпоследнее слагаемое в правую часть тождества.

k⁵ + 4k⁴ + 4k³ = k³ + 4k² + 4k.

Из правой и из левой части выносится общий множитель (k² + 4k +4):

k³(k² + 4k + 4) = k (k² + 4k + 4).

Всё переносится в левую часть уравнения, чтобы в правой остался 0:

k³(k² + 4k + 4) — k (k² + 4k + 4) = 0.

Снова необходимо вынести общий множитель:

(k³ k)(k² + 4k + 4) = 0.

Из первого полученного сомножителя можно вынести k. По формуле краткого умножения второй множитель будет тождественно равен (k + 2)²:

k (k² 1)(k + 2)² = 0.

Использование формулы разности квадратов:

k (k — 1)(k + 1)(k + 2)² = 0.

Поскольку произведение равно 0, если хотя бы один из его множителей нулевой, найти все корни уравнения не составит труда:

  1. k = 0,
  2. k — 1 = 0, k = 1,
  3. k + 1 = 0, k = -1,
  4. (k + 2)² = 0, k = -2.

На основании наглядных примеров можно понять, как запомнить формулы, их отличия, а также решить несколько практических задач с применением ФСУ. Задачи простые, и при их выполнении не должно возникнуть никаких сложностей.

Формулы сокращённого умножения. Алгебра, 7 класс: уроки, тесты, задания.
1. Формула квадрата суммы или квадрата разности, проверка правильности использования формулы

Сложность: лёгкое

1
2. Применение формулы разности квадратов

Сложность: лёгкое

1
3. Формула квадрата суммы, возведение многочлена в квадрат

Сложность: лёгкое

2
4. Формула разности квадратов

Сложность: лёгкое

1
5. Формула квадрата разности

Сложность: лёгкое

1
6. Формулы сокращённого умножения (формулировки)

Сложность: лёгкое

1
7. Произведение разности и суммы (обыкновенные дроби)

Сложность: среднее

3
8. Разность квадратов (степень)

Сложность: среднее

3
9. Разность квадратов (десятичные дроби)

Сложность: среднее

3
10. Произведение суммы и разности (целые числа)

Сложность: среднее

3
11. Значение выражения

Сложность: среднее

4
12. Квадрат суммы (десятичные дроби)

Сложность: среднее

5
13. Квадрат разности (обыкновенные дроби)

Сложность: среднее

5
14. Квадрат суммы (трином)

Сложность: среднее

5
15. Квадрат разности (трином)

Сложность: среднее

5
16. Разность кубов

Сложность: среднее

5
17. Квадрат разности (умножение на число)

Сложность: среднее

3
18. Произведение суммы двух чисел на неполный квадрат их разности

Сложность: сложное

3
19. Формулы сокращённого умножения (десятичные дроби)

Сложность: сложное

8
20. Разность квадратов (целые числа)

Сложность: сложное

7
21. Произведение суммы и разности (числовое выражение)

Сложность: сложное

5

Формулы сокращенного умножения

Рассмотрим на примерах применение формул сокращенного умножения.

Пример 4 Преобразуйте выражение в многочлен

Разложим выражение на множители с помощью формулы куба суммы

Пример 5 Преобразуйте используя формулу куба разности

Формула куба разности

Пример 6 Разложите на множители многочлен

Воспользуемся формулой суммы кубов

Пример 7 Разложите на множители многочлен

Воспользуемся формулой разности кубов

{n — 2} x \: dx $

,
Формула сокращения | Статья о формуле сокращения по Free Dictionary Индия считает, что любая формула снижения тарифов, согласованная под эгидой ВТО, должна основываться только на связанных ставках, а не на применяемых ставках. В ее поправке говорится, что формула сокращения парниковых газов должна учитывать «эквиваленты CO2, выбрасываемые из-за добыча и производственный процесс, транспортировка, распределение и изменения в землепользовании … ». В ссылке [1] Мурти попросил нас найти формулу сокращения для T (r, n).«Другими словами, плати больше, чтобы получить меньше взамен». Комиссар сказал, что, по его мнению, формула снижения тарифов может использоваться для доступа к несельскохозяйственным рынкам (NAMA), но она настолько расплывчата, что невозможно понять, как это улучшит возможности доступа к рынкам. Директива о качестве топлива регулирует только качество топлива ». И внесенная в таблицу поправка гласит, что формула сокращения выбросов парниковых газов должна учитывать «эквиваленты CO2, выбрасываемые в результате процесса добычи и добычи, транспортировки, распределения и изменений в землепользовании, за вычетом экономии выбросов эквивалентов CO2 в результате улавливания и хранения или связанных с поглотителями». на производство топлива.«Он был« особенно срочным »для продвижения переговоров по сельскому хозяйству, но он также приветствовал признаки сближения в формуле снижения тарифов для промышленных тарифов. Аннотация В этой статье приведена формула сокращения для последовательностей соотношений Smarandache LCM SLR (6) и SLR ( 7). Недавнее предложение G-20 о доступе к рынку требует формулы снижения тарифов с гарантией oflexibilityo для чувствительных и специальных продуктов. Стимулы, основанные на формулах снижения энергопотребления, включают платежи, а также кредиты под низкие проценты.ЖЕНЕВА — Соединенные Штаты и Европейский союз заявили, что они откажутся от усилий по созданию «смеси» между двумя предлагаемыми формулами снижения тарифов на сельскохозяйственную продукцию, заявили представители Всемирной торговой организации. Формулы сокращения, используемые для выражения многих эллиптических интегралы в терминах нескольких стандартных интегралов упрощаются путем изменения определения промежуточных «базовых интегралов». 2. Источники сообщили, что ВТО надеется завершить работу над формулами снижения тарифов на сельскохозяйственную продукцию к очередному неофициальному совещанию на уровне министров ВТО в Момбасе, Кения, в начале марта, и сосредоточиться на вопросах несельскохозяйственного сектора на тех же переговорах.,

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *