Размеры чертежей формата А0, А1, А2, А3, А4, А5
Основные форматы чертежей получены путем последовательного деления формата А0, площадь которого равна 1 м2, на две равные части параллельно меньшей стороне соответствующего формата. В таблице основные форматы выделены серым цветом.
Дополнительные форматы листов чертежей образуются увеличением коротких сторон основных форматов на величину, кратную их размерам.
| Обозначение формата | Размеры сторон формата, мм | Площадь формата, м2 |
|---|---|---|
| А0 | 841 x 1189 | 1 |
| А0 x 2 | 1189 x 1682 | 2 |
| А0 x 3 | 1189 x 2523 | 3 |
| А1 | 594 x 841 | 1/2 |
| А1 x 3 | 841 x 1783 | 3/2 |
| А1 x 4 | 841 x 2378 | 2 |
| А2 | 420 x 594 | 1/4 |
| А2 x 3 | 594 x 1261 | 3/4 |
| А2 x 4 | 594 x 1682 | 1 |
| А2 x 5 | 594 x 2102 | 5/4 |
| А3 | 297 x 420 | 1/8 |
| А3 x 3 | 420 x 891 | 3/8 |
| А3 x 4 | 420 x 1189 | 1/2 |
| А3 x 5 | 420 x 1486 | 5/8 |
| А3 x 6 | 420 x 1783 | 3/4 |
| А3 x 7 | 420 x 2080 | 7/8 |
| А4 | 210 x 297 | 1/16 |
| А4 x 3 | 297 x 630 | 3/16 |
| А4 x 4 | 297 x 841 | 1/4 |
| А4 x 5 | 297 x 1051 | 5/16 |
| А4 x 6 | 297 x 1261 | 3/8 |
| А4 x 7 | 297 x 1471 | 7/16 |
| А4 x 8 | 297 x 1682 | 1/2 |
| А4 x 9 | 297 x 1892 | 9/16 |
| А5 | 148 x 210 | 1/32 |
Предельные отклонения сторон форматов листов чертежей
| Размеры сторон формата, мм | Предельные отклонения, мм |
|---|---|
| До 150 | —+1,5 |
| Св. 150 до 600 | —+2,0 |
| Св. 600 | —+3,0 |
tekhnar.ru
Формат бумаги, размеры А0, А1, А2, А3, А4, А5, А6
Большая часть стандартной полиграфической продукции печатается стандартными форматами: А6 , А5, А4 , А3, А2, DL «евроформат» — 99×210 мм (1/3 А4) или же размерами, которые удобно ложатся на формат листа.
Это понятно, минимальное количество бумажного «отхода» при печати выгодно всем: производителям печатного оборудования, производителям бумаги, типографиям и полиграфическим центрам. Поэтому при разработке макета обязательно этот момент нужно учитывать.
Если Вы предложите типографии напечатать неформатное изделие, скорее всего, придется переплатить за бумагу, которая попадёт в мусор, а в лучшем случае на переработку. Главным образом это касается бумаг которые предназначены для цифровой и офсетной печати. А вот, например, дизайнерские картоны и бумаги имеют размер в большинстве случаев 700х1000 мм (примерно В1 формат 707х1000мм). При печати на таких бумагах нужно более тщательно подойти к размеру изделия, так как стоимость таких материалов на порядки выше.
Таблица форматов бумаги (размеры в мм), стандарт ISO 216
| А6 – 105х148 | А2 – 420х594 |
| А5 – 148х210 | А1 – 594х841 |
| А4 – 210х297 | А0 – 841х1189 |
| А3 – 297х420 |
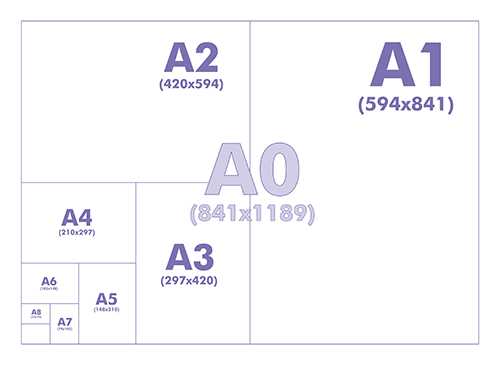
Таблица форматов бумаги (размеры в см)
| А6 – 10,5х14,8 | А2 – 42х59,4 |
| А5 – 14,8х21 | А1 – 59,4х84,1 |
| А4 – 21х29,7 | А0 – 84,1х118,9 |
| А3 – 29,7х42 |
Формат листа SRA3
Преимущественно, цифровые печатные машины имеют основной размер печатного листа SRA3 – 320х450 мм. Максимально и оптимально в этот размер войдут такие изделия (с учетом вылета под обрез 2мм на сторону)
А3 – 1 шт, А4 – 2 шт, А5 – 4 шт, А6 – 8 шт, DL (евроформат) – 6 шт, карманный календарь 100х70мм – 16 шт, визитка 90х50 мм – 24 шт.
Скачать раскладку на формате бумаги SRA3 .PDF
Скачать таблицу форматов бумаги .CDR
Создавая макет полиграфической продукции эту раскладку лучше держать под рукой, ведь понимая как этот процесс будет происходить в типографии, есть возможность неплохо сэкономить.
printexx.ru
Ответы@Mail.Ru: Помогите с алгеброй, сроооочнооо. Упростить выражение 3а (а + 2) – (а + 3)2 и найти его числовое значение при а =
3а*(а+2)-(а+3)*2=3a^2+6*a-2*а-6=3a^2+4*а-6 если а=-5 то значение выражения 3a^2+4*а-6=3*(-5)*(-5)-4*5-6=75-20-6=49
3а (а + 2) – (а + 3)2= (3а*2+ 6а) — (2а+6)= 3а*2 +4а-6 — квадратное уравнение, далее через дискриминант.. . надеюсь, умеете формулами пользоваться? ) Ну, или просто подставить заданное число…)
3а (а+2)-(а+3)2=3а в квадрате+6а-2а+6=9а в кубе -2а+6=7а в квадрате+6 7а в кв+6=-5 = 7авкв=-5+6=7авкв=1
Вот ссылка у меня там профиль: <a rel=»nofollow» href=»https://author24.ru/?ref=4fed5af13dc9c59b» target=»_blank»>https://author24.ru/?ref=4fed5af13dc9c59b</a>. Все решу с пояснениями.
touch.otvet.mail.ru
3(А2 – в2) – 2ав
4 | 2 | 1 | 2 | 0 | 2 | ||||||
при | А= | 3 | -2 | 0 | и | В= | 5 | -7 | -2 | ||
0 | -1 | 2 | 1 | 0 | -1 | ||||||
Имеем
4 | 2 | 1 | 4 | 2 | 1 | 22 | 3 | 6 | ||
А2= | 3 | -2 | 0 | 3 | -2 | 0 | = | 6 | 10 | 3 |
0 | -1 | 2 | 0 | -1 | 2 | -3 | 0 | 4 | ||
2 | 0 | 2 | 2 | 0 | 2 | 6 | 0 | 2 | ||
В2= | 5 | -7 | -2 | 5 | -7 | -2 | = | -27 | 49 | 26 |
1 | 0 | -1 | 1 | 0 | -1 | 1 | 0 | 3 |
16 | 3 | 4 | 48 | 9 | 12 | ||
А2 – В2 = | 33 | -39 | -23 | 99 | -117 | -69 | |
-4 | 0 | 1 | -12 | 0 | 3 |
4 | 2 | 1 | 2 | 0 | 2 | 19 | -14 | 3 | |||
АВ = | 3 | -2 | 0 | 5 | -7 | -2 | = | -4 | 14 | 10 | , |
0 | -1 | 2 | 1 | 0 | -1 | -3 | 7 | 0 |
38 | 6 | ||||||
2АВ = | -8 | 28 | 20 | ||||
-6 | 14 | 0 |
10 | 37 | 6 | |||||
3(A2 – B2) – 2AB = | 107 | -145 | -89 | ||||
-6 | -14 | 3 |
Умножение на единичную матрицу
На основании правила умножения матриц получаем:
АЕ = | а11 | а12 . | 1 | 0 | = | а11 | а |
а21 | а22 | 0 | 1 | а21 | а22 | ||
EA= | 1 | 0 . | а11 | а12 | = | а11 | а12 |
0 | 1 | а21 | а22 | а21 | а22 , | ||
т.е. АЕ = ЕА = А (11)
Произведение квадратной матрицы любого порядка на соответствующую единичную матрицу равняется первоначальной матрице. Таким образом, при умножении матриц единичная матрица играет роль единицы, поэтому и называется единичной.
Понятие обратной матрицы
Если А – квадратная матрица, то обратной по отношению к А называется матрица, которая, будучи умноженной на А (как справа, так и слева), даёт единичную матрицу. Обозначив обратную матрицу через А-1, запишем
А-1А = АА-1 = Е (12)
Если обратная матрица А-1 существует, то матрица А называется обратимой. Операция вычисления обратной матрицы называется обращением матрицы. Для того, чтобы квадратная матрица А имела обратную, необходимо и достаточно, чтобы матрица А была невырожденной.
studfiles.net
