ВЫСОТА (в геометрии) — это… Что такое ВЫСОТА (в геометрии)?
- ВЫСОТА (в геометрии)
- ВЫСОТА (в геометрии)
ВЫСОТА́, в геометрии — отрезок перпендикуляра, опущенного из вершины геометрической фигуры (напр., треугольника, пирамиды, конуса) на ее основание (или продолжение основания), а также длина этого отрезка. Высота призмы, цилиндра, шарового слоя, а также усеченных параллельно основанию пирамиды и конуса — расстояние между верхними и нижними основаниями.
Энциклопедический словарь. 2009.
- ВЫСОТА (в астрономии)
- ВЫСОЦКИЙ Михаил Иосифович
Смотреть что такое «ВЫСОТА (в геометрии)» в других словарях:
ВЫСОТА — в геометрии отрезок перпендикуляра, опущенного из вершины геометрической фигуры (напр., треугольника, пирамиды, конуса) на ее основание (или продолжение основания), а также длина этого отрезка. Высота призмы, цилиндра, шарового слоя, а также… … Большой Энциклопедический словарь
Высота (геометрич.) — Высота в геометрии, отрезок перпендикуляра, опущенного из вершины геометрической фигуры (например, треугольника, пирамиды, конуса) на её основание или продолжение основания, а также длина этого отрезка. В. призмы, цилиндра, шарового слоя,… … Большая советская энциклопедия
Высота — I Высота небесного светила, угол между направлением на светило и плоскостью истинного горизонта; см. Небесные координаты. II Высота в геометрии, отрезок перпендикуляра, опущенного из вершины геометрической фигуры (например,… … Большая советская энциклопедия
ВЫСОТА — 1) ВЫСОТА в астрономии см. Небесные координаты. 2) ВЫСОТА в геометрии отрезок перпендикуляра, опущенного из вершины геом. фигуры (напр., треугольника, трапеции, пирамиды, конуса) на её основание (или продолжение основания), а также длина этого… … Большой энциклопедический политехнический словарь
Высота (значения) — Высота размер или расстояние в вертикальном направлении. Другие значения: В астрономии: Высота светила угол между плоскостью математического горизонта и направлением на светило. В военном деле: Высота возвышенность рельефа. В… … Википедия
ВЫСОТА — (1) в геометрии а) плоской фигуры наибольший из перпендикуляров, опущенных из точек контура фигуры на её основание или его продолжение; б) пространственной фигуры наибольший из перпендикуляров, опущенных из граничных точек этой фигуры на… … Большая политехническая энциклопедия
высота — 3.4 высота (height): Размер самой короткой кромки карты. Источник: ГОСТ Р ИСО/МЭК 15457 1 2006: Карты идентификационные. Карты тонкие гибкие. Часть 1. Физические характеристики … Словарь-справочник терминов нормативно-технической документации
Высота (геометрия) — У этого термина существуют и другие значения, см. Высота (значения). Высота в элементарной геометрии отрезок перпендикуляра, опущенного из вершины геометрической фигуры (например, треугольника, пирамиды, конуса) на её основание или на… … Википедия
ВЫСОТА — в диофантовой геометрии некоторая численная функция на множестве решений диофантова уравнения. В простейшем случае целочисленного решения диофантова уравнения высота есть функция решения, равная В таком виде она встречается уже в методе спуска… … Математическая энциклопедия
Высота (геометрия) — это… Что такое Высота (геометрия)?
Высота в элементарной геометрии — отрезок перпендикуляра, опущенного из вершины геометрической фигуры (например, треугольника, пирамиды, конуса) на её основание или на продолжение основания. Под высотой также подразумевается длина этого отрезка.
Высота трапеции, призмы, цилиндра, шарового слоя, усеченных параллельно основанию — расстояние между верхним и нижним основаниями.
Высота треугольника
Высота треугольника — отрезок, опущенный из вершины треугольника перпендикулярно противоположной стороне.
Все высоты треугольника пересекаются в одной точке, называемой ортоцентром этого треугольника. — Эту теорему легко доказать, используя векторное тождество, справедливое для любых точек A, B, C, E, не обязательно даже лежащих в одной плоскости:
(Для доказательства следует взять в качестве точки E пересечение двух высот треугольника.)
Площадь треугольника равна половине произведения высоты треугольника на соответствующее основание. Кроме формулы, удобной для расчёта площади, из этого также следует, что длины высот треугольника обратно пропорциональны длинам соответствующих сторон.
Минимальная из высот треугольника обладает многими экстремальными свойствами. Например:
1. Минимальная ортогональная проекция треугольника на прямую, лежащую в плоскости треугольника, имеет длину, равную наименьшей из его высот.
2. Минимальный прямолинейный разрез в плоскости, через который можно протащить несгибаемую треугольную пластину, должен иметь длину, равную наименьшей из высот этой пластины.
3. При непрерывном движении двух точек по периметру треугольника друг навстречу другу, если они встречаются хотя бы дважды, тогда максимальное расстояние между точками во время их движения не может быть меньше длины наименьшей из высот треугольника.
dic.academic.ru
Свойства высоты для всех фигур, с примерами
Рассмотрим высоты треугольника и четырехугольника. У треугольника из каждой вершины можно опустить одну высоту (рис. 1). У четырехугольника из каждой вершины можно опустить две высоты на стороны, не смежные с данной вершиной (или на их продолжение) (рис. 2).
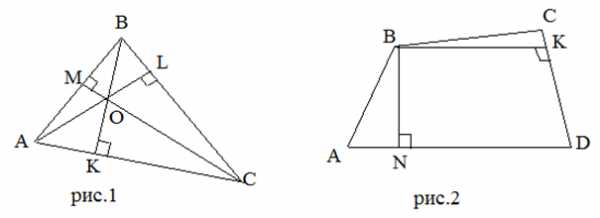
Свойства высоты геометрических фигур
- В треугольнике высоты пересекаются в одной точке, называемой ортоцентром. В остроугольном треугольнике высоты пересекаются внутри треугольника; в тупоугольном – вне треугольника; в прямоугольном – в вершине прямого угла.
- В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобных исходному.
- В остроугольном треугольнике две его высоты отсекают от него подобные треугольники.
- В равнобедренном треугольнике высота, опущенная на основание, является медианой и биссектрисой.
- В равностороннем треугольнике все высоты являются медианами и биссектрисами.
- Площадь треугольника вычисляется с помощью высоты и стороны, на которую она опущена:
- Площадь параллелограмма вычисляется по формуле:
где – сторона параллелограмма, – высота, опущенная на сторону .
- Площадь трапеции
где – основания трапеции, – высота трапеции.
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Высота (геометрия) — Википедия. Что такое Высота (геометрия)
Высота в элементарной геометрии — отрезок перпендикуляра, опущенного из вершины геометрической фигуры (например, треугольника, пирамиды, конуса) на её основание или на продолжение основания. Под высотой также подразумевается длина этого отрезка.
Высота трапеции, призмы, цилиндра, шарового слоя, усеченных параллельно основанию — расстояние между верхним и нижним основаниями.
Высота треугольника
Высота треугольника — отрезок, опущенный из вершины треугольника перпендикулярно противоположной стороне.
Все высоты треугольника пересекаются в одной точке, называемой ортоцентром этого треугольника. — Эту теорему легко доказать, используя векторное тождество, справедливое для любых точек A, B, C, E, не обязательно даже лежащих в одной плоскости:
- EA→⋅BC→+EB→⋅CA→+EC→⋅AB→=0{\displaystyle {\overrightarrow {EA}}\cdot {\overrightarrow {BC}}+{\overrightarrow {EB}}\cdot {\overrightarrow {CA}}+{\overrightarrow {EC}}\cdot {\overrightarrow {AB}}=0}
(Для доказательства следует взять в качестве точки E пересечение двух высот треугольника.)
Площадь треугольника равна половине произведения высоты треугольника на соответствующее основание. Кроме формулы, удобной для расчёта площади, из этого также следует, что длины высот треугольника обратно пропорциональны длинам соответствующих сторон.
Минимальная из высот треугольника обладает многими экстремальными свойствами. Например:
1. Минимальная ортогональная проекция треугольника на прямую, лежащую в плоскости треугольника, имеет длину, равную наименьшей из его высот.
2. Минимальный прямолинейный разрез в плоскости, через который можно протащить несгибаемую треугольную пластину, должен иметь длину, равную наименьшей из высот этой пластины.
3. При непрерывном движении двух точек по периметру треугольника друг навстречу другу, если они встречаются хотя бы дважды, тогда максимальное расстояние между точками во время их движения не может быть меньше длины наименьшей из высот треугольника.
wiki.sc
Высота (геометрия) Википедия
Высота в элементарной геометрии — отрезок перпендикуляра, опущенного из вершины геометрической фигуры (например, треугольника, пирамиды, конуса) на её основание или на продолжение основания. Под высотой также подразумевается длина этого отрезка.
Высота трапеции, призмы, цилиндра, шарового слоя, усеченных параллельно основанию — расстояние между верхним и нижним основаниями.
Высота треугольника[ | ]
Высота треугольника — отрезок, опущенный из вершины треугольника перпендикулярно противоположной стороне.
Все высоты треугольника пересекаются в одной точке, называемой ортоцентром этого треугольника. — Эту теорему легко доказать, используя векторное тождество, справедливое для любых точек
- EA→⋅BC→+EB→⋅CA→+EC→⋅AB→=0{\displaystyle {\overrightarrow {EA}}\cdot {\overrightarrow {BC}}+{\overrightarrow {EB}}\cdot {\overrightarrow {CA}}+{\overrightarrow {EC}}\cdot {\overrightarrow {AB}}=0}
(Для доказательства следует взять в качестве точки E пересечение двух высот треугольника.)
Площадь треугольника равна половине произведения высоты треугольника на соответствующее основание. Кроме формулы, удобной для расчёта площади, из этого также следует, что длины высот треугольника обратно пропорциональны длинам соответствующих сторон.
Минимальная из высот треугольника обладает многими экстремальными свойствами. Например:
1. Минимальная ортогональная проекция треугольника на прямую, лежащую в плоскости треугольника, имеет длину, равную наименьшей из его высот.
2. Минимальный прямолинейный разрез в плоскости, через который можно протащить несгибаемую треугольную пластину, должен иметь длину, равную наименьшей из высот этой пластины.
3. При непрерывном движении двух точек по периметру треугольника друг навстречу другу, если они встречаются хотя бы дважды, тогда максимальное расстояние между точками во время их движения не может быть меньше длины наименьшей из высот треугольника.
ru-wiki.ru
Высота (геометрия)
Высота в элементарной геометрии — отрезок перпендикуляра, опущенного из вершины геометрической фигуры (например, треугольника, пирамиды, конуса) на её основание или на продолжение основания. Под высотой также подразумевается длина этого отрезка.
Высота трапеции, призмы, цилиндра, шарового слоя, усеченных параллельно основанию — расстояние между верхним и нижним основаниями.
Высота треугольника
Основная статья: Высота треугольникаВысота треугольника — отрезок, опущенный из вершины треугольника перпендикулярно противоположной стороне.
Все высоты треугольника пересекаются в одной точке, называемой ортоцентром этого треугольника. — Эту теорему легко доказать, используя векторное тождество, справедливое для любых точек A, B, C, E, не обязательно даже лежащих в одной плоскости:
(Для доказательства следует взять в качестве точки E пересечение двух высот треугольника.)
Площадь треугольника равна половине произведения высоты треугольника на соответствующее основание. Кроме формулы, удобной для расчёта площади, из этого также следует, что длины высот треугольника обратно пропорциональны длинам соответствующих сторон.
Минимальная из высот треугольника обладает многими экстремальными свойствами. Например:
1. Минимальная ] проекция треугольника на прямую, лежащую в плоскости треугольника, имеет длину, равную наименьшей из его высот.
2. Минимальный прямолинейный разрез в плоскости, через который можно протащить несгибаемую треугольную пластину, должен иметь длину, равную наименьшей из высот этой пластины.
3. При непрерывном движении двух точек по периметру треугольника друг навстречу другу, если они встречаются хотя бы дважды, тогда максимальное расстояние между точками во время их движения не может быть меньше длины наименьшей из высот треугольника.
См. также
- Чевиа́на — отрезок (или продолжение отрезка), соединяющий вершину треугольника с точкой на противоположной ей стороне или на её продолжении.
- Высота
- Высота треугольника
- Ортоцентр
- Треугольник
Высота (геометрия) Информацию О

Высота (геометрия) Комментарии
Высота (геометрия)
Высота (геометрия)
Высота (геометрия) Вы просматриваете субъект
Высота (геометрия) что, Высота (геометрия) кто, Высота (геометрия) описание
There are excerpts from wikipedia on this article and video
www.turkaramamotoru.com
Высота (геометрич.) — это… Что такое Высота (геометрич.)?
- Высота (геометрич.)
- Высота в геометрии, отрезок перпендикуляра, опущенного из вершины геометрической фигуры (например, треугольника, пирамиды, конуса) на её основание или продолжение основания, а также длина этого отрезка. В. призмы, цилиндра, шарового слоя, усечённых параллельно основанию пирамиды и конуса — расстояние между верхним и нижним основаниями. На рис. изображены В. (h) треугольников, трапеции и усечённого конуса.
Большая советская энциклопедия. — М.: Советская энциклопедия. 1969—1978.
- Высокоэластическое состояние
- Высота апогея (перигея)
Смотреть что такое «Высота (геометрич.)» в других словарях:
Цилиндр (геометрич.) — Цилиндр (от греч. kýlindros ‒ валик, каток), тело, ограниченное замкнутой цилиндрической поверхностью и двумя секущими её параллельными плоскостями ‒ основаниями Ц. (рис.). Если основания перпендикулярны образующей, то Ц. называется прямым; в… … Большая советская энциклопедия
ПИФАГОРЕИЗМ — совокупность др. греч. филос. и научных концепций, восходящих к Пифагору (6 в. до н.э.) и основанному им замкнутому элитарному духовному обществу в «Великой Греции» (греч. города гос ва на юге Аппенинского полуострова и на востоке Сицилии). Почти … Философская энциклопедия
МНОГОМЕРНАЯ ГЕОМЕТРИЯ — геометрия пространств размерности, большей трех; термин применяется к тем пространствам, геометрия к рых была первоначально развита для случая трех измерений и только потом обобщена на число измерений n>3, прежде всего евклидово пространство,… … Математическая энциклопедия
Математика — (от греч. mathema значение, наука). В эпоху античности уровень развития М. был очень высок. Греки использовали накопл. в Вавилонии и Египте арифметич. и геометрич. знания, но достоверных данных, позволяющих точно определить их воздействие … Словарь античности
ОСВЕЩЕНИЕ — ОСВЕЩЕНИЕ. Различают естественное и искусственное О. Естественным называют О. от природных источников, гл.обр. от солнца, причем солнечные лучи могут освещать непосредственно, или отражаясь от луны, рассеиваясь в атмосфере, на облаках, на… … Большая медицинская энциклопедия
КРИСТАЛЛИЗАЦИЯ — образование кристаллов из паров, р ров, расплавов, из в ва в тв. состоянии (аморфном или другом кристаллическом), из электролитов в процессе электролиза (электрокристаллизация), а также при хим. реакциях. Для К. необходимо нарушение термодинамич … Физическая энциклопедия
Мелодия — (греч. melodia, от melos напев, песня и odn песня, пение) одноголосно выраженная музыкальная мысль (по И. В. Способину). В гомофонной музыке функция мелодии присуща обычно верхнему, ведущему голосу, тогда как второстепенные средние голоса … Музыкальная энциклопедия
ДИОФАНТОВА ГЕОМЕТРИЯ — диофантов анализ, область математики, посвященная изучению целочисленных и рациональных решений систем алгебраич. уравнений, или, иначе, изучению диофантовых уравнений, методами алгебраич. геометрии. Появление во 2 й пол. 19 в. теории алгебраич.… … Математическая энциклопедия
ЭЛЛИПТИЧЕСКАЯ КРИВАЯ — неособая полная алгебраическая кривая рода 1. Теория Э. к. является истоком большей части современной алгебраич. геометрии. Но исторически теория Э. к. возникла как часть анализа, как теория эллиптических интегралов и эллиптических функций.… … Математическая энциклопедия
ОПРЕДЕЛЕНИЕ МЕСТА СУДНА — установление фактич. места судна по наблюдениям береговых ориентиров визуально или с помощью радиолокаторов, по небесным светилам, по пеленгам радиомаяков, с помощью наземных радионавиг. систем или по спутниковым радионавиг. системам (РНС) с… … Морской энциклопедический справочник
dic.academic.ru
