Диаметр через длина окружности онлайн – Длина окружности или периметр круга

Калькулятор круга и шара. Рассчитать радиус, диаметр, длину окружности, площадь круга и шара, объем шара онлайн.

Калькулятор круга — это сервис, специально разработанный для расчета геометрических размеров фигур онлайн. Благодаря данному сервису Вы без проблем сможете определить любой параметр фигуры, в основе которой лежит круг. Например: Вы знаете объем шара, а необходимо получить его площадь. Нет ничего проще! Выберите соответствующий параметр, введите числовое значение и нажмите кнопку рассчитать. Сервис не только выдает результаты вычислений, но и предоставляет формулы, по которым они были сделаны. При помощи нашего сервиса вы без труда рассчитаете радиус, диаметр, длину окружности (периметр круга), площадь круга и шара, объем шара.

Вычислить радиус

Задача на вычисление значения радиуса – одна из самых распространенных. Причина тому достаточно проста, ведь зная этот параметр, вы без особого труда сможете определить значение любого другого параметра круга или шара. Наш сайт построен именно на такой схеме. Вне зависимости от того, какой вы выбрали исходный параметр, первым делом вычисляется значение радиуса и на его основе строятся все последующие вычисления. Для большей точности вычислений, сайт использует число Пи с округлением до 10-го знака после запятой.

Рассчитать диаметр

Расчет диаметра – самый простой вид расчета из тех, что умеет выполнять наш калькулятор. Получить значение диаметра совсем нетрудно и вручную, для этого совсем не надо прибегать к помощи интернета. Диаметр равен значению радиуса умноженному на 2. Диаметр – важнейший параметр круга, который чрезвычайно часто используется в повседневной жизни. Уметь его правильно рассчитать и использовать должен абсолютно каждый. Воспользовавшись возможностями нашего сайта, вы вычислите диаметр с большой точностью за доли секунды.

Узнать длину окружности

Вы даже не представляете, как много вокруг нас круглых объектов и какую важную роль они играют в нашей жизни. Умение рассчитать длину окружности необходимо всем, от рядового водителя, до ведущего инженера-проектировщика. Формула для вычисления длинны окружности очень проста: D=2Pr. Расчет можно легко провести как на листке бумаги, так и при помощи данного интернет помощника. Преимущество последнего в том, что он проиллюстрирует все вычисления рисунками. И ко всему прочему, второй способ намного быстрее.

Вычислить площадь круга

Площадь круга – как и все перечисленные перечисленные в этой статье параметры является основой современной цивилизации. Уметь рассчитать и знать площадь круга полезно всем без исключения слоям населения. Трудно представить область науки и техники, в которой не надо было бы знать, площадь круга. Формула для вычисления опять же нетрудная: S=PR². Эта формула и наш онлайн-калькулятор помогут Вам без лишних усилий узнать площадь любого круга. Наш сайт гарантирует высокую точность вычислений и их молниеносное выполнение.

Рассчитать площадь шара

Формула для расчета площади шара ничуть не сложнее формул, описанных в предыдущих пунктах. S=4Pr²

. Этот нехитрый набор букв и цифр уже многие годы дает людям возможность достаточно точно вычислять площадь шара. Где это может быть применено? Да везде! Например, вы знаете, что площадь земного шара равна 510 100 000 километров квадратных. Перечислять, где может быть применено знание этой формулы перечислять бесполезно. Слишком широка область применения формулы для вычисления площади шара.

Вычислить объем шара

Для вычисления объема шара используют формулу V=4/3(Pr³). Она была использована при создании нашего онлайн сервиса. Сайт tellaboutall.ru дает возможность рассчитать объем шара за считанные секунды, если вы Вам известен любой из следующих параметров: радиус, диаметр, длинна окружности, площадь круга или площадь шара. Так же вы можете применять его для обратного вычисления, например, чтобы зная объем шара, получить значение его радиуса или диаметра. Спасибо, что кратко ознакомились с возможностями нашего калькулятора круга. Надеемся, Вам у нас понравилось, и вы уже добавили сайт в закладки.

tellaboutall.ru

онлайн-калькулятор расчета через радиус, диаметр и длину окружности

С помощью нашего онлайн калькулятора можно найти площадь круга зная его радиус, диаметр, длину окружности.
3 основных формулы площади круга:

👉через радиус — S=πR².

👉через диаметр — S=¼πd².

👉через длину окружности — .

Через радиус

S=πR²

Через диаметр

S=¼πd²

Через длину окружности

Круг – множество точек плоскости, удаленных от заданной точки этой плоскости (центр круг) на расстояние, не превышающее заданное (радиус круга).

Окружность – замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра), лежащей в той же плоскости, что и кривая.

• r – радиус круга.
• d – диаметр круга.
• π (греческая буква пи) всегда равно 3,14 — обозначает константу, выражающую отношение длины окружности к его диаметру или площади круга к квадрату его радиуса.

Чтобы окончательно разобраться в теме «Круг и его площадь», смотрите видео урок на котором учитель математики понятно рассказывает все, что вам нужно знать.

Автор Cascading Style Sheets

hr-vector.com

Онлайн калькулятор: Сегмент круга

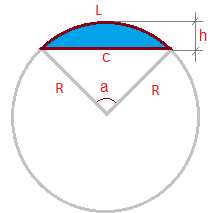
Сегмент круга

Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).

На рисунке:
L — длина дуги сегмента
c — хорда
R — радиус
a — угол сегмента
h — высота

Первый калькулятор рассчитывает параметры сегмента, если известен радиус и угол по следующим формулам:

Формулы вычисления параметров сегмента

Площадь сегмента:
[1]
Длина дуги:

Длина хорды:

Высота сегмента:

Угол в градусах, образуемый радиусами сектора

Точность вычисления

Знаков после запятой: 2

Сохранить share extension

Однако, как справедливо заметил наш пользователь:«на практике часто случается, что как радиус дуги, так и угол неизвестны»

(см. длина дуги ). Для этого случая для расчета площади сегмента и длины дуги можно использовать следующий калькулятор:

Точность вычисления

Знаков после запятой: 2

Угол (градусы)

 

Сохранить share extension

Калькулятор вычисляет радиус круга по длине хорды и высоте сегмента по следующей формуле:

Далее, зная радиус и длину хорды, легко найти угол сегмента по формуле:

Остальные параметры сегмента вычисляются аналогично первому калькулятору, по формулам, приведенным в начале статьи.

Следующий калькулятор вычисляет площадь сегмента по высоте и радиусу:

Точность вычисления

Знаков после запятой: 2

Угол (градусы)

 

planetcalc.ru

Длина окружности по диаметру

Здравствуйте! Давайте для начала вспомним с Вами, что такое длина окружности. Длина окружности — это грубо говоря, периметр окружности, который обозначается буквой . Для того, чтобы найти длину окружности используют формулу: 

   

, где  — радиус окружности, а  — это приблизительное постоянное число, которое равно 3,14.
Хорошо, возможно у Вас может также возникнуть вопрос, что такое радиус. Но если повторять, так повторять всё. Итак, радиус — отрезок, который соединяет центр окружности (либо же сферы) с любой точкой, которая лежит на окружности, а также является длиной этого отрезка. Радиус, как Вы уже поняли, обозначается буковкой  , либо же . Но давайте вспомним формулой, чтоб более чётко понять, что такое радиус. Итак, вот и формула: 

   

, где — это диаметр окружности.
А что ж такое диаметр?! Это отрезок, соединяющий две точки лежащие на окружности и проходящий через центр данной окружности. Он равносильно равен такой формуле: 

   

.
Хорошо. теперь, исходя из того,что мы узнали, можем ответить про то, что такое длина окружности по диаметру. Что ж, это не просто какое-то значение! Это просто отчасти формулировка формулы, как можно найти длину окружности, исходя из того, что мы знаем диаметр. И данная формула будет иметь такой вид: 

А теперь мы решим Вашу задачку. Итак, дана окружность, в которой известен диаметр, который равен 20 см. Давайте решать: 

   

 

   

 

   

Ответ:  см

ru.solverbook.com

Калькулятор онлайн — Вычисление длины окружности

Этот математический калькулятор онлайн поможет вам вычислить длину окружности. Программа для вычисления длины окружности не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения результата.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Если вы не знакомы с правилами ввода чисел, рекомендуем с ними ознакомиться.

Числа можно вводить целые или дробные.
Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.

Правила ввода десятичных дробей.
В десятичных дробях дробная часть от целой может отделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так: 2.5 или так 1,3

Правила ввода обыкновенных дробей.

В качестве числителя, знаменателя и целой части дроби может выступать только целое число.

Знаменатель не может быть отрицательным.

При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Ввод: -2/3
Результат: \( -\frac{2}{3} \)

Целая часть отделяется от дроби знаком амперсанд: &
Ввод: -1&5/7
Результат: \( -1\frac{5}{7} \)

www.math-solution.ru

No related posts.