Формула sin3a – Sin3a = расписать по формуле

как вывести забытую тригонометрическую формулу?

На олимпиаде по математике с большой степенью вероятности, а на внешнем независимом тестировании – уж наверняка встретятся задания по тригонометрии. Тригонометрию часто не любят за необходимость зубрить огромное количество трудных формул, кишащих синусами, косинусами, тангенсами и котангенсами. На сайте уже когда-то давались советы, как вспомнить забытую формулу, на примере формул Эйлера и Пиля.

А в этой статье мы постараемся показать, что достаточно твёрдо знать всего пять простейших тригонометрических формул, а об остальных иметь общее представление и выводить их по ходу дела. Это как с ДНК: в молекуле не хранятся полные чертежи готового живого существа. Там содержатся, скорее, инструкции по его сборке из имеющихся аминокислот. Так и в тригонометрии, зная некоторые общие принципы, мы получим все необходимые формулы из небольшого набора тех, которые нужно обязательно держать в голове.

Будем опираться на следующие формулы:

1. Основное тригонометрическое тождество: sin²a+cos²a = 1
2. Определение тангенса:
3. Определение котангенса:
4. Формула синуса суммы: sin(a+b) = sinacosb+cosasinb
5. Формула косинуса суммы: cos(a+b) = cosacosb—sinasinb

Из формул синуса и косинуса сумм, зная о чётности функции косинуса и о нечётности функции синуса, подставив -b вместо b, получаем формулы для разностей:

6. Синус разности: sin(a-b) = sinacos(-b)+cosasin(-b) = sinacosb—cosasinb
7. Косинус разности: cos(a-b) = cosacos(-b)—sinasin(-b) = cosacosb+sinasinb

Поставляя в эти же формулы a = b, получаем формулы синуса и косинуса двойных углов:

8. Синус двойного угла: sin2a = sin(a+a) = sinacosa+ cosasina = 2sinacosa
9. Косинус двойного угла: cos2a = cos(a+a) = cosacosa—sinasina = cos²a—sin²a

Аналогично получаются и формулы других кратных углов:

10. Синус тройного угла: sin3a = sin(2a+a) = sin2acosa+cos2asina = (2sinacosa)cosa+(cos²a—sin²a)sin
    a = 2sinacos²a+sinacos²a—sin³a = 3sinacos²a—sin³a = 3sina(1-sin²a)-sin³a = 3sina-4sin³a
11. Косинус тройного угла: cos3a = cos(2a+a) = cos2acosa—sin2asina = (cos²a—sin²a)cosa-(2sinacosa)sina = cos³a- sin²acosa-2sin²acosa = cos³a-3sin²acosa = cos³a-3(1-cos²a)cosa = 4cos³a-3cosa

Прежде чем двигаться дальше, рассмотрим одну задачу.
Дано: угол — острый.
Найти его косинус, если
Решение, данное одним учеником:
Т.к. , то sina = 3,а cosa = 4.
(Из математического юмора)

Итак, определение тангенса связывает эту функцию и с синусом, и с косинусом. Но можно получить формулу, дающую связь тангенса только с косинусом. Для её вывода возьмём основное тригонометрическое тождество: sin

²a+cos²a = 1 и разделим его на cos²a. Получим:

12. Связь тангенса и косинуса:

Так что решением этой задачи будет:

(Т.к. угол острый, при извлечении корня берётся знак +)

13. Аналогично получаем связь котангенса и синуса:

Формула тангенса суммы – ещё одна, тяжело поддающаяся запоминанию. Выведем её так:

14. Формула тангенса суммы: . Разделив числитель и знаменатель на произведение косинусов, получим:

Сразу выводится и

15. Формула тангенса двойного угла:

Из формулы косинуса двойного угла можно получить формулы синуса и косинуса для половинного. Для этого к левой части формулы косинуса двойного угла:

cos2a = cos²a—sin²a
прибавляем единицу, а к правой – тригонометрическую единицу, т.е. сумму квадратов синуса и косинуса.
cos2a+1 = cos²a—sin²a+cos²a+sin²a
2cos²a = cos2a+1
Выражая cosa через cos2a и выполняя замену переменных, получаем:

16. Косинус половинного угла:

Знак берётся в зависимости от квадранта.

Аналогично, отняв от левой части равенства единицу, а от правой — сумму квадратов синуса и косинуса, получим:

cos2a-1 = cos²a—sin²a—cos²a—sin²a
2sin²a = 1-cos2a

17. Cинус половинного угла:

И, наконец, чтобы преобразовать сумму тригонометрических функций в произведение, используем следующий приём. Допустим, нам нужно представить в виде произведения сумму синусов sina+sinb. Введём переменные x и y такие, что a = x+y, b+x-y. Тогда
sina+sinb = sin(x+y)+sin(x-y) = sinxcosy+cosx

siny+sinxcosy-cosxsiny = 2sinxcosy. Выразим теперь x и y через a и b.

Поскольку a = x+y, b = x-y, то . Поэтому

18. Представление суммы синусов в виде произведения:

Сразу же можно вывести

19. Формулу для разбиения произведения синуса и косинуса в сумму: sinacosb = 0.5(sin(a+b)+sin(a-b))

Рекомендуем потренироваться и вывести самостоятельно формулы для преобразования в произведение разности синусов и суммы и разности косинусов, а также для разбиения в сумму произведений синусов и косинусов. Проделав эти упражнения, вы досконально освоите мастерство вывода тригонометрических формул и не потеряетесь даже на самой сложной контрольной, олимпиаде или тестировании.

intelmath.narod.ru

sina+sin3a+sin5a+sin7a как решить пример ??

По-моему надо sina вынести за скобку.

наверно получится sin15a????

формула налицо

Есть формулы: <a rel=»nofollow» href=»http://mschool.kubsu.ru/cdo/shabitur/kniga/sprav/trigfunc/osnform/osnform.htm» target=»_blank»>http://mschool.kubsu.ru/cdo/shabitur/kniga/sprav/trigfunc/osnform/osnform.htm</a>

TEBE NADO PREOBRAZOVAT ETU SUMMU V PROIZVEDENIE? sina+sin3a+sin5a+sin7a = (sina + sin7a) + (sin3a + sin5a) = 2sin4a cos3a + 2sin4a cosa = 2sin4a(cos3a + cosa) = 4sin4a * cos2a * cosa. posmotri formuli u Николай Кирпичников. ne reshit, a preobrazovat! zapomni eto!

touch.otvet.mail.ru

sin (3п / 2)

Вычислим значение тригонометрического выражения несколькими возможными методами. Их можно использовать для вычисления синуса от других аргументов.

Метод таблицы значений синуса
Он чаще всего используется для синуса от основных значений аргумента, к которым также относится и аргумент .
Итак, используем таблицу.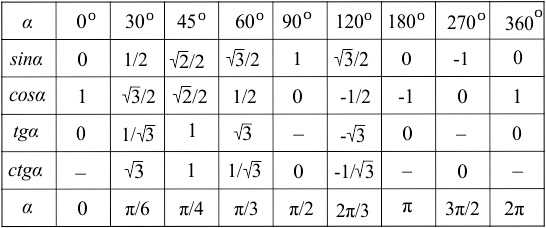

Из нее нас интересует столбик со значением аргумента и строка, в которой находятся значения синуса. На пересечении столбца и строки находится значение указанной функции от выбранного аргумента:

   

Метод тригонометрического круга
Популярным этот метод является в случае, когда таблицы значений синуса нет. Достаточно запомнить некоторые основные моменты и его можно использовать не только для вычисления значения синуса, но и косинуса, а также тангенса и котангенса.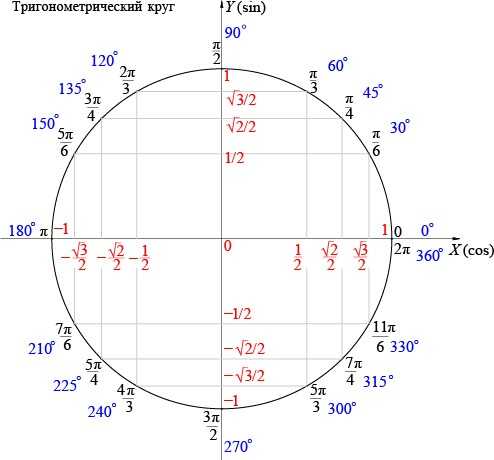

Рассмотрим основные моменты: значения синусов лежат на оси ординат (на оси Оу), а значения косинусов — на оси абсцисс (на оси Ох). Все аргументы функций расположены непосредственно на окружности.
Чтобы вычислить значений синуса от аргумента найдем на окружности нужное значение. Далее нужно спроецировать найденную точку на ось синусов, то есть на ось Оу. Полученное значение будет равно —1. Следовательно, равен —1.
Аналогично вычисляются и другие тригонометрические функции.

Метод использования графика
В школе при изучении тригонометрических функций изучают их графики. Как они выглядят запомнить несложно.

Для его использования нужно найти на оси Ох значение угла, а затем на оси Оу соответствующее значение функции.

ru.solverbook.com