Формула включения и исключения.
Чтобы найти мощность объединения двух непересекающихся множеств
нужно просто сложить их мощности: .
Если множества пересекаются,
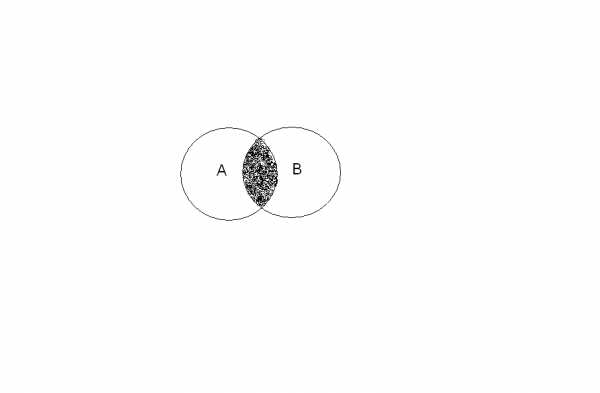
то
при сложении их мощностей каждый элемент
пересечения будет посчитан дважды.
Поэтому для правильного ответа необходимо
из суммы мощностей вычесть мощность их
пересечения:
. При этом каждый элемент объединения
будет посчитан ровно один раз.
При этом каждый элемент объединения
будет посчитан ровно один раз.
Пусть теперь имеется три множества:
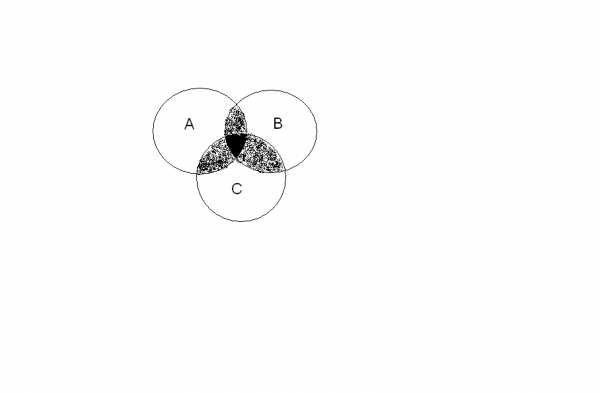
Теперь при сложении мощностей всех трех множеств каждый элемент, входящий ровно в два множества, будет посчитан дважды, а каждый элемент, входящий во все три множества, – трижды. Если из суммы мощностей вычесть мощности попарных пересечений, то по одному разу будут посчитаны элементы, входящие ровно в одно множество и ровно в два множества, но элементы, входящие во все три множества, не будут посчитаны ни разу. Поэтому для получения правильного ответа необходимо еще прибавить мощность пересечения всех трех множеств:
Аналогичная формула справедлива и в общем случае:
Докажем
эту формулу, называемую формулой
включения и исключения. Пусть элемент 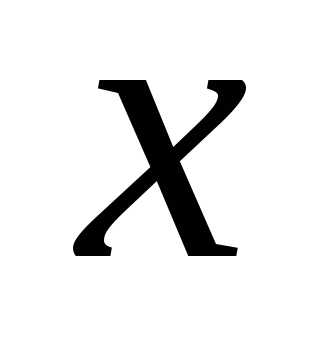 входит ровно в
входит ровно в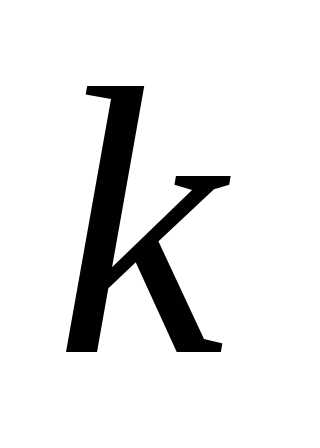 подмножеств
подмножеств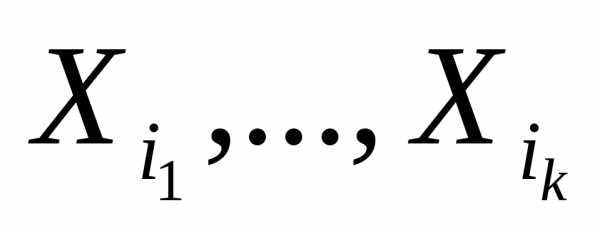 .
Вклад, который дает этот элемент в правую
часть, равен
.
Вклад, который дает этот элемент в правую
часть, равен
,
как это следует из тождества 4 для биномиальных коэффициентов (п. 1.2.). Поэтому вклад каждого элемента в правую часть будет равен единице, т.е. правая часть будет равна полному числу элементов, что и доказывает формулу.
В практических задачах часто имеется некоторое множество U и система его подмножеств U1,…,Um. Требуется найти число элементов множества U, не принадлежащих ни одному из множеств U1,…,Um . В этом случае формула включения и исключения выглядит следующим образом
.
Рассмотрим пример. В группе, состоящей из 20 человек, 6 знают немецкий, 7 – французский и 8 – английский язык, 3 человека знают немецкий и французский, 4 – немецкий и английский, 5 – французский и английский и один человек знает все 3 языка. Сколько человек не знают ни одного иностранного языка?
Другой пример. Пусть требуется найти число натуральных чисел, не превосходящих 100 и не делящихся ни на одно из чисел 3, 5, 7. Число чисел, делящихся на 3, равно [100/3]=33; на 5 – [100/5]=20; на 7 – [100/7]=14. Число чисел, делящихся на 3 и 5, равно [100/15]=6; на 3 и 7 – [100/21]=4, на 5 и 7 – [100/35]=2. Число чисел, делящихся на все три числа 3, 5 и 7, равно [100/105]=0. Поэтому искомое число равно 100–(33+20+14)+(6+4+2)–0=45.
Рассмотрим теперь пример посложнее. Пусть требуется найти число целочисленных решений системы
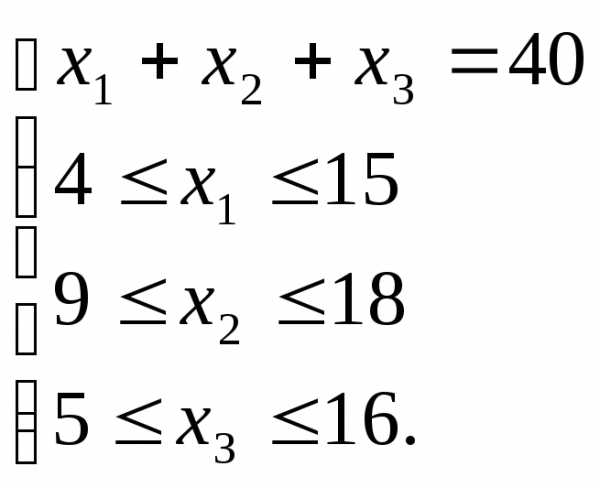
Формула включения и исключения оказывается полезной и здесь. Введем новые переменные ,,. Система перепишется в виде
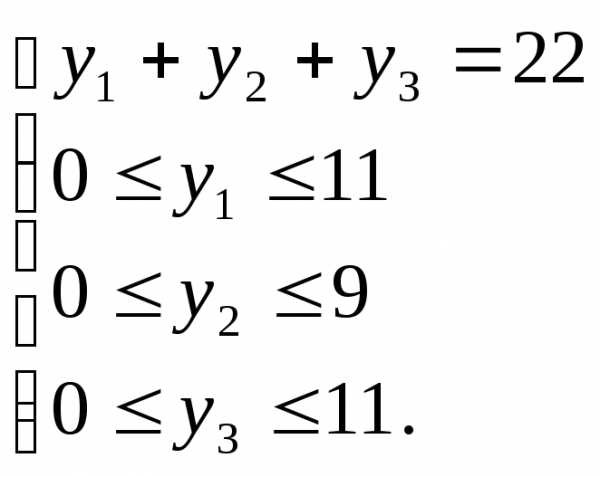
Пусть U – множество решений системы
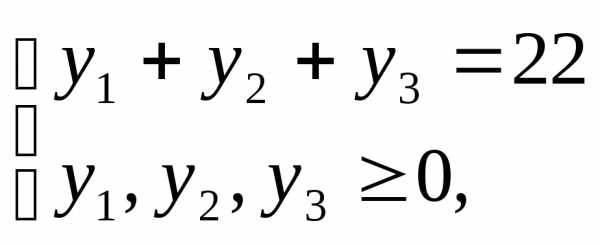
U1 – множество решений системы
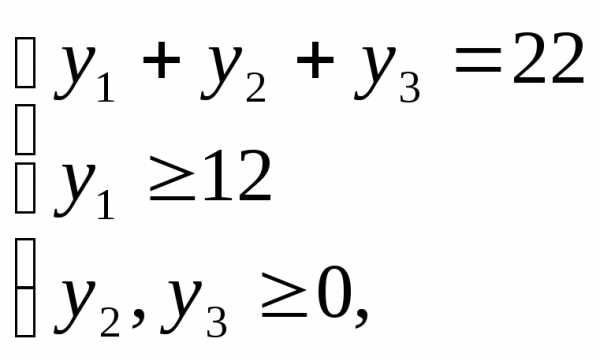
U2 – множество решений системы
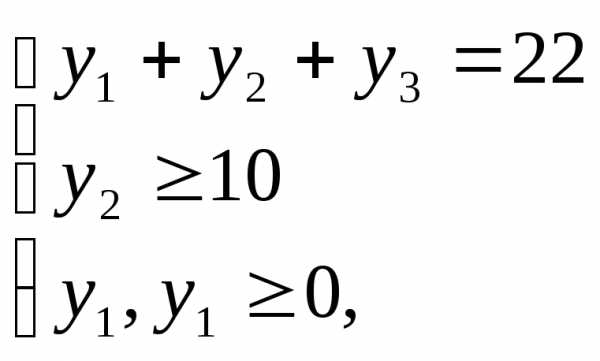
U3 – множество решений системы
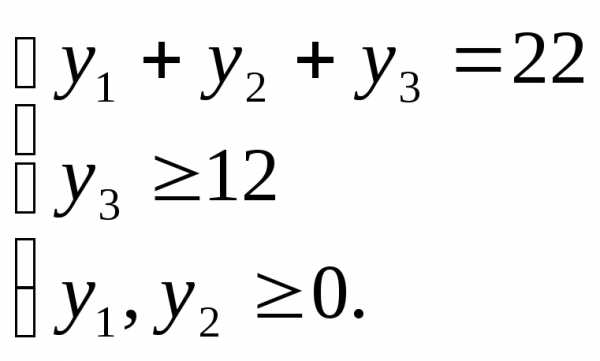
согласно п. 1.1.
Чтобы найти мощность множества U1, достаточно в соответствующей системе сделать замену . Это дает
.
Аналогично,
,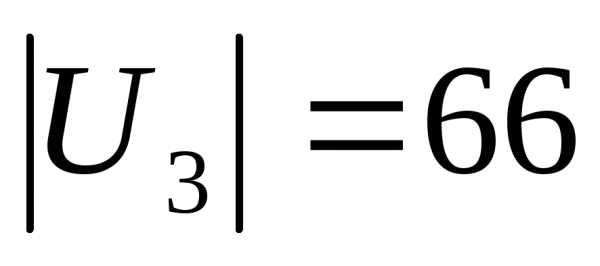 .
.
Далее, легко видеть, что
, ,.
Поэтому в соответствии с формулой включения и исключения число решений исходной системы равно
В
качестве ещё одного примера рассмотрим
известную задачу о беспорядках. Требуется
найти число перестановок чисел 1,2,…,n,
в которых никакое число i
не стоит на i
– ом месте. Всего перестановок 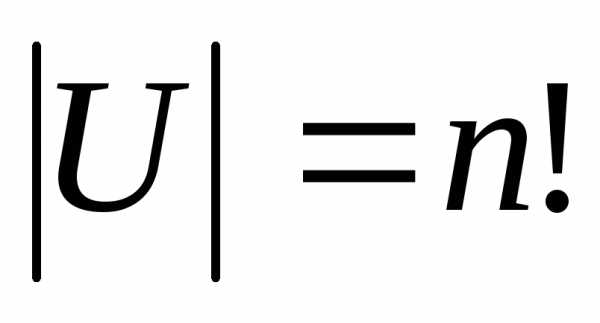 .
Перестановок, в которых числоi
стоит на i
– ом месте,
Перестановок, в которых два различных
числаi
и j
стоят на своих местах,
и т.д. По формуле включения и исключения
имеем
.
Перестановок, в которых числоi
стоит на i
– ом месте,
Перестановок, в которых два различных
числаi
и j
стоят на своих местах,
и т.д. По формуле включения и исключения
имеем
.
Отметим,
что выражение в скобках с ростом 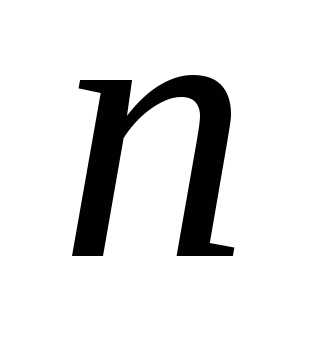 стремится к
стремится к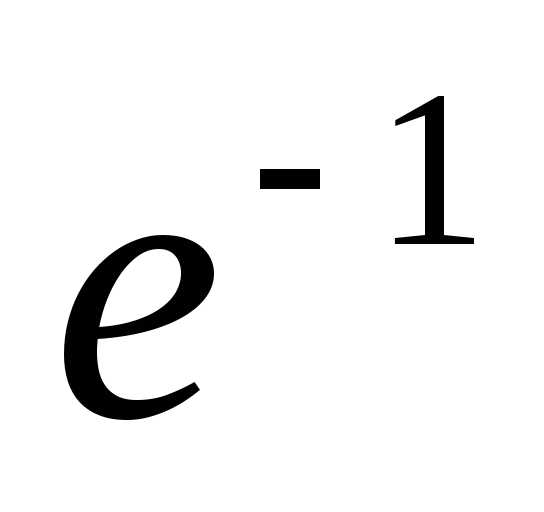 .
.
Вопросы для самопроверки.
В группе 5 студентов не занимается ни в одной спортивной секции, 10 студентов занимается ровно в одной из спортивных секций, 6 судентов ходят в две секции и один студент занимается в трех секциях. Сколько всего студентов в группе?
а) 22; б) 20; в) 25.
В группе 25 студентов. Из них в бассейн ходят 10 человек, в гимнастический зал – 8 человек, в волейбольную секцию – 6 человек. При этом 4 человека ходят одновременно в бассейн и на гимнастику, 3 человека – в бассейн и на волейбол и 2 человека – на гимнастику и на волейбол. Один человек ходит во все три секции. Сколько студентов группы не занимается в спортивных секциях?
а) 12; б) 9; в) 11.
Сколько натуральных чисел, не превосходящих 100, не делятся на 2 и 3? а) 30; б) 33; в) 34.
Формула включений и исключений
Пусть имеется N предметов, некоторые из которых обладают свойствами . При этом каждый предмет может либо не обладать ни одним из этих свойств, либо обладать одним или несколькими свойствами. Обозначим черезчисло предметов, обладающих свойствами
Если предмет не
обладает каким-либо свойством, то это
свойство пишем с чертой. Например,
—
число предметов, обладающих свойствами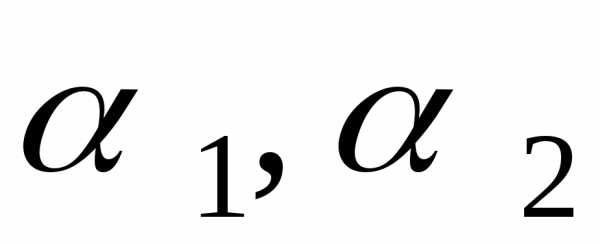 и не обладающих свойствами
и не обладающих свойствами .
Число предметов, не обладающих ни одним
из указанных свойств, обозначается по
этому правилу
.
Число предметов, не обладающих ни одним
из указанных свойств, обозначается по
этому правилу
Формула включений и исключений состоит в том, что
Здесь алгебраическая сумма распространена на все комбинации свойств (без учета их порядка), причем знак + ставится, если число учитываемых свойств четно, и знак — если это число нечетно.Общие указания к решению задач
Правила умножения и сложения можно использовать при решении задач самых различных типов. Формулу включений и исключений используют при подсчете числа объектов, обладающих или не обладающих определенными свойствами.
Пример 2. Из пункта А в пункт В можно добраться пароходом, поездом, автобусом, самолетом; из пункта В в пункт С – пароходом и автобусом. Сколькими способами можно добраться из пункта А в пункт С (рис. 6)?
Рис. 6. Варианты добраться до пункта С.
В задаче рассматриваются объекты: 1 – вид транспорта из пункта А в пункт В;
2 – вид транспорта из пункта
Нужно найти число способов выбора 1 и 2 объектов. Объект 1 можно выбрать четырьмя способами, объект 2 – двумя способами.
По правилу умножения объекты 1 и 2 можно выбрать способами.
Пример 3. Сколько существует четырехзначных двоичных чисел?
Если допустить, что числа могут начинаться с нуля, то когда каждую цифру числа можно выбрать двумя способами (в двоичной системе используются две цифры 0, 1). По правилу умножения получаем, что четырехзначных двоичных чисел будет .
Пример 4. Сколько четырехзначных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, если:
а) ни одна из цифр не повторяется более одного раза;
б) цифры могут повторяться?
Решение:
а) первую цифру можно выбрать пятью способами, это может быть любая цифра из цифр 1, 2, 3, 4, 5 (нуль не может быть первой цифрой потому, что в таком случае число не четырехзначное), вторую цифру можно выбрать пятью способами. Так как цифры не должны повторяться, то третью цифру можно выбрать четырьмя способами, четвертую цифру — тремя способами.
Согласно правилу умножения общее число способов равно
б) первую цифру можно выбрать пятью способами, а каждую следующую цифру шестью способами, так как цифры могут повторяться. Таким образом, число искомых чисел равно
Пример 5. В научно-исследовательском институте работает 67 человек. Из них 47 знают английский язык, 35 – немецкий и 23 – оба языка. Сколько человек в институте не знают ни английского, ни немецкого языков?
Решение. Коллектив сотрудников можно разбить на части:
первую из них составляют те, кто знает только английский язык;
вторую – те, кто знает только немецкий язык;
третью – те, кто знает оба языка;
четвертую – те, кто не знает ни одного, ни другого языка.
Применим формулу включений и исключений, для этого введем обозначения:
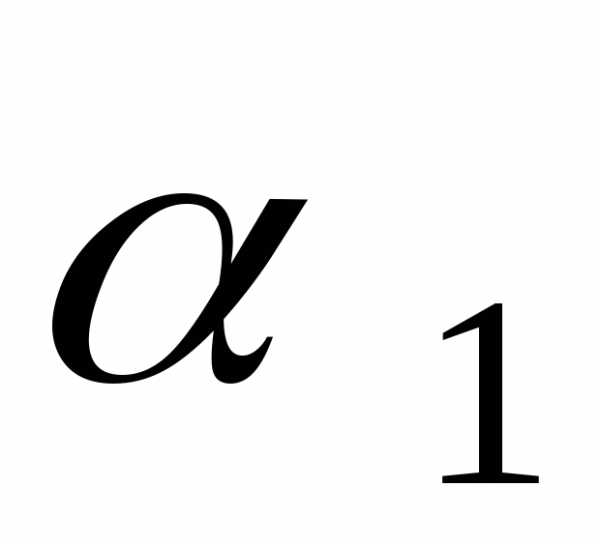 –знание английского
языка;
–знание английского
языка;
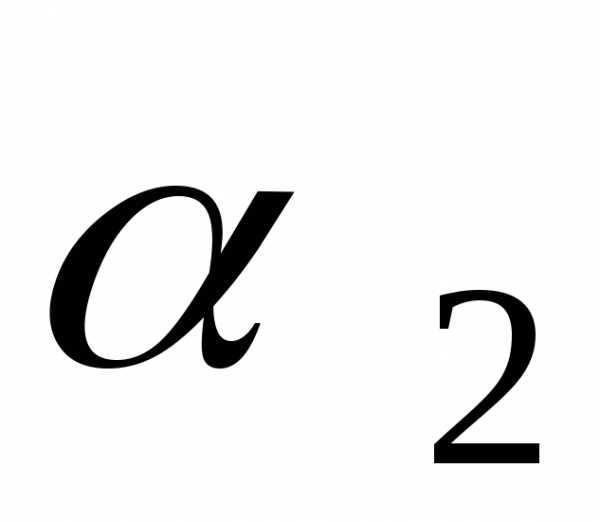 –знание немецкого
языка;
–знание немецкого
языка;
N – число сотрудников института;
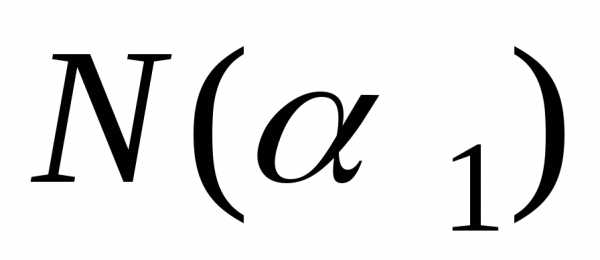 –число сотрудников,
знающих английский язык;
–число сотрудников,
знающих английский язык;
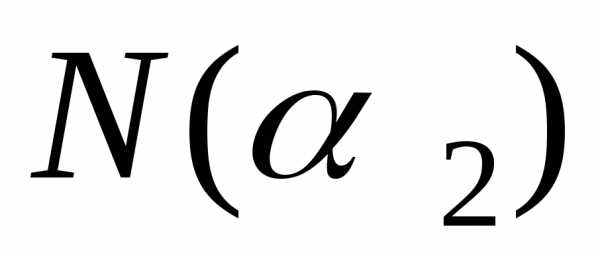 –число сотрудников,
знающих немецкий язык;
–число сотрудников,
знающих немецкий язык;
–число сотрудников, знающих оба языка;
–число сотрудников, не знающих ни одного языка.
По формуле включений и исключений получаем:

Пример 6. Пассажир оставил вещи в автоматической камере хранения, а когда пришел получать вещи, выяснилось, что он забыл номер. Он только помнит, что номер содержал числа 23 и 37. Чтобы открыть камеру, нужно правильно набрать пятизначный номер. Какое наибольшее количество номеров нужно перебрать, чтобы открыть камеру?
В данном случае возможны следующие взаимоисключающие комбинации из цифр:
? 2 3 3 7 ? 3 7 2 3
2 3 ? 3 7 3 7 ? 2 3
2 3 3 7 ? 3 7 2 3 ?
Знак ? стоит на месте забытой цифры.
Этой цифрой может быть любая из десяти цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Таким образом, каждой из 6 комбинаций соответствует 10 различных чисел. По правилу суммы получаем, что общее количество различных чисел равно .
studfiles.net
Формула включений-исключений — это… Что такое Формула включений-исключений?
Формула включений-исключений (или принцип включений-исключений) — комбинаторная формула, позволяющая определить мощность объединения конечного числа конечных множеств, которые в общем случае могут пересекаться друг с другом.
Случай двух множествНапример, в случае двух множеств формула включений-исключений имеет вид:
В сумме элементы пересечения учтены дважды, и чтобы компенсировать это мы вычитаем из правой части формулы. Справедливость этого рассуждения видна из диаграммы Эйлера-Венна для двух множеств, приведенной на рисунке справа.
Таким же образом и в случае множеств процесс нахождения количества элементов объединения состоит во включении всего, затем исключении лишнего, затем включении ошибочно исключенного и так далее, то есть в попеременном включении и исключении. Отсюда и происходит название формулы.
Впервые формулу включений-исключений опубликовал португальский математик Даниэль да Сильва (англ.) в 1854 году [1]. Но еще в 1713 году Николай Бернулли (англ.) использовал этот метод для решения задачи Монмора (англ.), известной как задача о встречах (фр. «Le problème des rencontres»)[2], частным случаем которой является задача о беспорядках. Также формулу включений-исключений связывают с именами французского математика Абрахама де Муавра[источник не указан 1272 дня] и английского математика Джозефа Сильвестра [3]. В теории вероятностей аналог принципа включений-исключений известен как формула Пуанкаре[1].
Формулировка
Формулу включений-исключений можно сформулировать в разных формах.
В терминах множеств
Пусть — конечные множества. Формула включений-исключений утверждает:
При получаем формулу для двух множеств, приведенную выше.
В терминах свойств
Принцип включений-исключений часто приводят в следующей альтернативной формулировке [4]. Пусть дано конечное множество , состоящее из элементов, и пусть имеется набор свойств . Каждый элемент множества может обладать или не обладать любым из этих свойств. Обозначим через количество элементов, обладающих свойствами (и, может быть, некоторыми другими). Также через обозначим количество элементов, не обладающих ни одним из свойств . Тогда имеет место формула:
Формулировка принципа включений-исключений в терминах множеств эквивалентна формулировке в терминах свойств. Действительно, если множества являются подмножествами некоторого множества , то в силу правил де Моргана (черта над множеством — дополнение в множестве ), и формулу включений-исключений можно переписать так:
Если теперь вместо «элемент принадлежит множеству » говорить «элемент обладает свойством », то мы получим формулировку принципа включений-исключений в терминах свойств, и наоборот.
Обозначим через количество элементов, обладающих в точности свойствами из набора .Тогда формулу включений-исключений можно переписать в следующей замкнутой форме (англ.)
Доказательство
Существует несколько доказательств формулы включений-исключений.
По индукции
Формулу включений-исключений можно доказать по индукции [1][5].
При формула включений-исключений тривиальна:
Пусть формула верна для , докажем ее для .
Пусть каждый элемент множества может обладать или не обладать любым из свойств . Применим формулу включений-исключений для свойств :
Теперь применим формулу для свойств к множеству объектов, для которых выполнено свойство :
Наконец, применим формулу для одного свойства к совокупности , объектов, которые не обладают свойствами :
Комбинируя выписанные три формулы, получим формулу включений-исключений для свойств . Что и требовалось доказать.
Комбинаторное доказательство
Рассмотрим произвольный элемент и подсчитаем, сколько раз он учитывается в правой части формулы включений-исключений[4].
Если элемент не обладает ни одним из свойств , то в правой части формулы он учитывается ровно 1 раз (в члене ).
Пусть элемент обладает в точности свойствами, скажем . Он дает по 1 в тех слагаемых суммы , для которых есть подмножество , и 0 для остальных. Число таких подмножеств по определению есть число сочетаний . Следовательно, вклад элемента в правую часть равен
При числа сочетаний равны нулю. Оставшаяся сумма в силу биномиальной теоремы равна
Таким образом, правая часть формулы включений-исключений учитывает каждый элемент, не имеющий указанных свойств точно по одному разу, а каждый элемент, обладающий хотя бы одним из свойств — нуль раз. Следовательно, она равна количеству элементов, не обладающих ни одним из свойств , то есть . Что и требовалось доказать.
Используя индикаторные функции
Пусть — произвольные (не обязательно конечные) множества, являющиеся подмножествами некоторого множества , и пусть — индикаторные функции (или, эквивалентно, свойств ).
Индикаторные функции их дополнений равны
а индикаторная функция пересечения дополнений:
Раскрывая скобки в правой части и еще раз используя тот факт, что индикаторная функция пересечения множеств равна произведению их индикаторных функций, получим
Это соотношение — одна из форм принципа включений-исключений. Оно выражает собой логическое тождество[1] и верно для произвольных множеств . В случае конечных множеств (и, соответственно, в предположении конечности множества ), просуммировав это соотношение по всем и воспользоваться тем, что для произвольного подмножества его мощность равна
получим формулировку принципа включений-исключений в терминах мощностей множеств (или в терминах свойств).
Применение
Задача о беспорядках
Основная статья: Задача о беспорядках
Классический пример использования формулы включений-исключений — задача о беспорядках [4]. Требуется найти число перестановок множества таких что для всех . Такие перестановки называются беспорядками.
Пусть — множество всех перестановок и пусть свойство перестановки выражается равенством . Тогда число беспорядков есть . Легко видеть, что — число перестановок, оставляющих на месте элементы , и таким образом сумма содержит одинаковых слагаемых. Формула включений-исключений дает выражение для числа беспорядков:
Это соотношение можно преобразовать к виду
Нетрудно видеть, что выражение в скобках является частичной суммой ряда . Таким образом, с хорошей точностью число беспорядков составляет долю от общего числа перестановок:
Вычисление функции Эйлера
Другой пример применения формулы включений-исключений — нахождение явного выражения для функции Эйлера [6].
Для целого положительного функция Эйлера дает количество чисел ряда , взаимно простых с . Найдем явное выражение для функции Эйлера.
Пусть каноническое разложение числа на простые множители имеет вид
Число взаимно просто с тогда и только тогда, когда ни один из простых делителей не делит . Если теперь свойство означает, что делит , то количество чисел взаимно простых с есть .
Количество чисел, обладающих свойствами равно , поскольку .
По формуле включений-исключений находим
Эта формула преобразуется к виду:
Вариации и обобщения
Принцип включения-исключения для вероятностей
Пусть — вероятностное пространство. Тогда для произвольных событий справедлива формула [1][5][7]
Эта формула выражает принцип включений-исключений для вероятностей. Ее можно получить из принципа включений-исключений в форме индикаторных функций:
Пусть — события вероятностного пространства , то есть . Возьмем математическое ожидание от обеих частей этого соотношения, и, воспользовавших линейностью математического ожидания и равенством для произвольного события , получим формулу включения-исключения для вероятностей.
Принцип включений-исключений в пространствах с мерой
Пусть — пространство с мерой. Тогда для произвольных измеримых множеств конечной меры имеет место формула включений-исключений:
Очевидно, принцип включений-исключений для вероятностей и для мощностей конечных множеств являются частными случаями этой формулы. В первом случае мерой является, естественно, вероятностная мера в соответствующем вероятностном пространстве: . Во втором случае в качестве меры берется мощность множества: .
Вывести принцип включений-исключений для пространств с мерой можно также, как для указанных частных случаев, из тождества для индикаторных функций:
Пусть — измеримые множества пространства , то есть . Проинтегрируем обе части этого равенства по мере , воспользуемся линейностью интеграла и соотношением , и получим формулу включений-исключений для меры.
Тождество максимумов и минимумов
Формула включений-исключений может рассматриваться как частный случай тождества максимумов и минимумов:
Это соотношение справедливо для произвольных чисел . В частном случае, когда мы получаем одну из форм принципа включений-исключений. В самом деле, если положить , где — произвольный элемент из , то получим соотношение для индикаторных функций множеств:
Обращение Мёбиуса
Пусть — конечное множество, и пусть — произвольная функция, определенная на совокупности подмножеств и принимающая действительные значения. Определим функцию следующим соотношением:
Тогда имеет место следующая формула обращения[8][9]:
Это утверждение является частным случаем общей формулы обращения Мёбиуса для алгебры инцидентности (англ.) совокупности всех подмножеств множества , частично упорядоченных по отношению включения .
Покажем, как из этой формулы следует принцип включения-исключения для конечных множеств. Пусть дано семейство подмножеств конечного множества , обозначим — множество индексов. Для каждого набора индексов определим как число элементов, входящих только в те множества , для которых . Математически это можно записать так:
Тогда функция , определенная формулой
дает количество элементов, каждый из которых входит во все множества , , и, быть может, еще в другие. То есть
Заметим далее, что — количество элементов, не обладающих ни одним из свойств:
С учетом сделанных замечаний запишем формулу обращения Мёбиуса:
Это есть в точности формула включений-исключений для конечных множеств, только в ней не сгруппированы слагаемые, относящиеся к одинаковым значениям .
См. также
Примечания
- ↑ 1 2 3 4 5 Риордан Дж. Введение в комбинаторный анализ = An Introduction to Combinatorial Analysis. — М.: Изд-во иностранной литературы, 1963. — С. 63-66. — 289 с.
- ↑ Weisstein, Eric W. Derangement (англ.) на сайте Wolfram MathWorld.
- ↑ Рыбников К. А. Введение в комбинаторный анализ. — 2-е изд. — М.: Изд-во МГУ, 1985. — С. 264. — 309 с.
- ↑ 1 2 3 Холл М. Комбинаторика = Combinatorial Theory. — М.: «Мир», 1970. — С. 18-20. — 424 с.
- ↑ 1 2 Рыбников К. А. Введение в комбинаторный анализ. — 2-е изд. — М.: Изд-во МГУ, 1985. — С. 69-73. — 309 с.
- ↑ Рыбников К. А. Введение в комбинаторный анализ. — 2-е изд. — М.: Изд-во МГУ, 1985. — С. 266. — 309 с.
- ↑ Боровков, А. А. Теория вероятностей. — 2-е изд. — М.: «Наука», 1986. — С. 24. — 431 с.
- ↑ Холл М. Комбинаторика = Combinatorial Theory. — М.: «Мир», 1970. — С. 30-31. — 424 с.
- ↑ Стенли Р. Перечислительная комбинаторика = Enumerative Combinatorics. — М.: «Мир», 1990. — С. 103-107. — 440 с.
Ссылки
dic.academic.ru
Формула включений-исключений
Теорема Эрдеша.
Результат, доказанный Полом Эрдёшем и Дьёрдем (Джорджем) Секерешем таков: для данных r, s они показали, что любая последовательность длины по крайней мере (r-1)(s-1)+1 содержит или монотонно возрастающую подпоследовательность длины r, или монотонно убывающую длины s. Для r=3 и s=2, формула говорит, что любая переста новка трёх чисел имеет возрастающую подпоследовательность длиной три или убывающую подпоследовательность длиной два. Пример: Из шести перестановок чисел 1,2,3:
-1,2,3 имеет возрастающую подпоследовательность длиной три
-1,3,2 имеет убывающую подпоследовательность 3,2
-2,1,3 имеет убывающую подпоследовательность 2,1
-2,3,1 имеет две убывающие подпоследовательности, 2,1 и 3,1
-3,1,2 имеет две убывающие подпоследовательности, 3,1 and 3,2
-3,2,1 имеет три убывающие подпоследовательности длины 2, 3,2, 3,1, и 2,1.
Теорема Эрдёша-Секереша может быть доказана несколькими разными способами; Майкл Стил дает обзор шести разных доказательств теоремы, в том числе с использованием принципа Дирихле и теоремы Дилворта.[2] Прочие способы доказательства, приводимые Стилом, включают оригинальное доказательство Эрдёша и Секереша и доказательство Блэквелла, Ловаса и самого Стила
Формула включений-исключений
Формула включений-исключений (или принцип включений-исключений) —комбинаторная формула, позволяющая определить мощность объединения конечного числа конечных множеств, которые в общем случае могут пересекаться друг с другом.
Например, в случае двух множеств формула включений-исключений имеет вид:
В сумме элементы пересечения учтены дважды, и чтобы компенсировать это мы вычитаем из правой части формулы.
Таким же образом и в случае множеств процесс нахождения количества элементов объединения состоит во включении всего, затем исключении лишнего, затем включении ошибочно исключенного и так далее, то есть в попеременном включении и исключении. Отсюда и происходит название формулы.
Впервые формулу включений-исключений опубликовал португальский математик Даниэль да Сильва в 1854 году. Но еще в 1713 году Николай Бернулли использовал этот метод для решения задачи Монмора, известной как задача о встречах, частным случаем которой является задача о беспорядках. Также формулу включений-исключений связывают с именами французского математика Абрахама де Муавра и английского математика Джозефа Сильвестра. В теории вероятностей аналог принципа включений-исключений известен как формула Пуанкаре.
5. Теорема о биекциях.
Биекция — это отображение, которое является одновременно и сюръективным и инъективным. При биективном отображении каждому элементу одного множества соответствует ровно один элемент другого множества, при этом, определено обратное отображение, которое обладает тем же свойством. Поэтому биективное отображение называют ещё взаимно-однозначным отображением(соответствием), одно-однозначным отображением. Если между двумя множествами можно установить взаимно-однозначное соответствие (биекция), то такие множества называются равномощными. С точки зрения теории множеств, равномощные множества неразличимы. Взаимно-однозначное отображение конечного множества в себя называется перестановкой (элементов этого множества). Функция называется биекцией (и обозначается ), если она:
Переводит разные элементы множества X в разные элементы множества Y (инъективность). Иными словами,
.
Любой элемент из Y имеет свой прообраз (сюръективность). Иными словами,
.
Теорема о инъекциях.
Отображение называется инъекцией (или вложением, или отображением «в»), если разные элементы множества X переводятся в разные элементы множества Y.
Формально это значит, что если два образа совпадают, то совпадают и прообразы ( ). Инъективность является необходимым условием биективности (достаточно вместе ссюръективностью).
Инъекцию можно также определить как отображение, для которого существует левое обратное, то есть инъективно, если существует такое, что .
Теорема о сурьекциях.
Отображение называется сюръективным (или сюръекцией, или отображением на Y), если каждый элемент множества Y является образом хотя бы одного элемента множества X, то есть . Для случая числовых функций это выражается как «функция, принимающая все возможные значения». Пример. — сюръективно.
Определение формулы АВ.
1)Простейшие высказ-я А,В,А1,А2 ..- формулы. 2)Если Φ,Ψ-формулы, то тогда (Φ), ( Φ)→( Ψ), ( Φ)&( Ψ), ( Φ)v ( Ψ), ( Φ)↔( Ψ).3)Др формул нет. Все формулы АВ построены таким обр-м. Договоренность о снятии скобок: связки по старшинству: 1,2v, &,3 →,↔.Поэтому в формуле (Φ) → Ψ, мы может убрать скобки и получить в итоге Φ → Ψ, исходя их старшинства связок.
Формулы АВ в юриспруденции.
У-убийство имело место после полуночи, С- Смит убийца,D-Джонс лжет, V-Джонс не встр ночью Смита.
V→Cv D
C→(V Λ Y)
Y→Cv D
C
(V→Cv D) Λ [C→(VΛ Y)]Λ ( Y→Cv D) →C
Попробуем подобрать значения С=л, V=и, Y=и, D=и. V,D,Y возможно. Возможно, что С не убийца. Вывод следователя был неполный. Он не учел все вещи. Эта формула бывает ложной. Т.е. с помощью математической логики мы пришли к заключению, что следователь не полностью исследовал все условия данного дела.
14.Полные системы логических связок.Определение. Множество функций алгебры логики называются полной системой, если любую функцию алгебры логики можно выразить формулой ——
Теорема: Система Ає{v, &, } – полна. Доказательство: Если функция алгебры логики f отличается от тождественного нуля, то А выражается в виде совершенной дизъюнктивной форме, в которую входит лишь дизъюнкция, конъюнкция, и отрицание. Если же f=0, то f есть x&x (ч.т.д). Лемма системы:
1.{x&y, x}2.{xVy, x}3.{x->y, x}4.{x|y} где x|y ~ (x&y) 5. {xΛy} где |xΛy| ~(xVy) полны
Доказательство.
1.x&y= (xVy) 2.xVy= (x&y) 3.x->y= xVy= (x&y)
А так как система Ає{v, &, } полна, то эти 3 пунка доказуемы.
4. x ~ xΛx; xVy ~ (xΛx) V (yΛy)
5. x ~ x|x; xVy ~ (x|x) V (y|y) ч.т.д
Понятие вывода.
Определение. Выводом из конечной совокупности формул H называется всякая конечная последовательность формул , всякий член которой удовлетворяет одному из следующих трех условий: 1) является одной из формул совокупности H; 2) является доказуемой формулой; 3) получается по правилу заключения из двух любых предшествующих членов последовательности .
Свойства вывода:
1) Всякий начальный отрезок вывода из совокупности H есть вывод из H.
2) Если между двумя соседними членами вывода из H вставить некоторый вывод из H, то полученная новая последовательность формул будет выводом из H.
3) Всякий член вывода из совокупности H, является формулой, выводимой из H.
Следствие. Всякий вывод из H является выводом его последней формулы.
4) Если , то всякий вывод из H является из W.
5) Для того, чтобы формула B была выводима из совокупности H, необходимо и достаточно, чтобы существовал вывод этой формулы из H.
Понятие вывода
ками вывода. Свойства:
23. Теорема о дедукции
Лемма Кальмара
29.Теорема полноты исчисления высказывний.
Общезначимые формулы.
Общезначимость аксиом ИП.
Определение. Формула А называется общезначимой тогда и только тогда, когда она истинна в каждой интерпретации.
Аксиомы ИП общезначимы.
Теорема о полноте ИП.
41. Системы одноместных предикатов формульных в арифметике. Определение 1. Одноместным предикатом Р(x) называется произвольная функция переменного x, определенная на множестве M и принимающая значение из множества {1; 0}. Множество М, на котором определен предикат Р(x), называется областью определения предиката Р(x). Множество всех элементов , при которых предикат принимает значения “истина” (1), называется множеством (областью) истинности предиката Р(x), т.е. множество истинности предиката Р(х)- это множество . Так, например, предикат Р(x) – “x – простое число” определен на множестве N, а множество истинности IP для него есть множество всех простых чисел.
Р(х) – “х есть простое число”
П(х) – “x=pa, где р-простое”
Sq(x) – “х есть квадрат нат. числа”
Сub(x) – “х есть куб нат. числа”
Even(x) – “х есть четное число”
Odd (x) – “х есть нечентное число”
Even(x)~ ØOdd (x)
42. Система одноместных операций формульных в арифметике. Предикаты, так же, как высказывания, принимают значения И или Л, поэтому и к предикатам и к высказываниям применимы все операции логики высказываний. Одноместная операция это такая операция, где участвует только одно высказывание или предикат. Логическое отрицание является одноместной операцией. Таблица истинности одноместной логической операции состоит из двух строк: два различных значения аргумента — «истина» (1) и «ложь» (0) и два соответствующих им значения функции. Логическая операция НЕ применяется к одному аргументу, в качестве которого может быть и простое, и сложное логическое выражение. Результатом операции НЕ является следующее: Результат операции отрицания истинен, когда исходное высказывание ложно, и наоборот. Приведем примеры отрицания: Высказывание «Земля вращается вокруг Солнца» истинно. Высказывание «Земля не вращается вокруг Солнца» ложно.
43. Система двухместных предикатов формульных в арифметике.Определение 1. Двухместным предикатом Р(x,y)называется функция двух переменных x и y, определенная на множестве М=М1хМ 2 и принимающая значения из множества {1;0}. В числе примеров двухместных предикатов можно назвать такие предикаты: Q(x, y) – “x=y” — предикат равенства, определенный на множестве RхR=R2;
44. Система двухместных операций формульных в арифметике.Предикаты, так же, как высказывания, принимают значения И или Л, поэтому и к предикатам и к высказываниям применимы все операции логики высказываний. Двухместная операция – операция в которой участвуют два высказывания или предиката. в таблице истинности двуместной логической операции — четыре строки: 4 различных сочетания значений аргументов — 00, 01, 10 и 11 и 4 соответствующих им значения функции. 45.Система двухместных операций формульных в арифметике.
Двуместные операции
z=lcm(x,y) наименьшее общее кратное
z=gcd(x,y) наибольший общий делитель
z=DIV(x,y) частное от деления x на y
z=MOD(x,y) остаток от деления x на y
z=exp(x,y) z=xy=eylnx
p=gcd(x,y) ~ [(x|p&y|p)&Av(v|x&v|y)=>v|p]
x=1 ~ A y [lcm(x,y)=y]
x=1 ~ A y [gcd(x,y)=x]
x=0 ~ A y [gcd(x,y)=y]
45.Определимость констант 0.1.2,… в системах не менее сильных чем следование.
Neib(x,y) ~ [(x=s(y) vy=s(x)]
SK(x)=y ~ S(S…(x)) /*K раз*/ =y
x=0 ~ -E y(S(y)=x)
x=1 ~ E y (S(y)=x & y=0)
x=2 ~ E y (S(y)=x & y=1)
Теорема Эрдеша.
Результат, доказанный Полом Эрдёшем и Дьёрдем (Джорджем) Секерешем таков: для данных r, s они показали, что любая последовательность длины по крайней мере (r-1)(s-1)+1 содержит или монотонно возрастающую подпоследовательность длины r, или монотонно убывающую длины s. Для r=3 и s=2, формула говорит, что любая переста новка трёх чисел имеет возрастающую подпоследовательность длиной три или убывающую подпоследовательность длиной два. Пример: Из шести перестановок чисел 1,2,3:
-1,2,3 имеет возрастающую подпоследовательность длиной три
-1,3,2 имеет убывающую подпоследовательность 3,2
-2,1,3 имеет убывающую подпоследовательность 2,1
-2,3,1 имеет две убывающие подпоследовательности, 2,1 и 3,1
-3,1,2 имеет две убывающие подпоследовательности, 3,1 and 3,2
-3,2,1 имеет три убывающие подпоследовательности длины 2, 3,2, 3,1, и 2,1.
Теорема Эрдёша-Секереша может быть доказана несколькими разными способами; Майкл Стил дает обзор шести разных доказательств теоремы, в том числе с использованием принципа Дирихле и теоремы Дилворта.[2] Прочие способы доказательства, приводимые Стилом, включают оригинальное доказательство Эрдёша и Секереша и доказательство Блэквелла, Ловаса и самого Стила
Формула включений-исключений
Формула включений-исключений (или принцип включений-исключений) —комбинаторная формула, позволяющая определить мощность объединения конечного числа конечных множеств, которые в общем случае могут пересекаться друг с другом.
Например, в случае двух множеств формула включений-исключений имеет вид:
В сумме элементы пересечения учтены дважды, и чтобы компенсировать это мы вычитаем из правой части формулы.
Таким же образом и в случае множеств процесс нахождения количества элементов объединения состоит во включении всего, затем исключении лишнего, затем включении ошибочно исключенного и так далее, то есть в попеременном включении и исключении. Отсюда и происходит название формулы.
Впервые формулу включений-исключений опубликовал португальский математик Даниэль да Сильва в 1854 году. Но еще в 1713 году Николай Бернулли использовал этот метод для решения задачи Монмора, известной как задача о встречах, частным случаем которой является задача о беспорядках. Также формулу включений-исключений связывают с именами французского математика Абрахама де Муавра и английского математика Джозефа Сильвестра. В теории вероятностей аналог принципа включений-исключений известен как формула Пуанкаре.
5. Теорема о биекциях.
Биекция — это отображение, которое является одновременно и сюръективным и инъективным. При биективном отображении каждому элементу одного множества соответствует ровно один элемент другого множества, при этом, определено обратное отображение, которое обладает тем же свойством. Поэтому биективное отображение называют ещё взаимно-однозначным отображением(соответствием), одно-однозначным отображением. Если между двумя множествами можно установить взаимно-однозначное соответствие (биекция), то такие множества называются равномощными. С точки зрения теории множеств, равномощные множества неразличимы. Взаимно-однозначное отображение конечного множества в себя называется перестановкой (элементов этого множества). Функция называется биекцией (и обозначается ), если она:
Переводит разные элементы множества X в разные элементы множества Y (инъективность). Иными словами,
.
Любой элемент из Y имеет свой прообраз (сюръективность). Иными словами,
.
Теорема о инъекциях.
Отображение называется инъекцией (или вложением, или отображением «в»), если разные элементы множества X переводятся в разные элементы множества Y.
Формально это значит, что если два образа совпадают, то совпадают и прообразы ( ). Инъективность является необходимым условием биективности (достаточно вместе ссюръективностью).
Инъекцию можно также определить как отображение, для которого существует левое обратное, то есть инъективно, если существует такое, что .
Теорема о сурьекциях.
Отображение называется сюръективным (или сюръекцией, или отображением на Y), если каждый элемент множества Y является образом хотя бы одного элемента множества X, то есть . Для случая числовых функций это выражается как «функция, принимающая все возможные значения». Пример. — сюръективно.
Определение формулы АВ.
1)Простейшие высказ-я А,В,А1,А2 ..- формулы. 2)Если Φ,Ψ-формулы, то тогда (Φ), ( Φ)→( Ψ), ( Φ)&( Ψ), ( Φ)v ( Ψ), ( Φ)↔( Ψ).3)Др формул нет. Все формулы АВ построены таким обр-м. Договоренность о снятии скобок: связки по старшинству: 1,2v, &,3 →,↔.Поэтому в формуле (Φ) → Ψ, мы может убрать скобки и получить в итоге Φ → Ψ, исходя их старшинства связок.
infopedia.su
Формула включений и исключений — 7 Июля 2016 — Примеры решений задач
Пусть задано конечное множество А. Число его элементов обозначим n(А). Найдем сколько элементов содержится в множестве А ∪ В. Основная формула нахождения числа элементов суммы двух множеств
n(А ∪ В) = n(А) + n(В) – n(А ∩ В) (1)
Действительно, n(А ∪ В) — это сумма числа элементов множеств А и В, но при подсчете элементы, принадлежащие А ∩ В учитывались дважды. С помощью формулы (1) можно получить формулы для определения числа элементов суммы любого числа множеств. Например,
n(А ∪ В ∪ С) = n(А ∪ (В ∪ С)) = n(А) + n(В ∪ С) – n(А ∩ (В ∪ С)) =
= n(А) + n(В) + n(С) – n(В ∩ С) – n((А ∩ В) ∪ (А ∩ С)) =
= n(А) + n(В) + n(С) – n(В ∩ С) – (n(А ∩ В) + n(А ∩ С) – n((А ∩ В) ∩ (А ∩ С))) =
=n(А) + n(В) + n(С) – n(В ∩ С) – n(А ∩ В) – n(А ∩ C) + n(А ∩ В ∩ С).
n(А ∪ В ∪ С) = n(А) + n(В) + n(С) – n(А ∩ В) – n(В ∩ С) – n(А ∩ C) + n(А ∩ В ∩ С) (2)
Формулы (1) и (2) называют формулами включений и исключений.
Примеры с подробным решением.
Задача 1. Из 100 школьников английский знают 42, немецкий — 30, французский — 28, английский и немецкий — 5, английский и французский — 10, немецкий и французский — 8, английский, немецкий и французский — 3 школьника. Сколько школьников не знают ни одного языка?
Решение. I способ.
Обозначим через А — множество школьников, знающих английский язык; N — множество школьников, знающих немецкий язык; F — множество школьников, знающих французский язык.
Тогда n(A) = 42, n(N) = 30, n(F) = 28, n(A ∩ N) = 5,
n(A ∩ F) = 10, n(N ∩ F) = 8, n(A ∩ N ∩ F) = 3.
Найдем с помощью формулы включений и исключений количество школьников, знающих хотя бы один из перечисленных иностранных языков.
n(A ∪ N ∪ F) = n(A) + n(N) + n(F) =
= n(A ∩ N) – n(A ∩ F) – n(N ∩ F) + n(A ∩ N ∩ F) =
= 42 + 30 + 28 – 5 – 10 – 8 + 3 = 80.
Следовательно, не знают ни одного иностранного языка:
100 – 80 = 20 школьников.
II способ.
Эту же задачу можно решить с помощью диаграммы Эйлера–Венна (рис. 1).
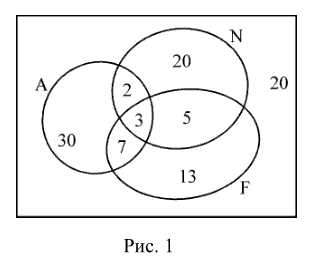
Так как 3 языка знают 3 школьника, то английский и немецкий знают 5 – 3 = 2, английский и французский — 10 – 3 = 7,
немецкий и французский — 8 – 3 = 5 школьников.
Только английский знают 42 –(2 + 3 + 7) = 30,
только немецкий — 30 – (2 + 3 + 5) = 20,
только французский — 28 – (3 + 5 + 7) = 13 школьников.
Ни одного языка не знают 100 – (2 + 3 + 5 + 7 + 13 + 20 + 30) = 20 школьников.
Задача 2. Сколько двузначных чисел не делятся ни на 2, ни на 3, ни на 5, ни на 11?
Решение. Обозначим: А — множество двузначных чисел, делящихся на 2;
В — множество двузначных чисел, делящихся на 3;
С — множество двузначных чисел, делящихся на 5;
D — множество двузначных чисел, делящихся на 11.
n(A ∪ B ∪ C ∪ D) — количество двузначных чисел, делящихся хотя бы на одно из чисел 2; 3; 5; 11.
n(A ∪ B ∪ C ∪ D) = n(A) + n(B) + n(C) + n(D) –
– n(A ∩ B) – n(A ∩ C) – n(A ∩ D) – n(B ∩ C) –
– n(B ∩ D) – n(C ∩ D) + n(A ∩ B ∩ C) + n(A ∩ B ∩ D) +
+ n(A ∩ C ∩ D) + n(B ∩ C ∩ D) – n(A ∩ B ∩ C ∩ D).
n(A) = 45, n(B) = 30, n(C) = 18, n(D) = 9,
n(A ∩ B) = 15, n(A ∩ C) = 9, n(A ∩ D) = 4, n(B ∩ C) = 6,
n(B ∩ D) = 3, n(C ∩ D) = 1, n(A ∩ B ∩ C) = 3,
n(A ∩ B ∩ D) = 1, n(A ∩ C ∩ D) = n(B ∩ C ∩ D) = n(A ∩ B ∩ C ∩ D) = 0.
Итак, n(A ∪ B ∪ C ∪ D) = 45 + 30 +18 + 9 – 15 – 9 – 4 – 6 – 3 – 1 + 3 + 1 = 68.
Так как всего 90 двузначных чисел, то чисел, не делящихся ни на одно из заданных чисел:
90 – 68 = 22.
Задача 3. Известно, что из n учеников спортом увлекаются a учеников, программированием b, математикой c, спортом и программированием d, спортом и математикой e, программированием и математикой f , спортом, математикой и программированием g учеников. Сколько учеников увлекается только программированием? Сколько учеников увлекается только математикой? Сколько учеников ничем не увлекается?
Вариант | n | a | b | c | d | e | f | g |
14 | 70 | 32 | 21 | 23 | 8 | 12 | 4 | 3 |
Решение. Пусть A —множество учеников, которые увлекаются спортом,
B — программированием, С — математикой.
Тогда |A| = 32, |B| = 21, |C| = 23, |A ∩ B| = 8, |A ∩ C| = 12, |B ∩ C| =4 |A ∩ B ∩ C| = 3
|(A ∩ B) ∪ ( B ∩ C) | = |A ∩ B| + |B ∩ C| − |A ∩ B ∩ C| = 8 + 4 – 3 = 9
Тогда, только программированием занимается 21 – 9 = 12 учеников.
|(A ∩ C) ∪ ( B ∩ C) | = |A ∩ C| + |B ∩ C| − |A ∩ B ∩ C| = 12 + 4 – 3 = 13
Тогда, только математикой занимается 23 – 13 = 10 учеников.
По формуле включений и исключений для трёх множеств находим число учеников увлекающихся спортом, программированием или математикой:
|A ∪ B ∪ C| = |A| + |B| + |C| − |A ∩ B| − |A ∩ C| − |B ∩ C| + |A ∩ B∩ C| = =32+21+23-8-12-4+3 = 55
Значит, ничем не увлекается 70 − 55 = 15 человек. Ответ: 15.
Упражнения
1. В спортивном классе обучаются 24 человека. Каждый учащийся занимается хотя бы одним видом спорта (баскетболом или волейболом), из них баскетболом и волейболом занимаются 12 человек. Сколько человек занимается только волейболом, если их в 3 раза больше, чем тех, кто занимается только баскетболом?
2. В одном украинском городе все жители говорят на русском или украинском языке. По-украински говорят 80 % всех жителей, а по-русски — 75 %. Сколько процентов всех жителей говорят на обоих языках?
3. Группа ребят отправилась в поход. Семеро из них взяли с собой бутерброды, шестеро — фрукты, пятеро — печенье. Четве- ро ребят взяли с собой бутерброды и фрукты, трое — бутерброды и печенье, двое — фрукты и печенье, а один — и бутерброды, и фрукты, и печенье. Сколько ребят пошли в поход?
4. Староста класса, в котором 40 человек, подводил итоги по успеваемости группы за I полугодие. Получилась следующая картина: из 40 учащихся не имеют троек по русскому языку 25 человек, по математике — 28 человек, по русскому языку и мате- матике — 16 человек, по физике — 31 человек, по физике и ма- тематике — 22 человека, по физике и русскому языку 16 человек. Кроме того, 12 человек учатся без троек по всем трем предметам. Классный руководитель, просмотрев результаты, сказал: «В тво- их расчетах есть ошибка». Составьте диаграмму Эйлера–Венна и объясните, почему это так.
5. В лаборатории института работают несколько человек. Каждый из них знает хотя бы один иностранный язык. 7 человек знают английский, 7 — немецкий, 8 — французский, 5 знают английский и немецкий, 4 — немецкий и французский, 3 — французский и английский, 2 человека знают все три языка. Сколько человек работает в лаборатории? Сколько из них знает только французский язык? Сколько человек знает ровно 1 язык?
6. Сколько целых чисел от 0 до 999 не делятся ни на 5, ни на 7, ни на 11?
Ответы: 1. 9. 2. 55 %. 3. 10. 4. Если на диаграмме Эйлера– Венна отметить данные в непересекающихся множествах класса, то общее число учащихся класса получится равным 42, а не 40, как сказано в условии. 5. 12; 3; 4. 6. 376.
www.reshim.su
Формула включений-исключений — Википедия
Формула включений-исключений (или принцип включений-исключений) — комбинаторная формула, позволяющая определить мощность объединения конечного числа конечных множеств, которые в общем случае могут пересекаться друг с другом. В теории вероятностей аналог принципа включений-исключений известен как формула Пуанкаре[1].
Случай двух множествНапример, в случае двух множеств формула включений-исключений имеет вид:
В сумме элементы пересечения учтены дважды, и чтобы компенсировать это мы вычитаем из правой части формулы. Справедливость этого рассуждения видна из диаграммы Эйлера-Венна для двух множеств, приведенной на рисунке справа.
Таким же образом и в случае множеств процесс нахождения количества элементов объединения состоит во включении всего, затем исключении лишнего, затем включении ошибочно исключенного и так далее, то есть в попеременном включении и исключении. Отсюда и происходит название формулы.
Формулу включений-исключений можно сформулировать в разных формах.
В терминах множеств[править]
Пусть — конечные множества. Формула включений-исключений утверждает:
При получаем формулу для двух множеств, приведенную выше.
В терминах свойств[править]
Принцип включений-исключений часто приводят в следующей альтернативной формулировке [2]. Пусть дано конечное множество , состоящее из элементов, и пусть имеется набор свойств . Каждый элемент множества может обладать или не обладать любым из этих свойств. Обозначим через количество элементов, обладающих свойствами (и, может быть, некоторыми другими). Также через обозначим количество элементов, не обладающих ни одним из свойств . Тогда имеет место формула:
Формулировка принципа включений-исключений в терминах множеств эквивалентна формулировке в терминах свойств. Действительно, если множества являются подмножествами некоторого множества , то в силу правил де Моргана (черта над множеством — дополнение в множестве ), и формулу включений-исключений можно переписать так:
Если теперь вместо «элемент принадлежит множеству » говорить «элемент обладает свойством », то мы получим формулировку принципа включений-исключений в терминах свойств, и наоборот.
Обозначим через количество элементов, обладающих в точности свойствами из набора .Тогда формулу включений-исключений можно переписать в следующей замкнутой форме (англ.)
Доказательство[править]
Существует несколько доказательств формулы включений-исключений.
Доказательство по индукции
Комбинаторное доказательство
Рассмотрим произвольный элемент и подсчитаем, сколько раз он учитывается в правой части формулы включений-исключений[2].
Если элемент не обладает ни одним из свойств , то в правой части формулы он учитывается ровно 1 раз (в члене ).
Пусть элемент обладает в точности свойствами, скажем . Он дает по 1 в тех слагаемых суммы , для которых есть подмножество , и 0 для остальных. Число таких подмножеств по определению есть число сочетаний . Следовательно, вклад элемента в правую часть равен
При числа сочетаний равны нулю. Оставшаяся сумма в силу биномиальной теоремы равна
Таким образом, правая часть формулы включений-исключений учитывает каждый элемент, не имеющий указанных свойств точно по одному разу, а каждый элемент, обладающий хотя бы одним из свойств — нуль раз. Следовательно, она равна количеству элементов, не обладающих ни одним из свойств , то есть . Что и требовалось доказать. ■
Доказательство через индикаторные функции
Пусть — произвольные (не обязательно конечные) множества, являющиеся подмножествами некоторого множества , и пусть — индикаторные функции (или, эквивалентно, свойств ).
Индикаторная функция их дополнений равна
а индикаторная функция пересечения дополнений:
Раскрывая скобки в правой части и ещё раз используя тот факт, что индикаторная функция пересечения множеств равна произведению их индикаторных функций, получаем:
Это соотношение — одна из форм принципа включений-исключений. Оно выражает собой логическое тождество[1] и верно для произвольных множеств . В случае конечных множеств (и, соответственно, в предположении конечности множества ), просуммировав это соотношение по всем и воспользоваться тем, что для произвольного подмножества его мощность равна
получим формулировку принципа включений-исключений в терминах мощностей множеств (или в терминах свойств). ■
Задача о беспорядках[править]
Классический пример использования формулы включений-исключений — задача о беспорядках[2]. Требуется найти число перестановок множества таких что для всех . Такие перестановки называются беспорядками.
Пусть — множество всех перестановок и пусть свойство перестановки выражается равенством . Тогда число беспорядков есть . Легко видеть, что — число перестановок, оставляющих на месте элементы , и таким образом сумма содержит одинаковых слагаемых. Формула включений-исключений дает выражение для числа беспорядков:
Это соотношение можно преобразовать к виду
Нетрудно видеть, что выражение в скобках является частичной суммой ряда . Таким образом, с хорошей точностью число беспорядков составляет долю от общего числа перестановок:
Вычисление функции Эйлера[править]
Другой пример применения формулы включений-исключений — нахождение явного выражения для функции Эйлера [4], выражающей количество чисел из , взаимно простых с .
Пусть каноническое разложение числа на простые множители имеет вид
Число взаимно просто с тогда и только тогда, когда ни один из простых делителей не делит . Если теперь свойство означает, что делит , то количество чисел взаимно простых с есть .
Количество чисел, обладающих свойствами равно , поскольку .
По формуле включений-исключений находим
Эта формула преобразуется к виду:
Вариации и обобщения[править]
Принцип включения-исключения для вероятностей[править]
Пусть — вероятностное пространство. Тогда для произвольных событий справедлива формула[1][3][5]
Эта формула выражает принцип включений-исключений для вероятностей. Её можно получить из принципа включений-исключений в форме индикаторных функций:
Пусть — события вероятностного пространства , то есть . Возьмем математическое ожидание от обеих частей этого соотношения, и, воспользовавших линейностью математического ожидания и равенством для произвольного события , получим формулу включения-исключения для вероятностей.
Принцип включений-исключений в пространствах с мерой[править]
Пусть — пространство с мерой. Тогда для произвольных измеримых множеств конечной меры имеет место формула включений-исключений:
Очевидно, принцип включений-исключений для вероятностей и для мощностей конечных множеств являются частными случаями этой формулы. В первом случае мерой является, естественно, вероятностная мера в соответствующем вероятностном пространстве: . Во втором случае в качестве меры берется мощность множества: .
Вывести принцип включений-исключений для пространств с мерой можно также, как для указанных частных случаев, из тождества для индикаторных функций:
Пусть — измеримые множества пространства , то есть . Проинтегрируем обе части этого равенства по мере , воспользуемся линейностью интеграла и соотношением , и получим формулу включений-исключений для меры.
Тождество максимумов и минимумов[править]
Формула включений-исключений может рассматриваться как частный случай тождества максимумов и минимумов:
Это соотношение справедливо для произвольных чисел . В частном случае, когда мы получаем одну из форм принципа включений-исключений. В самом деле, если положить , где — произвольный элемент из , то получим соотношение для индикаторных функций множеств:
Обращение Мёбиуса[править]
Пусть — конечное множество, и пусть — произвольная функция, определенная на совокупности подмножеств и принимающая действительные значения. Определим функцию следующим соотношением:
Тогда имеет место следующая формула обращения[6][7]:
Это утверждение является частным случаем общей формулы обращения Мёбиуса для алгебры инцидентности (англ.) совокупности всех подмножеств множества , частично упорядоченных по отношению включения .
Покажем, как из этой формулы следует принцип включения-исключения для конечных множеств. Пусть дано семейство подмножеств конечного множества , обозначим — множество индексов. Для каждого набора индексов определим как число элементов, входящих только в те множества , для которых . Математически это можно записать так:
Тогда функция , определенная формулой
даёт количество элементов, каждый из которых входит во все множества , и, быть может, ещё в другие. То есть
Заметим далее, что — количество элементов, не обладающих ни одним из свойств:
С учетом сделанных замечаний запишем формулу обращения Мёбиуса:
Это есть в точности формула включений-исключений для конечных множеств, только в ней не сгруппированы слагаемые, относящиеся к одинаковым значениям .
Впервые формулу включений-исключений опубликовал португальский математик Даниэль да Сильва (англ.) в 1854 году [1]. Но еще в 1713 году Николай Бернулли (англ.) использовал этот метод для решения задачи Монмора (англ.), известной как задача о встречах (фр. Le problème des rencontres)[8], частным случаем которой является задача о беспорядках. Также формулу включений-исключений связывают с именами французского математика Абрахама де Муавра[источник не указан 3271 день] и английского математика Джозефа Сильвестра [9].
- ↑ 1,01,11,21,31,4 Риордан Дж. Введение в комбинаторный анализ = An Introduction to Combinatorial Analysis. — М.: Изд-во иностранной литературы, 1963. — С. 63-66. — 289 с.
- ↑ 2,02,12,2 Холл М. Комбинаторика = Combinatorial Theory. — М.: «Мир», 1970. — С. 18-20. — 424 с.
- ↑ 3,03,1 Рыбников К. А. Введение в комбинаторный анализ. — 2-е изд. — М.: Изд-во МГУ, 1985. — С. 69-73. — 309 с.
- ↑ Рыбников К. А. Введение в комбинаторный анализ. — 2-е изд. — М.: Изд-во МГУ, 1985. — С. 266. — 309 с.
- ↑ Боровков, А. А. Теория вероятностей. — 2-е изд. — М.: «Наука», 1986. — С. 24. — 431 с.
- ↑ Холл М. Комбинаторика = Combinatorial Theory. — М.: «Мир», 1970. — С. 30-31. — 424 с.
- ↑ Стенли Р. Перечислительная комбинаторика = Enumerative Combinatorics. — М.: «Мир», 1990. — С. 103-107. — 440 с.
- ↑ Weisstein, Eric W. Derangement (англ.) на сайте Wolfram MathWorld.
- ↑ Рыбников К. А. Введение в комбинаторный анализ. — 2-е изд. — М.: Изд-во МГУ, 1985. — С. 264. — 309 с.
www.wikiznanie.ru
Реферат Формула включений-исключений
скачатьРеферат на тему:
План:
- Введение
- 1 Формулировка
- 1.1 В терминах множеств
- 1.2 В терминах свойств
- 2 Доказательство
- 2.1 По индукции
- 2.2 Комбинаторное доказательство
- 2.3 Используя индикаторные функции
- 3 Применение
- 3.1 Задача о беспорядках
- 3.2 Вычисление функции Эйлера
- 4 Вариации и обобщения
- 4.1 Принцип включения-исключения для вероятностей
- 4.2 Принцип включений-исключений в пространствах с мерой
- 4.3 Тождество максимумов и минимумов
- 4.4 Обращение Мёбиуса
Примечания
Введение
Формула включений-исключений (или принцип включений-исключений) — комбинаторная формула, позволяющая определить мощность объединения конечного числа конечных множеств, которые в общем случае могут пересекаться друг с другом.
Случай двух множеств
Например, в случае двух множеств формула включений-исключений имеет вид:
В сумме элементы пересечения учтены дважды, и чтобы компенсировать это мы вычитаем из правой части формулы. Справедливость этого рассуждения видна из диаграммы Эйлера-Венна для двух множеств, приведенной на рисунке справа.
Таким же образом и в случае множеств процесс нахождения количества элементов объединения состоит во включении всего, затем исключении лишнего, затем включении ошибочно исключенного и так далее, то есть в попеременном включении и исключении. Отсюда и происходит название формулы.
Впервые формулу включений-исключений опубликовал португальский математик Даниэль да Сильва (англ.) в 1854 году [1]. Но еще в 1713 году Николай Бернулли (англ.) использовал этот метод для решения задачи Монмора (англ.), известной как задача о встречах (фр. «Le problème des rencontres»)[2], частным случаем которой является задача о беспорядках. Также формулу включений-исключений связывают с именами французского математика Абрахама де Муавра и английского математика Джозефа Сильвестра [3]. В теории вероятностей аналог принципа включений-исключений известен как формула Пуанкаре[1].
1. Формулировка
Формулу включений-исключений можно сформулировать в разных формах.
1.1. В терминах множеств
Пусть — конечные множества. Формула включений-исключений утверждает:
При получаем формулу для двух множеств, приведенную выше.
1.2. В терминах свойств
Принцип включений-исключений часто приводят в следующей альтернативной формулировке [4]. Пусть дано конечное множество , состоящее из элементов, и пусть имеется набор свойств . Каждый элемент множества может обладать или не обладать любым из этих свойств. Обозначим через количество элементов, обладающих свойствами (и, может быть, некоторыми другими). Также через обозначим количество элементов, не обладающих ни одним из свойств . Тогда имеет место формула:
Формулировка принципа включений-исключений в терминах множеств эквивалентна формулировке в терминах свойств. Действительно, если множества являются подмножествами некоторого множества , то в силу правил де Моргана (черта над множеством — дополнение в множестве ), и формулу включений-исключений можно переписать так:
Если теперь вместо «элемент принадлежит множеству » говорить «элемент обладает свойством », то мы получим формулировку принципа включений-исключений в терминах свойств, и наоборот.
Обозначим через количество элементов, обладающих в точности свойствами из набора .Тогда формулу включений-исключений можно переписать в следующей замкнутой форме (англ.)
2. Доказательство
Существует несколько доказательств формулы включений-исключений.
2.1. По индукции
Формулу включений-исключений можно доказать по индукции [1][5].
При формула включений-исключений тривиальна:
Пусть формула верна для , докажем ее для .
Пусть каждый элемент множества может обладать или не обладать любым из свойств . Применим формулу включений-исключений для свойств :
Теперь применим формулу для свойств к множеству объектов, для которых выполнено свойство :
Наконец, применим формулу для одного свойства к совокупности , объектов, которые не обладают свойствами :
Комбинируя выписанные три формулы, получим формулу включений-исключений для свойств . Что и требовалось доказать.
2.2. Комбинаторное доказательство
Рассмотрим произвольный элемент и подсчитаем, сколько раз он учитывается в правой части формулы включений-исключений[4].
Если элемент не обладает ни одним из свойств , то в правой части формулы он учитывается ровно 1 раз (в члене ).
Пусть элемент обладает в точности свойствами, скажем . Он дает по 1 в тех слагаемых суммы , для которых есть подмножество , и 0 для остальных. Число таких подмножеств по определению есть число сочетаний . Следовательно, вклад элемента в правую часть равен
При числа сочетаний равны нулю. Оставшаяся сумма в силу биномиальной теоремы равна
Таким образом, правая часть формулы включений-исключений учитывает каждый элемент, не имеющий указанных свойств точно по одному разу, а каждый элемент, обладающий хотя бы одним из свойств — нуль раз. Следовательно, она равна количеству элементов, не обладающих ни одним из свойств , то есть . Что и требовалось доказать.
2.3. Используя индикаторные функции
Пусть — произвольные (не обязательно конечные) множества, являющиеся подмножествами некоторого множества , и пусть — индикаторные функции (или, эквивалентно, свойств ).
Индикаторные функции их дополнений равны
а индикаторная функция пересечения дополнений:
Раскрывая скобки в правой части и еще раз используя тот факт, что индикаторная функция пересечения множеств равна произведению их индикаторных функций, получим
Это соотношение — одна из форм принципа включений-исключений. Оно выражает собой логическое тождество[1] и верно для произвольных множеств . В случае конечных множеств (и, соответственно, в предположении конечности множества ), просуммировав это соотношение по всем и воспользоваться тем, что для произвольного подмножества его мощность равна
получим формулировку принципа включений-исключений в терминах мощностей множеств (или в терминах свойств).
3. Применение
3.1. Задача о беспорядках
Классический пример использования формулы включений-исключений — задача о беспорядках [4]. Требуется найти число перестановок множества таких что для всех . Такие перестановки называются беспорядками.
Пусть — множество всех перестановок и пусть свойство перестановки выражается равенством . Тогда число беспорядков есть . Легко видеть, что — число перестановок, оставляющих на месте элементы , и таким образом сумма содержит одинаковых слагаемых. Формула включений-исключений дает выражение для числа беспорядков:
Это соотношение можно преобразовать к виду
Нетрудно видеть, что выражение в скобках является частичной суммой ряда . Таким образом, с хорошей точностью число беспорядков составляет долю от общего числа перестановок:
3.2. Вычисление функции Эйлера
Другой пример применения формулы включений-исключений — нахождение явного выражения для функции Эйлера [6].
Для целого положительного функция Эйлера дает количество чисел ряда , взаимно простых с . Найдем явное выражение для функции Эйлера.
Пусть каноническое разложение числа на простые множители имеет вид
Число взаимно просто с тогда и только тогда, когда ни один из простых делителей не делит . Если теперь свойство означает, что делит , то количество чисел взаимно простых с есть .
Количество чисел, обладающих свойствами равно , поскольку .
По формуле включений-исключений находим
Эта формула преобразуется к виду:
4. Вариации и обобщения
4.1. Принцип включения-исключения для вероятностей
Пусть — вероятностное пространство. Тогда для произвольных событий справедлива формула [1][5][7]
Эта формула выражает принцип включений-исключений для вероятностей. Ее можно получить из принципа включений-исключений в форме индикаторных функций:
Пусть — события вероятностного пространства , то есть . Возьмем математическое ожидание от обеих частей этого соотношения, и, воспользовавших линейностью математического ожидания и равенством для произвольного события , получим формулу включения-исключения для вероятностей.
4.2. Принцип включений-исключений в пространствах с мерой
Пусть — пространство с мерой. Тогда для произвольных измеримых множеств конечной меры имеет место формула включений-исключений:
Очевидно, принцип включений-исключений для вероятностей и для мощностей конечных множеств являются частными случаями этой формулы. В первом случае мерой является, естественно, вероятностная мера в соответствующем вероятностном пространстве: . Во втором случае в качестве меры берется мощность множества: .
Вывести принцип включений-исключений для пространств с мерой можно также, как для указанных частных случаев, из тождества для индикаторных функций:
Пусть — измеримые множества пространства , то есть . Проинтегрируем обе части этого равенства по мере , воспользуемся линейностью интеграла и соотношением , и получим формулу включений-исключений для меры.
4.3. Тождество максимумов и минимумов
Формула включений-исключений может рассматриваться как частный случай тождества максимумов и минимумов:
Это соотношение справедливо для произвольных чисел . В частном случае, когда мы получаем одну из форм принципа включений-исключений. В самом деле, если положить , где — произвольный элемент из , то получим соотношение для индикаторных функций множеств:
4.4. Обращение Мёбиуса
Пусть — конечное множество, и пусть — произвольная функция, определенная на совокупности подмножеств и принимающая действительные значения. Определим функцию следующим соотношением:
Тогда имеет место следующая формула обращения[8][9]:
Это утверждение является частным случаем общей формулы обращения Мёбиуса для алгебры инцидентности (англ.) совокупности всех подмножеств множества , частично упорядоченных по отношению включения .
Покажем, как из этой формулы следует принцип включения-исключения для конечных множеств. Пусть дано семейство подмножеств конечного множества , обозначим — множество индексов. Для каждого набора индексов определим как число элементов, входящих только в те множества , для которых . Математически это можно записать так:
Тогда функция , определенная формулой
дает количество элементов, каждый из которых входит во все множества , , и, быть может, еще в другие. То есть
Заметим далее, что — количество элементов, не обладающих ни одним из свойств:
С учетом сделанных замечаний запишем формулу обращения Мёбиуса:
Это есть в точности формула включений-исключений для конечных множеств, только в ней не сгруппированы слагаемые, относящиеся к одинаковым значениям .
Примечания
- ↑ 12345Риордан Дж. Введение в комбинаторный анализ = An Introduction to Combinatorial Analysis. — М.: Изд-во иностранной литературы, 1963. — С. 63-66. — 289 с.
- Weisstein, Eric W. Derangement — mathworld.wolfram.com/Derangement.html (англ.) на сайте Wolfram MathWorld.
- Рыбников К. А. Введение в комбинаторный анализ. — 2-е изд. — М.: Изд-во МГУ, 1985. — С. 264. — 309 с.
- ↑ 123Холл М. Комбинаторика = Combinatorial Theory. — М.: «Мир», 1970. — С. 18-20. — 424 с.
- ↑ 12Рыбников К. А. Введение в комбинаторный анализ. — 2-е изд. — М.: Изд-во МГУ, 1985. — С. 69-73. — 309 с.
- Рыбников К. А. Введение в комбинаторный анализ. — 2-е изд. — М.: Изд-во МГУ, 1985. — С. 266. — 309 с.
- Боровков, А. А. Теория вероятностей. — 2-е изд. — М.: «Наука», 1986. — С. 24. — 431 с.
- Холл М. Комбинаторика = Combinatorial Theory. — М.: «Мир», 1970. — С. 30-31. — 424 с.
- Стенли Р. Перечислительная комбинаторика = Enumerative Combinatorics. — М.: «Мир», 1990. — С. 103-107. — 440 с.
wreferat.baza-referat.ru
