Как построить x y – Построение графиков функций онлайн

Как построить график функции y=m*f(x), если известен график функции y=f(x)

На этом уроке мы обсудим построение модификаций графиков вида у = m*f(x). Вначале мы вспомним, как строятся ранее изучаемые модификации графиков вида у = f(x±k) и у = f(x)±k. Далее мы рассмотрим построение графика функции вида у = m*f(x) на примере функции синуса и сформулируем общее правило для подобных преобразований. В конце урока мы решим несколько примеров на построение схематического графика.

Тема: Тригонометрические функции

Урок: Как построить график функции y=m∙f(x), если известен график функции y=f(x)

Вспомним известные нам правила преобразования графиков.

1) Построить графики функций

Например:

 получаем сдвигом кривой  на 1 вправо по оси x;

 получаем сдвигом кривой  на 1 влево по оси x.

2) Построить графики функций

Например:

 получаем сдвигом кривой  на 1 вверх по оси

y;

 получаем сдвигом кривой  на 1 вниз по оси y.

3) Построить график функции

Например:

Поместим значения функций в основных точках в таблицу.

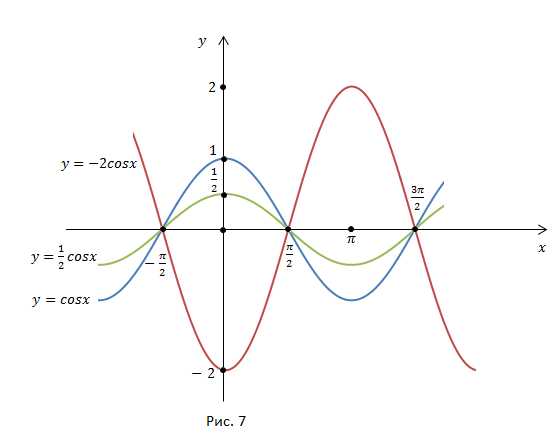
И построим графики функций  (рис. 3).

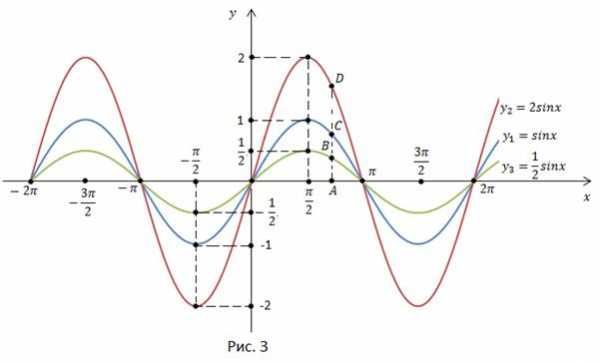
Исходную кривую необходимо растянуть или сжать в m раз. При  точки графика остаются без изменения.

Рассмотрим значения функций в основных точках при

И построим графики функций

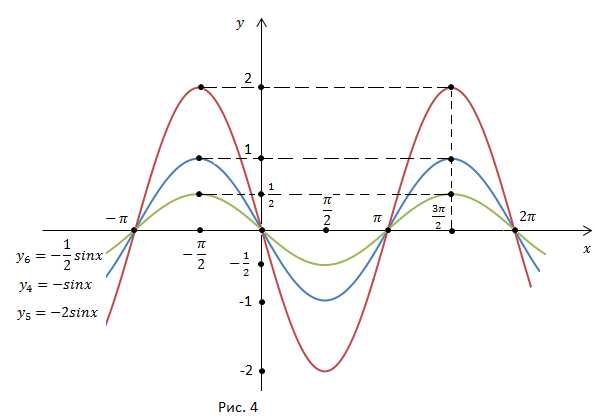
График функции симметричен графику функции  относительно оси x.

Правило получения кривой  из кривой

1. Точки пересечения кривой  c осью x сохраняются без изменений.

2. В остальных точках области определения ордината изменяется в m раз (рис. 5).

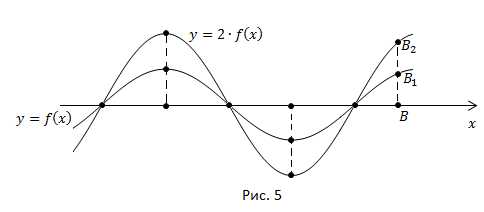
Используя правило, построим графики функций:

1) 

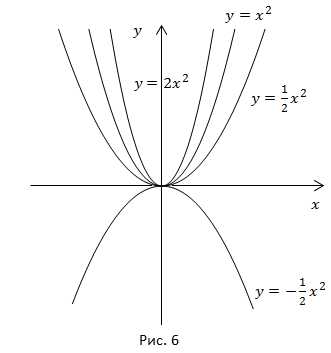
2) 

Мы вспомнили известные ранее правила преобразования графиков функций и вывели новое правило, по которому из графика функции  можно получить график функции , привели несколько примеров.

Правило будет использоваться и в дальнейшем, в частности, при исследовании гармонических колебаний.

 

Список литературы

1. Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2009.

2. Алгебра и начала анализа, 10 класс (в двух частях). Задачник  для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.

3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики).-М.: Просвещение, 1996.

4. Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.

5. Сборник задач по математике для поступающих во ВТУЗы (под ред. М.И.Сканави).-М.:Высшая школа, 1992.

6. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер.-К.: А.С.К., 1997.

7. Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.

8. Карп А.П. Сборник задач по алгебре и началам анализа : учеб. пособие для 10-11 кл. с углубл. изуч. математики.-М.: Просвещение, 2006.

 

Домашнее задание

Алгебра и начала анализа, 10 класс (в двух частях). Задачник  для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.

№№ 17.1 – 17.6.

 

Дополнительные веб-ресурсы

1. Математика (Источник).

2. Интернет-портал Problems.ru (Источник).

3. Образовательный портал для подготовки к экзаменам (Источник).

interneturok.ru

Как построить график функции у = f(x + t), если известен график функции у = f(x)

В этом уроке вы узнаете, как построить график функции y = f (x + t), если известен график функции y = f(x)

Конкретизируем задачу.

Дано:

Кривая ; график этой функции нам известен

 (действительное число)

Построить:

Это и есть задача нашего урока. Рассмотрение этой задачи начнем с простейших примеров.

Пример 1. Построить а) у = (х – 1)²; б) у = (х + 1)²

Дано:

у = х²(графиком данной функции является парабола (рис. 1).

Рис. 1. Парабола

Решение:

Поясним характер кривых, их взаимное расположение поясним с помощью таблицы.

х	-2	-1	0	1	2
у = х2	4	1	0	1	4
у = (х – 1)2	9	4	1	0	1
у = (х + 1)2	1	0	1	4	9

Строим график функции у = (х – 1)² (рис. 2):

Рис. 2. График функции у = (х – 1)²

Следует заметить, что кривая а) была получена сдвигом на 1 единицу вправо. Кривая же б) будет получена сдвигом на 1 единицу влево (что можно проверить, поставив полученные в таблице точки на координатную прямую) (рис. 3):

Рис. 3. Сдвиг графика

Заметим еще раз, что если к х прибавляется 1 единица, то сдвиг исходной прямой идет влево вдоль оси Ох, а если отнимается – то сдвиг графика идет вправо.

Вспомнить, когда сдвиг идет направо, а когда – налево, нам помогает самая характерная точка параболы – вершина параболы.

Значение у = 0 достигается этими функциями (рис. 4):

при х = 0, если у = х²

при х = 1, если у = (х – 1)²

при х = -1, если у = (х + 1)²

Рис. 4. Случаи, когда у = 0

Если у нас у = (х – 1)², то кривая сдвигается на 1 единицу вправо.

Если у нас у = (х + 1)², то кривая сдвигается на 1 единицу влево.

Мы рассмотрели конкретный случай с конкретными числами. Но вместо чисел, можно взять любое действительное число; вместо функции у = х²можно взять любую функцию. Получим важное правило.

Чтобы получить у = f(x + t), надо кривую у = f(x):

— сдвинуть на  единиц вправо, если

t < 0,

— сдвинуть на  единиц влево, если t > 0

 Это правило является центральным, и нам необходимо закрепить его на примерах.

Дано:

 

Построить:

а)

б)

Решение:

а) Строим график функции  и сдвигаем его на 1 единицу вправо (согласно правилу) (рис. 5):

Рис. 5. Иллюстрация к примеру а)

Эта гипербола не существует в точке  (вертикальная асимптота проходит в точке ).

Точка пересечения с осью Оу – -1, потому что у(0) = -1.

Задача а) решена.

б) Строим график функции  и сдвигаем его на 1 единицу влево (согласно правилу) (рис. 6):

Рис. 6. Иллюстрация к примеру б)

Эта гипербола не существует в точке .

Точка пересечения с осью Оу – 1, потому что у(0) = 1.

В построении графика  помогла точка разрыва графика (то есть точка ; вертикальная асимптота проходит в точке , что означает невозможность существования функции в данной точке.).

Обе задачи решены.

Из этой задачи мы можем сделать вывод, что, если правило забыто, то нам может помочь характерная особенность (например, точка разрыва в примере 1). Но иногда сдвигать график утомительно, тогда мы поступаем следующим образом:

Дано:

 

Построить:

а)

Решение:

Можно сдвинуть ось Оу. Кривая тогда останется на месте, однако масштаб по оси Ох придется изменить. Если сдвигать всю кривую для построения графика функции, то кривую надо сдвинуть на 1 единицу вправо. Но если мы сдвигаем ось Оу, то ее надо сдвинуть на 1 единицу влево.

Получим новую ось Oу(рис. 7):

      

Рис. 7. Иллюстрация к примеру 2

Асимптота проходит в точке , потому что в точке  функции не существует.

Задача решена сдвигом оси Оу. Итак, если затруднительно сдвигать кривую, то можно сдвинуть ось в ту или иную сторону.

         

Список литературы

1. Башмаков М.И. Алгебра 8 класс. – М.: Просвещение, 2004.
2. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5 издание. – М.: Просвещение, 2010.
3. Никольский С.М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра 8 класс. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2006.

 

Домашнее задание

1. № 19.11, 19.18, 19.24 стр. 116–120. Мордкович А.Г. Алгебра 8 класс. Задачник для учащихся общеобразовательных школ.– 12-е изд. – М.: Мнемозина, 2010. – 273 стр.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал Urokimatematiki.ru (Источник).
2. Интернет-портал Festival.1september.ru (Источник).
3. Интернет-портал Yaklass.ru (Источник).

interneturok.ru

Построение графиков функций по заданным параметрам»

Разделы: Математика, Информатика

---

Цели урока:

• научить строить графики элементарных математических функций с помощью табличного процессора Excel;
• показать возможности использования программы Excel для решения задач по математике;
• закрепить навыки работы с Мастером диаграмм.

Задачи урока:

• образовательная – знакомство учащихся с основными приемами построения графиков функций в программе Excel;
• развивающие – формирование у учащихся логического и алгоритмического мышления; развитие познавательного интереса к предмету; развитие умения оперировать ранее полученными знаниями; развитие умения планировать свою деятельность;
• воспитательные – воспитание умения самостоятельно мыслить, ответственности за выполняемую работу, аккуратности при выполнении работы.

Тип урока:

• комбинированный

Учебники:

Информатика. Базовый курс 2-е издание/Под ред. С.В. Симоновича. — СПб.: Питер, 2004.-640с.:ил.

Технические и программные средства:

• Персональные компьютеры;
• Приложение Windows – электронные таблицы Excel.
• Проектор

Раздаточный материал:

• Карточки с индивидуальными заданиями на построение графиков функций.

План урока.

1. Организационный момент – 3 мин.
2. Проверка домашнего задания –10 мин.
3. Объяснение нового материала –20 мин.
4. Применение полученных знаний –20 мин.
5. Самостоятельная работа. – 20 мин
6. Подведение итогов урока. Домашнее задание – 7 мин.

Ход урока

Организационный момент

Проверка готовности учащихся к уроку, отметка отсутствующих, объявление темы и цели урока

Проверка домашнего задания. (фронтальный опрос)

Вопросы для проверки

1. Что представляет собой рабочая область программы Excel?
2. Как определяется адрес ячейки?
3. Как изменить ширину столбца, высоту строки?
4. Как ввести формулу в Excel?
5. Что такое маркер заполнения и для чего он нужен?
6. Что такое относительная адресация ячеек?
7. Что такое абсолютная адресация ячеек? Как она задается?
8. Что такое колонтитулы? Как они задаются?
9. Как задать поля печатного документа? Как изменить ориентацию бумаги?
10. Что такое функциональная зависимость у = f(х)? Какая переменная является зависимой, а какая независимой?
11. Как ввести функцию в Excel?
12. Что такое график функции у = f(х)?
13. Как построить диаграмму в Excel?

Объяснение нового материала.

При объяснении нового материала может быть использован файл Excel с шаблонами задач (Приложение 1), который выводится на экран с помощью проектора

Сегодня мы рассмотрим применение табличного процессора Excel для графиков функций. На предыдущих практических вы уже строили диаграммы к различным задачам, используя Мастер диаграмм. Графики функций, так же как и диаграммы строятся с помощью Мастера диаграмм программы Excel.

Рассмотрим построение графиков функций на примере функции у = sin x.

Вид данного графика хорошо известен вам по урокам математики, попробуем построить его средствами Excel.

Программа будет строить график по точкам: точки с известными значениями будут плавно соединяться линией. Эти точки нужно указать программе, поэтому, сначала создается таблица значений функции у = f(х).

Чтобы создать таблицу, нужно определить

• отрезок оси ОХ, на котором будет строиться график.
• шаг переменной х, т.е. через какой промежуток будут вычисляться значения функции.

Задача 1.Построить график функции у = sin x на отрезке [– 2; 2] с шагом h = 0,5.

1. Заполним таблицу значений функции. В ячейку С4 введем первое значение отрезка: – 2
2. В ячейку D4 введем формулу, которая будет добавлять к лево-стоящей ячейки шаг: = В4 + $A$4
3. Маркером заполнения ячейки D4 заполним влево ячейки строки 4, до тех пор, пока получим значение другого конца отрезка: 2.
4. Выделим ячейку С5, вызовем Мастер функций, в категории математические выберем функцию SIN, в качестве аргумента функции выберем ячейку С4.
5. Маркером заполнения распространим эту формулу в ячейках строки 5 до конца таблицы.

Таким образом, мы получили таблицу аргументов (х) и значений (у) функции у = sin x на отрезке [-2;2] с шагом h = 0,5 :

x	-2	-1,75	-1,5	-1,25	-1	-0,75	-0,5	-0,25	0	0,25	0,5	0,75	1	1,25	1,5	1,75	2
y	-0,9092	-0,9839	-0,9974	-0,9489	-0,8414	-0,6816	-0,4794	-0,2474	0	0,2474	0,4794	0,6816	0,8414	0,9489	0,9974	0,9839	0,9092

6. Следующий шаг. Выделим таблицу и вызовем Мастер диаграмм. На первом шаге выберем во вкладке Нестандартные Гладкие графики.
7. На втором шаге во вкладке Ряд выполним:

В поле Ряд необходимо выделить ряд х и нажать на кнопку “Удалить” (график изменений х нам не нужен. График функции – это график изменения значений у)

В поле Подписи оси Х нажать на кнопку. Выделить в таблице ячейки со значениями х и нажмите на кнопку . Подписи по горизонтальной оси станут такими, как у нас в таблице.

8. На третьем шаге заполним вкладку Заголовки.

9. Пример полученного графика.

На самом деле пока это мало похоже на график функции в нашем привычном понимании.

Для форматирования графика:

• Вызовем контекстное меню оси ОУ. Затем, выберем пункт Формат оси…. Во вкладке Шкала установим: цена основного деления: 1. Во вкладке Шрифт установим размер шрифта 8пт.
• Вызовем контекстное меню оси ОХ. Выберем пункт Формат оси….

Во вкладке Шкала установим: пересечение с осью ОУ установите номер категории 5 (чтобы ось ОУ пересекала ось ОХ в категории с подписью 0, а это пятая по счету категория).

Во вкладке шрифт установите размер шрифта 8пт. Нажмите на кнопку ОК.

Остальные изменения выполняются аналогично.

Для закрепления рассмотрим еще одну задачу на построение графика функций. Эту задачу попробуйте решить самостоятельно, сверяясь с экраном проектора.

Применение полученных знаний.

Пригласить к проектору студента и сформулировать следующую задачу.

Задача 2. Построить график функции у = х³ на отрезке [– 3; 3] с шагом h = 0,5.

1. Создать следующую таблицу: Создать таблица значений функции у = f(х).

2. В ячейку С4 ввести первое значение отрезка: –3
3. В ячейку D4 ввести формулу, которая будет добавлять к лево-стоящей ячейки шаг: = В4 + $A$4
4. Маркером заполнения ячейки D3 заполнить влево ячейки строки 3, до тех пор, пока не будет получено значение другого конца отрезка: 3.
5. В ячейку С5 ввести формулу вычисления значения функции: = С4^3
6. Маркером заполнения скопировать формулу в ячейки строки 5 до конца таблицы.

Таким образом, должна получиться таблица аргументов (х) и значений (у) функции у = х³ на отрезке [–3;3] с шагом h = 0,5:

х	-3	-2,5	-2	-1,5	-1	-0,5	0	0,5	1	1,5	2	2,5	3
y	-27	-15,625	-8	-3,375	-1	-0,125	0	0,125	1	3,375	8	15,625	27

7. Выделить таблицу и вызвать мастер диаграмм. На первом шаге выбрать во второй вкладке Гладкие графики.
8. На втором шаге во вкладке Ряд выполнить:

• В поле Ряд выделить ряд х и нажать на кнопку “Удалить” (график изменений х нам не нужен. График функции – это график изменения значений у)
• В поле Подписи оси Х нажать на кнопку . Выделить в таблице ячейки со значениями х и нажать на кнопку . Подписи по горизонтальной оси станут такими, как у нас в таблице.

9. На третьем шаге заполнить вкладку Заголовки.

10. Пример полученного графика:
11. Оформить график.
12. Установить параметры страницы и размеры диаграмм таким образом, что бы все поместилось на одном листе альбомной ориентации.
13. Создать колонтитулы для данного листа (Вид Колонтитулы…):
14. Верхний колонтитул слева: график функции у = x³

Сохранить документ своей папке под именем График.

Самостоятельная работа.

Работа по карточкам с индивидуальными заданиями. (Приложение 2)

Пример карточки, с задачей в общем виде, выводится на экран с помощью проектора.

1. Построить график функции y=f(x) на отрезке [a;b] с шагом h=c
2. Установить параметры страницы и размеры графика таким образом, что бы все поместилось на одном листе альбомной ориентации.
3. Создать колонтитулы для данного листа (Вид Колонтитулы…):

• Верхний колонтитул слева: график функции y=f(x)
• Нижний колонтитул в центре: ваши Ф.И.О. и дата

4. Сохранить в своей папке под именем “Зачетный график”
5. Вывести документ на печать.

После выполнения задания правильность каждого варианта проверяется с помощью проектора.

Подведение итогов.

Домашнее задание.

Оценки за урок.

15.02.2006

Поделиться страницей:

xn--i1abbnckbmcl9fb.xn--p1ai