Чем отличается сочетание от размещения
Б. Паскаль и Ферма, изучая теорию азартных игр, были основателями нового раздела математики, называемого комбинаторикой. В ней изучается, какое количество комбинаций заданного типа можно составить из предложенных элементов.
Определение
Сочетания — соединения, каждое из которых составлено из k1 элементов, выбранных из n1 различных элементов, состав которых отличается хотя бы на один элемент.
Размещения — cоединения, каждое из которых составлено из k1 элементов, взятых из n1 различных элементов, у которых состав элементов или их порядок отличают их друг от друга.
к содержанию ↑Сравнение
Сочетания — соединения, содержащие k1 элементов, выбранных из n1 различных элементов. Сочетания отличаются друг от друга хотя бы на один элемент. Порядок следования элементов не важен. Число сочетаний равно n1 элементов.
Наборы, которых отличает только порядок следования элементов, но не состав, считаются одинаковыми. Отличие сочетаний друг от друга составом, но не порядком следования элементов.
Пример. Сочетание — нужно выбрать 3 предмета из 6. Есть предметы с номерами от 1 до 6. Выбираем из этого набора предметы в любом порядке с номерами 1, 4 и 6. Это и есть сочетание.
Размещениями называют соединения, каждое из которых содержит k1 элементов, взятых из n1 различных элементов, которых отличает друг от друга порядок или состав элементов. В размещениях не должно быть дубликатов.
Размещения отличают друг от друга состав элементов или их порядок. Из n1 элементов по к1 (к1 < n1). По-другому, из n1 элементов выбирают к1 элементов и размещают их на А позиций. Число размещений из n1 элементов по к1 обозначают символом Ак1n1 (читается: А из n1 по к1).

При этом две расстановки будут считаться разными, если у них есть отличие друг от друга хотя бы на один элемент. Или они состоят из одних и тех же предметов, но они расположены в разном порядке. Например, есть три элемента, размещаем их в определенном порядке: 15, 11, 12 или 11, 12, 15 или 12, 15,11. Это и есть размещение — различные комбинации с одними и теми же элементами. Число размещений больше числа сочетаний.
к содержанию ↑Выводы TheDifference.ru
- Сочетания отличаются от размещений только тем, что они не зависят от порядка следования элементов.
thedifference.ru
Перестановки, сочетания, размещения Основные определения и обозначения
Различные
упорядоченные множества, которые
отличаются лишь порядком элементов
(т.е. могут быть получены из того же
самого множества), называются перестановками
этого множества. Число различных
перестановок 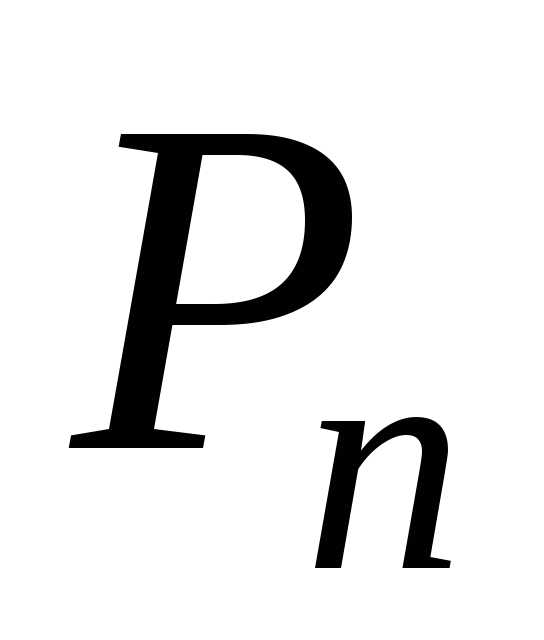 изn элементов
равно
изn элементов
равно 
Произвольное k – элементное подмножество n – элементного множества называется сочетанием из n элементов по k.
Число сочетаний 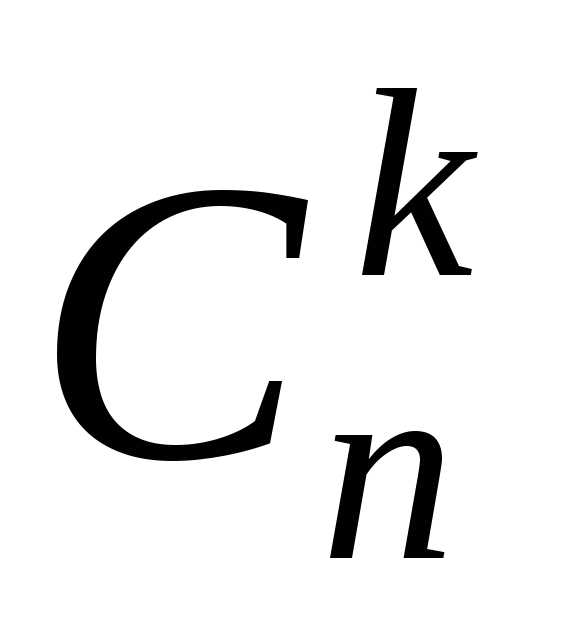 изn элементов
по k равно
изn элементов
по k равно 
Упорядоченные k – элементные подмножества из n элементов называются размещением из n элементов по k.
Число
размещений  изn элементов
по k равно
изn элементов
по k равно
Методические указания к решению задач
Применяя формулы числа перестановок, сочетаний и размещений, следует исходить из определений этих понятий.
Пример 7. Задано множество .
Составить всевозможные перестановки этого множества.
Всевозможные сочетания по два элемента.
Всевозможные размещения по два элемента.
Решение:

Пример 8. Сколько существует способов выбора из 7 человек комиссии, состоящей из 3 человек?
Решение. Число возможных составов комиссии равно числу всевозможных трехэлементных подмножеств множества, состоящего из 7 человек, т.е.
Пример 9. Сколькими способами можно разместить на полке 4 книги?
Решение. Искомое число способов равно числу способов упорядочения множества, состоящего из 4 элементов, т.е.
Пример 10. В студенческой группе 25 человек. Надо выбрать старосту группы, академорга и профорга. Сколькими способами может быть сделан выбор, если каждый член группы может занимать только один пост?
Решение. В данном примере из множества в 25 элементов нужно выбрать 3 элемента, но среди выбранных 3 элементов имеет значение порядок, так как здесь играет роль то, кто какой пост займет.
Например, выбор:
староста – Иванова, академорг – Алексеева, профорг – Петров отличается от выбора:
староста – Алексеева, академорг – Иванова, профорг – Петров.
Следовательно, число различных способов выбора равно числу размещений из 25 элементов по 3,
Пример 11. На профсоюзном собрании присутствует 50 человек. Необходимо выбрать делегацию из 5 человек на профсоюзную конференцию. Сколькими способами это можно сделать?
Решение. В данном примере из множества в 50 элементов нужно выбрать подмножество из 5, порядок которых не играет роли. Поэтому число способов выбора делегации равно
Пример 12. Сколькими способами можно упорядочить множество так, чтобы каждое четное число имело четный номер?
Решение. Здесь можно рассматривать 2 объекта: четные и нечетные числа.
Мест с четными номерами n. Таким образом, четные числа можно расставить n! способами. Общее число искомых перестановок по правилу умножения равно
Перестановки и сочетания с повторениями Основные определения и обозначения
До сих пор мы рассматривали предметы, которые были попарно различны. А теперь рассмотрим совокупности, в которых имеются одинаковые предметы.
Пусть имеются
предметы k различных
типов, число предметов первого типа
равно  ,
второго типа —
,
второго типа — k—го
типа —
k—го
типа — 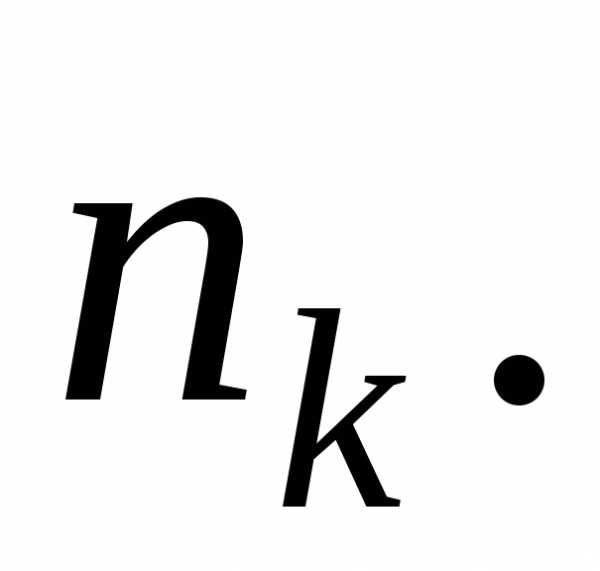
Число различных перестановок, которые можно сделать из даных элементов, равно
Число m – элементарных подмножеств, порядок в которых не принимается во внимание, равно
studfiles.net
Мастер-класс по теме «Элементы комбинаторики: перестановки, сочетания и размещения»
Разделы: Математика
Элементы комбинаторики: перестановки, сочетания, размещения.
“Число, положение и комбинация – три
взаимно пересекающиеся, но различные
сферы мысли, к которым можно
отнести все математические идеи”.
Джозеф Сильвестр (1844 г.)
Цели занятия.
Образовательные:
- познакомить студентов с новым разделом математики: «Комбинаторика», с его историей, основными понятиями и задачами, использованием в практических целях и в жизни человека;
- способствовать созданию учебного проекта как показатель качественного изучения темы занятия.
Развивающие:
- развивать аналитические способности, логическое мышление,
- индивидуальные способности каждого студента, создавая комфортную психологическую обстановку для каждого студента при обучении и создании проекта.
Воспитывающая:
- формировать активность личности студента, умение работать в группе, отвечать за свои поступки.
Оборудование: компьютеры, проектор, экран, презентация, электронные и на бумажных носителях тесты, задачи “Судоку”, кубики Рубика, папки для ВСР (внеаудиторная самостоятельная работа), рабочие тетради, чистые ватманы, калькуляторы, цветная бумага, клей, ножницы, фломастеры.
Ход занятия
I. Организационный момент
Перекличка
Сообщение целей и задач занятия: В связи с тем, что по дисциплине “Математика” на 2 курсе специальности “Технология деревообработки” на тему “Основные понятия комбинаторика: перестановки, размещения, сочетания” отводится 2 часа, а рассмотреть нужно много материала, решать задачи, создать проект, вам было выдано задание на внеаудиторную самостоятельную работу следующее: в литературе по истории математики, в энциклопедиях, в учебниках и в интернете найти материал о разделе математики, имеющем звучное название “комбинаторика”. Слайды № 1–2. Презентация
В календарно-тематическом плане по дисциплине “Математика” на 2 курсе специальности “Технология деревообработки” на тему “Основные понятия комбинаторика: перестановки, размещения, сочетания” отводится 2 часа. Изучить теоретический материал, решить задачи разных видов за такой временной промежуток невозможно. Для достижения глубокого изучения материала было выдано задание на внеаудиторную самостоятельную работу: в литературе по истории математики, в энциклопедиях, в учебниках и в интернете найти материал о разделе математики, имеющем звучное название “комбинаторика”. Слайды № 1–2.
Вопросов для внеаудиторной самостоятельной работы выделено было три:
- Определения комбинаторики.
- Ученые – математики — первооткрыватели этого раздела.
- Применение комбинаторики в современной жизни.
Запись даты, темы урока.
II. Работа над темой занятия
Вступление:
Комбинаторика ставится самостоятельным разделом математики, по сути – самостоятельной наукой лишь во второй половине XVII века, — в период, когда возникла теория вероятностей.
Таким образом, — комбинаторика – это самостоятельный раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчинённых тем или условиям, можно составить из заданных объектов.Комбинаторика – самостоятельная ветвь математической науки. Cлайд № 3
Термин “КОМБИНАТОРИКА” происходит от латинского слова “combina”, что в переводе на русский означает – “сочетать”, “соединять” — слайд № 4.
Как трактует это слово Большой Энциклопедический Словарь?
Комбинаторика – это раздел математики, в котором изучаются простейшие “соединения”: перестановки, размещения, сочетания. Этот раздел иначе называют “комбинаторный анализ”.
Сегодня мы будем рассматривать перестановки, размещения, сочетания, как соединения, как комбинаторные конфигурации.
Разделы комбинаторики:
Давайте вспомним известное вам из детства сказание о том, как богатырь или другой добрый молодец, доехав до развилки трех дорог, читает на камне: “Вперед поедешь – голову сложишь, направо поедешь – коня потеряешь, налево поедешь – меча лишишься”. А дальше уже говорится, как он выходит из того положения, в которое попал в результате выбора. Но выбирать разные пути или варианты приходится и современному человеку. Эти пути и варианты складываются в самые разнообразные комбинации. И целый раздел математики, именуемый КОМБИНАТОРИКОЙ, занят поисками ответов на вопросы: сколько всего есть комбинаций в том или ином случае, как из всех этих комбинаций выбрать наилучшую – слайд № 6.
Итак, комбинаторика – раздел математики, в котором изучается, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов.
Задачей комбинаторики можно считать задачу размещения объектов по специальным правилам и нахождение числа способов таких размещений.
Перестановки-соединения, которые можно составить из n предметов, меняя всеми возможными способами их порядок; число их
Количество всех перестановок из n элементов обозначают
Число n при этом называется порядком перестановки – слайд № 7–10.
Произведение всех натуральных чисел от n до единицы, обозначают символом n! (Читается “эн - факториал”). Используя знак факториала, можно, например, записать:
1! = 1,
2! = 2•1 = 2,
3! = 3 •2 •1 = 6,
4! = 4 •3 •2 •1 = 24,
5! = 5 •4 •3 •2 •1 = 120.
Необходимо знать, что 0!=1
Термин “перестановки” употребил впервые Якоб Бернулли в книге “Искусство предположений”.
Примеры решения задач:
Задача №1. Сколькими способами 7 книг разных авторов можно расставить на полке в один ряд?
Перестановками называют комбинации, состоящие из одних и тех же п различных элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок обозначается Рп и оно равно п!, т.е. Рп = п!, где п! = 1 * 2 * 3 * … п.
Решение: Р7 = 7!, где 7! = 1 * 2 * 3 * 4 * 5 * 6 * 7 =5040, значит существует 5040 способов осуществить расстановку книг.
Ответ: 5040 способов.
Задача № 2 (о квартете)
В знаменитой басне Крылова “Квартет” “Проказница мартышка, Осел, Козел да косолапый Мишка” исследовали влияние взаимного расположения музыкантов на качество исполнения.
Зададим вопрос: Сколько существует способов, чтобы рассадить четырех музыкантов?
Решение: на слайде
Размещения – соединения, содержащие по m предметов из числа n данных, различающихся либо порядком предметов, либо самими предметами; число их.
Cлайды № 11–13.
В комбинаторике размещением называется расположение “предметов” на некоторых “местах” при условии, что каждое место занято в точности одним предметом и все предметы различны.
В отличие от сочетаний размещения учитывают порядок следования предметов. Так, например, наборы < 2,1,3 > и < 3,2,1 > являются различными, хотя состоят из одних и тех же элементов {1,2,3} (то есть, совпадают как сочетания).
Термин “Размещение” употребил впервые Якоб Бернулли в книге “Искусство предположений”.
Примеры решения задач:
Задача № 1. Сколько можно составить телефонных номеров из 6 цифр каждый, так чтобы все цифры были различны? Это пример задачи на размещение без повторений.
Размещаются здесь десять цифр по 6. Значит, ответ на выше поставленную задачу будет:
Ответ:151200 способов
Задача № 2. В группе ТД – 21 обучается 24 студентов. Сколькими способами можно составить график дежурства по техникуму, если группа дежурных состоит из трех студентов?
Решение: число способов равно числу размещений из 24 элементов по 3, т.е. равно А243. По формуле находим
Ответ: 12144 способа
Сочетания-соединения, содержащие по m предметов из n, различающиеся друг от друга, по крайней мере, одним предметом; число их .
Таким образом, количество вариантов при сочетании будет меньше количества размещений. Cлайды № 14–16.
В комбинаторике сочетанием из n по m называется набор m элементов, выбранных из данных n элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений.
Термин “сочетание” впервые встречается у Блеза Паскаля в 1665 году.
Примеры решения задач:
Задача №1. Сколько трехкнопочных комбинаций существует на кодовом замке (все три кнопки нажимаются одновременно), если на нем всего 10 цифр?
Решение: Так как кнопки нажимаются одновременно, то выбор этих кнопок – сочетание. Отсюда возможно
Ответ: 120 вариантов.
Задача № 2. Сколько экзаменационных комиссий, состоящих из 3 членов, можно образовать из 10 преподавателей?
Решение: По формуле находим:
комиссий
Ответ: 120 комиссий.
Библиографическая справка – слайд № 17.
Общее у всех этих задач то, что их решением занимается отдельная область математики, называемая комбинаторикой. “Особая примета” комбинаторных задач – вопрос, который всегда можно сформулировать так, чтобы он начинался словами: “Сколькими способами…?”. Cлайд № 18.
3. Решение задач: тексты задач с решениями в приложении 1 – начало на слайде № 19.
4. Исторические сведения о комбинаторике на слайдах № 20–21 (частично даны сведения при изучении темы, остальные данные для проекта студенты возьмут из материалов для ВСР).
5. Связи комбинаторики на слайдах № 22–31 (частично даны сведения при изучении темы, остальные данные для проекта студенты возьмут из материалов для ВСР).
6. Выдвижение гипотезы. Гипотеза – это научное предположение, выдвигаемое для объяснения каких-нибудь явлений, вообще – предположение, требующее подтверждения.
Выдвигается гипотеза: Комбинаторика интересна и имеет широкий спектр практической направленности — слайд № 32.
7. Метод проектов: три группы студентов и группа преподавателей выполняют проект по теме: “Комбинаторика”, используя знания, полученные на занятии, а также материалы, подготовленные по заданию на ВСР: различные определения комбинаторики, ученые – математики - первооткрыватели этого раздела, применение комбинаторики в современной жизни.
8. Защита проектов: при защите проекта сделать вывод: подтверждает ли проект выдвинутую гипотезу или опровергает.
9. Тестирование: Часть студентов тестируется на компьютерах, остальные – на бумажных носителях по теме занятия. По мере выполнения тестов студенты решают задачу “Судока” или собирают кубик Рубика.
10. При выходе из кабинета каждый студент выбирает прямоугольник по цвету, соответствующему надписями “всё понятно и усвоено”, “трудно и не всё понятно”, “не понятно и не усвоено”, и опускает в соответствующий конверт.
Информационные ресурсы
1. Фадеев Д.К., Никулин М.С., Соколовский. Элементы высшей математики для школьников. Москва. “Наука”, 1987 год.
2. Грэхем Р., Кнут Д.А., Паташник О. Конкретная математика.. Москва “Мир”, 1998 г.
3. Богомолов Н.В. Практические занятия по математике: Учеб. Пособие для техникумов, Москва. “Высшая Школа, 1983.
4. Перельман Я.И. “Занимательная алгебра. Занимательная геометрия, Москва, АСТ “Астрель”, 2002 год.
5. Савин А.П. “Энциклопедический словарь юного математика”, Москва “Педагогика”, 1985.
6. Сканави М.И. “Сборник задач по математике для поступающих в вузы”, Москва, “Высшая школа”, 1998 г.
7. Вентцель Е.С. Теория вероятностей. – 4-е изд. - М.: Наука, 1969.
8. Элементы теории вероятностей. Математика. Приложение к газете «Первое сентября», № 41, 42.
9. http//portfolio.1september.ru
10. Лютикас В.С. Факультативный курс по математике: Теория вероятностей, Москва, “ Просвещение”, 1990.
11. Гнеденко Б.В., Хинчин А.Я. Элементарное введение в теорию вероятностей. — 6-е изд. — М.: Наука, 1964.
12. Андреева Е. В. “Комбинаторные задачи”, Москва, “Чистые пруды”, 2005 г.
Приложение 1
20.06.2011
xn--i1abbnckbmcl9fb.xn--p1ai
Формулы размещения, сочетания, перестановки — Студопедия.Нет
Основные понятия комбинаторики: правила сложения и умножения, формулы размещений, сочетаний, перестановок
Понятие о комбинаторике
Комбинаторика – ветвь математики, изучающая различные комбинации и перестановки объектов. Возникла комбинаторика в 17 веке. Развивалась наука в 18 веке благодаря научным трудам итальянских ученых Кардано, Тартальи, Галилея; французских математиков Паскаля и Ферма; немецких ученых Лейбница и Эйлера. Впервые название науки «комбинаторика» ввел Леонард Эйлер.
Первоначально комбинаторика возникла на основе азартных игр. К таким играм относятся: карты, кости, шашки, шахматы, нарды. Выигрывает в них тот, кто лучше изучил выигрышные комбинации, просчитал все возможные исходы на несколько шагов вперед и избежал проигрыша.
Не только игры давали пищу для комбинаторных размышлений. Разведчики, дипломаты, стремясь к тайне переписки, изобретали различные шифры и коды.
В современном обществе с развитием ЭВМ комбинаторика добилась новых успехов. Она применяется довольно широко: в теории случайных процессов; в статистике; в математическом программировании; в вычислительной математике; в военном искусстве; в управлении и т.д.
С помощью комбинаторики, например, была решена проблема «четырех красок». Любую географическую карту можно раскрасить в четыре цвета так, что никакие две страны, имеющие общие границы, не будут окрашены в один цвет.
Правила умножения и сложения
Установим два важных правила, которые часто применяются при решении комбинаторных задач. Для этого рассмотрим решение следующей задачи.
Пример 1.В группе студентов 30 человек. Необходимо выбрать старосту и профорга. Сколькими способами можно это сделать?
Решение. Старостой может быть выбран любой из 30 учащихся, т.е. существует 30 способов выбора старосты. После того как староста уже выбран, профоргом можно выбрать любого из оставшихся 29 учащихся. Таким образом, одному способу выбора старосты соответствует 29 способов выбора профорга. Следовательно, общее число способов выбора старосты и профорга равно 30*29=870.
Рассуждения, которые были проведены при решении предыдущих задач, подтверждают справедливость следующего простого утверждения.
Правило умножения.Пусть требуется выполнить одно за другим какие-то k действий. Если первое действие можно выполнить n1 способами, второе действие – n2 способами, третье – n3 способами и так до k-го действия, которое можно выполнить nк способами, то все к действий вместе могут бать выполнены n1∙ n2∙ n3∙…∙ nк способами.
Это правило дает удобный универсальный метод решения многих комбинаторных задач.
Пример 2.Четыре мальчика и четыре девочки садятся на 8 расположенных подряд стульев, причем мальчики садятся на места с четными номерами, а девочки — на места с нечетными номерами. Сколькими способами можно это сделать?
Первый мальчик может сесть на любое из четырех четных мест, второй – на любое из оставшихся трёх мест, третий – на любое из оставшихся двух мест. Последнему мальчику предоставляется всего одна возможность. Согласно правилу умножения, мальчики могут занять четыре места 4*2*3*1=24 способами. Столько же возможностей имеют и девочки. Таким образом, согласно правилу умножения, мальчики и девочки могут занять все стулья 24*24=576 способами.
Пример 3.Нефтекамский завод «Искож» выпускает трикотажные изделия. На складеимеется 20 изделий 1-го сорта и 30 изделий 2-го сорта. Необходимо выбрать два изделия одного сорта. Сколько способов выбора двух изделий возможно в данной ситуации, если учитывается порядок выбора изделий?
Условимся первым действием считать выбор изделий 1-го сорта, вторым – выбор изделий 2-го сорта. По правилу умножения два изделия 1-го сорта можно выбрать 20*19=380 способами. Аналогично, два изделия 2-го сорта можно выбрать 30*29=870 способами. Согласно условию задачи следует выбрать два изделия одного сорта, не важно какого. Это могут быть либо изделия 1-го сорта, либо изделия 2-го сорта. Таким образом, должно быть выполнено либо первое действие, либо второе, но не первое действие, а затем второе. Эти действия не могут быть выполнены одновременно, поскольку они взаимно исключают друг друга. Поэтому общее число способов выбора изделий одного сорта равно 380+870=1250.
Соображения, которые были приведены при решении последней задачи, позволяют сформулировать правило сложения.
Правило сложения.Если два действия взаимно исключают друг друга, причем одно из них можно выполнить m способами, а другое – n способами, то выполнить одно любое из этих действий можно n+m способами.
Это правило легко распространить на любое конечное число действий.
Формулы размещения, сочетания, перестановки
Комбинаторика занимается вопросами о том, сколько комбинаций определенного типа можно составить из данных элементов. Группы, составленные из каких-либо элементов, называются соединениями.
Пусть имеется некоторое множество, содержащее конечное число членов. Например, множество учебных групп в колледже, множество книг на полке, множество населенных пунктов в данной области или, например, множество целых положительных чисел, меньших 10, и т.д. Все элементы такого множества можно пронумеровать, т.е. каждому элементу множества можно поставить в соответствие одно из чисел: 1, 2, 3, 4, …,n; в результате получается некоторая последовательность элементов данного множества, которые обычно записывают в виде а1, а2, а2, …, ап. Такие “ занумерованные” множества будем называть упорядоченными. Таким образом, упорядоченное множество представим в виде некоторой последовательности, что будет использовано в дальнейшем. Очевидно, если в упорядоченном множестве поменять местами хотя бы два его элемента, то получим новое упорядоченное множество, которому будет соответствовать новая последовательность элементов данного множества. Введем определение факториала.
Определение.Произведение всех натуральных чисел от 1 до п включительно называют n − факториалом и пишутn! = 1∙2∙3∙4∙…∙(n – 1)∙n
Определение. Размещением из n элементов по m в каждом называются такие соединения, которые отличаются друг от друга либо самими элементами (хотя бы одним), либо порядком их расположения.
Пример 4. Пусть имеется множество, содержащее четыре буквы:{A, B, С; Д}. Таких размещений 12: AB, AC, AD, BC, BD, CD, BA, CA, DA, CB, DB, DC.
Заметим, что размещения отличаются порядком входящих в них элементов и их составом. Размещения АВ и ВА содержат одинаковые буквы, но порядок их расположения различен. Поэтому эти размещения считаются разными.
Пример 5.Следующие последовательности цифр являются размещениями по 4 элемента из 10 элементов множества:{0,1,2,3,4,5,6,7,8,9,}: 3021, 4590, 8612, 7485, 1234.
В последнем примере не выписаны все возможные размещения, так как таких размещений более 5000.
На практике чаще представляет интерес количество размещений, а не их конкретный вид. Число размещений из nэлементов по mбудем обозначать символом Атп,где m<nилиm=n.
Теорема.Число размещений из n элементов по m равно
Пример 6.Сколько можно записать четырехзначных чисел, используя без повторения все десять цифр?
Так как в любом числе важную роль играет порядок входящих в него цифр, то для ответа на поставленный вопрос, очевидно, следует определить число размещений из 10 цифр по 4:
А410 = 10!/6!=7*8*9*10=5040.
Однако все последовательности из 4 цифр представляют собой четырёхзначное число, поскольку среди них есть и такие, у которых на 1-м месте находится 0. Найдем число таких последовательностей. Так как у рассматриваемых последовательностей на 1-м месте уже стоит 0, то следует выбрать ещё 3 цифры из оставшихся 9. Найдем число размещений из 9 по 3: А39=9!/6!=7*8*9=504. Таким образом, искомое число четырехзначных чисел равно разности А410 — А39 =5040-504=4536.
Рассмотрим теперь отдельно случай, когда m=n. Соответствующие этому случаю размещения называются перестановками.
Перестановками из n элементов называются такие соединения из всех n элементов которые отличаются друг от друга порядком расположения элементов.
Пример 7.Пусть имеются числа 3, 5, 7. Этому множеству чисел соответствует 6 перестановок: 357, 375, 537, 573, 753,735.
Пример 8.Слова “барк” и “краб” образованы в результате перестановки букв, составляющих слово “брак”. Число таких перестановок равно 24, так как
А44 = 4!/0!=4!=1*2*3*4=24.
Отметим, что перестановки состоят из одних и тех же элементов, но отличающихся между собой порядком. Число перестановок nразличных элементов будем обозначать символом Рп .
Теорема.Число перестановок n различных элементов равно n!, т.е. =n!
Так как перестановки являются частным случаем размещений, то при n=mполучаем
= =n!/0!=n!
Пример 9.Сколькими способами можно расставить 9 различных книг на полке, чтобы определенные четыре книги стояли рядом?
Способ 1. Будем считать выделенные книги за одну книгу. Тогда для шести книг существует Р6=6!=720 перестановок. Однако четыре определенные книги можно переставить между собой Р4=4!=24 способами. По правилу умножения имеем Р6 ∙ Р4 =720∙24=17 280.
Способ 2.Возможны следующие случаи: первая из четырёх книг стоит на 1-м месте, тогда четвёртая стоит на 4-м месте; первая книга стоит на 2-м месте, а четвертая стоит на 5-м месте, первая стоит на 6-м месте, тогда четвертая стоит на последнем, 9-м месте. Число таких случаев равно шести. Сами книги могут быть переставлены Р4=4!=24 способами. Значит, по правилу умножения выделенные четыре книги можно расставить 6∙Р4=144 способами. Оставшиеся 5 книг можно переставить Р5=5!=120 способами. Воспользовавшись снова правилом умножения, приходим к тому же результату, который был получен при первом способе решения: Р4∙6∙Р5 = Р6 ∙ Р4 = 17 280.
Если два различных размещения состоят из одинаковых элементов некоторого множества, то они обязательно отличаются порядком входящих в них элементов. Иногда возникает необходимость не учитывать порядок элементов, входящих в размещение. В этом случае все m!размещений, которые состоят из одних и тех же элементов, считаются неразличимыми.
Предположим, что из чисел 3, 5, 7 необходимо составить различные произведения двух чисел. Таких произведений только три: 3∙5=15, 3∙7=21,5∙7=35. Это объясняется тем, что произведения вида 3∙5 и 5∙3 совпадают, так как порядок сомножителей, входящих в произведение, не учитывается. Если требуется из указанных цифр составить двузначные числа, то таких чисел уже шесть. Запишем эти числа: 35, 53, 37, 73, 57, 75. Как видно, здесь уже пришлось учитывать порядок цифр.
При выборе делегации в составе 3 человек из 30 учащихся не надо учитывать порядок выбранных делегатов, так как все члены делегации равноправны. Однако, выбирая физорга, старосту, профорга из тех же учащихся, порядок уже приходится учитывать. Каждый конкретный результат выбора из 30 учащихся делегации в составе 3 человек – это сочетание из 30 по 3 в отличие от размещения из 3 по 3.
Сочетаниями из n элементов по m в каждом называются такие соединения, которые отличаются друг от друга хотя бы одним элементом.
Пример 10.Необходимо выбрать в подарок 4 из 10 имеющихся различных книг. Сколькими способами можно это сделать?
Из смысла задачи следует, что порядок выбора книг не играет роли. Здесь важен только их состав. Как известно из предыдущего (см. задачу 5), число размещений из 10 по 4 равно А410=5040. Пусть теперь выбраны 4 книги из 10. Число таких возможных выборов, где не учитывается порядок выбранных книг, равно С410. Однако каждому из этих сочетаний будут соответствовать Р4=24 перестановки выбранных книг. Тогда выбор 4 книг из 10 с учетом их порядка по правилу умножения возможен С410 ∙ Р4 способами. С другой стороны, число указанных способов – это число размещений А410. Таким образом, число возможных способов выбора подарка равна 210.
Теорема.Число сочетаний из n элементов по m равно
Пример 11. Имеется 10 белых и 5 черных шаров. Сколькими способами можно выбрать 7 шаров, чтобы среди них были 3 черных?
Решение. Среди выбранных шаров 4 белых и 3 черных. Белые шары можно выбрать С410 =10!/4!∙6!=210 способами. Черные шары можно выбрать С35 =5!/3!∙2!=10 способами. Тогда по правилу умножения искомое число способов равно С410 ∙ С35 =2100.
Пример 12. Десять команд участвуют в розыгрыше первенства России по хоккею, лучшие из которых занимают 1-е, 2-е и 3-е места. Две команды, занявшие последние места, не будут участвовать в следующем таком же первенстве. Сколько разных вариантов результата первенства может быть, если учитывать только положение первых трех и последних двух команд?
Решение. Первые три места могут быть распределены А310=10!/7!=720 способами. В результате останется семь команд, две из которых выбывают из следующего первенства. Так как в этом случае порядок выбывших команд не важен, то это может произойти С27=7!/2!∙5!=21 способами. Согласно правилу умножения получаем, что число разных результатов первенства равно А310∙ С27=15 120. [4]
Упражнения для закрепления
1. Сколько трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6, если цифры могут повторяться?
2. Сколько существует пятизначных чисел, которые одинаково читаются слева направо и справа налево?
3. В классе десять предметов и пять уроков в день. Сколькими способами можно составить расписание на один день?
4. Сколькими способами можно выбрать 4 делегата на конференцию, если в группе 20 человек?
5. Сколькими способами можно разложить восемь различных писем по восьми различным конвертам, если в каждый конверт кладется только одно письмо?
6. Из трех математиков и десяти экономистов надо составить комиссию, состоящую из двух математиков и шести экономистов. Сколькими способами это можно сделать?
7. Вычислить:
1) 2) 3)
8. Решите уравнения:
1) ; 2) 3) 4)
Контрольные вопросы
1. Что является предметом изучения комбинаторики?
2. Сформулируйте правило произведения и правило сложения.
3. Какие соединения называют размещениями?перестановками
4. Какие множества называют упорядоченными?
5. Какие соединения называют сочетаниями?
6. Дайте определение факториала.
studopedia.net
Перестановки, размещения, сочетания
Характерная примета в задачах из области комбинаторики – вопрос в них обычно можно сформулировать так, чтобы он начинался со слов: «Сколькими способами…».
Первые задачи такого типа встречались уже, например, в древней и средневековой Индии.
«О друг, назови число различных ожерелий, которые можно получить из бриллиантов, сапфиров, изумрудов, кораллов и жемчугов» (Махавира, IX в.). Условие этой задачи, возможно, не очень понятно; судя по решению, здесь речь идет об ожерельях, которые бы отличались не по количеству или расположению камней одного и того же типа, а по наличию тех или иных камней – например, ожерелье из бриллиантов, из бриллиантов и кораллов, из бриллиантов, изумрудов и жемчугов и т. д.
| Решение | |||||||||||||||||||||||||||||||||||
|
Конечно, эту задачу можно решить простым перебором вариантов, но можно кое-что заметить. В разных ожерельях камни каждого конкретного вида могут наличествовать либо отсутствовать. Например, бриллианты могут быть, а могут не быть – две возможности. Как при наличии бриллиантов, так и при их отсутствии сапфиры могут быть, а могут или не быть – итого четыре возможности. И при наличии, и при отсутствии бриллиантов и сапфиров изумруды могут быть, а могут не быть, – итого восемь возможностей. И т. д. Следовательно, всего вариантов 25 = 32, правда, нужно еще вычесть один вариант отсутствия всех пяти камней (такое ожерелье, с точки зрения здравого смысла, ожерельем не является). Итак, ответ в задаче – 31 возможное ожерелье.
|
«Повар готовит различные блюда с шестью вкусовыми оттенками: острым, горьким, вяжущим, кислым, соленым, сладким. Друг, скажи, каково число всех разновидностей» (Шридхара, IX–X вв.).
| Решение |
|
Аналогично решению предыдущей задачи получаем 26 – 1 = 64 – 1 = 63. |
Классическими понятиями комбинаторики являются перестановки, размещения и сочетания.
Перестановкой называется какой-либо способ упорядочения данного множества. Чтобы найти число всех перестановок множества из n предметов (это число обозначается Pn, от французского permutation – перестановка) – например, число способов, которыми можно расставить n томов на книжной полке, – обычно рассуждают таким образом. Первым можно поставить любой из n предметов, вторым – любой из (n – 1) оставшихся предметов, третьим любой из (n – 2) оставшихся предметов и т. д. В результате число перестановок будет равно произведению n множителей n (n – 1) (n – 2) … ∙ 3 ∙ 2 ∙ 1.
|
Рис. 1. Перестановки (варианты размещения четырех предметов по четырем ячейкам) |
Упорядоченная совокупность m предметов, выбираемых из исходных n предметов, называется размещением из n по m. С помощью рассуждений, аналогичных предыдущим, нетрудно найти, что число размещений из n по m (оно обозначается , от французского arrangement – размещение) равно произведению m множителей
| n (n – 1) (n – 2) … (n – m + 2) (n – m + 1). |
|
Рис. 2. Размещения (варианты размещения четырех предметов по трем ячейкам) |
Наконец, неупорядоченная совокупность m предметов, выбираемых из исходных n предметов, называется сочетанием из n по m. Число сочетаний обозначается , от французского combinaison – сочетание. Поскольку одному и тому же сочетанию соответствует Pm размещений (получаемых с помощью различных перестановок одного и того же набора m элементов), число сочетаний из n по m меньше числа размещений из n по m в Pm раз:
|
Рис. 3. Сочетания (неупорядоченные размещения) |
Впервые понятия перестановки, размещения и сочетания в их взаимосвязи появились в написанной на древенееврейском языке арифметике (1321 г.) жившего в Провансе (Юго-Восточная Франция) Льва Герсонида, или Леви бен Гершона, однако его труд не был известен большинству последующих европейских математиков. В основном элементы комбинаторики были открыты и упорядочены математиками XVII и начала XVIII вв.
Например, термин permutation – перестановка – появился в учебнике «Теория и практика арифметика» (1656 г.) у работавшего в Лувене и Антверпене (ныне Бельгия) преподавателя математики Андре Таке, учебники которого получили большое распространение в XVII–XVIII вв. Понятие размещений и равенство вновь появились только у Я. Бернулли, давшего наиболее полное изложение комбинаторики во второй части «Искусства предположений», изданного в 1713 г. спустя четыре года после смерти автора и ставшего фундаментальной работой по теории вероятностей.
А вот история сочетаний, как мы сейчас убедимся, более давняя: а именно, числа сочетаний – оказывается, ни что иное, как давно знакомые нам биномиальные коэффициенты, которые мы (вслед за Эйлером) обозначали
Дело тут вот в чем: число – это коэффициент при an – mbm в разложении выражения (a + b)n. Когда бином (a + b) возводится в n-ую степень, т. е. перемножаются n выражений (a + b), множитель bm получается из m выражений (a + b), а an – m – из оставшихся (n – m) таких же выражений. Коэффициент равен числу, указывающему, сколько раз произведение an – mbm появляется в этом разложении, т. е. сколько раз можно выбрать m из n множителей. Слово combinaison – сочетание – употреблял уже Б. Паскаль, который, как уже было указано, уделил большое внимание свойствам биномиальных сочетаний, образующих треугольник Паскаля.
Соответственно, на числа сочетаний переносятся все уже известные свойства биномиальных коэффициентов, в частности, свойство
Это свойство можно доказать новым способом, исходя из комбинаторного смысла чисел . Сумма – это совокупное число, которым можно выбрать последовательно из n имеющихся элементов: ноль элементов (это можно сделать только одним способом), один элемент (это, разумеется, можно сделать n способами), два элемента и т. д., наконец, n элементов (снова одним способом). Каково же это суммарное число? Обратимся к способу решения вышеприведенной задачи об ожерельях! В данном сочетании первый элемент либо присутствует, либо нет – две возможности. Независимо от первого, второй либо присутствует, либо нет – значит, для присутствия или отсутствия первого и второго четыре возможности. Независимо от первого и второго, третий может присутствовать, может не присутствовать – итого 8 возможностей и т. д. Всего получается 2n всевозможных сочетаний, где каждый элемент может присутствовать, а может и отсутствовать, вплоть до одновременного отсутствия всех n элементов (единственный возможный вариант сочетания из n по 0): правда, индийская задача как раз этот – единственный – случай и исключала: ожерелье вовсе без камней – вообще не ожерелье.
Также по-новому, исходя из комбинаторного определения сочетаний, можно доказать и свойство , гарантирующее, вместе с очевидными равенствами , что числа сочетаний можно найти с помощью треугольника Паскаля. Попробуйте!
| Доказательство | ||||
По определению, число сочетаний из n по m – это число способов, которыми можно из n предметов выбрать m, порядок которых неважен. Как-либо выделим (n – 1) предмет из данных n. Тогда составить неупорядоченную совокупность m предметов из n данных можно, либо выбрав все m лишь из выделенных (n – 1), либо взять один невыделенный предмет, а оставшиеся (m – 1) выбрать из выделенных (n – 1) предмета. Получается, что общее число способов, которым можно создать неупорядоченную совокупность m предметов из n данных, равно числу способов, которым можно из (n – 1) предметов выбрать m, плюс число способов, которым из (n – 1) предметов можно выбрать (m – 1). Таким образом,
|
Т. н. мультипликативное представление биномиальных коэффициентов
| = (n (n – 1) (n – 2) … (n – m + 2) (n – m + 1)) / (m (m – 1) (m – 2) … ∙ 3 ∙ 2 ∙ 1) |
впервые (после Леви бен Гершона) установил парижский преподаватель математики П. Эригон (1634 г.), но широкую известность оно получило благодаря работе Паскаля «Трактат об арифметическом треугольнике», опубликованной в 1665 г. после смерти автора. Пожалуй, проще всего этот результат доказывается с помощью равенства . Впрочем, мы сейчас обычно записываем «мультипликативное представление» несколько иначе, с помощью знака факториала. Факториалом натурального числа n называется произведение всех натуральных чисел от 1 до n. Факториалом 0 считается 1. Термин «факториал» впервые предложил французский математик Л. Ф. А. Арбогаст (1800 г.). Факториал числа n обозначается n! Это обозначение ввел в 1808 г. немецкий математик К. Крамп. Итак, n! = 1 ∙ 2 ∙ 3 ∙ … ∙ n, 0! = 1. В этих обозначениях
Pn = n!,
Что касается самого слова «комбинаторика», то оно восходит к «Рассуждению о комбинаторном искусстве» двадцатилетнего Лейбница (1666 г.), которое положило начало этому разделу математики как самостоятельной науке. «Рассуждение» Лейбница содержало ряд теорем о сочетаниях и перестановках, но, кроме того, автор провозглашал весьма широкую применимость новой науки к таким разнообразным предметам, как замки, органы, силлогизмы, смешение цветов, стихосложение, логика, геометрия, военное искусство, грамматика, юриспруденция, медицина и богословие. В дальнейшем Лейбниц продолжил вынашивать грандиозный замысел комбинаторики, полагая, что, как обычная математика занимается большим и малым, единым и многим, целым и частью, так комбинаторика должна заниматься одинаковым и различным, похожим и непохожим, абсолютным и относительным местоположением. Лейбниц предвидел приложения комбинаторики к кодированию и декодированию, к играм, статистике, теории наблюдений. Следует отметить, что, хотя ныне мы понимаем комбинаторику более узко, тем не менее, предвидения Лейбница относительно развития математических теорий, относящихся к указанным предметам, ныне вовсе не выглядят такими беспочвенными, какими казались в его время.
school-collection.iv-edu.ru
Перестановки, размещения, сочетания
Характерная примета в задачах из области комбинаторики – вопрос в них обычно можно сформулировать так, чтобы он начинался со слов: «Сколькими способами…».
Первые задачи такого типа встречались уже, например, в древней и средневековой Индии.
«О друг, назови число различных ожерелий, которые можно получить из бриллиантов, сапфиров, изумрудов, кораллов и жемчугов» (Махавира, IX в.). Условие этой задачи, возможно, не очень понятно; судя по решению, здесь речь идет об ожерельях, которые бы отличались не по количеству или расположению камней одного и того же типа, а по наличию тех или иных камней – например, ожерелье из бриллиантов, из бриллиантов и кораллов, из бриллиантов, изумрудов и жемчугов и т. д.
| Решение | |||||||||||||||||||||||||||||||||||
|
Конечно, эту задачу можно решить простым перебором вариантов, но можно кое-что заметить. В разных ожерельях камни каждого конкретного вида могут наличествовать либо отсутствовать. Например, бриллианты могут быть, а могут не быть – две возможности. Как при наличии бриллиантов, так и при их отсутствии сапфиры могут быть, а могут или не быть – итого четыре возможности. И при наличии, и при отсутствии бриллиантов и сапфиров изумруды могут быть, а могут не быть, – итого восемь возможностей. И т. д. Следовательно, всего вариантов 25 = 32, правда, нужно еще вычесть один вариант отсутствия всех пяти камней (такое ожерелье, с точки зрения здравого смысла, ожерельем не является). Итак, ответ в задаче – 31 возможное ожерелье.
|
«Повар готовит различные блюда с шестью вкусовыми оттенками: острым, горьким, вяжущим, кислым, соленым, сладким. Друг, скажи, каково число всех разновидностей» (Шридхара, IX–X вв.).
| Решение |
|
Аналогично решению предыдущей задачи получаем 26 – 1 = 64 – 1 = 63. |
Классическими понятиями комбинаторики являются перестановки, размещения и сочетания.
Перестановкой называется какой-либо способ упорядочения данного множества. Чтобы найти число всех перестановок множества из n предметов (это число обозначается Pn, от французского permutation – перестановка) – например, число способов, которыми можно расставить n томов на книжной полке, – обычно рассуждают таким образом. Первым можно поставить любой из n предметов, вторым – любой из (n – 1) оставшихся предметов, третьим любой из (n – 2) оставшихся предметов и т. д. В результате число перестановок будет равно произведению n множителей n (n – 1) (n – 2) … ∙ 3 ∙ 2 ∙ 1.
|
Рис. 1. Перестановки (варианты размещения четырех предметов по четырем ячейкам) |
Упорядоченная совокупность m предметов, выбираемых из исходных n предметов, называется размещением из n по m. С помощью рассуждений, аналогичных предыдущим, нетрудно найти, что число размещений из n по m (оно обозначается , от французского arrangement – размещение) равно произведению m множителей
| n (n – 1) (n – 2) … (n – m + 2) (n – m + 1). |
|
Рис. 2. Размещения (варианты размещения четырех предметов по трем ячейкам) |
Наконец, неупорядоченная совокупность m предметов, выбираемых из исходных n предметов, называется сочетанием из n по m. Число сочетаний обозначается , от французского combinaison – сочетание. Поскольку одному и тому же сочетанию соответствует Pm размещений (получаемых с помощью различных перестановок одного и того же набора m элементов), число сочетаний из n по m меньше числа размещений из n по m в Pm раз:
|
Рис. 3. Сочетания (неупорядоченные размещения) |
Впервые понятия перестановки, размещения и сочетания в их взаимосвязи появились в написанной на древенееврейском языке арифметике (1321 г.) жившего в Провансе (Юго-Восточная Франция) Льва Герсонида, или Леви бен Гершона, однако его труд не был известен большинству последующих европейских математиков. В основном элементы комбинаторики были открыты и упорядочены математиками XVII и начала XVIII вв.
Например, термин permutation – перестановка – появился в учебнике «Теория и практика арифметика» (1656 г.) у работавшего в Лувене и Антверпене (ныне Бельгия) преподавателя математики Андре Таке, учебники которого получили большое распространение в XVII–XVIII вв. Понятие размещений и равенство вновь появились только у Я. Бернулли, давшего наиболее полное изложение комбинаторики во второй части «Искусства предположений», изданного в 1713 г. спустя четыре года после смерти автора и ставшего фундаментальной работой по теории вероятностей.
А вот история сочетаний, как мы сейчас убедимся, более давняя: а именно, числа сочетаний – оказывается, ни что иное, как давно знакомые нам биномиальные коэффициенты, которые мы (вслед за Эйлером) обозначали
Дело тут вот в чем: число – это коэффициент при an – mbm в разложении выражения (a + b)n. Когда бином (a + b) возводится в n-ую степень, т. е. перемножаются n выражений (a + b), множитель bm получается из m выражений (a + b), а an – m – из оставшихся (n – m) таких же выражений. Коэффициент равен числу, указывающему, сколько раз произведение an – mbm появляется в этом разложении, т. е. сколько раз можно выбрать m из n множителей. Слово combinaison – сочетание – употреблял уже Б. Паскаль, который, как уже было указано, уделил большое внимание свойствам биномиальных сочетаний, образующих треугольник Паскаля.
Соответственно, на числа сочетаний переносятся все уже известные свойства биномиальных коэффициентов, в частности, свойство
Это свойство можно доказать новым способом, исходя из комбинаторного смысла чисел . Сумма – это совокупное число, которым можно выбрать последовательно из n имеющихся элементов: ноль элементов (это можно сделать только одним способом), один элемент (это, разумеется, можно сделать n способами), два элемента и т. д., наконец, n элементов (снова одним способом). Каково же это суммарное число? Обратимся к способу решения вышеприведенной задачи об ожерельях! В данном сочетании первый элемент либо присутствует, либо нет – две возможности. Независимо от первого, второй либо присутствует, либо нет – значит, для присутствия или отсутствия первого и второго четыре возможности. Независимо от первого и второго, третий может присутствовать, может не присутствовать – итого 8 возможностей и т. д. Всего получается 2n всевозможных сочетаний, где каждый элемент может присутствовать, а может и отсутствовать, вплоть до одновременного отсутствия всех n элементов (единственный возможный вариант сочетания из n по 0): правда, индийская задача как раз этот – единственный – случай и исключала: ожерелье вовсе без камней – вообще не ожерелье.
Также по-новому, исходя из комбинаторного определения сочетаний, можно доказать и свойство , гарантирующее, вместе с очевидными равенствами , что числа сочетаний можно найти с помощью треугольника Паскаля. Попробуйте!
| Доказательство | ||||
По определению, число сочетаний из n по m – это число способов, которыми можно из n предметов выбрать m, порядок которых неважен. Как-либо выделим (n – 1) предмет из данных n. Тогда составить неупорядоченную совокупность m предметов из n данных можно, либо выбрав все m лишь из выделенных (n – 1), либо взять один невыделенный предмет, а оставшиеся (m – 1) выбрать из выделенных (n – 1) предмета. Получается, что общее число способов, которым можно создать неупорядоченную совокупность m предметов из n данных, равно числу способов, которым можно из (n – 1) предметов выбрать m, плюс число способов, которым из (n – 1) предметов можно выбрать (m – 1). Таким образом,
|
Т. н. мультипликативное представление биномиальных коэффициентов
| = (n (n – 1) (n – 2) … (n – m + 2) (n – m + 1)) / (m (m – 1) (m – 2) … ∙ 3 ∙ 2 ∙ 1) |
впервые (после Леви бен Гершона) установил парижский преподаватель математики П. Эригон (1634 г.), но широкую известность оно получило благодаря работе Паскаля «Трактат об арифметическом треугольнике», опубликованной в 1665 г. после смерти автора. Пожалуй, проще всего этот результат доказывается с помощью равенства . Впрочем, мы сейчас обычно записываем «мультипликативное представление» несколько иначе, с помощью знака факториала. Факториалом натурального числа n называется произведение всех натуральных чисел от 1 до n. Факториалом 0 считается 1. Термин «факториал» впервые предложил французский математик Л. Ф. А. Арбогаст (1800 г.). Факториал числа n обозначается n! Это обозначение ввел в 1808 г. немецкий математик К. Крамп. Итак, n! = 1 ∙ 2 ∙ 3 ∙ … ∙ n, 0! = 1. В этих обозначениях
Pn = n!,
Что касается самого слова «комбинаторика», то оно восходит к «Рассуждению о комбинаторном искусстве» двадцатилетнего Лейбница (1666 г.), которое положило начало этому разделу математики как самостоятельной науке. «Рассуждение» Лейбница содержало ряд теорем о сочетаниях и перестановках, но, кроме того, автор провозглашал весьма широкую применимость новой науки к таким разнообразным предметам, как замки, органы, силлогизмы, смешение цветов, стихосложение, логика, геометрия, военное искусство, грамматика, юриспруденция, медицина и богословие. В дальнейшем Лейбниц продолжил вынашивать грандиозный замысел комбинаторики, полагая, что, как обычная математика занимается большим и малым, единым и многим, целым и частью, так комбинаторика должна заниматься одинаковым и различным, похожим и непохожим, абсолютным и относительным местоположением. Лейбниц предвидел приложения комбинаторики к кодированию и декодированию, к играм, статистике, теории наблюдений. Следует отметить, что, хотя ныне мы понимаем комбинаторику более узко, тем не менее, предвидения Лейбница относительно развития математических теорий, относящихся к указанным предметам, ныне вовсе не выглядят такими беспочвенными, какими казались в его время.
files.school-collection.edu.ru
8. Перестановки, размещения, , сочетания
В комбинаторных задачах комбинации предметов могут отличаться одна от другой числом предметов, их составом и порядком.
Пример. В отделении 5 новобранцев: Белкин, Пенкин, Фенькин, Свечкин и Овечкин. Их учат рассчитываться по порядку. Каждый раз их перестраивают по – новому и расчет повторяется. Сколько раз сержант может повторить это упражнение разными способами?
Можно обозначить солдат первыми буквами их фамилий. Например, ПСОФБ означает порядок, в котором солдаты расположились на построении. Все комбинации отличаются порядком букв и называются перестановками.
Пусть дано множество из N элементов. Занумеруем их от 1 до N.
Перестановкой из N элементов называется всякий способ нумерации этих элементов.
Теорема 2. Число всех различных перестановок из N элементов равно N!
Доказательство. Всякую перестановку из N элементов можно получить с помощью N действий: первое действие – выбор первого элемента, второе действие – выбор второго элемента и т. д., N – е действие – выбор элемента с номером N.
Первый элемент можно выбрать N Различными способами; второй выбирается из оставшихся N – 1 элементов, поэтому число всех способов выполнения второго действия будет N – 1. Далее останется N – 2 элемента, их можно разместить N – 2 способами. И т. д. Последнее действие можно выполнить одним способом. По правилу умножения число всех способов выполнения действий, т. е. число перестановок, равно (так обозначается функция факториал, т. е. произведение всех членов натурального ряда до N Включительно). ■
Число перестановок обозначается РN:
(4)
В случае с новобранцами (N = 5) РN = 5! = 120.
Пример. Свидетель происшествия запомнил, что четырехзначный номер автомобиля, скрывшегося с места происшествия, начинается с цифры 1, а завершается на 4, причем все цифры разные. Сколько автомобилей должна проверить автоинспекция?
Решение. Вторую и третью цифры надо выбирать из восьми, а именно из 0, 2, 3, 5, 6, 7, 8, 9. Если выбрать вторую цифру восемью способами, то для третьей цифры останется 7 вариантов. Отсюда 8×7 = 56 способов.
Нужно перебрать из восьми цифр по две с учетом их порядка, поскольку 1674 и 1764 – разные номера. Такие комбинации называют размещениями.
Размещением из N элементов по K называется всякая перестановка из K элементов, выбранных каким – либо способом из данных N элементов.
Число размещений обозначается .
Теорема 3. Число всех размещений из N элементов по K вычисляется по формуле:
(5)
(в этой формуле K сомножителей).
Доказательство. Аналогично теореме 2. Каждое размещение можно получить с помощью K действий. Первое действие можно выполнить N способами, второе – N— 1 способами и т. д., K действие – (N – K + 1) способами. По правилу умножения , что и требовалось доказать. ■
Для рассмотренного выше примера .
Пример. Из 10 депутатов поселкового совета 7 проголосовали «за». Каково число всех возможных вариантов голосования?
Здесь порядок выбора не играет роли, поэтому комбинации отличаются только составом лиц. Такие комбинации называются сочетаниями.
Сочетанием из N элементов по K называется всякая совокупность K элементов, выбранных каким – либо способом из данных N элементов.
Теорема 4. Число всех сочетаний из N элементов по K вычисляется по формуле:
(6)
Доказательство. Возьмем какое – нибудь сочетание из N элементов по K:
(A, B, C, … , F) — здесь K букв.
Переставляя эти элементы всевозможными способами, получим K! всех размещений из N элементов по K одного и того же состава. Таким образом, из одного сочетания получается K! размещений. Следовательно, из сочетаний получится размещений, т. е. . Отсюда
, что и требовалось доказать. ■
В последнем примере = 10, = 7,
Другая формула для числа сочетаний имеет вид:
Теорема 5.Свойство :
(7)
Доказательство. Если из N элементов выбрать K элементов, то останется (N – K) элементов. Следовательно, каждому сочетанию из N элементов по K соответствует определенное сочетание из N элементов по (N – K ). Поэтому число тех и других сочетаний одинаково, что и требовалось доказать. ■
Формула (7) сокращает вычисления, например:
По определению 0! = 1, .
Числа называются биномиальными коэффициентами, с их помощью записывается так называемая формула бинома Ньютона:
Эту формулу можно доказать методом математической индукции.
| < Предыдущая | Следующая > |
|---|
matica.org.ua
