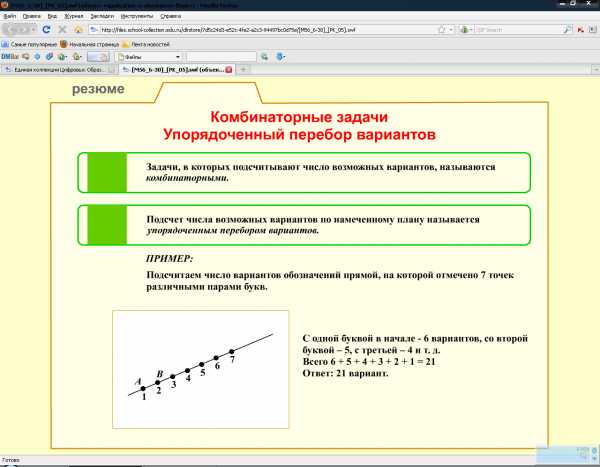
Методы решения комбинаторных задач
При решении многих практических задач приходится использовать комбинации элементов, выбирать из данной совокупности те, которые имеют определенные свойства, и размещать их в определенном порядке. Такие задачи называются комбинаторными. Раздел математики, посвящённый решению задач выбора и расположения элементов в соответствии с данными условиями, называется комбинаторикой. Термин «комбинаторика» происходит от латинского слова «combina», что в переводе на русский язык означает – «сочетать», «соединять».
Выбранные группы элементов называют соединениями. Если все элементы соединения разные, то получаем соединения без повторений, которые и рассмотрим ниже.
Большинство комбинаторных задач решается с помощью двух основных правил – правила суммы и правила произведения.
| Выбор правила | Выбор правила |
| Правило суммы | Правило произведения |
| Если некоторый объект А можно выбрать m способами, а другой объект В можно выбрать n способами, то выбор объекта либо А, либо В можно осуществить m + n способами. | Если объект А можно выбрать m способами и если после каждого такого выбора объект В можно выбрать n способами, то выбор пары А и В можно осуществить m · n способами. |
Задача 1.
В магазине «Все для чая» есть 6 разных чашек и 4 разных блюдца. Сколько вариантов чашки и блюдца можно купить?
Решение.
Чашку мы можем выбрать 6-ю способами, а блюдце 4-я способами. Так как нам надо купить пару чашку и блюдце, то это можно сделать 6 · 4 = 24 способами (по правилу произведения).
Ответ: 24.
Для успешного решения комбинаторных задач надо еще и правильно выбрать формулу, по которой искать количество нужных соединений. В этом поможет следующая схема.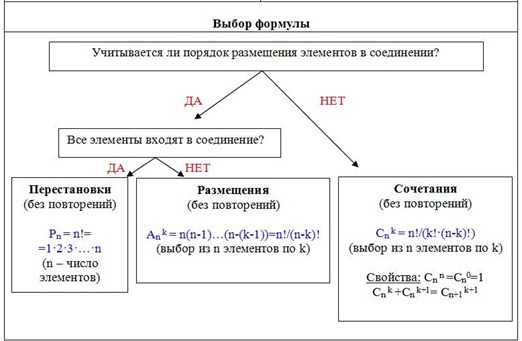
Рассмотрим решение нескольких задач на разные виды соединений без повторений.
Задача 2.
Найдите количество трехзначных чисел, которые можно составить из цифр 1, 2, 3, 4, 5, 6, 7, если цифры в числе повторяться не могут.
Решение.
Для выбора формулы выясняем, что для чисел, которые мы будем составлять, порядок учитывается и не все элементы одновременно выбираются. Значит, это соединение – размещение из 7 элементов по 3. Воспользуемся формулой для числа размещений: A73 = 7(7 – 1)(7 – 2) = 7 · 6 · 5 = 210 чисел.
Ответ: 210.
Задача 3.
Сколько существует семизначных телефонных номеров, в которых все цифры разные, а номер не может начинаться с нуля?
Решение.
На первый взгляд эта задача такая же, как и предыдущая, но сложность в том, что надо не учитывать те соединения, которые начинаются с нуля. Значит необходимо из существующих 10-ти цифр составить все семизначные номера телефонов, а потом от полученного числа отнять количество номеров, начинающихся с нуля. Формула будет иметь вид:
A107 – A96 = 10 · 9 · 8 · 7 · 6 · 5 · 4 – 9 · 8 · 7 · 6 · 5 · 4 = 544 320.
Ответ: 544 320.
Задача 4.
Сколькими способами можно расставить на полке 12 книг, из которых 5 книг – это сборники стихотворений, так, чтобы сборники стояли рядом?
Решение.
Сначала примем 5 сборников условно за одну книгу, потому что они должны стоять рядом. Так как в соединении существенным есть порядок, и все элементы используются, значит это перестановки из 8 элементов (7 книг + условная 1 книга). Их количество Р8. Далее будем переставлять между собой только сборники стихотворений. Это можно сделать Р5 способами. Поскольку нам нужно расставить и сборники, и другие книги, то воспользуемся правилом произведения. Следовательно, Р8 · Р5 = 8! · 5!. Число способов будет большим, поэтому ответ можно оставить в виде произведения факториалов.Ответ: 8! · 5!
Задача 5.
В классе 16 мальчиков и 12 девочек. Для уборки территории возле школы нужно 4 мальчика и 3 девочки. Сколькими способами можно их выбрать со всех учеников класса?
Решение.
Сначала отдельно выберем 4 мальчика из 16 и 3 девочки из 12. Так как порядок размещения не учитывается, то соответственные соединения – сочетания без повторений. Учитывая необходимость одновременного выбора и мальчиков, и девочек, используем правило произведения. В результате число способов будет вычисляться таким образом:
С164 · С123 = (16!/(4! · 12!)) · (12!/(3! · 9!)) = ((13 · 14 · 15 · 16) / (2 · 3 · 4)) ·((10 · 11 · 12) / (2 · 3)) = 400 400.
Ответ: 400 400.
Таким образом, успешное решение комбинаторной задачи зависит от правильного анализа ее условия, определения типа соединений, которые будут составляться, и выбора подходящей формулы для вычисления их количества.
Остались вопросы? Не знаете, как решать комбинаторные задачи?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!
Зарегистрироваться
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
blog.tutoronline.ru
Комбинаторные задачи 6 класс — ТолВИКИ
Автор урока
Астапова Александра Анатольевна
Место работы: МБУ «Школа № 32 г.о. Тольятти
сайт МБУ «Школа №32»
Название урока
Решение комбинаторных задач
Предмет, класс
математика, 6 класс
Цели урока
Ввести понятие комбинаторики; сформировать представление о комбинаторных задачах; научить строить дерево возможных вариантов; повторить сложение и вычитание дробей с разными знаменателями; развитие логического мышления.
Ход урока
1. Организационный момент
Учитель объясняет тему урока и цель.
2. Новый материал объяснить в ходе решения трех задач.
Презентация «Комбинаторика» (Приложение 1).
Задача№1
Государственные флаги многих стран состоят из горизонтальных или вертикальных полос разных цветов. Сколько существует различных флагов, состоящих из двух горизонтальных полос одинаковой ширины и разного цвета – белого, красного и синего?
Решение:
Пусть верхняя полоса флага – белая (Б). Тогда нижняя полоса может быть красной (К) или синей (С). Получили две комбинации – два варианта флага. Если верхняя полоса флага – красная, то нижняя может быть белой или синей. Получим ещё два варианта флага. Пусть, наконец, верхняя полоса – синяя, тогда нижняя может быть белой или красной. Это ещё два варианта флага. Всего получили 3 • 2 = 6 комбинаций – шесть вариантов флагов.
Задачи, решая которые приходится составлять различные комбинации из конечного числа элементов и подсчитывать число комбинаций, получили названиекомбинаторных .
Раздел математики, в котором рассматривают такие задачи, называют комбинаторикой. Комбинаторика (от латинского combinare) означает “соединять, сочетать”.
Задача 2
Сколько трехзначных чисел можно составить из цифр 1, 3, 5, 7? Используя в записи числа каждую из них не более одного раза?
Решение:
Чтобы ответить на этот вопрос, выпишем все такие числа. Пусть на первом месте стоит цифра 1. На втором месте может быть записана любая из цифр 3, 5, 7. Запишем, например, на втором месте цифру 3. Тогда в качестве третьей цифры можно взять 5 или 7. Получим два числа 135 и 137. Если на втором месте записать цифру 5, то в качестве третьей цифры можно взять цифру 3или 7. В этом случае получим числа 153 и 157. Если же, наконец, на втором месте записать цифру 7, то получим числа 173 и 175. Итак, мы составили все числа, которые начинаются с цифры 1. Таких чисел шесть: 135, 137, 153, 157, 173, 175. Аналогичным способом можно составить числа, которые начинаются с цифры 2,с цифры 5, с цифры 7.
Полученные результаты запишем в четыре строки, в каждой из которых шесть чисел:
135, 137, 153, 157, 173, 175, 315, 317, 351, 357, 371, 375, 513, 517, 531, 537, 571, 573, 713, 715, 731, 735, 751, 753,
Таким образом, из цифр 1, 3, 5, 7 (без повторения цифр) можно составить 24 трехзначных числа.
Проведенный перебор вариантов проиллюстрирован на так называемом дереве возможных вариантов. Ответ на вопрос, поставленный в задаче, можно получить, не выписывая сами числа. Рассуждая так. Первую цифру можно выбрать 4 способами. Так как после выбора первой цифры останутся 3, то вторую цифру можно выбрать уже 3 способами. Наконец, третью цифру можно выбрать (из оставшихся двух) 2 способами. Следовательно, общее число искомых трехзначных чисел равно произведению 4 • 3 • 2, т.е. 24. Ответ на поставленный в задаче вопрос мы нашли, используя комбинаторное правило умножения. Пусть имеется n элементов и требуется выбрать один за другим некоторые k элементов. Если первый элемент можно выбрать n1 способами, после чего второй элемент можно выбрать из оставшихся элементов n2 способами, затем третий элемент n3 способами и т. д., то число способов, которыми могут быть выбраны все k элементов, равно произведению n1 • n2 • n3 • …• nk.
Задача 3 Из города А в город В ведут две дороги, из города В в город С – три дороги, из города С до пристани – две дороги. Туристы хотят проехать из города А через города В и С к пристани. Сколькими способами они могут выбрать маршрут?
Решение: Путь из А в В туристы могут выбрать двумя способами. Далее в каждом случае они могут проехать из В в С тремя способами. Значит, имеются 2 • 3 вариантов маршрута из А в С. Так как из города С на пристань можно попасть двумя способами, то всего существует 2 • 3 • 2, т.е. 12 способов выбора туристами маршрута из города А к пристани. 3. Тренировочные упражнения (Задания в виде презентации «Комбинаторика» или карточек.).
Задание 1 Сколько существует флагов составленных из трёх горизонтальных полос одинаковой ширины и различных цветов –белого, зелёного, красного и синего? Есть ли среди них флаг Российской Федерации. (Ребята самостоятельно решают задачу. Решив задачу, проверяют ответ, вставив пропущенные числа. Ответ в задаче и в примере одинаковый.)

Решение: Таким образом, 4 • 3 • 2 = 24 флага. Ответ: 24 флага, да.
Задание 2
Сколько различных трехзначных чисел (без повторения цифр) можно составить из нечётных цифр, которые являются кратными 5. Прежде чем решать эту задачу, давайте повторим, какие цифры нечётные? Какие числа являются кратными 5.
Решение: Нечётные цифры: 1, 3, 5, 7, 9. В данном случае, чтобы число было кратным 5, оно должно оканчиваться на 5. Составим дерево возможных вариантов.
Таким образом, 4 • 3 • 1 = 12 чисел.
Задание 3 В школьной столовой предлагают 2 первых блюда: борщ, лапша – и 4 вторых блюда: пельмени, котлеты, гуляш, рыба. Сколько обедов из двух блюд может заказать посетитель. Перечислите их.
Решение: 1 блюдо: Б Л 2 возможности 2 блюдо: П К Г Р П К Г Р по 4 Таким образом, 2 • 4 = 8 различных обедов: Борщ, пельмени; Лапша, пельмени; Борщ, котлеты; Лапша, котлеты; Борщ, гуляш; Лапша, гуляш; Борщ, рыба; Лапша, рыба.
Задание 4 Учащиеся 6 класса решили обменяться фотографиями. Сколько фотографий для этого потребуется, если в классе 11 учащихся. Решение: 11 человек по 10 фотографий. 11 • 10 = 110 (фотографий). Ответ: 110 фотографий.
Задание 5 Из села Ташла в село Пискалы ведут три дороги, а из села Пискалы в город Тольятти – четыре дороги. Сколькими способами можно попасть из села Тащла в город Тольятти через село Пискалы?
Решение: 3 дороги по 4 варианта, т.е. 3 • 4 = 12 (способов). Ответ: 12 способов.
Задание 6 В кафе имеются четыре первых блюда, пять вторых и два третьих. Сколькими способами посетители кафе могут выбрать обед, состоящий из первого, второго и третьего блюд?
Решение: 4 • 5 • 2 = 40 (способов) Ответ: 40 способов.
Итог урока
– Какие задачи называются комбинаторными?
– Что означает слово «комбинаторика»?
– Как формулируется комбинаторное правило умножения?–
Домашние задание
Придумать и решить три комбинаторных задачи
Презентация
Презентация к уроку «Решение комбинаторных задач
Фото отчет
Материалы по формирующему и итоговому оцениванию
Итоговое оценивание с помощью смайликов
Материалы по сопровождению урока
Литература:
1. Учебник «Математика 6» Н.Я.Виленкин, В.И.Жохов и др. Москва: «Мнемозина», 2006.
2. Учебник И.И. Зубарева, А.Г. Мордкович Москва: «Мнемозина», 2005
3. Алгебра. Элементы статистики и теории вероятностей. Учебное пособие под редакцией С.А.Теляковского. Москва: «Просвещение», 2005.
wiki.tgl.net.ru
Урок математики в 6 классе «Решение комбинаторных задач»
Математика 6 класс
Тема: «Решение комбинаторных задач».
Составила Арзуманова К. В. – учитель физики, математики
Цели:
Образовательная – ознакомить учащихся с методами решения комбинаторных задач; научить применять методы полного перебора всех возможных вариантов и умножения.
Развивающая – развивать логическое мышление, интерес к изучению математики. грамотную математическую речь.
Воспитательная – воспитывать внимание и аккуратность в оформлении заданий.
Тип урока: изучение нового материала
Оборудование: доска, учебники, компьютер, проектор, презентация к уроку (образец в приложении)
План урока:
1. Организационный момент. Приветствие.
2. Изучение нового материала.
3. Рефлексия. Закрепление.
4. Итоги урока.
ХОД УРОКА
1. Приветствие.
2. Устный счёт. Угадай тему урока.
1) 1/8 + 1/4; 2) 2/15 ∙ 0; 3) 7 – 3/8; 4) 57/9 – 21/6; 5) 11/2 ∙ 2/9; 6) 61/2 + 31/4; 7) 4/5 ∙ ¾; 8) 4 + 22/5;
9) 3/8 ∙ 7/12; 10) 3/4 – 1/3; 11) 3/8 ∙ 1; 12) 2/15 ∙ 4; 13) 3 ∙ 11/2.
к
о
м
б
и
н
а
т
о
р
и
к
а
А) Введение понятия комбинаторика. (Слайд)
Учитель. Комбинаторика – раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчинённых тем или иным условиям, можно составить из заданных объектов.
Б) Что значит решить комбинаторную задачу. (Слайд)
Учитель. Решить комбинаторную задачу – это значит выписать все возможные комбинации, составленные из чисел, слов, предметов и др., отвечающих условию задачи.
В разделе представлены комбинаторные задачи на размещение, сочетание, перестановки с повторением и без повторения элементов. Используется естественный, доступный детям всех возрастов метод решения комбинаторных задач с помощью непосредственного перебора возможных вариантов (комбинаций).
В) Решение задачи методом полного перебора всех возможных вариантов. (Слайд)
Сколько двузначных чисел можно составить, используя цифры 1; 4; 7?
Решение: Для того чтобы не пропустить и не повторить ни одного из чисел, будем выписывать их в порядке возрастания:
11; 14; 17; (начали с 1)
41; 44; 47; (начали с 4)
71; 74; 77; (начали с 7)
Таким образом, из трёх данных цифр можно составить всего 9 различных двузначных чисел.
Ответ: 9 чисел.
3. Решение задач методом полного перебора на доске и в тетрадях. (Слайд)
Учащиеся. Сколько существует флагов составленных из трёх горизонтальных полос одинаковой ширины и различных цветов – белого, зелёного, красного и синего?
Вопрос:
Есть ли среди них флаг Российской Федерации?
Что означают цвета Российского флага? (Слайд)
(Белый цвет символизирует благородство и откровенность;
Синий цвет — верность, честность, безупречность и целомудрие;
Красный цвет — мужество, смелость, великодушие и любовь).
4. Решение задач с помощью дерева возможных вариантов на доске и в тетрадях. (Слайд)
Учитель. Существует общий подход к решению самых разных комбинаторных задач с помощью составления специальных схем. Внешне такая схема напоминает дерево, отсюда название – дерево возможных вариантов. При правильном построении дерева ни один из возможных вариантов решения не будет потерян.
5. Задача. (Слайд)
Рассмотрим задачу о составлении трехзначных чисел из цифр 1; 4; 7. Для её решения построим схему-дерево возможных вариантов, которое наглядно показывает решение задачи.
6. Решение задач с использованием дерева возможных вариантов на доске и в тетрадях. (Слайд)
Учащиеся. Мама на рынке купила фрукты: груши, бананы, яблоки, виноград, мандарины, абрикосы. Сколькими способами мама может разложить эти фрукты по вазам?
Сообщение о фруктах. Американский психолог И. Канн утверждает в своей книге «1001 способ раскрытия своей личности», что привязанность к тем или иным фруктам или ягодам обнаруживает черты вашего характера. Итак, познаем себя через плоды.
Виноград – эти люди умеют хранить тайны не только свои, но и чужие; энергичные, весёлые.
Бананы – любители бананов волевые, мужественные, легкоранимые личности; мечтатели.
Мандарины – это покладистые личности, у них лёгкий характер, они очень коммуникабельны.
Абрикосы – это внимательные и чуткие люди, умеющие дружить; не любят посягательства на свою свободу.
Груши – это оптимисты, преданные друзья, прекрасно поддерживают разговоры на любую тему; душа компании.
Яблоки – это трудолюбивые, усердные в работе люди; по характеру устойчивы и стабильны, всегда добиваются своей цели и их трудно свернуть с пути, который они выбрали. (Слайд).
7. Правило умножения в комбинаторных задачах. (Слайд )
Учитель. Для комбинаторной задачи с умножением можно построить дерево вариантов, но такое дерево строить станет намного сложнее, именно поэтому используется метод умножения, чтобы запись была короче.
Рассмотрим этот метод на примере одной задачи:
На обед в школьной столовой предлагается 2 супа,3 вторых блюда и 4 разных сока. Сколько различных обедов можно составить по предложенному меню?
Суп 2 Вторые блюда 3 Сок 4
Решение: 2 x 3 x 4 = 24
Ответ: Можно составить 24 варианта различных обедов.
8. Решение задач с использованием дерева возможных вариантов на доске и в тетрадях. (Слайд)
Учащиеся. Сколькими способами можно посадить деревья: берёзу, клён, осину, липу, рябину так, чтобы деревья не повторялись?
Сообщение о деревьях биодонорах.
Деревья обладают огромными запасами биоэнергии и способностью её восстанавливать. Издавна известно, что человеку, родившемуся под определенным знаком Зодиака, соответствует свое дерево.
Знак Зодиака
Дерево-донор
Овен
слива
Телец
мирт
Близнецы
лавр
Рак
ива
Лев
дуб
Дева
яблоня
Весы
бук
Скорпион
рябина
Стрелец
пальма
Козерог
сосна
Водолей
инжир
Рыбы
вяз
9. Перестановки в комбинаторных задачах. (Слайд)
Учитель. В комбинаторике часто приходиться решать задачу о том, сколькими способами можно расположить в ряд или, как говорят математики, упорядочить все элементы некоторого множества. Каждое из таких расположений называют перестановкой.
Задача. Андрей, Борис и Василий входят в комнату по одному. Сколько у них есть способов это сделать?
Решение. Пусть первым войдёт Андрей, но тогда вторым может войти Борис или Василий, то есть имеются две возможности. Аналогично есть две возможности, если первым войдёт Борис и если первым войдёт Василий. Таким образом, 6 возможностей.
Ответ: 6 способов.
10. Решите задачу на перестановки. (Слайд)
Учащиеся. Меню ученика должно включать в себя витамины группы А, В1, С, Р. Сколько существует вариантов меню так, чтобы витамины не повторялись.
Сообщения о витаминах.
Если у человека не хватает какого-то витамина, то он чувствует себя дискомфортно. Например, если у человека недостаточно витамина:
С – частые простуды, нарушение сна, кровоточащие десны;
А – шероховатость кожи, слезотечение, светобоязнь;
В1 – головные боли, снижение памяти, плаксивость, одышка, сердцебиение;
В2 – бессонница, апатия, плохой запах изо рта, шелушение губ;
В12 – желтый цвет лица, ранняя седина, выпадение волос, головокружение, онемение и покалывание в руках и ногах;
Р – слабость, извращение вкуса, болезненность языка;
Е – нарастающая мышечная усталость;
D – боль в области костей, в мышцах, часто потеет голова.
Чтобы мы были здоровы, бодры, веселы нужно соблюдать здоровый образ жизни. Есть много фруктов, заниматься спортом, делать утреннюю зарядку.
11. Итог урока
12 Спасибо за урок.
www.metod-kopilka.ru
Урок по математике на тему: «Комбинаторные задачи», 6 класс
Тема урока «Комбинаторные задачи», 6 класс
Цели урока:
— обобщить и систематизировать знания о комбинаторных задачах;
— повторить способы решения комбинаторных задач;
— совершенствовать навыки решения данных задач;
— развивать умение дискуссионной и групповой работы;
— развитие коммуникативных компетенций;
— формирование умений мыслить системно, находить творческий подход в своей работе;
— умение создать и защитить минипроект по теме «Комбинаторные задачи».
Выставка творческих работ по теме «Комбинаторные задачи»
Презентация. Приложение №1.
Класс разбит на 5 групп.
Ход занятия
Организационный момент.
Учитель. В вашем, 6 а классе, много ребят творческих, участвующих во всевозможных олимпиадах, конкурсах, проектах. Недавно были подведены результаты заочной российской олимпиады «Авангард», где участвовали ребята. Сегодня они получают дипломы призёров данной олимпиады. ( 5 человек).
Мы закончили изучать интересную тему, учились решать задачи по данной теме, выполняли творческое задание. Как эта тема называлась и чему мы научились, изучая данную тему?
Актуализация знаний.
Кто вспомнит, что это за раздел математики, комбинаторные задачи?
(ответы учащихся)
Сообщение ученицы. Слайд №3.
Комбинаторика – раздел математики, в котором изучают вопросы о том, сколько различных комбинаций, подчинённых тем или иным условиям можно составить из данных объёктов. Выбором объектов и расположением их в том или ином порядке приходиться заниматься чуть ли не во всех областях человеческой деятельности. Например, конструктору, разрабатывающему новую модель механизма, учёному-агроному, планирующему сельхозкультуры на нескольких полях, химику, изучающему строение молекул.
С аналогичными задачами, получившими название комбинаторных, люди столкнулись в глубокой древности. В Китае увлекались составлением магических квадратов, в Древней Греции подсчитывали число различных комбинаций длинных и коротких слогов стихотворных размеров. Комбинаторные задачи возникли в связи с такими играми, как шашки, шахматы, карты, кости и др.Чтобы их решить, нужно было уметь подсчитывать число различных комбинаций, подчинённых тем или иным условиям.
Кто напомнит, какими способами мы научились решать комбинаторные задачи? Слайд №4.
Перебор возможных вариантов.
Таблицей.
Дерево возможных вариантов.
Правило умножения.
Правило треугольника.
С помощью графов.
Презентация способов решения задач. (Выступает с презентацией ученица, слайды с №5 по №10). Учащиеся работают в группах.
А сейчас мы вспомним отдельно каждый способ. Я вам буду предлагать задачу, вы в группах решите ёё и скажете правильный ответ. Затем проверим решение с помощью презентации.
1.Перебор возможных вариантов.
Сколько существует двухзначных чисел, составленных из цифр: 0, 5, 8 ?
Решение. 58, 50, 80, 85.
Ответ: 4 числа.
2. Таблицей.
Алла, Бэла, Валентина и Галина во время майского праздника подарили друг другу по одному цветку. Причём каждая девочка подарила каждой по одному цветку. Сколько всего цветков было подарено?
Решение.
Ответ: 12 цветков.
А
Б
В
Г
А
——
+
+
+
Б
+
___
+
+
В
+
+
—-
+
Г
+
+
+
—-
3.Дерево возможных вариантов.
Никита, Борис, Виктор, и Григорий играли в шахматы. Каждый сыграл по 1 партии. Сколько сыграно партий?
Решение.
Никита
Борис Виктор Григорий
Виктор Григорий Григорий
Ответ. 6 партий.
Правило умножения.
В меню в столовой предложены на выбор 3 первых блюда, 5 вторых и 4 третьих блюд. Сколько различных вариантов обедов, состоящих из 1 первого, 1 второго и 1 третьего блюда, можно составить из предложенного меню?
Решение. 3*5*4=60
Ответ: 60 блюд.
5.Правило треугольника.
Встретились 5 приятелей и обменялись рукопожатиями. Сколько всего сделано рукопожатий?
Решение.
1 2 3 4 5
1 — + + + +
2 — — + + +
3 — — — + +
4 — — — — +
— — — — — Ответ: 10 рукопожатий.
6.С помощью графа.
По окончанию деловой встречи 4 специалиста обменялись визитными карточками (каждый вручил свою карточку каждому). Сколько визитных карточек было роздано?
Решение.
Ответ. 12 визиток
4.Работа в группах. Слайд №11.
Сейчас я предлагаю каждой группе решить задачу одну и ту же, но разными способами. Каждая группа оформляет своё решение на листе фломастерами.
Задача. Андрей, Борис, Виктор и Григорий после возвращения из спортивного лагеря подарили друг другу на память свои фотографии. Причём каждый мальчик подарил каждому по 1 фотографии. Сколько всего фотографий было подарено?
Решение задач вывешивается на доске. Выполняется анализ решения задач каждой группы.
Защита минипроектов. Слайд № 12.
Каждый из вас дома выполнил творческую работу. Кто–то сам составил и решил задачи несколькими способами, другие нашли задачи в интернете и тоже их представили. Послушаем наиболее удачные и интересные работы.
(Выступление 5 учащихся)
Итог урока. Домашнее задание.
Слайд № 13. Знаешь ли ты?
Как прочитать и решить такой пример?
10!
6!
8!
Поищите в справочной литературе, в интернете ответ на этот вопрос.
Учитель. Рефлексия. Итак, мы закончили изучать тему из раздела Комбинаторики. Интересно ли было решать комбинаторные задачи? Понравился ли урок? (Учащиеся показывают рисунки рожицы с улыбкой или грустные).
Нам ещё предстоит познакомиться с другим разделом математики: теорией вероятности. Это тоже интересная тема. Но о ней мы поговорим позже.
infourok.ru
Урок по математики «Решение комбинаторных задач»
Урок-путешествие
по теме
«Решение комбинаторных задач»
Класс: 6
Предмет: математика
Тип урока: объяснение нового материала
Цели:
Образовательные:
— создать представление о комбинаторике как разделе математики;
— формировать умение решать комбинаторные задачи путем перебора возможных вариантов с помощью дерева вариантов или путем перестановки закодированных элементов;
— познакомить учащихся с решением комбинаторных задач и с использованием правила умножения;
— показать применение знаний, полученных на уроках математики, на практике.
Развивающие:
— развивать логическое мышление, устную математическую речь, внимание, память и воображение через интеллектуальные задания;
— развивать умение решать комбинаторные задачи по правилу умножения;
— развивать творческий потенциал и самооценку через творческие задания.
Воспитательные:
— продолжить воспитание познавательного интереса к предмету и повышение мотивации к учению по средствам ИКТ;
— способствовать воспитанию самостоятельности и умению работать в парах.
Учебники и дидактические материалы:
— Мордкович А.Г. и др. «События. Вероятности. Статистическая обработка данных. 7-9 кл.» — М.: Мнемозина, 2003
— Виленкин Н.Я. и др. «Математика 6 класс» — М.: Мнемозина, 2008
— Дорофеев и др. «Математика 6 кл.» — М.: Просвещение, 1996
— Макарычев Ю.Н. и др. «Элементы статистики и теории вероятностей. Алгебра 7-9 классы» — М.: Просвещение, 2008
— Ткачева М.В., Федорова Н.Е. «Элементы статистики и вероятность. 7-9 кл.» — М.: Просвещение, 2006
ХОД УРОКА:
Организационный момент.
Здравствуйте, ребята. Сегодня на уроки мы с вами научимся решать задачи , а из какого они раздела вы узнаете когда разгадаете кроссворд. Наш сегодняшний урок-путешествие в страну Знаний начинается.
Станция «Любознайкино»
Ну вот, ребята , вы узнали, отгадав ребус (Комбинаторика). Мы вспомним из математики 5 класса решение комбинаторных задач путем перебора вариантов и построения дерева возможных вариантов и познакомимся с новым способом – правилом умножения.
Нам часто приходится иметь дело с задачами, в которых нужно подсчитать число всех возможных способов расположения некоторых предметов или число всех возможных способов как это действие осуществить. Разные пути или варианты, которые приходится выбирать человеку, складываются в самые разнообразные комбинации.
Комбинаторика – это раздел математики, посвященный решению задач на перебор различных вариантов, удовлетворяющих каким-либо условиям. Здесь изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов.
Латинское слово combinare означает «соединять, сочетать».
В комбинаторных задачах обычный вопрос: сколькими способами, сколько вариантов… Рождение комбинаторики как раздела математики связано с трудами великих французских математиков XVII века Блеза Паскаля и Пьера Ферма.
Существует очень много задач, в которых рассматриваются различные ситуации выбора. Однако, несмотря на все разнообразие комбинаторных задач, можно выделить среди них группы однотипных. В этих задачах речь идет о разных предметах, приводятся разные ситуации, но ход их решения одинаков, и именно поэтому такие задачи можно объединить в отдельные группы. С такими задачами мы встречались с вами в 5 классе.
Например: Сколько трехзначных чисел можно составить из цифр 0, 2, 4, если цифры в записи числа не повторяются?
Составим схему рассуждений.
Первая цифра 2 4
Вторая цифра 0 4 0 2
Третья цифра 4 0 2 0
Решение: 204, 240, 402,420 – 4 числа.
Способы решения таких задач перебором возможных вариантов используются при наличии нескольких решений. При записи возможных вариантов, их схемы изображаются, как дерево с разветвленными ветвями, которое так и называется «дерево возможных вариантов».
Решим эту задачу другим способом.
На первом месте может быть только две цифры (2 или 4), на втором – две из оставшихся, а на третьем – одна. Таким образом, 2 ∙ 2 ∙ 1 = 4
Станция» Решайкино.»
Рассмотрим другие задачи.
Задача 1. Сколько четных двузначных чисел можно составить из цифр 0, 1, 2, 4, 5, 7?
02
4
1
10
12
14
2
20
22
24
4
40
42
44
5
50
52
54
7
70
72
74
Решение.
Первые цифры искомых чисел: 1, 2, 4, 5, 7, так как в двузначном числе на первом месте может стоять любая цифра, кроме 0. Так как нужно составить четные двузначные числа, то второй цифрой искомых чисел могут быть: 0, 2, 4.
Составим таблицу: 5 строк (цифры 1, 2, 4, 5, 7) и 3 столбца (цифры 0, 2, 4) соответственно.
Заполняем клетки: первая цифра числа равна метке строки, а вторая цифра – метке столбца. По строкам и столбцам мы перечисляем все возможные варианты, значим, искомых чисел будет столько же, сколько клеток в таблице, то есть 3 ∙ 5 = 15.
Ответ: из цифр 0, 1, 2, 4, 5, 7 можно составить 15 четных двузначных чисел.
Учитель: В этой задаче мы осуществили полный перебор всех возможных вариантов (комбинаций). Поэтому подобные задачи называются комбинаторными.
Задача 2. На завтрак в школьной столовой любой ученик может выбрать булочку, ватрушку, кекс или сочник, а запить их он может соком, чаем или компотом. Сколько вариантов завтрака предлагается в школьной столовой?
Решение. Собираем все варианты в таблицу.
Булочка (Б)Ватрушка (В)
Пирожок (П)
Сок (С)
С Б
С В
С П
Чай (Ч)
Ч Б
Ч В
Ч П
В таблице 2 строки и 3 столбца, которые образуют 6 клеток. Так как выбор еды и напитка происходит независимо, то в каждой клетке будет стоит один из возможных вариантов завтрака. Значит, всего вариантов столько, сколько клеток в таблице, то есть 6. Напиток можно выбрать двумя способами (сок или чай), а еду тремя способам.
Ответ: 2 ∙ 3 = 6 столовая предлагает 6 вариантов завтрака.
Задача 3. У Розы есть розовая, желтая, красная кофта и черная, зеленая, синяя юбки. Сколько различных нарядов можно составить из них?
Решение: Составим дерево возможных вариантов.
При этом возможные варианты, объекты в нем записываются
кодом. При записи объектов кодом используются буквы или
цифры. Сколько ветвей у дерева в схеме, столько решений
у задачи.
РЧ, РЗ, РС; ЖЧ, ЖЗ, ЖС; КЧ, КЗ, КС.
Кофту можно выбрать тремя способами и юбку тремя способам.
3 · 3 = 9 (нарядов)
Учитель: Что вы заметили при решении этих задач?
(Задачи разные, но решения совершенно одинаковые).
— Совершенно верно. А основаны они на общем правиле умножения
Задача 4. Государственные флаги некоторых стран состоят из трех горизонтальных полос разного цвета. Сколько существует различных вариантов флагов с белой, синей и красной полосой?
Запомни:
Если объект a можно выбрать m способами, а объект b можно выбрать k
способами, то выбор пары (a, b) можно осуществить m · k способами.
Станция «Закрепляйкино.»
Примеры задач:
1. Мастер должен обшить 12 стульев обшивкой красного, коричневого и зеленого цвета. Сколькими способами он может это сделать? (12 стульев и 3 цвета, значит 12 ∙ 3 = 36)
2. Сколькими способами можно выбрать гласную и согласную буквы из слова «правило»?
(3 гласных и 4 согласных, значит 3 ∙ 4 = 12)
3. На первой полке стоит 5 книг, а на второй 10. Сколькими способами можно выбрать одну книгу с первой полки и одну со второй? (5 ∙ 10 = 50)
4. Сколько существует пятизначных чисел, которые одинаково читаются слева направо и справа налево?
Решение: В таких числах последняя цифра будет такая же, как и первая, а предпоследняя – как и вторая. Третья цифра будет любой. Это можно представить в виде XYZYX, где Y и Z любые цифры, а X – не ноль. Значит по правилу произведения количество цифр одинаково читающихся как слева направо, так и справа налево равно 9 ∙ 10 ∙ 10 = 900 вариантов.
Станция»Сумейка.»
Самостоятельная работа.
1 вариант.
№ 53 6 ∙ 5 ∙ 4 ∙ 3 ∙ 2 ∙ 1 = 720 способов; 2 ∙ 5 ∙ 4 ∙ 3 ∙ 2 ∙ 1 = 240 способов
№ 410 10 ∙ 9 ∙ 8 ∙ 7 = 1540 номеров
2 вариант.
№ 517 25 ∙ 24 = 600 способов
№ 915 27; 57; 87; 387; 357; 537; 837
Вопросы ученикам:
Какие задачи называют комбинаторными?
Какие задачи называют задачами на перестановки?
В чем состоит правило умножения при решении комбинаторных задач?
Продолжите предложение по нашей теме
— Мы знаем … (как решать комбинаторные задачи по правилу умножения)
— Мы умеем … (проводить анализировать и делать выводы)
— Мы можем применить … (правило умножения при решении комбинаторных задач)
Рефлексия: Оцените результаты своей деятельности на уроке.
Выберите смайлик и приклейте в свою тетрадь.
Какое впечатление у вас об уроке? Что вам понравилось, а что нет?
Что было интересного и что еще нужно изменить? Что у вас получилось, и что нет?
Над чем еще вам нужно поработать и что повторить?
Домашнее задание: № 24, № 262, № 355, придумать одну задачу по теме.
Спасибо всем за урок.
infourok.ru
элективный курс по математике в 6 классе «Решение комбинаторных задач».
МАОУ «Белоярская СОШ №1»Элективный курс по математике в 6 классе «Решение комбинаторных задач».
Учитель: Перепилица Н.Ф.
Пояснительная записка.
В настоящее время теория вероятностей завоевала очень серьёзное место в науке и прикладной деятельности. Её идеи, методы и результаты не только используются, но буквально пронизывают все естественные и технические науки, экономику, планирование, организацию производства, связи, а также такие далёкие, казалось бы, от математики науки, как лингвистику и археологию.
Сейчас без достаточно развитых представлений о случайных событиях и их вероятностях, невозможно полноценно работать в физике, химии, биологии, управлять производственными процесса.
Расчёт вероятностей во многих случаях приводит к комбинаторным задачам. Поэтому в последние годы необычайно возросла роль комбинаторных методов не только в самой математике, но и в её многочисленных приложениях: ф физике, химии, биологии, лингвистике, технике, экономике.
Важнейшим направлением модернизации школьного курса математики на современном этапе является включение в него элементов статистики, комбинаторики и теории вероятностей.
Понятие множества является также одним из основных понятий современной математики. В настоящее время большинство разделов математики построено на теоретико- множественной базе.
Понимание основных идей теории множеств помогает внести ясность и в вопросы школьной математики. Основные понятия теории множеств настолько просты, что ввести их в обучение математике можно в 6 классе. Данная тема помогает увлечь ребят, разбудить их фантазию, научить рассуждать.
Роль комбинаторики коренным образом изменилась с появлением компьютеров: она превратилась в область , находящуюся на магистральном пути развития науки. Поэтому важно как можно раньше начать знакомить учащихся с комбинаторными методами и комбинаторным подходом.
Введение элементов комбинаторики в 5, 6 классах- важнейшая учебно- мотодическая задача.
Изучение этой темы способствует развитию у учащихся « комбинаторного» мышления, расширению их математического кругозора, облегчает усвоение в дальнейшем элементов теории вероятностей.
Предложенный курс является продолжением ознакомления школьников с теоретико- вероятностным и статистическим мышлением.
Цель курса: формирование у учащихся элементарных стохастических знаний,
развитие комбинаторного и вероятностно- статистического
мышления.
Задачи курса:
Учить решать разнообразные задачи, способствующие формированию комбинаторного мышления:
Познакомить учащихся с элементами теории множеств;
Дать представление учащимся о том, как математика количественно оценивает возможность появления того или иного события;
Учит в
educontest.net
Деятельность учителя | Деятельность ученика | УУД | ||||
личностные | регулятивные | познавательные | коммуникативные | |||
1. Организационный момент. (2 мин) | Объясняет тему урока и цель. — Тема сегодняшнего урока «Комбинаторика в нашей жизни». Как вы думаете, чем мы будем заниматься? Как можно по-другому сформулировать тему урока? | Рассуждают и один из предложенных вариантов записывают на доску и в рабочие карты. Например, «Решение комбинаторных задач» или «Методы решения комбинаторных задач». | Умение оформлять свои мысли в устной форме. Умение слушать и понимать речь других | |||
2.Мотивация к учебной деятельности (5 мин) | Девиз нашего урока: СЛАЙД 2. Часто в нашей жизни мы вынуждены делать выбор. Для того, чтобы определить, что правильно нужно пересмотреть все варианты. Сделать мы это сможем с помощью комбинаторики. Теперь поговорим о том, что за этот урок мы должны сделать.(Наиболее правильные учитель записывает на доску) — Это цель урока для всего класса. Мне хочется, чтобы вы подумали и записали на листочках (рабочая карта), что конкретно ВЫ хотите получить от этого урока. Отнеситесь серьёзно к выполнению этого задания. И может кто-нибудь захочет озвучить своё желание? — Посмотрите внимательно на ваши листы, что осталось незаполненным? (графа «МОГУ») К ней мы вернёмся в конце урока. | Дети предлагают варианты и записывают в графу «НАДО» в своих рабочих картах. Учащиеся в течении 1-2 минут записывают свои мысли в рабочую карту в графе «ХОЧУ». | Самоопределение-мотивация учения. | Умение определять и формулировать цель на уроке с помощью учителя. | Умение ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя. Самостоятельное выделение познавательной цели. | Умение слушать и понимать речь других |
3. Устный счет (5 мин) | Выполните задание http://fcior.edu.ru/catalog/meta/3/mc/class/mi/5/p/page.html. Положительные и отрицательные числа. | Выполняют задания устного счета и сразу проверяют свои результаты. | Умение применять имеющиеся знания: находить ответы на вопросы, используя свой жизненный опыт. | |||
4. Актуализация опорных знаний (5 мин) | В начале урока прозвучали два понятия: «комбинаторика» и «комбинаторная задача». Вспомним из 5 класса, что означают эти понятия. Если возникли трудности, то на ваших листах есть подсказки. Вам необходимо вставить пропуски, дописав пропущенные слова. Мной были подобраны самые простые толкования этих математических терминов. СЛАЙД 3.
| Обсуждение идёт сообща, учащиеся результат записывают в рабочую карту. | Осознание ответственности за общее дело. | Умение проговаривать последовательность действий на уроке | Умение преобразовывать информацию из одной формы в другую | Умение оформлять свои мысли в устной и письменной форме, аргументация своего мнения, учёт разных мнений учащихся. |
5. Решение задач на повторение (15 мин) | 1.А сейчас мы переходим к решению комбинаторных задач. Для начала вспомним примеры этих задач, которые вы решали в 5 классе (учащиеся называют по несколько предметов). Решим следующую задачу (работа в тетрадях): сколько двузначных чисел можно составить из цифр 1, 5, 9 при условии, что цифры не повторяются (задача есть в картах и презентации). На решение вам отводится только 2 минуты. Потом ответы сверим. СЛАЙД 4. — Как вы решали данную задачу? Как можно назвать этот метод решения комбинаторных задач? 2.Усложним задачу. Сколько трехзначных чисел можно составить из цифр 1,3,5,7, используя в записи числа каждую из них не более одного раза? (работа в тетрадях) Подумайте, применим ли здесь метод перебора, да или нет, почему? (обсуждение) Вспомните из 5 класса, какие интересные фигуры мы рисовали при решении таких задач? (показать пример из учебника Виленкина Н.Я. «Математика. 5 класс»). Как они называются? Может кто-нибудь попробует изобразить дерево вариантов для этой задачи и подсчитать количество чисел? СЛАЙД 5-6. | Учащиеся на местах (индивидуальная работа) решают предложенную задачу методом перебора (большинство). После того, как время закончилось, проверяются ответы и выписываются полученные комбинации. Учащиеся объясняют суть решения, предлагают названия метода. После обсуждения идёт работа с картой: постепенное заполнение столбцов таблицы «Методы решения комбинаторных задач» (Приложение 1) | Умение проговаривать последовательность действий на уроке; высказывать своё предположение. | Умение применять имеющиеся знания: находить ответы на вопросы, используя свой жизненный опыт. Ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя. Анализ, сравнение, обобщение, подведение под понятие, постановка и формулирование проблемы, построение речевого высказывания. | Умение осознанно и произвольно строить речевое высказывание в устной форме. Слушать и понимать речь других; работать в группе, выполнять различные роли Уметь оформлять мысли в устной и письменной форме | |
6.Физминутка (3 мин) | Раз, два, три, четыре, пять – Все умеем мы считать. Раз! Подняться, потянуться. Два! Согнуться, разогнуться. Три! В ладоши три хлопка, Головою три кивка. На четыре – руки шире. Пять – руками помахать. Шесть — за парту мы присели. Значит, хватит отдыхать! | Выполняют физические упражнения. | Планирование собственной деятельности, распределение нагрузки и отдых в процессе ее выполнения. Формирование привычки к охране своего здоровья. | |||
7. Решение задач на повторение (5 мин) | СЛАЙД 7. | Учащиеся вспоминают правило нахождения факториала, вспоминают названия метода. Продолжают работу работа с картой. Во время работы с картой проговаривают названия методов решения задач. | Умение применять имеющиеся знания: находить ответы на вопросы, используя свой жизненный опыт. | Уметь оформлять мысли в письменной форме. | ||
8.Закрепление материала (25 мин) | -Это была задача на правило умножения. Все 3 правила из 5 класса мы повторили, осталось посмотреть, как вы умеете решать комбинаторные задачи разными методами. Задание 1. Сколько существует флагов составленных из трёх горизонтальных полос одинаковой ширины и различных цветов –белого, зелёного, красного и синего? Задание 2. Сколько различных трехзначных чисел (без повторения цифр) можно составить из нечётных цифр, которые являются кратными 5. Задание 3 В школьной столовой предлагают 2 первых блюда: борщ, лапша – и 4 вторых блюда: пельмени, котлеты, гуляш, рыба. Сколько обедов из двух блюд может заказать посетитель. Задание 4 Учащиеся 6 класса решили обменяться фотографиями. Сколько фотографий для этого потребуется, если в классе 11 учащихся. Решение: 11 человек по 10 фотографий. Ответ: 110 фотографий. Задание 5. СЛАЙД 16-17. Из села Терновка в село Родничок ведут три дороги, а из села Родничок в город Балашов – четыре дороги. Сколькими способами можно попасть из села Терновка в город Балашов через село Родничок? | Решают задачи самостоятельно с последующей проверкой со слайда, слабые ученики выполняют задания под руководством учителя. Вспоминают нечетные числа и что значит кратно числу. Решают задачи под руководством учителя с последующей проверкой со слайда. | Умение планировать своё действие в соответствии с поставленной задачей | Выбор наиболее эффективных способов решения задач в зависимости от конкретных условий. Умение действовать по алгоритму Умение классифицировать и систематизировать.Умение устанавливать аналогии. Выполнение действий по алгоритму, построение логической цепи рассуждений, анализ, обобщение, подведение под понятие. Рефлексия способов и условий действия. | Выражение своих мыслей, использование речевых средств для решения коммуникационных задач, достижение договорённости и согласование общего решения | |
9. Физминутка (2 мин) | Рисуй глазами треугольник. Теперь его переверни Вершиной вниз. Ты по периметру веди. Рисуй восьмерку вертикально. Ты головою не крути, А лишь глазами осторожно Ты вдоль по линиям води И на бочок ее клади. Теперь следи горизонтально, И в центре ты остановись. Зажмурься крепко, не ленись. Глаза открываем мы, наконец. Зарядка окончилась. Ты молодец!» | Выполняют упражнения для глаз. | Планирование собственной деятельности, распределение нагрузки и отдых в процессе ее выполнения. Формирование привычки к охране своего здоровья. | |||
10.Повторение (8 мин) | Выполните самостоятельную работу с самопроверкой и поставьте себе оценку. http://www.matematika-na.ru/5class/mat_5_30.php
| Уметь вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок. | ||||
11. Подведение итогов урока (7 мин) | – Какие задачи называются комбинаторными? http://files.school-collection.edu.ru/dlrstore/7d5c24d3-e52c-4fe2-a2c3-94497bc0d75e/%5BM56_6-30%5D_%5BPK_05%5D.swf А теперь мы обратим своё внимание на ту таблицу, которую мы весь урок постепенно заполняли. Сейчас вы поработаете в группах: 1 группа – метод перебора, 2 группа – дерево вариантов, 3 группа – правило умножения. Ваша задача: из рассмотренных задач и из всего сказанного выделить достоинства и недостатки каждого метода. СЛАЙД 18. Название метода | Достоинства метода | Недостатки метода | |||
Метод перебора | Наглядность, возможность увидеть все варианты. «Теоретически» можно решить любую комбинаторную задачу | Очень длительный, можно пропустить варианты | ||||
Дерево вариантов | Наглядность, возможность увидеть все варианты | Очень громоздкий и длительный. Не все задачи могут быть решены с его помощью | Учащиеся заполняют таблицу (групповая работа). Всего минуты 2-3, потом проверка. Если время позволяет, учащиеся могут перенести таблицу с слайда (готовую) в свою карту. | Анализ, сравнение, обобщение, подведение под понятие. Умение ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя | Умение оформлять свои мысли в устной форме. Умение слушать и понимать речь других Умение с достаточной полнотой и точностью выражать свои мысли. | |
12. Рефлексия ученика и учителя (5 мин) | — Все молодцы! Отлично поработали на уроке. Осталось до конца заполнить ваши листы. Это графа «МОГУ». Перечислите и кратко запишите, что вы уже можете или знаете, связанное с комбинаторикой и комбинаторными задачами. Молодцы! Вы уже многое знаете и многое еще узнаете в старших класса по комбинаторике. В заключении урока я хотела, чтобы вы ответили, а точнее дописали, на 3 вопроса:
Листки мне ваши сдайте, я их верну. Спасибо за урок! | Способность к самооценке на основе критерия успешности учебной деятельности | Способность к самооценке на основе критерия успешности учебной деятельности. Контроль и оценка процесса и результатов деятельности. Адекватное понимание причин успеха / неуспеха в учебной деятельности. Личностное самоопределений. | Рефлексия способов и условий действия. Анализ и синтез. | Умение оформлять свои мысли в устной и письменной форме; слушать и понимать речь других | |
13. Домашнее задание (3 мин) | На дом вам нужно будет придумать задачу на комбинаторное правило умножения. №№ 80,108,160 . СЛАЙД 19. | Записывают домашнее задание. |
doc4web.ru