Тестовые задания на тему «Упрощение логических функций»
Контрольная работа № 2
«Упрощение логических функций»
1 вариант
1. Упростите выражение:
а)
б)
в)
г)
2. С помощью таблиц истинности докажите правильность упрощения (для примеров в и г)
Контрольная работа № 2
«Упрощение логических функций»
2 вариант
1. Упростите выражение:
а)
б)
в)
г)
2. С помощью таблиц истинности докажите правильность упрощения (для примеров в и г)
Контрольная работа № 2
«Упрощение логических функций»
3 вариант
1. Упростите выражение:
а)
б)
в)
г)
2. С помощью таблиц истинности докажите правильность упрощения (для примеров
Контрольная работа № 2
«Упрощение логических функций»
4 вариант
1. Упростите выражения:
а)
б)
в)
г)
2. С помощью таблиц истинности докажите правильность упрощения (для примеров в и г)
Контрольная работа № 2
«Упрощение логических функций»
5 вариант
1. Упростите выражения:
а)
б)
в)
г)
2. С помощью таблиц истинности докажите правильность упрощения (для примеров в и г)
Контрольная работа № 2
«Упрощение логических функций»
6 вариант
1. Упростите выражения:
а)
б)
в)
г)
2. С помощью таблиц истинности докажите правильность упрощения (для примеров в и г)
Контрольная работа № 2
«Упрощение логических функций»
7 вариант
1. Упростите выражения:
а)
б)
в)
г)
2. С помощью таблиц истинности докажите правильность упрощения (для примеров в и г)
Контрольная работа № 2
«Упрощение логических функций»
8 вариант
1. Упростите выражения:
а)
б)
в)
г)
2. С помощью таблиц истинности докажите правильность упрощения (для примеров в и г)
Контрольная работа № 2
«Упрощение логических функций»
9 вариант
1. Упростите выражения:
а)
б)
в)
г)
2. С помощью таблиц истинности докажите правильность упрощения (для примеров
Контрольная работа № 2
«Упрощение логических функций»
10 вариант
1. Упростите выражения:
а)
б)
в)
г)
2. С помощью таблиц истинности докажите правильность упрощения (для примеров в и г)
Контрольная работа № 2
«Упрощение логических функций»
1 вариант
1. Упростите выражение:
а)
б)
в)
г)
2. С помощью таблиц истинности докажите правильность упрощения (для примеров в и г)
Контрольная работа № 2
«Упрощение логических функций»
2 вариант
1. Упростите выражение:
а)
б)
в)
г)
2. С помощью таблиц истинности докажите правильность упрощения (для примеров в и г)
Контрольная работа № 2
«Упрощение логических функций»
3 вариант
1. Упростите выражение:
а)
б)
в)
г)
2. С помощью таблиц истинности докажите правильность упрощения (для примеров в и г)
Контрольная работа № 2
«Упрощение логических функций»
4 вариант
1. Упростите выражения:
а)
б)
в)
г)
2. С помощью таблиц истинности докажите правильность упрощения (для примеров в и г)
Контрольная работа № 2
«Упрощение логических функций»
5 вариант
1. Упростите выражения:
а)
б)
в)
г)
2. С помощью таблиц истинности докажите правильность упрощения (для примеров
Контрольная работа № 2
«Упрощение логических функций»
6 вариант
1. Упростите выражения:
а)
б)
в)
г)
2. С помощью таблиц истинности докажите правильность упрощения (для примеров в и г)
Контрольная работа № 2
«Упрощение логических функций»
7 вариант
1. Упростите выражения:
а)
б)
в)
г)
2. С помощью таблиц истинности докажите правильность упрощения (для примеров в и г)
Контрольная работа № 2
«Упрощение логических функций»
8 вариант
1. Упростите выражения:
а)
б)
в)
г)
2. С помощью таблиц истинности докажите правильность упрощения (для примеров в и г)
Контрольная работа № 2
«Упрощение логических функций»
9 вариант
1. Упростите выражения:
а)
б)
в)
г)
2. С помощью таблиц истинности докажите правильность упрощения (для примеров в и г)
Контрольная работа № 2
«Упрощение логических функций»
10 вариант
1. Упростите выражения:
а)
б)
в)
г)
2. С помощью таблиц истинности докажите правильность упрощения (для примеров в и г)
Ответы:
1 а) 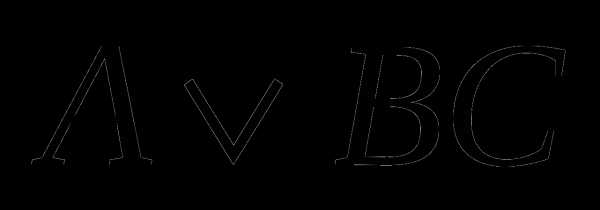 2 а)
2 а) 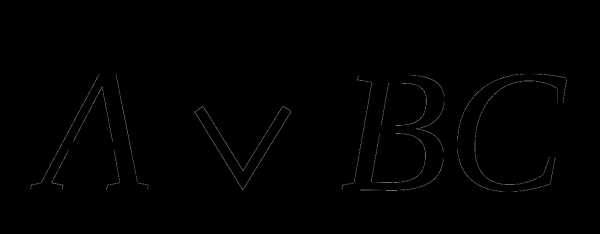 3 а)
3 а) 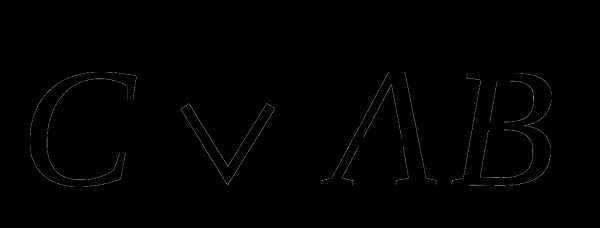
 б)
б)  б)
б) в)  в)
в)  в) В
в) В
г) 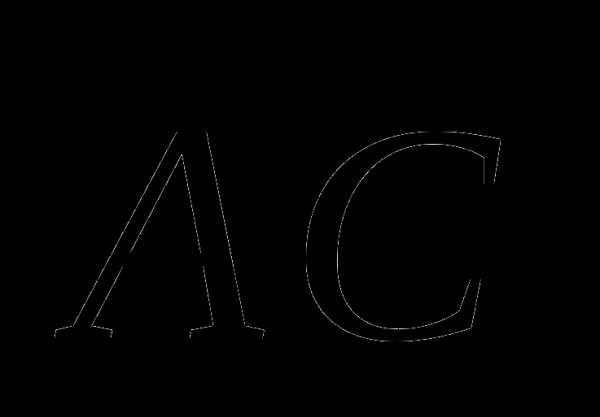 г) г)
г) г) 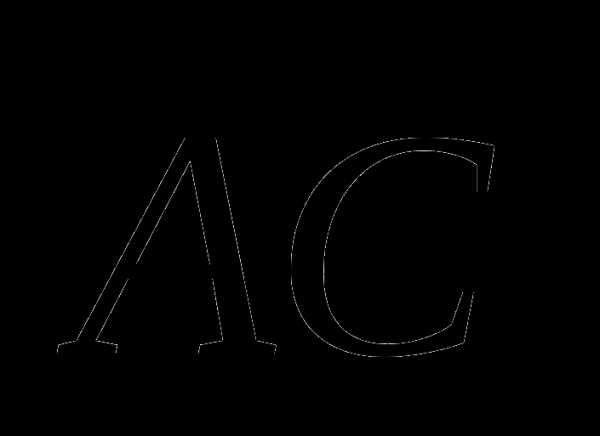
4 а) 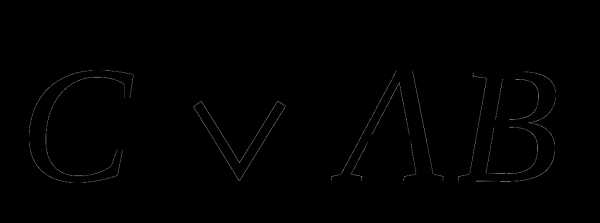 5 а)
5 а) 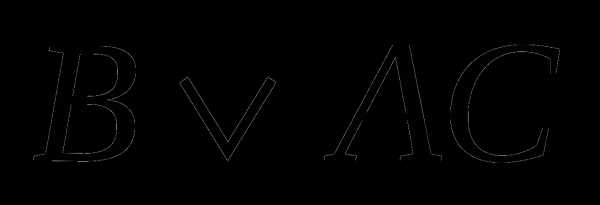 6 а)
6 а) 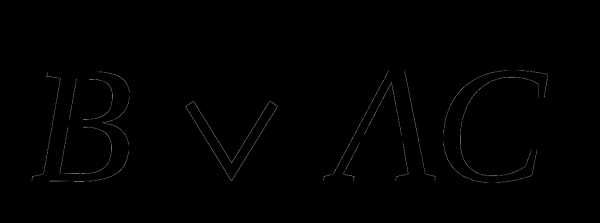
б) 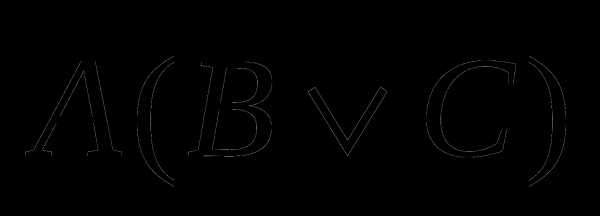 б)
б) 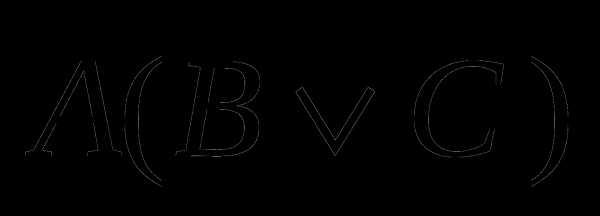 б)
б) 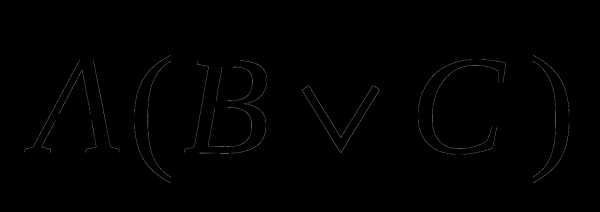
в) 
г)  г) г)
г) г) 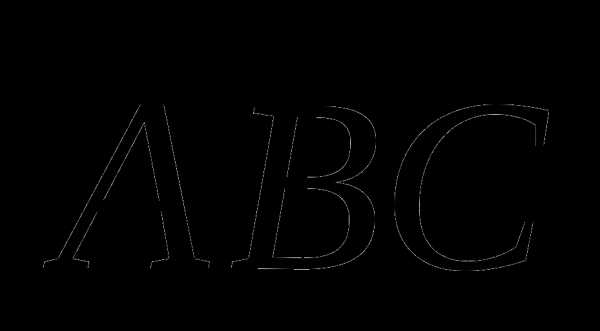
7 а) 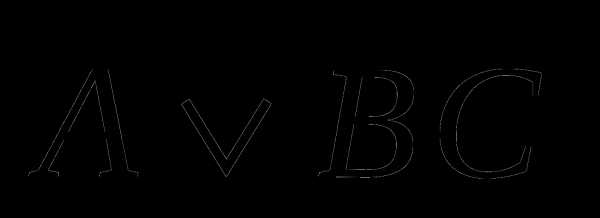 8 а)
8 а) 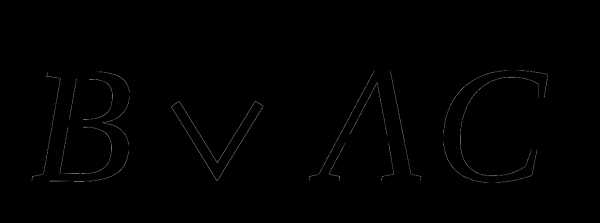 9 а)
9 а)  10 а)
10 а) 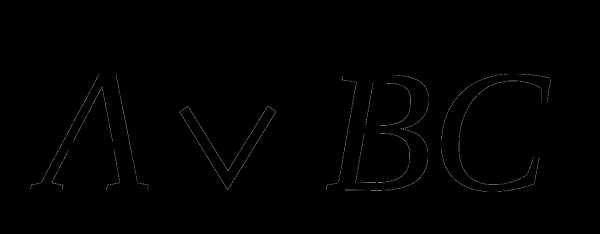
б)  б)
б)  б)
б)  б)
б) 
в)  в)
в) 
г) г) г) г) 
Таблицы истинности:
1 в)
1
8
2
3
4
6
5
7
9
А
В


АВ
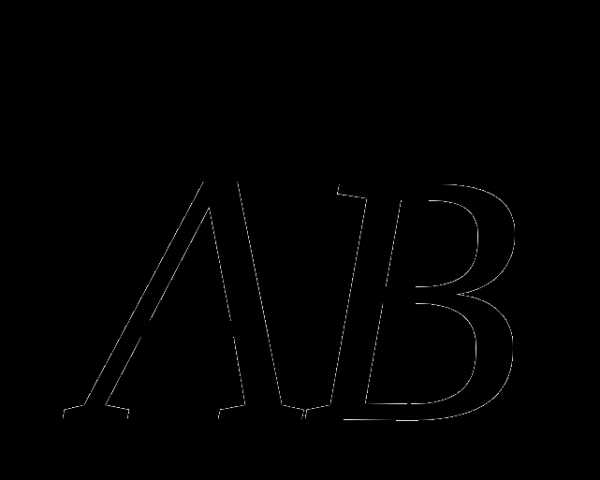
B V 1
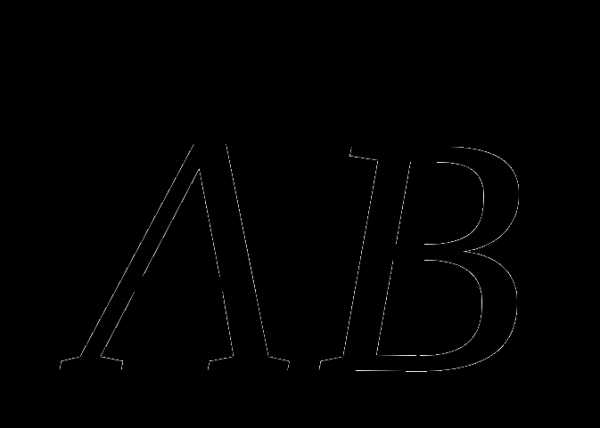

2→3
4B
A→

67
8→9
1
1
0
0
1
0
1
0
0
1
1
0
1
1
1
1
0
0
1
0
1
1
0
1
1
0
1
0
0
0
0
1
1
0
0
1
1
1
1
1
1
1
0
0
0
0
0
1
1
0
1
1
0
1
1
0
1
0
0
0
1 г)
A
B
C


infourok.ru
Примеры упрощения логических формул с использованием законов логики
Просмотр содержимого документа
«Примеры упрощения логических формул с использованием законов логики»

Примеры упрощения логических выражений с использованием законов логики

Пример 1 : Упростить выражение:
Решение:
Применим для скобки закон Де Моргана. Получим:
По закону двойного отрицания:
Применим формулу поглощения:
Ответ:

Пример 2 : Упростить выражение:
Решение:
Применим закон Де Моргана. Получим:
По закону двойного отрицания:
Применим сочетательный закон:
, следовательно, получим:
Ответ:

Пример 3 : Упростить выражение:
Решение:
Применим в обеих скобках закон Де Моргана:
По закону двойного отрицания получим:
Перед нами формула склеивания, т.е. значение нашего выражения равно А.
Ответ: А

Пример 4 : Упростить выражение:
Решение:
Применим к первой скобке закон Де Моргана, а во второй заметим, что . Тогда получим:
По закону двойного отрицания:
Перед нами снова формула склеивания. Результат будет равен А.
Ответ: А

Пример 5 :
Решение:
Для первой скобки применим закон: , а для второй:
Получим:
Применим сочетательный закон:
Очевидно, что: , а
Ответ: 1

Пример 6 : Упростить выражение:
Решение:
Применим для скобки закон Де Моргана. Получим:
Сформируем скобки в соответствии с сочетательным законом:
По аналогии с предыдущим примером получим:
Ответ: 1
multiurok.ru
построение и упрощение :: SYL.ru
Главная задача логики – выяснить, является ли некоторое утверждение ложным или его можно считать истинным. Для этого было изобретено несколько методов. Разработаны способы определения того, истина это или ложь, на основе других высказываний и их атрибутов. Логическое выражение – базовое понятие науки, и его параметры определяют, какие операции могут быть совершены.
Общие термины
Сегодня логика изучается в форме математической логики. В ее основе исключительно формальные методы познания. Один из ключевых разделов направления – алгебра логики. Она специализируется только на сложных объектах и методах, позволяющих установить их параметры. Используются строго алгебраические способы изучения.
Наука называется алгеброй Буля, так как автором ее является Джордж Буль, сформулировавший свои основные идеи в 1854 году, когда он выпустил фундаментальную книгу. Буль поставил перед собой задание изучить операции, на основании которых функционирует человеческий ум, понять, каков механизм рассуждений, описать его символами. Добившись в этом успеха, он сумел создать новую науку.
Логические выражения в программировании
Условное логическое выражение представляет собой некоторые переменные и постоянные, которые классифицируются простыми. Все объекты объединены между собой сравнением. В результате вычисления удается получить некоторое конечное условное выражение: истина либо ложь.
Наиболее применима логика в программировании. На примере языка Паскаль можно выделить наиболее важные операции, используемые на практике:
- определение большего из двух;
- определение меньшего из двух;
- вычисление меньшего либо равного;
- вычисление большего либо равного;
- определение равенства двух выражений;
- заключение, что выражения не равны между собой.
Если при программировании необходимо построить логическое выражение, но сравниваются между собой вещественные числа, учтен должен быть следующий факт: представление чисел неточно, так как обязательно происходит округление. Это означает, что операция вычисления строгого равенства не может быть точной. Опытные программисты рекомендуют по возможности избегать обращаться к этой операции, поскольку велика вероятность, что равенство в итоге будет посчитано как ложное, не являясь таковым.
Пример: x = (2.23*x/2.23)
Согласитесь, визуально видна истинность формулы. Но при записи ее в компьютерный код и неизбежности погрешности округления при расчетах она окажется ложной.
Еще один тонкий момент: условное логическое выражение обязательно записывается в скобках, если оно является операндом. Правило следует из разработанной иерархии операций. Например, сравнение по своему приоритету ниже прочих, а логических операции – высокий. Чтобы изменить относительно такого порядка процесс расчета конкретного примера, придется расставить скобки.
Основа науки
Под объектом в логике принято понимать такое повествование, о котором точно сообщают, что оно является ложью, истиной. Значение логического выражения, когда оно истинно, записывают единицей, второй вариант обозначается нулем.
Под логическими операциями принято понимать такие действия (как правило, мыслительный процесс), которые в итоге дают увеличение знаний, а также ведут к формированию совершенно новых объектов.
Логическое выражение бывает устным, можно его записать. Оно включается в объекты наряду с константами. Выражение напрямую зависит от переменных объектов, становясь либо единицей, либо нулем.
Если пришлось столкнуться со сложным высказыванием, нужно помнить, что оно включает в себя сложные простые выражения, для соединения которых применялись логические операции.
Логика выделяет ключевые операции, именуемые:
- конъюнкция;
- эквивалентность;
- дизъюнкция;
- импликация;
- инверсия.
Для решения практически любого примера их будет достаточно.
Конъюнкция
Под этим термином принято понимать такую сложную операцию, которая может быть истиной, лишь если оба простых составляющих являются истиной. Прочие варианты считаются ложными.
Записывается так: F = А & В.
Таблица:
Дизъюнкция
В этой ситуации истинность логических выражений определяется, исходя из анализа значения (единица и ноль) составляющих простых выражений. Если оба они ложны, то функция также имеет значение «ноль». В противном случае ее значение равняется единице.
Записывается так: F = A + B.
Таблица:
Инверсия
Термин обозначает операцию, когда происходит превращение в ложное выражение, прежде бывшего истинным, и наоборот. Если исходный объект верный, в результате получаем ложный, а если изначально была ложь, она трансформируется в истину.
Таблица:
Равнозначность
Это логическое выражение лишь в том случае будет значить единицу, когда оба выражения в примере значат одно и то же.
Таблица:
Импликация
Термин применяется к такому сложному выражению логики, которое ложно, если из истины следует ложь. Прочие ситуации: значение равняется единице. Операция применяется для двух простых объектов, из которых одно называют условием, а другое – следствием.
Таблица:
Операции: логические нюансы
Зная, какое логическое выражение используется в качестве объекта, можно правильно вычислить результат. При этом следует помнить, что операции в логике – это как в арифметике те операции, которые необходимы для взаимодействия с числами. Логические операции помогают строить логически выражения – это также является параллелью с алгеброй.
В составе логических выражений встречаются константы и переменные. Первые имеют конкретное значение – ноль либо единицу. В случае если выражение в себя включает некоторые переменные, оно тем самым будет задавать булеву функцию, чье значение вычисляется на основании аргументов. Значения аргументов для каждой задачи указаны в условиях. Необходимо просто подставить их в выражение, после чего вести дальнейший расчёт.
Любое логическое выражение может иметь собственную таблицу истинности, то есть объект, детально во всех вариациях описывающий, какие значения и когда принимает функция, если использован конкретный набор переменных. Одна строчка такой таблицы – один набор исходных условий для вычисления. Если в функции задействовано N переменных, то строк вдвое больше.
Таблицы истинности
Выделяют следующие общие свойства, характерные всякой таблице:
- уже упомянутое число строк, вдвое превышающее количество переменных;
- число столбцов таблицы на один превышает количество задействованных переменных.
Вне зависимости от того, каково множество значений переменных, заданное в условии, всегда можно сформулировать такое выражение, которое будет равняться единице на определенном наборе переменных.
Записывается это как «дизъюнкция конъюнкций». На практике это означает, что можно построить некоторое выражение, имея перед собой готовую таблицу истинности. Конечно, объемы этой таблицы могут существенно усложнить задачу математика.
Упрощения
Нередко бывают ситуации, когда математическое выражение требует для адекватности решения упрощения. Есть определенные преобразования, применимые в булевой логике.
В частности, одно выражение можно заменить на другое, являющееся эквивалентным. Проверяют эквивалентность, анализируя таблицы истинности. Если они совпадают, можно проводить замену. Здесь вступает в действие правило подставной, когда в объекте А меняется на некоторое подвыражение Р, присутствовавшее здесь ранее Q, и получается выражение В. По всем расчетам оно эквивалентно А.
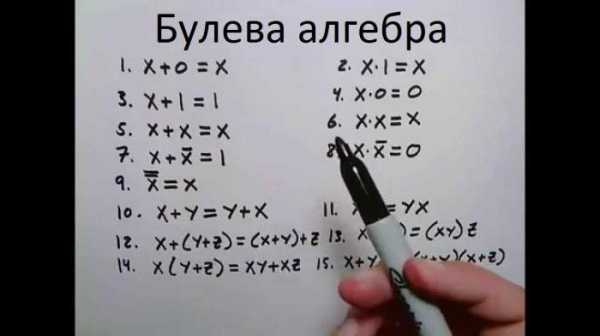
Упрощение логических выражений принято именовать минимизацией. Главная задача минимизации – это представить функцию в таком виде, когда букв, операций имеется наименьшее число из возможных. Добиться желаемого можно одним из двух вариантов:
- алгебраическим;
- графическим.
Алгебраический метод
Упростить логическое выражение алгебраическим методом можно, упростив формулу. Это производится уже описанными выше эквивалентными преобразованиями. При этом необходимо учитывать тождества и правила, существующие в булевой алгебре.
Упрощенное выражение от того, которое необходимо было решить изначально, отличается в первую очередь количеством букв. Впрочем, нередки задачи, когда приходится доказывать эквивалентность исходного выражения и полученного в результате упрощения. Производится это сличением таблиц истинности.
Если в примере представлены элементарные высказывания, можно добиться их видоизменения, прибегая не только к общим правилам, но и к тем, что связаны с операциями над множествами.
При анализе высказывания, связанного со множествами, нередко оптимальный вариант – сводить выражения до импликации, когда члены уже не содержат импликации.
www.syl.ru
Урок №5 Упрощение логических выражений (10 класс)
Тема урока: Упрощение логических выражений с использованием законов логики.
Образовательная – изучение способов решения разнообразных заданий по упрощению логических выражений с использованием законов логики;Развивающая — создать условия для развития познавательного интереса учащихся, способствовать развитию памяти, внимания, логического мышления;
Воспитательная: способствовать воспитанию умения выслушивать мнение других, воспитание воли и настойчивости для достижения конечных результатов.
Тип урока: комбинированный урок
Оборудование: компьютер, мультимедийный проектор, презентация 5.
Ход урока
Повторение и актуализацию опорных знаний. Проверка домашнего задания (15 минут)
На предыдущих уроках мы познакомились с основными законами алгебры логики, научились использовать эти законы для упрощения логических выражений.
Выполним проверку домашнего задания по упрощению логических выражений:
а)
б)
Самостоятельная работа
1 вариантУпростить следующее логическое выражение:
Решение:
2 вариант
Упростить следующее логическое выражение:
Решение:
Ознакомление с темой урока. Изложение нового материала (30 мин).
Мы продолжаем изучать основы логики и тема нашего сегодняшнего урока «Упрощение логических выражений с использованием законов логики». Изучив данную тему, вы узнаете способы решения разнообразных заданий, содержащихся в ЕГЭ, по упрощению логических выражений с использованием законов логики.
Каково наименьшее натуральное число X, при котором высказывание ¬(X·X < 9) → (X >(X + 2)) будет ложным?
Решение: Преобразуем исходное выражение, используя законы логики
Выражение будет ложным когда обе его части будут ложными:
(Х>(X+2)) – ложь, тогда (X*X<9) – ложь. Следовательно (Х*Х>=9) – истина.
Наименьшее значение Х, при котором верно это неравенство 3.
Ответ: 3.
2). Укажите значения переменных K, L, M, N, при которых логическое выражение
(¬K M) → (¬L M N) ложно.
Ответ запишите в виде строки из четырех символов: значений переменных K, L, M и N (в указанном порядке). Так, например, строка 1101 соответствует тому, что K=1, L=1, M=0, N=1.
Решение:
Преобразуем выражение (¬K M) → (¬L M N), используя законы логики
Выражение ложно, когда оба слагаемые ложны. Второе слагаемое равно 0, если M=0, N=0, L=1. В первом слагаемом K=0, так как М=0, а  .
.
Ответ: 0100
3). Для какого из указанных значений числа Х истинно выражение
1) 0 2) 2 3) 4 4) 7
Решение: преобразуем выражение
Будем поочередно подставлять значения числа Х в данное выражение и определять значение выражения. Можно решение записать в виде следующей таблицы:
Дан фрагмент таблицы истинности выражения F:
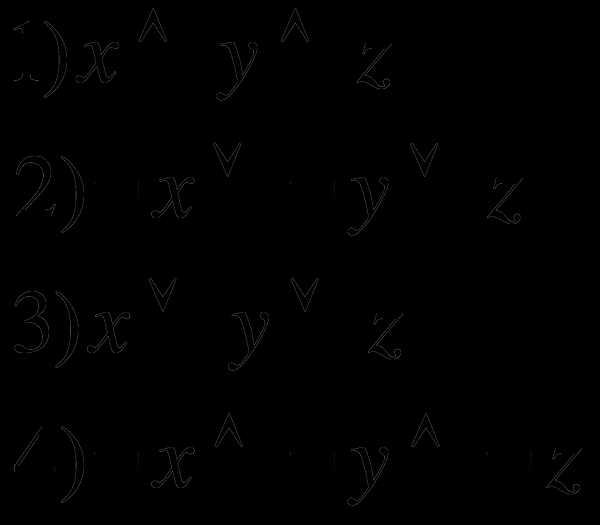
Решение:
Преобразуем логические выражения и определим значения этих выражений при указанных значениях аргументов:
Х*Y*Z
X+Y+Z
Укажите, какое логическое выражение равносильно выражению
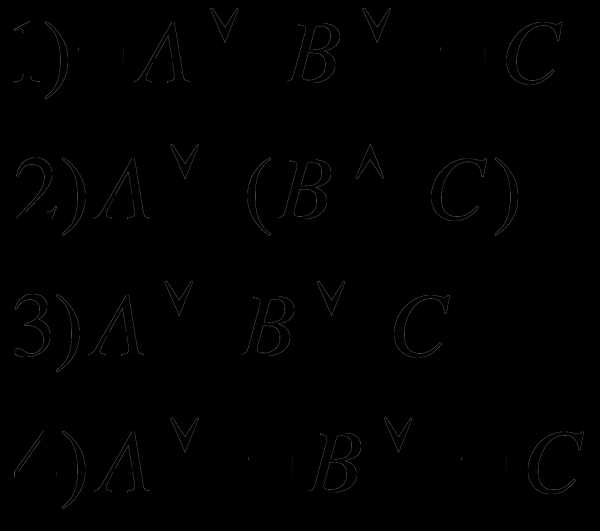
Решение:
Преобразуем запись исходного выражения и предложенных вариантов, используя законы логики:
1)
2) A+(B*C)
3) A+B+C
4)
Ответ: 2
6). Какое из приведенных имен удовлетворяет логическому условию:
(первая буква согласнаявторая буква согласная)(предпоследняя буква гласнаяпоследняя буква гласная)?
1) КРИСТИНА 2) МАКСИМ 3) СТЕПАН 4) МАРИЯ
Решение:
Преобразуем исходное выражение, используя законы логики:
(первая буква гласная или вторая буква согласная) и (предпоследняя буква согласная или последняя буква гласная)=1
Результаты анализа представим в виде таблицы:
Задание на дом
1. Какое из приведенных слов удовлетворяет логическому условию:
(первая буква согласная→вторая буква согласная) ٨ (последняя буква гласная → предпоследняя буква гласная)?
Если таких слов несколько, укажите наименьшее из них.
1) АННА 2) МАРИЯ 3) ОЛЕГ 4) СТЕПАН
2. Укажите, какое логическое выражение равносильно выражению
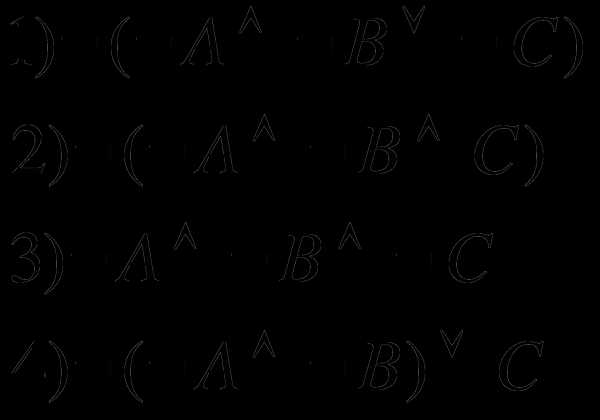
3. Дан фрагмент таблицы истинности выражения F:
0Какое выражение соответствует F?
infourok.ru
41)Алгебра логики. Упрощение логических выражений.
Алгебра логики— раздел математической логики, в котором изучаются логические операции над высказываниями. Высказывания могут быть истинными, ложными или содержащими истину и ложь в разных соотношениях.
Равносильные преобразования логических формул имеют то же назначение, что и преобразования формул в обычной алгебре. Они служат для упрощения формул или приведения их к определённому виду путем использования основных законов алгебры логики.
Под упрощением формулы понимают равносильное преобразование, приводящее к формуле, которая либо содержит по сравнению с исходной меньшее число операций конъюнкции и дизъюнкции и не содержит отрицаний неэлементарных формул, либо содержит меньшее число вхождений переменных.
Некоторые преобразования логических формул похожи на преобразования формул в обычной алгебре (вынесение общего множителя за скобки, использование переместительного и сочетательного законов и т.п.), тогда как другие преобразования основаны на свойствах, которыми не обладают операции обычной алгебры (использование распределительного закона для конъюнкции, законов поглощения, склеивания, де Моргана и др.). Рассмотрим на примерах некоторые приемы и способы, применяемые при упрощении логических формул:
1):сначала добиваемся, чтобы знак отрицания стоял только перед отдельными переменными, а не перед их комбинациями, для этого дважды применяем правило де Моргана; затем используем закон двойного отрицания.
2) : к отрицаниям формул применяется правило де Моргана; используются законы двойного отрицания и склеивания.
42) Алгебра логики. Функциональные схемы.
Алгебра логики— раздел математической логики, в котором изучаются логические операции над высказываниями. Высказывания могут быть истинными, ложными или содержащими истину и ложь в разных соотношениях. Функциональная схема – это логическая диаграмма, графический (геометрический, точнее — топологический) аппарат математической логики, показывающий её работу.
Доказать законы алгебры логики можно с помощью диаграммы Эйлера-Венна, которая является функциональной схемой.
Леонард Эйлер при решении задач изображал множества с помощью кругов, и в его честь этот метод был назван «методом кругов Эйлера». Однако такой прием очень полезен и при решении логических задач, когда с помощью кругов изображаются высказывания. После Эйлера метод получил развитие в работах других ученых, однако наибольшего расцвета графические методы достигли в работах логика Венна, поэтому такие схемы называют «диаграммами Эйлера-Венна».
Закон де Моргана (Если существует операция логического умножения двух и более элементов, операция «и»—(A&B), то для того, чтобы найти обратное от всего суждения~(A&B), необходимо найти обратное от каждого элемента и объединить их операцией логического сложения,операцией «или»— (~A+~B). Закон работает аналогично в обратном направлении:~(A+B)= (~A&~B)) . Докажем его с помощью диаграммы эйлера-венна.
Для наглядного представления левой части равенства выполним последовательно: заштрихуем оба круга (применим дизъюнкцию) серым цветом, затем для отображения инверсии заштрихуем область за пределами кругов черным цветом:
Для визуального представления правой части равенства выполним последовательно: заштрихуем область для отображения инверсии (¬А) серым цветом и аналогично область ¬В также серым цветом; затем для отображения конъюнкции нужно взять пересечение этих серых областей (результат наложения представлен черным цветом):Видим, что области для отображения левой и правой части равны. Что и требовалось доказать.
studfiles.net
3.3. Преобразование логических выражений и схем
Преобразование логических выражений часто сводится к их упрощению. При этом надо использовать законы алгебры логики (табл. 1.8), обратив особое внимание на приемы замены отдельной переменной или константы формулой.
Преобразование логических схем (ЛС) можно выполнить так. Записать логическую функцию, реализуемую ЛС, затем упростить полученное выражение и составить новую ЛС, реализующую его.
3.3.1. Примеры
Пример 3.6. Упростить логическое выражение: .
По закону дистрибутивности вынесем a за скобки:
.
По закону исключенного третьего скобочное выражение заменяем логической константой 1:
.
Используем закон исключения констант:
.
Замечание 3.4. Готовых «рецептов» какие и в каком порядке применять законы алгебры логики для упрощения выражений нет и не может быть. Умение приходит с опытом.
Пример 3.7. Упростить логическое выражение: .
Введем вспомогательный
логический множитель 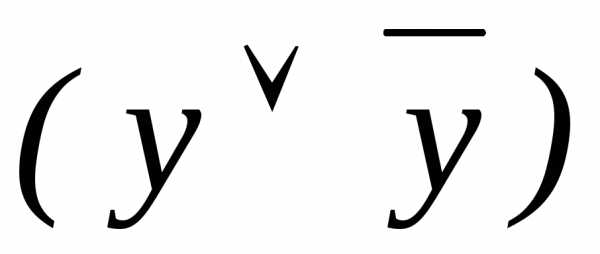 :
:
.
На основании дистрибутивного закона раскрываем скобки и комбинируем (в соответствии с переместительным законом) два крайних и два средних логических слагаемых:
Используем закон поглощения:
.
Пример 3.8. Требуется упростить: .
Способ 1. Применим закон дистрибутивности:
.
К выражению в скобках применим закон противоречия:
.
Применим закон исключения констант:
.
Способ 2. Перемножим скобки (как в обычной алгебре чисел) на основании дистрибутивного закона:
.
К логическому слагаемому применим закон идемпотентности, потом два средних слагаемых сгруппируем и общий логический множитель вынесем за скобки, заменим последнее слагаемое (на основании закона противоречия) логической константой 0:
.
Используем законы исключенного третьего и исключения констант:
.
Используем закон исключения констант:
.
Применяем закон идемпотентности
.
Пример 3.9. Упростить ЛС из примера 2.1 (рис. 2.2). Логическое выражение, описывающее ЛС, имеет вид: .
Применим ко второму слагаемому закон де Моргана:
.
Применяем закон двойного отрицания:
.
Последнее выражение
это неравнозначность относительно
логических выражений  и
и .
Поэтому имеем:
.
Поэтому имеем:
.
Осталось нарисовать ЛС.
Пример 3.10. Составить логическую схему, реализующую логическую функцию f(x, y, z), заданную таблицей истинности (табл. 3.5).
Выберем строки таблицы, где значения функции равны 1. Таких строк 3, т. е. функция равна 1 только для этих трех наборов переменных. Отсюда выражение для функции можно записать так:
.
Таблица 3.5 | |||
Таблица f(x, y, z) | |||
x | y | z | f |
0 | 0 | 0 | 0 |
0 | 0 | 1 | 0 |
0 | 1 | 0 | 1 |
0 | 1 | 1 | 1 |
1 | 0 | 0 | 0 |
1 | 0 | 1 | 0 |
1 | 1 | 0 | 1 |
1 | 1 | 1 | 0 |
Полученное выражение
можно упростить. Для этого сгруппируем
первые два слагаемых и вынесем множитель 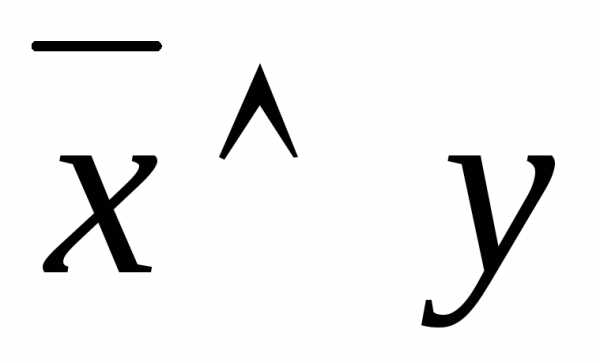 за скобки:
за скобки:
.
Применяя законы исключенного третьего и исключения констант, имеем:
.
Вынесем логический множитель y за скобки, а к скобочному выражению применим закон поглощения:
.
Применяя закон де Моргана имеем:
.
Получилась очень простая логическая схема (рис. 3.5):
studfiles.net
Презентация на тему: Упростить логические выражения:
F (x z) (x z) (y z)x ( y z)
Здесь для первых двух скобок применена формула склеивания
F(A, B,C) (A B C) (A B C)
(A B) (C C) A B1 A B
(Аv A) B=1 B=B
(A (AvB) (Bv B)= (закон исключенного третьего (44))
=A (AvB) 1=A (A B)= (конъюнкция с И)
=(A A) (A B)= (закон идемпотентности (34)) =A (A B)= A (закон поглощения (37))

Задания на упрощение выражений и таблицы истинности
1. F=¬(X (¬(¬Y X)))
2. F= ¬(X (¬ X ¬Y))
3.F=¬X (¬X Y ¬Y)
4.F =B(A+AB)
5. F=(A+C)(A+C)(B+C)
6. F=AB+AB+AB+BC7.F=D+ABC(B+C)
8.F =ABC+AB+ABC+ABC
9.F =AB+BC+C A
10.F =A×B+A
11.F=A+A+B+B×AB12.F=A×B+AB+AB

13.F =(A +B) ® (B +C)
14.F =A+B×C
15.F =((C +B) ®B)AB) ®B
16.F =ABC+(BC+A)
17.F =(AB+A)B
18.F =A×BC+ABC+ABC
19.F =A×B×C+ABC+ABC
20.F =A×BC+ABC+ABC
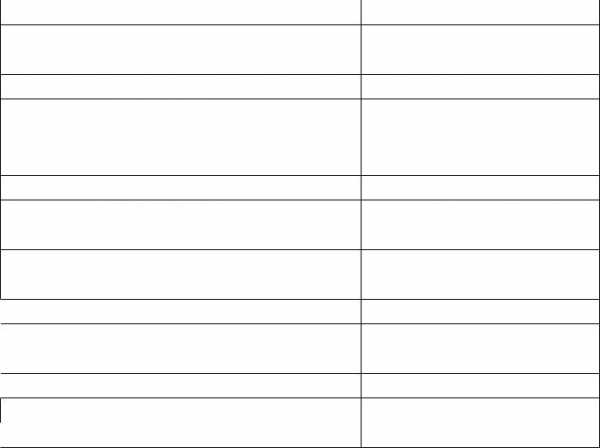
Задание. Заполните правую колонку таблицы названиями наиболее подходящих логических операций.
В естественном языке | В логике | |
…и… |
|
|
…или… |
|
|
Неверно, что… |
| |
…хотя… |
|
|
…в том и только в том случае… |
| |
…но… |
|
|
…а… |
|
|
…если… | то… |
|
…однако… |
| |
…тогда и только тогда, когда… |
| |
Либо… | либо… |
|
…необходимо и достаточно…
Из… следует…
…влечет…
…равносильно…
…необходимо…
…достаточно…
По горизонтали:
2.Мысль, в которой что-либоутверждается или отрицается.
5.Это повествовательное предложение, о котором можно сказать, истинно оно или ложно.
6.Логическое умножение.
7.Логическое сложение.
9.Форма мышления, в которой отражаются существенные признаки отдельного предмета или класса однородных предметов.
10.Наука о законах и формах мышления.
По вертикали:
1.Частица, используемая для образования сложного высказывания.
3.Прием мышления, посредством которого из исходного знания получается новое знание.
4.Одно из двух возможных значений, которые могут принимать логические формулы.
studfiles.net
