Умножение матрицы на вектор, формула и примеры
Умножение матрицы на вектор производится по правилу «строка на столбец». При умножении матрицы на вектор-столбец число столбцов в матрице должно совпадать с числом строк в векторе-столбце. Результатом умножения матрицы на вектор-столбец есть вектор-столбец:
При умножении матрицы на вектор-строку, умножаемая матрица может быть только вектором-столбцом, причем количество строк в векторе-столбце должно совпадать с количеством столбцов в векторе-строке. Результатом такого умножения будет квадратная матрица соответствующей размерности:
Примеры умножения матриц на вектора
| Понравился сайт? Расскажи друзьям! | |||
умножение матрицы на вектор | C++ для приматов
Даны квадратная матрица [latex]A[/latex] порядка [latex]n[/latex], векторы [latex]x[/latex] и [latex]y[/latex] с [latex]n[/latex] элементами. Получить вектор [latex]A(x+y)[/latex].
Примеры:
| Размерность матрицы | Матрица | Вектор x | Вектор y | Результирующий вектор A(x+y) |
| 2 | 2 3 3 2 | 3 4 | 5 6 | 46 44 |
| 3 | 2 1 4 5 2 6 3 4 8 | 2 2 2 | 4 4 4 | 42 78 90 |
| 4 | 1 2 3 4 3 4 1 6 2 3 8 1 4 5 0 8 | 1 2 3 4 | 5 4 3 2 | 60 84 84 102 |
| 5 | 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 | 4 6 7 8 0 | 2 8 9 3 1 | 0 0 16 0 0 |
Алгоритм решения: Вводим матрицу [latex]A[/latex] порядка [latex]n[/latex]. Вводим векторы [latex]x[/latex] и [latex]y[/latex], прибавляем векторы [latex]x[/latex] и [latex]y[/latex]. После умножаем матрицу [latex]A[/latex] на вектор [latex]x + y[/latex] и получаем вектор [latex]A(x + y)[/latex]. С помощью цикла выводим результирующий вектор.
Код программы :
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
#include <iostream> using namespace std; int main() { int n; cin >> n; int x[n]; int y[n]; int z[n]; int A[n][n]; int result_vector[n]; for (int i = 0; i < n; i++){ for (int j = 0; j < n; j++) cin >> A[i][j]; } for (int i = 0; i < n; i++){ cin>>x[i]; } for (int i = 0; i < n; i++){ cin>>y[i]; } for (int i = 0; i < n; i++){ z[i]=x[i]+y[i]; } for(int i=0; i<n; i++) { result_vector[i]=0; for(int j=0; j<n; j++) { result_vector[i]+=A[i][j]*z[j]; } } for(int i=0; i<n; i++) { cout << result_vector[i] << endl; } return 0; } |
Оригинал кода можно увидеть перейдя по ссылке
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 |
import java.util.*; import java.lang.*; import java.io.*; /* Name of the class has to be «Main» only if the class is public. */ class Ideone { public static void main (String[] args) throws java.lang.Exception { int n; Scanner in = new Scanner(System.in); n = in.nextInt(); double []x = new double[n]; double []y = new double[n]; double []z = new double[n]; double [] result_vector = new double[n]; double [][] A = new double[n][n]; for (int i = 0; i < n; i++){ for (int j = 0; j < n; j++){ A[i][j]=in.nextDouble(); } } for (int i = 0; i < n; i++){ x[i]=in.nextDouble(); } for (int i = 0; i < n; i++){ y[i]=in.nextDouble(); } for (int i = 0; i < n; i++){ z[i]=x[i]+y[i]; } for(int i=0; i<n; i++) { result_vector[i]=0; for(int j=0; j<n; j++) { result_vector[i]+=A[i][j]*z[j]; } } for(int i=0; i<n; i++) { System.out.printf(«%.6f «,result_vector[i]); } } } |
Оригинал кода можно увидеть перейдя по ссылка
Posted in 6. Многомерные массивы. Tagged умножение матрицы на вектор.Задача. Дана квадратная матрица порядка n. Получить вектор Ab, где b-вектор, элементы которого вычисляются по формулам:
[latex]b_{i}=\begin{cases}\frac{1}{i^{2}+2} & \text{, if i mod 2=0} \\ \frac{1}{i} & \text{, other case } \end{cases}[/latex]
i=(1,…,n).
Тесты:
| Вход | Выход | Комментарий |
| 4 1 2 1 1 1 3 6 9 1 2 1 1 1 6 3 18 | 1.72222 4 1.72222 4 | Пройден |
| 3 0 0 0 1 1 1 2 2 2 | 0 1.5 3 | Пройден |
| 4 1 2 2 9 3 4 1 18 1 1 1 1 0 0 0 0 | 2.5 5 1.55556 0 | Пройден |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
#include <iostream> using namespace std;
int main() { int n; cin>>n; double b[n]; for (int i=0; i<n; i++) { if((i+1)%2==0) b[i]=1.0/((i+1)*(i+1) + 2); else b[i]=1.0/(i+1); }
double A[n][n]; for (int i=0; i<n; i++) for (int j=0; j<n; j++) cin>>A[i][j]; double Ab[n]; for (int i=0; i<n; i++) { Ab[i]=0; for (int j=0; j<n; j++) { Ab[i]+=A[i][j]*b[j]; } } for (int i=0; i<n; i++) cout<<Ab[i]<<» «; return 0; } |
Решение:
Согласно условию находим вектор b. По формуле [latex]Ab_{i}=\sum_{j=1}^{n}A_{ij}b_{j}[/latex], i=(0,…,n) находим произведение матрицы на вектор.
С работой программы можно ознакомится здесь.
Posted in 6. Многомерные массивы. Tagged квадратная матрица, умножение матрицы на вектор.cpp.mazurok.com
Как умножить вектор на матрицу 🚩 умножение матрица на вектор 🚩 Математика
Автор КакПросто!
В теории матриц вектором называется матрица, имеющая только один столбец или только одну строку. Умножение такого вектора на другую матрицу происходит по общим правилам, однако имеет и свои особенности.
Статьи по теме:
Инструкция
По определению произведения матриц умножение возможно только в том случае, если количество столбцов первого множителя равно количеству строк второго. Следовательно, вектор-строку удастся умножить только на матрицу, в которой столько же строк, сколько элементов в вектор-строке. Аналогично, вектор-столбец можно умножить только на матрицу, в которой столько же столбцов, сколько элементов в вектор-столбце. Умножение матриц некоммутативно, то есть если A и B — матрицы, то A*B ≠ B*A. Более того, существование произведения A*B вовсе не гарантирует существования произведения B*A. Например, если матрица A имеет размеры 3*4, а матрица B — 4*5, то произведение A*B — матрица размером 3*5, а B*A не определено.Пусть задан: вектор-строка A = [a1, a2, a3 … an] и матрица B размерности n*m, элементы которой равны:
[b11, b12, b13, … b1m;
b21, b22, b23, … b2m;
…
bn1, bn2, bn3, … bnm].
Cj = ∑ai*bij (i = 1 … n, j = 1 … m).
Иными словами, для нахождения i-того элемента произведения нужно умножить каждый элемент вектора-строки на соответствующий ему по порядку элемент i-того столбца матрицы и просуммировать эти произведения.
Аналогично, если задана матрица A размерности m*n и вектор-столбец B размерности n*1, то их произведение будет вектором-столбцом размерности m*1, i-тый элемент которого равен сумме произведений элементов вектора-столбца B на соответствующие им элементы i-той строки матрицы A.
Если A — вектор-строка размерности 1*n, а B — вектор-столбец размерности n*1, то произведение A*B является числом, равным сумме произведений соответствующих элементов этих векторов:c = ∑ai*bi (i = 1 … n).
Это число называется скалярным, или внутренним, произведением.
Результат умножения B*A в этом случае является квадратной матрицей размерности n*n. Ее элементы равняются:Cij = ai*bj (i = 1 … n, j = 1 … n).
Такая матрица называется внешним произведением векторов.
Совет полезен?
Статьи по теме:
Не получили ответ на свой вопрос?
Спросите нашего эксперта:
www.kakprosto.ru
Параллельные методы умножения матрицы на вектор
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
ГОУВПО “ПЕРМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ”
Кафедра прикладной математики и информатики
Параллельные методы умножения матрицы на вектор
( лаба №1 )
Пермь 2010
Цель лабораторной работы.
Реализация последовательного и параллельных алгоритмов умножения матрицы на вектор при использовании 2-х ядерной вычислительной системы с общей памятью.
Постановка задачи.
В результате умножения матрицы
и вектора , получается вектор , каждый i -ый элемент которого есть результат скалярного умножения i -й строки матрицы (обозначим эту строчку ) и вектора .Тем самым получение результирующего вектора
предполагает повторение однотипных операций по умножению строк матрицы и вектора . Каждая такая операция включает умножение элементов строки матрицы и вектора ( операций) и последующее суммирование полученных произведений (операций).Общее количество необходимых скалярных операций есть величина
.- Поcледовательный алгоритм умножения матрицы на вектор
void SerialResultCalculation(double* pMatrix, double* pVector,
double* pResult, int Size) {
int i, j; // Loop variables
for (i=0; i<Size; i++) {
pResult[i]=0;
for (j=0; j<Size; j++)
pResult[i] += pMatrix[i*Size+j]*pVector[j];
}
}
- Умножение матрицы на вектор при разделении данных по строкам.
Базовая подзадача — скалярное умножение одной строки матрицы на вектор. После завершения вычислений каждая базовая подзадача определяет один из элементов вектора результата c .
В общем виде схема информационного взаимодействия подзадач в ходе выполняемых вычислений показана на рис.1. Количество вычислительных операций для получения скалярного произведения одинаково для всех базовых подзадач.
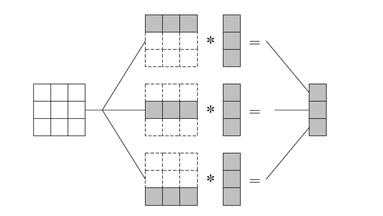
Рисунок 1 . Организация вычислений при выполнении параллельного алгоритма умножения матрицы на вектор, основанного на разделении матрицы по строкам.
Каждый поток параллельной программы использует только «свои» данные, ему не требуются данные, которые в данный момент обрабатывает другой поток, нет обмена данными между потоками, не возникает необходимости синхронизации. Т.е. практически нет накладных расходов на организацию параллелизма (за исключением расходов на организацию и закрытие параллельной секции), и можно ожидать линейного ускорения. Однако, как будет видно из представленных результатов, ускорение далеко от линейного.
Время решения задачи одним потоком складывается из времени, когда процессор непосредственно выполняет вычисления, и времени, которое тратится на чтение необходимых для вычислений данных из ОП в кэш. При этом время, необходимое на чтение данных, может в несколько раз превосходить время счета.
Процесс выполнения последовательного алгоритма умножения матрицы на вектор может быть представлен диаграммой, изображенной на рис.2.
Рисунок 2. Диаграмма состояний процесса выполнения последовательного алгоритма
умножения матрицы на вектор.
Время выполнения последовательного алгоритма складывается из времени вычислений и времени доступа к памяти:
, где — это количество выполненных операций, — время выполнения одной операции, — размерность матрицы. , где — объем данных, которые необходимо закачать в кэш процессора, — скорость доступа (пропускная способность канала доступа) ОП.Таким образом,
.Для оценки
, измерим время выполнения последовательного алгоритма при, т.к. матрица и вектор полностью поместятся в кэш ВЭ. (У нас размер кэш равен 2048 кбайт, поэтому ). Чтобы исключить необходимость выборки данных из ОП, перед началом вычислений заполним матрицу и вектор случайными числами – выполнение этого действия гарантирует закачку данных в кэш. Далее при решении задачи все время будет тратиться на вычисления, так как нет необходимости загружать данные из ОП.
Получим
0,00000308.Тогда
Теперь, оценим
при : 8 121 537 238,29В таблице 1 и на рис.3 представлено сравнение реального времени последовательного алгоритма умножения матрицы на вектор и теоретического.
Таблица 1. Сравнение экспериментального и теоретического времени выполнения последовательного
алгоритма умножения матрицы на вектор.
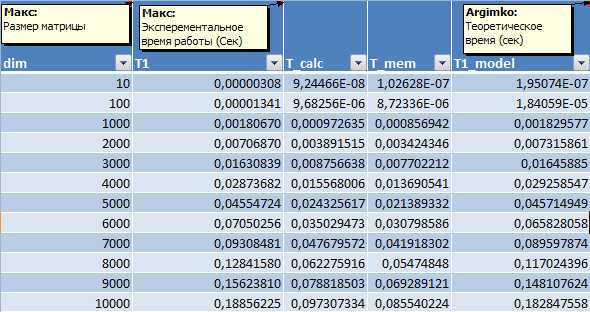
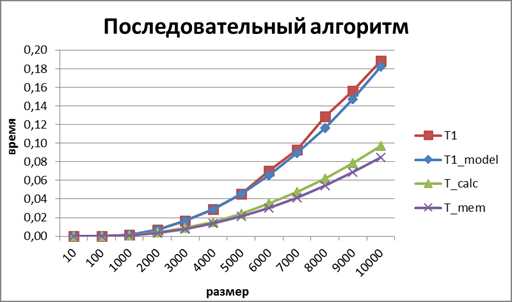
Рисунок 3. График зависимости экспериментального и теоретического времени выполнения последовательного алгоритма от объема исходных данных (ленточное разбиение матрицы по строкам
В многоядерных процессорах Intel архитектуры Core 2 Duo ядра процессоров разделяют общий канал доступа к памяти. Т.е., несмотря на то, что вычисления могут выполняться ядрами параллельно , доступ к памяти осуществляется строго последовательно. Следовательно, время
выполнения параллельного алгоритма в системе с вычислительными элементами, с использованием потоков и при описанной выше схеме доступа к памяти может быть оценено при помощи следующего соотношения: .void ParallelResultCalculation_rows (double* pMatrix, double* pVector,
double* pResult, int Size) {
int i, j; // Loop variables
#pragma omp parallel private (i,j)
#pragma omp for
for (i=0; i<Size; i++) {
for (j=0; j<Size; j++)
pResult[i] += pMatrix[i*Size+j]*pVector[j];
}
}
Результаты вычислительных экспериментов приведены в таблице 2. Времена выполнения алгоритмов указаны в секундах.
Ускорение есть результат деления времени работы последовательного алгоритма на время работы параллельного.
Таблица 2. Результаты вычислительных экспериментов для параллельного алгоритма умножения
матрицы на вектор при ленточной схеме разделении данных по строкам.
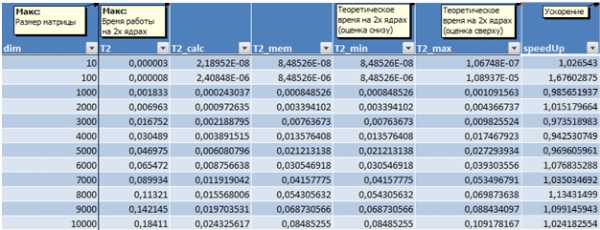
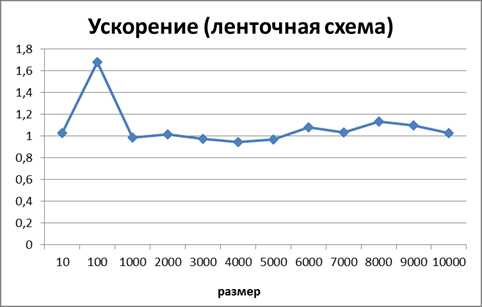
Рисунок 4. Зависимость ускорения от количества исходных данных при выполнении параллельного алгоритма умножения матрицы на вектор, основанного на ленточном горизонтальном разбиении матрицы
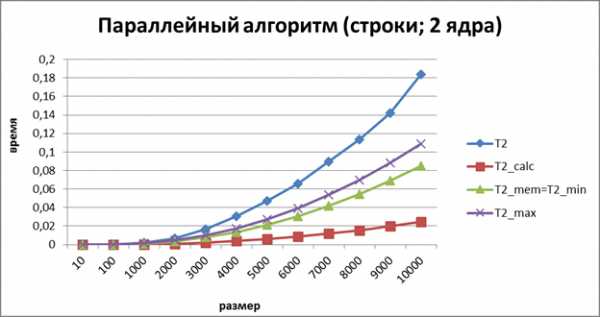
Рисунок 5. График зависимости экспериментального и теоретического времени выполнения параллельного алгоритма от объема исходных данных при использовании двух потоков (ленточное разбиение матрицы по строкам)
mirznanii.com
Алгоритм умножения матрицы на вектор
Алгоритм умножения матрицы (для простоты возьмем квадратную матрицу) размерности на вектор размерности можно представить как скалярных умножений векторов, получающихся из строк матрицы на вектор . Если строки матрицы слоистым образом распределены по процессорам и вектор хранится на каждом процессоре, то параллельный алгоритм можно записать следующим образом:
Шаг 1: на
Шаг 2: на
Шаг 3:
На втором шаге на каждом процессоре параллельно вычисляются соответствующие блоки результирующего вектора , затем (если это необходимо) на третьем шаге они пересылаются на первый процессор.
Предположим, что столбцы матрицы распределены слоистым образом по процессорам. В этом случае необходимо модифицировать алгоритм с учетом хранения матрицы. Результат матрично-векторного произведения можно получить, умножив каждый столбец матрицы на соответствующий элемент вектора и сложив получившиеся вектора. Степень параллелизма этого алгоритма меньше, чем в предыдущем, и обусловлена тем, что приходится осуществлять суммирование.
Условно, по шагам алгоритм записывается следующим образом:
Шаг 1: на
Шаг 2: на
Шаг 3: на
Шаг
4:
Шаг 5: на
На втором шаге осуществляется покомпонентное умножение векторов, на третьем – частичное суммирование, на четвертом – пересылка частичных сумм на первый процессор, на последнем – завершающее суммирование.
Матрично-векторное умножение обычно является частью более широкого процесса вычислений и для выбора того или иного алгоритма главную роль играет способ хранения и в момент, когда требуется их произведение. Например, если и уже находятся в памяти -го процессора, то эффективнее использовать второй алгоритм, хотя степень параллелизма в нем ниже, чем в первом. Еще один важный фактор при выборе параллельного алгоритма — желаемое расположение результата по окончании операции умножения: во втором алгоритме вектор-результат размещается в памяти одного процессора, тогда как в первом он распределен по процессорам.
program EXAMPLE
include
‘mpif.h’integer my_id, np, comm, tag, count, ierr, n,q
integer i,j,k
integer a(100,100),b(100)
integer c(100,100),a1(100,100),a2(100,100)
integer status(MPI_STATUS_SIZE)
double precision t1,tfinish
call MPI_Init(ierr)
comm=MPI_COMM_WORLD
call MPI_Comm_rank(COMM, my_id, ierr)
call MPI_Comm_size(COMM, np, ierr)
print *, ‘Process ‘, my_id, ‘ of ‘, np, ‘ is alive’
! Инициализация матриц
t1=MPI_Wtime()
call MPI_Bcast(n,1,MPI_INTEGER,0,COMM,ierr)
call MPI_Bcast(b,n,MPI_INTEGER,0,COMM,ierr)
call MPI_Scatter(a,int(n*n/np),MPI_INTEGER,a1,
* int(n*n/np),MPI_INTEGER,0,COMM,ierr)
c=0
do j=1,n,1
do i=1,int(n/np),1
do k=1,n,1
c(i+int(n/np)*my_id,j)=
*c(i+int(n/np)*my_id,j)+a1(k,i)*b(k)
end do
end do
end do
call MPI_Reduce(c,a2,n*n,MPI_INTEGER,MPI_SUM,
*0, COMM,ierr)
t1=MPI_Wtime()-t1
write(*,*) ‘Dim = ‘,n,’ the time is ‘,t1
call MPI_Finalize(ierr)
stop
end
Задание: Алгоритм умножения матриц
Реализовать любой вариант параллельного умножения матриц.
Пример:
Приведенные параллельные алгоритмы матрично-векторного произведения естественным образом обобщаются на задачу умножения матриц. Приведенные же ниже алгоритмы будут обсуждаться с точки зрения того, как хранились матрицы до операции произведения и после нее.
Для простоты возьмем квадратные матрицы и размерности .
Первый вариант параллельного алгоритма матричного умножения будем строить, предполагая, что матрица распределена по процессорам слоистым образом по строкам, а матрица — целиком. В этом случае искомый результат можно получить, выполнив параллельно на каждом процессоре скалярных произведений.
Приведем алгоритм:
Шаг 1: на
Шаг 2: на (причем циклы по индексам расположены в следующей последовательности
Шаг 3:
Второй вариант параллельного алгоритма матричного умножения будем строить, предполагая, что матрица распределена по процессорам слоистым образом по столбцам, а матрица — целиком. В этом случае искомый результат можно получить, выполнив параллельно на каждом процессоре умножение соответствующих столбцов матрицы на соответствующие элементы строк матрицы , затем необходимо осуществить частичное суммирование получившихся произведений и на последнем шаге, переслав матрицы с частичными суммами на один процессор, закончить суммирование. Алгоритм опустим ввиду его громоздкости и очевидности.
Возможные способы хранения исходных матриц порождают другие алгоритмы. Например, матрица распределена по процессорам слоистым образом по строкам, а матрица — целиком, или распределена по процессорам слоистым образом по столбцам, а — целиком. Алгоритмы при этом схожи с рассмотренными выше.
Возможно также построение алгоритмов, которые основаны на блочном распределении матриц и по процессорам.
Если разбиения обеих матриц на блоки согласованы, то
,
где или — миноры соответствующих матриц. Это представление можно реализовать разными алгоритмами. Пусть, например, число процессоров равно (числу миноров матрицы . При условии, что матрицы и распределены соответствующим образом по процессорам, все миноры матрицы можно вычислять одновременно.
studfiles.net
Умножение матрицы на вектор при разделении данных по строкам
Данный алгоритм основан на представлении матрицы непрерывными наборами (горизонтальными полосами) строк. Полученные полосы распределяются по процессорам вычислительной системы. Вектор b копируется на все процессоры. Перемножение полосы матрицы на вектор (а данная операция может быть выполнена процессорами параллельно) приводит к получению блока элементов результирующего вектора с. Для объединения результатов расчета и получения полного вектора c на каждом из процессоров вычислительной системы необходимо выполнить операцию обобщенного сбора данных.
4.2.2. Умножение матрицы на вектор при разделении данных по столбцам
Другой подход к параллельному умножению матрицы на вектор основан на разделении исходной матрицы на непрерывные наборы (вертикальные полосы) столбцов. Вектор b при таком подходе разделен на блоки. Вертикальные полосы исходной матрицы и блоки вектора распределены между процессорами вычислительной системы.
Параллельный алгоритм умножения матрицы на вектор начинается с того, что каждый процессор i выполняет умножение своей вертикальной полосы матрицы А на блок элементов вектора b, в итоге на каждом процессоре получается вектор промежуточных результатов c'(i). Далее для получения элементов результирующего вектора с процессоры должны обменяться своими промежуточными данными между собой.
4.2.3. Умножение матрицы на вектор при блочном разделении данных
Рассмотрим теперь параллельный алгоритм умножения матрицы на вектор, который основан на ином способе разделения данных – на разбиении матрицы на прямоугольные фрагменты (блоки). При таком способе разделения данных исходная матрица A представляется в виде набора прямоугольных блоков. Вектор b также должен быть разделен на блоки. Блоки матрицы и блоки вектора распределены между процессорами вычислительной системы. Логическая (виртуальная) топология вычислительной системы в данном случае имеет вид прямоугольной двумерной решетки. Размеры процессорной решетки соответствуют количеству прямоугольных блоков, на которые разбита матрица A. На процессоре pi,j, находящемся на пересечении i-й строки и j-го столбца процессорной решетки, располагается блок Ai,j матрицы A и блок bj вектора b.
После перемножения блоков матрицы A и вектора b каждый процессор pi,j будет содержать вектор частичных результатов c'(i,j). Поэлементное суммирование векторов частичных результатов для каждой горизонтальной строки процессорной решетки позволяет получить результирующий вектор c.
4.3. Матричное умножение
Задача умножения матрицы на матрицу определяется соотношениями:
(для простоты изложения материала будем предполагать, что перемножаемые матрицы A и B являются квадратными и имеют порядок n×n). Как следует из приведенных соотношений, вычислительная сложность задачи является достаточно высокой (оценка количества выполняемых операций имеет порядок n3).
Основу возможности параллельных вычислений для матричного умножения составляет независимость расчетов для получения элементов сij результирующей матрицы C. Тем самым, все элементы матрицы C могут быть вычислены параллельно при наличии n2 процессоров, при этом на каждом процессоре будет располагаться по одной строке матрицы A и одному столбцу матрицы B. При меньшем количестве процессоров подобный подход приводит к ленточной схеме разбиения данных, когда на процессорах располагаются по несколько строк и столбцов (полос) исходных матриц.
Другой широко используемый подход для построения параллельных способов выполнения матричного умножения состоит в применении блочного представления матриц, при котором исходные матрицы A, B и результирующая матрица C рассматриваются в виде наборов блоков (как правило, квадратного вида некоторого размера m×m). Тогда операцию матричного умножения матриц A и B в блочном виде можно представить следующим образом:
где каждый блок Cij матрицы C определяется в соответствии с выражением:
Полученные блоки Cij также являются независимыми, и, как результат, возможный подход для параллельного выполнения вычислений может состоять в расчетах, связанных с получением отдельных блоков Cij, на разных процессорах. Применение подобного подхода позволяет получить многие эффективные параллельные методы умножения блочно-представленных матриц.
studfiles.net
2.3.2 Умножение матрицы на вектор
Задача умножения матрицы на вектор определяется соотношениями
.
Тем самым, получение результирующего вектора y предполагает повторения n однотипных операций по умножению строк матрицы A и вектора x. Получение каждой такой операции включает поэлементное умножение элементов строки матрицы и вектора x и последующее суммирование полученных произведений. Общее количество необходимых скалярных операций оценивается величиной
.
Как следует из выполняемых действий при умножении матрицы и вектора, параллельные способы решения задачи могут быть получены на основе параллельных алгоритмов суммирования.
Выполним анализ информационных зависимостей в алгоритме умножения матрицы на вектор для выбора возможных способов распараллеливания. Как можно заметить
выполняемые при проведении вычислений операции умножения отдельных строк матрицы на вектор являются независимыми и могут быть выполнены параллельно;
умножение каждой строки на вектор включает независимые операции поэлементного умножения и тоже могут быть выполнены параллельно;
суммирование получаемых произведений в каждой операции умножения строки матрицы на вектор могут быть выполнены по одному из ранее рассмотренных вариантов алгоритма суммирования (последовательный алгоритм, модифицированная схема).
Таким образом, максимально необходимое количество процессоров определяется величиной
.
Использование такого количества процессоров может быть представлено следующим образом. Множество процессоров разбивается нагрупп
,
каждая из которых представляет набор процессоров для выполнения операции умножения отдельной строки матрицы на вектор. В начале вычислений на каждый процессор группы пересылаются элемент строки матрицы и соответствующий элемент вектора. Далее каждый процессор выполняет операцию умножения. Последующие затем вычисления выполняются по каскадной схеме суммирования. Для иллюстрации на рис. 3.3 приведена вычислительная схема для процессоров группыпри размерности матрицы.[13] Для реализации алгоритма воспользуемся модельюSIMD.
Рис. 3.3. Вычислительная схема операции умножения строки матрицы на вектор
Вычислим эффективность алгоритма умножения матрицы на вектор. По закону Амдала ускорение можно определить следующим образом
, 
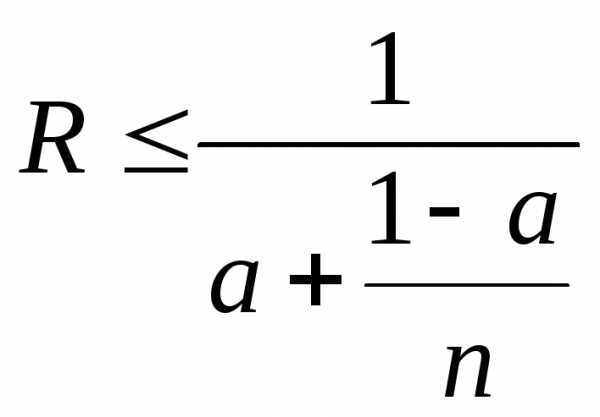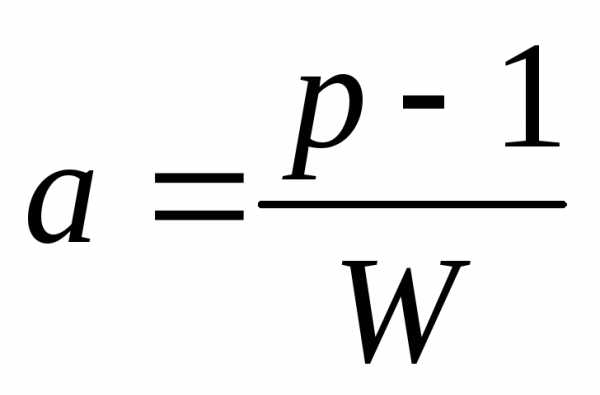, W =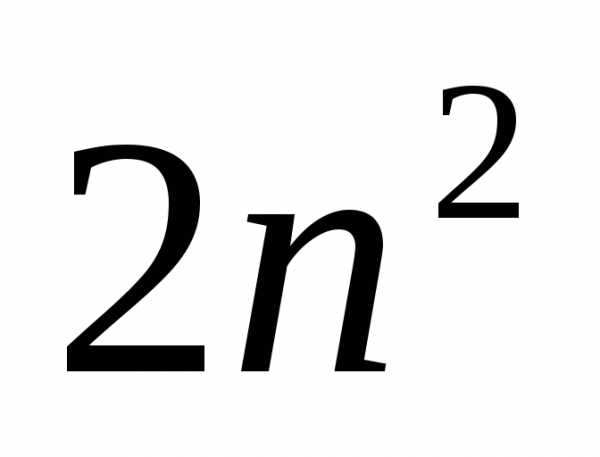 
.
2.3.3 Матричное умножение
Задача умножения матрицы на матрицу определяется соотношениями
,
.
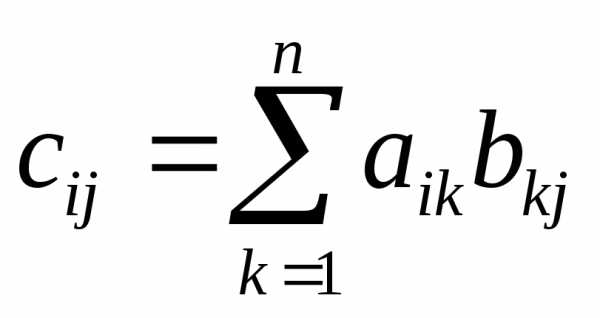(для простоты изложения материала будем предполагать, что перемножаемые матрицы иявляются квадратными и имеют порядок).
Анализ возможных способов параллельного выполнения данной задачи может быть проведен по аналогии с рассмотрением задачи умножения матрицы на вектор.
Задача матричного умножения требует для своего решения выполнение большого количества операций (скалярных умножений и сложений). Информационный граф алгоритма при большом размере матриц становится достаточно объемным и, как результат, непосредственный анализ этого графа затруднен. После выявления информационной независимости выполняемых вычислений могут быть предложены многочисленные способы распараллеливания алгоритма.
С другой стороны, алгоритм выполнения матричного умножения может быть рассмотрен как процесс решения независимых подзадач умножения матрицына столбцы матрицы. Введение макроопераций, как можно заметить по рис. 3.4, приводит к более компактному представлению информационного графа алгоритма, значительно упрощает проблему выбора эффективных способов распараллеливания вычислений, позволяет использовать типовые параллельные методы выполнения макроопераций в качестве конструктивных элементов при разработке параллельных способов решения сложных вычислительных задач.
Рис. 3.4. Вычислительная схема матричного умножения при использовании макроопераций умножения матрицы A на столбец матрицы B
Важно отметить, что процесс введения макроопераций может осуществляться поэтапно с последовательно возрастающим уровнем детализации используемых операций. Так, для задачи матричного умножения после построения графа вычислений на основе макроопераций умножения матрицы на вектор может быть выполнено рассмотрение каждой макрооперации как последовательности независимых операций скалярного произведения векторов и т.п. Подобная иерархическая декомпозиционная методика построения параллельных методов решения сложных задач является одной из основных в параллельном программировании и широко используется в практике.
При построении параллельных способов выполнения матричного умножения наряду с рассмотрением матриц в виде наборов строк и столбцов широко используется блочное представление матриц. Выполним более подробное рассмотрение данного способа организации вычислений.
Пусть количество процессоров составляет , а количество строк и столбцов матрицы является кратным величине, т.е.. Представим исходные матрицы,и результирующую матрицув виде наборов прямоугольных блоков размера. Тогда операцию матричного умножения матрицив блочном виде можно представить следующим образом:
,
где каждый блок матрицыопределяется в соответствии с выражением
.
Информационный граф алгоритма умножения при подобном представлении матриц показан на рис. 3.5 (на рисунке представлен фрагмент графа для вычисления только одного блока матрицы ). При анализе этого графа можно обратить внимание на взаимную независимость вычислений блоковматрицы. Как результат, возможный подход для параллельного выполнения вычислений может состоять в выделении для расчетов, связанных с получением отдельных блоков, разных процессоров. Применение подобного подхода позволяет получить многиеэффективные параллельные методы умножения блочно-представленных матриц; один из алгоритмов данного класса рассматривается ниже.
Рис. 3.5. Информационный граф матричного умножения при блочном представлении матриц
В основе алгоритма используем модель SIMD. Сгруппируем матрицы А и С по количеству процессов р. Предадим процессам матрицу В, сгруппированные матрицы А и С. Каждый процесс вычисляет свою группу (операции умножения и сложения) и формирует часть матрицы С. Затем возвращает их главному процессу.
Вычислим эффективность алгоритма умножения матриц. По закону Амдала ускорение можно определить следующим образом
, 
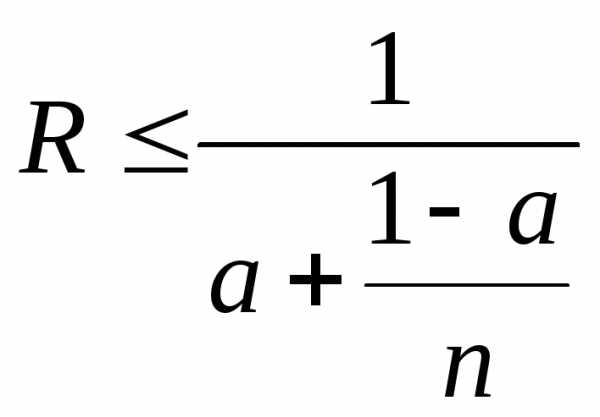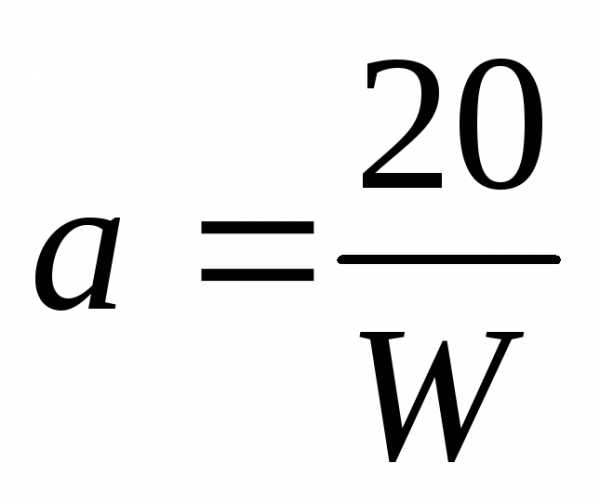, W= .
studfiles.net