Множество значений функции
Определение 1
Функцией, заданной на множестве $X$ и принимающей значения из множества $Y$ называют некую закономерность, по которой каждому элементу из множества $X$ соответствует лишь один и только один элемент из множества $Y$.
Из этого определения следует, что множество (область) значений функции — это те значения функции $y(x)$, которые она может принимать соответственно области её определения. Теперь перейдём к следующему определению.
Определение 2
Область (множество) значений функции на некотором рассматриваемом отрезке — это интервал значений, которые функция принимает на этом рассматриваемом отрезке.
Чаще всего в учебной литературе встречается термин «множество значений функции». Кратко его обозначают $E(f)$.
Как определить область значения функции
Для определения множества значений функции пользуются графическим методом, методом поисков минимума и максимума, вычислением производной и другими.
Определение множества значений функции графическим методом
Графический метод подразумевает построение графика функции и изучение этого графика. Этот метод наиболее удобен, если не известна какая-либо закономерность изменения функции $f(x)$, а есть только набор произвольных точек или собственно сам график.
Пример 1
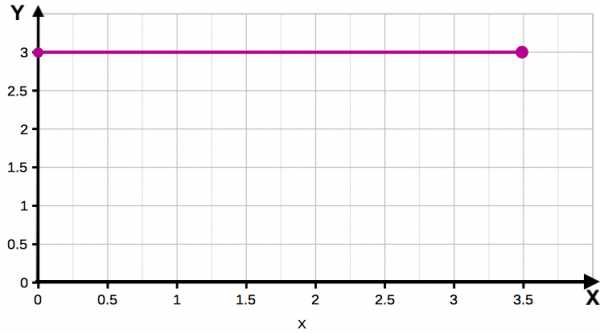
Рисунок 1. Определение множества значений функции графическим методом
На данном рисунке область значений функции $y=f(x)$ равна $E(y)=3$, так как на протяжении всего отрезка функция $y$ не меняет своего значения и всегда равна $3$, тогда как область определения функции $D(y)=[0;3.5]$.
Скобки в данном случае для области определения функции необходимо использовать квадратные, так как обе точки закрашены, то есть включены в отрезок. В случае если точки не закрашены, они не включаются в отрезок и тогда применяются круглые скобки.
Метод нахождения области значения функции через производную
Метод нахождения области значения функции через производную состоит в том, чтобы сначала оценить область её определения (то есть определить те значения, которые может принимать аргумент $x$, а затем осуществить процедуру нахождения самой производной. После этого осуществляют поиск значений $x$, при которых производная функции равна нулю и при которых производная не существует.
Рассмотрим пример нахождения области значений функции через производную.
Пример 2
Дана функция $f(x)=\sqrt{16-x^2}$. Найдите область её значений.
Сначала определяем, какие значения может принимать $x$ для существования функции.
При значении $x^2>16$ под корнем получается отрицательное число, а это значит, что область определения функции от $[-4;4]$ включительно.
Теперь найдём производную функции:
$(\sqrt{16-x^2})’=-\frac{x}{\sqrt{16-x^2}}$
Если в знаменателе производной нуль, то производной не существует, в данном случае это условие выполняется при $x=±4$.
Приравниваем производную к нулю и находим значения $x$. Производная данной функции принимает нулевое значение при $x=0$. Теперь подставляем найденные значения производной в нашу функцию, и получаем, что наименьшее значение функции — это $f(4)$ и $f(-4)$, при этих значениях функция равна нулю, а наибольшее значение $f(x)$ — при $x=0$, в этой точке функция равна $16$.
Метод поиска минимума и максимума
Метод поиска минимума и максимума основан на том, чтобы найти максимальное и и минимальное значение, которые функция принимает на изучаемой области.
Пример 3
Определите область значений функции:
$y=6-4sinx$
Проанализируем данную функцию. Так как минимальное значение синуса равно минус единице, а а максимальное — единице, то подставив эти значения получаем, что $max(f(x))=10$ при $x=\frac{3π}{2}$, а минимум $min(f(x))=2$ при $x=\frac{π}{2}$. Следовательно, множество значений, которые может принимать данная функция — $E(x)=[2;10]$.
Разница между областью значения и областью определения функции
Стоит обратить внимание, что область значений функции — не одно и то же с термином «область определения функции».
Определение 3
Область определения функции $D(y)$ — это диапазон таких значений переменной $x$, при которых существует функция $y(x)$.
Например, рассмотрим функцию $y(x)=x^2$. В данном случае область определения этой функции будет множеством вещественных (действительных) чисел $\mathbb{R}$, а сама функция будет принимать значения только положительных действительных чисел $\mathbb{R}^+$, так как вещественное число, возведённое в квадрат, не может давать отрицательное значение. То есть, в этом примере множество значений функции — это множество положительных вещественных чисел $\mathbb{R}^+$.
Также имеют место случаи, когда область определения функции совпадает с областью значений. В качестве иллюстрации можно рассмотреть функцию $y(x)=2x$. За аргумент $x$ данная функция может принимать любое действительное число из множества $\mathbb{R}$, а значения, которые будет принимать сама функция — это удвоенные числа из множества всех действительных чисел. То есть, в данном случае областью значений $E(y)$ будет также всё множество вещественных чисел $\mathbb{R}$.
spravochnick.ru
5.2. Множество значений функции.
1º. Множеством (областью) значений E(y)функцииy=f(x)называется множество всех таких чиселy0, для каждого из которых найдется числоx0такое, чтоf(x0)=y0.
2º. Областью значений всякого многочлена
четной степени является промежуток 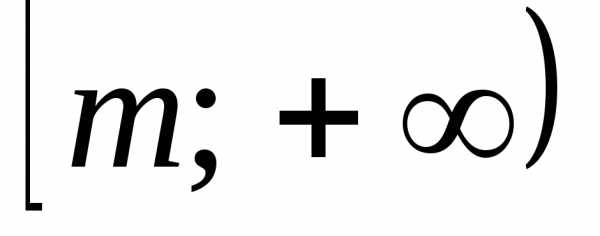 ,
гдеm– наименьшее
значение этого многочлена, либо промежуток
,
гдеm– наименьшее
значение этого многочлена, либо промежуток ,
гдеn– наибольшее
значение этого многочлена.
,
гдеn– наибольшее
значение этого многочлена.
Областью значений всякого многочлена нечетной степени является R.
3º. Области значений основных элементарных функций:
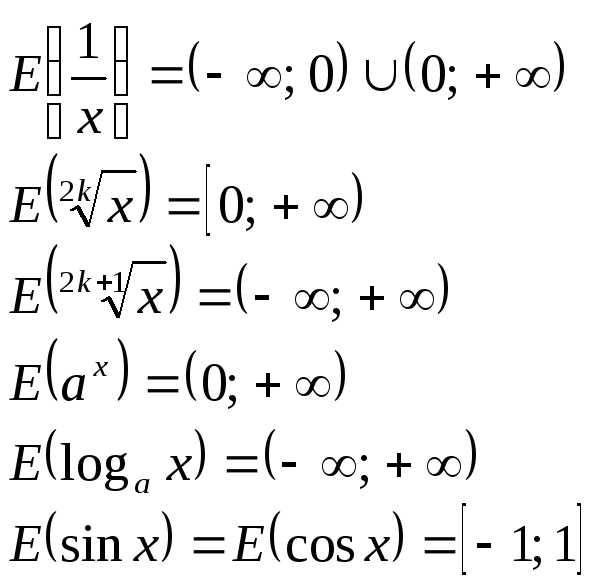
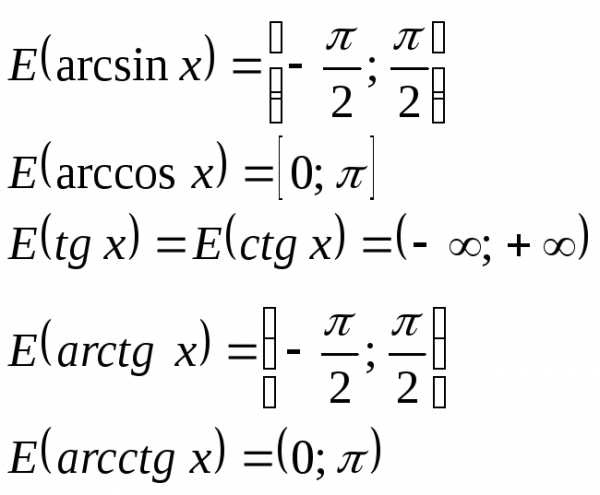
Пример 15. Найти множество значений
функции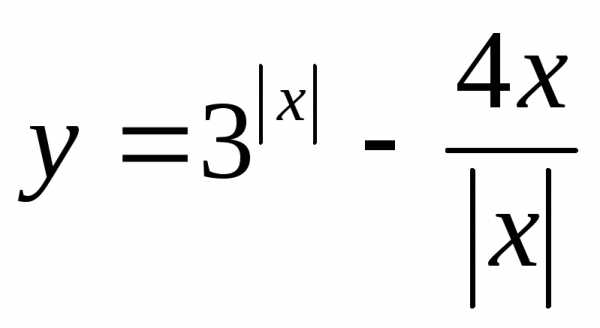 ,
еслиx≤1.
,
еслиx≤1.
Решение: Данная функция не определена при x=0и, следовательно, задана на множестве.
Рассмотрим x<0,
тогда|x|=-xи функция принимает вид.
Так какдляx<0, то.
Таким образом, на промежутке функция принимает значения от 5 до +∞.
функция принимает значения от 5 до +∞.
Если x>0, то|x|=xи функция имеет вид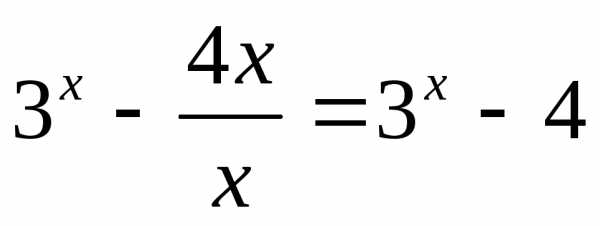 .
Так какдля
.
Так какдля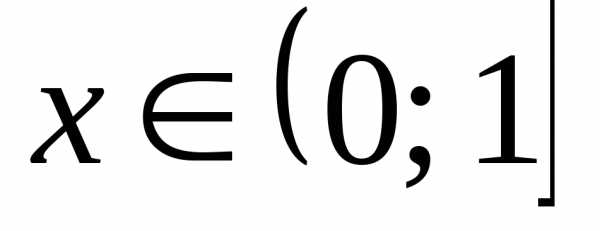 ,
то.
,
то.
Ответ: .
Дидактический материал.
Решите неравенства:
1. 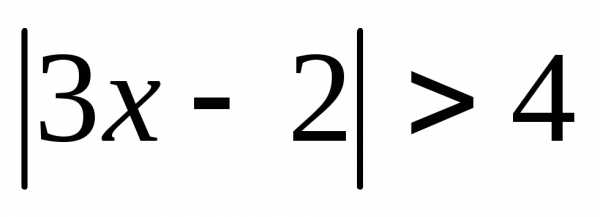 ; 2.
; 2.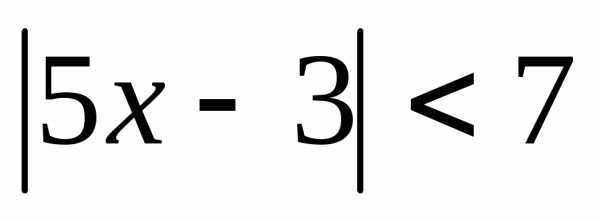 ; 3.;
; 3.;
4. ; 5.; 6.;
7. ; 8.; 9.;
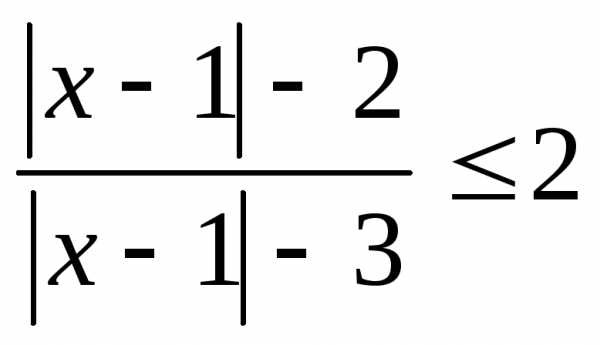 ; 11.
; 11.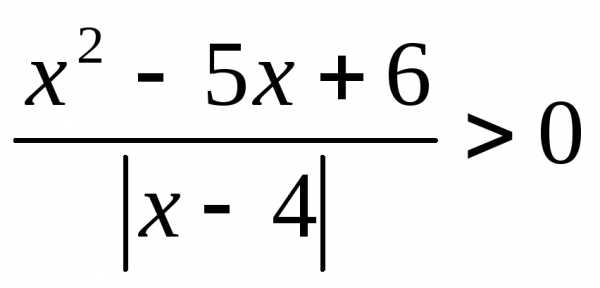 ; 12.
; 12.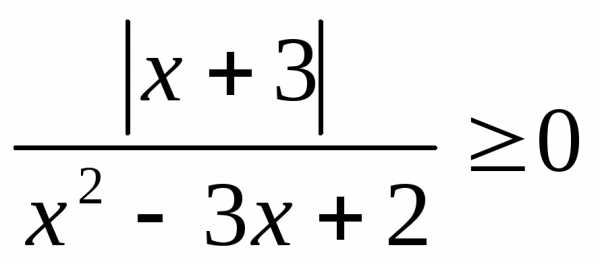 ;
;13. ; 14.;
15. ; 16.;
17. ; 18..
19. При каких xточки
графика функции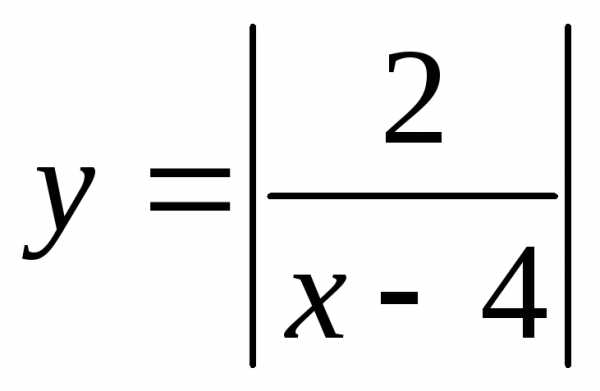 лежат
выше прямой
лежат
выше прямой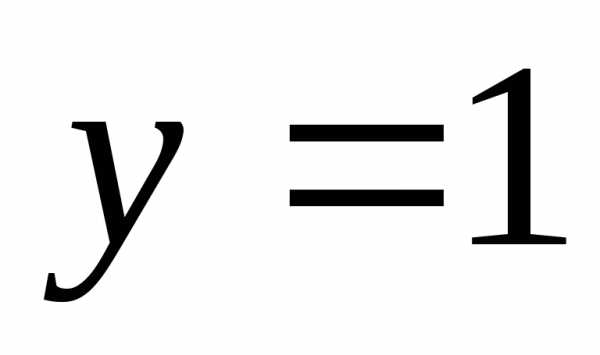 ?
?
20. При каких xточки
графика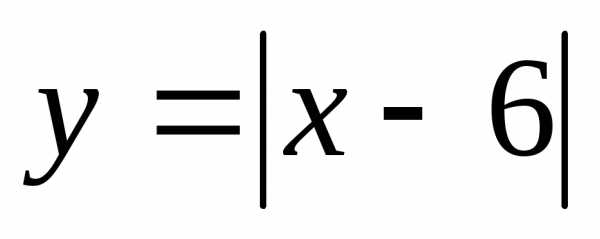 лежат не ниже точек графика функции?
лежат не ниже точек графика функции?
Найти множество значений функции:
21. 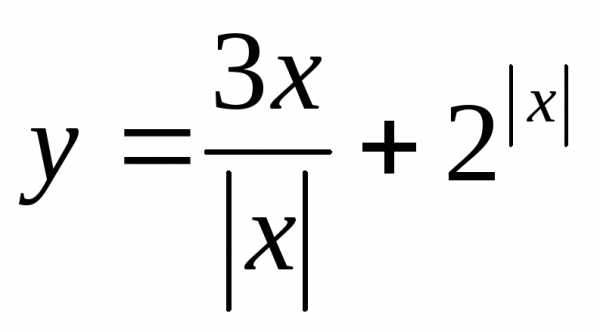 ,
если
,
если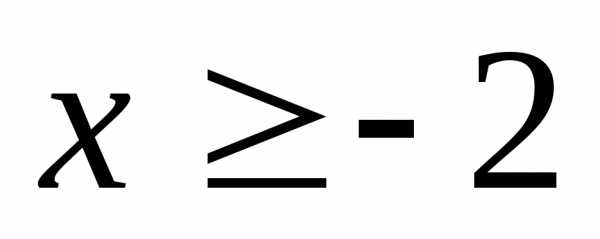 ; 22.
; 22.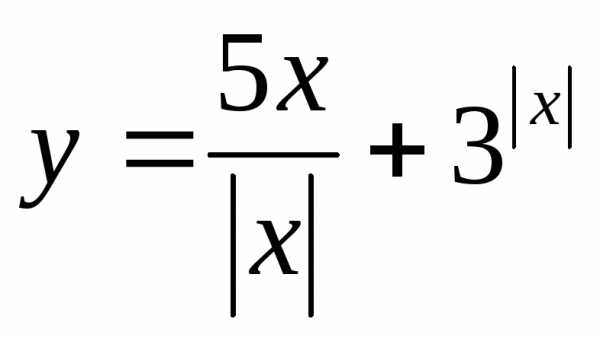
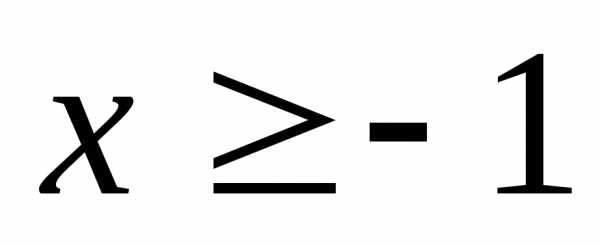 .
.Тема №6. Иррациональные уравнения.
1º. Иррациональнымназывают уравнение, в котором переменная содержится под знаком корня.
При решении иррациональных уравнений применяют 2 метода: метод возведения в степень обеих частей уравнения и метод введения новой переменной (замены переменной).
2º. Метод возведения обеих частей уравнения в одну и ту же степеньсостоит в следующем:
а) преобразуют заданное иррациональное уравнение к виду ;
б) возводят обе части полученного уравнения в n-ую степень:;
в) учитывая, что 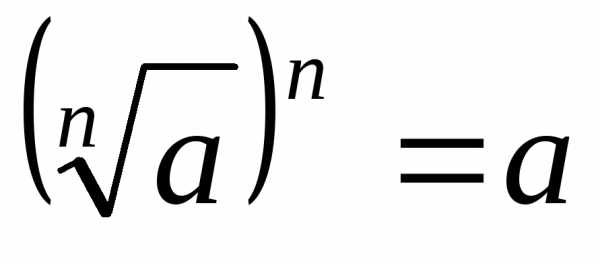 ,
получают уравнениеи решают его.
,
получают уравнениеи решают его.
3º. Следует учитывать, что при возведении обеих частей уравнения в четную степень возможно появление посторонних корней. В этом случае обязательна
Пример 16. Решить уравнение .
Решение: Преобразуем уравнение к виду и возведем обе части его в квадрат. Получим:
Еще раз возведем обе части уравнения в квадрат:
Откуда получим:
Проверка: 1) При x=5имеем:. Таким образом,x=5является корнем заданного уравнения.
2) . Таким образом,x=197– посторонний корень.
Ответ: 5.
4º. Метод замены переменнойпродемонстрируем на примере.
Пример 17. Решить уравнение .
Решение: Область определения уравнения:
Пусть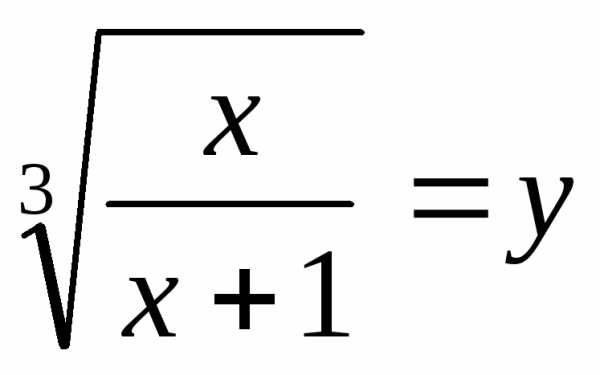
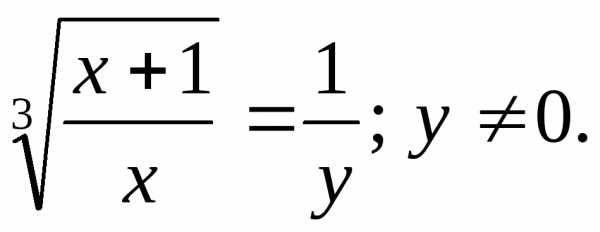 ПоэтомуОтсюда:
ПоэтомуОтсюда:1) Получили неверное числовое равенство, значит, в этом случае нет корней.
2)
Ответ: -8/7.
Дидактический материал.
Решите уравнения:
1. ; 2.;
3. ; 4.;
5. ; 6.;
7. ; 8.;
9. ; 10..
Найдите наименьший корень уравнения:
11. ; 12.;
13. .
Найдите произведение всех корней уравнения:
14. ; 15..
Решите уравнения:
16. ; 17.;
18. 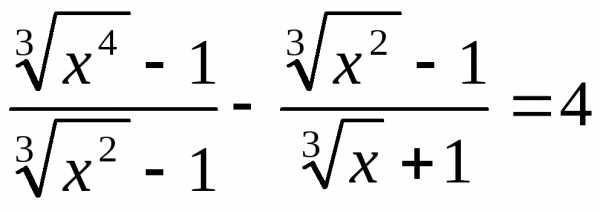 .
.
Тема №7. Показательные уравнения.
7.1. Методы решения показательных уравнений.
1º. Показательными уравнениями называют уравнения, содержащие переменную в показателе степени.
Решение показательных уравнений основано на свойстве степени: две степени с одним и тем же основание равны тогда и только тогда, когда равны их показатели.
2º. Основные способы решения показательных уравнений
1) простейшее уравнение
имеет решение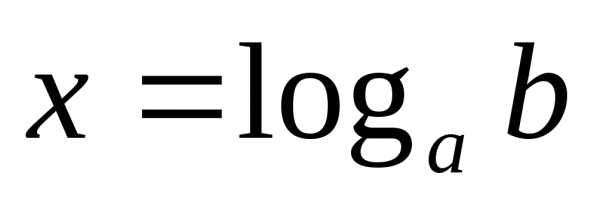 ;
;
2) уравнение вида логарифмированием по основаниюa сводят к виду;
3) уравнение вида равносильно уравнению;
4) уравнение вида
равносильно уравнению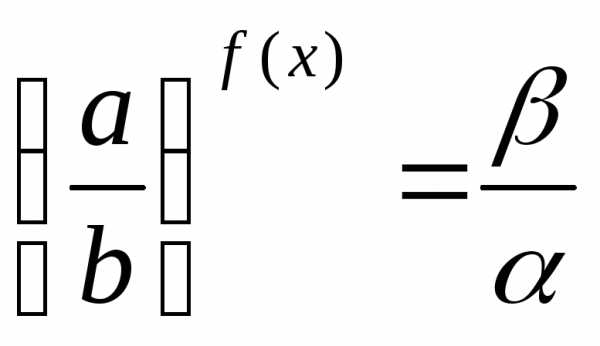 .
.
5) уравнение вида 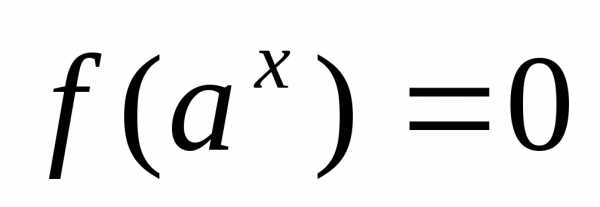 через замену
через замену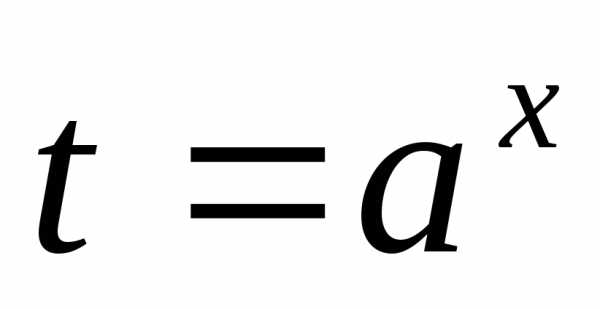 сводят к уравнению
сводят к уравнению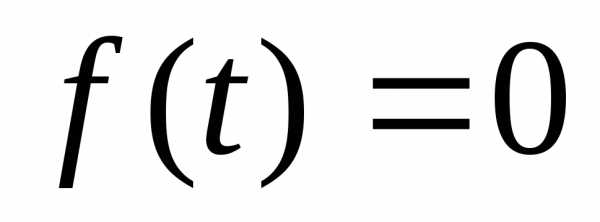 ,
а затем решают совокупность простейших
показательных уравнений
,
а затем решают совокупность простейших
показательных уравнений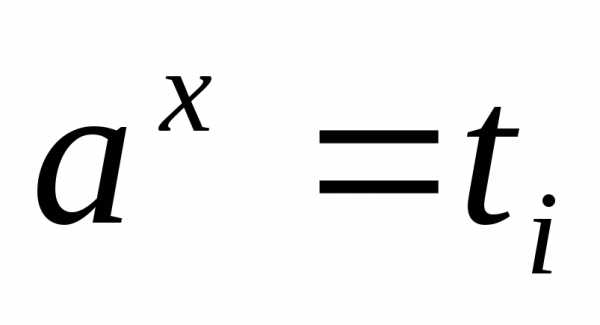 ;
;
6) уравнение со взаимно обратными
величинами
заменой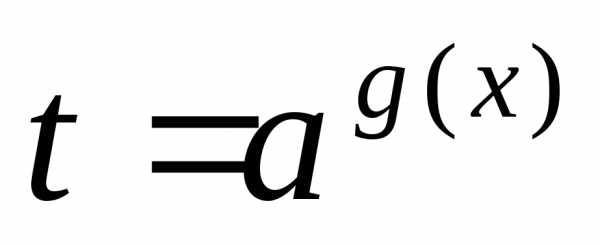
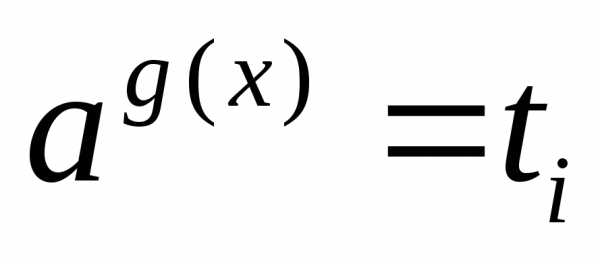 ;
; 7) уравнения, однородные относительно ag(x)иbg(x)при условиивидачерез замену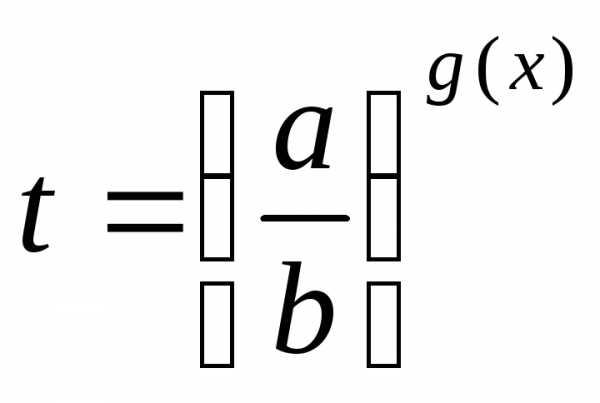 сводят к уравнению,
а затем решают совокупность уравнений
сводят к уравнению,
а затем решают совокупность уравнений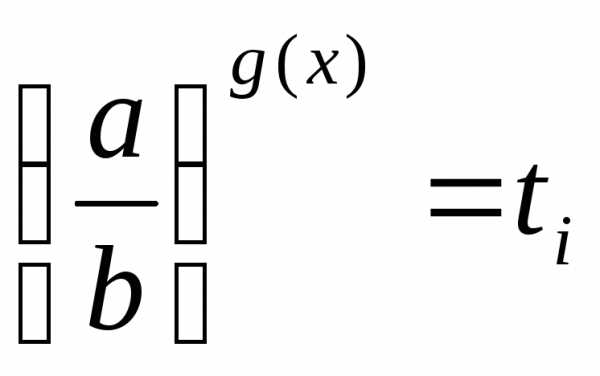 .
.
studfiles.net
5.2. Множество значений функции.
1º. Множеством (областью) значений
2º. Областью значений всякого многочлена
четной степени является промежуток 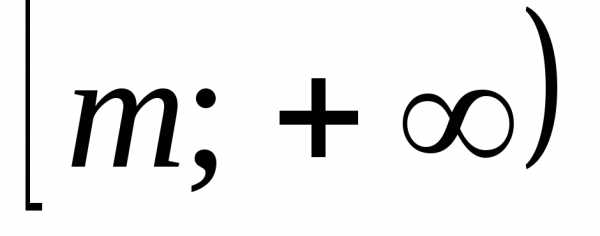 ,
гдеm– наименьшее
значение этого многочлена, либо промежуток
,
гдеm– наименьшее
значение этого многочлена, либо промежуток ,
гдеn– наибольшее
значение этого многочлена.
,
гдеn– наибольшее
значение этого многочлена.
Областью значений всякого многочлена нечетной степени является R.
3º. Области значений основных элементарных функций:
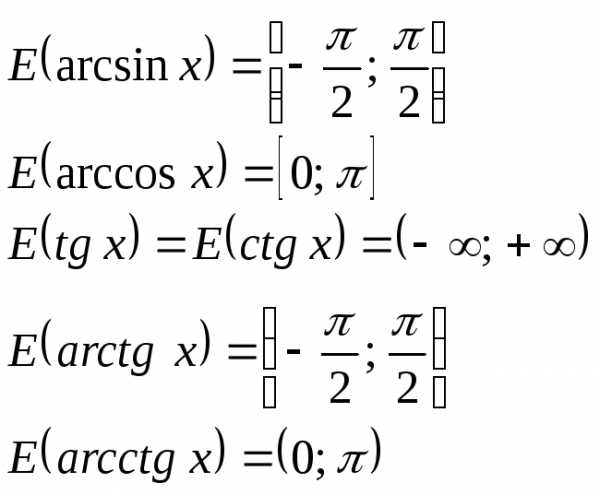
Пример 15. Найти множество значений
функции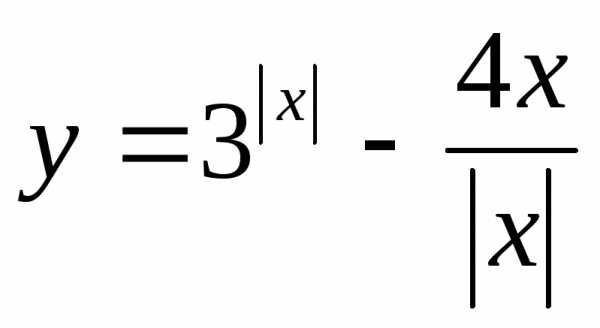
Решение: Данная функция не определена при x=0и, следовательно, задана на множестве.
Рассмотрим x<0,
тогда|x|=-xи функция принимает вид.
Так какдляx<0, то.
Таким образом, на промежутке функция принимает значения от 5 до +∞.
функция принимает значения от 5 до +∞.
Если x>0, то|x|=xи функция имеет вид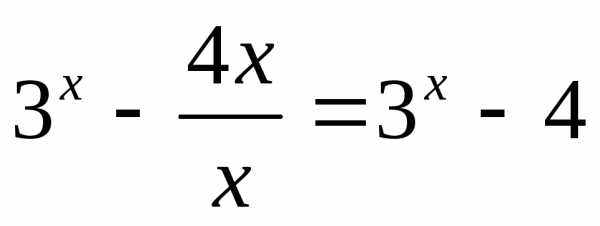 .
Так какдля
.
Так какдля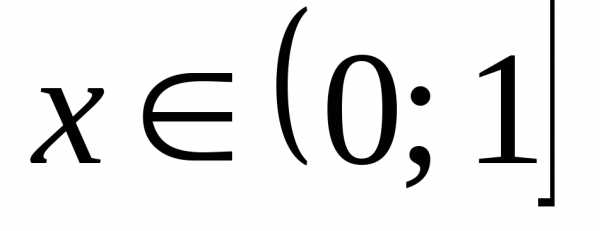 ,
то.
,
то.
Ответ: .
Дидактический материал.
Решите неравенства:
1. 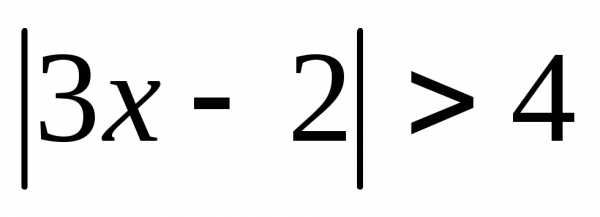 ; 2.
; 2.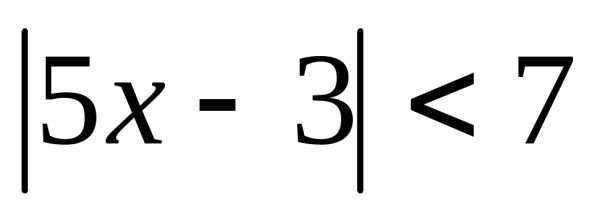
4. ; 5.; 6.;
7. ; 8.; 9.;
10. 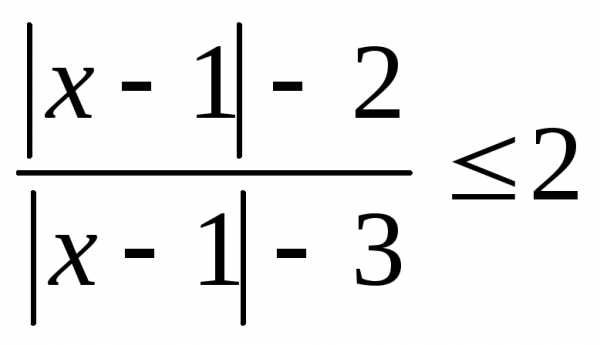 ; 11.
; 11.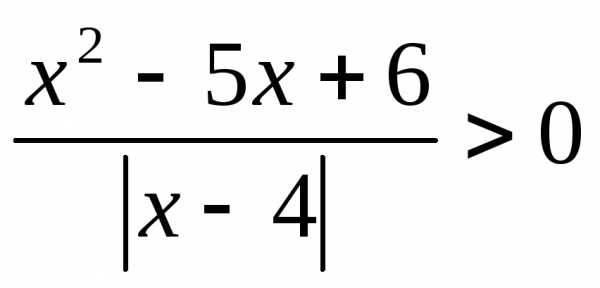 ; 12.
; 12.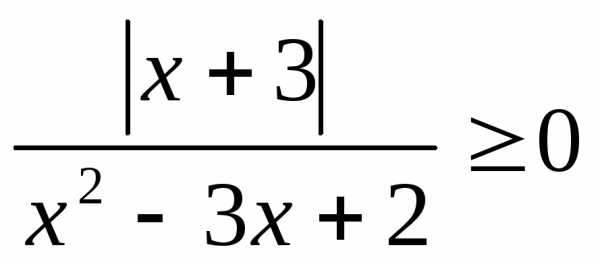 ;
;
13. ; 14.;
15. ; 16.;
17. ; 18..
19. При каких xточки
графика функции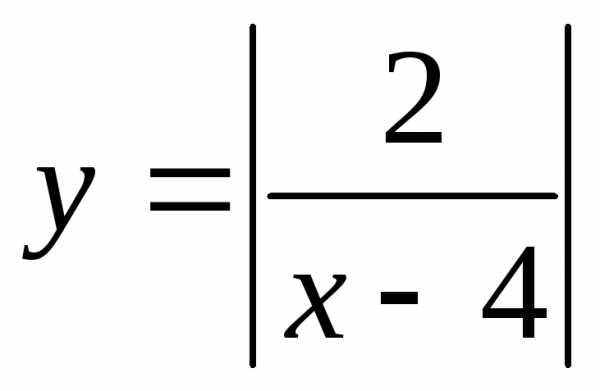 лежат
выше прямой
лежат
выше прямой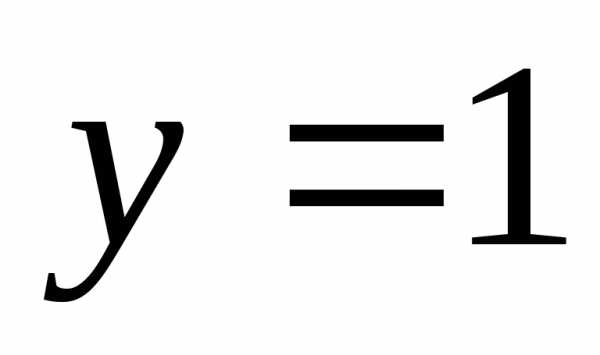 ?
?
20. При каких xточки
графика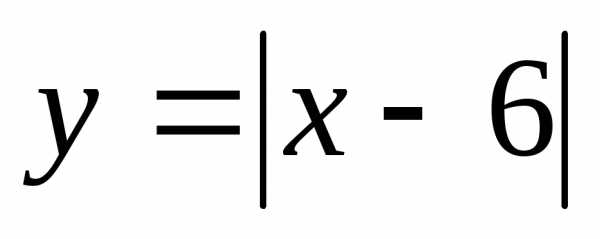 лежат не ниже точек графика функции?
лежат не ниже точек графика функции?
Найти множество значений функции:
21. 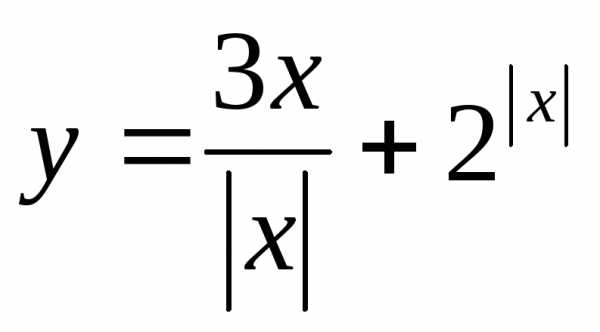 ,
если
,
если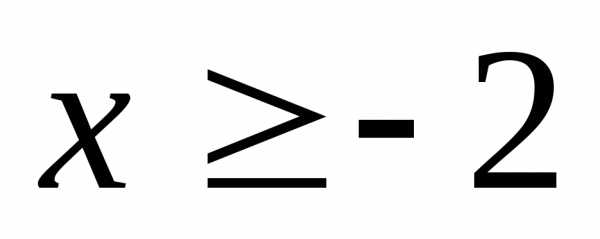 ; 22.
; 22.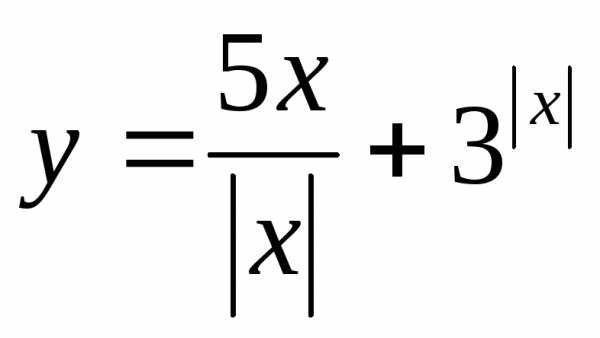 ,
если
,
если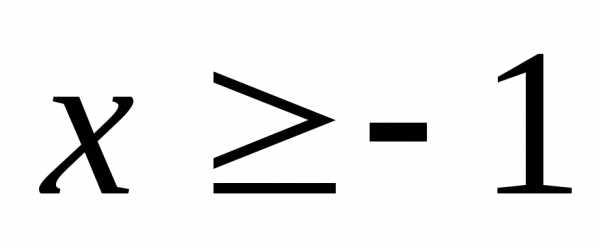 .
.
Тема №6. Иррациональные уравнения.
1º. Иррациональнымназывают уравнение, в котором переменная содержится под знаком корня.
При решении иррациональных уравнений применяют 2 метода: метод возведения в степень обеих частей уравнения и метод введения новой переменной (замены переменной).
2º. Метод возведения обеих частей уравнения в одну и ту же степеньсостоит в следующем:
а) преобразуют заданное иррациональное уравнение к виду ;
б) возводят обе части полученного уравнения в n-ую степень:;
в) учитывая, что 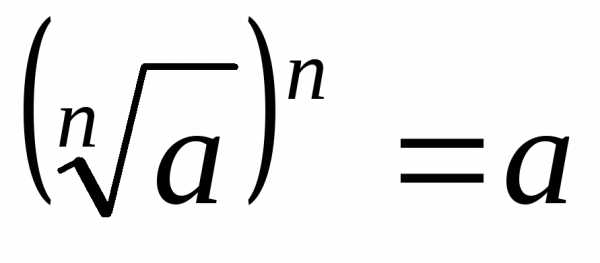 ,
получают уравнениеи решают его.
,
получают уравнениеи решают его.
3º. Следует учитывать, что при возведении обеих частей уравнения в четную степень возможно появление посторонних корней. В этом случае обязательна проверка найденных корнейпутем их подстановки в исходное уравнение.
Пример 16. Решить уравнение .
Решение: Преобразуем уравнение к виду и возведем обе части его в квадрат. Получим:
Еще раз возведем обе части уравнения в квадрат:
Откуда получим:
Проверка: 1) При x=5имеем:. Таким образом,x=5является корнем заданного уравнения.
2) . Таким образом,x=197– посторонний корень.
Ответ: 5.
4º. Метод замены переменнойпродемонстрируем на примере.
Пример 17. Решить уравнение .
Решение: Область определения уравнения:
Пусть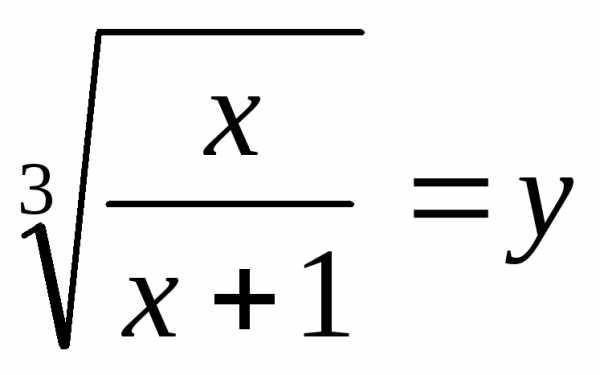 ,
тогда
,
тогда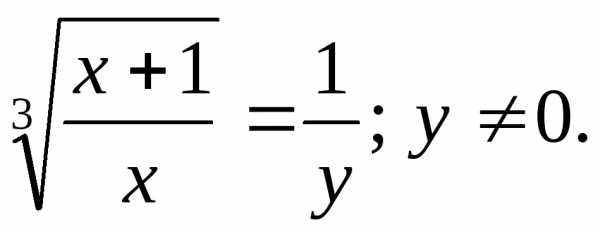 ПоэтомуОтсюда:
ПоэтомуОтсюда:
1) Получили неверное числовое равенство, значит, в этом случае нет корней.
2)
Ответ: -8/7.
Дидактический материал.
Решите уравнения:
1. ; 2.;
3. ; 4.;
5. ; 6.;
7. ; 8.;
9. ; 10..
Найдите наименьший корень уравнения:
11. ; 12.;
13. .
Найдите произведение всех корней уравнения:
14. ; 15..
Решите уравнения:
16. ; 17.;
18. 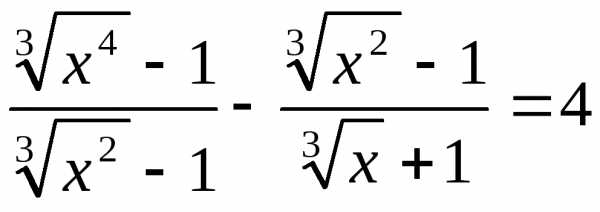 .
.
Тема №7. Показательные уравнения.
7.1. Методы решения показательных уравнений.
1º. Показательными уравнениями называют уравнения, содержащие переменную в показателе степени.
Решение показательных уравнений основано на свойстве степени: две степени с одним и тем же основание равны тогда и только тогда, когда равны их показатели.
2º. Основные способы решения показательных уравнений:
1) простейшее уравнение
имеет решение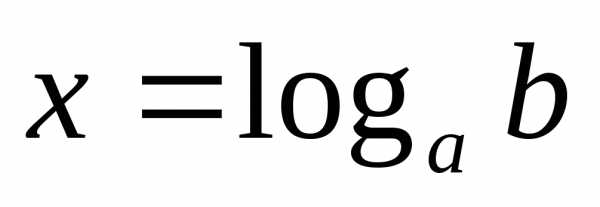 ;
;
2) уравнение вида логарифмированием по основаниюa сводят к виду;
3) уравнение вида равносильно уравнению;
4) уравнение вида
равносильно уравнению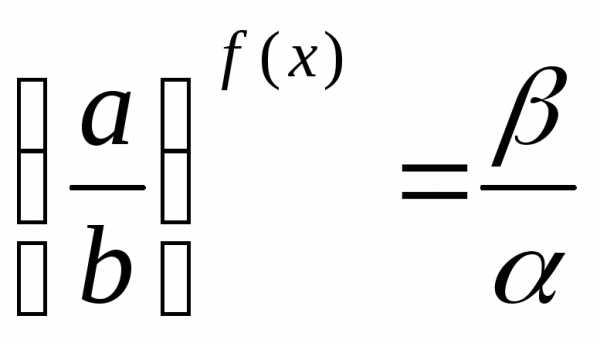 .
.
5) уравнение вида 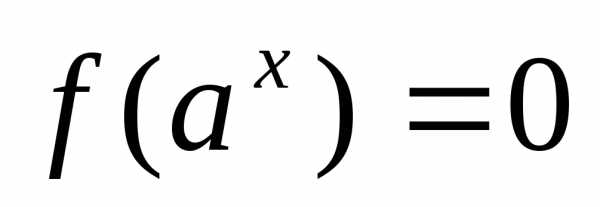 через замену
через замену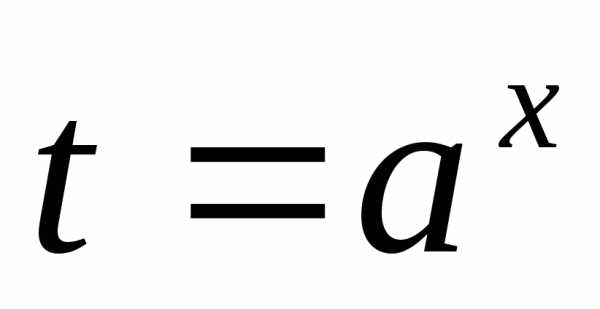 сводят к уравнению
сводят к уравнению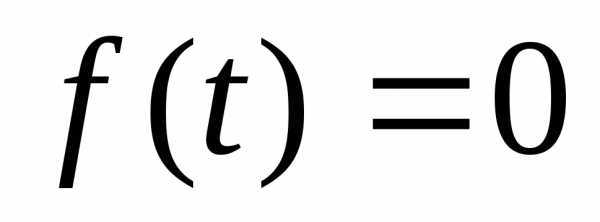 ,
а затем решают совокупность простейших
показательных уравнений
,
а затем решают совокупность простейших
показательных уравнений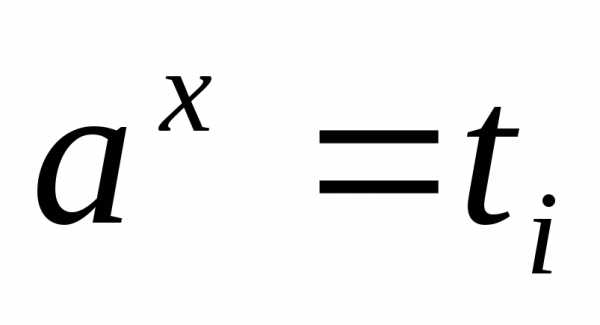 ;
;
6) уравнение со взаимно обратными
величинами
заменой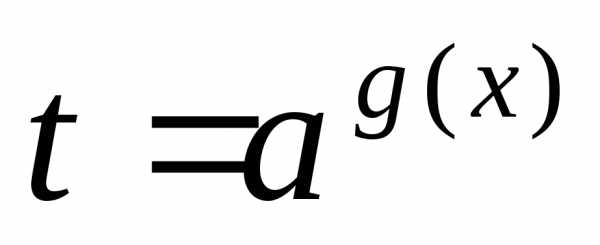 сводят к уравнению,
а затем решают совокупность уравнений
сводят к уравнению,
а затем решают совокупность уравнений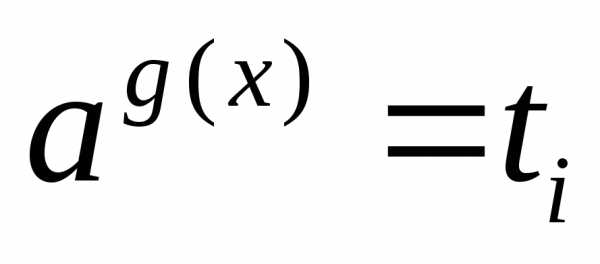 ;
;
7) уравнения, однородные относительно ag(x)иbg(x)при условиивидачерез замену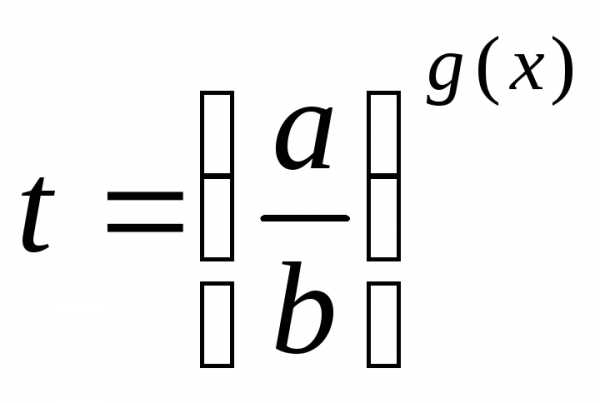 сводят к уравнению,
а затем решают совокупность уравнений
сводят к уравнению,
а затем решают совокупность уравнений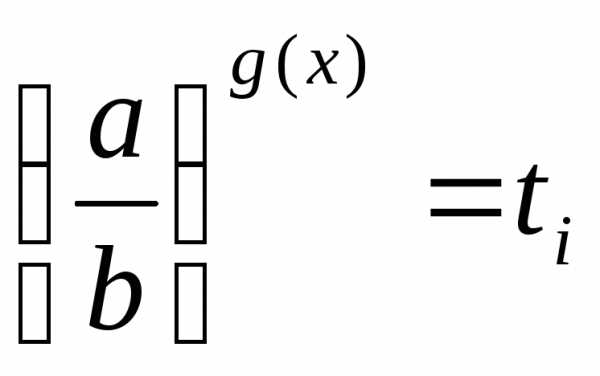 .
.
studfiles.net
5.2. Множество значений функции.
1º. Множеством (областью) значений E(y)функцииy=f(x)называется множество всех таких чиселy0, для каждого из которых найдется числоx0такое, чтоf(x0)=y0.
2º. Областью значений всякого многочлена
четной степени является промежуток 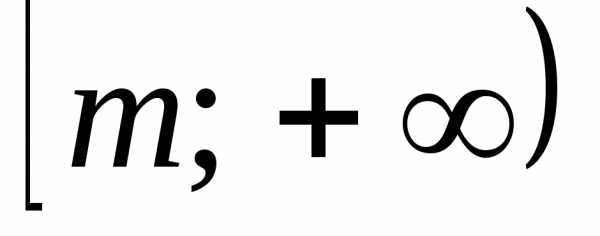 ,
гдеm– наименьшее
значение этого многочлена, либо промежуток
,
гдеm– наименьшее
значение этого многочлена, либо промежуток ,
гдеn– наибольшее
значение этого многочлена.
,
гдеn– наибольшее
значение этого многочлена.
Областью значений всякого многочлена нечетной степени является R.
3º. Области значений основных элементарных функций:
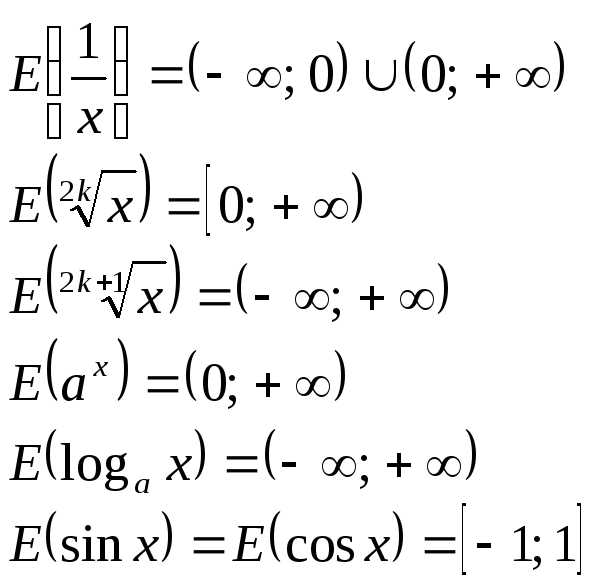
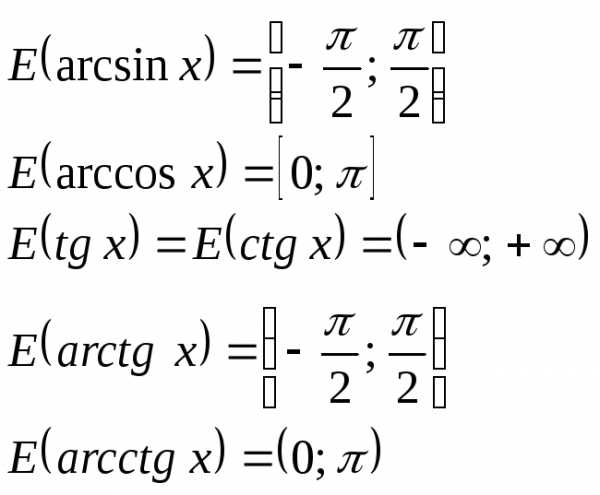
Пример 15. Найти множество значений
функции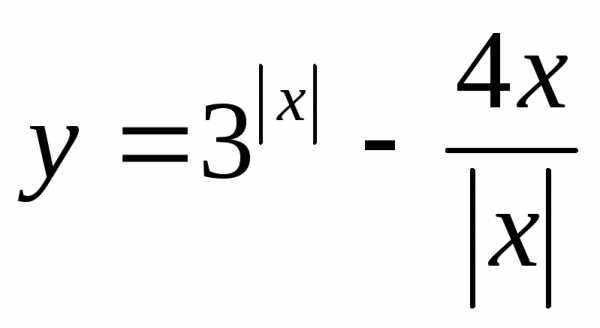 ,
еслиx≤1.
,
еслиx≤1.
Решение: Данная функция не определена при x=0и, следовательно, задана на множестве.
Рассмотрим x<0,
тогда|x|=-xи функция принимает вид.
Так какдляx<0, то.
Таким образом, на промежутке функция принимает значения от 5 до +∞.
функция принимает значения от 5 до +∞.
Если x>0, то|x|=xи функция имеет вид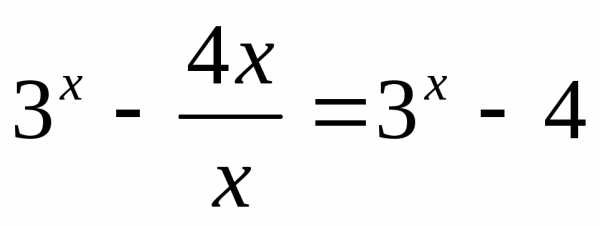 .
Так какдля
.
Так какдля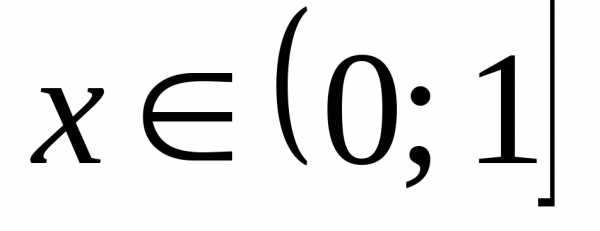 ,
то.
,
то.
Ответ: .
Дидактический материал.
Решите неравенства:
1. 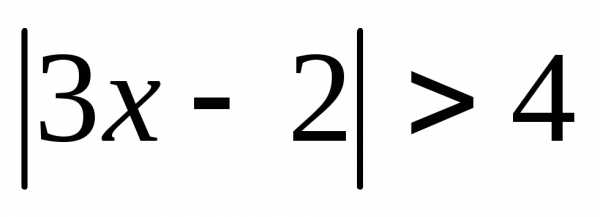 ; 2.
; 2.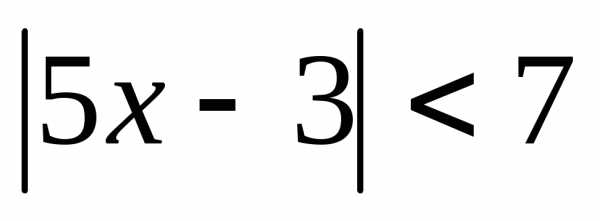 ; 3.;
; 3.;
4. ; 5.; 6.;
7. ; 8.; 9.;
10. 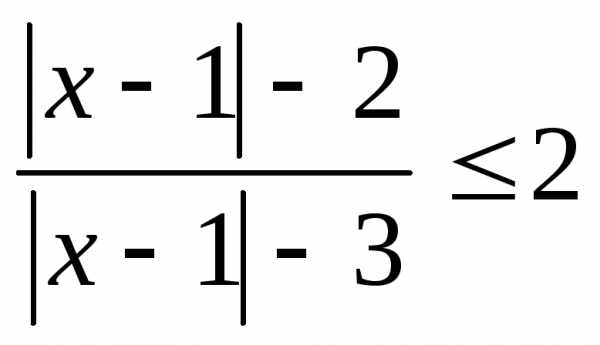 ; 11.
; 11.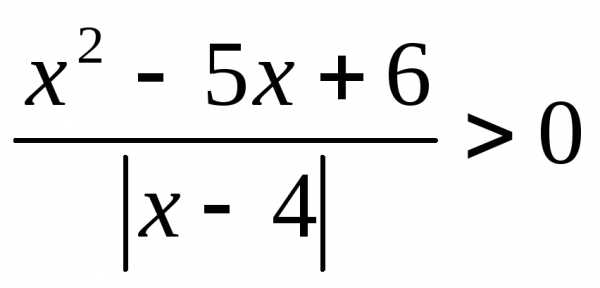 ; 12.
; 12.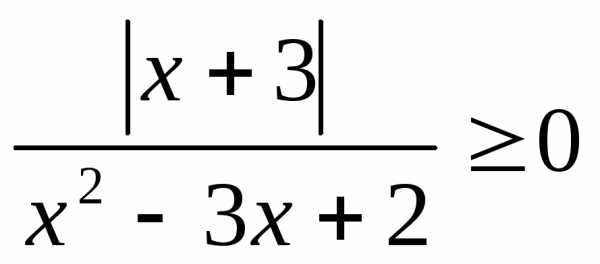 ;
;
13. ; 14.;
15. ; 16.;
17. ; 18..
19. При каких xточки
графика функции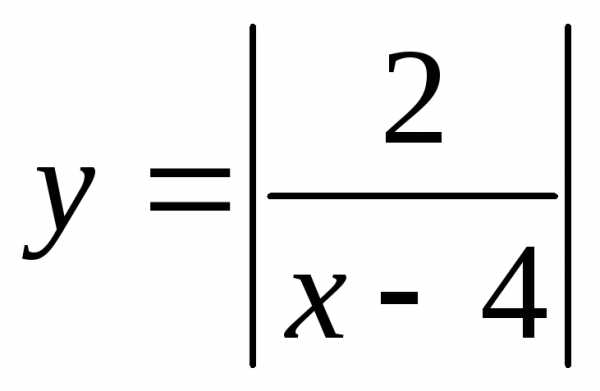 лежат
выше прямой
лежат
выше прямой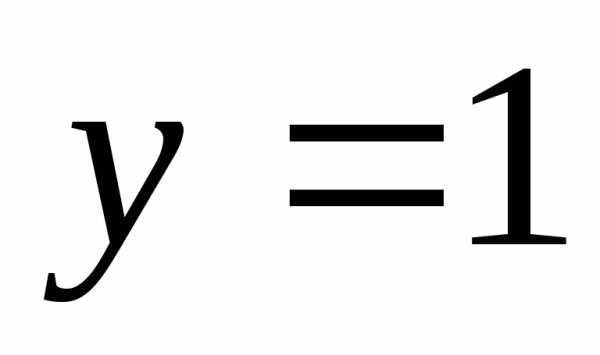 ?
?
20. При каких xточки
графика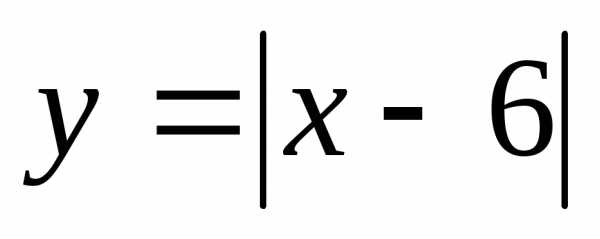 лежат не ниже точек графика функции?
лежат не ниже точек графика функции?
Найти множество значений функции:
21. 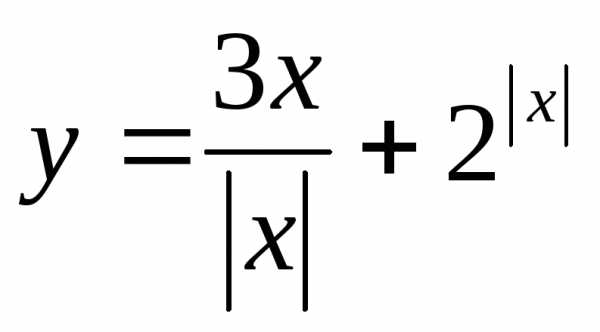 ,
если
,
если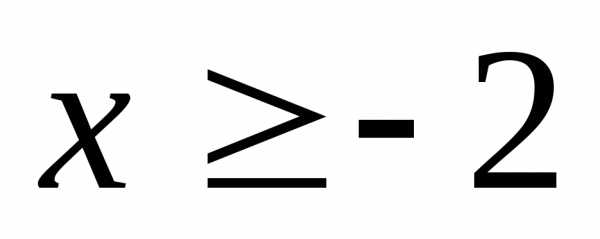 ; 22.
; 22.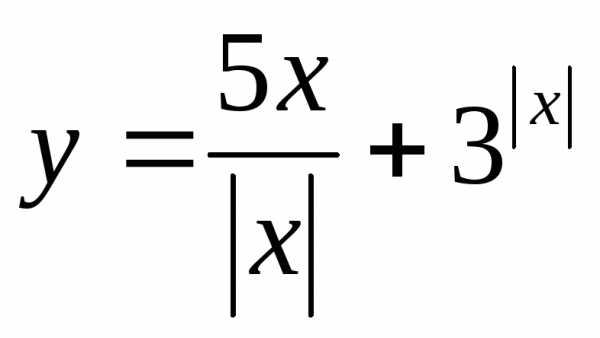 ,
если
,
если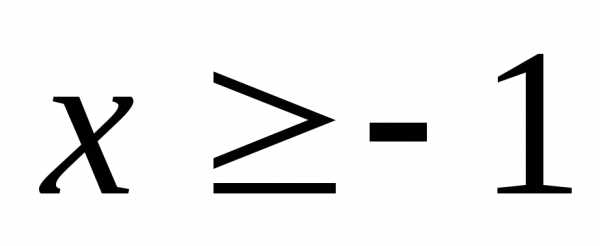 .
.
Тема №6. Иррациональные уравнения.
1º. Иррациональнымназывают уравнение, в котором переменная содержится под знаком корня.
При решении иррациональных уравнений применяют 2 метода: метод возведения в степень обеих частей уравнения и метод введения новой переменной (замены переменной).
2º. Метод возведения обеих частей уравнения в одну и ту же степеньсостоит в следующем:
а) преобразуют заданное иррациональное уравнение к виду ;
б) возводят обе части полученного уравнения в n-ую степень:;
в) учитывая, что 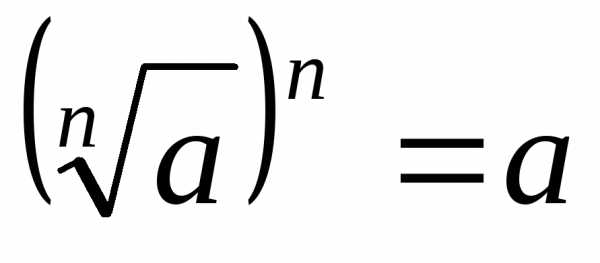 ,
получают уравнениеи решают его.
,
получают уравнениеи решают его.
3º. Следует учитывать, что при возведении обеих частей уравнения в четную степень возможно появление посторонних корней. В этом случае обязательна проверка найденных корнейпутем их подстановки в исходное уравнение.
Пример 16. Решить уравнение .
Решение: Преобразуем уравнение к виду и возведем обе части его в квадрат. Получим:
Еще раз возведем обе части уравнения в квадрат:
Откуда получим:
Проверка: 1) При x=5имеем:. Таким образом,x=5является корнем заданного уравнения.
2) . Таким образом,x=197– посторонний корень.
Ответ: 5.
4º. Метод замены переменнойпродемонстрируем на примере.
Пример 17. Решить уравнение .
Решение: Область определения уравнения:
Пусть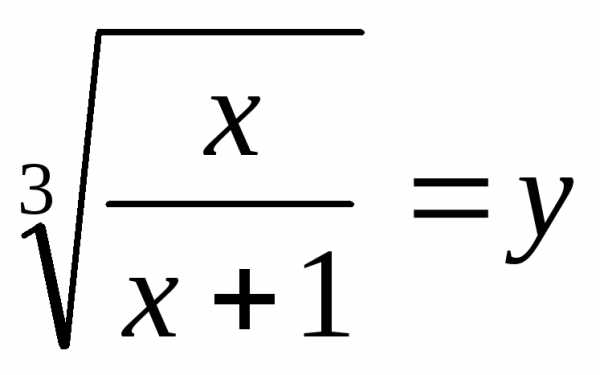 ,
тогда
,
тогда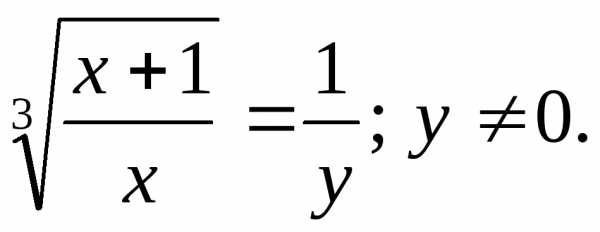 ПоэтомуОтсюда:
ПоэтомуОтсюда:
1) Получили неверное числовое равенство, значит, в этом случае нет корней.
2)
Ответ: -8/7.
Дидактический материал.
Решите уравнения:
1. ; 2.;
3. ; 4.;
5. ; 6.;
7. ; 8.;
9. ; 10..
Найдите наименьший корень уравнения:
11. ; 12.;
13. .
Найдите произведение всех корней уравнения:
14. ; 15..
Решите уравнения:
16. ; 17.;
18. 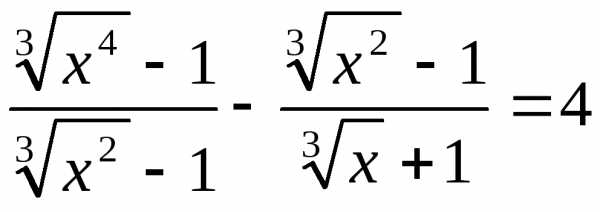 .
.
Тема №7. Показательные уравнения.
7.1. Методы решения показательных уравнений.
1º. Показательными уравнениями называют уравнения, содержащие переменную в показателе степени.
Решение показательных уравнений основано на свойстве степени: две степени с одним и тем же основание равны тогда и только тогда, когда равны их показатели.
2º. Основные способы решения показательных уравнений:
1) простейшее уравнение
имеет решение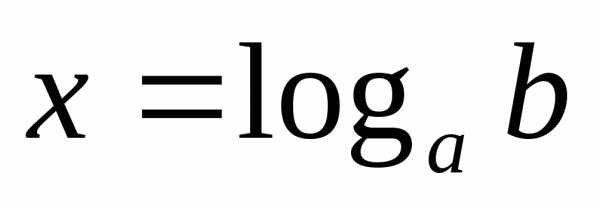 ;
;
2) уравнение вида логарифмированием по основаниюa сводят к виду;
3) уравнение вида равносильно уравнению;
4) уравнение вида
равносильно уравнению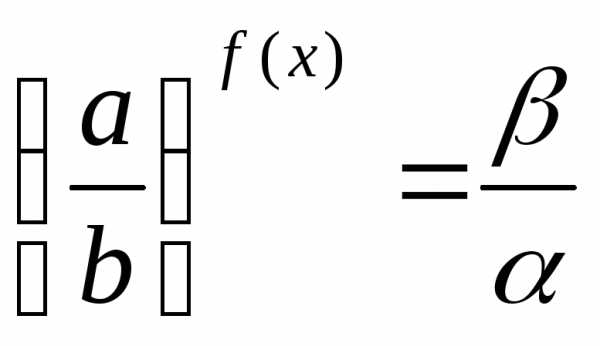 .
.
5) уравнение вида 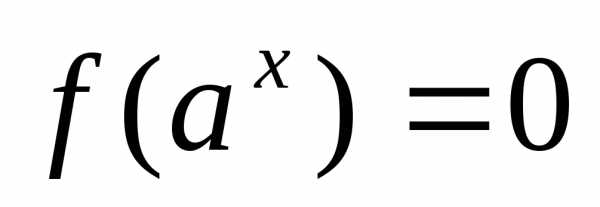 через замену
через замену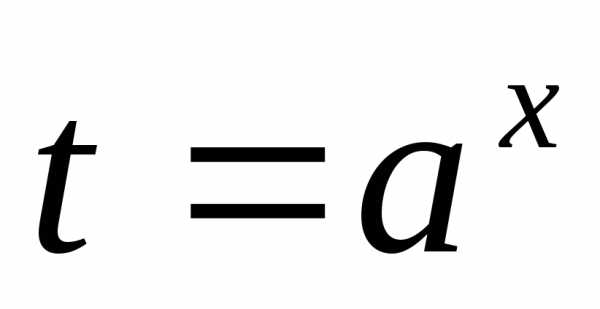 сводят к уравнению
сводят к уравнению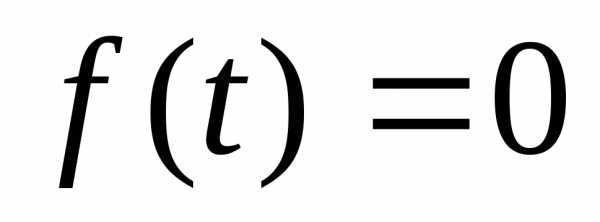 ,
а затем решают совокупность простейших
показательных уравнений
,
а затем решают совокупность простейших
показательных уравнений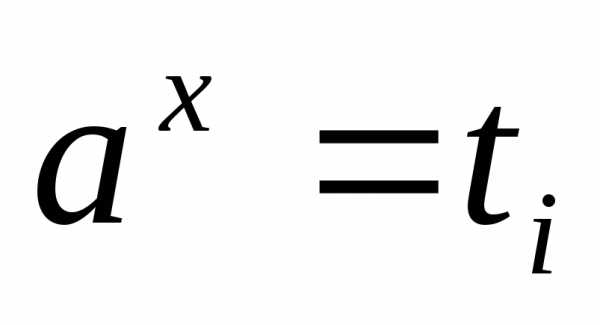 ;
;
6) уравнение со взаимно обратными
величинами
заменой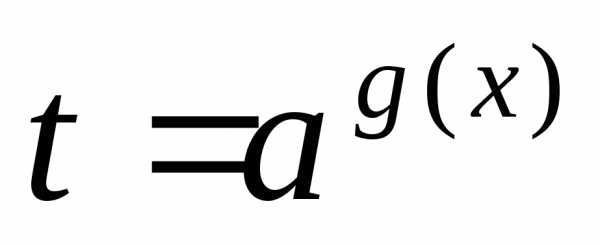 сводят к уравнению,
а затем решают совокупность уравнений
сводят к уравнению,
а затем решают совокупность уравнений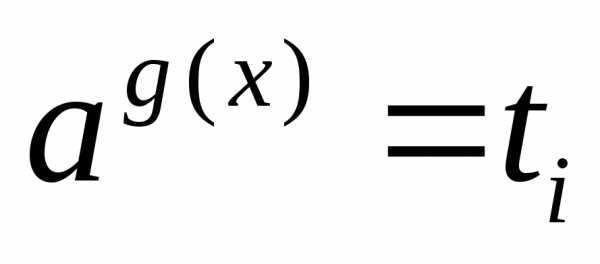 ;
;
7) уравнения, однородные относительно ag(x)иbg(x)при условиивидачерез замену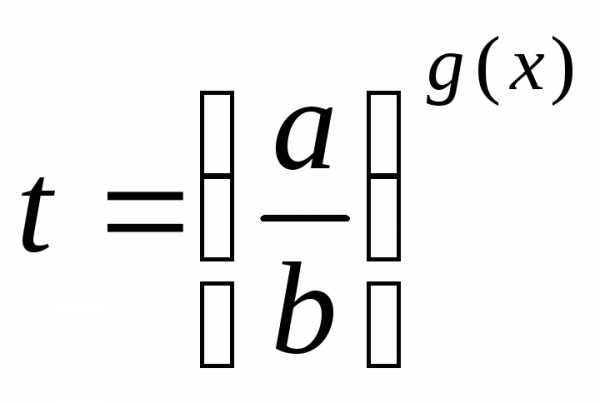 сводят к уравнению,
а затем решают совокупность уравнений
сводят к уравнению,
а затем решают совокупность уравнений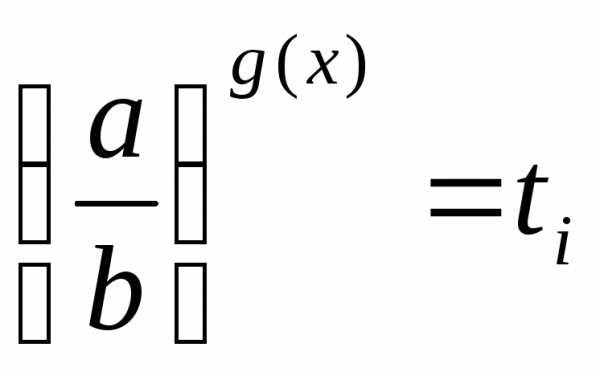 .
.
studfiles.net
5.2. Множество значений функции.
1º. Множеством (областью) значений E(y)функцииy=f(x)называется множество всех таких чиселy0, для каждого из которых найдется числоx0такое, чтоf(x0)=y0.
2º. Областью значений всякого многочлена
четной степени является промежуток 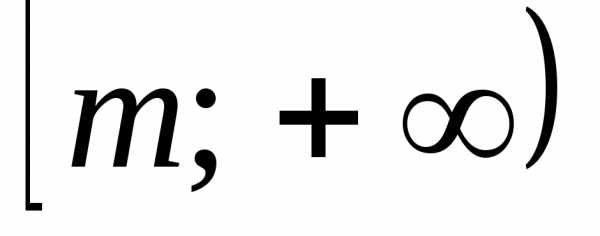 ,
гдеm– наименьшее
значение этого многочлена, либо промежуток
,
гдеm– наименьшее
значение этого многочлена, либо промежуток ,
гдеn– наибольшее
значение этого многочлена.
,
гдеn– наибольшее
значение этого многочлена.
Областью значений всякого многочлена нечетной степени является R.
3º. Области значений основных элементарных функций:
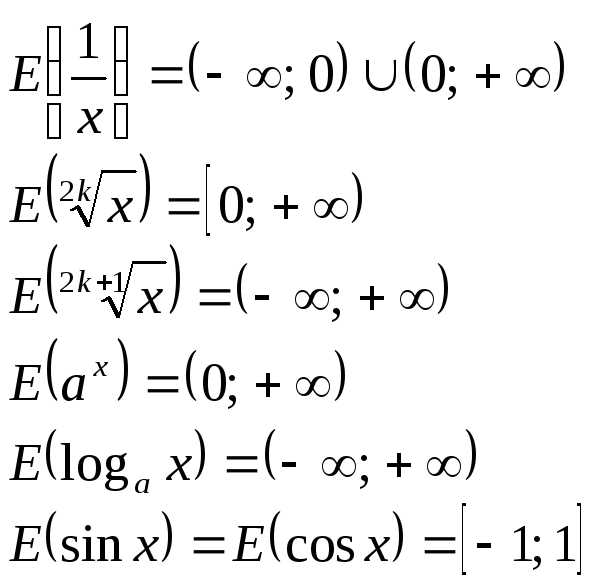
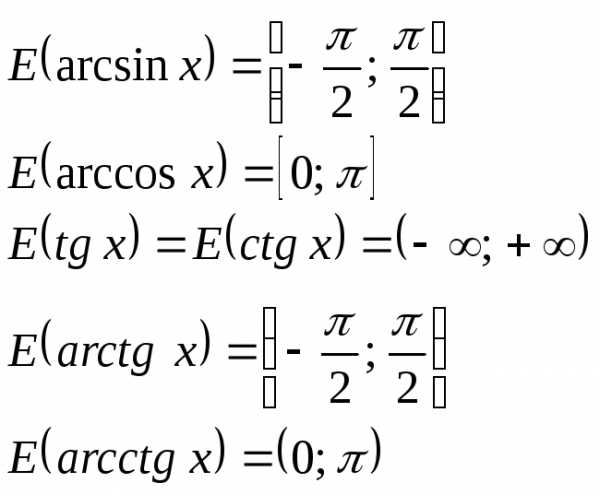
Пример 15. Найти множество значений
функции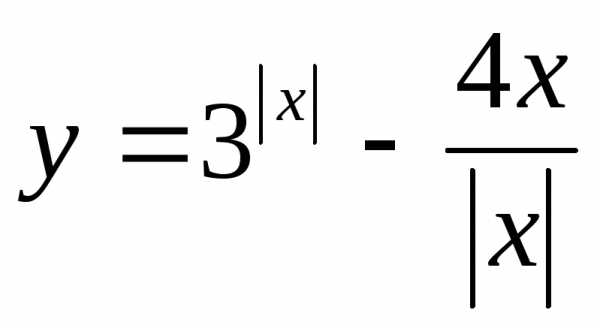 ,
еслиx≤1.
,
еслиx≤1.
Решение: Данная функция не определена при x=0и, следовательно, задана на множестве.
Рассмотрим x<0,
тогда|x|=-xи функция принимает вид.
Так какдляx<0, то.
Таким образом, на промежутке функция принимает значения от 5 до +∞.
функция принимает значения от 5 до +∞.
Если x>0, то|x|=xи функция имеет вид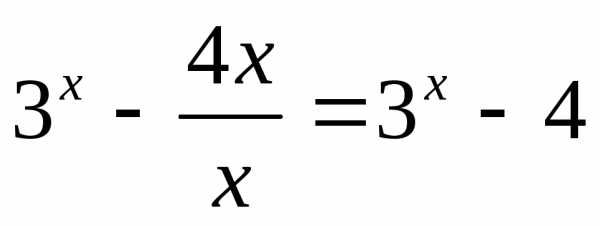 .
Так какдля
.
Так какдля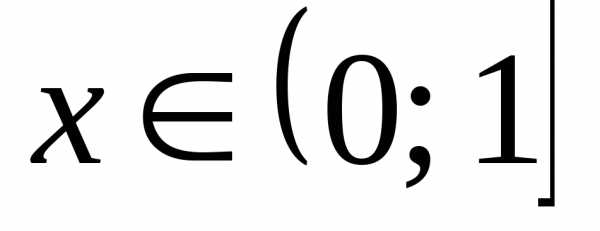 ,
то.
,
то.
Ответ: .
Дидактический материал.
Решите неравенства:
1. 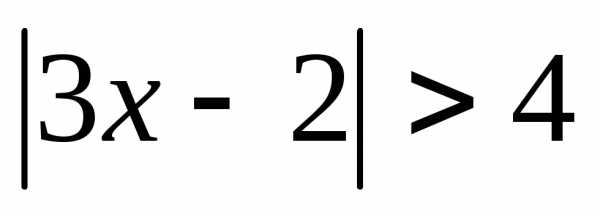 ; 2.
; 2.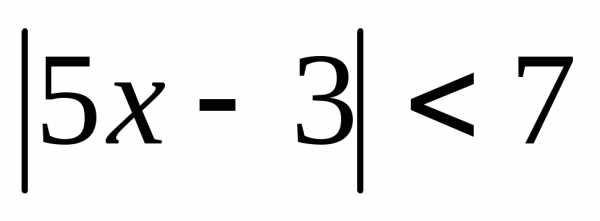 ; 3.;
; 3.;
4. ; 5.; 6.;
7. ; 8.; 9.;
10. 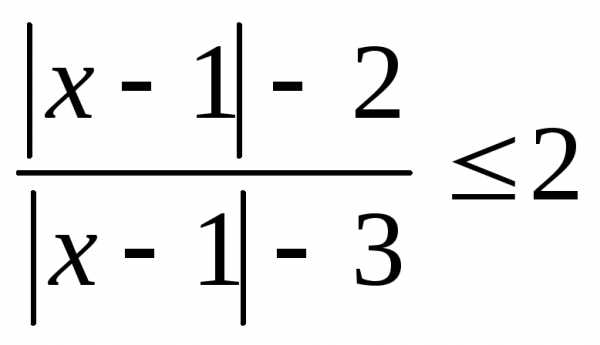 ; 11.
; 11.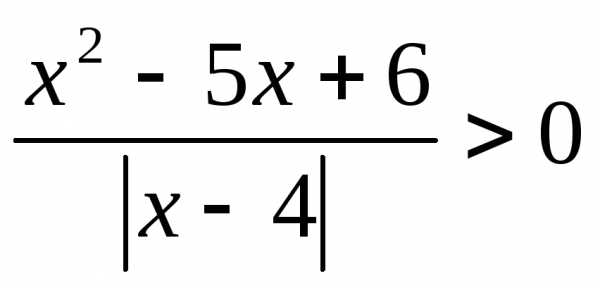 ; 12.
; 12.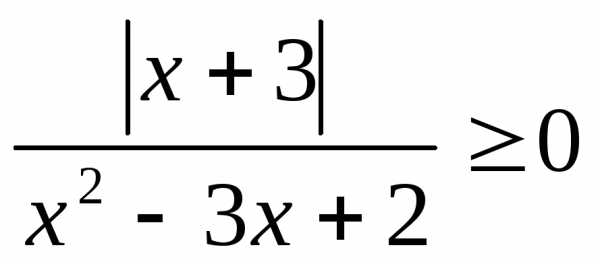 ;
;
13. ; 14.;
15. ; 16.;
17. ; 18..
19. При каких xточки
графика функции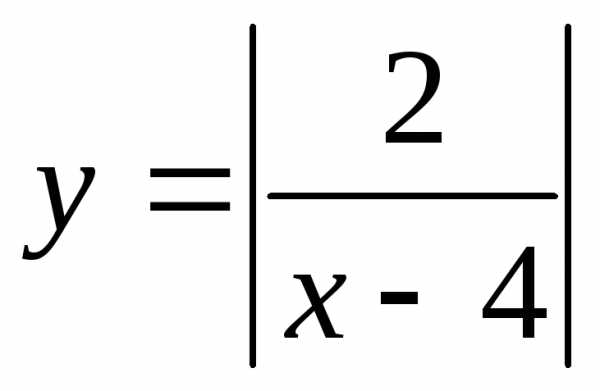 лежат
выше прямой
лежат
выше прямой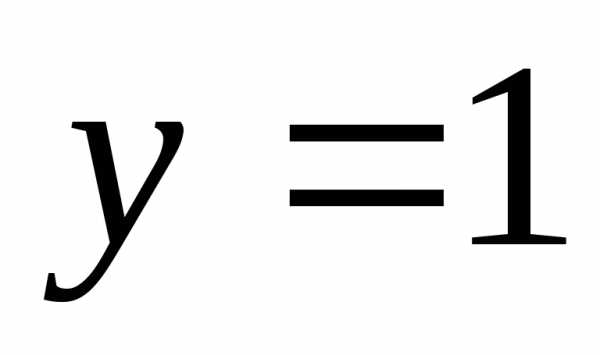 ?
?
20. При каких xточки
графика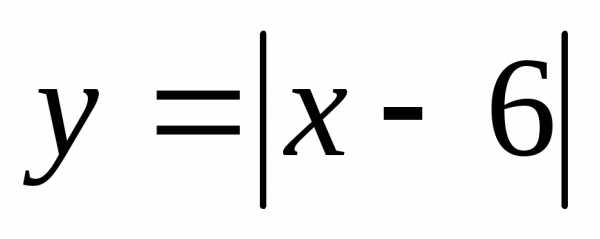 лежат не ниже точек графика функции?
лежат не ниже точек графика функции?
Найти множество значений функции:
21. 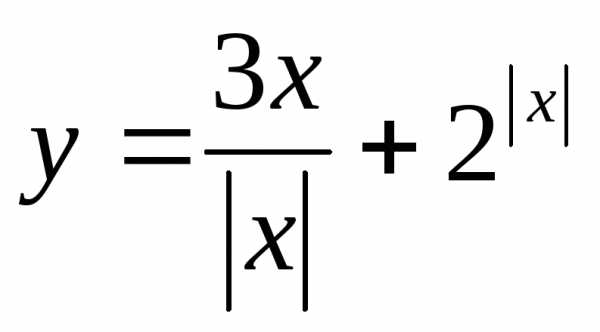 ,
если
,
если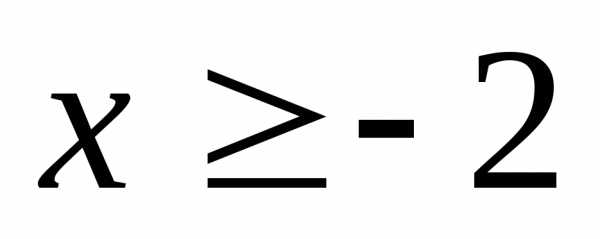 ; 22.
; 22.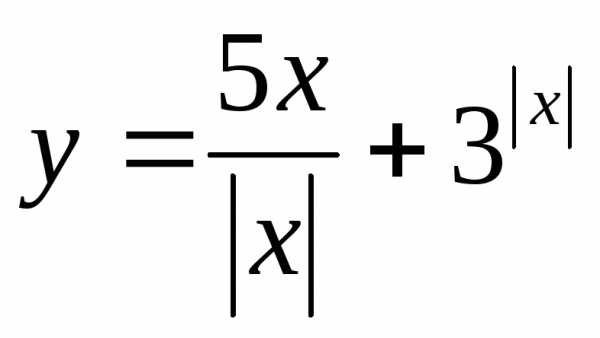 ,
если
,
если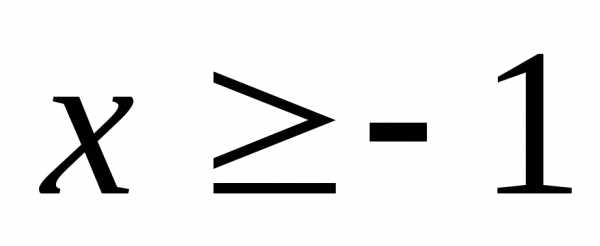 .
.
Тема №6. Иррациональные уравнения.
1º. Иррациональнымназывают уравнение, в котором переменная содержится под знаком корня.
При решении иррациональных уравнений применяют 2 метода: метод возведения в степень обеих частей уравнения и метод введения новой переменной (замены переменной).
2º. Метод возведения обеих частей уравнения в одну и ту же степеньсостоит в следующем:
а) преобразуют заданное иррациональное уравнение к виду ;
б) возводят обе части полученного уравнения в n-ую степень:;
в) учитывая, что 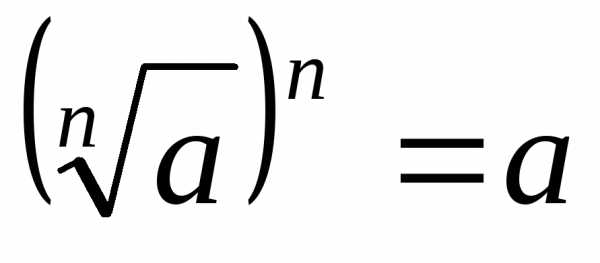 ,
получают уравнениеи решают его.
,
получают уравнениеи решают его.
3º. Следует учитывать, что при возведении обеих частей уравнения в четную степень возможно появление посторонних корней. В этом случае обязательна проверка найденных корнейпутем их подстановки в исходное уравнение.
Пример 16. Решить уравнение .
Решение: Преобразуем уравнение к виду и возведем обе части его в квадрат. Получим:
Еще раз возведем обе части уравнения в квадрат:
Откуда получим:
Проверка: 1) При x=5имеем:. Таким образом,x=5является корнем заданного уравнения.
2) . Таким образом,x=197– посторонний корень.
Ответ: 5.
4º. Метод замены переменнойпродемонстрируем на примере.
Пример 17. Решить уравнение .
Решение: Область определения уравнения:
Пусть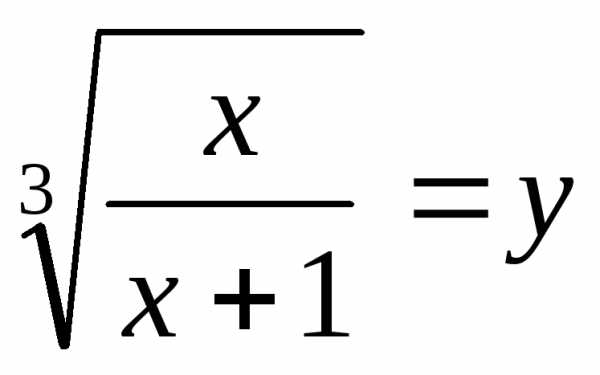 ,
тогда
,
тогда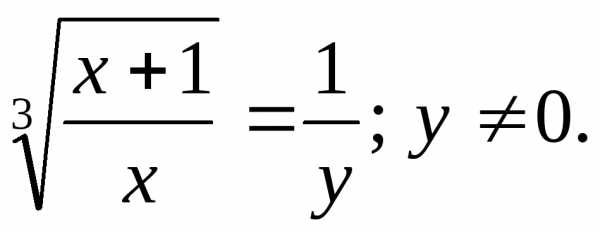 ПоэтомуОтсюда:
ПоэтомуОтсюда:
1) Получили неверное числовое равенство, значит, в этом случае нет корней.
2)
Ответ: -8/7.
Дидактический материал.
Решите уравнения:
1. ; 2.;
3. ; 4.;
5. ; 6.;
7. ; 8.;
9. ; 10..
Найдите наименьший корень уравнения:
11. ; 12.;
13. .
Найдите произведение всех корней уравнения:
14. ; 15..
Решите уравнения:
16. ; 17.;
18. 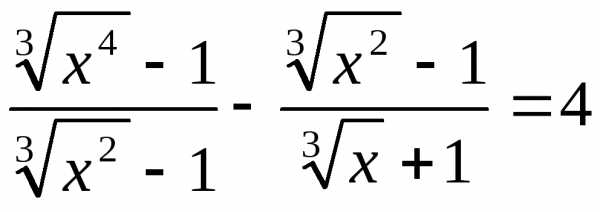 .
.
Тема №7. Показательные уравнения.
7.1. Методы решения показательных уравнений.
1º. Показательными уравнениями называют уравнения, содержащие переменную в показателе степени.
Решение показательных уравнений основано на свойстве степени: две степени с одним и тем же основание равны тогда и только тогда, когда равны их показатели.
2º. Основные способы решения показательных уравнений:
1) простейшее уравнение
имеет решение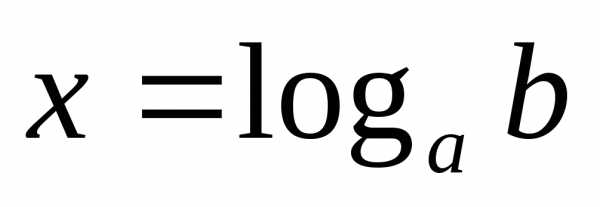 ;
;
2) уравнение вида логарифмированием по основаниюa сводят к виду;
3) уравнение вида равносильно уравнению;
4) уравнение вида
равносильно уравнению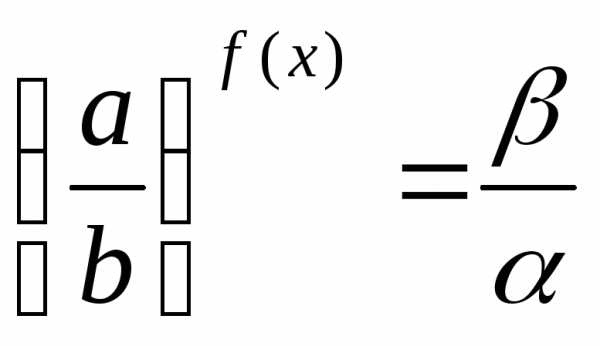 .
.
5) уравнение вида 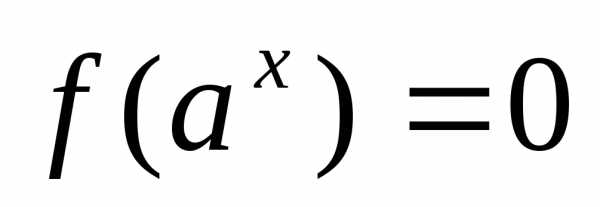 через замену
через замену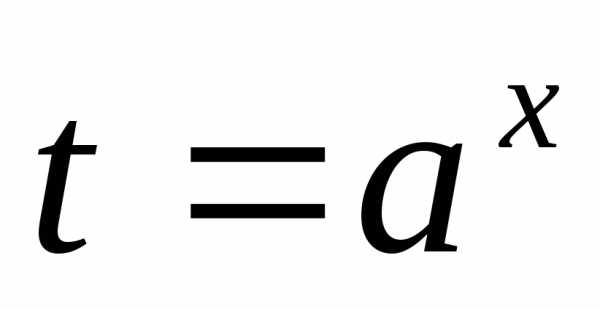 сводят к уравнению
сводят к уравнению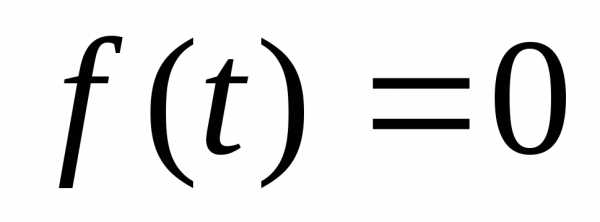 ,
а затем решают совокупность простейших
показательных уравнений
,
а затем решают совокупность простейших
показательных уравнений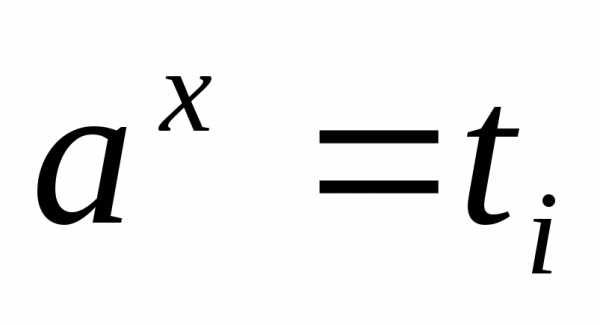 ;
;
6) уравнение со взаимно обратными
величинами
заменой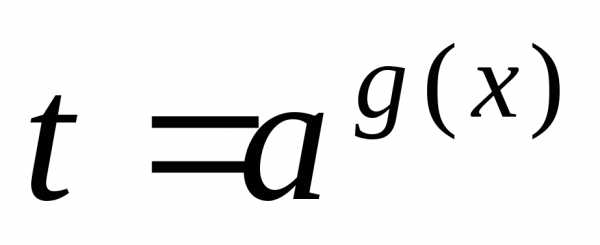 сводят к уравнению,
а затем решают совокупность уравнений
сводят к уравнению,
а затем решают совокупность уравнений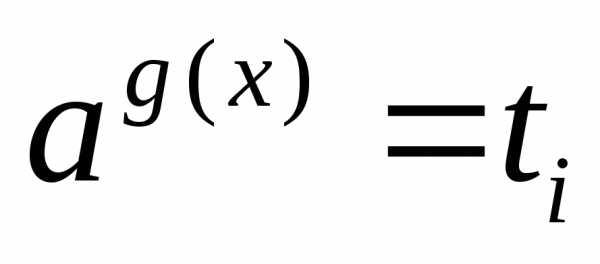 ;
;
7) уравнения, однородные относительно ag(x)иbg(x)при условиивидачерез замену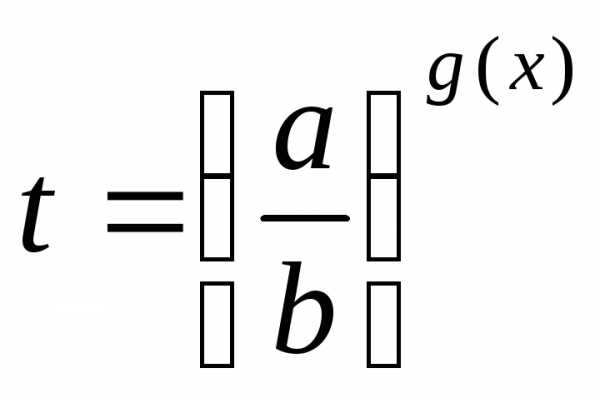 сводят к уравнению,
а затем решают совокупность уравнений
сводят к уравнению,
а затем решают совокупность уравнений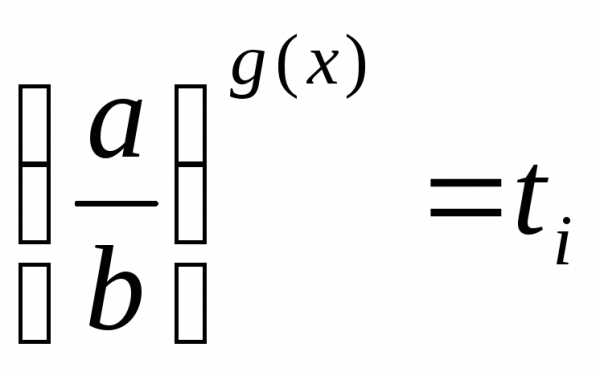 .
.
studfiles.net
| (Ф. Хаусдорф.) ‘ quotes[1]='»Математика — это язык, на котором написана книга природы.»(Г. Галилей) ‘ quotes[2]='»Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает настойчивость и упорство в достижении цели.»(А. Маркушевич) ‘ quotes[3]='»Рано или поздно всякая правильная математическая идея находит применение в том или ином деле.»(А.Н. Крылов) ‘ quotes[4]='»Если вы хотите участвовать в большой жизни, то наполняйте свою голову математикой. Она окажет вам потом огромную помощь во всей вашей работе.»(М.И. Калинин) ‘ quotes[5]='»Разве ты не заметил, что способный к математике изощрен во всех науках в природе?»(Платон) ‘ quotes[6]='»Математика есть лучшее и даже единственное введение в изучение природы.»(Д.И. Писарев) ‘ quotes[7]='»Вдохновение нужно в геометрии не меньше, чем в поэзии.»(А.С. Пушкин) ‘ quotes[8]='»Геометрия полна приключений, потому что за каждой задачей скрывается приключение мысли. Решить задачу – это значит пережить приключение.»(В. Произволов) ‘ quotes[9]='»В математике есть своя красота, как в живописи и поэзии.»(Н.Е. Жуковский) ‘ quotes[10]='»Химия – правая рука физики, математика – ее глаз.»(М.В. Ломоносов) ‘ quotes[11]='»Математику уже затем учить надо, что она ум в порядок приводит.»(М.В. Ломоносов) ‘ quotes[12]='»Математика — это язык, на котором говорят все точные науки.»(Н.И. Лобачевский) ‘ quotes[13]='»Именно математика дает надежнейшие правила: кто им следует – тому не опасен обман чувств.»(Л. Эйлер) ‘ quotes[14]='»Числа не управляют миром, но они показывают, как управляется мир.»(И. Гете) ‘ quotes[15]='»Было бы легче остановить Солнце, легче было сдвинуть Землю, чем уменьшить сумму углов в треугольнике или свести параллели к схождению…»(В.Ф. Каган) ‘ quotes[16]='»Счет и вычисления — основа порядка в голове.»(Песталоцци) ‘ quotes[17]='»Величие человека — в его способности мыслить.»(Б. Паскаль) ‘ quotes[18]='»Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их.»(Д.Пойа) ‘ quotes[19]='»Предмет математики столь серьезен, что не следует упускать ни одной возможности сделать его более занимательным.»(Б. Паскаль) ‘ quotes[20]='»В математических вопросах нельзя пренебрегать даже самыми мелкими ошибками.»(И. Ньютон) ‘ quotes[21]='»Первое условие, которое надлежит выполнять в математике, — это быть точным, второе — быть ясным и, насколько можно, простым.»(Л. Карно) ‘ quotes[22]='»Много из математики не остается в памяти, но когда поймешь ее, тогда легко при случае вспомнить забытое.»(М.В. Остроградский) ‘ quotes[23]='»Математика — это цепь понятий: выпадет одно звенышко — и не понятно будет дальнейшее.»(Н.К. Крупская) ‘ quotes[24]='»Математика уступает свои крепости лишь сильным и смелым.»(А.П. Конфорович) ‘ quotes[25]='»Доказательство — это рассуждение, которое убеждает.»(Ю.А. Шиханович) ‘ quotes[26]='»В каждой естественной науке заключено столько истины, сколько в ней есть математики.»(И. Кант) ‘ var whichquote= Math.floor(Math.random()*(quotes.length)) document.write(quotes[whichquote]) |
free-math.ru
Лекция 19. Функция. Область определения и множество значений функции.
Функция — одно из важнейших математических понятий.
Определение: Если каждому числу из некоторого множества x поставлено в соответствие единственное число y, то говорят, что на этом множестве задана функция y(x). При этом x называют независимой переменной или аргументом, а y — зависимой переменной или значением функции или простофункцией.
Говорят также, что переменная y является функцией от переменной x.
Обозначив соответствие некоторой буквой, например f, удобно писать: y=f (x), то есть, значение y получается из аргумента x с помощью соответствия f. (Читают: y равно f от x.) Символом f (x) обозначают значение функции, соответствующее значению аргумента, равному x.
Пример 1 Пусть функция задается формулой y=2x2–6. Тогда можно записать, что f(x)=2x2–6. Найдем значения функции для значений х, равных, например, 1; 2,5;–3; т. е. найдем f(1), f(2,5), f(–3):
f(1)=2•12–6=–4;
f(2,5)=2•2,52–6=6,5;
f(–3)=2•(–3)2–6= 12.
Заметим, что в записи вида y=f (x) вместо f употребляют и другие буквы: g, и т. п.
Определение: Область определения функции — это все значения x, при которых существует функция.
Если функция задана формулой и ее область определения не указана, то считают, что область определения функции состоит из всех значений аргумента, при которых формула имеет смысл.
Другими словами, область определения функции, заданной формулой, является все значения аргумента, за исключением тех, которые приводят к действиям, которые мы не можем выполнить. На данный момент мы знаем только два таких действия. Мы не можем делить на нуль и не можем извлечь квадратный корень из отрицательного числа.
Определение: Все значения, которые принимает зависимая переменная образуют область значения функции.
Область определения функции, описывающей реальный процесс, зависит от конкретных условий его протекания. Например, зависимость длины l железного стержня от температуры нагревания t выражается формулой , где l0 начальная длина стержня, а —коэффициент линейного расширения. Указанная формула имеет смысл при любых значениях t. Однако, областью определения функцииl=g(t) является промежуток в несколько десятков градусов, для которого справедлив закон линейного расширения.
Пример.
Укажите область значений функции y = arcsinx.
Решение.
Областью определения арксинуса является отрезок [-1; 1]. Найдем наибольшее и наименьшее значение функции на этом отрезке.
Производная положительна для всех x из интервала (-1; 1), то есть, функция арксинуса возрастает на всей области определения. Следовательно, наименьшее значение она принимает при x = -1, а наибольшее при x = 1.
Мы получили область значений функции арксинуса .
Найдите множество значений функции на отрезке [1; 4].
Решение.
Найдем наибольшее и наименьшее значение функции на данном отрезке.
Определим точки экстремума, принадлежащие отрезку [1; 4]:
Вычисляем значения исходной функции на концах отрезка и в точках :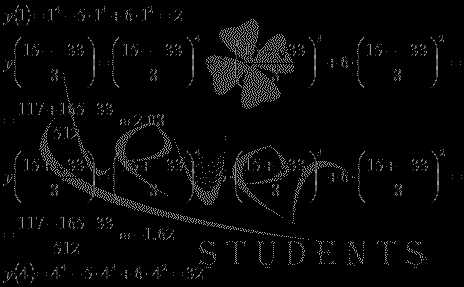
Следовательно, множеством значений функции на отрезке является интервал .
Сейчас покажем, как находить множество значений непрерывной функции y = f(x) на открытых интервалах (a; b), .
Сначала определяем точки экстремума, экстремумы функции, промежутки возрастания и убывания функции на данном интервале. Далее вычисляем односторонние пределы на концах интервала и (или) пределы на бесконечности (то есть, исследуем поведение функции на границах открытого интервала или на бесконечности). Этой информации достаточно, чтобы найти множество значений функции на таких промежутках.
Похожие статьи:
poznayka.org
